Molecular dynamics simulation of the structure and interfacial free energy barriers of mixtures of ionic liquids and divalent salts near a graphene wall
Víctor
Gómez-González
a,
Borja
Docampo-Álvarez
a,
Trinidad
Méndez-Morales
a,
Oscar
Cabeza
b,
Vladislav B.
Ivaništšev
 c,
Maxim V.
Fedorov
de,
Luis J.
Gallego
a and
Luis M.
Varela
*a
c,
Maxim V.
Fedorov
de,
Luis J.
Gallego
a and
Luis M.
Varela
*a
aGrupo de Nanomateriales, Fotónica y Materia Blanda. Departamento de Física de Partículas, Facultade de Física, Universidade de Santiago de Compostela, Campus Vida s/n, E-15782 Santiago de Compostela, Spain. E-mail: luismiguel.varela@usc.es
bDepartamento de Física, Facultade de Ciencias, Universidade da Coruña, Campus A Zapateira s/n, E-15071 A Coruña, Spain
cInstitute of Chemistry, University of Tartu, Ravila 14a, Tartu 50411, Estonia
dSkolkovo Institute of Science and Technology, 3 Nobel Street, Moscow 143026, Russian Federation
eDepartment of Physics, Scottish University Physics Alliance (SUPA), University of Strathclyde, John Anderson Bldg, 107 Rottenrow, Glasgow, G4 0NG, UK
First published on 9th December 2016
Abstract
A molecular dynamics study of mixtures of 1-butyl-3-methylimidazolium tetrafluoroborate ([BMIm][BF4]) with magnesium tetrafluoroborate (Mg[BF4]2) confined between two parallel graphene walls is reported. The structure of the system is analyzed by means of ionic density profiles, lateral structure of the first layer close to the graphene surface and angular orientations of imidazolium cations. Free energy profiles for divalent magnesium cations are calculated using two different methods in order to evaluate the height of the potential barriers near the walls, and the results are compared with those of mixtures of the same ionic liquid and a lithium salt (Li[BF4]). Preferential adsorption of magnesium cations is analyzed using a simple model and compared to that of lithium cations, and vibrational densities of states are calculated for the cations close to the walls analyzing the influence of the graphene surface charge. Our results indicate that magnesium cations next to the graphene wall have a roughly similar environment to that in the bulk. Moreover, they face higher potential barriers and are less adsorbed on the charged graphene walls than lithium cations. In other words, magnesium cations have a more stable solvation shell than lithium ones.
1 Introduction
Room-temperature ionic liquids (ILs) are currently considered as novel media for many potential applications.1,2 Their most important property is perhaps their ability to be used as “universal” solvents, but they also have many other interesting properties,3,4 including a wide electrochemical window. These make them attractive candidates for their use as electrolytes in future electrochemical devices such as batteries, supercapacitors or fuel cells, as it has been pointed out in several recent reviews.5–8So called “designer solvents” or “task-specific ionic liquids” (usually with fluoroanions) are practically non-electroactive, so they should usually be mixed with a suitable redox-active salt for their use in electrochemical devices. The studies performed so far in this area have been mainly focused on systems comprising ILs and salts of lithium or other alkali metals.9–30 However, salts with divalent cations should in principle be potentially more efficient in energy-storage systems, and some of them (like Mg2+) are much more abundant, cheaper and safer than Li+ cations. Accordingly, it is important to investigate in detail mixtures of ILs and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes and compare their electrochemical ability with those of their 1
1 electrolytes and compare their electrochemical ability with those of their 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes analogous. Some theoretical studies on bulk mixtures of ILs with 2
1 electrolytes analogous. Some theoretical studies on bulk mixtures of ILs with 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes have recently been performed. For instance, Gómez-González et al.31 have used molecular dynamics (MD) simulations to investigate the properties of protic and aprotic ILs with magnesium and calcium salts. A main feature of these amphiphilically nano-organized liquids is the so called “nanostructured solvation”,31–35 a phenomenon which is qualitatively similar to that occurring in the analogous mixtures with 1
1 electrolytes have recently been performed. For instance, Gómez-González et al.31 have used molecular dynamics (MD) simulations to investigate the properties of protic and aprotic ILs with magnesium and calcium salts. A main feature of these amphiphilically nano-organized liquids is the so called “nanostructured solvation”,31–35 a phenomenon which is qualitatively similar to that occurring in the analogous mixtures with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes, and which consists of selective solvation of the solute species in the nanocavities of the same polar character. This peculiar organization of the dense ionic mixture and the associated solvation of ions in this environment are at the origin of the high energy barriers for cation transport to the electrochemical interfaces.36,37 On the other hand, some experimental results related to electrolyte–electrode systems using mixtures of ILs and 2
1 electrolytes, and which consists of selective solvation of the solute species in the nanocavities of the same polar character. This peculiar organization of the dense ionic mixture and the associated solvation of ions in this environment are at the origin of the high energy barriers for cation transport to the electrochemical interfaces.36,37 On the other hand, some experimental results related to electrolyte–electrode systems using mixtures of ILs and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes have been reported.38–41 However, to the best of our knowledge, computational studies on mixtures of ILs containing multivalent cations near walls (a situation of special relevance for both theoretical and technological reasons) have not been reported so far.
1 electrolytes have been reported.38–41 However, to the best of our knowledge, computational studies on mixtures of ILs containing multivalent cations near walls (a situation of special relevance for both theoretical and technological reasons) have not been reported so far.
In the work described here we performed MD simulations of mixtures of 1-butyl-3-methylimidazolium tetrafluoroborate ([BMIm][BF4]) with magnesium tetrafluoroborate (Mg[BF4]2) confined between two parallel graphene surfaces. Our aim was threefold: (i) to obtain a complete information on these systems, both for neutral and charged graphene surfaces, for which we computed molecular density profiles, angular orientations of IL cations, preferential adsorption, free energy profiles, 2D density maps and vibrational densities of states of the salt cations; (ii) to compare our results with those obtained in ref. 36 and 37 for their analogous, graphene-confined [BMIm][BF4]–Li[BF4] mixtures; and (iii) to determine to which extent our results for confined mixtures differ from those obtained in ref. 31 for bulk [BMIm][BF4]–Mg[BF4]2 mixtures.
The essential technical details of the method used are sketched in Section 2, our results are presented and discussed in Section 3 and in Section 4 we summarize our main conclusions.
2 Simulation details
For all the simulations present in this paper, the GROMACS 5.0.2 package42 was used, setting the OPLS-AA force field developed by Jorgensen43 for different organic liquids in order to parametrize the ions. The simulations were carried out using several steps to ensure proper minimization and stabilization of the systems. Once the system was stabilized, a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ns stabilization run followed by a simulation run of 30
ns stabilization run followed by a simulation run of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ns were performed to have enough statistics in order to calculate reliable densities. These simulation times are usually considered to be long enough to attain equilibrium in these IL–salt mixtures.32 This final configuration was used as an initial configuration to calculate the Helmholtz free energy profile A(z), where z is the distance between a probe metal ion and the graphene wall: a probe of magnesium salt ion was introduced in the mixture (removing another one at random), minimizing and stabilizing again the energy of the system. Then, pulling the probe several different initial configurations for the simulation run were generated, each one with a different and fixed z position, so the forces acting in the probe at each distance could be calculated. A simulation run of 1 ns was performed for each distance. The time step of the simulations was 1
ns were performed to have enough statistics in order to calculate reliable densities. These simulation times are usually considered to be long enough to attain equilibrium in these IL–salt mixtures.32 This final configuration was used as an initial configuration to calculate the Helmholtz free energy profile A(z), where z is the distance between a probe metal ion and the graphene wall: a probe of magnesium salt ion was introduced in the mixture (removing another one at random), minimizing and stabilizing again the energy of the system. Then, pulling the probe several different initial configurations for the simulation run were generated, each one with a different and fixed z position, so the forces acting in the probe at each distance could be calculated. A simulation run of 1 ns was performed for each distance. The time step of the simulations was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fs, although some were carried out using a time step of 0.5
fs, although some were carried out using a time step of 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fs due to the extremely high Newtonian forces present in these systems. For all these steps, and to control the temperature of the system, a temperature coupling constant of 0.5
fs due to the extremely high Newtonian forces present in these systems. For all these steps, and to control the temperature of the system, a temperature coupling constant of 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ps was used.
ps was used.
The temperature of the systems was set to T = 450 K and the annealing temperature used in the annealing steps was T = 1000 K. The salt molar fractions in all the systems were %salt = {0, 10 and 25}. For the two non-zero molar fractions, 1000 and 600 ionic pairs of IL were used, respectively. The number of Mg[BF4]2 salt molecules was calculated for each situation by considering each ionic pair as a single unit in the calculation of molar fractions. All other relevant information concerning the force field and parametrization of the atoms can be found in ref. 36.
3 Results and discussion
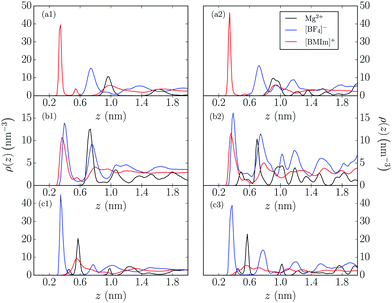
As mentioned previously, in this section we present and discuss the results for densities of all species in the ionic liquid–salt mixtures, angular orientations of imidazolium cations, free energy profiles, preferential adsorption, 2D density maps and vibrational density of states (vDOS) of the magnesium cation in the mixtures.Number densities, ρ(z), of all species in the mixtures were calculated to study the structure near the graphene walls, and the results are shown in Fig. 1. Note that for these calculations the positions of cations and anions were computed considering the C atom between the two N atoms of the imidazolium ring (C2) and the B atom (B1), respectively.
As can be seen in that figure, even uncharged graphene walls have an important effect on the structure of the liquid, as it was reported in the past,36,44–47 with the large structural differences compared to the bulk appearing in two layers close to graphene. As in [BMIm][BF4]–1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes mixtures,36,37 there is a first layer of cations followed closely by one of anions. For high salt concentrations, salt cations are solvated close to this first shell of anions. At greater distance from the wall, a second (first at low concentration of salt) shell of salt cations appears, also close to a second shell of anions and a small, diffuse shell of cations, contrary to 10% mixtures where Mg2+ can appear only in the second layer of the electric double layer. Beyond this second layer, the interfacial inhomogeneous structure starts to fade away and the system gets progressively closer to homogeneous bulk.
1 electrolytes mixtures,36,37 there is a first layer of cations followed closely by one of anions. For high salt concentrations, salt cations are solvated close to this first shell of anions. At greater distance from the wall, a second (first at low concentration of salt) shell of salt cations appears, also close to a second shell of anions and a small, diffuse shell of cations, contrary to 10% mixtures where Mg2+ can appear only in the second layer of the electric double layer. Beyond this second layer, the interfacial inhomogeneous structure starts to fade away and the system gets progressively closer to homogeneous bulk.
On the other hand, in simulations with charged graphene walls a strong layering of charge leading to an overcompensation of the charge of the previous layer is observed, in agreement with a large body of reported results,8,44,48–57 a fact which was also found in mixtures with lithium salts.36,37 It is interesting to note that with charged graphene walls, the structure of the system is weakly dependent on salt concentration: the effect of the electric field is strong in these cases and it seems to anchor divalent cations and cancel out other possible effects coming from statistics. Due to this layering of charge, and provided they are strongly solvated by IL anions, salt cations are closer to the positively charged wall than to the negatively charged one, as has also been reported previously.37
However, the most important observation is that, contrary to their homologous Li+ cation,36 no Mg2+ cation is found at graphene walls. The divalent cations seem unable to desolvate from BF4− anions and cross the IL's layered region close to the wall. Therefore, although kinetically they can jump the barriers in the electric double layer with a certain probability, in the final stationary state they are stuck between the layers of charge.
Fig. 2 shows the distance of closest approach of salt cation to the graphene wall as a function of the wall charge, calculated from the number density profiles. There we can see that, in the negatively charged wall, the Mg2+ cation is placed around 0.9 nm, close to where Li+ cation was in the analogous system.36 It is also interesting to note that the behaviour of the mixtures changes markedly with the concentration of the added salt in this case. The distance from the first peak of the number density curves to the graphene wall decreases with concentration for the negatively charged and neutral walls, while it is approximately constant for the positively charged wall. Moreover, we can see that for the 25% molar fraction, Mg2+ cations are placed almost as close to the wall as Li+ cations at both neutral and negatively charged graphene walls, while they are much further away in the case of the positively charged walls. Finally, in all cases the distance of salt cations to the wall is reduced as the electrode surface charge increases, at least in the charge window (−1, +1) e nm−2, a behavior that was also observed in the case of Li+ cations.
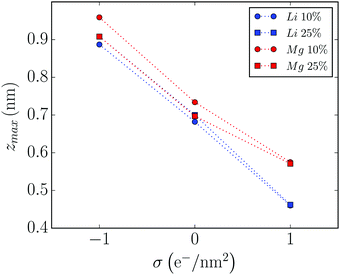 | ||
| Fig. 2 Distances from the first peak of the density profile relative to the graphene wall for Mg2+ cations, for all the molar fractions and wall charges studied in this paper (for comparison, also shown are the results obtained in ref. 36 for the analogous mixtures of Li+ cations). Dashed lines are guides to the eye. | ||
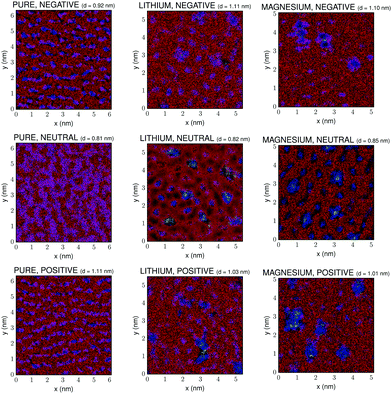
Fig. 3 shows the (x, y) lateral structure within a 3D slab close to the graphene surface for the pure IL, and for the mixtures containing 10% molar fraction of Li[BF4] and Mg[BF4]2. A cutoff number density was set in this figure in order to represent only the highest density regions, which are the most reliable ones since they are not so dependent on poor statistics as those regions with lower densities. The thickness of this layer, d, has been chosen from the number density plots in Fig. 1 guaranteeing that in all cases it contains at least one entity of each of the different species in the mixture, in order to clearly observe the effect of the mixing process on the structure of the IL–graphene interface. All the information of the 3D distribution of ions inside this slab of the electric double layer is summarised in the 2D plot shown in Fig. 3.
It is worth mentioning that the apparent non-smoothness of the shape of the regions associated to cations and anions in Fig. 3 could be an artifact arising from non-ergodicity of the simulations or from the position of the represented slab. However, we must indicate that the used simulation times (40 ns including stabilization and production phases) are conventionally considered to be long enough to attain equilibrium in IL–salt mixtures and for the different species to be in their diffusive regimes.58 Moreover, in what the position and size of the slab are concerned, different possibilities were tested. First of all, we must mention that the whole lateral size of the slab in the xy-plane is plotted, and that several values of its width d were tested with no significant improvement of the qualitative appearance of the results, so the final chosen value was the one that included at least one entity of all the species in the mixture without smearing out the different nanoregions in a too significant way, so their qualitative differences for different compositions of the mixtures could be clearly visible at a glance. The apparent non-smoothness observed in the plots could be possibly related to poor statistics arising from the low number of ions in the simulation or to the 2D representation of the 3D slab.
First of all, we can observe that, as previously reported for IL–water mixtures,59 transitions from ordered stripes to ordered phases with hexagonal symmetry take place upon doping. The same effect is observed charging the walls in the case of the pure IL, as can be seen in the column on the left in Fig. 3. This is in agreement with the results reported by Rotenberg and Salanne,60 who computationally described potential-driven ordering transitions in the first adsorbed layer that had been previously found experimentally (see ref. 60 and references therein). Moreover, it is noteworthy that the plots in Fig. 3 are not just simple 2D representations of the xy layer at the wall, but they contain 3D information of the whole slab next to it. Indeed, two consecutive layers of cations and anions are shown that lie closer to the wall than the chosen cutoff distance. This specific representation gives a taste of the 3D structuring of the electric double layer since the superposition of ions in different layers is shown in mixed colors (e.g. pink colors in Fig. 3 reflect the superposition of cations and anions of the IL in different layers of the slab). As we can see, the addition of salt to the IL induces a decrease of the size of the pink regions, indicating a severe 3D restructuring of the electric double layer. This effect is clearly more intense in the case of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes, since they much more efficiently induce the formation of clusters of Mg2+ and BF4− anions. Indeed, a 3D structure for the electric double layer such as the one predicted by Kornyshev and Qiao61 is clearly present in these systems. Apparently, a herringbone interfacial 3D structure appears, implying that the first layers are coupled due to the strong charge density present in ILs, which also gets reinforced by the charge that salt cations introduce in the system.62,63
1 electrolytes, since they much more efficiently induce the formation of clusters of Mg2+ and BF4− anions. Indeed, a 3D structure for the electric double layer such as the one predicted by Kornyshev and Qiao61 is clearly present in these systems. Apparently, a herringbone interfacial 3D structure appears, implying that the first layers are coupled due to the strong charge density present in ILs, which also gets reinforced by the charge that salt cations introduce in the system.62,63
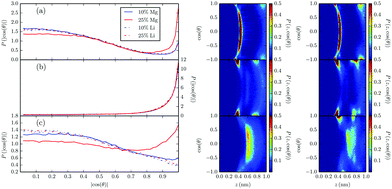
The orientations of imidazolium cations in the first layer were considered in order to further analyze the electric double layer in these mixtures. Taking θ as the angle between the vector normal to the walls (parallel to the z-axis) and a vector normal to the imidazolium ring, we calculated the probability distribution functions for ring orientations as a function of |cos(θ)| and/or the distance to the wall, z, which are shown in Fig. 4.
There we see that imidazolium ring orientations in all the studied situations seem to be very similar to those in [BMIm][BF4]–Li[BF4] mixtures except for 25% Mg[BF4]2 molar fraction. This clear difference between Mg2+ cations at 25% molar fraction and the other cases was also seen above for the distance of the first layer of salt cations to the wall, and it is probably related to these results, because the position of the Mg2+ cation influences the imidazolium cation ring orientation due to its higher charge density with respect to Li+ cation. At neutral walls, the most probable configuration for imidazolium cation rings is to lie almost parallel to the wall, independently of the added salt concentration. Charging the wall changes neatly the distribution of orientations. Near negative walls, a large region of almost constant probability is present, meaning that the cation can be between 90° and 65° with almost equal probability, but low angle orientations are not so probable because a probability minimum appears near the negatively charged wall, although the probability of lying flat on the wall is higher and increases with salt concentration. In addition to this, the other effect of the concentration is to shift the position of the minimum to higher angles. Meanwhile, for positively charged walls the behaviour of the angular probability at 10% salt molar fraction is the same as that of mixtures with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes: imidazolium cations tend to lie near 90° with the wall, and the probability steadily decreases until a minimum is found for the normal configuration; however, at 25% salt molar fraction this normal configuration is slightly preferred and a broad minimum appears at around |cos(θ)| = 0.7. This difference with [BMIm][BF4]–1
1 electrolytes: imidazolium cations tend to lie near 90° with the wall, and the probability steadily decreases until a minimum is found for the normal configuration; however, at 25% salt molar fraction this normal configuration is slightly preferred and a broad minimum appears at around |cos(θ)| = 0.7. This difference with [BMIm][BF4]–1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes mixtures may be simply an effect of the lack of statistics for cations near positive walls (as can be clearly seen in P(z,cos
1 electrolytes mixtures may be simply an effect of the lack of statistics for cations near positive walls (as can be clearly seen in P(z,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), where the layered structure is very diffuse compared to the other systems), but it also could be reflecting, as indicated above, a physical effect related to the higher charge density of divalent cations, which modifies more markedly the ionic environment and may induce a change in the solvation of divalent cations in the electric double layer with respect to monovalent ones.
θ), where the layered structure is very diffuse compared to the other systems), but it also could be reflecting, as indicated above, a physical effect related to the higher charge density of divalent cations, which modifies more markedly the ionic environment and may induce a change in the solvation of divalent cations in the electric double layer with respect to monovalent ones.
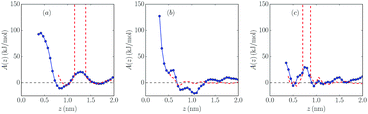
In order to shed more light on the distribution of salt cations at the interface, the Helmholtz free energy profiles A(z) were calculated using a potential of the mean force (PMF) method:46,47,64
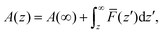 | (1) |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) (z′) is the average force acting over a probe of the cation fixed at z′ during the simulation run, as well as by the probability method:65
(z′) is the average force acting over a probe of the cation fixed at z′ during the simulation run, as well as by the probability method:65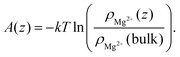 | (2) |
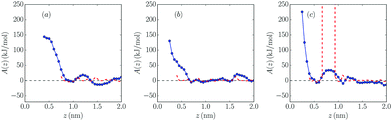
In Fig. 5 and 6, free energy profiles for the two studied molar fractions of Mg2+ calculated using both methods are shown. The lack of statistics we mentioned before produces some divergences in the curves of the probability methods in positions where no salt cation is present, which was solved using PMF-based A(z) curves. However, as we can see in eqn (1), A(∞) is not well-defined, so an “offset” was fixed far from the wall to the values predicted by the probability method, since these data have there the smallest uncertainty due to the calculation procedure in eqn (1).
As can be seen, in the systems with charged walls free energy barriers appear close to the wall: in the negatively charged wall, their heights are 20 kJ mol−1 and 18 kJ mol−1 for 10% and 25% mixtures, respectively, while their values are higher in the positively charged wall (38 kJ mol−1 and 34 kJ mol−1, respectively), as expected. It is shown that increasing salt concentration softly reduces the height of all barriers, which favors the presence of salt cations at the electrochemical interface. A similar result was reported for mixtures with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes.36 However, no clear dependence of the barrier values on the molar fraction of the added salt was found in ref. 37. In this latter reference it is clearly shown that the height of these barriers is related to the strength of the solvation of the cations in the dense interfacial solvation structures in these electrolytes.
1 electrolytes.36 However, no clear dependence of the barrier values on the molar fraction of the added salt was found in ref. 37. In this latter reference it is clearly shown that the height of these barriers is related to the strength of the solvation of the cations in the dense interfacial solvation structures in these electrolytes.
Comparing the results with those for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes,34,36 it seems that monovalent cations face smaller barriers between the bulk and direct contact with the electrode. In the neutral system no clear barriers were found apart from the ones created by the first layer of cations and anions, which prevents the salt cation approaching the wall, in contrast with the results for 1
1 electrolytes,34,36 it seems that monovalent cations face smaller barriers between the bulk and direct contact with the electrode. In the neutral system no clear barriers were found apart from the ones created by the first layer of cations and anions, which prevents the salt cation approaching the wall, in contrast with the results for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes reported by Méndez-Morales et al.36
1 electrolytes reported by Méndez-Morales et al.36
In Table 1 the preferential adsorption measure Δω(Xn+) (Xn+ = Li+, Mg2+) is shown for mixtures with magnesium salt, as well as its comparison with mixtures with lithium salt. This magnitude was introduced by Docampo-Álvarez et al.59 in order to discuss the effect of confinement on water adsorption in its mixtures with ionic liquids, and can also be used here to get additional insight on the preferential adsorption of salt cations near the electrochemical interface. Δω(Xn+) compares deviation of density of salt cations near the wall relative to that corresponding to a homogeneous density between the electrodes. This magnitude represents the difference between the probability P(Xn+) of finding salt cations within a given distance to the wall, δ, and δ/L (L being the width of the cell), which gives this same probability on the homogeneous density situation: Δω(Xn+) = P(Xn+) − δ/L. Therefore, positive values of Δω represent preferential adsorption of the salt cation, while negative values correspond to depletion. In our system we take δ for each wall charge as the distance of the first salt cation density minimum to the wall with the corresponding charge, so we only take into account the first salt cation layer.
| 10% | 25% | ||||
|---|---|---|---|---|---|
| σ (e nm−2) | Li+ | Mg2+ | σ (e nm−2) | Li+ | Mg2+ |
| −1 | −0.039 | −0.029 | −1 | −0.022 | −0.024 |
| 0 | 0.009 | −0.013 | 0 | −0.025 | −0.022 |
| +1 | 0.025 | 0.010 | +1 | 0.015 | 0.007 |
The results obtained show that Δω(Xn+) increases with the charge of the wall in all cases. It also appears that depletion occurs more markedly when the wall is negatively charged, as we reported above, as a consequence of the strong solvation of Mg2+ cations by [BF4]− anions. In the opposite situation, when the wall is positively charged, a preferential adsorption is registered for this same reason, as has been reported previously.37 It is noteworthy mentioning that in the neutral wall case, for 25% salt molar fraction there is no practical difference between the values of Δω(Xn+) and those for the negatively charged wall. Regarding the salt valence effect, Li+ cation has higher values of Δω for 10% salt molar fraction except when the wall is negatively charged. In the other two situations, it is clearly seen that Li+ cations are adsorbed more strongly than Mg2+ ones, as expected. At 25% salt molar fraction, however, both salts behave more similarly.
Finally, we also calculated the vDOS for the cations of the added magnesium salt located closest to the wall, using the same method as in ref. 31, and the results are shown in Fig. 7, together with those for bulk cations. Comparing the vDOS for Mg2+ cations in the layers closest to the walls with those in the bulk reveals that there is a slight red shift of the modes at 12 and 19.7 THz, while a small blue-shift appears for the 13.3 THz mode. This is a little bit more clearly visible for the positively charged wall. All these modes are related to the “types of coordination” between Mg2+ cations and the anions surrounding them.31 This red shift means that salt cations are less strongly bound in their cages in the bulk than they are in the interfacial region. Opposite behavior was reported in ref. 59 for water molecules in dense ionic environments. This is probably an effect of the wall slightly reinforcing the bulk structure, in which salt cations are highly confined in the polar nanoregions (i.e. a slightly stronger solvation of cations near the wall is detected).31 It seems that near the electrode, salt cations can move less freely than in bulk. Regarding vDOS comparison with wall charge, the biggest change is produced when Mg2+ ion is placed near the negative wall. These effects, however, are not very significant, so we conclude that monovalent and divalent cations have a very similar ionic environment at the interface because they are separated from the wall by the interfacial/solvation layer.
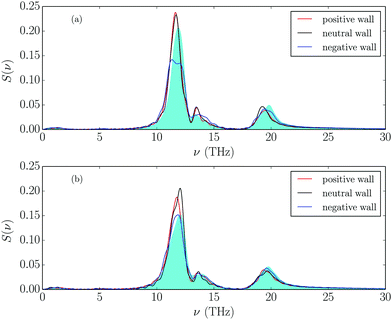 | ||
| Fig. 7 vDOS comparison of Mg2+ cation in bulk (shaded in blue) and near the charged walls. (a) 10% molar fraction, (b) 25% molar fraction of salt. | ||
4 Conclusions
In this paper, we performed molecular dynamics simulations of mixtures of [BMIm][BF4] with Mg[BF4]2 between two parallel graphene walls, and the results were compared with those obtained in ref. 33 and 37 for similar mixtures with Li[BF4]. The structure of the mixtures near the electrodes was analyzed by means of number density profiles of all species and angular orientations of imidazolium cations. Similar results were observed for salts of both monovalent and divalent cations. Moreover, for the same molar fraction of salt, magnesium salts were seen to exhibit a similar qualitative behaviour, which also happened when comparing their bulk mixtures. However, divalent cations are not as present at the interfaces as their monovalent counterparts.On the other hand, free energy profiles for magnesium cations were calculated using both potential of the mean force and probability methods in order to obtain the potential barriers for the transference of cations to the walls. We found that divalent cations must overcome higher potential barriers than monovalent ones, which makes the transference of the divalent cations at the negative electrode much more difficult than the transference of monovalent cations. Due to the well-known overcompensation of charge at the interface and the very strong solvation of the Mg2+ cations in the interfacial layers, Mg2+ cations could not approach the negative electrode, and preferential adsorption is only registered for positively charged walls. Higher valence increased the adsorption for positively charged walls, but this phenomenon decreased for negatively charged ones at low concentrations of salt.
Our current results suggest that added salts exert a deep influence in the 2D (within layers) and 3D structures of the IL in the neighborhood of the walls. Moreover, we can see that divalent cations of the added salt are much more effective in inducing the nucleation of the anions within the electric double layer than monovalent ones, reflecting a stronger solvation of the divalent cations in their dense ionic environments.
Vibrational densities of states of magnesium cations were calculated for magnesium cations near the neutral, positively charged and negatively charged graphene walls, and also for their bulk mixtures. The results indicated that the ionic caging of the salt cation, which was already very strong in bulk mixtures, is generally reinforced by the presence of the electrode, so salt cations move less freely in confined systems than in the bulk media. Hence, we conclude that, despite their undoubted usefulness for electrochemical devices due to large electrochemical windows, these dense ionic media significantly hinder cation transport to the electrodes, although not more strongly for divalent cations than for monovalent ones. This undesirable feature could be reduced by tuning the structure of the electrode or the composition of the electrolyte (cosolvent addition), which demands more careful analysis. However, the enhanced cation blockade in the highly ordered electric double layer of ILs could be also useful for energy storage devices, if it prevents from the IL decomposition. Thus, the role of ionic cages formed by the added salt might be two-fold, and requires closer examination using ab initio or reactive force field molecular dynamics.
To sum up, the results shown in this paper for [BMIm][BF4]–Mg[BF4]2 mixtures confined between two parallel graphene surfaces, which were compared with those previously reported for analogous mixtures with a lithium salt, appear to indicate that the major effect of valence is to further prevent the salt cation approaching the charged electrode (at least for low molar fraction of salt) due to stronger solvation of divalent cations in these dense ionic environments. However, whether this rather counterintuitive result has a more general validity is a question that warrants further investigation. Accordingly, it is expected that the results presented in this paper will motivate further studies to get a broader view of the valence dependence of IL–salt mixtures between two graphene surfaces (or other appropriate layered or non-layered 2D materials), in order to see whether or not 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (or, more generally, multivalent) electrolytes are worse than 1
1 (or, more generally, multivalent) electrolytes are worse than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes for their use in batteries. However, taking into consideration all the results we obtained in this work, we can assert that Mg2+ behaves roughly the same way as Li+.
1 electrolytes for their use in batteries. However, taking into consideration all the results we obtained in this work, we can assert that Mg2+ behaves roughly the same way as Li+.
Acknowledgements
The authors wish to thank Prof. Ruth M. Lynden-Bell for her invaluable advice and most useful discussions. The financial support of the Spanish Ministry of Economy and Competitiveness (Projects MAT2014-57943-C3-1-P, MAT2014-57943-C3-3-P and FIS2012-33126) is gratefully acknowledged. Moreover, this work was funded by the Xunta de Galicia (AGRUP2015/11). All these research projects were partially supported by FEDER. V. G.-G. thanks the Spanish Ministry of Education for his FPU grant. Facilities provided by the Galician Supercomputing Centre (CESGA) are also acknowledged. The study was also supported by Estonian Personal Research Project PUT1107. Funding from the European Union (COST Actions CM1206 and MP1303) is also acknowledged.References
- R. D. Rogers and K. R. Seddon, Science, 2003, 302, 792–793 CrossRef PubMed
.
- K. R. Seddon, Nat. Mater., 2003, 2, 363–365 CrossRef CAS PubMed
.
-
P. Wasserscheid and T. Welton, Ionic liquids in synthesis, Wiley Online Library, 2003 Search PubMed
.
- J. Dupont, R. F. de Souza and P. A. Z. Suarez, Chem. Rev., 2002, 102, 3667–3692 CrossRef CAS PubMed
.
- D. R. MacFarlane, M. Forsyth, P. C. Howlett, J. M. Pringle, J. Sun, G. Annat, W. Neil and E. I. Izgorodina, Acc. Chem. Res., 2007, 40, 1165–1173 CrossRef CAS PubMed
.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed
.
- X. Lu, G. Burrell, F. Separovic and C. Zhao, J. Phys. Chem. B, 2012, 116, 9160–9170 CrossRef CAS PubMed
.
- M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed
.
- H. Sakaebe and H. Matsumoto, Electrochem. Commun., 2003, 5, 594–598 CrossRef CAS
.
- B. García, S. Lavallée, G. Perron, C. Michot and M. Armand, Electrochim. Acta, 2004, 49, 4583–4588 CrossRef
.
- W. A. Henderson and S. Passerini, Chem. Mater., 2004, 16, 2881–2885 CrossRef CAS
.
- M. Diaw, A. Chagnes, B. Carré, P. Willmann and D. Lemordant, J. Power Sources, 2005, 146, 682–684 CrossRef CAS
.
- Q. Zhou, W. A. Henderson, G. B. Appetecchi and S. Passerini, J. Phys. Chem. C, 2010, 114, 6201–6204 CAS
.
- S. Y. Lee, H. H. Yong, Y. J. Lee, S. K. Kim and S. Ahn, Green Chem., 2005, 109, 13663–13667 CAS
.
- I. Nicotera, C. Oliviero, W. A. Henderson, G. B. Appetecchi and S. Passerini, J. Phys. Chem. B, 2005, 109, 22814–22819 CrossRef CAS PubMed
.
- M. Castriota, T. Caruso, R. G. Agostino, E. Cazzanelli, W. A. Henderson and S. Passerini, J. Phys. Chem. A, 2005, 109, 92–96 CrossRef CAS PubMed
.
- J. Lassègues, J. Grondin and D. Talaga, Phys. Chem. Chem. Phys., 2006, 8, 5629–5632 RSC
.
- E. Markevich, V. Baranchugov and D. Aurbach, Electrochem. Commun., 2006, 8, 1331–1334 CrossRef CAS
.
- J. Xu, J. Yang, Y. NuLi, J. Wang and Z. Zhang, J. Power Sources, 2006, 160, 621–626 CrossRef CAS
.
- S. Seki, Y. Kobayashi, H. Miyashiro, Y. Ohno, A. Usami, Y. Mita, N. Kihira, M. Watanabe and N. Terada, J. Phys. Chem. B, 2006, 110, 10228–10230 CrossRef CAS PubMed
.
- M. Egashira, H. Todo, N. Yoshimoto, M. Morita and J. Yamaki, J. Power Sources, 2007, 174, 560–564 CrossRef CAS
.
- Y. Saito, T. Umecky, J. Niwa, T. Sakai and S. Maeda, J. Phys. Chem. B, 2007, 111, 11794–11802 CrossRef CAS PubMed
.
- V. Borgel, E. Markevich, D. Aurbach, G. Semrau and M. Schmidt, J. Power Sources, 2009, 189, 331–336 CrossRef CAS
.
- J. Lassègues, J. Grondin, C. Aupetit and P. Johansson, J. Phys. Chem. A, 2009, 113, 305–314 CrossRef PubMed
.
- B. G. Nicolau, A. Sturlaugson, K. Fruchey, M. C. C. Ribeiro and M. D. Fayer, J. Phys. Chem. B, 2010, 114, 8350–8356 CrossRef CAS PubMed
.
- Q. Zhou, K. Fitzgerald, P. D. Boyle and W. A. Henderson, Chem. Mater., 2010, 22, 1203–1208 CrossRef CAS
.
- S. Menne, J. Pires, M. Anouti and A. Balducci, Electrochem. Commun., 2013, 31, 39–41 CrossRef CAS
.
- H. Yoon, G. Lane, Y. Shekibi, P. Howlett, M. Forsyth, A. Best and D. MacFarlane, Energy Environ. Sci., 2013, 6, 979–986 CAS
.
- F. Castiglione, A. Famulari, G. Raos, S. V. Meille, A. Mele, G. B. Appetecchi and S. Passerini, J. Phys. Chem. B, 2014, 118, 13679–13688 CrossRef CAS PubMed
.
- L. Aguilera, J. Völkner, A. Labrador and A. Matic, Phys. Chem. Chem. Phys., 2015, 17, 27082–27087 RSC
.
- V. Gómez-González, B. Docampo-Álvarez, O. Cabeza, M. V. Fedorov, R. M. Lynden-Bell, L. J. Gallego and L. M. Varela, J. Chem. Phys., 2015, 143, 124507 CrossRef PubMed
.
- T. Méndez-Morales, J. Carrete, S. Bouzón-Capelo, M. Pérez-Rodrguez, O. Cabeza, L. J. Gallego and L. M. Varela, J. Phys. Chem. B, 2013, 117, 3207–3220 CrossRef PubMed
.
- T. Méndez-Morales, J. Carrete, O. Cabeza, O. Russina, A. Triolo, L. J. Gallego and L. M. Varela, J. Phys. Chem. B, 2014, 118, 761–770 CrossRef PubMed
.
- T. Méndez-Morales, J. Carrete, J. R. Rodrguez, Ó. Cabeza, L. J. Gallego, O. Russina and L. M. Varela, Phys. Chem. Chem. Phys., 2015, 17, 5298–5307 RSC
.
- O. Russina, R. Caminiti, T. Méndez-Morales, J. Carrete, O. Cabeza, L. J. Gallego, L. M. Varela and A. Triolo, J. Mol. Liq., 2015, 205, 16–21 CrossRef CAS
.
- T. Méndez-Morales, J. Carrete, M. Pérez-Rodríguez, O. Cabeza, L. J. Gallego, R. M. Lynden-Bell and L. M. Varela, Phys. Chem. Chem. Phys., 2014, 16, 13271–13278 RSC
.
- V. Ivaništšev, T. Méndez-Morales, R. M. Lynden-Bell, O. Cabeza, L. J. Gallego, L. M. Varela and M. V. Fedorov, Phys. Chem. Chem. Phys., 2016, 18, 1302–1310 RSC
.
- G. T. Cheek, W. E. O'Grady, S. Z. El Abedin, E. M. Moustafa and F. Endres, J. Electrochem. Soc., 2008, 155, D91–D95 CrossRef CAS
.
- G. A. Giffin, A. Moretti, S. Jeong and S. Passerini, J. Phys. Chem. C, 2014, 118, 9966–9973 CAS
.
- G. Vardar, A. E. S. Sleightholme, J. Naruse, H. Hiramatsu, D. J. Siegel and C. W. Monroe, ACS Appl. Mater. Interfaces, 2014, 6, 18033–18039 CAS
.
- S. Saha, T. Taguchi, N. Tachikawa, K. Yoshii and Y. Katayama, Electrochim. Acta, 2015, 183, 42–48 CrossRef CAS
.
- D. V. D. Spoel, E. Lindahl, B. Hess, A. R. V. Buuren, E. Apol, P. J. Meulenhoff, D. P. Tieleman, A. L. T. M. Sijbers, K. A. Feenstra, R. V. Drunen and H. J. C. Berendsen, Gromacs User Manual version 4.6.7, http://www.Gromacs.org, 2014.
- W. L. Jorgensen, J. Phys. Chem., 1986, 90, 1276–1284 CrossRef CAS
.
- R. S. Payal and S. Balasubramanian, ChemPhysChem, 2012, 13, 1764–1771 CrossRef PubMed
.
- S. A. Kislenko, I. S. Samoylov and R. H. Amirov, Phys. Chem. Chem. Phys., 2009, 11, 5584–5590 RSC
.
- M. V. Fedorov and R. M. Lynden-Bell, Phys. Chem. Chem. Phys., 2012, 14, 2552–2556 RSC
.
- R. M. Lynden-Bell, A. I. Frolov and M. V. Fedorov, Phys. Chem. Chem. Phys., 2012, 14, 2693–2701 RSC
.
- C. Pinilla, M. G. Del Pópolo, R. M. Lynden-Bell and J. Kohanoff, J. Phys. Chem. B, 2005, 109, 17922–17927 CrossRef CAS PubMed
.
- A. A. Kornyshev, J. Phys. Chem. B, 2007, 111, 5545–5557 CrossRef CAS PubMed
.
- M. V. Fedorov and A. A. Kornyshev, Electrochim. Acta, 2008, 111, 6835–6840 CrossRef
.
- S. Maolin, Z. Fuchun, W. Guozhong, F. Haiping, W. Chunlei, C. Shimou, Z. Yi and H. Jun, J. Chem. Phys., 2008, 128, 134504 CrossRef PubMed
.
- G. Feng, J. S. Zhang and R. Qiao, J. Phys. Chem. C, 2009, 113, 4549–4559 CAS
.
- S. A. Kislenko, I. S. Samoylov and R. H. Amirov, Phys. Chem. Chem. Phys., 2009, 11, 5584–5590 RSC
.
- S. Wang, S. Li, Z. Cao and T. Yan, J. Phys. Chem. C, 2010, 114, 990–995 CAS
.
- Q. Dou, M. L. Sha, H. Y. Fu and G. Z. Wu, J. Phys.: Condens. Matter, 2011, 23, 175001 CrossRef CAS PubMed
.
- V. Ivaništšev, S. O'Connor and M. V. Fedorov, Electrochem. Commun., 2014, 48, 61–64 CrossRef
.
- V. Ivaništšev, K. Kirchner, T. Kirchner and M. V. Fedorov, J. Phys.: Condens. Matter, 2015, 27, 102101 CrossRef PubMed
.
- M. Salanne, Phys. Chem. Chem. Phys., 2015, 17, 14270–14279 RSC
.
- B. Docampo-Álvarez, V. Gómez-González, H. Montes-Campos, J. M. Otero-Mato, T. Méndez-Morales, O. Cabeza, L. J. Gallego, R. M. Lynden-Bell, V. B. Ivaništšev, M. V. Fedorov and L. M. Varela, J. Phys.: Condens. Matter, 2016, 28, 464001 CrossRef PubMed
.
- B. Rotenberg and M. Salanne, J. Phys. Chem. Lett., 2015, 6, 4978–4985 CrossRef CAS PubMed
.
- A. A. Kornyshev and R. Qiao, J. Phys. Chem. C, 2014, 118, 18285–18290 CAS
.
- K. Kirchner, T. Kirchner, V. Ivaništšev and M. Fedorov, Electrochim. Acta, 2013, 110, 762–771 CrossRef CAS
.
- J. Wallauer, M. Drüschler, B. Huber and B. Roling, Z. Naturforsch., B: J. Chem. Sci., 2013, 68, 1143–1153 CAS
.
- V. Ivaništšev, M. V. Fedorov and R. M. Lynden-Bell, J. Phys. Chem. C, 2014, 118, 5841–5847 Search PubMed
.
-
J. P. Hansen and I. R. McDonald, Theory of simple liquids, Academic Press, Oxford, 1986 Search PubMed
.
| This journal is © the Owner Societies 2017 |