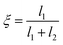Quantum and classical inter-cage hopping of hydrogen molecules in clathrate hydrate: temperature and cage-occupation effects

Abstract

Building on our previous work (J. Phys. Chem. C, 2016, 120, 16561), using an empirical model we run both classical and path-integral molecular dynamics simulations for a type II clathrate hydrate containing different amounts of guest H₂ molecules from 1 to 5 molecules per large cage, with results presented at temperatures of 50, 100 K and 200 K. We present results for the density isosurfaces of the guest molecules at all different occupations and temperatures, showing how the density approaches the perfect tetrahedral structure which has been found for the n = 4 case in which each molecule sits on the vertex of a tetrahedron about the centre of each large cage. We calculate free-energy profiles of the molecules over the volume interior to the cage, and using umbrella sampling, we also calculate the free energy barrier for the molecule to hop between cages. We show that this barrier reduces almost linearly for n = 1–3 molecules per large cage, but becomes larger than would be expected (from extrapolation) for the n = 4 case, with this departure from linearity becoming larger at lower temperatures. We show that, perhaps counter-intuitively, these barriers tend to increase with raising the temperature, and also counter-intuitively that quantisation of the nuclei acts to increase the barriers. Finally, for the n = 4 case, a comparison is made between the empirical model results and those from an ab initio molecular dynamics calculation, which shows that qualitative agreement exists between the two models.

---

Introduction

The type II clathrate hydrate is a water-ice crystal with a structure consisting of ‘large’ and ‘small’ polyhedral cages, with H-bonded water molecules forming the vertex of each polyhedron. The large cages are hexadecahedral 5¹²6⁴ polyhedra – i.e. they contain twelve pentagonal faces (water pentamers) and four hexagonal faces (water hexamers) – whereas the small cages are 5¹² dodecahedrons.

These clathrates only form around the presence of ‘guest’ molecules, trapped within the cages, and in this work we shall be studying a hydrogen clathrate-hydrate in which the water cages contain guest H₂ molecules.

Both the instantaneous and average numbers of guest molecules per cage is not fixed, with the hydrogens having the ability to ‘hop’ between adjacent cages, over a medium sized energy barrier (typically 10–40 kJ mol⁻¹ between large cages), and where the average number of hydrogen molecules is determined by formation conditions. Typically, the small cages are thought to contain either one or two H₂ molecules, whereas the large cages can contain anywhere up to four guest hydrogens. Indeed, we will find it convenient to label these occupations using the notation L4 for n = 4 guest molecules in the large cage, etc.

Given enough time, the hydrogen molecules can diffuse throughout the lattice, as the hydrogen molecules performing successive hops from one cage to another. By far the lowest energy barrier for inter-cage hopping is between adjacent large cages, which are connected by a shared hexagonal face (water hexamer), and in order to complete this hop, the guest molecule has to squeeze through the middle of one of the four hexamers in each large cage. Molecules can also hop in and out of the smaller dodecahedral cages, but to do so it must fit through one of the twelve pentagonal faces of the dodecahedron, which is energetically much higher in energy than passing through the hexagonal faces of the larger cage.

In our previous paper,¹ we calculated the free-energy barriers for guest H₂ molecules to hop between adjoining large cages in a type II clathrate hydrate at 200 K for n = 1 to 5 occupancies. Results were shown for both classical calculations – calculated via molecular dynamics together with an umbrella sampling method, in which multiple simulations are run with a tagged H₂ constrained to different regions along the path connecting both cages – and for quantum calculations in which nuclear quantisation effects are accounted for with path-integral molecular dynamics, which was also run with umbrella sampling. In this work it was shown that, perhaps contrary to expectations, these free-energy barriers tend to increase with increasing temperature, which we explained as being due to the low entropy at the transition state, when the molecule is ‘squeezing’ through the water hexameter connecting each pair of adjacent large cages.

It is worth mentioning that these findings were in direct disagreement with the calculations of Trinh et al.,² who ran ab initio molecular dynamics calculations together with umbrella sampling to calculate the exact same free-energy barriers under a DFT potential energy surface. Contrary to our findings, Trinh et al. find that this energy barrier substantially decreases upon raising the temperature (from 0 to 100 K). It may be that this disagreement is due to the different potential energy surfaces used – we used an empirical model, vs. their use of DFT with a BLYP functional augmented with a local DZPM basis set. Or it may be that there is a methodological problem, but we readily admit that there is nothing in the description of their methodology that we find questionable.

It is also worth mentioning that at 100 K, Trinh et al. found quite small free-energy barriers for inter-cage hopping of H₂ molecules between adjacent large cages, finding barriers that are typically less than half the size of those we find using our empirical model. This perhaps implies that our empirical model has a very different potential energy surface from the DFT potential energy surface used by Trinh et al. Having said that, it is striking that, as shown in our previous paper, the 50 K barrier energies calculated from our empirical model actually give quite good agreement with Trinh's 0 K results, suggesting that the most importance difference between our calculations is that of the temperature dependence of the barriers. To help settle this question, in this work we will present some of our own results from ab initio molecular dynamics calculations under a DFT potential energy surface.

Using an empirical model, Sebastianelli et al. have run diffusion Monte Carlo (DMC) calculations³ for the ground state for n = 1–5 occupation numbers, and path-integral molecular dynamics calculations⁴ at five temperatures from 25 to 200 K for n = 2 and n = 4 large-cage occupation numbers. These simulations were done for a single large cage, with the waters held rigid. In order to elucidate the structure, density isosurfaces were calculated for the spatial distribution of H₂ guest molecules within the cage and various distribution functions were calculated as a function of distances/angles the H₂ molecules make with respect to each-other and the centre of the cage. Their results clearly show that for the L4 occupation, within each large cage, the H₂ guest molecules favour a tetrahedral structure, with this tetrahedron having a definite orientation with respect to the cage polyhedron. At low temperatures each H₂ sits on the vertex of a tetrahedron, but as the temperature is increased the molecules start to sample off-tetrahedral positions. These results were found to be consistent with the structure proposed by Lokshin et al.,⁵ obtained by fitting to neutron diffraction data of D₂ in a type II clathrate hydrate. Lokshin et al. found that below 50 K the neutron diffraction data can be modelled by assuming that the guest D₂ molecules occupy tetrahedral sites within the large cage, but that at higher temperatures the structure is better explained by the molecules occupying a nearly spherical density distribution about the large-cage centres.

Several authors have investigated isolated large cages using quantum-chemistry/first-principles methods. Alavi and Ripmeester⁶ calculated a ∼24 kJ mol⁻¹ energy barrier for a single H₂ molecule to leave an isolated rigid large cage through one of its four hexagonal faces, finding little difference between using a B3LYP or a MP2 potential energy surface (with a 6-311++G(d,p) basis set). Patchkovskii and Tse⁷ also used a combination of MP2 and DFT in their study in which they estimate the occupation numbers inside large and small cages, finding occupations of 3.96 and 2 respectively at 250 K.

In this work, we shall use molecular-dynamics simulation coupled with umbrella sampling with an empirical interaction potential to systematically explore the energetics, structure and free-energies for guest H₂ molecules in a type II clathrate with large-cavity occupation numbers ranging from n = 1 to 5 and temperatures of 50, 100 and 200 K. Both classical and path-integral results will be shown. Particular attention will be paid to the behaviour of the free-energy barrier for inter-cage hopping of hydrogen molecules between adjacent large cages.

To an extent, we will cover some of the same ground as Sebastianelli et al., in particular largely repeating their calculation of density isosurfaces, but in our study we will use a clathrate hydrate lattice in periodic boundary conditions, whereas Sebastianelli et al.'s calculations used a (good) approximation of placing the guest molecules in an isolated rigid large cage.

This work will also build on the results of our previous paper,¹ where we first presented classical and path-integral calculations for the H₂ clathrate hydrate, showing how the inter-cage hopping free-energies change with cage occupation. Here, we extend our earlier calculations by switching to a 2D free-energy surface which much better elucidates the structure of the hydrogen guest molecules within the cages, and which correlates well with the density isosurface calculations. We also provide a much more systematic study of the results for different temperatures.

Methodology

Molecular-dynamics simulations

Molecular dynamics simulations were run using an empirical model on a periodic cubic cell containing 136 water molecules forming a type II clathrate structure, consisting of eight large cages and 16 small cages. All simulations are run at constant temperature, using a Nosé–Hoover chain thermostat.^8–10 Long-range interactions are handled by the Ewald-summation method.¹¹

In this work we shall use the same empirical model as used in our previous paper,¹ in which the water is described by the TIP4P 2005 intermolecular potential energy surface,¹² and the H₂ molecules and their interactions with water are described by the model of Alavi et al.¹³ The reader is referred to our previous paper¹ for full model details.

In this work, results will also be presented from path-integral molecular dynamics calculations, which give a successively improvable approximation to the equilibrium statistics upon quantisation of the nuclei.

The accuracy of the path-integral simulation is dependent on the number of replicas used. In our previous paper, it was shown that at 200 K, just four replicas is sufficient to give good convergence of the free-energy profiles for H₂ molecules moving from one cage to another, and we have kept the same number of replicas for this work. In the path-integral method, every time the temperature is halved the number of replicas should be doubled in order to keep the same accuracy, and so eight replicas were used for the 100 K results and sixteen for the simulations at 50 K.

Ab initio molecular-dynamics simulation

Ab initio molecular-dynamics (MD) simulations were done within the framework of density functional theory (DFT) in generalised-gradient approximation (GGA). We employed DRSLL exchange–correlation functional,^14,15 which involves van der Waals interaction via explicit non-local correlation correction. The functional was recently shown to perform exceptionally well for liquid water.^16–21 Born–Oppenheimer type of MD was carried out on hydrate models. Equations of motions were propagated with time step 0.2 fs in canonical (NVT) ensemble. System temperature was imposed at 258 K by a Nose–Hoover thermostat^8,9 with fictitious mass 120 Ry fs². Charge density in each MD step was converged to accuracy 10⁻⁴ a.u. The calculations were performed in DZP basis set using program SIESTA.²²

Free energies

In our previous paper¹ we calculated the free energy for a tagged H₂ molecule to move between adjacent large cages (a geometry depicted in Fig. 1), where the free energy is given as F = F(ξ) with ξ being a reaction coordinate defined from
with l₁, l₂ being the distance of the centre of mass of the tagged hydrogen molecule to the centres of two adjacent cages, separated by a bridging hexamer.

Fig. 1 An H₂ guest molecule in an adjacent pair of large cages in the clathrate hydrate structure. The two cages interface via a water hexamer.

The free energy is related to the probability distribution P(ξ) via

P(ξ) = Ae^−βF(ξ)

where A is a normalisation constant.

The reaction coordinate ξ is chosen such that it spans the movement of a tagged molecule from the centre of one cage, at ξ = 0, to the centre of an adjoining cage at ξ = 1, with ξ = 0.5 corresponding to the tagged molecule being halfway between the two cages inside a bridging water hexamer.

In our previous paper the umbrella-sampling method²³ was used to obtain the free energy surface F(ξ) over the hard to sample barrier relating to the hopping of a H₂ molecule between adjoining cages. In this method, multiple molecular-dynamics simulations are performed, each including a different quadratic bias potential in the Hamiltonian used to constrain that simulation to a different region of the reaction coordinate. This bias potential has the form

where ξ₀ is a constant, used to constrain that simulation to the vicinity of ξ = ξ₀, with k being a force-constant determining the strength of the constraint. Using the WHAM algorithm of Kumar et al.,²⁴ results from the different simulations are then combined to produce a free energy surface which spans the entire region of interest.

In our previous work, for each free energy curve we ran trajectories with ξ₀ = 0.0, 0.05–0.50 in steps of 0.05 and having a force constant k = 1000 kJ mol⁻¹. These trajectories were supplemented with two more trajectories to ensure better sampling of the transition state region, with ξ₀ = 0.5 and having k = 1500 and 2000 kJ mol⁻¹. Finally a trajectory with k = 0 was used, which is the same as having no bias potential and so is identical to running a normal thermostatted MD simulation. Another thing which makes this last case special is that because there is no bias potential, results can be averaged not just over a single tagged molecule (as is the case with other trajectories), but over all the H₂ molecules and cages in the system, thus giving much better statistics than would otherwise be the case.

In doing the calculations for this work, we realised that the umbrella-sampling trajectories with k = 1000 kJ mol⁻¹ and ξ₀ < 0.35 make virtually no contribution to the final free energy curve, and so here these trajectories are simply omitted. The reason why is easy to find – these trajectories are sampling parts of the free energy curve that are already very well sampled by the special, zero force constant, k = 0 trajectory and so add little more to the statistics.

One problem with the above approach is that ξ is perhaps not the most physically intuitive coordinate, and so in this work we will shift to different coordinates, x and y, respectively the perpendicular and parallel distances of the centre of mass of the tagged molecule from the centre of the bridging hexamer (see Fig. 2). We feel that this new choice of coordinates allows for a more complete and easier to interpret analysis of the free-energy surface F(x,y) over the region of interest.

Fig. 2 The (x, y) coordinate system used in the 2D free-energy surface plots. The centre of the tagged H₂ molecule is at x + y, where x is a vector running from the centre of and perpendicular to the plane of the bridging hexamer connecting two adjacent large cages, y is a vector running parallel to the plane of the hexamer and where x and y are mutually orthogonal.

In fact, in this work, the simulations were still performed using umbrella sampling in the original ξ reaction coordinate, with the results then being transformed to the x and y coordinates via first calculating the probability distributions P(x,y;ξ) for all ξ values over all umbrella-sampling runs, then, transforming according to

where P(ξ), is the probability distribution for ξ, which is calculated via the umbrella sampling in ξ.

In addition to the above calculations, we shall also be presenting equivalent results calculated with the path-integral molecular dynamics method, thus accounting for quantisation of the nuclei.

As in our previous paper, we will also present results for a quantised analogue of the umbrella-sampling free-energy curves, which are generated by adding an umbrella-sampling bias potential in the so-called centroid coordinates of the path-integral to the path-integral molecular-dynamics Hamiltonian. The reader is referred to our previous paper and its ESI† for a full description of exactly how this is done.

Isosurface calculation

Following Sebastianelli et al.,⁴ we shall also be presenting results for isosurfaces of constant probability densities for the H₂ molecules inside each large cage at the different temperatures and cage occupancies considered and where the results are calculated with respect to a definite cage orientation. Essentially this involves taking a volumetric 3D histogram in x, y and z of the coordinates of the H₂ molecular centre of masses over all time steps. Third party software can then be used to find and plot the constant density isosurfaces. In this work, we use VMD²⁵ to plot both the isosurfaces and the molecular graphics.

Sebastianelli et al. worked with a single isolated rigid cage, but it is a little more tricky for our case in which we wish to average the data over multiple large flexible cages in periodic boundary conditions and where the cages don't even all share the same orientations.

Our solution to this problem is to first find the four vectors from the geometric centre of the cage to the centres of the four hexagonal faces in each large cage. These hexagonal faces are positioned tetrahedrally around the cage, and so the four vectors form a close approximation to the vertices of a tetrahedron. Then a linear combination of the four tetrahedral vectors is found that produces a set of three orthonormal axes for each cage; this can be done by way of an orthogonal transformation. In the frame of these orthonormal axes, each large cage has a fixed orientation, and so these vectors can be used to define a standard axes for results collection. This process is done afresh for each cage individually and for each time-frame of the simulation over which results are collected. Finally, to get the best statistics, each data point is replicated over all symmetries of the surrounding large cage.

Results and discussion

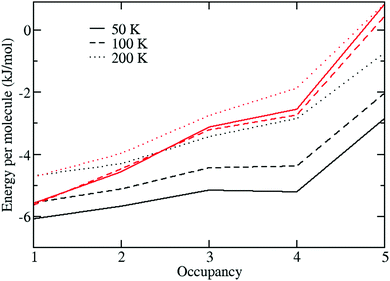
Energetics

We begin by showing in Fig. 3 the calculated energy per H₂ molecule of a H₂ molecule in a large cage with respect to the gas-phase for the different large-cage occupancies and temperatures considered.

Fig. 3 Energy change per large cage guest H₂ molecule with respect to the gas-phase at different temperatures as a function of large-cage occupancy. Black lines are classical results and red are path-integral. See text for details.

The energy change is calculated from

ΔU = (U_n − U₀)/N_mol − U_g,

where U_n is the energy of a clathrate cell with L_n occupancy, i.e. having n H₂ molecules per large cage, U₀ is the energy of a clathrate cell with L₀ occupancy, N_mol is the number of large-cage H₂ molecules in the cell, and U_g is the energy per molecule of a gas-phase H₂ molecule at that temperature.

These results show that the energy per molecule is lowest (i.e., most negative) for the L1 occupation case. However, for the classical calculations, ΔU remains negative even up to L5 and so it should be energetically favourable for up to and including five guest molecules to fill up each large cage. The situation is slightly different for the path-integral case, which predicts an increasing destabilisation for the higher occupancies, and in particular gives a positive energy difference for the L5 occupancy. Thus, these calculations predict that under quantisation of the nuclei, the large cages should fill up to a maximum occupancy of four guest molecules per large cage. Similar behaviour was seen by Sebastianelli et al. in their 0 K DMC calculations of H₂ molecules within a single large rigid cage who also found that quantisation makes it energetically unfavourable to place five molecules inside each large cage. And these results are also consistent with the findings of Patchkovskii and Tse⁷ who estimate an occupation number of 3.96 inside the large cages at 250 K.

Also note that the path-integral results show only a small difference for the ΔU values between 50 and 100 K, indicating that this is close to their ground state energies.

Structure and free-energy surfaces

Fig. 4 shows the isosurfaces of constant probability densities for the hydrogen molecule center of masses in the large cages, where the results are obtained from an average over an MD simulation and averaging over all the large cages in the simulation cell.

Fig. 4 Isosurfaces for the different occupations and different temperatures. The darker solid surface represents 20% of the maximum density. The transparent grey surface represents 10%.

These pictures should be compared to their equivalents in Fig. 5, which shows the free-energy surfaces F(x,y) in the interior of the cages, with enhanced sampling along one ‘neck’ connecting an adjacent large cage, as obtained from the umbrella-sampling calculations. The path-integral free-energy distributions are visually quite similar and so have been presented in the ESI† (cf. Fig. S1).

Fig. 5 Free-energy surfaces F(x,y) for the different occupations and different temperatures, where the colour corresponds to the free-energy value in kJ mol, and x and y are the perpendicular and parallel distances from the center of the bridging hexamer.

Looking at both figures, we see that in the L1 case, the H₂ molecule inside each cage is confined to a near spherical volume of about 2 Angstroms in radius, but doesn't have much preference for where it resides, showing a near uniform distribution about the volume.

The L2 isosurface looks similar, but a look at the free-energy surface shows that the two H₂ molecules quite strongly avoid the center of the cage, with there being a sizable free energy barrier for a molecule to sit at the center. Clearly this is not simply due to the interaction between the guest molecules and the cage, or else it would have shown up in the L1 results. Instead, it must be due to the repulsion between H₂ molecules.

The L3 isosurface shows that, for this occupancy, the distribution has begun to lose its rotational symmetry, with the H₂ molecules now showing a preference for sitting on the edges of a tetrahedron. This becomes even clearer for the L4 isosurface, in which the tetrahedral geometry can be naturally satisfied, not just on average, but instantaneously as well.

Finally, the preference for tetrahedral sites persists even for the L5 occupancy, although given that not all five molecules can instantaneously fill the four edges of a tetrahedron, it must be assumed that at any instant at least one molecule is forced into an off-tetrahedral location.

Each site sits directly behind the center of one of the four tetrahedrally positioned water hexamer faces in the cage, which helps explain why the H₂ molecules have a preference for those sites – the H₂ molecules experiencing less intermolecular repulsion with the waters here than behind the smaller pentagonal faces. That the cage shares the symmetries of the tetrahedron must also help.

For all that the tetrahedral structure is evident, it should be noted that we observe quite a small (less than 5 kJ mol⁻¹) free energy barrier for the molecules to pass between sites which likely represents the rotation of the tetrahedron as a whole to a different orientation.

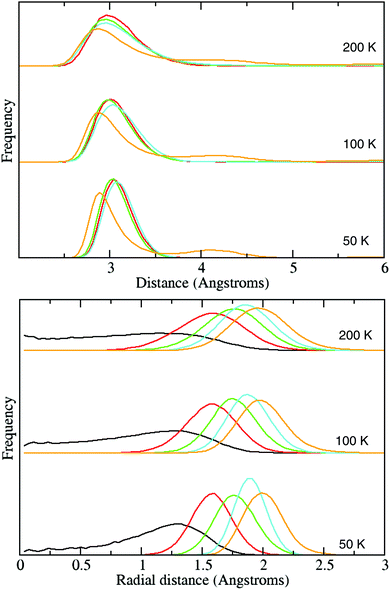
Fig. 6 shows two different distribution functions of the H₂ molecules within the large cages as calculated with classical molecular dynamics. The path-integral results are very similar, and so are presented in ESI† (cf. Fig. S2).

Fig. 6 H₂ centre-of-mass distribution functions (classical). Top: Intermolecular separation between H₂ centres of mass inside each cage. Bottom: Radial distance of H₂ centres of mass from the cage centre. (Divided by r² to give the frequency per unit shell volume.) Colour scheme: Black, red, green, cyan, orange corresponds to L1, L2, L3, L4, L5.

In the top figure is shown the intermolecular H₂ centre-of-mass distribution, and the figure below shows the radial distribution of H₂ centres of mass from the centre of the large cage.

As previously done by Sebastianelli et al.⁴ using their empirical model, it is instructive to compare our model results with those obtained by Lokshin et al.⁵ who modelled a clathrate-hydrate structure containing guest D₂ molecules to neutron diffraction data. Lokshin et al. find that at temperatures below 50 K, their data was best explained by each large cage containing four D₂ molecules in the tetrahedral structure, in which the intermolecular distance is 2.93 Å and the radial distance is 1.8 Å. Our classical L4/50 K results actually agree very well with these numbers given that we find peak-positions of 3.1 Å and 1.9 Å for the intermolecular and radial distances respectively. Sebastianelli et al. appear to get similar good agreement.

The intermolecular distributions show little difference between the n = 1 to 4 occupancies, all exhibiting a single peak at ∼3 Å. This is consistent with the L4 case having a tetrahedral geometry in which all guest hydrogens are mutually equidistant. There is a notable change for the L5 case in which the main peak shifts to a shorter distance and a second peak develops at just over 4 Å. Presumably, this is simply due to the geometrical fact that there exists no equidistant configuration for 5 points in three dimensions, i.e. for five molecules, there must be a second nearest neighbour distance.

The radial distribution functions show much more variety over the different large cage occupancies. As we have seen before, the L1 result shows that the single guest molecule is free to move over the interior of the cage, but that at higher occupancies, this centre region becomes excluded due to intermolecular repulsion. It is also notable that the average radial distance from the large cage-centre becomes larger with the addition of each extra guest molecule, again presumably due to competing intermolecular repulsion effects. Finally, note how the n = 2 to 5 distributions show a single peak, indicating that the guest hydrogens are more or less confined to the surface of a sphere.

Most of the findings in this section are in agreement with the work of Sebastianelli et al., who presented clear evidence for the tetrahedral structure adopted by guest H₂ molecules in the L4 cages. It should be noted that these authors also describe a ‘qualitative change’ taking place between below 50–100 K and above in which the structure changes from the purely tetrahedral one, having a definite orientation with respect to the surrounding cage, to one in which the guest molecules start to sample other minima involving off-site positions. Looking at our results, although it is certainly true that at the lowest temperatures, the structure inside the L4 cage becomes almost perfectly tetrahedral, nothing we've seen indicates that there is anything other than a smooth increase in sampling higher energy configurations with increasing temperatures.

Inter-cage hopping barriers

There is also a (much larger) free energy barrier for a H₂ molecule to leave its cage, almost always through the middle of one of the hexagonal faces into an adjoining cage (the pentagonal faces having a much higher barrier for traversal). These free energy barriers can be seen in Fig. 5, along the thin necks on the right-hand side of each plot. Note that, in reality, there are equivalent pathways through each of the four hexamers, but our umbrella sampling only enhances the sampling along one of those four.

In order to see these free energy barriers clearer, in Fig. 7 we have also plotted the 1D free energies F(x) where x is the perpendicular distance of the H₂ molecular center of mass from the center of the bridging water hexamer. Both the classical and the path-integral results are shown, with the path-integral results displayed with a sign change to the x coordinate, such that the barriers can be more easily visually compared.

Fig. 7 Free-energy F(x) for the different occupations and different temperatures, where x is the perpendicular distance from the centre of the bridging hexamer.

It is seen that these barriers are quite large, being in the range 10–30 kJ mol⁻¹, and are dependent on both the cage occupation and the temperature.

As seen in our previous paper, we observe that, somewhat surprisingly, these barriers tend to increase with temperature. (Of course, we should still expect that the rates themselves will not decrease as the temperature is raised.) We think this is because of entropic effects – the entropy is lower in the region of the transition state than in the body of the cage, giving a negative sign for the difference in entropy between these two regions: ΔS = S^TS − S^cage < 0. Thus, all other things being equal, the free energy difference between the minimum and the transition state ΔF = ΔU − TΔS will tend to increase with temperature.

It is worth noting though that there is one case which goes against this trend. The L4 occupancy has free-energy barriers which decrease with increasing temperature, with the effect being more pronounced in the path-integral data. We speculate that this is because the L4 case has a lower relative entropy than the other occupancies, with the molecules being able to pack perfectly into the four tetrahedral sites available per cage.

As noted in our previous paper, each path-integral calculation consistently shows a larger barrier than its classical analogue, with the difference being largest at the lowest temperatures and lower occupancies. Our explanation for this somewhat counterintuitive result is that quantization increases the effective size of the H₂ molecules, making it harder for them to squeeze through the bridging water hexamers connecting adjacent cages. We will expand on this at the end of this subsection.

Finally, note that most of the path-integral results once again show little difference between 50 and 100 K, indicating that at this temperature the H₂ molecules are close to their ground state. However, there still seems to be a substantial difference in the L4 occupation free-energy barrier over this temperature range.

Fig. 8 shows the classical and the path integral free-energy barriers as a function of occupancy for the different temperatures studied. As before, it is seen that the path-integral free-energy barriers are consistently larger than their classical analogues. It is also clear that these barriers tend to get smaller with increasing occupancy, with the L5 barriers being significantly smaller than the L1 barriers at each temperature. However, once again it is found that the L4 occupancy behaves somewhat anomalously, with the L4 barrier at 50 K and 100 K being larger than the L3 value at the same temperature. And again, we explain this by the fact that the L4 occupancy allows for perfect packing of the H₂ molecules into the tetrahedral vacancies, allowing for enhanced stability over the transition states. Also and perhaps not surprisingly, the L4 case has the largest observed barriers for the H₂ guest molecules to move between tetrahedral sites within one large cage.

Fig. 8 Free energy barriers for different occupancies for the temperatures studied. Black lines are the classical results and red represent path-integral results.

Moving past the quadruple occupation case, the L5 occupancy is seen to have significantly smaller barriers than would be expected from extrapolating from the near-linear trend seen in the L1–L3 results. Yet again this result can be explained with reference to the tetrahedral packing – the L5 case having one too many molecules per large cage for them all to fit into tetrahedral sites appears to allow for free movement of guest molecules through the clathrate structure.

Returning to the question of the effective size of the H2 molecules, Fig. 9 shows the root mean square (r.m.s.) radius of the nuclear path-integral paths for the O nuclei in the water molecules and the H nuclei in both the water and H₂ molecules for the L1 case at the three different temperatures studied. Only the L1 case is shown, as nearly identical results were found for other occupations.

Fig. 9 (top) RMS path-integral path radius for H and O nuclei in the L1 case at three different temperatures. (bottom left) r.m.s. HH bond-length distribution using both classical and quantum simulations. (bottom right) Angular distribution of angle each replica H₂ makes with centroid H₂.

Given their lighter mass, it is not surprising that the water-molecule H nuclei have a larger path radius than the O nuclei. However, it is notable that, at all temperatures, the H nuclei in H₂ molecules have a significantly larger path radius than their equivalents in H₂O. These radii also show significant variation with temperature, and at 50 K the H nuclei in H₂ path radius is a remarkable ∼0.4 Å, which is more than half the size of the HH bond distance of ∼0.75 Å.

Turning to the bottom-left of Fig. 9, we can see that the path-integral H₂ bond length distribution hardly changes with temperature. This is somewhat surprising given the massive temperature variation in the H path radii seen in the top of the figure. However, the explanation can be seen in the bottom right of Fig. 9, which shows the distribution of angles that each path-integral replica H₂ makes with its centroid H₂ (the centroid being the average over all replica). This figure shows that decreasing the temperature causes the path H₂ molecules to spread out over a greater angular region, i.e., in directions perpendicular to the bond vector. Thus, the nuclear radii are getting bigger, but in the angular direction, as opposed to along the bond direction.

The above finding is perhaps not too surprising given that the H₂ molecules are not bonded to anything and so are behaving like rigid rotors, in that they are almost completely free to rotate about their axes. This is in contrast to the water molecules, which are of course mutually hydrogen-bonded to each other, and so do not have the same freedom to rotate over all angles.

The above is consistent with our argument that nuclear quantum effects cause the effective size of the H₂ molecules to increase with decreasing temperature, which we claim makes it harder for the molecules to squeeze through the hexamers connecting adjacent cages, so giving rise to larger free-energy barriers.

It is interesting to compare our findings to double-well systems where quantisation of the nuclei acts to lower the barriers. For example, Benoit et al.²⁶ performed a computational study of the behaviour of protons in the transition of ice VIII to ice VII under high pressure, in which each water proton starts out confined to one side of a O–H⋯O double well until the O nuclei approach close enough for the proton to be shared symmetrically between the well pair. These authors found that quantisation of the nuclei via path-integral simulation allows the proton to become symmetrised at a lower pressure than observed using classical statistics, indicating the existence of a lower effective barrier when nuclear quantum effects are included – presumably due to quantum tunnelling effects.

That the above example shows a lowering of the barrier with quantisation whereas we observe a raising in the H₂ hopping barrier reflects, we reason, qualitative difference in barrier types. The O–H⋯O barrier is simply due to the potential energy surface having a higher energy when the proton is in the middle than when it resides in either of the two wells. Comparing this to the arguably more complex barrier of the H₂ hopping between hydrate cages in which the H₂ has to thread through the centre of a hexamer connecting adjacent cages. In this case, size effects appear to play a much more significant rôle: the larger the molecule, the harder it will be for it to pass through the hexamer. As we have shown, the quantisation of the nuclei increases the effective size of the H nuclei resulting in a net overall raising of the effective barrier height. Nevertheless, it is surely the case that tunnelling plays a rôle, just that it is not a dominant one, at least at the temperatures studied. Also, it should be noted that the ∼20 kJ mol⁻¹ hopping barrier is quite large and wide, meaning that tunnelling may well be insignificant at these temperatures.

Comparison to DFT

In order to judge the accuracy of our empirical model, we have also performed ab initio molecular dynamics simulations for the L4 quadruple occupation case, with a comparison to the empirical model results shown in Fig. 10.

Fig. 10 Comparison between DFT and empirical model results for the L4 occupancy at 260 K. Top: Probability isosurfaces. Middle: Free energy surfaces F(x,y). Bottom: Free energy F(x).

For the purposes of this comparison, we ran both simulations at 260 K, which is about the highest possible pre-melting temperature. This relatively high temperature was chosen in order that the DFT simulation would have the best chance of overcoming any barriers.

From this figure, it can be seen that there are somewhat significant differences between the DFT and empirical model free energies, and so it seems the best we can hope for with this empirical model is a qualitative description of the system. Still, both potential energy surfaces show evidence of tetrahedral packing of the guest H₂ molecules.

Umbrella sampling was not used with the DFT calculations, and so, unfortunately, we do not know how large the barrier is for a hopping event under the DFT potential energy surface, however the ab initio MD results show that it appears to be at least 15 kJ mol⁻¹ in size, which can be compared to the empirical model barrier of 20 kJ mol⁻¹.

We can compare our L4 DFT result to the work of Trinh et al.,² who used ab initio molecular dynamics calculations to calculate the free-energy barriers for the n = 1 to 6 large-cage guest molecule H₂ occupations. And although their calculations were run at 100 K compared to our 260 K calculation, it is interesting to note that they report an inter-cage hopping free-energy barrier of just 9 kJ mol⁻¹ for the L4 case, which seems considerably smaller than our value, of at least 15 kJ mol⁻¹. It may be that the difference between our calculations is explained by the fact that Trinh et al. are using a functional which does not include van der Waals interactions. Such interactions will modify the H-bond interaction, perhaps making it more difficult for the water–water hydrogen bonds to change size as a H₂ molecules passes through the hexamers. However, we admit that this is speculative and will need to be tested in future work.

Summary and conclusions

The main aim of this paper has been to explore the temperature dependence and dependence on cage occupancy of the free-energies for H₂ molecules inside a type II clathrate hydrate lattice, using both classical and quantum statistics. We were in particular concerned with the barriers for H₂ molecules to move from one large cage to another.

Somewhat surprisingly, it is seen these inter-cage barriers tend to get larger with temperature and also surprisingly that the inclusion of nuclear quantum effects acts to increase the size of the barriers with respect to their classical analogues, with the largest changes being seen at the lower temperatures. We explained how these changes are likely a result of nuclear quantisation acting to increase the effective size of the H₂ molecules, making it harder for them to thread through the water hexamers connecting adjacent cages. Also, we confirmed that nuclear quantisation increases the effective size by causing the H nuclei to spread out over the radial directions of each H₂ molecule.

Though not in such detail, both these effects were shown in our previous paper. However, in this work we have placed the behaviour of these free-energy surfaces in the context of the tetrahedral packing favoured by the H₂ molecules in the large cages. In particular, it was shown that the L4 case behaves somewhat anomalously, having a larger barrier for inter-cage hopping than would be expected from extrapolation from the smaller occupation values, with the difference becoming more pronounced at lower temperatures. The L4 case also behaves anomalously in that it has a barrier which decreases with increasing temperature, unlike all other cases examined.

It was also shown that the inter-cage hopping barrier drops off unexpectedly quickly for the L5 case, which we explained as being due to this occupancy having one H₂ molecule too many with respect to a perfect tetrahedral packing.

We also explored the effects of quantising the nuclear degrees of freedom via path-integral molecular dynamics, showing how this quantisation acts to increase the inter-cage hopping barriers over the equivalent classical results, with the classical-quantum difference being largest at the lowest temperatures. Quantisation was also found to have a significant effect on the energetics determining the capacity of each cage, such that with nuclear quantum effects included, the system can only be expected to hold a maximum of four molecules per large cage, whereas classically, for this potential, the number can be as large as five.

Finally, for the L4 case we made comparisons between density functional theory ab initio molecular dynamics and our empirical model results, finding that there is only qualitative agreement between the two. Nevertheless both potential energy surfaces predict a tetrahedral ordering of the guest H2 molecules and both show reasonably large inter-cage hopping barriers of more than 15 kJ mol⁻¹. However, it would obviously be a boon to find or develop an empirical model which is closer to ab initio data.

Acknowledgements

The authors acknowledge Science Foundation Ireland (SFI/15/ERC/I3142) for funding.

References

1. C. J. Burnham and N. J. English, Free-Energy Calculations of the Intercage Hopping Barriers of Hydrogen Molecules in Clathrate Hydrates, J. Phys. Chem. C, 2016, 120, 16561.
2. T. T. Trinh, M. H. Waage, T. S. V. Erp and S. Kjelstrup, Low Barriers for Hydrogen Diffusion in Sii Clathrate, Phys. Chem. Chem. Phys., 2015, 17, 13808–13812.
3. F. Sebastianelli, M. Xu and Z. Bačić, Quantum Dynamics of Small H2 and D2 Clusters in the Large Cage of Structure Ii Clathrate Hydrate: Energetics, Occupancy, and Vibrationally Averaged Cluster Structures, J. Phys. Chem., 2008, 129, 244706.
4. A. Witt, F. Sebastianelli, M. E. Tuckerman and Z. Bačić, Path Integral Molecular Dynamics Study of Small H2 Clusters in the Large Cage of Structure Ii Clathrate Hydrate: Temperature Dependence of Quantum Spatial Distributions, J. Phys. Chem. C, 2010, 114, 20775.
5. K. A. Lokshin, Y. Zhao, D. He, W. L. Mao, H.-K. Mao, R. J. Hemley, M. V. Lobanov and M. Greenblatt, Structure and Dynamics of Hydrogen Molecules in the Novel Clathrate Hydrate by High Pressure Neutron Diffraction, Phys. Rev. Lett., 2004, 93, 125503.
6. S. Alavi and J. A. Ripmeester, Hydrogen-Gas Migration through Clathrate Hydrate Cages, Angew. Chem., 2007, 46, 6102.
7. S. Patchkovskii and J. S. Tse, Thermodynamic Stability of Hydrogen Clathrates, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14645.
8. S. Nosé, A Unified Formulation of the Constant Temperature Molecular Dynamics Methods, J. Chem. Phys., 1984, 81, 511.
9. W. G. Hoover, Canonical Dynamics: Equilibrium Phase-Space Distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 31, 1695.
10. G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé–Hoover Chains: The Canonical Ensemble Via Continuous Dynamics, J. Chem. Phys., 1992, 97, 2635.
11. W. Smith, Elements of Molecular Dynamics, 2015.
12. J. L. F. Abascal and C. Vega, A General Purpose Model for the Condensed Phases of Water: Tip4p/2005, J. Chem. Phys., 2005, 123, 234505.
13. S. Alavi, J. A. Ripmeester and D. D. Klug, Molecular-Dynamics Study of Structure Ii Hydrogen Clathrates, J. Chem. Phys., 2005, 123, 024507.
14. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, van der Waals Density Functional for General Geometries, Phys. Rev. Lett., 2004, 92, 246401.
15. G. Román-Pérez and J. M. Soler, Efficient Implementation of a van der Waals Density Functional: Application to Double-Wall Carbon Nanotubes, Phys. Rev. Lett., 2009, 103, 096102.
16. J. Wang, G. Román-Pérez, J. M. Soler, E. Artacho and M.-V. Fernández-Serra, Density, Structure, and Dynamics of Water: The Effect of van der Waals Interactions, J. Chem. Phys., 2011, 134, 024516.
17. C. Zhang, J. Wu, G. Galli and F. Gygi, Structural and Vibrational Properties of Liquid Water from van der Waals Density Functionals, J. Chem. Theory Comput., 2011, 7, 3054.
18. F. Corsetti, E. Artacho, J. M. Soler, S. S. Alexandre and M.-V. Fernández-Serra, Room Temperature Compressibility and Diffusivity of Liquid Water from First Principles, J. Chem. Phys., 2013, 139, 194502.
19. A. Bankura, A. Karmakar, V. Carnevale, A. Chandra and M. L. Klein, Structure, Dynamics, and Spectral Diffusion of Water from First-Principles Molecular Dynamics, J. Phys. Chem. C, 2014, 118, 29401.
20. N. J. English, Structural Properties of Liquid Water and Ice Ih from Ab Initio Molecular Dynamics with a Non-Local Correlation Functional, Energies, 2015, 8, 9383.
21. M. J. Gillan, D. Alfè and A. Michaelides, Perspective: How Good Is Dft for Water?, J. Chem. Phys., 2016, 144, 130901.
22. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, The Siesta Method for Ab Initio Order-N materials, J. Phys.: Condens. Matter, 2002, 14, 2745.
23. G. M. Torrie and J. P. Valleau, Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling, J. Comp. Physiol., 1977, 23, 187.
24. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method, J. Comput. Chem., 1992, 13, 1011.
25. W. Humphrey, A. Dalke and K. Schulten, Vmd – Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33.
26. M. Benoit, D. Marx and M. Parrinello, Tunnelling and Zero-Point Motion in High-Pressure Ice, Nature, 1998, 392, 258.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp06531g

---