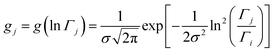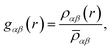Open Access Article
Open Access ArticleDynamics of an amorphous pharmacologically active compound – diazepam: a QENS study combined with molecular dynamics simulations†
Aleksandra Pajzderska *a,
Miguel A. Gonzalezb,
Jan P. Embs
*a,
Miguel A. Gonzalezb,
Jan P. Embs c,
Jadwiga Mielcarekd and
Jan W. Wąsickiae
c,
Jadwiga Mielcarekd and
Jan W. Wąsickiae
aA. Mickiewicz University, Faculty of Physics, Umultowska 85, Poznan, Poland. E-mail: apajzder@amu.edu.pl
bInstitute Laue Langevin, 71 Avenue des Martyrs, Grenoble, France
cLaboratory for Neutron Scattering and Imaging, Paul Scherrer Institut, 5232 Villigen, Switzerland
dPoznan University of Medical Sciences, Poznan, Poland
eThe NanoBioMedical Centre, Umultowska 85, Poznan, Poland
First published on 17th July 2017
Abstract
The dynamics of methyl groups in crystalline and amorphous diazepam were investigated by a combination of molecular dynamics simulations and quasielastic neutron spectroscopy methods. The reorientation of the methyl group with a single correlation time was detected in crystalline diazepam. On the other hand, methyl group rotations in the amorphous sample cannot be represented by a single relaxation time and a distribution of correlation times approximated by a log-normal function is needed to explain both the simulation and neutron results. Additionally, MD simulations showed that the intermolecular part of the interactions due to the different environment around each methyl group is responsible for the distribution of correlation times observed experimentally.
1. Introduction
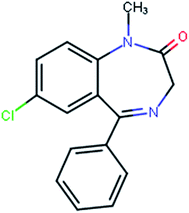
The study of amorphous forms of pharmacological active substances is becoming increasingly important due to the fact that they are often less thermodynamically stable and can show higher bioavailability1–5 than the corresponding crystalline forms. It is therefore of interest to evaluate the molecular dynamics of amorphous active pharmaceutical ingredients since it is believed that mobility is one of the main factors that govern their physical stability.6,7 Investigations of amorphous forms are still a challenge, although very different experimental methods can be applied for the physico-chemical and dynamical characterization, including thermal analysis, X-ray powder diffraction, Fourier transform infrared spectroscopy (FT-IR), solid-state nuclear magnetic resonance (ssNMR) and neutron spectroscopy.8 Moreover, the macroscopic properties of amorphous substances could depend on the dynamics of molecular fragments.9 Thus, the understanding of the dynamics of functional groups, including methyl groups, is of general interest in drug design.Diazepam belongs to the family of benzodiazepine derivatives, a group of medicaments having a wide spectrum of activity along four main lines: antianxiety, sedative and sleep-inducing, anticonvulsive and reducing muscle tension.10 The molecule is built of a condensed benzodiazepine ring and a chlorobenzene ring, with a methyl group attached to the nitrogen atom at position 1 in the benzodiazepine ring (Fig. 1).
The diazepam molecule contains only one methyl group and therefore, it is an excellent system to study the role of intra- and intermolecular interactions in determining the properties of pharmaceuticals in either crystalline or amorphous forms. In the past, we have studied the physical properties of crystalline diazepam by calorimetric, infrared absorption and nuclear magnetic resonance (NMR) methods. The investigation of its dynamics was complemented by a density functional theory (DFT) study of the vibrational frequencies and infrared intensities and the calculation of steric hindrances. The results indicate the occurrence of reorientation jumps of the CH3 group with a threefold barrier of height about 8 kJ mol−1,11 which is typical value for reorientation of methyl groups.12–15 Later we focused on the amorphous sample, obtained by the melting and quench-cooling method and used NMR and atom–atom potential energy calculations to determine the distribution of energy barriers for the reorientation of methyl groups, finding that there is a distribution of energy barriers varying from ∼2 to ∼13 kJ mol−1.16 These calculations permitted also a separation of energy contributions coming from intra- and from inter-molecular interactions, with the former suggesting the possibility of a modification of the conformation of the diazepam molecule in the amorphous phase.
The drawback of atom–atom potential calculations is that they are performed under the static approximation, i.e. assuming that the neighbouring molecules are motionless. Nevertheless, the agreement between the energy barrier distribution obtained in this way for diazepam with that obtained from NMR measurements implies that the approximation is reasonably satisfactory.
However, in order to analyse the dynamics of amorphous diazepam in more detail and get further insight into the dynamical behaviour of this compound, in this paper we apply the molecular dynamics (MD) method to obtain and compare the correlation times of methyl group reorientations in crystalline and amorphous diazepam. In this way, we take into account the intra- and intermolecular interactions and their modulation caused by the reorientation of methyl groups belonging to neighbouring molecules. The calculated correlation times are confronted with those measured for crystalline and amorphous diazepam using quasielastic neutron scattering (QENS). MD simulations permit the analysis of molecular motions whose time scale is comparable with that of QENS results and allow to trace the behaviour of individual methyl groups. Both methods are especially adequate for this kind of study, since they operate over essentially the same time and length scales, ideally complementing each other. The usefulness of such a combined approach resides in the direct confrontation of experimental and theoretical results. This allows us, on one hand, to validate the potential used in the MD simulations and, on the other hand, to use the MD trajectories as a guide for interpreting the experimental data and model the dynamical properties of the samples studied.
2. Experimental
2.1. Sample
Crystalline diazepam (7-chloro-1,3-dihydro-1-methyl-5-phenyl-2H-1,4-benzodiazepin-2-one) was purchased in hermetically sealed containers from GlaxoSmithKline Pharmaceuticals S.A., Poznań. The quality of the sample was checked and described in our previous paper.11Amorphous diazepam was prepared by melt-quench cooling methods, i.e. the sample was heated at ca. 10 K min−1 up to 425 K (∼10 degrees above the melting temperature), kept at this temperature for approximately 10 min and then the melt was cooled down to 200 K (with a cooling rate equal to 20 K min−1).
2.2. Computational details
Molecular Dynamics (MD) simulations of crystalline and amorphous diazepam were performed using DL_POLY Classic.17 Crystalline diazepam was simulated using a supercell of dimensions 38.8 × 40.0 × 39.9 Å3 constructed on the basis of X-ray diffraction (XRD) data18 and containing 180 diazepam molecules. An amorphous cell containing 200 molecules was constructed using the Amorphous Cell module built in the Materials Studio package.19MD simulations were performed in the temperature range 200–300 K at constant NVT. The temperature was controlled using Berendsen's thermostat20 with a relaxation constant of 1 ps. Periodic boundary conditions were applied in all directions. We used the cvff force field.21 A cut-off distance of 19 Å was applied for the van der Waals forces and the electrostatic interactions were treated using the Ewald summation method with the same cutoff in real space. In all cases a time step of 1 fs was used and the systems were equilibrated during 1 ns. The trajectory was saved every 1 ps for a total simulation time of 10 ns. The analysis of the trajectories was then performed using nMoldyn 3 (ref. 22) and self-written programs.
Methods
QENS measurements of crystalline and amorphous samples were done on the time-of-flight spectrometer FOCUS (PSI, SINQ). The sample was placed in a specially designed container consisting in a hermetically closed aluminum hollow cylinder (mass of sample = 0.89 g). QENS spectra were taken in the Q-range 0.3–1.8 Å−1 using a PG002 monochromator, giving an incoming neutron wavelength λ0 = 5.75 Å and an energy resolution equal to ∼0.036 meV (FWHM). First, the crystalline sample was measured at the following temperatures: 26 K, 100 K, 150 K, 200 K, 250 K, 300 K and 350 K. Then, it was heated up to 425 K and amorphous diazepam was prepared by melt-quench cooling methods and measured at the same temperatures as the crystal. Powder diffraction spectra (which are measured simultaneously on FOCUS) allowed us to follow the phase transitions and the disappearance of Bragg peaks confirmed the amorphisation of the sample. The sample holder was weighted before and after the measurements to confirm that it was hermetic and no mass losses were detected. Additionally, an empty container and a vanadium sample were measured at room temperature to be used in the background and normalization procedures, respectively.Raw data were treated with the DAVE package,23 which performs the standard corrections, including background subtraction and self-absorption correction. Then, using a vanadium spectrum as an elastic scattering standard the intensities were normalised in order to correct for different detector efficiencies. Finally, detectors where Bragg peaks influenced the collected spectra were removed from further analysis in order to focus only on the incoherent quasielastic neutron scattering.
3. Results and discussion
3.1. Molecular dynamics simulations
Fig. 2 shows two snapshots corresponding to the initial configuration of the crystalline and amorphous simulation boxes on which the MD calculations were performed. | ||
| Fig. 2 Crystalline (left) and amorphous (right) simulation boxes used in the molecular dynamics simulations. | ||
ACF(t) = 〈![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) CH(t0)· CH(t0)·![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) CH(t0 + t)〉, CH(t0 + t)〉,
| (1) |
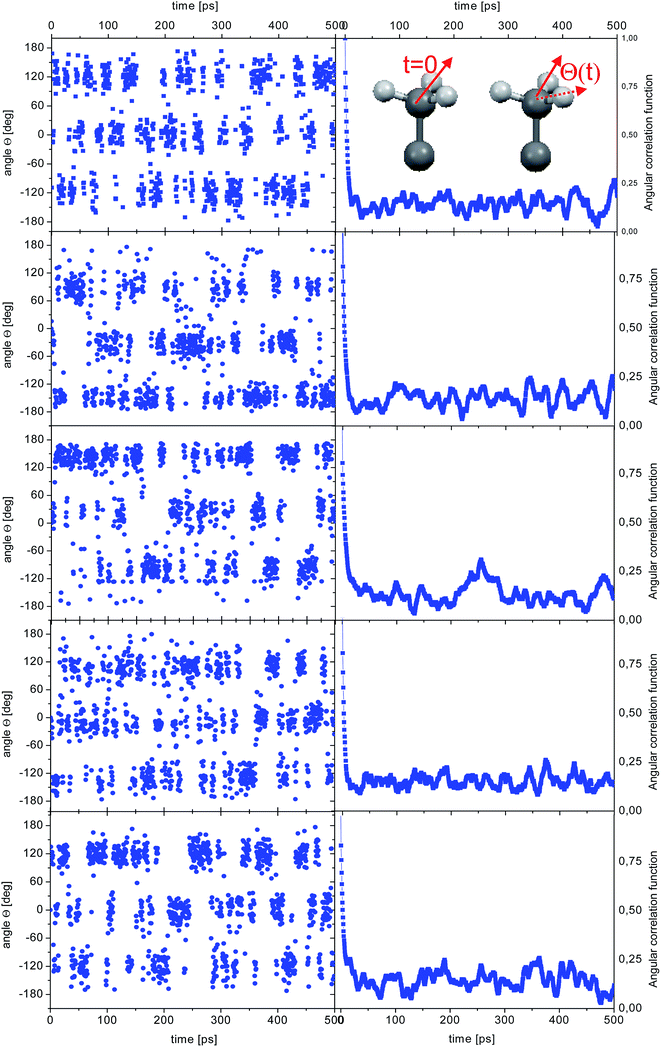
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) CH(t0 + t) is the vector along one C–H bond of a methyl group at time t0 + t and the brackets indicate an average over all methyl groups in the system and possible origins t0. The ACFs can be fitted using a single exponential function (ACF(t) ∼ exp(−t/τc)), where τc is the correlation time. The angular correlation function (ACF) was calculated both as an average of all the methyl groups and for each individual methyl groups. The results obtained at 300 K are shown in Fig. 3.
CH(t0 + t) is the vector along one C–H bond of a methyl group at time t0 + t and the brackets indicate an average over all methyl groups in the system and possible origins t0. The ACFs can be fitted using a single exponential function (ACF(t) ∼ exp(−t/τc)), where τc is the correlation time. The angular correlation function (ACF) was calculated both as an average of all the methyl groups and for each individual methyl groups. The results obtained at 300 K are shown in Fig. 3.
Unsurprisingly, the behaviour of all the methyl groups in the crystal is very similar, and all of them show comparable relaxation times. With decreasing temperature, the methyl reorientation slows down as expected. The temperature dependence of the average correlation time is displayed in Fig. 4, which also shows the τc dependence obtained using the activation parameters from the earlier NMR measurements and an Arrhenius relation (solid line) and those derived from QENS data (next section of this work). The three sets of correlation times are in excellent agreement, suggesting that the method of calculation, as well as the partial charges and force field employed to describe the dynamic properties of diazepam are a good choice and can be extended to the amorphous sample.
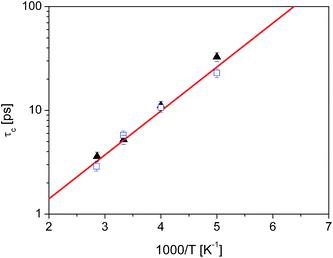 | ||
Fig. 4 Temperature dependence of the correlation time for methyl reorientation in crystalline diazepam:  QENS data QENS data  MD simulations, solid line: NMR data.16 MD simulations, solid line: NMR data.16 | ||
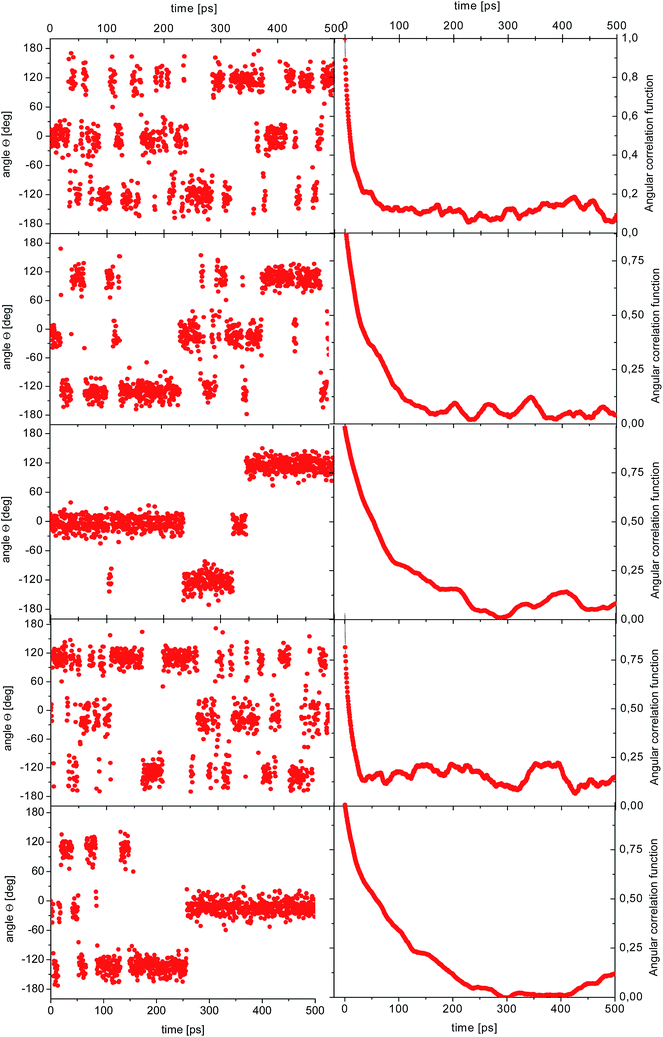 | ||
| Fig. 5 Time dependence of the angle θ(t) for the reorientation of selected methyl groups in the simulation of amorphous diazepam (left) and corresponding ACFs (right). | ||
As before, the ACF of each methyl group was calculated individually and fitted by a single exponential function from which the correlation times were extracted. The shortest correlation time found is 0.5 ps, while the longest is ∼50 ps (at 300 K) or ∼200 ps (lower temperatures), indicating a very broad distribution of relaxation times. In order to characterize such a distribution, we show in Fig. 6 the histogram obtained by representing the number of molecules (or methyl groups) characterised by a given correlation time τc. At 350 K this distribution is highly non-symmetric and shows a single maximum at τc ≈ 2 ps followed by a long tail extending to very long times. With decreasing temperature, the reorientation slows down (so the maxima are shifted towards longer times) and the distribution of correlation times extends, indicating that an increased number of methyl groups is characterised by longer correlation times.
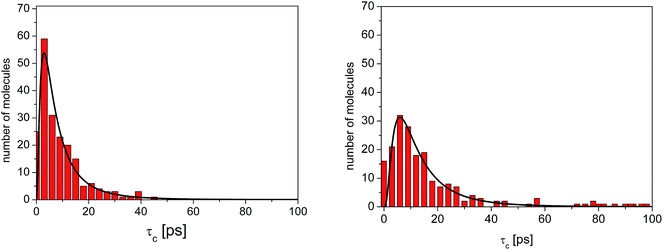 | ||
| Fig. 6 Distribution of correlation times for the reorientation of methyl groups in amorphous diazepam extracted from MD simulations (rectangles) at 300 K (left) and 250 K (right). The solid lines correspond to the curves obtained by fitting this distribution with a log-normal function (eqn (2)). | ||
The distributions shown in Fig. 6 can be well described by the log-normal function:
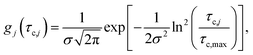 | (2) |
3.2. Quasielastic neutron scattering
As mentioned above, apart from the QENS spectra, during the same measurements also the neutron diffraction patterns were recorded. They are shown in Fig. 1S† for both crystalline and amorphous diazepam measured at room temperature. As expected, the crystal exhibits well pronounced diffraction peaks appearing at scattering angles that agree with those generated on the basis of the known crystallographic structure. For the amorphous sample, no diffraction peaks are observed, and only a very broad peak (a halo) is seen with a maximum at about 50 degrees, confirming that the quench-cooling process succeeded in producing an amorphous sample.| S(Q,ω) = A0(Q)δ(ω) + (1 − A0(Q))L(ω) + B(Q,ω), | (3) |
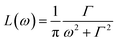 is a Lorentz function of half-width at half-maximum Γ and B(Q,ω) describes the linear background. They were fitted using the STR_FIT program in Lamp24 which enables numerical convolution with the instrumental resolution function R(Q,ω) determined from a measurement of a vanadium standard sample.
is a Lorentz function of half-width at half-maximum Γ and B(Q,ω) describes the linear background. They were fitted using the STR_FIT program in Lamp24 which enables numerical convolution with the instrumental resolution function R(Q,ω) determined from a measurement of a vanadium standard sample.Two important parameters are extracted from the fit: the correlation time (inversely proportional to the half-width of the Lorentz function Γ) and A0(Q), which provides information about the geometry of the dynamic process. Thus, this phenomenological fit permits us to determine the EISF in a model independent way. Assuming jumps of methyl groups between three equidistant sites on a circle of radius r, the corresponding EISF can be written as:25
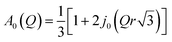 | (4) |
While all atoms in the sample contribute to the EISF, the contribution from the hydrogen atoms represents more than 90% of the total scattering, so the contribution from other atoms (nitrogen, carbon, oxygen, and chlorine) can be neglected. Furthermore in the crystalline sample we can assume that only the methyl groups move within the time scale given by the finite resolution of the spectrometer. Therefore the measured elastic incoherent structure factor (EISF) can be written as
| EISF = c + (1 − c)·A0(Q) | (5) |
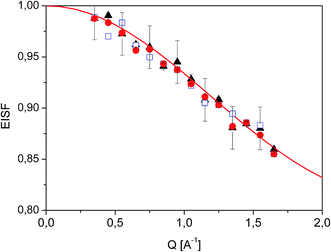 | ||
Fig. 7 Experimental EISF extracted from QENS data at T = 350 K ( ), 300 K ( ), 300 K ( ) and 250 K ( ) and 250 K ( ). The solid line shows the expected EISF corresponding to a methyl rotation between three equivalent positions while the other atoms of the diazepam molecule remain immobile (eqn (5)). ). The solid line shows the expected EISF corresponding to a methyl rotation between three equivalent positions while the other atoms of the diazepam molecule remain immobile (eqn (5)). | ||
In the range 250–350 K, the EISF obtained does not depend on temperature (Fig. 7) and is perfectly described by the model assuming the reorientation of one methyl group. Therefore all the spectra were re-fitted using this specific model corresponding to jumps between three positions:
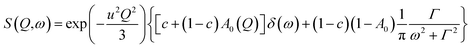 | (6) |
where exp(−u2Q2/3) is the Debye–Waller factor. Again this model describes very well the experimental data, as shown in Fig. 8, but now using only two parameters, r and Γ, as the Q-dependence of A0(Q) is now given by eqn (6).
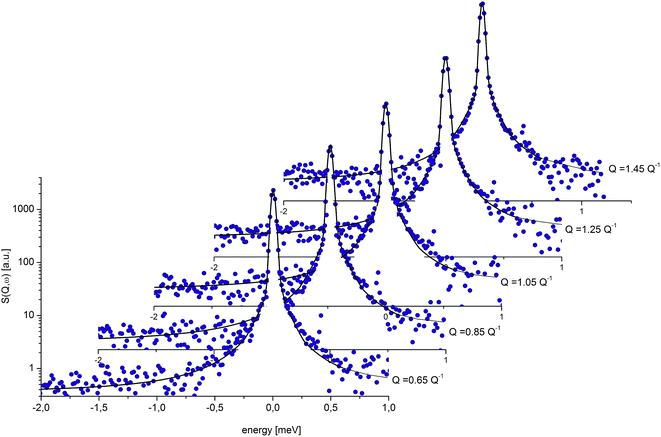 | ||
| Fig. 8 QENS spectra for crystalline diazepam at 250 K. The solid line shows the fits given by eqn (6). | ||
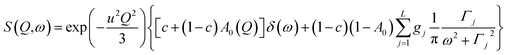 | (7) |
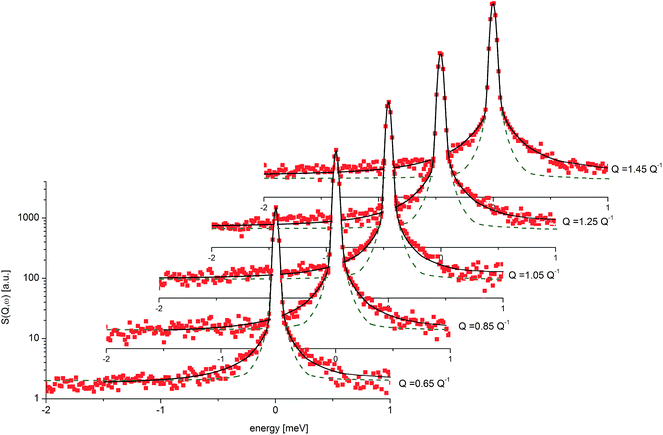 | ||
| Fig. 9 QENS spectra for amorphous diazepam at 250 K. The solid lines correspond to the fits obtained using eqn (7), while the dashed lines to those using eqn (6). The difference between both fits shows clearly that the model assuming only one correlation time (one single Lorentzian function) cannot describe well the experimental data. | ||
This model is based on the rotation distribution model26 that considers a distribution of jumping rates and has been applied in polymers,27,28 in low molecular-weight glasses29,30 or in glass-forming liquids in soft confinement.31 For each jumping distance, instead of a single Γi value, a distribution of HWHMs is used. The distribution is represented by L values of the HWHM (Γj) with associated weights gj taken from a log-normal distribution of standard deviation σ and normalized such that 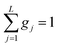 . The Γj are chosen equally spaced on a logarithmic scale in the range
. The Γj are chosen equally spaced on a logarithmic scale in the range 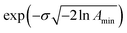 ,
, 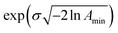 , where Amin is the cut-off chosen for the value of the distribution function with respect to its maximum. Here we used L = 21 and Amin = 0.1.
, where Amin is the cut-off chosen for the value of the distribution function with respect to its maximum. Here we used L = 21 and Amin = 0.1.
Fig. 9 presents an example of the QENS spectra of amorphous diazepam measured at 250 K and several Q values together with the results of the fits obtained with eqn (7). As mentioned above, the half-width Γj obtained from the fitting of the QENS spectra is directly related to the correlation time τc. As each Lorentz function of width Γj represents a contribution described by the weight gj, it is possible to obtain a distribution of correlation times. They are shown in Fig. 10 together with the distribution obtained from the MD simulations (see Fig. 6). Both present similar characteristics, although the experimental one cannot be estimated beyond a few tens of ps due to the time-window of FOCUS spectrometer.
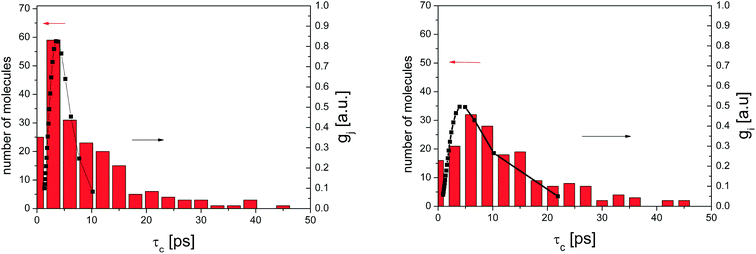 | ||
| Fig. 10 Distribution of correlation times for amorphous diazepam as obtained from MD simulation (rectangles) and from the fit of QENS data at 300 K (left) and 250 K (right) with eqn (7) (solid lines). | ||
3.3. Analysis of intra- and intermolecular interactions
In order to determine the origin of the very different behaviour in crystalline and amorphous diazepam, the MD trajectories were used to probe the intra- and intermolecular structure by means of the partial and total radial distribution functions (RDF). The latter is computed as:
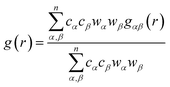 | (8) |
And each partial RDF is given by:
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) αβ represents the average density over the whole simulation box, cα and cβ correspond to the concentration numbers of atoms of type α and β, respectively and wα and wβ to their respective weights in the total RDF (e.g. neutron scattering lengths or X-ray form factors when comparing with neutron or X-ray diffraction data, but here set to 1 for all the atoms).
αβ represents the average density over the whole simulation box, cα and cβ correspond to the concentration numbers of atoms of type α and β, respectively and wα and wβ to their respective weights in the total RDF (e.g. neutron scattering lengths or X-ray form factors when comparing with neutron or X-ray diffraction data, but here set to 1 for all the atoms).
The total intramolecular RDF (Fig. 11) shows several well-resolved peaks and their positions and widths are very similar for crystalline and amorphous samples, clearly indicating that the molecular geometry is almost identical in both phases and reflecting the relative rigidity of the diazepam molecule.
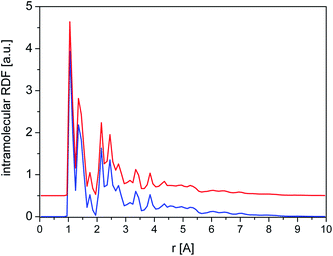 | ||
| Fig. 11 Total intramolecular RDF calculated for crystalline (blue line) and amorphous (red line) cluster. | ||
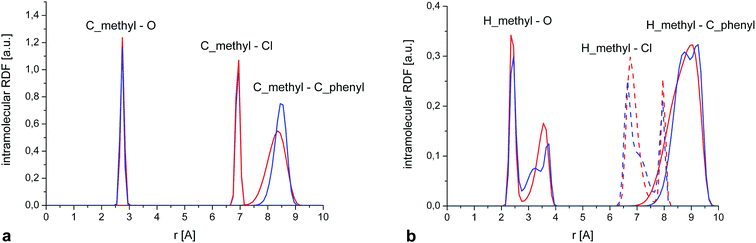
This is further confirmed by a closer examination of the distribution of intramolecular distances (Fig. 12a) between the C of the methyl group and three reference atoms situated in each of the rings forming the molecule, i.e. O, Cl and the C situated at the extreme of the phenyl ring. Again, the positions and width of those peaks are almost identical for both phases. Only the last RDF (peak at ∼8.5 Å) is slightly broader in the amorphous system, suggesting some additional flexibility of the phenyl ring compared to the crystal. We also calculated the equivalent RDFs for the hydrogen of the methyl groups, which show some additional structure (Fig. 12b), but there are no significative differences between crystal and amorphous that could explain the different dynamical behaviour of the methyl group in both phases.
The nature of the local environment has been determined by calculating the RDF individually for each methyl group, i.e.
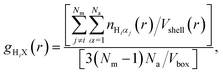 | (9) |
In the case of the crystal (Fig. 13), we see that the environment around the methyl group is very similar for each molecule, as expected, explaining that the CH3 rotation can be described by a single correlation time. Also contributions from different atoms to RDF are very similar to each other (Fig. 2S†).
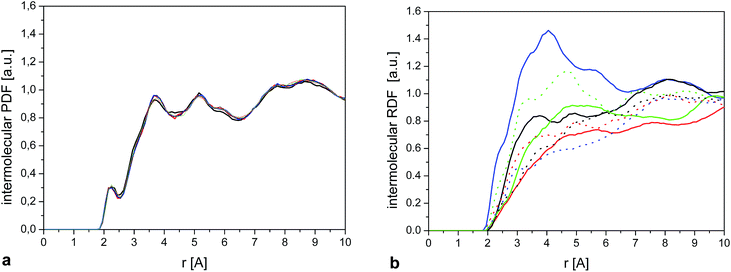 | ||
| Fig. 13 (a) Intermolecular HiX RDF (eqn (9)) calculated for a single methyl group. The 3 curves show the result for 6 randomly selected molecules. (b) As (a) for 6 randomly selected molecules in the amorphous sample. | ||
On the other hand, we observe significant differences between the molecules in the amorphous system. Fig. 13b shows the intermolecular RDF for six selected molecules from the amorphous system and Fig. 2S† the separate contributions from different types of atoms for these molecules. The RDF around each methyl group in the amorphous phase is very different, so it comes as no surprise that they will also have different rotational correlation times.
It is tempting to try to link the individual correlation times previously obtained (e.g. Fig. 5) with the different steric hindrances exemplified by the RDFs shown above. Although we explored this path, we could not establish any obvious correlation. This is due to the fact that the effective rotational potential felt by a methyl group will emerge from the combination of all the intra- and inter-molecular interactions which have different magnitudes and ranges (torsional potential, van der Waals interactions with different values of σ, and electrostatic potential). Therefore the only conclusion that we can extract is that the variety of environments in the disordered phase of diazepam results in a distribution of correlation times that can be well represented by a log-normal function, as shown in Fig. 10.
4. Conclusions
In this paper, by combining molecular dynamics simulations and quasielastic neutron scattering we have investigated in detail the dynamics of methyl groups in crystalline and amorphous diazepam. Our results can be summarised as follows:(1) Molecular dynamics simulations performed for crystalline diazepam confirmed the occurrence of reorientations of methyl groups and permitted the determination of the temperature dependence of their characteristic correlation times, which are in very good agreement with those obtained from NMR and QENS measurements.
(2) Molecular dynamics simulations revealed that the correlation times of reorientations of methyl groups in the amorphous sample cannot be characterized by a single correlation time, but by a distribution of correlation times approximated by a log-normal function.
(3) The QENS spectra obtained for the crystalline sample could be fitted assuming a simple model consisting of a δ-function and one single Lorentzian function of width Γ.
(4) The spectra of amorphous diazepam are more complex and could be fitted by the modified rotation distribution model – a log-Gaussian model (following from MD simulations) that assumes a distribution of jumping rates, so instead of a single Γ value, a distribution of widths is used.
(5) MD simulations showed that the distribution of correlation times observed experimentally are due to intermolecular effects and the variety of local environments around the methyl group that one can have in the amorphous sample.
In summary, molecular dynamics simulations have allowed us to obtain a more detailed understanding of the dynamics of molecular fragments in crystalline and amorphous drugs, shedding new light on the origin of the distribution of correlation times in amorphous systems also observed in QENS experiments.
Acknowledgements
The work has been partially financed by the National Science Centre of Poland, Grant No. 2015/17/B/ST5/00104 and has been supported in part by PL-Grid Infrastructure. A. P. would like to thank the Institut Laue Langevin (France) for an invitation as a visiting scientist. This work is based on experiments performed at the Swiss spallation neutron source SINQ, Paul Scherrer Institute, Villigen, Switzerland.References
- A. M. Thayer, Form and Function, Chem. Eng. News, 2007, 85, 17–30 Search PubMed.
- A. M. Thayer, Finding Solutions, Chem. Eng. News, 2010, 88, 13–18 Search PubMed.
- T. Einfalt, O. Planinsek and K. Hrovat, Methods of Amorphization and Investigation of the Amorphous State, Acta Pharm., 2013, 63, 305–334 CrossRef CAS PubMed.
- B. C. Hancock and G. Zografi, Characteristics and Significance of the Amorphous State in Pharmaceutical Systems, J. Pharm. Sci., 1997, 86, 1–12 CrossRef CAS PubMed.
- P. Srinarong, S. Kouwen, M. R. Visser, W. L. Hinrichs and H. W. Frijlink, Effect of Drug–carrier Interaction on the Dissolution Behavior of Solid Dispersion Tablets, Pharm. Dev. Technol., 2010, 15, 460–468 CrossRef CAS PubMed.
- A. Paudel, M. Geppi and G. van den Monter, Structural and Dynamic Properties of Amorphous Solid Dispersions: the Role of Solid State Nuclear Magnetic Resonance Spectroscopy and Relaxometry, J. Pharm. Sci., 2014, 103, 2635–2662 CrossRef CAS PubMed.
- S. Baghel, H. Cathcart and N. J. O'Reilly, Polymeric Amorphous Solid Dispersions: A Review of Amorphization, Crystallization, Stabilization, Solid-State Characterization, and Aqueous Solubilization of Biopharmaceutical Classification System Class II Drug, J. Pharm. Sci., 2016, 105, 2527–2544 CrossRef CAS PubMed.
- P. Gao, Amorphous Pharmaceutical Solids: Characterization, Stabilization, and Development of Marketable Formulations of Poorly Soluble Drugs with Improved Oral Absorption, Mol. Pharm., 2008, 5, 903–904 CrossRef CAS PubMed.
- For example: Y. Aso, S. Yoshioka and S. Kojima, Molecular Mobility-Based Estimation of the Crystallization Rates of Amorphous Nifedipine and Phenobarbital in poly(vinylpyrrolidone) Solid Dispersions, J. Pharm. Sci., 2004, 93, 384–391 CrossRef CAS PubMed.
- F. Qashu, T. H. Figueiredo, V. Aroniadou-Anderjaska, J. P. Apland and M. F. Braga, Diazepam Administration After Prolonged Status Epilepticus Reduces Neurodegeneration in the Amygdala but not in the Hippocampus During Epileptogenesis, Amino Acids, 2010, 38, 189–197 CrossRef CAS PubMed.
- J. Mielcarek, D. M. Nowak, A. Pajzderska, B. Peplinska and J. Wasicki, A Hybrid Method for Estimation of Molecular Dynamics of Diazepam-Density Functional Theory Combined with NMR and FT-IR spectroscopy, Int. J. Pharm. Res. Scholars, 2011, 404, 19–26 CAS.
- J. Wąsicki, D. P. Kozlenko, S. E. Pankov, P. Bilski, A. Pajzderska, B. C. Hancock, A. Medek, W. Nawrocik and B. N. Savenko, NMR Search for Polymorphic Phase Transformations in Chlorpropamide form-A at High Pressures, J. Pharm. Sci., 2009, 98, 1426–1437 CrossRef PubMed.
- A. Pajzderska, D. M. Chudoba, J. Mielcarek and J. Wasicki, Calorimetric, FTIR and 1H NMR Measurements in Combination with DFT Calculations for Monitoring Solid-State Changes of Dynamics of Sibutramine Hydrochloride, J. Pharm. Sci., 2012, 101, 3799–3810 CrossRef CAS PubMed.
- E. R. Andrew, B. Peplinska and M. Kempka, Molecular Dynamics in Solid l-adrenaline by Proton NMR, Solid State Nucl. Magn. Reson., 1998, 10, 117–121 CrossRef CAS PubMed.
- C. Smuda, S. Busch, R. Schellenberg and T. Unruh, Methyl Group Dynamics in Polycrystalline and Liquid Ubiquinone Q0 Studied by Neutron Scattering, J. Phys. Chem. B, 2009, 113, 916–922 CrossRef CAS PubMed.
- A. Pajzderska, M. Jarek, J. Mielcarek and J. Wasicki, Analysis of the Distribution of Energy Barriers in Amorphous Diazepam on the Basis of Computationally Supported NMR Relaxation Data, J. Phys. Chem. B, 2016, 120, 10723–10728 CrossRef CAS PubMed.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, DL_POLY_3: New Dimensions In Molecular Dynamics Simulations via Massive Parallelism, J. Mater. Chem., 2006, 16, 1911–1918 RSC.
- A. Camerman and N. Camerman, Stereochemical Basis of Anticonvulsant Drug Action. II. Molecular Structure of Diazepamu, J. Am. Chem. Soc., 1972, 94, 268–272 CrossRef CAS PubMed.
- Materials Studio Modelling Environment, Version 6.5, Accelrys, Inc., San Diego, CA, 2009 Search PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. van Gunsteren, A. DiNola and J. R. Haak, Molecular Dynamics with Coupling to an External Bath, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS.
- P. Dauber-Osguthorpe, V. A. Roberts, D. J. Osguthorpe, J. Wolff, M. Genest and A. T. Hagler, Structure and energetics of ligand binding to proteins: Escherichia coli dihydrofolate reductase-trimethoprim, a drug-receptor system, Proteins: Struct., Funct., Genet., 1988, 4, 31–47 CrossRef CAS PubMed.
- K. Hinsen, E. Pellegrini, S. Stachura and G. R. Kneller, nMoldyn 3: Using Task Farming for a Parallel Spectroscopy-oriented Analysis of Molecular Dynamics Simulations, J. Comput. Chem., 2012, 33, 2043–2048 CrossRef CAS PubMed.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, DAVE: A Comprehensive Software Suite for the Reduction, Visualization, and Analysis of Low Energy Neutron Spectroscopic Data, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358 CrossRef CAS PubMed.
- D. Richard, M. Ferrand and G. J. Kearley, Analysis and Visualisation of Neutron-Scattering Data, J. Neutron Res., 1996, 4, 33–39 CrossRef.
- M. Bee, Quasielastic Neutron Scattering: Principles and Applications in Solid State Chemistry, Biology, and Material Science, Adam Hilger, Bristol, Philadelphia, 1988 Search PubMed.
- A. Chahid, A. Alegría and J. Colmenero, Methyl Group Dynamics in Poly(vinyl methyl ether). A Rotation Rate Distribution Model, Macromolecules, 1994, 27, 3282–3288 CrossRef CAS.
- A. C. Genix, A. Arbe, J. Colmenero, J. Wuttke and D. Richter, Neutron Scattering and X-ray Investigation of the Structure and Dynamics of Poly(ethyl methacrylate), Macromolecules, 2012, 45, 2522–2536 CrossRef CAS.
- F. Alvarez, A. Alegría and J. Colmenero, Origin of the Distribution of Potential Barriers for Methyl Group Dynamics in Glassy Polymers: A Molecular Dynamics Simulation in Polyisoprene, Macromolecules, 2000, 33, 8077–8084 CrossRef CAS.
- A. J. Moreno, A. Alegria and J. Colmenero, Methyl Group Dynamics in Glassy Toluene: A Neutron Scattering Study, J. Chem. Phys., 2001, 115, 8958–8966 CrossRef CAS.
- A. J. Moreno, A. Alegrıa, J. Colmenero and B. Frick, Methyl Group Dynamics from Tunneling to Hopping in NaCH3CO2·3H2O: Comparison Between a Crystal and its Glassy Counterpart, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 134202 CrossRef.
- R. Zorn, M. Mayorova, D. Richter and B. Frick, Inelastic Neutron Scattering Study of a Glass-Forming Liquid in Soft confinement, Soft Matter, 2008, 4, 522–533 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra06133a |
| This journal is © The Royal Society of Chemistry 2017 |