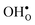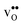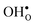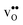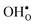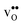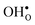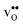On the relationship between chemical expansion and hydration thermodynamics of proton conducting perovskites
Received
10th December 2015
, Accepted 26th February 2016
First published on 1st March 2016
Abstract
In this contribution, we determine the compositional dependence of the chemical expansion and entropy of hydration of the proton conducting perovskites BaZrO3, BaSnO3, BaCeO3, and SrZrO3 by first principles phonon calculations. The calculations reveal that the cubic BaZrO3 and BaSnO3, which display the least favourable hydration enthalpies, −72 and −65 kJ mol−1, respectively, exhibit the most favourable entropies, −108 and −132 J mol−1 K−1, respectively. The strong compositional dependency of the hydration entropy primarily originates from the entropy gain upon filling the oxygen vacancy, which is closely related to the chemical expansion coefficient of oxygen vacancies, and thus the chemical expansion upon hydration. The chemical expansion coefficient of oxygen vacancies is more negative for the cubic than the orthorhombic perovskites, leading to a considerably larger chemical expansion upon hydration of the former. The calculations therefore suggest that challenges associated with chemical expansion upon hydration of BaZrO3 proton conducting electrolytes to some extent can be avoided, or reduced, by partial substitution of Zr by Ce.
1 Introduction
Protons dissolve in many oxides1 through hydration of oxygen vacancies, resulting in high temperature proton conduction with potentials for important applications such as in fuel cells and gas separation membranes. The relative dominance of protons and oxygen vacancies is determined by the enthalpy and entropy of the hydration reaction| | 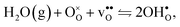 | (1) |
with the corresponding equilibrium constant:| | 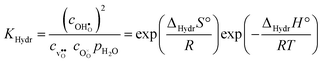 | (2) |
where ci are the molar concentrations of protons, oxygen vacancies, and lattice oxygen species. The enthalpy of this reaction can be evaluated by both indirect2 and direct measurements,3–5 or computationally, and correlates with various materials' parameters.5–9 The entropy on the other hand, has never been measured directly, and its nature and compositional dependence is in general poorly understood. We recently determined ΔHydrS° of BaZrO3 computationally,10 and revealed that its major contribution is the vibrational entropy of oxygen vacancies 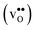 , in addition to loss of water vapour. Although the vibrational contribution from protons was found to be small, there is a significant configurational contribution due to their site degeneracy around the oxide ions in the perovskite structure. In this contribution, we continue our efforts to understand the entropy of hydration, by for the first time assessing its compositional dependence and relationship with the chemical expansion, computationally.
, in addition to loss of water vapour. Although the vibrational contribution from protons was found to be small, there is a significant configurational contribution due to their site degeneracy around the oxide ions in the perovskite structure. In this contribution, we continue our efforts to understand the entropy of hydration, by for the first time assessing its compositional dependence and relationship with the chemical expansion, computationally.
ΔHydrH° has been shown to correlate with material specific parameters such as the difference in the electronegativity of the B- and A-site cations8 and the tolerance factor,9 which has been argued to reflect its dependence on the basicity, or partial charge density of the oxide ions.7,11 ΔHydrS°, however, seemingly does not display any similar correlations,8 which partly may stem from the large scatter in the experimental range of values. Further, the compositional dependence of ΔHydrS° is less intuitive than that of ΔHydrH° as it is related to both the chemical expansion of the material upon 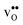 and
and 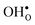 formation, the bonding strengths of H+ and O2−, and the local structural relaxations induced by the two defects.
formation, the bonding strengths of H+ and O2−, and the local structural relaxations induced by the two defects.
To assess the compositional and structural dependency of ΔHydrS°, we evaluate the vibrational formation entropies of 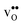 and
and 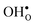 from first principles phonon calculations, and the configurational contribution originating from the site degeneracy of protons (and oxygen vacancies). We have chosen to focus on four structurally different proton conducting perovskites; BaZrO3, BaSnO3, BaCeO3 and SrZrO3. The two former take on a cubic structure (Pm
from first principles phonon calculations, and the configurational contribution originating from the site degeneracy of protons (and oxygen vacancies). We have chosen to focus on four structurally different proton conducting perovskites; BaZrO3, BaSnO3, BaCeO3 and SrZrO3. The two former take on a cubic structure (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), while the two latter adopt an orthorhombic structure (Pnma), thus allowing us to judge the effect of both symmetry and composition on ΔHydrS°. As shown in Table 1, the experimental ΔHydrH° and ΔHydrS° for these perovskites cover a wide range of values, with the cubic BaZrO3 and BaSnO3 exhibiting the least exothermic ΔHydrH°, but also the least negative (most favourable) ΔHydrS°.
m), while the two latter adopt an orthorhombic structure (Pnma), thus allowing us to judge the effect of both symmetry and composition on ΔHydrS°. As shown in Table 1, the experimental ΔHydrH° and ΔHydrS° for these perovskites cover a wide range of values, with the cubic BaZrO3 and BaSnO3 exhibiting the least exothermic ΔHydrH°, but also the least negative (most favourable) ΔHydrS°.
Table 1 Selected experimentally determined hydration enthalpies (ΔHydrH°) and entropies (ΔHydrS°) of acceptor doped BaZrO3, BaSnO3, BaCeO3 and SrZrO3
|
|
ΔHydrH° (kJ mol−1) |
ΔHydrS° (J mol−1 K−1) |
|
BaZrO
3
|
| 10 mol% Y6 |
−80 |
−89 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
BaSnO
3
|
| 5 mol% Y12 |
−46 |
−95 |
| 12.5 mol% Y12 |
−50 |
−88 |
| 12.5 mol% Y13 |
−59 |
−97 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
BaCeO
3
|
| 10 mol% Y2 |
−162 |
−167 |
| 10 mol% Y11 |
−135 |
−141 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
SrZrO
3
|
| 5 mol% Yb14 |
−106 |
−127 |
First principles phonon calculations allow us to determine both ΔHydrH° and ΔHydrS° as a function of temperature, and explore the individual contributions that constitute both thermodynamic parameters. The calculations are performed under constant volume and/or constant/zero pressure conditions, in order to separate contributions from local relaxations and chemical expansion to the vibrational entropies.
2 Thermodynamic formalism
2.1 Defect formation thermodynamics
The free energy of defect formation, ΔFFdefect (or ΔFGdefect) is given by| | 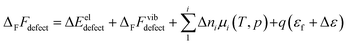 | (3) |
where ΔEeldefect is the total energy difference between the defective and perfect supercells, while ΔFFvibdefect is the vibrational (phonon) contribution to the formation energy. Further, Δni is the change in the number of atoms i with chemical potential μi, q is the effective charge of the defect, εf is the Fermi level and Δε aligns the core potentials of the perfect and the defective supercells to remedy shifts in the band edges due to the jellium background charge. The chemical potential of H2O is given by| | 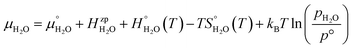 | (4) |
where the zero-point energy 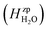 , is obtained from the calculated vibrational frequency of a H2O molecule, while
, is obtained from the calculated vibrational frequency of a H2O molecule, while 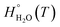 and
and 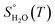 are taken from thermodynamic tables.15 The standard chemical potential,
are taken from thermodynamic tables.15 The standard chemical potential, 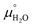 , is set to the calculated total electronic energy of the isolated H2O molecule.
, is set to the calculated total electronic energy of the isolated H2O molecule.
The contribution from phonons to the free energy, Fvib(T) or Gvib(T), and entropy, Svib(T), is in the harmonic approximation given by
| | 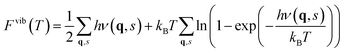 | (5) |
| | 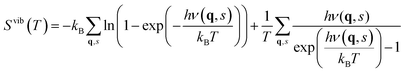 | (6) |
where
ν(
q,
s) are the phonon frequencies throughout the
q-space. Although the vibrational frequencies in principle should be evaluated at all
q-points, the phonon spectra for the defective cells were only evaluated at the
Γ-point of the defective supercells due to their large sizes. From
eqn (6), the vibrational formation entropy of a defect is simply
| | | ΔFSvibdefect = Svibdefect(T) − Svibbulk(T), | (7) |
and similar for Δ
FHvibdefect, and Δ
FFvibdefect or Δ
FGvibdefect. Note that we are assuming a negligible change in the thermal expansion coefficient upon defect formation, such that Δ
FSvibdefect and Δ
FGvibdefect calculated by full volume relaxations represent zero/constant pressure properties. We are currently also exploring anharmonic contributions to the defect formation entropies and thermal expansion of BaCeO
3 in more detail, which indicate that these contributions are of minor importance for the defect thermodynamics of BaCeO
3.
2.2 Hydration thermodynamics
The enthalpy and entropy of hydration according to eqn (1) can readily be determined from eqn (3)–(7):| | 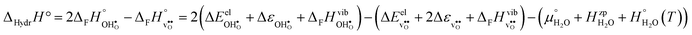 | (8) |
| | 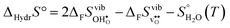 | (9) |
Upon experimental determination of ΔHydrS° by curve fitting of eqn (2) to e.g. water uptake data from thermogravimetric measurements, it is usually assumed that the number of regular positions for 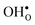 and
and 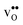 equal the number of oxide ions per formula unit.2 For perovskites,
equal the number of oxide ions per formula unit.2 For perovskites, 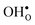 is normally found to take on a number of different configurations around each oxide ion, depending on the crystal structure. Further, in oxides where
is normally found to take on a number of different configurations around each oxide ion, depending on the crystal structure. Further, in oxides where 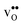 preferentially forms on one of the several structurally distinct oxide ions, the number of regular positions for
preferentially forms on one of the several structurally distinct oxide ions, the number of regular positions for 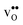 is lower than the concentration of O lattice sites. The number of proton positions (NH) around each oxide ion and the number of vacancy configurations (Nv) affect the chemical potential of
is lower than the concentration of O lattice sites. The number of proton positions (NH) around each oxide ion and the number of vacancy configurations (Nv) affect the chemical potential of 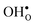 and
and 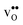 , and thus KHydr. Not accounting for these configurations when evaluating defect thermodynamics by curve fitting results in an apparent hydration entropy, ΔHydrS°app, which, in addition to the vibrational contributions, also includes configurational contributions:
, and thus KHydr. Not accounting for these configurations when evaluating defect thermodynamics by curve fitting results in an apparent hydration entropy, ΔHydrS°app, which, in addition to the vibrational contributions, also includes configurational contributions:
| | 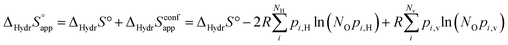 | (10) |
NO is the number of oxide ions per formula unit, while
pi,H and
pi,v are the conditional probabilities for occupation of each configuration at an oxide ion by
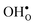
and
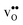
, respectively. The general expression for the probability of occupation of a given configuration is for instance for the proton given by
| | 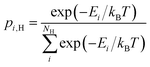 | (11) |
where
Ei are the relative energies of the different
NH configurations around the
NO oxide ions (3 for perovskites). It is important to note that Δ
HydrSconfapp in
eqn (10) only accounts for the configurational contributions stemming from distributing a proton or an oxygen vacancy over
NH and
Nv configurations at one specific oxide ion, as the remaining contributions are accounted for through the mass action law (
eqn (2)). At higher temperatures or in perovskites where the different
NH and
Nv are degenerate,
eqn (10) converges to
| | ΔHydrS°app = ΔHydrS° + 2R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(NH) ln(NH) | (12) |
3 Computational details
The first principles calculations are performed with the plane-wave Density Functional Theory (DFT) approach within the VASP (v.5.3.5) code,16,17 at the GGA-PBE18 and/or LDA19 level with a constant plane-wave cut-off energy of 500 eV. For the cubic BaZrO3 and BaSnO3, all defect calculations were performed with 3 × 3 × 3 (135 atoms) supercell expansions, while 2 × 2 × 2 supercells (160 atoms) were used for orthorhombic BaCeO3 and SrZrO3. Electronic integration was performed using a 2 × 2 × 2 Monkhorst-Pack k-mesh over the supercell. Further, all calculations were performed using a reciprocal projection scheme, with ionic and electronic convergence criteria of 10−4 eV Å−1 and 10−8 eV, respectively. The number of electrons in the supercell was adjusted to simulate the desired charge state of the defects, which was compensated by a homogeneous, opposite background charge. Finally, the defect calculations were performed both by fixing the volume to that of the defect-free bulk, or by relaxing both the supercell shape and its volume, in order to simulate constant volume, or zero/constant pressure conditions, respectively.
The phonon frequencies were calculated within the harmonic approximation using finite ionic displacements of ±0.01 Å. Fourier transform and diagonalisation of the dynamical matrix were performed using the phonopy code.20,21 While BaZrO3, BaCeO3 and SrZrO3 displayed no imaginary modes, BaSnO3 exhibited imaginary modes at the R-point of the Brillouin zone with the GGA-PBE functional. With the LDA functional however, all modes of BaSnO3 were found to be positive and this functional was therefore chosen to avoid erroneous contributions to the vibrational thermodynamics. All electronic contributions to the defect thermodynamics were, however, evaluated with the GGA-PBE functional – for consistency.
Table 2 shows the calculated lattice parameters and unit cell volumes of the four included perovskites. As is typically observed, GGA consistently overestimates the lattice parameters slightly, while the LDA parameters for BaSnO3 are somewhat underestimated.
Table 2 Calculated lattice parameters and unit cell volumes (per f.u.) for BaZrO3, BaSnO3, BaCeO3 and SrZrO3. For BaSnO3, the results refer to calculations with the LDA functional, while the GGA results are given in parentheses
|
|
BaZrO3 |
BaSnO3 |
BaCeO3 |
SrZrO3 |
| DFT |
Exp.22 |
DFT |
Exp.23 |
DFT |
Exp.24 |
DFT |
Exp.25 |
|
a (Å) |
4.236 |
4.19 |
4.096 (4.188) |
4.118 |
6.289 |
6.235 |
5.859 |
5.815 |
|
b (Å) |
— |
|
— |
|
8.865 |
8.781 |
8.254 |
8.196 |
|
c (Å) |
— |
|
— |
|
6.286 |
6.212 |
5.819 |
5.786 |
|
V (Å3) |
75.96 |
73.6 |
68.74 (73.44) |
69.83 |
87.62 |
85.03 |
70.83 |
68.94 |
4 Results and discussion
4.1 Site degeneracy and configurational entropy
The orientation of the protonic defect around each oxide ion has previously been shown to depend on the symmetry of the structure, but also on the lattice constant/volume of the unit cell.26 In BaZrO3, BaSnO3, BaCeO3 and SrZrO3, the proton takes on a position along the bisector of two O connecting lines and there are thus 4 proton positions per oxide ion.26–30 While these positions are degenerate in BaZrO3 and BaSnO3, they are non-degenerate in the orthorhombic BaCeO3 and SrZrO3. In the denser SrTiO3, on the other hand, protons have been argued to take on a position along the edge of the TiO6 polyhedra, resulting in 8 equivalent positions around each oxide ion.31,32 Our calculations are in general agreement with those of refs 26–30 showing that all included compositions exhibit proton positions at, or close to, the bisector of two oxygen connecting lines (see Fig. 1). The site is 4-fold degenerate in BaZrO3 and BaSnO3, while BaCeO3 and SrZrO3 display 4 unique minima around each of the O1 and O2 ions within 0.20 and 0.18 eV of each other, respectively (cf.Fig. 1 for SrZrO3). In BaCeO3 and SrZrO3, we also find that 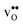 is favoured by merely 70 and 60 meV, for BaCeO3 and SrZrO3, respectively, at the O1 compared to the O2 site. As shown in Fig. 2, the non-degenerate proton and oxygen vacancy configurations in SrZrO3 and BaCeO3 render the configurational contribution to the hydration entropy temperature dependent. At the lowest temperatures, the contribution is actually negative due to the preference for occupation of the O1 site by oxygen vacancies. However, due to the small energy difference between the various proton and oxygen vacancy configurations, the configurational contribution approaches that for BaZrO3 even at ∼600 K. Both SrZrO3 and BaCeO3 also undergo several phase transitions upon heating, which may affect the relative stability of the different proton and vacancy configurations. Hence, the configurational contribution to ΔHydrS° is approximately 2R
is favoured by merely 70 and 60 meV, for BaCeO3 and SrZrO3, respectively, at the O1 compared to the O2 site. As shown in Fig. 2, the non-degenerate proton and oxygen vacancy configurations in SrZrO3 and BaCeO3 render the configurational contribution to the hydration entropy temperature dependent. At the lowest temperatures, the contribution is actually negative due to the preference for occupation of the O1 site by oxygen vacancies. However, due to the small energy difference between the various proton and oxygen vacancy configurations, the configurational contribution approaches that for BaZrO3 even at ∼600 K. Both SrZrO3 and BaCeO3 also undergo several phase transitions upon heating, which may affect the relative stability of the different proton and vacancy configurations. Hence, the configurational contribution to ΔHydrS° is approximately 2R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(4) (23 J K−1 mol−1) within the majority of the experimental temperature window (600–1100 K) for all included perovskites. Any compositional dependence of ΔHydrS°, in contrast to the conclusions of Tauer et al.,33 is therefore of a purely vibrational nature, and will be the focus in the remaining parts of this contribution.
ln(4) (23 J K−1 mol−1) within the majority of the experimental temperature window (600–1100 K) for all included perovskites. Any compositional dependence of ΔHydrS°, in contrast to the conclusions of Tauer et al.,33 is therefore of a purely vibrational nature, and will be the focus in the remaining parts of this contribution.
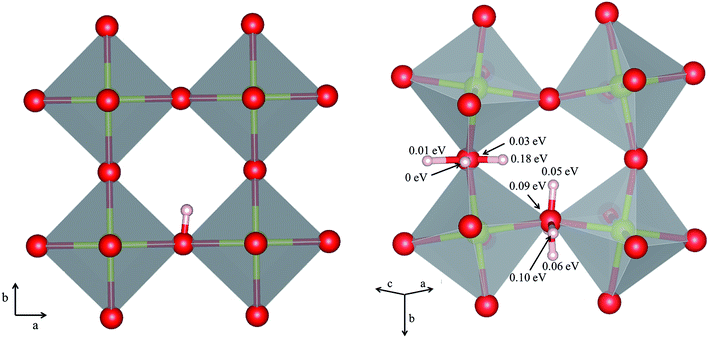 |
| | Fig. 1 Proton positions in (left) BaZrO3 and (right) SrZrO3 with b as the apical axis. For SrZrO3 we also report the stability (in eV) of the different configurations relative to the most stable configuration around the O1 ion. | |
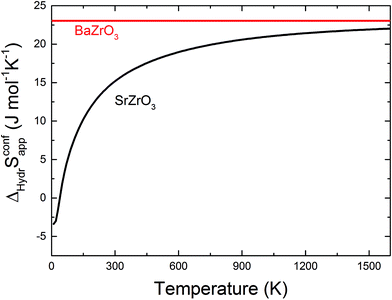 |
| | Fig. 2 Configurational contribution to ΔHydrS° when neglecting the site degeneracy of protons and oxygen vacancies (ΔHydrSconfapp) of BaZrO3 and SrZrO3 as a function of temperature according to eqn (10). | |
4.2 Chemical expansion
In our previous contribution on BaZrO3,10 the formation volume of a defect was shown to have major implications for its formation entropy under zero/constant pressure conditions. In addition, the formation volume determines the chemical expansion coefficient of defects, and thus also the chemical expansion of the material upon e.g. hydration (eqn (1)).
The normalised volumetric chemical expansion coefficient, εi, of a defect i is here taken as:34
| | 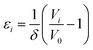 | (13) |
where
Vi and
V0 are the volumes of the defective and perfect supercells, respectively, while
δ is the defect concentration in mole fractions (1/27 for BaZrO
3 and BaSnO
3, and 1/32 for BaCeO
3 and SrZrO
3). Correspondingly, the chemical expansion upon hydration (
eqn (1)) may be quantified through
| | 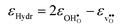 | (14) |
where
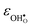
and
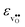
are the chemical expansion coefficients of
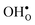
and
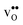
, respectively.
εHydr is thus given as the relative expansion upon hydration of 1 mole of
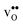
, and with respect to the volume of the
defect-free lattice. Experimentally, however, chemical expansion coefficients are taken as the relative volume of the hydrated and dry materials –
i.e. relative to the
defective lattice. Experimental
εHydr will therefore appear somewhat larger than those determined computationally in this work and in
e.g.ref. 34.
Table 3 shows the calculated chemical expansion coefficients and formation volumes of 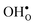 and
and 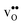 (both linear and volumetric), along with the chemical expansion upon hydration. All expansion coefficients are given per mole of formed defect. Both defects lead to anisotropic relaxations of the supercell for the four perovskites, even for the cubic BaZrO3 and BaSnO3, where
(both linear and volumetric), along with the chemical expansion upon hydration. All expansion coefficients are given per mole of formed defect. Both defects lead to anisotropic relaxations of the supercell for the four perovskites, even for the cubic BaZrO3 and BaSnO3, where 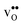 leads to a tetragonal cell, in line with experimental reports.7,35,36 For all compositions, both defects display negative formation volumes and are thus smaller than the native oxide ions, with
leads to a tetragonal cell, in line with experimental reports.7,35,36 For all compositions, both defects display negative formation volumes and are thus smaller than the native oxide ions, with 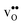 leading to a considerably larger contraction than
leading to a considerably larger contraction than 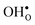 .
. 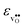 increases (less negative) notably in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, while
increases (less negative) notably in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, while 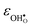 follows the opposite trend. The calculated εHydr are comparable with the experimentally determined values, although the experimental values vary considerably with the dopant concentration, and the adopted method (which most likely originates from uncertain proton concentrations). Hence, the compositional dependence of εHydr is somewhat unclear from the experimental values. Our calculated εHydr on the other hand decreases notably in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, which stems from both the decreasing
follows the opposite trend. The calculated εHydr are comparable with the experimentally determined values, although the experimental values vary considerably with the dopant concentration, and the adopted method (which most likely originates from uncertain proton concentrations). Hence, the compositional dependence of εHydr is somewhat unclear from the experimental values. Our calculated εHydr on the other hand decreases notably in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, which stems from both the decreasing 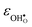 and the increasing
and the increasing 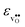 . Interestingly, these results therefore indicate that issues associated with the chemical expansion of BaZrO3 electrolytes upon hydration may for instance be reduced by adopting BaZrO3–BaCeO3 solid solutions.
. Interestingly, these results therefore indicate that issues associated with the chemical expansion of BaZrO3 electrolytes upon hydration may for instance be reduced by adopting BaZrO3–BaCeO3 solid solutions.
Table 3 Linear (εa, εb, εc) and volumetric (εi) chemical expansion coefficients, formation volumes (ΔFVi), of 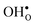 and
and 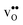 , and chemical expansion coefficient upon hydration (εHydr) for the included perovskites. The
, and chemical expansion coefficient upon hydration (εHydr) for the included perovskites. The 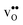 in BaZrO3 and BaSnO3 is aligned with the Zr(Sn)-
in BaZrO3 and BaSnO3 is aligned with the Zr(Sn)-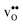 -Zr(Sn) axis parallel to the a-axis, while in BaCeO3 and SrZrO3 it is parallel to the b-axis. Note that the calculations on BaSnO3 are performed with the LDA functional
-Zr(Sn) axis parallel to the a-axis, while in BaCeO3 and SrZrO3 it is parallel to the b-axis. Note that the calculations on BaSnO3 are performed with the LDA functional
|
|
BaZrO3 |
BaSnO3 |
BaCeO3 |
SrZrO3 |
|
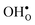
|
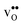
|
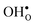
|
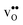
|
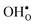
|
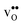
|
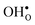
|
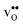
|
|
ε
i,a
|
0.0158 |
−0.0496 |
0.007 |
−0.0379 |
−0.0475 |
−0.1111 |
−0.0463 |
−0.1176 |
|
ε
i,b
|
−0.0566 |
−0.0952 |
−0.0540 |
−0.0973 |
−0.0429 |
−0.0688 |
−0.0110 |
−0.0323 |
|
ε
i,c
|
−0.0178 |
−0.0952 |
−0.0138 |
−0.0973 |
0.0238 |
−0.0454 |
−0.0116 |
−0.0560 |
| ΔFVi |
−4.44 Å3 |
−18.1 Å3 |
−4.14 Å3 |
−15.9 Å3 |
−5.86 Å3 |
−19.7 Å3 |
−4.87 Å3 |
−14.6 Å3 |
|
ε
i
|
−0.0587 |
−0.239 |
−0.060 |
−0.232 |
−0.067 |
−0.225 |
−0.069 |
−0.206 |
|
ε
Hydr
|
0.122 |
0.111 |
0.0911 |
0.068 |
|
ε
ExpHydr
|
0.160 (In doped),37
0.176 (Y doped),6
0.115–0.227 (Y doped)38
|
— |
0.030–0.099 (Yb doped),390.151 (Y doped)38 |
— |
4.3 Defect entropies
Fig. 3 shows the vibrational contribution to the formation entropy 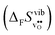 of
of 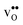 in SrZrO3 and BaZrO3 calculated under constant volume and zero/constant pressure conditions. For both compounds,
in SrZrO3 and BaZrO3 calculated under constant volume and zero/constant pressure conditions. For both compounds, 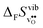 is negative, and significantly more negative under zero/constant pressure than under constant volume conditions – which stems from a blue shift of the phonon spectrum due to the negative formation volume of
is negative, and significantly more negative under zero/constant pressure than under constant volume conditions – which stems from a blue shift of the phonon spectrum due to the negative formation volume of 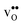 .10 Further, the effect is more noticeable for BaZrO3 than for SrZrO3, in line with the more negative formation volume of
.10 Further, the effect is more noticeable for BaZrO3 than for SrZrO3, in line with the more negative formation volume of 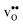 in BaZrO3. Similar effects of volume relaxation on
in BaZrO3. Similar effects of volume relaxation on 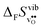 were also found for BaSnO3 and BaCeO3.
were also found for BaSnO3 and BaCeO3.
 |
| | Fig. 3
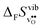 of SrZrO3 and BaZrO3 calculated under constant volume or zero/constant pressure (i.e., relaxed volume) conditions. of SrZrO3 and BaZrO3 calculated under constant volume or zero/constant pressure (i.e., relaxed volume) conditions. | |
Fig. 4 shows 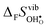 and
and 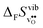 for the four included perovskites, calculated under zero/constant pressure conditions. For all compositions,
for the four included perovskites, calculated under zero/constant pressure conditions. For all compositions, 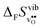 is significantly more negative than
is significantly more negative than 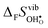 , and also shows a stronger compositional dependence. While all
, and also shows a stronger compositional dependence. While all 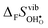 fall within 15 J mol−1 K−1 of each other throughout the temperature interval,
fall within 15 J mol−1 K−1 of each other throughout the temperature interval, 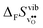 differs by as much as 80 J mol−1 K−1 at 1000 K between BaZrO3 and SrZrO3. The compositional variation of
differs by as much as 80 J mol−1 K−1 at 1000 K between BaZrO3 and SrZrO3. The compositional variation of 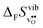 to some extent follows
to some extent follows 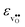 , with the two cubic perovskites, BaZrO3 and BaSnO3, displaying significantly more negative entropies than the orthorhombic SrZrO3 and BaCeO3. Hence, the compositional dependence of
, with the two cubic perovskites, BaZrO3 and BaSnO3, displaying significantly more negative entropies than the orthorhombic SrZrO3 and BaCeO3. Hence, the compositional dependence of 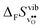 partly stems from the changes in
partly stems from the changes in 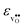 through the series, and partly from varying local structural relaxations around the defect (as reflected by the compositional dependence of
through the series, and partly from varying local structural relaxations around the defect (as reflected by the compositional dependence of 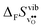 under constant volume conditions, see Fig. 3).
under constant volume conditions, see Fig. 3).
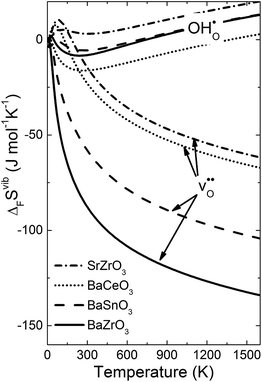 |
| | Fig. 4 Calculated 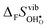 and and 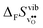 for the four included perovskites calculated under zero/constant pressure conditions. for the four included perovskites calculated under zero/constant pressure conditions. | |
4.4 Hydration thermodynamics
Fig. 5 compares the calculated enthalpies (a) and entropies (b) of hydration according to eqn (1) for BaZrO3, BaSnO3, SrZrO3 and BaCeO3. Interestingly, the vibrational contribution to ΔHydrH° results in a slight temperature dependence, and ΔHydrH° therefore becomes less negative with increasing temperature for all compositions. Experimentally, ΔHydrH° is determined from eqn (2) over a wide temperature interval such that the temperature dependence of ΔHydrH° (and ΔHydrS°) is not observed. In a recent work,3 we indicated, from combined thermogravimetric measurements of water uptake and differential scanning calorimetry (TG-DSC), that ΔHydrH° of Sc and In doped BaTiO3 actually displays weak temperature dependencies in accordance with Fig. 5. The experimentally determined ΔHydrH° and ΔHydrS° listed in Table 1 should therefore be compared with the temperature averaged ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° and ΔHydr
° and ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° from linearisation of the computational ΔHydrG° vs. T (see Table 4). For comparative reasons, ΔHydr
° from linearisation of the computational ΔHydrG° vs. T (see Table 4). For comparative reasons, ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) °app values in Table 4 represent the temperature averaged apparent entropy of hydration, i.e. including the configurational contribution according to eqn (11) (23 J mol−1 K−1 for all compositions).
°app values in Table 4 represent the temperature averaged apparent entropy of hydration, i.e. including the configurational contribution according to eqn (11) (23 J mol−1 K−1 for all compositions).
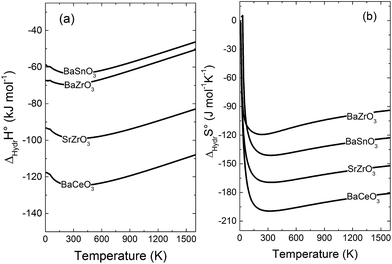 |
| | Fig. 5 Calculated (a) enthalpy and (b) entropy of hydration of BaZrO3, BaSnO3, SrZrO3 and BaCeO3. | |
Table 4 Temperature averaged standard hydration enthalpy and entropy of BaZrO3, BaSnO3, SrZrO3 and BaCeO3. For consistency with experimental values, a constant configurational contribution of 23 J mol−1 K−1 to ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° has been included for all compositions
° has been included for all compositions
|
|
ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° (kJ mol−1) ° (kJ mol−1) |
ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) °app (J mol−1 K−1) °app (J mol−1 K−1) |
| BaZrO3 |
−65 |
−84 |
| BaSnO3 |
−60 |
−109 |
| SrZrO3 |
−97 |
−141 |
| BaCeO3 |
−122 |
−171 |
The ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° values are, as expected, very close to the low temperature ΔHydrH° in Fig. 5, and are in reasonable agreement with the experimental ranges of enthalpies for all compositions in Table 1. The calculated values also reflect the experimentally observed compositional dependence, with the two cubic perovskites displaying significantly less exothermic enthalpies than the two orthorhombic members. Also the calculated ΔHydr
° values are, as expected, very close to the low temperature ΔHydrH° in Fig. 5, and are in reasonable agreement with the experimental ranges of enthalpies for all compositions in Table 1. The calculated values also reflect the experimentally observed compositional dependence, with the two cubic perovskites displaying significantly less exothermic enthalpies than the two orthorhombic members. Also the calculated ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° values are in good agreement with the experimental values in Table 1. The entropies display a distinct compositional dependence, and are in general less negative for the cubic BaZrO3 and BaSnO3 than for the orthorhombic SrZrO3 and BaCeO3. The less negative ΔHydrS° of BaZrO3 and BaSnO3 stabilises protons compared to in the orthorhombic BaCeO3 and SrZrO3, in line with Kreuer's remark that the favourable proton transport properties of BaZrO3 stems from entropic stabilisation of protons.6 As noted in Fig. 3,
° values are in good agreement with the experimental values in Table 1. The entropies display a distinct compositional dependence, and are in general less negative for the cubic BaZrO3 and BaSnO3 than for the orthorhombic SrZrO3 and BaCeO3. The less negative ΔHydrS° of BaZrO3 and BaSnO3 stabilises protons compared to in the orthorhombic BaCeO3 and SrZrO3, in line with Kreuer's remark that the favourable proton transport properties of BaZrO3 stems from entropic stabilisation of protons.6 As noted in Fig. 3, 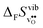 is the dominant vibrational contribution to ΔHydrS°, and also shows a stronger compositional dependency than
is the dominant vibrational contribution to ΔHydrS°, and also shows a stronger compositional dependency than 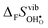 . Hence, one may argue that the entropic stabilisation of protons in BaZrO3/BaSnO3 is, more precisely, a result of entropic destabilisation of
. Hence, one may argue that the entropic stabilisation of protons in BaZrO3/BaSnO3 is, more precisely, a result of entropic destabilisation of 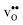 .
.
Turning to the hydration enthalpy, the strong compositional dependency (cf.Table 4) is generally in line with experimental observations; orthorhombic perovskites exhibit more exothermic values than the cubic, i.e. it becomes more exothermic with a decreasing electronegativity difference between the B- and A-site cations, but also with a decreasing Goldschmidt tolerance factor.8,9 These correlations are usually attributed to the basicity/ionicity of the oxide, which affects the bonding strength of 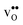 and
and 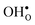 ; the oxide with the most exothermic hydration enthalpies exhibits the most stable protonic defects, and the most unstable oxygen vacancies (i.e. most stable oxide ions). There is further a striking correlation between both the calculated and experimental ΔHydr
; the oxide with the most exothermic hydration enthalpies exhibits the most stable protonic defects, and the most unstable oxygen vacancies (i.e. most stable oxide ions). There is further a striking correlation between both the calculated and experimental ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° and ΔHydr
° and ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° values, with the compound displaying the most exothermic ΔHydr
° values, with the compound displaying the most exothermic ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° (BaCeO3) also displaying the most negative (least favorable) ΔHydr
° (BaCeO3) also displaying the most negative (least favorable) ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) °. The correlation between ΔHydr
°. The correlation between ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° and ΔHydr
° and ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° is far from intuitive since ΔHydr
° is far from intuitive since ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° depends on both
° depends on both 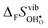 and
and 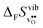 , neither of which correlate directly with either
, neither of which correlate directly with either 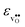 ,
, 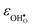 or εHydr, or the volume of the unit cells, as one might expect. The contributions to
or εHydr, or the volume of the unit cells, as one might expect. The contributions to 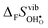 and
and 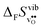 are related to both the vibrational frequency of protons and oxide ions, local relaxations upon protonation and filling of the
are related to both the vibrational frequency of protons and oxide ions, local relaxations upon protonation and filling of the 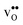 , in addition to the chemical expansion of the unit cell upon hydration. These properties can again be related to the size of the cations in the perovskite structure (which determines the unit cell volume and symmetry), and their electronegativity (which determines the interatomic bonding strengths), which – somewhat speculatively – explains the observed correlation between ΔHydr
, in addition to the chemical expansion of the unit cell upon hydration. These properties can again be related to the size of the cations in the perovskite structure (which determines the unit cell volume and symmetry), and their electronegativity (which determines the interatomic bonding strengths), which – somewhat speculatively – explains the observed correlation between ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° and ΔHydr
° and ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) °. Conclusively, the oxide exhibiting the most stable protons and least stable vacancies enthalpy-wise, also exhibits weaker entropic destabilisation of vacancies, and thus the least favourable entropies of hydration.
°. Conclusively, the oxide exhibiting the most stable protons and least stable vacancies enthalpy-wise, also exhibits weaker entropic destabilisation of vacancies, and thus the least favourable entropies of hydration.
5 Conclusions
We have in this work assessed the thermodynamics of hydration, with emphasis on vibrational contributions, and the chemical expansion of the four proton conducting perovskites BaZrO3, BaSnO3, BaCeO3 and SrZrO3 from first principles phonon calculations. The calculations show that both 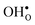 and
and 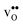 are smaller than the native oxide ions in all materials. Further,
are smaller than the native oxide ions in all materials. Further, 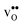 is significantly smaller than the proton and is therefore the main contributor to the chemical expansion of the materials upon hydration. The chemical expansion shows a distinct compositional dependence, and decreases in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3. As such, proton conducting electrolytes composed of BaZrO3–BaCeO3 or BaZrO3–SrZrO3 solid solutions should be less prone to issues stemming from chemical expansion upon hydration than pure BaZrO3 electrolytes. There is further a significant contribution from phonons to the formation entropy of both
is significantly smaller than the proton and is therefore the main contributor to the chemical expansion of the materials upon hydration. The chemical expansion shows a distinct compositional dependence, and decreases in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3. As such, proton conducting electrolytes composed of BaZrO3–BaCeO3 or BaZrO3–SrZrO3 solid solutions should be less prone to issues stemming from chemical expansion upon hydration than pure BaZrO3 electrolytes. There is further a significant contribution from phonons to the formation entropy of both 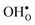 and
and 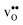 . The contribution is most pronounced for
. The contribution is most pronounced for 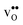 , and negative for all compositions, and becomes less negative in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, i.e. with increasing (less negative) chemical expansion of
, and negative for all compositions, and becomes less negative in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, i.e. with increasing (less negative) chemical expansion of 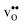 . Both the calculated ΔHydrH° and ΔHydrS° are in good agreement with the experimental ranges of values, and display a distinct compositional dependence. ΔHydrS° is in general less negative (more favourable) for the cubic BaZrO3 and BaSnO3 than the orthorhombic members, reflecting its dependence on the vibrational formation entropy, and again the chemical expansion, of
. Both the calculated ΔHydrH° and ΔHydrS° are in good agreement with the experimental ranges of values, and display a distinct compositional dependence. ΔHydrS° is in general less negative (more favourable) for the cubic BaZrO3 and BaSnO3 than the orthorhombic members, reflecting its dependence on the vibrational formation entropy, and again the chemical expansion, of 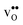 . Interestingly, there is a general correlation between ΔHydrH° and ΔHydrS°; the two cubic members display the least exothermic ΔHydrH°, but also the least negative (and thus most favourable) ΔHydrS° – an effect which may stem from both parameters being related to the bonding strengths of O2− and H+.
. Interestingly, there is a general correlation between ΔHydrH° and ΔHydrS°; the two cubic members display the least exothermic ΔHydrH°, but also the least negative (and thus most favourable) ΔHydrS° – an effect which may stem from both parameters being related to the bonding strengths of O2− and H+.
Acknowledgements
The authors gratefully acknowledge the Research Council of Norway (RCN), project “HydraThermPro” (project number 214252), and the Centre for Materials Science and Nanotechnology, for financial support. We also thank the Norwegian Metacenter for Computational Science (NOTUR) for computational resources and excellent support (project NN4604k).
References
- H. Iwahara, T. Esaka, H. Uchida and N. Maeda, Solid State Ionics, 1981, 3–4, 359–363 CrossRef CAS.
- K. D. Kreuer, Solid State Ionics, 1999, 125, 285–302 CrossRef CAS.
- T. S. Bjørheim, S. M. H. Rahman, S. G. Eriksson, C. S. Knee and R. Haugsrud, Inorg. Chem., 2015, 54, 2858–2865 CrossRef PubMed.
- C. Kjølseth, L.-Y. Wang, R. Haugsrud and T. Norby, Solid State Ionics, 2010, 181, 1740–1745 CrossRef.
- A. Løken, C. Kjølseth and R. Haugsrud, Solid State Ionics, 2014, 267, 61–67 CrossRef.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- K. D. Kreuer, S. Adams, W. Münch, A. Fuchs, U. Klock and J. Maier, Solid State Ionics, 2001, 145, 295–306 CrossRef CAS.
- T. Norby, M. Widerøe, R. Glöckner and Y. Larring, Dalton Trans., 2004, 3012–3018 RSC.
- T. S. Bjørheim, A. Kuwabara, I. Ahmed, R. Haugsrud, S. Stølen and T. Norby, Solid State Ionics, 2010, 181, 130–137 CrossRef.
- T. S. Bjørheim, E. A. Kotomin and J. Maier, J. Mater. Chem. A, 2015, 3, 7639–7648 Search PubMed.
- A. Løken, T. S. Bjørheim and R. Haugsrud, J. Mater. Chem. A, 2015, 3, 23289–23298 Search PubMed.
- Y. Wang, A. Chesnaud, E. Bevillon and G. Dezanneau, Solid State Ionics, 2012, 214, 45–55 CrossRef CAS.
- Y. Wang, A. Chesnaud, E. Bevillon, J. Yang and G. Dezanneau, Int. J. Hydrogen Energy, 2011, 36, 7688–7695 CrossRef CAS.
- F. Krug and T. Schober, J. Am. Ceram. Soc., 1997, 80, 794–796 CrossRef CAS.
-
M. W. Chase Jr, Nist-janaf Thermochemical Tables, The American Institute of Physics for The National Institute of Standards and Technology, New York, 4th edn, 1998 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- I. Levin, T. G. Amos, S. M. Bell, L. Farber, T. A. Vanderah, R. S. Roth and B. H. Toby, J. Solid State Chem., 2003, 175, 170–181 CrossRef CAS.
- E. Bévillon, A. Chesnaud, Y. Wang, G. Dezanneau and G. Geneste, J. Phys.: Condens. Matter, 2008, 20, 145217 CrossRef.
- A. J. Jacobson, B. C. Tofield and B. E. F. Fender, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 956–961 CrossRef CAS.
- A. Ahtee, M. Ahtee, A. M. Glazer and A. W. Hewat, Acta Crystallogr., Sect. B: Struct. Crystallogr.
Cryst. Chem., 1976, 32, 3243–3246 CrossRef.
- J. Hermet, M. Torrent, F. Bottin, G. Dezanneau and G. Geneste, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104303 CrossRef.
- M. E. Björketun, P. G. Sundell and G. Wahnström, Faraday Discuss., 2007, 134, 247–265 RSC.
- G. Geneste, A. Ottochian, J. Hermet and G. Dezanneau, Phys. Chem. Chem. Phys., 2015, 17, 19104–19118 RSC.
- R. A. Davies, M. S. Islam and J. D. Gale, Solid State Ionics, 1999, 126, 323–335 CrossRef CAS.
- R. Hempelmann, M. Soetratmo, O. Hartmann and R. Wäppling, Solid State Ionics, 1998, 107, 269–280 CrossRef CAS.
- M. Cherry, M. S. Islam, J. D. Gale and C. R. A. Catlow, J. Phys. Chem., 1995, 99, 14614–14618 CrossRef CAS.
- E. Matsushita and T. Sasaki, Solid State Ionics, 1999, 125, 31–37 CrossRef CAS.
- T. Tauer, R. O'Hayre and J. W. Medlin, Solid State Ionics, 2011, 204–205, 27–34 CrossRef CAS.
- E. Jedvik, A. Lindman, M. Benediktsson and G. Wahnström, Solid State Ionics, 2015, 275, 2–8 CrossRef CAS.
- K. D. Kreuer, Annu. Rev. Mater. Res., 2003, 33, 333–359 CrossRef CAS.
- F. Giannici, M. Shirpour, A. Longo, A. Martorana, R. Merkle and J. Maier, Chem. Mater., 2011, 23, 2994–3002 CrossRef CAS.
- F. G. Kinyanjui, S. T. Norberg, I. Ahmed, S. G. Eriksson and S. Hull, Solid State Ionics, 2012, 225, 312–316 CrossRef CAS.
- A. K. E. Andersson, S. M. Selbach, C. S. Knee and T. Grande, J. Am. Ceram. Soc., 2014, 97, 2654–2661 CrossRef CAS.
- Y. Yamazaki, F. Blanc, Y. Okuyama, L. Buannic, J. C. Lucio-Vega, C. P. Grey and S. M. Haile, Nat. Mater., 2013, 12, 647–651 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
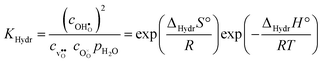
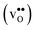 , in addition to loss of water vapour. Although the vibrational contribution from protons was found to be small, there is a significant configurational contribution due to their site degeneracy around the oxide ions in the perovskite structure. In this contribution, we continue our efforts to understand the entropy of hydration, by for the first time assessing its compositional dependence and relationship with the chemical expansion, computationally.
, in addition to loss of water vapour. Although the vibrational contribution from protons was found to be small, there is a significant configurational contribution due to their site degeneracy around the oxide ions in the perovskite structure. In this contribution, we continue our efforts to understand the entropy of hydration, by for the first time assessing its compositional dependence and relationship with the chemical expansion, computationally.
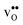 and
and 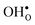 formation, the bonding strengths of H+ and O2−, and the local structural relaxations induced by the two defects.
formation, the bonding strengths of H+ and O2−, and the local structural relaxations induced by the two defects.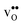 and
and 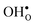 from first principles phonon calculations, and the configurational contribution originating from the site degeneracy of protons (and oxygen vacancies). We have chosen to focus on four structurally different proton conducting perovskites; BaZrO3, BaSnO3, BaCeO3 and SrZrO3. The two former take on a cubic structure (Pm
from first principles phonon calculations, and the configurational contribution originating from the site degeneracy of protons (and oxygen vacancies). We have chosen to focus on four structurally different proton conducting perovskites; BaZrO3, BaSnO3, BaCeO3 and SrZrO3. The two former take on a cubic structure (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), while the two latter adopt an orthorhombic structure (Pnma), thus allowing us to judge the effect of both symmetry and composition on ΔHydrS°. As shown in Table 1, the experimental ΔHydrH° and ΔHydrS° for these perovskites cover a wide range of values, with the cubic BaZrO3 and BaSnO3 exhibiting the least exothermic ΔHydrH°, but also the least negative (most favourable) ΔHydrS°.
m), while the two latter adopt an orthorhombic structure (Pnma), thus allowing us to judge the effect of both symmetry and composition on ΔHydrS°. As shown in Table 1, the experimental ΔHydrH° and ΔHydrS° for these perovskites cover a wide range of values, with the cubic BaZrO3 and BaSnO3 exhibiting the least exothermic ΔHydrH°, but also the least negative (most favourable) ΔHydrS°.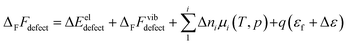
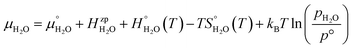
 , is obtained from the calculated vibrational frequency of a H2O molecule, while
, is obtained from the calculated vibrational frequency of a H2O molecule, while 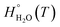 and
and 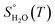 are taken from thermodynamic tables.15 The standard chemical potential,
are taken from thermodynamic tables.15 The standard chemical potential, 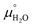 , is set to the calculated total electronic energy of the isolated H2O molecule.
, is set to the calculated total electronic energy of the isolated H2O molecule.
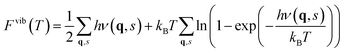
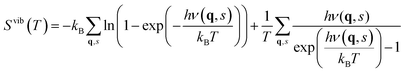
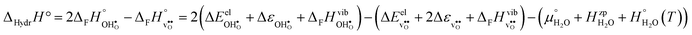
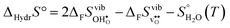
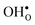 and
and 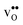 equal the number of oxide ions per formula unit.2 For perovskites,
equal the number of oxide ions per formula unit.2 For perovskites, 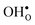 is normally found to take on a number of different configurations around each oxide ion, depending on the crystal structure. Further, in oxides where
is normally found to take on a number of different configurations around each oxide ion, depending on the crystal structure. Further, in oxides where 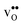 preferentially forms on one of the several structurally distinct oxide ions, the number of regular positions for
preferentially forms on one of the several structurally distinct oxide ions, the number of regular positions for 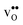 is lower than the concentration of O lattice sites. The number of proton positions (NH) around each oxide ion and the number of vacancy configurations (Nv) affect the chemical potential of
is lower than the concentration of O lattice sites. The number of proton positions (NH) around each oxide ion and the number of vacancy configurations (Nv) affect the chemical potential of 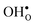 and
and 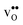 , and thus KHydr. Not accounting for these configurations when evaluating defect thermodynamics by curve fitting results in an apparent hydration entropy, ΔHydrS°app, which, in addition to the vibrational contributions, also includes configurational contributions:
, and thus KHydr. Not accounting for these configurations when evaluating defect thermodynamics by curve fitting results in an apparent hydration entropy, ΔHydrS°app, which, in addition to the vibrational contributions, also includes configurational contributions: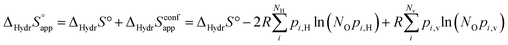
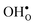 and
and 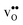 , respectively. The general expression for the probability of occupation of a given configuration is for instance for the proton given by
, respectively. The general expression for the probability of occupation of a given configuration is for instance for the proton given by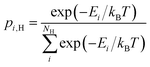
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(NH)
ln(NH)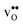 is favoured by merely 70 and 60 meV, for BaCeO3 and SrZrO3, respectively, at the O1 compared to the O2 site. As shown in Fig. 2, the non-degenerate proton and oxygen vacancy configurations in SrZrO3 and BaCeO3 render the configurational contribution to the hydration entropy temperature dependent. At the lowest temperatures, the contribution is actually negative due to the preference for occupation of the O1 site by oxygen vacancies. However, due to the small energy difference between the various proton and oxygen vacancy configurations, the configurational contribution approaches that for BaZrO3 even at ∼600 K. Both SrZrO3 and BaCeO3 also undergo several phase transitions upon heating, which may affect the relative stability of the different proton and vacancy configurations. Hence, the configurational contribution to ΔHydrS° is approximately 2R
is favoured by merely 70 and 60 meV, for BaCeO3 and SrZrO3, respectively, at the O1 compared to the O2 site. As shown in Fig. 2, the non-degenerate proton and oxygen vacancy configurations in SrZrO3 and BaCeO3 render the configurational contribution to the hydration entropy temperature dependent. At the lowest temperatures, the contribution is actually negative due to the preference for occupation of the O1 site by oxygen vacancies. However, due to the small energy difference between the various proton and oxygen vacancy configurations, the configurational contribution approaches that for BaZrO3 even at ∼600 K. Both SrZrO3 and BaCeO3 also undergo several phase transitions upon heating, which may affect the relative stability of the different proton and vacancy configurations. Hence, the configurational contribution to ΔHydrS° is approximately 2R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(4) (23 J K−1 mol−1) within the majority of the experimental temperature window (600–1100 K) for all included perovskites. Any compositional dependence of ΔHydrS°, in contrast to the conclusions of Tauer et al.,33 is therefore of a purely vibrational nature, and will be the focus in the remaining parts of this contribution.
ln(4) (23 J K−1 mol−1) within the majority of the experimental temperature window (600–1100 K) for all included perovskites. Any compositional dependence of ΔHydrS°, in contrast to the conclusions of Tauer et al.,33 is therefore of a purely vibrational nature, and will be the focus in the remaining parts of this contribution.

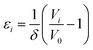
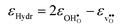
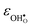 and
and 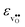 are the chemical expansion coefficients of
are the chemical expansion coefficients of 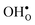 and
and 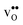 , respectively. εHydr is thus given as the relative expansion upon hydration of 1 mole of
, respectively. εHydr is thus given as the relative expansion upon hydration of 1 mole of 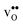 , and with respect to the volume of the defect-free lattice. Experimentally, however, chemical expansion coefficients are taken as the relative volume of the hydrated and dry materials – i.e. relative to the defective lattice. Experimental εHydr will therefore appear somewhat larger than those determined computationally in this work and in e.g.ref. 34.
, and with respect to the volume of the defect-free lattice. Experimentally, however, chemical expansion coefficients are taken as the relative volume of the hydrated and dry materials – i.e. relative to the defective lattice. Experimental εHydr will therefore appear somewhat larger than those determined computationally in this work and in e.g.ref. 34.
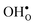 and
and 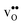 (both linear and volumetric), along with the chemical expansion upon hydration. All expansion coefficients are given per mole of formed defect. Both defects lead to anisotropic relaxations of the supercell for the four perovskites, even for the cubic BaZrO3 and BaSnO3, where
(both linear and volumetric), along with the chemical expansion upon hydration. All expansion coefficients are given per mole of formed defect. Both defects lead to anisotropic relaxations of the supercell for the four perovskites, even for the cubic BaZrO3 and BaSnO3, where 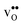 leads to a tetragonal cell, in line with experimental reports.7,35,36 For all compositions, both defects display negative formation volumes and are thus smaller than the native oxide ions, with
leads to a tetragonal cell, in line with experimental reports.7,35,36 For all compositions, both defects display negative formation volumes and are thus smaller than the native oxide ions, with 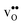 leading to a considerably larger contraction than
leading to a considerably larger contraction than 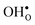 .
. 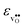 increases (less negative) notably in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, while
increases (less negative) notably in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, while 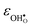 follows the opposite trend. The calculated εHydr are comparable with the experimentally determined values, although the experimental values vary considerably with the dopant concentration, and the adopted method (which most likely originates from uncertain proton concentrations). Hence, the compositional dependence of εHydr is somewhat unclear from the experimental values. Our calculated εHydr on the other hand decreases notably in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, which stems from both the decreasing
follows the opposite trend. The calculated εHydr are comparable with the experimentally determined values, although the experimental values vary considerably with the dopant concentration, and the adopted method (which most likely originates from uncertain proton concentrations). Hence, the compositional dependence of εHydr is somewhat unclear from the experimental values. Our calculated εHydr on the other hand decreases notably in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, which stems from both the decreasing 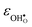 and the increasing
and the increasing 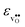 . Interestingly, these results therefore indicate that issues associated with the chemical expansion of BaZrO3 electrolytes upon hydration may for instance be reduced by adopting BaZrO3–BaCeO3 solid solutions.
. Interestingly, these results therefore indicate that issues associated with the chemical expansion of BaZrO3 electrolytes upon hydration may for instance be reduced by adopting BaZrO3–BaCeO3 solid solutions.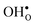 and
and 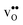 , and chemical expansion coefficient upon hydration (εHydr) for the included perovskites. The
, and chemical expansion coefficient upon hydration (εHydr) for the included perovskites. The 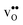 in BaZrO3 and BaSnO3 is aligned with the Zr(Sn)-
in BaZrO3 and BaSnO3 is aligned with the Zr(Sn)-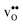 -Zr(Sn) axis parallel to the a-axis, while in BaCeO3 and SrZrO3 it is parallel to the b-axis. Note that the calculations on BaSnO3 are performed with the LDA functional
-Zr(Sn) axis parallel to the a-axis, while in BaCeO3 and SrZrO3 it is parallel to the b-axis. Note that the calculations on BaSnO3 are performed with the LDA functional
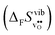 of
of 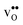 in SrZrO3 and BaZrO3 calculated under constant volume and zero/constant pressure conditions. For both compounds,
in SrZrO3 and BaZrO3 calculated under constant volume and zero/constant pressure conditions. For both compounds, 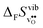 is negative, and significantly more negative under zero/constant pressure than under constant volume conditions – which stems from a blue shift of the phonon spectrum due to the negative formation volume of
is negative, and significantly more negative under zero/constant pressure than under constant volume conditions – which stems from a blue shift of the phonon spectrum due to the negative formation volume of 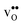 .10 Further, the effect is more noticeable for BaZrO3 than for SrZrO3, in line with the more negative formation volume of
.10 Further, the effect is more noticeable for BaZrO3 than for SrZrO3, in line with the more negative formation volume of 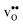 in BaZrO3. Similar effects of volume relaxation on
in BaZrO3. Similar effects of volume relaxation on 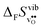 were also found for BaSnO3 and BaCeO3.
were also found for BaSnO3 and BaCeO3.

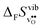 of SrZrO3 and BaZrO3 calculated under constant volume or zero/constant pressure (i.e., relaxed volume) conditions.
of SrZrO3 and BaZrO3 calculated under constant volume or zero/constant pressure (i.e., relaxed volume) conditions.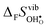 and
and 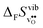 for the four included perovskites, calculated under zero/constant pressure conditions. For all compositions,
for the four included perovskites, calculated under zero/constant pressure conditions. For all compositions, 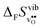 is significantly more negative than
is significantly more negative than 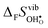 , and also shows a stronger compositional dependence. While all
, and also shows a stronger compositional dependence. While all 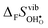 fall within 15 J mol−1 K−1 of each other throughout the temperature interval,
fall within 15 J mol−1 K−1 of each other throughout the temperature interval, 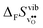 differs by as much as 80 J mol−1 K−1 at 1000 K between BaZrO3 and SrZrO3. The compositional variation of
differs by as much as 80 J mol−1 K−1 at 1000 K between BaZrO3 and SrZrO3. The compositional variation of 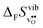 to some extent follows
to some extent follows 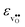 , with the two cubic perovskites, BaZrO3 and BaSnO3, displaying significantly more negative entropies than the orthorhombic SrZrO3 and BaCeO3. Hence, the compositional dependence of
, with the two cubic perovskites, BaZrO3 and BaSnO3, displaying significantly more negative entropies than the orthorhombic SrZrO3 and BaCeO3. Hence, the compositional dependence of 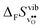 partly stems from the changes in
partly stems from the changes in 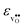 through the series, and partly from varying local structural relaxations around the defect (as reflected by the compositional dependence of
through the series, and partly from varying local structural relaxations around the defect (as reflected by the compositional dependence of 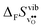 under constant volume conditions, see Fig. 3).
under constant volume conditions, see Fig. 3).
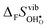 and
and 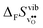 for the four included perovskites calculated under zero/constant pressure conditions.
for the four included perovskites calculated under zero/constant pressure conditions.![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° and ΔHydr
° and ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° from linearisation of the computational ΔHydrG° vs. T (see Table 4). For comparative reasons, ΔHydr
° from linearisation of the computational ΔHydrG° vs. T (see Table 4). For comparative reasons, ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) °app values in Table 4 represent the temperature averaged apparent entropy of hydration, i.e. including the configurational contribution according to eqn (11) (23 J mol−1 K−1 for all compositions).
°app values in Table 4 represent the temperature averaged apparent entropy of hydration, i.e. including the configurational contribution according to eqn (11) (23 J mol−1 K−1 for all compositions).
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° has been included for all compositions
° has been included for all compositions
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° (kJ mol−1)
° (kJ mol−1)![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) °app (J mol−1 K−1)
°app (J mol−1 K−1)![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° values are, as expected, very close to the low temperature ΔHydrH° in Fig. 5, and are in reasonable agreement with the experimental ranges of enthalpies for all compositions in Table 1. The calculated values also reflect the experimentally observed compositional dependence, with the two cubic perovskites displaying significantly less exothermic enthalpies than the two orthorhombic members. Also the calculated ΔHydr
° values are, as expected, very close to the low temperature ΔHydrH° in Fig. 5, and are in reasonable agreement with the experimental ranges of enthalpies for all compositions in Table 1. The calculated values also reflect the experimentally observed compositional dependence, with the two cubic perovskites displaying significantly less exothermic enthalpies than the two orthorhombic members. Also the calculated ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° values are in good agreement with the experimental values in Table 1. The entropies display a distinct compositional dependence, and are in general less negative for the cubic BaZrO3 and BaSnO3 than for the orthorhombic SrZrO3 and BaCeO3. The less negative ΔHydrS° of BaZrO3 and BaSnO3 stabilises protons compared to in the orthorhombic BaCeO3 and SrZrO3, in line with Kreuer's remark that the favourable proton transport properties of BaZrO3 stems from entropic stabilisation of protons.6 As noted in Fig. 3,
° values are in good agreement with the experimental values in Table 1. The entropies display a distinct compositional dependence, and are in general less negative for the cubic BaZrO3 and BaSnO3 than for the orthorhombic SrZrO3 and BaCeO3. The less negative ΔHydrS° of BaZrO3 and BaSnO3 stabilises protons compared to in the orthorhombic BaCeO3 and SrZrO3, in line with Kreuer's remark that the favourable proton transport properties of BaZrO3 stems from entropic stabilisation of protons.6 As noted in Fig. 3, 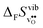 is the dominant vibrational contribution to ΔHydrS°, and also shows a stronger compositional dependency than
is the dominant vibrational contribution to ΔHydrS°, and also shows a stronger compositional dependency than 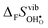 . Hence, one may argue that the entropic stabilisation of protons in BaZrO3/BaSnO3 is, more precisely, a result of entropic destabilisation of
. Hence, one may argue that the entropic stabilisation of protons in BaZrO3/BaSnO3 is, more precisely, a result of entropic destabilisation of 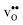 .
.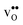 and
and 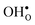 ; the oxide with the most exothermic hydration enthalpies exhibits the most stable protonic defects, and the most unstable oxygen vacancies (i.e. most stable oxide ions). There is further a striking correlation between both the calculated and experimental ΔHydr
; the oxide with the most exothermic hydration enthalpies exhibits the most stable protonic defects, and the most unstable oxygen vacancies (i.e. most stable oxide ions). There is further a striking correlation between both the calculated and experimental ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° and ΔHydr
° and ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° values, with the compound displaying the most exothermic ΔHydr
° values, with the compound displaying the most exothermic ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° (BaCeO3) also displaying the most negative (least favorable) ΔHydr
° (BaCeO3) also displaying the most negative (least favorable) ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) °. The correlation between ΔHydr
°. The correlation between ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° and ΔHydr
° and ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° is far from intuitive since ΔHydr
° is far from intuitive since ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) ° depends on both
° depends on both 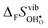 and
and 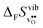 , neither of which correlate directly with either
, neither of which correlate directly with either 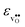 ,
, 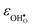 or εHydr, or the volume of the unit cells, as one might expect. The contributions to
or εHydr, or the volume of the unit cells, as one might expect. The contributions to 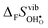 and
and 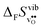 are related to both the vibrational frequency of protons and oxide ions, local relaxations upon protonation and filling of the
are related to both the vibrational frequency of protons and oxide ions, local relaxations upon protonation and filling of the 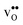 , in addition to the chemical expansion of the unit cell upon hydration. These properties can again be related to the size of the cations in the perovskite structure (which determines the unit cell volume and symmetry), and their electronegativity (which determines the interatomic bonding strengths), which – somewhat speculatively – explains the observed correlation between ΔHydr
, in addition to the chemical expansion of the unit cell upon hydration. These properties can again be related to the size of the cations in the perovskite structure (which determines the unit cell volume and symmetry), and their electronegativity (which determines the interatomic bonding strengths), which – somewhat speculatively – explains the observed correlation between ΔHydr![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ° and ΔHydr
° and ΔHydr![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) °. Conclusively, the oxide exhibiting the most stable protons and least stable vacancies enthalpy-wise, also exhibits weaker entropic destabilisation of vacancies, and thus the least favourable entropies of hydration.
°. Conclusively, the oxide exhibiting the most stable protons and least stable vacancies enthalpy-wise, also exhibits weaker entropic destabilisation of vacancies, and thus the least favourable entropies of hydration.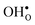 and
and 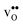 are smaller than the native oxide ions in all materials. Further,
are smaller than the native oxide ions in all materials. Further, 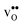 is significantly smaller than the proton and is therefore the main contributor to the chemical expansion of the materials upon hydration. The chemical expansion shows a distinct compositional dependence, and decreases in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3. As such, proton conducting electrolytes composed of BaZrO3–BaCeO3 or BaZrO3–SrZrO3 solid solutions should be less prone to issues stemming from chemical expansion upon hydration than pure BaZrO3 electrolytes. There is further a significant contribution from phonons to the formation entropy of both
is significantly smaller than the proton and is therefore the main contributor to the chemical expansion of the materials upon hydration. The chemical expansion shows a distinct compositional dependence, and decreases in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3. As such, proton conducting electrolytes composed of BaZrO3–BaCeO3 or BaZrO3–SrZrO3 solid solutions should be less prone to issues stemming from chemical expansion upon hydration than pure BaZrO3 electrolytes. There is further a significant contribution from phonons to the formation entropy of both 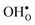 and
and 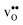 . The contribution is most pronounced for
. The contribution is most pronounced for 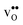 , and negative for all compositions, and becomes less negative in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, i.e. with increasing (less negative) chemical expansion of
, and negative for all compositions, and becomes less negative in the order BaZrO3 → BaSnO3 → BaCeO3 → SrZrO3, i.e. with increasing (less negative) chemical expansion of 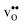 . Both the calculated ΔHydrH° and ΔHydrS° are in good agreement with the experimental ranges of values, and display a distinct compositional dependence. ΔHydrS° is in general less negative (more favourable) for the cubic BaZrO3 and BaSnO3 than the orthorhombic members, reflecting its dependence on the vibrational formation entropy, and again the chemical expansion, of
. Both the calculated ΔHydrH° and ΔHydrS° are in good agreement with the experimental ranges of values, and display a distinct compositional dependence. ΔHydrS° is in general less negative (more favourable) for the cubic BaZrO3 and BaSnO3 than the orthorhombic members, reflecting its dependence on the vibrational formation entropy, and again the chemical expansion, of 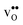 . Interestingly, there is a general correlation between ΔHydrH° and ΔHydrS°; the two cubic members display the least exothermic ΔHydrH°, but also the least negative (and thus most favourable) ΔHydrS° – an effect which may stem from both parameters being related to the bonding strengths of O2− and H+.
. Interestingly, there is a general correlation between ΔHydrH° and ΔHydrS°; the two cubic members display the least exothermic ΔHydrH°, but also the least negative (and thus most favourable) ΔHydrS° – an effect which may stem from both parameters being related to the bonding strengths of O2− and H+.