Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Formation of semi-dilute adhesion domains driven by weak elasticity-mediated interactions
Nadiv
Dharan
a and
Oded
Farago
ab
aDepartment of Biomedical Engineering, Ben Gurion University of the Negev, Be'er Sheva 84105, Israel
bIlse Katz Institute for Nanoscale Science and Technology, Ben Gurion University of the Negev, Be'er Sheva 84105, Israel
First published on 6th July 2016
Abstract
Cell–cell adhesion is established by specific binding of receptor and ligand proteins anchored in the cell membranes. The adhesion bonds attract each other and often aggregate into large clusters that are central to many biological processes. One possible origin of attractive interactions between adhesion bonds is the elastic response of the membranes to their deformation by the bonds. Here, we analyze these elasticity-mediated interactions using a novel mean-field approach. Our analysis of systems at different densities of bonds, ϕ, reveals that the phase diagram, i.e., the binodal and spinodal lines, exhibit a nearly universal behavior when the temperature T is plotted against the scaled density x = ϕξ2, where ξ is the linear size of the membrane's region affected by the presence of a single isolated bond. The critical point (ϕc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , Tc) is located at very low densities, and slightly below Tc we identify phase coexistence between two low-density phases. Dense adhesion domains are observed only when the height by which the bonds deform the membranes, h0, is much larger than their thermal roughness, Δ, which occurs at very low temperatures T ≪ Tc. We, thus, conclude that the elasticity-mediated interactions are weak and cannot be regarded as responsible for the formation of dense adhesion domains. The weakness of the elasticity-mediated effect and its relevance to dilute systems only can be attributed to the fact that the membrane's elastic energy saturates in the semi-dilute regime, when the typical spacing between the bonds r ≳ ξ, i.e., for x ≲ 1. Therefore, at higher densities, only the mixing entropy of the bonds (which always favors uniform distributions) is thermodynamically relevant. We discuss the implications of our results for the question of immunological synapse formation, and demonstrate that the elasticity-mediated interactions may be involved in the aggregation of these semi-dilute membrane domains.
, Tc) is located at very low densities, and slightly below Tc we identify phase coexistence between two low-density phases. Dense adhesion domains are observed only when the height by which the bonds deform the membranes, h0, is much larger than their thermal roughness, Δ, which occurs at very low temperatures T ≪ Tc. We, thus, conclude that the elasticity-mediated interactions are weak and cannot be regarded as responsible for the formation of dense adhesion domains. The weakness of the elasticity-mediated effect and its relevance to dilute systems only can be attributed to the fact that the membrane's elastic energy saturates in the semi-dilute regime, when the typical spacing between the bonds r ≳ ξ, i.e., for x ≲ 1. Therefore, at higher densities, only the mixing entropy of the bonds (which always favors uniform distributions) is thermodynamically relevant. We discuss the implications of our results for the question of immunological synapse formation, and demonstrate that the elasticity-mediated interactions may be involved in the aggregation of these semi-dilute membrane domains.
I. Introduction
The cellular membrane has the ability to adhere to different biological elements, including the extracellular matrix (ECM), the cytoskeleton and other cells. Cellular adhesion is mediated by several adhesion proteins (e.g., cadherins, integrins, and proteins from the immunoglobulin superfamily) that form specific bonds with receptors embedded in the adhesive element.1 These adhesion bonds often aggregate into macroscopically large adhesion clusters, such as focal adhesions, adherens junctions and gap junction plaques.2–4 In addition to providing mechanical stability to cells, these adhesion domains are essential for numerous biological processes, including signal transduction,5 T-cell activation,6 and tissue formation.7 Therefore, it is paramount to gain a comprehensive understanding of the biophysical principles that govern the formation of adhesion clusters.Over the past two decades, many studies have been conducted in order to better understand the biophysical interactions playing a role in the formation of adhesion clusters.8,9 Special attention has been directed to the effective interactions that are induced by membrane elasticity and thermal undulations. These non-specific interactions have also been studied in relation to condensation of trans-membrane proteins (membrane “inclusions”),10–12 and in the broader context of “Casimir-like” interactions in condensed matter.13 Specifically to the problem of adhesion domains, membrane mediated interactions between adhesion bonds originate from two interrelated mechanisms operating in concert. The first mechanism is related to the suppression of membrane thermal fluctuations by the adhesion bonds, which locally fix the membrane's height.14 The resulting loss in the membrane's fluctuation entropy can be partially mitigated if the adhesion bonds aggregate into a single domain. The second mechanism stems from local membrane deformations imposed by the pinning points, which can trigger a redistribution of the adhesion bonds in order to minimize the elastic curvature energy.15 Thus, membrane elasticity and thermal fluctuations induce a potential of mean force (PMF) between the adhesion bonds. The main challenge in deriving expressions for membrane mediated interactions arises from their many-body character,16i.e., their non-trivial dependence on the spatial distribution of the adhesion bonds.
Theoretical studies of membrane mediated interactions are often based on Helfrich's elasticity theory.17 Within the framework of this model, the membrane is considered as a two dimensional sheet fluctuating over a flat adhesive surface. Using the Monge gauge representation and assuming a small membrane curvature, the elastic energy can be expressed by the effective Hamiltonian
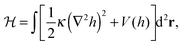 | (1) |
A commonly used practice in membrane elasticity studies is to assume that the membrane's free energy has the same form as eqn (1), with a renormalized bending modulus and with V(h) representing an effective potential between the surface and the membrane's mean height profile.18 Using this approach, Bruinsma, Goulian and Pincus studied the thermodynamics of domains of gap junctions.19 Two regimes with distinct expressions for V(h) have been proposed, corresponding to different membrane–surface interactions. In the first regime, coined the Helfrich regime, the bending modulus κ is small and, therefore, thermal fluctuations of the membranes are significant. The membrane interacts with the surface via thermal collisions, creating an effective repulsive potential V(h) ∼ (h − h0)−2.20 The resulting free energy has been analyzed within a mean-field picture assuming a lattice of equally spaced gap junctions, and was found to grow logarithmically with the lattice spacing. This result has received support from coarse-grained membrane simulations.21 Another prediction of ref. 19 was that due to the fluctuation-induced attraction between the gap junctions, the temperature is renormalized downward. This prediction was later examined in several computational studies, which demonstrated that, indeed, the renormalized temperature is about third to half of the thermodynamic temperature.22–25 These findings highlight the important role of thermal fluctuations in facilitating the conditions required for adhesion cluster formation. The fact that the renormalized temperature remains positive implies that in order to achieve aggregation of adhesion bonds, other attractive interactions must also be present.
The second regime examined in ref. 19, termed the van der Waals regime, is characterized by small thermal fluctuations, which allows one to consider a Lennard-Jones type potential between the membrane and the surface. For small deviations from the potential's minimum, a quadratic approximation for 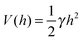 can be assumed. In contrast to the Helfrich regime where the range of the fluctuation-induced interactions diverges, the elasticity-mediated interactions in the van der Waals regime span over a characteristic healing length
can be assumed. In contrast to the Helfrich regime where the range of the fluctuation-induced interactions diverges, the elasticity-mediated interactions in the van der Waals regime span over a characteristic healing length
| ξ = (κ/γ)1/4, | (2) |
In the past few years, attempts to develop a more rigorous statistical mechanical treatment of the van der Waals regime have been made. Considering the elastic energy given by eqn (1) with a harmonic confining potential 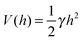 , the partition function of the system is given by
, the partition function of the system is given by
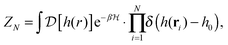 | (3) |
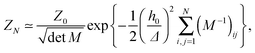 | (4) |
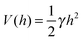 and without (N = 0) adhesion bonds. The coupling matrix M appearing in eqn (4) is given by
and without (N = 0) adhesion bonds. The coupling matrix M appearing in eqn (4) is given by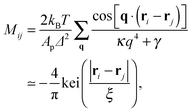 | (5) |
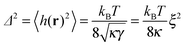 | (6) |
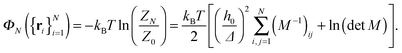 | (7) |
An interesting observation was made by Speck, Reister and Seifert, who argued that for small thermal roughness (Δ ≪ h0) the model depicted by eqn (7) belongs to the two dimensional Ising universality class.28 Furthermore, if the healing length ξ is smaller than the typical distance between the bonds, the model can be mapped onto a lattice-gas with nearest neighbor interactions. By estimating the effective interaction parameter between adhesion bonds occupying neighboring sites, the authors of ref. 28 were able to draw the phase diagram of the system and estimate the critical temperature below which clusters appear.
Despite the insights gained from previous studies, a satisfactory description of the thermodynamic behavior of the model described by eqn (7) is still lacking. Here, we take another look at this problem and derive a more accurate picture of the phase diagram, for a wide range of healing lengths, ξ, and adhesion bond densities, ϕ. Our investigation relies on a novel mean-field treatment of the system's free energy. We obtain the spinodal and binodal curves and locate the critical temperature of the system, Tc, above which adhesion domains do not form. Results for different systems exhibit data collapse when (Δ/h0)2 ∼ T/Tc is plotted as a function of the rescaled density ξ2ϕ. Interestingly, we find that the critical point is located at extremely low densities, which is linked to the many-body membrane mediated PMF. Therefore, close to critically, phase coexistence is found between two extremely dilute phases, while dense domains form only for T ≪ Tc, i.e., when each bond deforms the membrane considerably.
The paper is organized as follows: in Section II we introduce our mean-field theoretical treatment. This approach involves calculations of the elastic energy of systems with randomly distributed adhesion bonds at various densities. These calculations, which are described in Section II A, yield the expression for the mean-field energy of the system. The free energy is then obtained by combining the energy with the mean-field mixing entropy. In Section II B, we analyze the dependence of the free energy on the density of the bonds, and draw the phase diagram of the system, i.e., the binodal and spinodal lines. We discuss and summarize our findings in Section III.
II. Mean-field theory
The PMF, ΦN, given by eqn (7) corresponds to a system with a given spatial distribution of N fixed adhesion bonds. The thermodynamics of a system with N mobile bonds is characterized by the free energy F, which depends on the bond density ϕ = aN/Ap, where a is the microscopic unit area for which 0 ≤ ϕ ≤ 1. The free energy F can be derived from the corresponding partition function F = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z, where
Z, where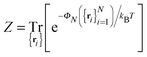 | (8) |
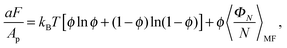 | (9) |
We are interested in the so called van der Waals regime (see Section I), which is characterized by small thermal roughness Δ. Following previous studies,19,28 we will also make the assumption that each adhesion bond causes a deformation h0 significantly larger than Δ. This allows us to drop the second term on the r.h.s. of eqn (7) accounting for the entropy of the thermal fluctuations, which leaves only the first term representing the elastic energy of the ground state. The latter can be estimated by considering a lattice of adhesion bonds with spacing 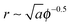 , which gives an energy landscape that depends on the ratio r/ξ. This approach yields good analytical expressions for the elastic energy only in the limits r/ξ ≫ 1 and r/ξ ≪ 1;19 however, it fails to capture the correct thermodynamic behavior in the intermediate regime r/ξ ∼ 1 where the lattice distribution does not necessarily represent the energy of a typical random distribution of adhesion bonds. Here, we take a different approach and derive an empirical expression for the dependency of the elastic energy on the bonds' density. We computationally obtain this expression by (i) generating membranes with random, rather than ordered, distributions of adhesion bonds, (ii) finding the membrane profile that minimizes the Helfrich elastic energy of each realization, and (iii) describing the computational data for the elastic energy by a fitting function, which applies to the entire range of densities.
, which gives an energy landscape that depends on the ratio r/ξ. This approach yields good analytical expressions for the elastic energy only in the limits r/ξ ≫ 1 and r/ξ ≪ 1;19 however, it fails to capture the correct thermodynamic behavior in the intermediate regime r/ξ ∼ 1 where the lattice distribution does not necessarily represent the energy of a typical random distribution of adhesion bonds. Here, we take a different approach and derive an empirical expression for the dependency of the elastic energy on the bonds' density. We computationally obtain this expression by (i) generating membranes with random, rather than ordered, distributions of adhesion bonds, (ii) finding the membrane profile that minimizes the Helfrich elastic energy of each realization, and (iii) describing the computational data for the elastic energy by a fitting function, which applies to the entire range of densities.
A. Energy calculations
The ground state Helfrich energy corresponding to a random distribution of adhesion bonds is given by the first term on the r.h.s. of eqn (7) and can, in principle, be computed by inverting the coupling matrix (5). In practice, this involves a computationally expensive process and, thus, we adopt a different strategy based on the direct minimization of the Helfrich Hamiltonian. This is done by considering a triangular lattice with lattice spacing l. Each site, i, represents a small membrane segment of area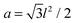 , and is characterized by a local height variable hi. On the lattice, N sites are randomly chosen for the locations of the adhesion bonds, at which we set hi = h0. The discrete analogue of the Helfrich Hamiltonian (1) is
, and is characterized by a local height variable hi. On the lattice, N sites are randomly chosen for the locations of the adhesion bonds, at which we set hi = h0. The discrete analogue of the Helfrich Hamiltonian (1) is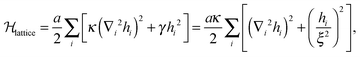 | (10) |
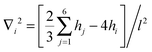 , with the sum j = 1,…,6 running over the six nearest neighbors of site i. Starting with hi = h0 at all sites, we simulate Langevin dynamics30 without the noise term (i.e., at zero temperature),
, with the sum j = 1,…,6 running over the six nearest neighbors of site i. Starting with hi = h0 at all sites, we simulate Langevin dynamics30 without the noise term (i.e., at zero temperature), 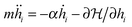 , which quickly brings the system to the ground state profile. We measure all lengths in units of the lattice spacing l = 1, and the energy scale is set to kBT = 1. The density of bonds is given by ϕ = N/Ns, where Ns is the number of lattice sites. Most of the calculations were performed on a triangular lattice of 104 × 120 sites (with periodic boundary conditions) that has an aspect ratio close to 1. We calculate the elastic energy of numerous random realizations at various densities ϕ ≤ 0.1 and for several values of ξ varying from ξ = 5 to ξ = 10. These values for the correlation length are chosen such that (i) ξ is sufficiently larger than the lattice spacing l = 1, which reduces the numerical errors associated with the discrete nature of eqn (10) to less than a few percent, and (ii) ξ is much smaller than the system linear size, to avoid finite size effects.
, which quickly brings the system to the ground state profile. We measure all lengths in units of the lattice spacing l = 1, and the energy scale is set to kBT = 1. The density of bonds is given by ϕ = N/Ns, where Ns is the number of lattice sites. Most of the calculations were performed on a triangular lattice of 104 × 120 sites (with periodic boundary conditions) that has an aspect ratio close to 1. We calculate the elastic energy of numerous random realizations at various densities ϕ ≤ 0.1 and for several values of ξ varying from ξ = 5 to ξ = 10. These values for the correlation length are chosen such that (i) ξ is sufficiently larger than the lattice spacing l = 1, which reduces the numerical errors associated with the discrete nature of eqn (10) to less than a few percent, and (ii) ξ is much smaller than the system linear size, to avoid finite size effects.
From eqn (5)–(7) (omitting the second term on the r.h.s.), we infer that for a given set of model parameters (κ, h0, ξ, ϕ), the average elastic energy has the form
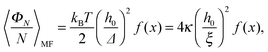 | (11) |
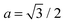 , this yields the decaying form
, this yields the decaying form 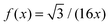 for x ≫ 1. Taking these considerations into account, we propose the following expression for the scaling function:
for x ≫ 1. Taking these considerations into account, we propose the following expression for the scaling function: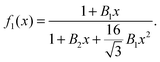 | (12) |
In Fig. 1 we plot the computational results (triangles) for the elastic energy per bond, normalized by 4κ(h0/ξ)2, which defines f(x) in eqn (11). The data, which are plotted against the scaled density x = ξ2ϕ, exhibit an excellent data collapse over the entire range x ≤ 10. The solid curve represents the fitting of the data to the form f1(x) given by eqn (12), with the parameters B1 ≃ 5.08 and B2 ≃ 9.87 that give the best fit. The scatter of the computational data is due to the randomness of the simulated configurations. As expected, the scatter is larger for small values x ≪ 1, where the interaction between the closer pairs of adhesion bonds dominates the energy of the configuration. In fact, for some configurations in this regime, we find f(x) to be slightly larger than unity. This feature is to be expected, and follows from the non-monotonicity of Kelvin's function defining the elements of the coupling matrix M [see eqn (5)]. For x ≪ 1, the PMF between the bonds can be approximated by the sum of pair potentials, as was assumed in ref. 26. By setting N = 2 in eqn (5) and (7), it is easy to confirm that the pair PMF is slightly repulsive at large bond separations. We, therefore, conclude that the scaling function f(x) should be non-monotonic: it first increases for very small values of x, before dropping to zero at larger values. Furthermore, from the fact that Kelvin's function converges exponentially to zero for large arguments, one can also conclude that the derivative of the scaling function df/dx = 0 at x = 0. These features of f(x) in the x → 0 limit are not accounted for by the scaling form f1(x) proposed by eqn (12). Therefore, we also consider the three fitting parameter scaling function
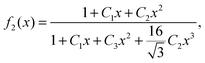 | (13) |
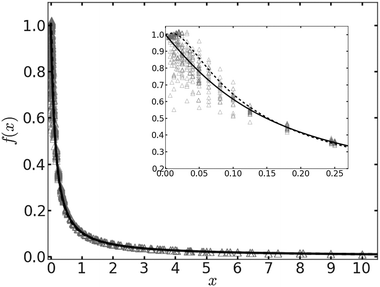 | ||
| Fig. 1 The scaling function for the elastic energy f(x) [see eqn (11)] as a function of the scaled density x. The numerical results are represented by triangles. The solid and dashed curves depict, respectively, the fitting functions f1(x) [eqn (12)] and f2(x) [eqn (13)] to the data. The inset shows an enlarged view of the data and the fitting functions for x ≪ 1. | ||
B. Phase diagram
Plugging eqn (11) into eqn (9), the mean-field free energy, F, of a system with adhesion bond concentration ϕ and correlation length ξ reads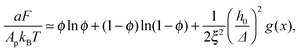 | (14) |
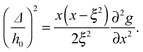 | (15) |
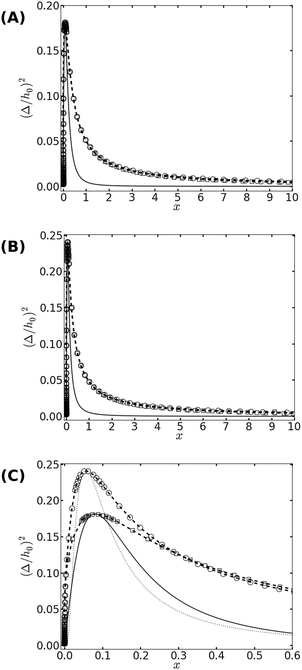 | ||
| Fig. 2 (A) The phase diagram corresponding to the free energy equation [eqn (14)] with f(x) = f1(x) given by eqn (12). The binodal curve is represented by symbols (with dashed lines serving as guides to the eye), where squares and circles represent data for ξ = 5 and ξ = 10, respectively. The two binodal curves nearly overlap with each other. The spinodal curves, which are represented by the solid (for ξ = 5) and dotted (for ξ = 10) lines, are also indistinguishable. (B) Same as (A), but for f(x) = f2(x) in eqn (14). (C) A zoom on the vicinity of the critical point, where the differences between the scaling functions f1(x) and f2(x) are visible. Binodal curves are plotted using squares for f1(x) and circles for f2(x). The spinodal lines are represented by the solid and dotted lines for f1(x) and f2(x), respectively. The phase diagrams are calculated for ξ = 10. | ||
III. Discussion and summary
Looking at the phase diagram depicted in Fig. 2, the one feature that stands out is that the critical point is found at very low densities. The precise value of the critical scaled density xc is, of course, unknown since it depends on the form of the scaling function f(x) [see Fig. 2(C)], and because the mean-field picture is not adequate in the vicinity of the critical point. Nevertheless, it is fair to conclude from the data in Fig. 2 that xc < 0.1, which implies that ϕc = xc/ξ2 ≪ 10−2 (unless the correlation length is microscopically small, i.e., ξ ∼ 1). The critical temperature Tc can be related to the elastic deformation energy due to a single bond Φ1/kBT = 0.5(h0/Δ)2. From Fig. 2 we read that the critical temperature satisfies Φ1 ≃ 2 − 3kBTc. Another noticeable feature in Fig. 2 is the fact that the spinodal and binodal curves of membranes with different values of ξ overlap with each other when plotted against the scaled density x. This does not a priori follow from the data collapse exhibited in Fig. 1, because of the mixing entropy contribution to the free energy. The latter depends on the density ϕ rather than the scaled density x. At low densities, however, we can use the approximation (1 − ϕ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − ϕ) ≃ −ϕ in eqn (9), and then it can be easily shown that the spinodal line [r.h.s. of eqn (15)] becomes only a function of x. Thus, the observation in Fig. 2 that the phase diagram depends on the scaled density is related to the fact that our investigation focuses on membranes with low densities of bonds.
ln(1 − ϕ) ≃ −ϕ in eqn (9), and then it can be easily shown that the spinodal line [r.h.s. of eqn (15)] becomes only a function of x. Thus, the observation in Fig. 2 that the phase diagram depends on the scaled density is related to the fact that our investigation focuses on membranes with low densities of bonds.
The fact that the critical point is located at very low densities means that, slightly below Tc, we expect phase coexistence between two low-density phases. From Fig. 2 we also notice that for x ≳ 1, phase separation occurs only when the temperature drops significantly to roughly T ≲ 0.2Tc. This implies that low density systems with large ξ will not phase separate unless the bonds strongly deform the membrane (h0 ≫ Δ). In the two phase region of such a system, the scaled density of the condensed phase x ≳ 1 which, depending on the value of ξ, could mean that the density ϕ is quite low. We term low-density (ϕ ≪ 1) regions with scaled density x ∼ 1 as semi-dilute, and conclude that the elasticity-mediated interactions may indeed lead to the formation of such semi-dilute domains.
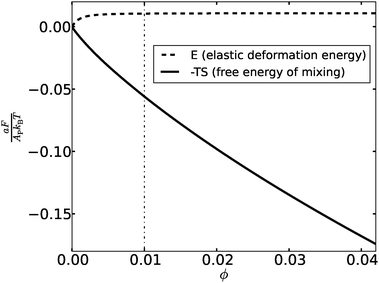
The “weakness” of the elasticity-mediated effect and its inability to induce formation of dense adhesion domains can be understood by looking at the variation of the total elastic deformation energy [second term on the r.h.s. of eqn (14)] with the density of the bonds ϕ. The elastic energy E, normalized per unit area, is plotted in Fig. 3 for membranes with (h0/Δ)2 = 20 (corresponding to T ∼ 0.2Tc) and ξ = 10. Also shown in Fig. 3 is the free energy of mixing −TS (S denotes the mixing entropy), per unit area, given by the first term on the r.h.s. of eqn (14). Both contributions to the free energy are given in units of the thermal energy kBT. We observe that the total elastic deformation energy increases with ϕ but, somewhat surprisingly, saturates at extremely low densities. The dashed-dotted vertical line in Fig. 3 at ϕ = 0.01 corresponds to x = ξ2ϕ = 1, and one can read from the data that the elastic energy of the membrane barely increases for x ≳ 0.5. The interpretation of this finding is that one needs a semi-dilute distribution of about one bond per area ξ2 to cause the membrane to adopt nearly flat configurations with h ∼ h0. Above the scaled density x ∼ 0.5, the membrane elastic energy becomes thermodynamically irrelevant, leaving us with only the mixing entropy term which always favors uniform distributions. This explains why phase separation into regions with distinct concentrations of bonds is possible only at densities below ϕ ∼ 0.5ξ−2. To state the last conclusion somewhat differently – the elasticity-mediated PMF induces an attraction between the bonds only if their separation is larger than ξ. This is an interesting collective (many-body) effect, exhibiting an “opposite” trend compared to the pair PMF, which is attractive at separations smaller than ξ and is screened off at larger distances. The pair PMF may play an attractive role only between two relatively isolated bonds in inhomogeneous distributions, but such configurations fall outside the framework of the mean-field picture presented in this work.
To put our findings in a biological context, we look at the example of the immunological synapse (IS), which forms the contact area between the T-cell lymphocyte and a target cell. Specifically, the cell–cell adhesion is mediated via binding between T-cell receptors (TCR) and MHC-peptide (MHCp) complexes, and between integrin LFA1 and its ligand ICAM-1.31 These two types of adhesion bonds form a unique structure, in which TCR–MCHp bonds are clustered in its center, while the LFA1–ICAM1 bonds aggregate in the periphery of synapse. It is believed that the central domain, i.e., the TCR–MHCp rich area, plays a pivotal role in T-cell activation.32 Typically, the bond density within the synapse is around 100 bonds per square micrometer, and the bond lengths are 14 nm and 41 nm for TCR–MHCp and LFA1–ICAM1 bonds, respectively.33 We recall that in the model presented here, h0 represents the local membrane deformation imposed by a bond relative to the resting height of the membrane. Thus, if we consider the resting separation between the two membranes in the IS to be dictated by the longer bonds, we can estimate the deformation to simply be the difference between the two bond lengths, h0 ≃ 27 nm. Taking the membrane bending rigidity to be κ ≃ 15kBT and the harmonic potential strength as γ ≃ 6 × 105kBT μm−4,34 we arrive at the values x ≃ 0.5 and (Δ/h0)2 ≃ 0.057 for the coordinates of this point in the phase diagram displayed in Fig. 2. Remarkably, the point lies in the two-phase region of the phase diagram, close to the binodal line. This raises the possibility that the TCR–MHCp rich domain may be the semi-dilute phase coexisting with a dilute phase of vanishingly small density. Thus, we speculate that the elasticity-mediated interactions may play an important role in the condensation of the TCR–MHCp signaling domain. They provide attraction which enables the TCR–MHCp bonds to spontaneously aggregate into domains with density comparable to that existing in the IS central zone. This finding is in line with several recent studies suggesting that passive thermodynamic processes can describe the short-time condensation of adhesion clusters of the IS, without evoking any active processes in the cytoskeleton (see, e.g., ref. 35 and references therein). Forces stemming from cytoskeletal activity may be essential during the later stages of IS pattern formation and stabilization.36,37 Introducing such active processes into the equilibrium thermodynamic framework presented here is a task for future studies.
Acknowledgements
This work was supported by the Israel Science Foundation (ISF) through grant number 1087/13.References
- B. Alberts, D. Bray, J. Lewis, M. Raff, K. Roberts and J. D. Watson, Mol. Biol. Cell, Garland, New York, 1994 Search PubMed.
- A. L. Berrier and K. M. Yamada, J. Cell. Physiol., 2007, 213, 565 CrossRef CAS PubMed.
- T. J. Harris and U. Tepass, Nat. Rev. Mol. Cell Biol., 2010, 11, 502 CrossRef CAS PubMed.
- F. F. Bukauskas, et al. , Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 2556 CrossRef CAS PubMed.
- S. K. Akiyama, Hum. Cell, 1996, 9, 181 CAS.
- C. R. Monks, et al. , Nature, 1998, 395, 82 CrossRef CAS PubMed.
- K. Vleminckx and R. Kemler, BioEssays, 1999, 21, 211 CrossRef CAS PubMed.
- A. S. Smith and E. Sackman, ChemPhysChem, 2009, 10, 66 CrossRef CAS PubMed.
- T. R. Weikl and R. Lipowsky, in Advances in Planar Lipid Bilayers and Liposomes, ed. A. Leitmannova Liu, Elsevier, 2006, vol. 5, ch. 4, pp. 63–127 Search PubMed.
- M. Goulian, R. Bruinsma and P. A. Pincus, Europhys. Lett., 1993, 22, 145 CrossRef CAS.
- T. R. Weikl, M. M. Kozlov and W. Helfrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 6988 CrossRef CAS.
- P. G. Dommersnes, J. B. Fournier and P. Galatola, Europhys. Lett., 1998, 42, 233 CrossRef CAS.
- M. Kardar and R. Golestanian, Rev. Mod. Phys., 1999, 71, 1233 CrossRef CAS.
- O. Farago, in Advances in Planar Lipid Bilayers and Liposomes, ed. A. Iglič, Elsevier, 2011, vol. 14, ch. 5, pp. 129–155 Search PubMed.
- B. Różycki, R. Lipowsky and T. R. Weikl, New J. Phys., 2010, 12, 095003 CrossRef.
- R. Golestanian, M. Goulian and M. Kardar, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6725 CrossRef CAS.
- W. Helfrich, Z. Naturforsch., 1973, 28c, 693 Search PubMed.
- O. Farago and P. Pincus, J. Chem. Phys., 2004, 120, 2934 CrossRef CAS PubMed.
- R. Bruinsma, M. Goulian and P. Pincus, Biophys. J., 1994, 67, 746 CrossRef CAS PubMed.
- W. Helfrich, Z. Naturforsch., 1978, 33a, 305 CAS.
- O. Farago, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 050902(R) CrossRef PubMed.
- T. R. Weikl and R. Lipowsky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 011903 CrossRef CAS PubMed.
- N. Weil and O. Farago, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 81 CrossRef CAS PubMed.
- N. Dharan and O. Farago, J. Chem. Phys., 2014, 141, 024903 CrossRef PubMed.
- T. Bihr, U. Seifert and A. S. Smith, New J. Phys., 2015, 18, 083016 CrossRef.
- T. Speck and R. L. C. Vink, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031923 CrossRef PubMed.
- D. Schmidt, T. Bihr, U. Seifert and A. S. Smith, Europhys. Lett., 2012, 99, 38003 CrossRef.
- T. Speck, E. Reister and U. Seifert, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 021923 CrossRef PubMed.
- M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions: with formulas, graphs, and mathematical tables, Dover, New York, 1972 Search PubMed.
- N. Grønbech-Jensen and O. Farago, Mol. Phys., 2013, 111, 983 CrossRef.
- A. Grakoui, et al. , Science, 1999, 285, 221 CrossRef CAS PubMed.
- S. K. Bromley, et al. , Annu. Rev. Immunol., 2001, 19, 375 CrossRef CAS PubMed.
- D. Coombs, M. Dembo, C. Wofsy and B. Goldstein, Biophys. J., 2004, 86, 1408 CrossRef CAS PubMed.
- A. K. Chattopadhyay and N. J. Burroughs, Europhys. Lett., 2007, 77, 48003 CrossRef.
- A. Carlson and L. Mahadevan, PLoS Comput. Biol., 2015, 11, e1004481 Search PubMed.
- N. J. Burroughs and C. Wülfing, Biophys. J., 2002, 83, 1784 CrossRef CAS PubMed.
- T. R. Weikl, M. Asfaw, H. Krobath, B. Różycki and R. Lipowsky, Soft Matter, 2009, 5, 3213 RSC.
| This journal is © The Royal Society of Chemistry 2016 |