DOI:
10.1039/C6SM00990E
(Paper)
Soft Matter, 2016,
12, 6621-6648
Critical Casimir interactions between Janus particles
Received
27th April 2016
, Accepted 13th June 2016
First published on 22nd July 2016
Abstract
Recently there has been strong experimental and theoretical interest in studying the self-assembly and the phase behavior of patchy and Janus particles, which form colloidal suspensions. Although in this quest a variety of effective interactions have been proposed and used in order to achieve a directed assembly, the critical Casimir effect stands out as being particularly suitable in this respect because it provides both attractive and repulsive interactions as well as the potential of a sensitive temperature control of their strength. Specifically, we have calculated the critical Casimir force between a single Janus particle and a laterally homogeneous substrate as well as a substrate with a chemical step. We have used the Derjaguin approximation and compared it with results from full mean field theory. A modification of the Derjaguin approximation turns out to be generally reliable. Based on this approach we have derived the effective force and the effective potential between two Janus cylinders as well as between two Janus spheres.
I. Introduction
The critical Casimir effect has been predicted1 as a classical analogue of the celebrated Casimir effect in quantum electrodynamics.2 The former is induced by the confinement of order parameter fluctuations in a system close to its critical point Tc, whereas the latter is due to the confinement of vacuum fluctuations. Upon approaching Tc the bulk correlation length ξ, characterizing the exponential decay of the two-point order parameter correlation function, increases algebraically as ξ(t = (T − Tc)/Tc → 0±) = ξ±0|t|−ν, with a bulk critical exponent ν and non-universal amplitudes ξ±0. If ξ becomes comparable with the size of the system, the so-called critical Casimir force arises which acts as an effective force on the confining surfaces of the system. The energy scale of the critical Casimir effect is set by kBT and its strength can be sensitively tuned by minute temperature changes. This effective force can be attractive as well as repulsive depending on the boundary conditions for the order parameter at the surfaces. In contrast to the quantum mechanical Casimir effect, the sign of the critical Casimir force can be chosen by modifying exclusively the surface chemistry of the confinement. An experimentally convenient realization of the critical Casimir effect is provided by binary liquid mixtures, for which the boundary conditions on the confining surfaces correspond to the adsorption preference for one of the components of the mixture (e.g. hydrophilic/hydrophobic surfaces).
The first experimental evidence for critical Casimir forces was provided only indirectly by studying the thickness of thin wetting films in classical binary liquid mixtures3,4 near demixing, as well as in mixtures of 3He/4He5,6 and liquid 4He close to their normal-superfluid transition.7,8 Corresponding Monte Carlo simulations for the film geometry9–14 are in very good quantitative agreement with the experiments. The first direct measurement of the critical Casimir effect15 was performed by monitoring optically the thermal motion of a single spherical colloid, immersed in a binary liquid mixture of water and 2,6-lutidine close to demixing and near a chemically homogeneous substrate. The experimental results are in excellent agreement with corresponding theoretical predictions,15–17 which make use of the Derjaguin approximation (DA)18 with Monte Carlo (MC) simulation results for the film geometry as input. A full MC simulation for the sphere-wall geometry has been performed only recently.19 Other theoretical studies rely on field-theoretical methods.20–24
Independently, at the same time strong experimental and theoretical interest emerged in patchy colloidal particles with chemically heterogeneous surface properties and in Janus particles with “two faces”—a topic which has been popularized by the nobel prize lecture of de Gennes.25 These particles have the potential to be building blocks for directed self-assembly of new materials, such as the kagome open-lattice structure.26–28 Topical reviews concerning both experimental and theoretical aspects of patchy particles are provided in ref. 29 and 30. From an experimental point of view, the fabrication of such particles poses a research challenge in itself,31–33 followed by the experimental observation of their (self-)assembly behavior.26,34,35
In principle, any anisotropic surface structure gives rise to an orientation dependent behavior caused by surface mediated interactions, e.g. due to surface charges36,37 or critical fluctuations. In this sense, the critical Casimir effect is a viable candidate to achieve a controlled self-assembly, as demonstrated experimentally by the trapping of homogeneous colloids adjacent to chemically patterned substrates,38,39 in very good agreement with corresponding theoretical predictions.39,40
The study of Janus particles subjected to the critical Casimir effect represents a rather new research issue, encompassing a few promising experimental investigations.41,42 The critical Casimir effect provides a controllable effective interaction which can be directed by both attraction and repulsion between the patches of the particles, depending on the design and surface treatment of the particles. The surfaces can also be modified in order to change boundary conditions for the order parameter of the underlying continuous phase transition of the solvent, e.g. by producing a surface with only weak adsorption preference for one of the two species forming the binary liquid solvent,43 though here we shall consider only the strong adsorption limit. In an experimental setup, along the lines of ref. 15, 38 and 41, the Janus particles considered here would be composed of a hydrophilic and a hydrophobic half.
Concerning the modeling of effective interactions between patchy particles, the main body of theoretical research is, however, dominated by the simple Kern–Frenkel model.44 This model assumes short-ranged on–off “bond-like” interactions and is employed in simulations of self-assembly behavior,45 in numerical studies of the phase diagram of patchy particles,46–49 in Monte Carlo simulations,50 or is embedded into other theoretical frameworks, ranging from Wertheim's association theory over integral-equation theory to self-consistent phonon theory.51–53 In contrast, at the critical point T = Tc of the solvent the critical Casimir forces are long-ranged, and can be both attractive and repulsive, but the strengths of attraction and repulsion differ. In order to understand the behavior of patchy particles in a critical solvent it is therefore necessary to work out the distinguishing features of the critical Casimir interaction compared to those of the simple Kern–Frenkel model, which assumes a square-well potential and the interaction between two patches only.
Our theoretical analysis of the critical Casimir interaction between Janus particles is structured as follows: in Section II we present the theoretical background of our method, starting with a brief introduction to finite size scaling for the present system. Within a two-pronged approach, we outline both the full numerical mean field calculations valid in spatial dimension d = 4, as well as the Derjaguin approximation used for d = 3 and d = 4.
Since previously a significant theoretical effort was put into the investigation of the interaction with patterned substrates,39,54–57 in Section III we first consider a cylindrical Janus particle close to a homogeneous substrate. The Derjaguin approximation implies an intriguing link in the description between the presence of chemical steps on a striped surface and of the chemical step on a Janus particle. We investigate this link which is confirmed by the order parameter distribution to occur in the modified form also within mean field theory (MFT). This result is then employed for a Janus particle floating above a substrate with a chemical step.
In Section IV we draw on this knowledge in order to establish within the Derjaguin approximation the force and the effective interaction potential between two Janus cylinders close to each other, but with a constraint on their orientation. In Section V we present the force and the interaction potential between two Janus spheres for arbitrary orientations of the two particles. The derivation of the corresponding scaling function can be found in Appendices A, B, and C. Finally, in Section VI we conclude and provide an outlook.
II. Theoretical background
A. Finite size scaling
Close to a critical point of a fluid, thermal fluctuations become correlated over macroscopic distances and are, to a large extent, independent of microscopic details. Upon approaching the critical demixing point Tc of a binary liquid mixture at its critical concentration, the bulk correlation length diverges as ξ±(t = (T − Tc)/Tc → 0±) = ξ±0|t|−ν, with the critical exponent ν ≃ 0.63 in d = 3 and ν = 1/2 in d = 4.58 The sign of t is chosen such that t > 0 corresponds to the homogeneous, mixed state, whereas t < 0 corresponds to the two phase region. Many experiments are performed advantageously in binary liquid mixtures with a lower critical point;15,16,38,39,41,42 in this case one has t = (Tc − T)/Tc.
According to finite size scaling, in the vicinity of its bulk critical point a (partially) finite system is described by universal scaling functions, which depend only on the shape of the sample and on coarse features of the system, summarized by universality classes. Here, we focus on the case of binary liquid mixtures, which belong to the Ising universality class, for which the scalar order parameter ϕ is defined as the deviation of the number density of one species from its value at criticality.
Accordingly, the critical Casimir force is described by a universal scaling function uniquely determined by the bulk universality class58 (here: Ising), the surface universality class59,60 (here: normal transition with symmetry-breaking boundary conditions (+) and (−)), the spatial dimension (here: d = 3 and d = 4 in mean field theory), and the geometry of the confinement61–63 (here: cylinders, spheres, and planar walls).
In the case of the film geometry with two flat, parallel, homogeneous, and macroscopically large walls at distance l, renormalization group theory predicts the following form for the critical Casimir force f(a,b) per area of the wall:64
| | 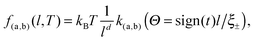 | (1) |
where the subscript (a,b) indicates the pair of boundary conditions (BCs) (a) and (b) characterizing the two walls. In the absence of a bulk ordering field and for infinitely strong surface fields, the scaling function
k(a,b) depends only on a single scaling variable, which is given by the sign of the reduced temperature
t and the film thickness
l in units of the bulk correlation length
ξ± (with ± taken for
t ≷ 0). We emphasize that
eqn (1) describes the behavior of the singular contribution to the effective force acting on the confining walls, in addition to any background forces,
e.g. van der Waals forces.
At the critical point T = Tc, ξ± diverges and the scaling function of the force k(a,b) between two walls reduces to a universal number referred to as the critical Casimir amplitude (see ref. 61; the notation differs slightly)
| | | k(a,b)(l/ξ± = 0) = Δ(a,b), | (2) |
which leads to an algebraic decay ∼
l−d of the critical Casimir force as a function of the film thickness. In contrast, off criticality the critical Casimir force decays exponentially as a function of
l/
ξ±. For the symmetry-breaking BCs (−,−) or (+,−) valid for binary liquid mixtures and for
t > 0, the critical Casimir force is expected to decay as (see
ref. 16, 40 and 65)
| | 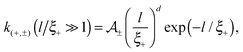 | (3) |
where
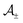
are universal amplitudes.
16
B. Mean field theory
Within MFT, the bulk and surface critical phenomena belonging to the Ising universality class are described by the standard Landau–Ginzburg–Wilson fixed point Hamiltonian59,60| | 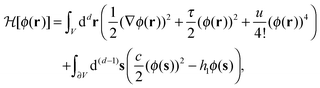 | (4) |
which is a functional of the order parameter profile ϕ(r) of the fluid such as the difference between the local concentration of one of the two species and its critical value in a binary liquid mixture. The Hamiltonian consists of a bulk term representing a d-dimensional liquid-filled volume V and a term describing the confining surface ∂V of this volume, e.g. provided by the surfaces of colloids immersed in the binary mixture, with ϕ(r)|∂V = ϕ(s) evaluated at the boundary ∂V. Within MFT, the parameter τ is proportional to the reduced temperature t as τ = t/(ξ+0)2,61 while the coupling constant u > 0 ensures the stability of 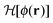 for t < 0 in the demixed phase; u is dimensionless in d = 4. In order to treat off-critical concentrations, the expression in eqn (4) can be extended to contain a term proportional to a bulk field h. The surface enhancement c and the symmetry breaking surface field h1 determine the BC. We focus on the so-called normal surface universality class, which is generic for liquids, with c = 0 and the two fixed point values h1 = ±∞. This leads to a divergence of ϕ → ±∞ at the surface of the colloids corresponding to what is denoted as the (+) and (−) BC.60 Concerning the numerical implementation, the divergence is realized by a short distance expansion close to the surface.66,67 Within MFT, only the order parameter configuration with the largest statistical weight
for t < 0 in the demixed phase; u is dimensionless in d = 4. In order to treat off-critical concentrations, the expression in eqn (4) can be extended to contain a term proportional to a bulk field h. The surface enhancement c and the symmetry breaking surface field h1 determine the BC. We focus on the so-called normal surface universality class, which is generic for liquids, with c = 0 and the two fixed point values h1 = ±∞. This leads to a divergence of ϕ → ±∞ at the surface of the colloids corresponding to what is denoted as the (+) and (−) BC.60 Concerning the numerical implementation, the divergence is realized by a short distance expansion close to the surface.66,67 Within MFT, only the order parameter configuration with the largest statistical weight 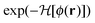 is considered and fluctuations of the order parameter are neglected. Within this approximation the free energy follows from
is considered and fluctuations of the order parameter are neglected. Within this approximation the free energy follows from 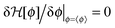 . The MFT order parameter profile defined as m = 〈ϕ〉/ϕt minimizes the Hamiltonian
. The MFT order parameter profile defined as m = 〈ϕ〉/ϕt minimizes the Hamiltonian 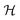 , where
, where 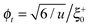 is the non-universal amplitude of the bulk order parameter ϕb = ϕt|t|β, β = 1/2 in d = 4 and β ≃ 0.33 in d = 3. MFT captures correctly the critical behavior above the upper critical dimension dc = 4, with logarithmic corrections in d = 4. In the context of renormalization group theory, the MFT results represent also the leading order contribution within an expansion in terms of ε = 4 − d. There are only two independent non-universal bulk amplitudes,59,60 such as ϕt and ξ+0.
is the non-universal amplitude of the bulk order parameter ϕb = ϕt|t|β, β = 1/2 in d = 4 and β ≃ 0.33 in d = 3. MFT captures correctly the critical behavior above the upper critical dimension dc = 4, with logarithmic corrections in d = 4. In the context of renormalization group theory, the MFT results represent also the leading order contribution within an expansion in terms of ε = 4 − d. There are only two independent non-universal bulk amplitudes,59,60 such as ϕt and ξ+0.
For a film confined by two planar walls, the MFT scaling functions of the critical Casimir force have been determined analytically65 and, inter alia, the critical Casimir amplitudes for the symmetry breaking BC have been found as 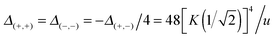 , where K is the complete elliptic integral of the first kind.
, where K is the complete elliptic integral of the first kind.
For the geometries studied here within MFT, the Hamiltonian 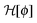 has been minimized numerically using a three-dimensional finite element method in order to obtain the order parameter profiles. The system is assumed to be translationally invariant along an extra dimension in d = 4. The critical Casimir forces are determined directly from the order parameter profile using the stress-tensor method.23,65,68
has been minimized numerically using a three-dimensional finite element method in order to obtain the order parameter profiles. The system is assumed to be translationally invariant along an extra dimension in d = 4. The critical Casimir forces are determined directly from the order parameter profile using the stress-tensor method.23,65,68
The scaling function k(a,b)(Θ) in eqn (1) covers the full range Θ ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) with Θ < 0 for t < 0 and Θ > 0 for t > 0, respectively. We note that the scaling variable Θ = sign(t)l/ξ± contains distinct denominators ξ±0 for t ≷ 0 in accordance with the universal ratio Rξ = ξ+0/ξ−0 = 1.96 in d = 358 and
with Θ < 0 for t < 0 and Θ > 0 for t > 0, respectively. We note that the scaling variable Θ = sign(t)l/ξ± contains distinct denominators ξ±0 for t ≷ 0 in accordance with the universal ratio Rξ = ξ+0/ξ−0 = 1.96 in d = 358 and 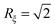 in d = 4.69 Here, we focus on t ≥ 0, for which the solvent is in the homogeneous, mixed phase. This relates to the common experimental situation in which the critical behavior near the lower critical point of a binary liquid mixture is studied upon approaching Tc along a thermodynamic path from below (e.g.ref. 15, 38, 40–42 and 70).
in d = 4.69 Here, we focus on t ≥ 0, for which the solvent is in the homogeneous, mixed phase. This relates to the common experimental situation in which the critical behavior near the lower critical point of a binary liquid mixture is studied upon approaching Tc along a thermodynamic path from below (e.g.ref. 15, 38, 40–42 and 70).
C. Derjaguin approximation
The Derjaguin approximation (DA) is a common technique to extend theoretically results for planar geometry, which can be derived directly, to curved objects, which are more common in practice. This approximation builds on the additivity of forces. Accordingly, a curved surface is sliced into infinitesimally small surface elements and the total force is calculated by summing up the individual planar wall–wall contributions k(a,b) from the surface elements vis-à-vis, with (a) and (b) indicating the BC at the two surfaces. In the case of a spherical object, its surface is divided into thin rings of radius ρ,16,22 whereas the surface of cylindrical objects is decomposed into parallel pairs of infinitesimally narrow stripes at lateral positions ±ρ.57,71 For both types of objects, the distance of each element from a planar wall is given by 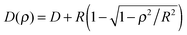 , where D is the closest distance between the particle surface with radius R and the planar wall. Since the DA holds only in the limit of large particle radii R, i.e. Δ = D/R → 0, it is often16,22,57 used in conjunction with the further “parabolic distance approximation” D(ρ) ≈ D(1 + ρ2/(2RD)). For comparison, the surface-to-surface distance
, where D is the closest distance between the particle surface with radius R and the planar wall. Since the DA holds only in the limit of large particle radii R, i.e. Δ = D/R → 0, it is often16,22,57 used in conjunction with the further “parabolic distance approximation” D(ρ) ≈ D(1 + ρ2/(2RD)). For comparison, the surface-to-surface distance  either between two spheres or between two cylinders increases twice as fast with ρ; correspondingly, within the “parabolic distance approximation” one has in these two cases D(ρ) ≈ D(1 + ρ2/(RD)).
either between two spheres or between two cylinders increases twice as fast with ρ; correspondingly, within the “parabolic distance approximation” one has in these two cases D(ρ) ≈ D(1 + ρ2/(RD)).
For Janus particles, the basic DA approach remains the same. However, for them the force contribution switches spatially between k(+,+) = k(−,−) and k(+,−) = k(+,−) due to the variation of the BC across the surface(s). Assuming again additivity and neglecting edge effects, the summation over these force contributions can be performed after appropriately subdividing the surface and grouping the surface elements according to the various pairs of BCs. For two Janus spheres this is presented in detail in Appendix B.
The DA for these geometries is based on the scaling function of the force for the film geometry. For d = 4 this is adopted directly from our independent MFT calculations for two parallel walls (see below). In d = 3 the scaling function of the force for the film geometry has been obtained from MC simulations.10,11,14,72,73 Here, we rely on the numerical estimate referred to as “approximation (i)” in Fig. 9 and 10 of ref. 11. The systematic uncertainty of the overall amplitude of these scaling functions can, in the worst case, reach up to 10–20%,11 which also affects our predictions. However, the impact on the scaling functions normalized by the critical amplitude Δ(+,+) is greatly reduced to a relative level of at most 5%.57
It has been shown that the DA is most reliable for t ≥ 0,19,71 whereas for the (+,−) BC and t < 0 clear deviations from the DA occur, which can be explained in terms of the formation of an interface surrounding the particles.71
III. General aspects concerning Janus particles
A. Implications of the DA for a cylindrical particle above a substrate
Before we address the subject of the effective interaction between two Janus particles, we assess the quality of the DA for the configuration of a single Janus cylinder above a substrate, which is limited, inter alia, by its underlying assumption of additivity of the forces. The analysis in this section follows Fig. 1(a) by first restating the case of a homogeneous particle above a substrate with a chemical step, and then by introducing a Janus particle above a homogeneous substrate before considering a Janus particle above a substrate step, which will connect to the case of two Janus particles.
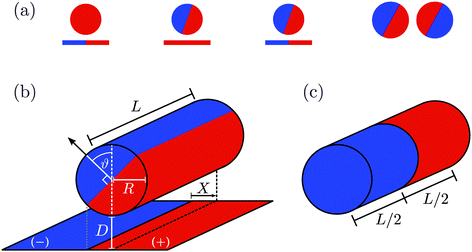 |
| | Fig. 1 (a) Sideview sketches of all types of configurations considered in the present study: chemically homogeneous cylinder vs. substrate with a chemical step – Janus cylinder (as in (b)) vs. homogeneous substrate – Janus cylinder vs. substrate with a chemical step – two Janus cylinders or two Janus spheres without a substrate. (b) Janus cylinder in d = 3 with the chemical step along the cylinder axis, shown in proximity and parallel to a planar substrate. The orientation of the Janus cylinder is given by the angle ϑ between the normal of the equatorial plane of the Janus cylinder and the substrate normal. The substrate may also feature a chemical step parallel to the cylinder, at a lateral position X which measures the distance between the projection of the cylinder axis (dotted line) and the chemical step at the substrate. (c) Second variant of a Janus cylinder in d = 3, with the chemical step perpendicular to the axis of the cylinder. For a discussion of this variant see ref. 71. | |
First, we clarify the ambiguous definition of a (hyper-)cylinder in higher dimensions (d ≥ 4). In the present context, a cylinder in d = 4 is a geometrical object with radius R and two lengths L and L4, defined by the volume x2 + y2 ≤ R2, 0 ≤ z ≤ L and 0 ≤ w ≤ L4, where w is the coordinate in the extra dimension and L4 is the length in that direction.74 We will use the (d − 2) dimensional length  in order to denote
in order to denote  in d = 3 and
in d = 3 and 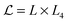 in d = 4.
in d = 4.
The Janus character due to the BC at the surface of a cylinder can be realized in two distinct ways in d = 3 [see Fig. 1(b) and (c)] and in three ways in d = 4. The two possibilities in d = 3 are evident with the chemical step, separating two domains of BCs, either running along the length of the cylinder, cutting it into two half-cylinders [Fig. 1(b)], or perpendicular to the length of the cylinder, cutting it into two cylinders of half the length [Fig. 1(c)]. It has been demonstrated that the latter case can be constructed within DA by a straightforward combination of two cylinders (see ref. 71). The former case, however, requires a new analysis, which is carried out in the present study. The third case, occurring for a cylinder in d = 4, has the step in the BC in the extra dimension, rendering two equal sized hypercylinders with different BCs. This is of limited practical use regarding the comparison with results in d = 3. We therefore restrict our description to the “natural” choice of a Janus cylinder being composed of two half-cylinders, both in d = 3 and in d = 4.
In order to set the stage, we recall the case of a chemically homogeneous cylinder close to a substrate with a chemical step (see Fig. 1(a)). The lateral position of the cylinder axis relative to a chemical step in parallel to the substrate is denoted by X (see Fig. 1(b)). Moreover, we always consider the cylinder to be parallel to the substrate (and to the step). The critical Casimir force 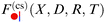 between a homogeneous cylindrical particle of length L and radius R, and a substrate with a step, at a lateral position X, has the scaling form (see eqn (D1) in Appendix D of ref. 57)
between a homogeneous cylindrical particle of length L and radius R, and a substrate with a step, at a lateral position X, has the scaling form (see eqn (D1) in Appendix D of ref. 57)
| | 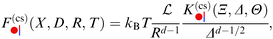 | (5) |
with the dimensionless scaling variables
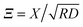
,
Δ =
D/
R, and
Θ = ±
D/
ξ±(
T) (with sign(
Θ) = sign(
t)) in
d dimensions. The scaling function
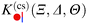
of the force

can be decomposed as
57| | 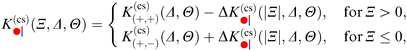 | (6) |
where (see eqn (D3) in
ref. 57)
| | 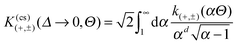 | (7) |
is the scaling function of the force within DA for a homogeneous cylindrical particle (+ or −) close to a homogeneous substrate (+ or −), and thus does not depend on
Ξ. The scaling function
k(+,±) for the slab geometry serves as an input, which is obtained either from MFT calculations for the film geometry in
d = 4 or from an interpolation of MC data provided in
ref. 11 for
d = 3. The choice of signs in
eqn (6) reflects
Ξ ≷ 0, chosen such that the direction of positive
X points to the side of the step with the same BC as the colloid (see
Fig. 1(a)) which is (+) in the present notation.
The excess scaling function  involving the step position X is given within DA by (see eqn (D6) in ref. 57)
involving the step position X is given within DA by (see eqn (D6) in ref. 57)
| | 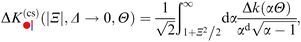 | (8) |
where Δ
k =
k(+,+) −
k(+,−) < 0 is the difference between the slab scaling functions for distinct BCs, which is negative for all temperatures
Θ. Note that

depends only on the absolute value of the scaled distance
Ξ, because the inverted position is equivalent to a switch of the BC of the step, which is covered by
eqn (6).
As a function of the scaled temperature Θ, in Fig. 2(a) we compare the scaling function of the force  obtained within DA for d = 4 viaeqn (6)–(8) (dashed curves) with the corresponding full MFT results (solid lines) determined by numerical minimization of the Hamiltonian. As expected from ref. 57, in Fig. 2(a) the DA scaling function approximates the full MFT results well for the geometry of a homogeneous cylinder above a substrate step, shown for various scaled step positions Ξ on both sides of the step.
obtained within DA for d = 4 viaeqn (6)–(8) (dashed curves) with the corresponding full MFT results (solid lines) determined by numerical minimization of the Hamiltonian. As expected from ref. 57, in Fig. 2(a) the DA scaling function approximates the full MFT results well for the geometry of a homogeneous cylinder above a substrate step, shown for various scaled step positions Ξ on both sides of the step.
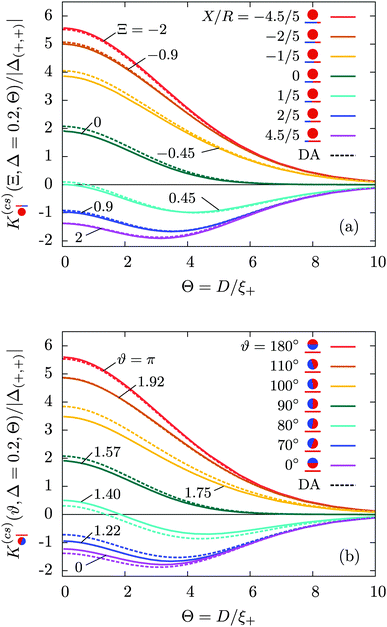 |
| | Fig. 2 (a) Scaling function  of the force between a homogeneous cylindrical particle above a substrate with a chemical step at various scaled lateral positions Ξ. (b) Scaling function of the force of the force between a homogeneous cylindrical particle above a substrate with a chemical step at various scaled lateral positions Ξ. (b) Scaling function of the force  between a Janus cylinder and a homogeneous substrate for various orientations ϑ. The full MFT results are shown as solid lines, whereas the corresponding DA scaling functions are shown as dashed lines. The DA yields a qualitatively adequate approximation for the MFT scaling functions, with varying quantitative deviations in (a) and (b). between a Janus cylinder and a homogeneous substrate for various orientations ϑ. The full MFT results are shown as solid lines, whereas the corresponding DA scaling functions are shown as dashed lines. The DA yields a qualitatively adequate approximation for the MFT scaling functions, with varying quantitative deviations in (a) and (b). | |
In accordance with the second sketch in Fig. 1(a), we now consider a Janus cylinder, but placed above a homogeneous substrate. The corresponding critical Casimir force 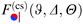 depends on the orientation angle ϑ (Fig. 1(b)) of the Janus cylinder. The scaling form remains the same as in the previous case, i.e.,
depends on the orientation angle ϑ (Fig. 1(b)) of the Janus cylinder. The scaling form remains the same as in the previous case, i.e.,
| | 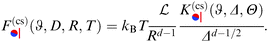 | (9) |
Comparing in
Fig. 1(a) the sketch for the case of a homogeneous cylinder near a stepped substrate with the case of a Janus cylinder above a homogeneous substrate, one realizes that for a suitable orientation
ϑ of the Janus cylinder the same pairings of BCs between the substrate and the particle enter the DA. Projecting the equatorial plane of a Janus cylinder onto a homogeneous substrate yields a distance
X =
XJ =
R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ between the (left) edge of the projection and the projection of the cylinder axis (
Fig. 1(b)). Conversely, the projection of the axis of a homogeneous cylinder onto a substrate with a chemical step renders a distance
X between them (
Fig. 1(b)). Choosing
X =
XJ =
R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ, within DA the sums of the surface elements
vis-à-vis for these two configurations are the same and thus yield the same force. In terms of the present scaling function the relation
X =
XJ translates into
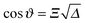
. This implies that within DA the scaling function

of the force between a Janus cylinder and a homogeneous substrate follows from
eqn (6)–(8) upon substituting
X =
R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ therein.
Fig. 2(b) shows for a Janus cylinder next to a homogeneous wall as a function of the scaled temperature
Θ the full MFT results (solid lines) for various orientations
ϑ (chosen independently from
Fig. 2(a)). The corresponding DA scaling functions are shown as dashed lines. In
Fig. 2(b), for the same distance
Δ = 1/5, the DA scaling functions appear to deviate slightly more from the corresponding full MFT results than those in
Fig. 2(a).
In order to assess quantitatively the difference between DA and full MFT, it is more suitable to compare the corresponding scaling functions  and
and 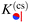 of the force for fixed scaled temperature Θ as a function of the scaling variable
of the force for fixed scaled temperature Θ as a function of the scaling variable 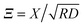 , which either corresponds to the lateral position X of the axis of a homogeneous cylinder relative to a chemical step on the substrate, or to the orientation
, which either corresponds to the lateral position X of the axis of a homogeneous cylinder relative to a chemical step on the substrate, or to the orientation 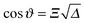 of a Janus cylinder above a homogeneous substrate. Accordingly, for the two scaled temperatures Θ = 1 and Θ = 5.65 in Fig. 3 we show the full MFT scaling function
of a Janus cylinder above a homogeneous substrate. Accordingly, for the two scaled temperatures Θ = 1 and Θ = 5.65 in Fig. 3 we show the full MFT scaling function 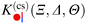 of the force for the homogeneous cylinder-step geometry [eqn (5)] as solid lines and the full MFT scaling function
of the force for the homogeneous cylinder-step geometry [eqn (5)] as solid lines and the full MFT scaling function  of a Janus cylinder next to a homogeneous substrate [eqn (9)] as dashed lines. The two values of Θ, here and in subsequent figures, are chosen to represent on the one hand values very close to Tc, and on the other hand those approaching Tc, but within the range of the monotonic decay of the scaling function (see also Fig. 2). In the spirit of the aforementioned equivalence within DA, the orientation angle ϑ of the Janus cylinder is related to the distance X between the projected axis of a homogeneous cylinder and the chemical step at the wall via the DA relation Ξ = Δ−1/2
of a Janus cylinder next to a homogeneous substrate [eqn (9)] as dashed lines. The two values of Θ, here and in subsequent figures, are chosen to represent on the one hand values very close to Tc, and on the other hand those approaching Tc, but within the range of the monotonic decay of the scaling function (see also Fig. 2). In the spirit of the aforementioned equivalence within DA, the orientation angle ϑ of the Janus cylinder is related to the distance X between the projected axis of a homogeneous cylinder and the chemical step at the wall via the DA relation Ξ = Δ−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ. For Δ = 1 in Fig. 3(a), there is a visible difference between the two scaling functions. However, for Δ = 1/5 in Fig. 3(b), which is closer to the DA limit Δ ≪ 1, the difference is considerably smaller. For comparison, in gray the scaling function of the force within DA is shown, which approximates both MFT scaling functions for Δ ≪ 1.
ϑ. For Δ = 1 in Fig. 3(a), there is a visible difference between the two scaling functions. However, for Δ = 1/5 in Fig. 3(b), which is closer to the DA limit Δ ≪ 1, the difference is considerably smaller. For comparison, in gray the scaling function of the force within DA is shown, which approximates both MFT scaling functions for Δ ≪ 1.
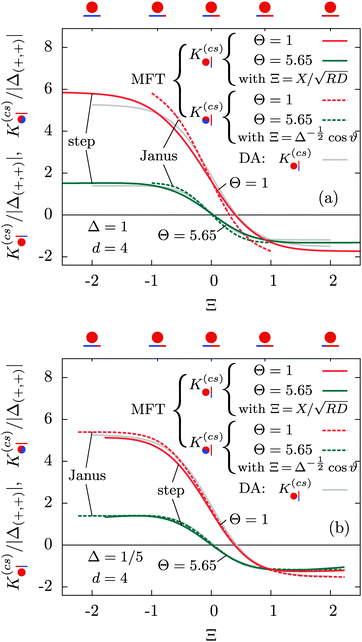 |
| | Fig. 3 Comparison of the scaling functions of the force  between a homogeneous cylinder above a chemical step on the substrate (solid lines) and between a homogeneous cylinder above a chemical step on the substrate (solid lines) and  for a Janus cylinder above a homogeneous substrate (dashed lines). The DA (valid for Δ ≪ 1) implies the same scaling function in both cases (gray lines), provided the tilt angle ϑ of the Janus cylinder (see Fig. 1(b)) is related to the scaled step position on the substrate as Ξ = Δ−1/2 for a Janus cylinder above a homogeneous substrate (dashed lines). The DA (valid for Δ ≪ 1) implies the same scaling function in both cases (gray lines), provided the tilt angle ϑ of the Janus cylinder (see Fig. 1(b)) is related to the scaled step position on the substrate as Ξ = Δ−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ. The full mean field results for ϑ. The full mean field results for  (step) and (step) and 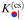 (Janus) are shown for Δ = 1 in (a) and Δ = 1/5 in (b), each for the two scaled temperatures Θ = 1 (red; close to Tc) and Θ = 5.65 (green; within the monotonic decay of (Janus) are shown for Δ = 1 in (a) and Δ = 1/5 in (b), each for the two scaled temperatures Θ = 1 (red; close to Tc) and Θ = 5.65 (green; within the monotonic decay of  as a function of Θ). From (a) it can be seen that within full MFT the correspondence between the case of a homogeneous cylinder above a chemical step on the substrate and a Janus particle above a homogeneous substrate does not hold in general. It holds roughly for Θ = 5.65 and further away from Tc, but not close to Tc (such as for Θ = 1). However, for Δ = 1/5 in (b), i.e. close to the DA limit of Δ ≪ 1, the correspondence of the two scaling functions within DA carries over to the MFT results. As a guide to the eye, visualizations of the geometry corresponding to certain values of Ξ are provided at the top of the panels. as a function of Θ). From (a) it can be seen that within full MFT the correspondence between the case of a homogeneous cylinder above a chemical step on the substrate and a Janus particle above a homogeneous substrate does not hold in general. It holds roughly for Θ = 5.65 and further away from Tc, but not close to Tc (such as for Θ = 1). However, for Δ = 1/5 in (b), i.e. close to the DA limit of Δ ≪ 1, the correspondence of the two scaling functions within DA carries over to the MFT results. As a guide to the eye, visualizations of the geometry corresponding to certain values of Ξ are provided at the top of the panels. | |
Thus it appears that the MFT results of both geometries approach each other in the limit of Δ → 0. This raises the question whether the relation between the two configurations, as implied by DA, reflects a more general foundation beyond DA.
B. Comparison of forces in terms of order parameter profiles
In contrast to the DA, the MFT minimization technique renders equilibrium order parameter profiles for each scaled temperature Θ. Nonetheless, the DA implies a certain structure of the order parameter profile, even though in general it is ignorant concerning the profile.
The reduced MFT order parameter profiles m(r) for a homogeneous cylinder above a chemical step are depicted in Fig. 4(a) for Θ = 1 and in Fig. 4(b) for Θ = 5.65. In this example, the geometric parameters have been chosen such that D = R, i.e. Δ = 1; the colloid with the (+) BC is positioned at X = −0.9R on the left side of the step with the opposite (−) BC there, and the cylinder axis is normal to the cut plane of the order parameter profiles, which are invariant along the cylinder axis. The profiles are taken for Θ > 0 at the critical concentration, i.e. in the mixed phase, in which the order parameter differs from zero primarily only near the surfaces. Due to the opposing BC on the colloid and on the left half of the substrate surface, the profile must cross zero (green line), although this does not indicate the formation of an actual interface. The gray line represents the zero crossing (at the same temperature) of the profile between a homogeneous particle and a homogeneous substrate, but with an opposing BC. In the case of a chemical step on the substrate, the DA implicitly assumes that the order parameter profile follows that for a homogeneous substrate up to the lateral position x = 0 of the step (Fig. 4(a) and (b)). Generally, Fig. 4(a) and (b) show that the actual zero crossing (green) follows closely the homogeneous case (gray), as assumed by the DA, up to a certain lateral position. However, the point of deviation between the green and the gray lines occurs at a lateral position which is to the left of the step position, because the actual zero crossing line (green) smoothly bends towards the step. The curvature of this bending depends on the temperature and broadens upon increasing the correlation length (i.e. decreasing Θ).
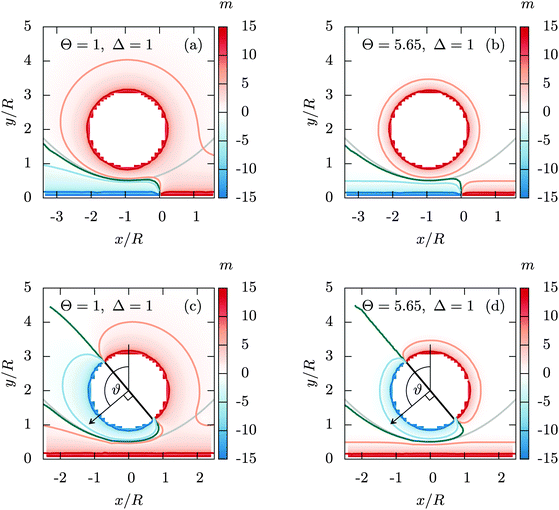 |
| | Fig. 4 Reduced order parameter profiles m as obtained from MFT in d = 4 and in units of the amplitude ϕt of the bulk order parameter ϕb = ϕt|t|1/2. The values of the order parameter are color coded, with red for positive values and blue for negative values, following the convention for the BC in Fig. 1. For Θ = 1 (a) depicts a homogeneous cylinder with the (+) BC at X = −0.9R above a substrate with a chemical step between the (+) BC for x > 0 and the (−) BC for x < 0. Panel (b) features the same geometry at Θ = 5.65, i.e. further away from Tc. For comparison, in (c) a Janus cylinder above a homogeneous substrate with the (+) BC is shown for Θ = 1 and in (d) for Θ = 5.65. The orientation of the Janus cylinder is taken as ϑ = 130°, so that cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ = −0.64. We have included certain isolines of the profile as a guide to the eye. The green line represents the zero crossing of the profiles, which has a special significance discussed in the main text. The gray curve indicates the zero crossing expected (at the same temperate) for the profile in the case that both the particle and the substrate are homogeneous, but with opposite BCs. ϑ = −0.64. We have included certain isolines of the profile as a guide to the eye. The green line represents the zero crossing of the profiles, which has a special significance discussed in the main text. The gray curve indicates the zero crossing expected (at the same temperate) for the profile in the case that both the particle and the substrate are homogeneous, but with opposite BCs. | |
In Fig. 4(c) and (d), the configuration of a Janus cylinder above a homogeneous substrate is shown in comparison to (a) and (b), for the scaled temperature Θ = 1 and Θ = 5.65. The orientation ϑ of the Janus cylinder has been chosen such that the configuration (a) and (b) and the configuration (c) and (d) yield forces within MFT which are approximately equal to each other. For both scaled temperatures, this was found to be the case for ϑ ≈ 130°, which deviates significantly from the DA relation ϑ = cos−1(X/R) = 154° for X/R = −0.9. Such a deviation is expected to occur away from the DA limit of Δ ≪ 1 [compare Fig. 3(a) and (b)]. For the Janus particles, we find that the zero crossing of the profiles (green line) again follows the one for a homogeneous colloid (gray line), but now bending towards the Janus equator on the particle. A systematic analysis reveals that one always finds equal values of the force in MFT for the step on the surface and for the Janus particle whenever the bending and the extension of the zero crossing line are closely mirroring each other in the two geometries. The reason for the equality of these forces within MFT goes right back to eqn (4). The Hamiltonian depends on the gradient of the order parameter profile, which relates to the bending of the zero line, but only via its square, which is independent of the direction of the bending. In Fig. 4(c) and (d) there is also an upper green zero crossing line, which is absent in (a) and (b). This line contributes only little to the force because it is relatively straight and because in that region the order parameter is small.
Based on the knowledge of the full MFT order parameter profiles, we construct a phenomenological relation beyond the DA relation of Ξ = Δ−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, which seeks to incorporate the bending of the zero crossing line. The base of this idea follows from ref. 71, where a similar principle was used successfully in order to reconcile DA with MFT results.
ϑ, which seeks to incorporate the bending of the zero crossing line. The base of this idea follows from ref. 71, where a similar principle was used successfully in order to reconcile DA with MFT results.
In Fig. 5, we sketch the essential features of a Janus cylinder of radius R, close to a homogeneous wall at distance D; the actual zero crossing line of the order parameter profile is shown in green (which is taken from Fig. 4(c), but here serves to represent a generic case), and the zero crossing implied by DA is shown as a solid light gray line. The dotted, vertical dark gray line indicates the original DA relation, which cuts off the solid gray zero crossing line (of the homogeneous system with the opposing BC at the colloid and substrate surface) at the projected position of the Janus equator. The visual agreement of the zero crossing lines can be improved by considering the DA for a fictitious scaled colloid (the blue and red semi-rings), with an effective radius of ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = R + pD and an effective surface-to-surface distance
= R + pD and an effective surface-to-surface distance ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = (1 − p)D, so that the zero crossing line follows the solid light gray line. This yields an improved scaled position (dotted, vertical light gray line)
= (1 − p)D, so that the zero crossing line follows the solid light gray line. This yields an improved scaled position (dotted, vertical light gray line)
| | 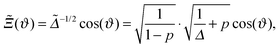 | (10) |
where
p is a free parameter which describes the rescaling of the particle size.
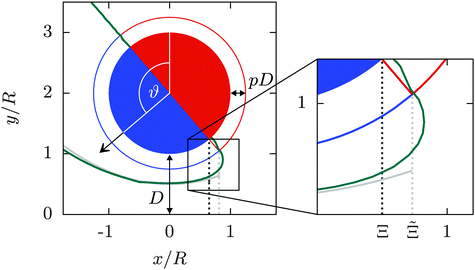 |
| | Fig. 5 A generic sketch depicting the essential features of a Janus cylinder at a distance D above a homogeneous substrate, tilted by an angle ϑ, akin to Fig. 4(c) and (d). An example for the actual zero crossing line of the order parameter profile, as found within full MFT, is shown in green. The zero crossing implied by the DA is shown in gray (solid light gray line, light and dark gray vertical dotted lines). In DA, the zero crossing is taken into account up to the scaled position Ξ = Δ−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ of the step in the BC of the Janus particle, projected onto the substrate along the normal of the substrate (dark gray dotted line). The improved DA relation ϑ of the step in the BC of the Janus particle, projected onto the substrate along the normal of the substrate (dark gray dotted line). The improved DA relation 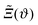 in eqn (10) follows the same principle, but applied to a fictitious particle of increased radius R + pD, with the rescaling parameter p, resulting in the solid light gray zero crossing line and the light gray vertical dotted line. The inset provides a magnified view of the relevant features. in eqn (10) follows the same principle, but applied to a fictitious particle of increased radius R + pD, with the rescaling parameter p, resulting in the solid light gray zero crossing line and the light gray vertical dotted line. The inset provides a magnified view of the relevant features. | |
Independently, we have calculated the scaling functions of the force within full MFT as a function of the position X of a homogeneous cylinder relative to a stepped substrate and for the orientation ϑ of the Janus cylinder, at fixed scaled temperatures Θ and distances Δ. Via linear interpolation within the two MFT scaling functions, we have extracted those values of X and ϑ for which both scaling functions of the force render the same value, which in turn renders a relation between the numeric values of ϑ and X. The proposed model 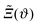 in eqn (10) can be checked against this discrete set {Ξ,ϑ}. We note that the projected, scaled step position
in eqn (10) can be checked against this discrete set {Ξ,ϑ}. We note that the projected, scaled step position 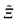 is proportional to
is proportional to ![[capital Delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10b.gif) −1/2 > Δ−1/2 for p > 0, i.e. for the same orientation ϑ, the scaled step position
−1/2 > Δ−1/2 for p > 0, i.e. for the same orientation ϑ, the scaled step position 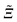 is larger than Ξ. However, for values of Ξ ≫ 1, the scaling function of the force saturates (see Fig. 3) and relating Ξ and ϑ numerically via the force within MFT becomes rather error-prone. This discredits fitting assumptions beyond the linear order. However, the relation in eqn (10), linearized around
is larger than Ξ. However, for values of Ξ ≫ 1, the scaling function of the force saturates (see Fig. 3) and relating Ξ and ϑ numerically via the force within MFT becomes rather error-prone. This discredits fitting assumptions beyond the linear order. However, the relation in eqn (10), linearized around 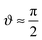 by using
by using 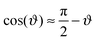 , results in a reasonable fit for p ≈ 1/4. Within fitting errors, the fit parameter p does not depend noticeably on the scaled temperature Θ and the scaling variable Δ. The value of the rescaling parameter p = 1/4 is in line with the presentation in Fig. 5, as it places the surface of the fictitious colloid halfway between the physical particle and the zero crossing line.
, results in a reasonable fit for p ≈ 1/4. Within fitting errors, the fit parameter p does not depend noticeably on the scaled temperature Θ and the scaling variable Δ. The value of the rescaling parameter p = 1/4 is in line with the presentation in Fig. 5, as it places the surface of the fictitious colloid halfway between the physical particle and the zero crossing line.
For comparison, Fig. 6 demonstrates the improved performance of the phenomenological relation 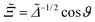 in eqn (10) with p = 1/4 compared with that of the approach used in Fig. 3, even for Δ = 1.
in eqn (10) with p = 1/4 compared with that of the approach used in Fig. 3, even for Δ = 1.
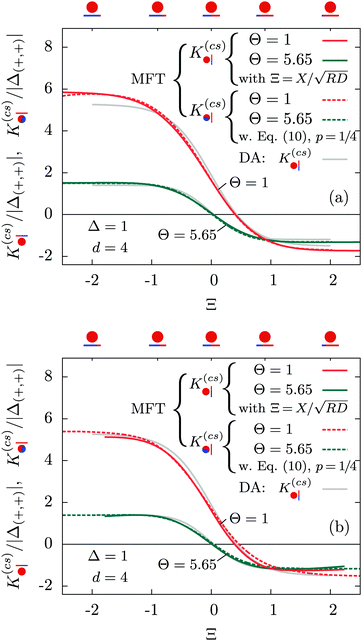 |
| | Fig. 6 The same as Fig. 3 but replacing Ξ by 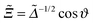 (eqn (10) with p = 1/4) for (eqn (10) with p = 1/4) for  . In this case, the correspondence between the scaling functions of the two configurations . In this case, the correspondence between the scaling functions of the two configurations  and and  holds within full MFT, for values of Δ outside the DA limit Δ ≪ 1. holds within full MFT, for values of Δ outside the DA limit Δ ≪ 1. | |
As a final remark, we emphasize that, in the above approach, within DA we counted the force to be normal to the substrate. An approach alternative to the DA considers the forces to be normal to the surface of the particle,75 which, however, leads to the same formal expressions for the critical Casimir forces. The improved DA relation in eqn (10) can be interpreted as a partial consideration of forces directed normal to the particle surface, with p being a weighting factor for the two force directions (see Fig. 5).
C. Cylindrical Janus particle above a chemical step
Here we analyze fully the case depicted in Fig. 1(b) of a single cylindrical Janus particle floating above a chemical step on the substrate. The cylindrical particle is taken to be oriented horizontally and all chemical steps are parallel to each other. Within DA, the configuration of a Janus particle above a step relates to the case of two walls each endowed with a chemical step, shifted with respect to each other,76 but accounting for distinct distance relations between the surface elements appearing in DA. Since the presence of two chemical steps can have a profound, non-additive effect on the order parameter profile, one has to check whether this spoils the usefulness of the relation introduced in eqn (10).
Within DA and for special configurations, the scaling function of the force 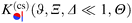 between a chemical step on the substrate and a Janus particle with orientation ϑ and its center shifted by
between a chemical step on the substrate and a Janus particle with orientation ϑ and its center shifted by 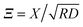 from the substrate step attains certain limiting expressions. For an upright orientation ϑ = 0 it has the same value as the scaling function
from the substrate step attains certain limiting expressions. For an upright orientation ϑ = 0 it has the same value as the scaling function 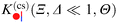 of the force between a homogeneous cylinder and a stepped substrate. If the Janus cylinder is positioned far away from the step, i.e. Ξ ≫ 1,
of the force between a homogeneous cylinder and a stepped substrate. If the Janus cylinder is positioned far away from the step, i.e. Ξ ≫ 1, 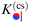 reduces to the scaling function of a Janus cylinder above a homogeneous substrate, then
reduces to the scaling function of a Janus cylinder above a homogeneous substrate, then 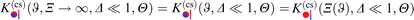 (where Ξ(ϑ) = Δ−1/2cos
(where Ξ(ϑ) = Δ−1/2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ or is given by eqn (10); analogously for Ξ → −∞).
ϑ or is given by eqn (10); analogously for Ξ → −∞).
Thus, similar to 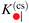 in eqn (6) and (7), the scaling function
in eqn (6) and (7), the scaling function 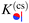 can be decomposed as
can be decomposed as 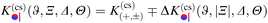 , where K(cs)(+,±) again refers to the scaling function of the force between a homogeneous cylinder and a homogeneous substrate (the rules when to use the upper and lower signs depend on ϑ and Ξ; see below):
, where K(cs)(+,±) again refers to the scaling function of the force between a homogeneous cylinder and a homogeneous substrate (the rules when to use the upper and lower signs depend on ϑ and Ξ; see below):
| | 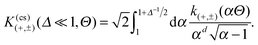 | (11) |
However, here the rhs of
eqn (11) carries a finite upper limit of integration,
i.e. without explicitly setting
Δ → 0. But the expression is still valid only in the DA limit
Δ ≪ 1. The dependence on nonzero values of
Δ ensures consistency with the scaling function of the excess force
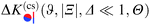
. The latter depends on the position of the Janus cylinder relative to the substrate step (again only
via the scaled absolute value |
Ξ| of the distance) and on the orientation
ϑ ∈ [−π,π]. The sign of the position
Ξ and the sign of the orientation
ϑ can be chosen according to different conventions. Here, the coordinates are chosen such that
ϑ > 0 rotates the normal of the equatorial plane of the Janus particle towards that side of the substrate which has the same BC,
i.e. here, the rotation is counter-clockwise towards the side
Ξ < 0 (see
Fig. 1(b)). We note that the force is invariant under reflection at the plane normal to the substrate and containing the cylinder axis (
ϑ → −
ϑ,
Ξ → −
Ξ and exchange of the BC on the substrate),
i.e.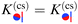
. Utilizing this symmetry, the decomposition reads
| | 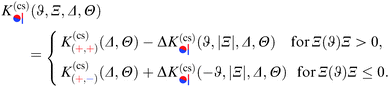 | (12) |
(Note that, as indicated, in
eqn (12), only in the first factor of the conditions,
Ξ is replaced by
Ξ(
ϑ) =
Δ−1/2cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ or, alternatively, by
eqn (10).) The condition
Ξ(
ϑ)
Ξ ≷ 0 considers in which direction the Janus cylinder is tilting (
e.g. Ξ(
ϑ) ∝ cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ > 0 ⇒ upwards) and over which side of the step it levitates (
via Ξ). Additionally, the equivalences
k(+,+) =
k(−,−) and
k(+,−) =
k(−,+) of the interaction between homogeneous, planar, and parallel walls lead to an invariance of the scaling function

upon inverting the normal of the particle,
i.e. ϑ →
ϑ ± π (such that
ϑ ∈ [−π,π]) and exchanging the BC of the substrate step (but without changing the position
Ξ), so that
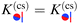
.
The excess scaling function  is obtained from the careful DA summation of the corresponding surface elements:
is obtained from the careful DA summation of the corresponding surface elements:
| | 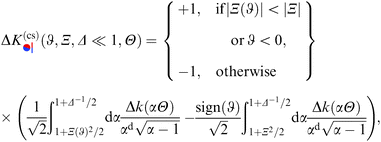 | (13) |
which has the structure of the difference between two expressions, resembling the scaling function corresponding to the chemical step on the substrate as in
eqn (8). The intricate prefactor effectively exchanges
Ξ(
ϑ) ↔
Ξ if |
Ξ(
ϑ)| ≥ |
Ξ|, which affects the sign only if
ϑ ≥ 0. Note that

depends on
ϑ only
via the sign and
via |
Ξ(
ϑ)| ∝ |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ|. One can verify that both the symmetry operations of reflection (
ϑ → −
ϑ) as well as inversion (
ϑ →
ϑ ± π such that
ϑ ∈ [−π,π]) yield the same result for the excess scaling function,
i.e.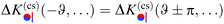
. Note that neither reflecting the position
Ξ → −
Ξ nor exchanging the BC affects

, but only
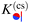
.
In Fig. 7, we compare the DA with the full MFT results for the scaling function 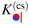 for two separations Δ = 1 in (a) and Δ = 1/5 in (b), with the step on the substrate fixed at Ξ = 0 (red sets of squares and lines). Within DA, this represents a peculiar configuration in that the orientations ϑ = ±π/2 of the Janus particle correspond to configurations in which both the step on the particle and the one on the substrate share a common vertical plane (see the sketches below the horizontal axis). At ϑ = −π/2, due to the opposing BC between all DA surface elements, the force (red lines) is repulsive (>0). For Δ = 1, around ϑ = −π/2 the DA result slightly overestimates the MFT result. Similarly, the special orientation at ϑ = π/2 leads to an attractive force (<0); here, however, for Δ = 1, DA clearly underestimates the MFT results. The cusplike shape of the scaling function around the maximum and minimum is an artifact of the DA; MFT renders a smooth and broader curve. In general, the MFT results are slightly more attractive and less repulsive than those predicted by DA. Nonetheless, for Δ ≪ 1 [Fig. 7(b)] DA and MFT agree rather well, even at ϑ = ±π/2. This is reassuring because for these orientations the shortcomings of the DA are particularly pronounced. As implied by the DA and in view of its reliability, the overall shape of the scaling function
for two separations Δ = 1 in (a) and Δ = 1/5 in (b), with the step on the substrate fixed at Ξ = 0 (red sets of squares and lines). Within DA, this represents a peculiar configuration in that the orientations ϑ = ±π/2 of the Janus particle correspond to configurations in which both the step on the particle and the one on the substrate share a common vertical plane (see the sketches below the horizontal axis). At ϑ = −π/2, due to the opposing BC between all DA surface elements, the force (red lines) is repulsive (>0). For Δ = 1, around ϑ = −π/2 the DA result slightly overestimates the MFT result. Similarly, the special orientation at ϑ = π/2 leads to an attractive force (<0); here, however, for Δ = 1, DA clearly underestimates the MFT results. The cusplike shape of the scaling function around the maximum and minimum is an artifact of the DA; MFT renders a smooth and broader curve. In general, the MFT results are slightly more attractive and less repulsive than those predicted by DA. Nonetheless, for Δ ≪ 1 [Fig. 7(b)] DA and MFT agree rather well, even at ϑ = ±π/2. This is reassuring because for these orientations the shortcomings of the DA are particularly pronounced. As implied by the DA and in view of its reliability, the overall shape of the scaling function 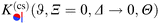 , within MFT and as a function of ϑ, is consistent with the dependence of the scaling function of the force between two patterned, planar substrates on a lateral shift (see ref. 76).
, within MFT and as a function of ϑ, is consistent with the dependence of the scaling function of the force between two patterned, planar substrates on a lateral shift (see ref. 76).
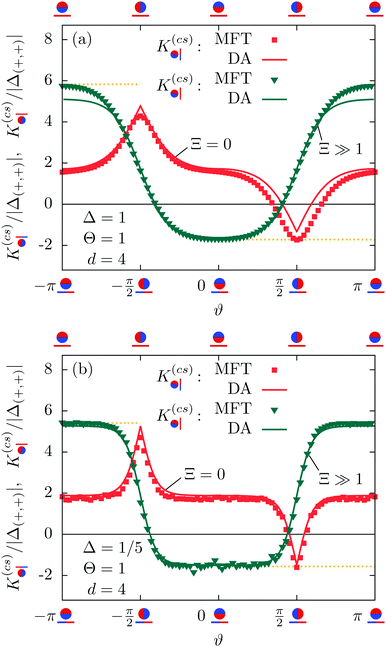 |
| | Fig. 7 (a) Scaling function 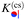 of the force between a Janus cylinder and a step on the substrate (in red), as a function of the particle orientation ϑ for Ξ = 0. The solid lines represent the results within DA, whereas the squares correspond to numerical MFT results for a separation Δ = D/R = 1. The green lines and triangles represent the scaling function of the force between a Janus cylinder and a step on the substrate (in red), as a function of the particle orientation ϑ for Ξ = 0. The solid lines represent the results within DA, whereas the squares correspond to numerical MFT results for a separation Δ = D/R = 1. The green lines and triangles represent the scaling function  of the force which corresponds to the case of a homogeneous substrate, or equally, to the case of a step that is far away from the particle, i.e. |Ξ| ≫ 1 [see eqn (6)]. (b) The same, but for Δ = 1/5. Both in (a) and (b), the MFT values of the scaling functions K(cs)(+,+) and K(cs)(+,−) [eqn (11)] for the fully attractive (<0) and repulsive (>0) cases, respectively, of a homogeneous cylinder and a homogeneous substrate are indicated by dotted golden lines. At the top of the panels, we indicate configurations with the Janus cylinder above a homogeneous substrate corresponding to certain points of the green curve for Ξ ≫ 1. Similarly, at the bottom of the panels, configurations are shown with the Janus particle directly above the step corresponding to the red curve, i.e. Ξ = 0. of the force which corresponds to the case of a homogeneous substrate, or equally, to the case of a step that is far away from the particle, i.e. |Ξ| ≫ 1 [see eqn (6)]. (b) The same, but for Δ = 1/5. Both in (a) and (b), the MFT values of the scaling functions K(cs)(+,+) and K(cs)(+,−) [eqn (11)] for the fully attractive (<0) and repulsive (>0) cases, respectively, of a homogeneous cylinder and a homogeneous substrate are indicated by dotted golden lines. At the top of the panels, we indicate configurations with the Janus cylinder above a homogeneous substrate corresponding to certain points of the green curve for Ξ ≫ 1. Similarly, at the bottom of the panels, configurations are shown with the Janus particle directly above the step corresponding to the red curve, i.e. Ξ = 0. | |
We point out that the DA curves shown in Fig. 6 are based on the improved relation given by eqn (10). For the original DA relation Ξ(ϑ) = Δ−1/2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, the agreement between DA and MFT turns out to be poorer in Fig. 7(a), i.e. for Δ = 1, but remains comparable to the good agreement evident in Fig. 7(b), i.e. for Δ = 1/5 (see also Fig. 3). We find that the explicit dependence on Δ introduced by eqn (10) and (11) does not improve the agreement between DA and MFT for the strongly attractive or repulsive configurations: in Fig. 7(a) see the difference between the green line and the green symbols as well as the dotted golden lines which refer to MFT results for K(cs)(+,+) < 0 and K(cs)(+,−) > 0. However, the dependence on Δ of the MFT scaling functions for the case of a homogeneous cylinder and substrate has a different cause.71 Within DA, a dependence on Δ has been introduced via the DA relation Ξ(ϑ) = Δ−1/2cos
ϑ, the agreement between DA and MFT turns out to be poorer in Fig. 7(a), i.e. for Δ = 1, but remains comparable to the good agreement evident in Fig. 7(b), i.e. for Δ = 1/5 (see also Fig. 3). We find that the explicit dependence on Δ introduced by eqn (10) and (11) does not improve the agreement between DA and MFT for the strongly attractive or repulsive configurations: in Fig. 7(a) see the difference between the green line and the green symbols as well as the dotted golden lines which refer to MFT results for K(cs)(+,+) < 0 and K(cs)(+,−) > 0. However, the dependence on Δ of the MFT scaling functions for the case of a homogeneous cylinder and substrate has a different cause.71 Within DA, a dependence on Δ has been introduced via the DA relation Ξ(ϑ) = Δ−1/2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ or viaeqn (10) along with the dependence on ϑ. Thus, the good agreement between the slopes of the DA and MFT scaling functions shown in Fig. 7 as a function of ϑ for different Δ values indicates the consistency of these relations beyond the DA limit.
ϑ or viaeqn (10) along with the dependence on ϑ. Thus, the good agreement between the slopes of the DA and MFT scaling functions shown in Fig. 7 as a function of ϑ for different Δ values indicates the consistency of these relations beyond the DA limit.
From these findings we conclude that the DA, although for Δ ≳ 1 it deviates quantitatively from the MFT results in d = 4, exhibits no basic flaws. In fact, studying the implication of the use of the DA in this section has revealed that the parameters Ξ and ϑ, associated with the positions of the chemical steps on the substrate and on the Janus cylinder, are related according to Ξ(ϑ) = Δ−1/2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ. The modified scaling variable
ϑ. The modified scaling variable 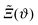 (eqn (10)) improves quantitatively the agreement with the full MFT results. We consider these properties as a justification to study below two Janus particles based on DA only.
(eqn (10)) improves quantitatively the agreement with the full MFT results. We consider these properties as a justification to study below two Janus particles based on DA only.
IV. Two Janus cylinders
Reassured by the result that DA can be used reliably for describing the force acting on a single Janus particle near a substrate, in this section we determine the force and the effective potential between two Janus cylinders within DA and without the substrate. For reasons of simplicity, we assume the long axes of the two cylinders to be parallel to each other, i.e. the positions and rotations of the cylinders are confined to a plane. This amounts to consider effectively discs in a two-dimensional system but with interactions corresponding to an embedding solvent in d = 3 or d = 4. In view of the experimental interest in such Janus particles, in the following figures we depict the scaling function in d = 3. This is accomplished by taking the wall-wall scaling functions k(a,b), which are needed as input for the DA, from ref. 11, i.e. from numerical simulations in d = 3.
According to renormalization group theory the singular part of the force between two Janus cylinders consists of prefactors which produce the unit of a force (kBT/R), the reduced length 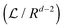 and a dimensionless scaling function
and a dimensionless scaling function 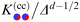 , as in the case of two homogeneous cylinders:77
, as in the case of two homogeneous cylinders:77
| | 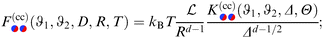 | (14) |
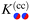
is the universal scaling function of the force between two Janus cylinders with equal radius
R,
ϑ1 and
ϑ2 are the orientations of the two Janus particles, and
Δ =
D/
R and
Θ = ±
D/
ξ±(
T) are dimensionless scaling variables for the surface-to-surface distance and the temperature, respectively. This scaling form is of the same type as the one in
eqn (5) for a homogeneous cylindrical particle above a stepped substrate and to the one in
eqn (9) for a Janus cylinder above a homogeneous substrate; however, the corresponding scaling functions are distinct. Within DA, for certain configurations
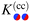
and,
e.g.,
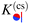
can attain the same values as the corresponding scaling functions for homogeneous particles. Within the corresponding expressions (see
eqn (12)),
K(cs)(+,±) for a homogeneous cylindrical particle and a homogeneous substrate is stronger by a factor of
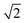
compared with
K(cc)(+,±) for two homogeneous cylinders.
A. Derjaguin approximation
Within DA, the force 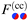 between two Janus cylinders orientated top-to-bottom [(ϑ1,ϑ2) = (0,0) and (±π,±π)], bottom-to-bottom [(0,±π)], or top-to-top [(±π,0)] is identical to the force between two homogeneous cylinders F(cc)(a,b)77 with (a,b) as the BC of the sides facing each other (compare Fig. 7). Upon construction this follows from the fact that for these configurations, the equatorial planes are orthogonal to the axis connecting the centers of the particles. Analogously as in eqn (12), we express the force between two Janus cylinders
between two Janus cylinders orientated top-to-bottom [(ϑ1,ϑ2) = (0,0) and (±π,±π)], bottom-to-bottom [(0,±π)], or top-to-top [(±π,0)] is identical to the force between two homogeneous cylinders F(cc)(a,b)77 with (a,b) as the BC of the sides facing each other (compare Fig. 7). Upon construction this follows from the fact that for these configurations, the equatorial planes are orthogonal to the axis connecting the centers of the particles. Analogously as in eqn (12), we express the force between two Janus cylinders  relative to the force F(cc)(+,±) between two homogeneous cylinders, yielding
relative to the force F(cc)(+,±) between two homogeneous cylinders, yielding| | 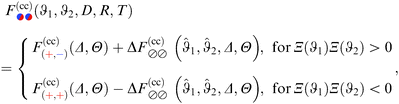 | (15) |
with Ξ(ϑi) = Δ−1/2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi and where, without the loss of generality, we introduced the reduced angles
ϑi and where, without the loss of generality, we introduced the reduced angles 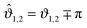 such that
such that 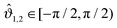 . Note that a shift of ±π amounts to reflecting the normals n1 and n2 at the corresponding equatorial plane of particles ① and ②, respectively. The subscript of the excess scaling function
. Note that a shift of ±π amounts to reflecting the normals n1 and n2 at the corresponding equatorial plane of particles ① and ②, respectively. The subscript of the excess scaling function 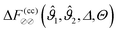 is not colored in order to emphasize that only the reduced angles enter. As in the previous case, the form given by eqn (15) is manifestly invariant against that reflection while also exchanging the BCs of the particles. For instance, for any configuration with ϑ1,2 ∈ [−π/2,π/2], i.e. Ξ(ϑ1) Ξ(ϑ2) > 0, one has
is not colored in order to emphasize that only the reduced angles enter. As in the previous case, the form given by eqn (15) is manifestly invariant against that reflection while also exchanging the BCs of the particles. For instance, for any configuration with ϑ1,2 ∈ [−π/2,π/2], i.e. Ξ(ϑ1) Ξ(ϑ2) > 0, one has| | 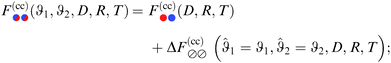 | (16) |
if instead ϑ2 is reflected to ϑ2′ = ϑ2 + π, one has Ξ(ϑ2′) = Δ−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2′ < 0, leading to
ϑ2′ < 0, leading to| | 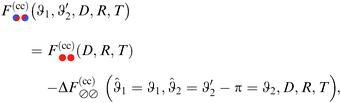 | (17) |
which corresponds to exchanging the BC. The subscript of the forces  and
and  between homogeneous particles has been colored in order to visualize the BC. We additionally enforce
between homogeneous particles has been colored in order to visualize the BC. We additionally enforce 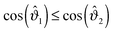 . The expressions for
. The expressions for  for all other configurations can be reduced to those in eqn (15) by exchanging the BC (a,b), by appropriately setting
for all other configurations can be reduced to those in eqn (15) by exchanging the BC (a,b), by appropriately setting 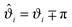 with i = {1,2}, and by switching the labeling
with i = {1,2}, and by switching the labeling 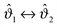 . In this sense, in the following we drop the hat of
. In this sense, in the following we drop the hat of 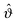 in favor of a lighter notation. Note that Ξ(ϑ1) Ξ(ϑ2) = 0 is exempted from the cases considered in eqn (15); in this limiting case the conditions should be read as abbreviations for
in favor of a lighter notation. Note that Ξ(ϑ1) Ξ(ϑ2) = 0 is exempted from the cases considered in eqn (15); in this limiting case the conditions should be read as abbreviations for 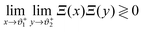 , i.e. the right-sided limit from above.78
, i.e. the right-sided limit from above.78
Dividing up the force as in eqn (15) leads, in conjunction with eqn (14), to an analogous separation of the scaling function of the critical Casimir force between two Janus cylinders. To this end, we introduce a new scaling function
| | 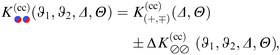 | (18) |
where the signs adhere to
eqn (15) and (compare
eqn (11))
| | 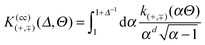 | (19) |
is the scaling function of the critical Casimir force between two homogeneous cylinders with the (+,∓) BC.
77 For homogeneous particles, the limit
Δ → 0, in which DA holds, can be carried out explicitly, so that in
eqn (19) the upper limit of integration reaches infinity. On the other hand, Δ
K(cc)⊘⊘ depends on
Δ via Ξ(
ϑ1,2) =
Δ1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2
ϑ1,2 within DA. In order for the separation in
eqn (18) to be consistent, both scaling functions
K(cc)(+,∓) and Δ
K(cc)⊘⊘ need to retain their dependence on
Δ. Nonetheless, the scaling functions within DA are expected to hold only for small but nonzero
Δ; keeping the dependence on
Δ is not necessarily a refinement (see Section III).
The scaling function ΔK(cc)⊘⊘ is constructed from the sum of surface elements as sketched in Fig. 8. This is similar to the case of two opposing structured substrates,54,76 but with the appropriately varying distance between the surface elements. Thus, we introduce the chemical step-like (i.e. dependence on Ξ) force scaling function (compare eqn (8) and (13))
| | 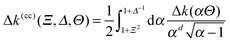 | (20) |
with the scaling variable
Ξ determined by the projected lateral step position of the Janus equator. For simplicity, we use the DA projection
Ξ(
ϑ1,2) =
Δ−1/2cos(
ϑ1,2), instead of the improved relation discussed in Section III. The complete scaling function of the force is found to be given by
| | 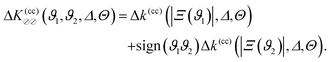 | (21) |
We point out the similarity between
eqn (13) and (21). However, in comparison, the sign-prefactor in
eqn (13) is superseded by the imposed restriction |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1| ≤ |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2|. Moreover, the factor −sign(
ϑ1) is replaced by sign(
ϑ1ϑ2); a configuration
ϑ1 > 0 and
ϑ2 > 0 results in a projected step–step configuration with opposite signs for the step positions
Ξ(
ϑ1) and
Ξ(
ϑ2) (see
Fig. 8(a)), thus, compared to
eqn (13), changing the sign of the term. This concise representation of Δ
K(cc)⊘⊘ in terms of the sign function is possible only for the reduced domain
. Special configurations of the two Janus cylinders, for which the scaling functions of the force require explicit considerations, are analyzed analytically in Appendix A.
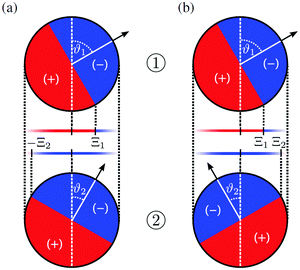 |
| | Fig. 8 Sketch of the geometry for the Derjaguin approximation concerning the force between two Janus cylinders ① and ② for ϑ2 > 0 in (a) and ϑ2 < 0 in (b). The cylinder axes are supposed to extend out of the plane of view. The angles ϑ1 and ϑ2 of the orientation are relative to the axis connecting the centers of the two particles. All orientations can be mapped onto the principal domain  . The middle parts show the unrolled surfaces of the Janus cylinders opposing each other. The construction of the DA for two Janus cylinders is akin to the interaction between two structured substrates interacting,54,76 considering, however, only the portion of the chemical structure that ranges from −R to +R, i.e. from −Δ−1/2 to +Δ−1/2 in terms of the scaling variable, and using the appropriate local surface-to-surface distance. In its straightforward version, the DA projects the Janus equators to step positions at Ξ1,2 ≡ Ξ(ϑ1,2) = Δ−1/2 . The middle parts show the unrolled surfaces of the Janus cylinders opposing each other. The construction of the DA for two Janus cylinders is akin to the interaction between two structured substrates interacting,54,76 considering, however, only the portion of the chemical structure that ranges from −R to +R, i.e. from −Δ−1/2 to +Δ−1/2 in terms of the scaling variable, and using the appropriate local surface-to-surface distance. In its straightforward version, the DA projects the Janus equators to step positions at Ξ1,2 ≡ Ξ(ϑ1,2) = Δ−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϑ1,2). Additionally, depending on sign(ϑ1ϑ2), either the left or the right edge of the equatorial plane enters into the projection, leading to opposite step positions ±Ξ1,2. cos(ϑ1,2). Additionally, depending on sign(ϑ1ϑ2), either the left or the right edge of the equatorial plane enters into the projection, leading to opposite step positions ±Ξ1,2. | |
In Fig. 9 we show the scaling function of the force between two Janus cylinders in d = 3 as a function of the scaled temperature Θ = D/ξ+ > 0 (i.e. for t > 0), for several orientations of the two Janus cylinders. The configuration ϑ1 = 0 and ϑ2 = 0 in Fig. 9(a) corresponds to the scaling function between two homogeneous cylinders with opposing BCs which is repulsive for all temperatures t > 0 (see Appendix A). Variations of the orientations out of this configuration lead to only small changes of the force between the cylinders. Even a significant rotation of ϑ2 = 77° results only in a small change in the scaling function. Around the perpendicular orientation ϑ2 = 90°, the force is much more sensitive to small tilts. For ϑ1 = 0 and orientations of the second Janus cylinder close to ϑ2 = 180°, the force is attractive for all temperatures t > 0 (see again Appendix A). If, however, particle 1 is rotated by 90° relative to the axis connecting the centers, and ϑ2 = 270° (see Fig. 9(b)), the scaling function of the force is more sensitive to changes in the orientation. The configuration ϑ1 = 90°, ϑ2 = 180° is geometrically equivalent to the one with ϑ1 = 0°, ϑ2 = 90°; in the former case the force is less sensitive to rotations of the second particle with ϑ2 = 180°.
 |
| | Fig. 9 The scaling function 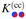 of the force between two Janus cylinders, within DA in d = 3, as a function of scaled temperature Θ = D/ξ+ for various orientations. The scaling function is normalized by the absolute value of the universal critical Casimir amplitude Δ(+,+). The wall–wall scaling function k(a,b)(L/ξ±), which, inter alia, determines Δ(+,+), is taken from MC results for the film geometry in ref. 11. (a) Configurations with ϑ1 = 0 for the orientation of particle ① for various orientation angles ϑ2 of particle ②, as visualized in the legend. (b) The case of ϑ1 = π/2 for various orientations ϑ2 of particle ②. The scaling function for the configuration ϑ1 = ϑ2 = 0 matches (repulsive) one of the two homogeneous cylindrical particles with the opposing BC, whereas the scaling function for the configuration ϑ1 = 0, ϑ2 = π equals the (attractive) one between two homogeneous cylinders with the same BC. The orientation angles belonging to the other curves have been chosen in order to visualize the particular sensitivity and insensitivity of the scaling function around the top-to-bottom, top-to-top, and bottom-to-bottom configurations, respectively. The angle ϑi is the one between the axis connecting the centers of the particles and the normal of the equatorial plane of particle i (see Fig. 8). of the force between two Janus cylinders, within DA in d = 3, as a function of scaled temperature Θ = D/ξ+ for various orientations. The scaling function is normalized by the absolute value of the universal critical Casimir amplitude Δ(+,+). The wall–wall scaling function k(a,b)(L/ξ±), which, inter alia, determines Δ(+,+), is taken from MC results for the film geometry in ref. 11. (a) Configurations with ϑ1 = 0 for the orientation of particle ① for various orientation angles ϑ2 of particle ②, as visualized in the legend. (b) The case of ϑ1 = π/2 for various orientations ϑ2 of particle ②. The scaling function for the configuration ϑ1 = ϑ2 = 0 matches (repulsive) one of the two homogeneous cylindrical particles with the opposing BC, whereas the scaling function for the configuration ϑ1 = 0, ϑ2 = π equals the (attractive) one between two homogeneous cylinders with the same BC. The orientation angles belonging to the other curves have been chosen in order to visualize the particular sensitivity and insensitivity of the scaling function around the top-to-bottom, top-to-top, and bottom-to-bottom configurations, respectively. The angle ϑi is the one between the axis connecting the centers of the particles and the normal of the equatorial plane of particle i (see Fig. 8). | |
B. Scaling function of the effective pair potential
Concerning thermodynamic properties, the effective pair potential between particles is of even more direct importance than the force because it is experimentally more easily accessible. Within the present study, we consider only the effective pair interaction between two Janus particles. A recent experimental study of the many-body effects in critical Casimir forces79 shows that the three-body contributions can be relevant. Similar deviations can be expected for three and more Janus particles.
The effective interaction potential  between two parallel Janus cylinders can be determined from the force F according to
between two parallel Janus cylinders can be determined from the force F according to
| |  | (22) |
with
z and
D as surface-to-surface distances. This can be cast into the scaling form
| | 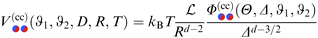 | (23) |
where the scaling function
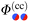
of the potential follows the same partition as the force in
eqn (15) so that
| | 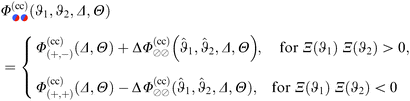 | (24) |
with
Ξ(
ϑi) =
Δ−1/2cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi
ϑi and where
| | 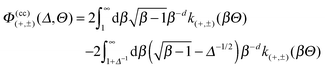 | (25) |
is the scaling function of the effective interaction potential between two homogeneous cylinders.
77 The Janus-induced excess scaling function Δ
Φ(cc)⊘⊘ in the reduced domain of
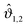
(see the previous subsection) follows from integrating
eqn (20) and (21). This keeps the general structure of the force scaling function, leading to
| | | ΔΦ(cc)(⊘⊘)(ϑ1,ϑ2,Δ,Θ) = ΔΦ(cc)s(|Ξ1|,Δ,Θ) + sign(ϑ1ϑ2) ΔΦ(cc)s(|Ξ2|,Δ,Θ), | (26) |
with
Ξi =
Ξ(
ϑi) and with the chemical step-like scaling function of the potential (compare
eqn (20)):
| | 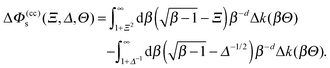 | (27) |
Since the dimensionless scaling function
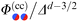
of the potential describes an energy in units of
kBT and per reduced length
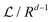
of the cylinders, it is useful to present it as an energy landscape in terms of the orientation angles
ϑ1 and
ϑ2, for a fixed scaled temperature
Θ and a fixed reduced distance
Δ =
D/
R (see
Fig. 10). This facilitates a thermodynamic interpretation. For example, it relates to the typical experimental setup in which the temperature is fixed and the formation of clusters is attributed to a minimum of the effective interaction potential. Invoking the critical Casimir effect alone, which leads to an irreversible aggregation, is insufficient to describe the distance dependence of effective interactions between colloids in suspension. Typically, in addition to the critical Casimir effect, there are repulsive electrostatic interactions due to counterions, which are short-ranged and prevent coagulation of the colloids. If, however, these additional interactions are basically isotropic (
e.g. due to a more or less homogeneous charge distribution on the colloid surface), the critical Casimir potential considered here is the only orientation dependent interaction and thus fully responsible for any orientation dependent behavior during the clustering of Janus particles close to
Tc.
 |
| | Fig. 10 The scaling function 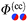 of the effective potential between two Janus cylinders in d = 3 presented in (a) as a free energy landscape in terms of the orientations ϑ1 and ϑ2 for the fixed scaled temperature Θ = 1 and the fixed reduced distance Δ = 1/5. The value of the scaling function is color coded ranging from blue for a minimum in the energy to red for a maximum in the energy. The landscape exhibits broad and flat plateaus; four free energy isolines (white, each consisting of three disconnected pieces), indicating a low value, zero, the mean value between the minimum and the maximum energy, and a high value, are drawn as a guide to the eye. Two straight horizontal paths are shown as a dashed red (ϑ2 = π/2) and as a dashed green line (ϑ2 = π/4). The scaling function of the potential along these paths is shown in (b) as a function of ϑ1. The points of each curve correspond to the scaling function for a specific geometric configuration (ϑ1, ϑ2) = (π/2, π/4). For the green curve selected configurations are indicated at the top of the panel, for the red curve examples are provided at the bottom. For each pair of particles the upper one is called ① and the lower one ②. of the effective potential between two Janus cylinders in d = 3 presented in (a) as a free energy landscape in terms of the orientations ϑ1 and ϑ2 for the fixed scaled temperature Θ = 1 and the fixed reduced distance Δ = 1/5. The value of the scaling function is color coded ranging from blue for a minimum in the energy to red for a maximum in the energy. The landscape exhibits broad and flat plateaus; four free energy isolines (white, each consisting of three disconnected pieces), indicating a low value, zero, the mean value between the minimum and the maximum energy, and a high value, are drawn as a guide to the eye. Two straight horizontal paths are shown as a dashed red (ϑ2 = π/2) and as a dashed green line (ϑ2 = π/4). The scaling function of the potential along these paths is shown in (b) as a function of ϑ1. The points of each curve correspond to the scaling function for a specific geometric configuration (ϑ1, ϑ2) = (π/2, π/4). For the green curve selected configurations are indicated at the top of the panel, for the red curve examples are provided at the bottom. For each pair of particles the upper one is called ① and the lower one ②. | |
The free energy landscape in Fig. 10(a) exhibits two broad minima (blue color) around (ϑ1,ϑ2) = (±π,0) and (ϑ1,ϑ2) = (0,π), which correspond to the two equally stable configurations of the blue sides facing each other, i.e. (−,−) BC, and the red sides facing each other, i.e. (+,+) BC, respectively (see Fig. 8 and 9). These two ground states are connected by a narrow valley along the line ϑ2 = π − ϑ1, which corresponds to configurations which emerge from (ϑ1 = 0, ϑ2 = π) upon counter-rotating both particles. In Fig. 10(a) two selected paths are marked by dashed lines with the scaling function shown, as a function of ϑ1 only, in Fig. 10(b). The resulting red and green curves are, unsurprisingly, reminiscent of the scaling function for the force acting between a Janus cylinder and a step (see Fig. 7). This extends the equivalence of substrate steps and Janus particles discussed before. The wedge-like shape of the valley trough is an artifact of DA. Based on previous findings (Fig. 7), we expect the actual potential landscape to be similar, but slightly broadened and smoother. The broad plateaus correspond to repulsive configurations (colored in red) with opposing BCs on those surface parts of the particles which face each other. The free energy landscape can be continued periodically with respect to ϑ1 and ϑ2, resulting in a checkerboard pattern. The occurrence of broad maxima and minima gives credit to the on–off “bond-like” character of the interaction used in the Kern–Frenkel model.44 Interestingly however, for the critical Casimir potential less than 50% of all configurations are actually attractive despite the Janus characteristic. There are additional characteristic features of the critical Casimir potential with important thermodynamic consequences, such as the discrepancy in strength of attraction and repulsion, the discussion of which we leave to future studies.
V. Janus spheres
The effective interaction between parallel, cylindrical Janus particles is conveniently described by only two orientational degrees of freedom. While this constrained setup poses an additional experimental challenge, the behavior of spherical colloids can, instead, be studied straightforwardly. Therefore, in the following we determine the scaling function of the force and of the effective pair potential between two spherical Janus particles, without constraints on the orientation.
We consider a conventional sphere in d = 3, for which the Janus characteristics are unambiguous. In d = 4, we consider a three-dimensional sphere extended along an extra dimension with a length L4, which is formally called a hyper-cylinder (rather than a hyper-sphere). This definition is distinct from the hyper-cylinder discussed before. In the context of spheres, 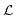 denotes
denotes 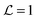 in d = 3 and
in d = 3 and 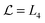 in d = 4.
in d = 4.
A. Scaling function of the force
The force between two Janus spheres depends, in principle, on their orientation vectors n1 and n2 and the vector r12 connecting their centers.80 The force takes the scaling form| | 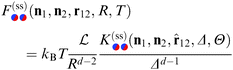 | (28) |
where for the scaling function, the connecting vector r12 = (D + 2R)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 = R(Δ + 2)
12 = R(Δ + 2)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 is expressed in terms of the surface-to-surface distance D along the direction
12 is expressed in terms of the surface-to-surface distance D along the direction ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 = r12/|r12|. Note that in the case of two spheres, at Tc the force decays as Δ−(d−1) with distance,16 compared to Δ−(d−1/2) for the force between two cylinders (see eqn (14)). As in the case of Janus cylinders, we decompose the scaling function
12 = r12/|r12|. Note that in the case of two spheres, at Tc the force decays as Δ−(d−1) with distance,16 compared to Δ−(d−1/2) for the force between two cylinders (see eqn (14)). As in the case of Janus cylinders, we decompose the scaling function 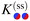 of the force into a part given by the scaling function K(ss)(+,±) between two homogeneous spheres16
of the force into a part given by the scaling function K(ss)(+,±) between two homogeneous spheres16| | 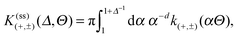 | (29) |
and an excess scaling function ΔK(ss)⊘⊘:| | 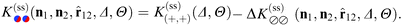 | (30) |
In contrast to the preceding sections, here we do not bear out explicitly all possible cases within the scaling function 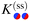 . Instead we divide them into ΔK(ss)⊘⊘, because the underlying symmetries are less intuitive and transparent. This leaves one with the arbitrary choice of whether to relate ΔK(ss)⊘⊘ to K(ss)(+,+)(Δ, Θ) or K(ss)(+,−)(Δ, Θ); we follow the definition in eqn (30). Note that it is not necessary to express ΔK(ss)⊘⊘ in terms of reduced angles, because as a spherical coordinate ϑ1,2 ∈ [0,π] is a reduced angle by definition. Again, the uncolored subscript emphasizes invariance with respect to the shift ϑi → ϑi ± π.
. Instead we divide them into ΔK(ss)⊘⊘, because the underlying symmetries are less intuitive and transparent. This leaves one with the arbitrary choice of whether to relate ΔK(ss)⊘⊘ to K(ss)(+,+)(Δ, Θ) or K(ss)(+,−)(Δ, Θ); we follow the definition in eqn (30). Note that it is not necessary to express ΔK(ss)⊘⊘ in terms of reduced angles, because as a spherical coordinate ϑ1,2 ∈ [0,π] is a reduced angle by definition. Again, the uncolored subscript emphasizes invariance with respect to the shift ϑi → ϑi ± π.
Determining completely the excess scaling function ΔK(ss)⊘⊘ requires careful considerations of all possible orientations. It turns out that within DA, the force necessarily depends only on the relative coordinates, because the interaction is expressed via the overlap of surface elements projected along the connecting vector r12. This is worked out in detail in Appendix B, using spherical coordinates n1 = (ϕ1,ϑ1) and n2 = (ϕ2,ϑ2). Thus the interaction depends only on the polar angles ϑ1 and ϑ2, and the dependence on ϕ1 and ϕ2 reduces to one on the angle difference α = ϕ2 − ϕ1 (see Fig. 11).
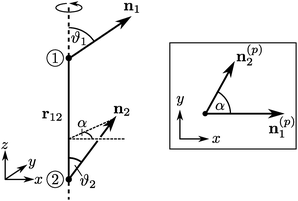 |
| | Fig. 11 Generic sketch of the orientations of the Janus spheres ① and ② defining the azimuthal angle α = ϕ2 − ϕ1, and the polar angles ϑ1 and ϑ2 of the relative coordinate system which has the z-axis aligned with the vector r12 and orientated such that ϕ1 = 0. Left: Side view with a slight perspective in order to depict α. Right: Top view of the same configuration, with n(p)i being the projection of ni onto the xy plane. The DA considers pairs of surface elements projected along r12, thus effectively representing a top-down view. Rotating the frame of reference, so that ϕ1 ≠ 0 but α = ϕ2 − ϕ1 is kept constant, does not affect the interaction in that case. | |
For comparison, we briefly consider the pair potential between two point dipoles of strength μ:
| | 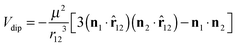 | (31) |
Written similarly in the relative coordinate system connecting the two dipoles, these render
ni·
r12 = cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi
ϑi and
n1·
n2 = cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2 + sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos(
ϕ1 −
ϕ2). Thus, concerning the dependence on the orientations, the critical Casimir interaction between two Janus spheres exhibits the same level of complexity as the dipole–dipole interaction.
Here, we provide the excess scaling function ΔK(ss)⊘⊘ as a function of ϑ1, ϑ2, and the relative coordinate α (see Appendix B):
| | 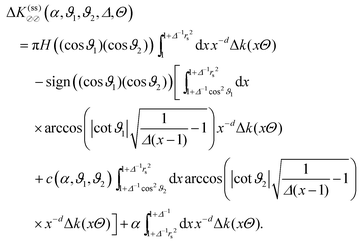 | (32) |
As before one has Δ
k =
k(+,+) −
k(+,−) < 0. The first term with the Heaviside step function
H((cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1)(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2)) as a prefactor effectively serves the same purpose as the case analysis within the scaling functions of previous geometries (see,
e.g.,
eqn (15), with
Ξ(
ϑ1)
Ξ(
ϑ2) ∝ (cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1)(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2)). Additionally, Δ
K(ss)⊘⊘ depends non-trivially on
α,
ϑ1, and
ϑ2,
inter alia,
via the dimensionless radius
rs =
Rs(
α,
ϑ1,
ϑ2)/
R (see
eqn (B8)) of a particular ring of surface elements occurring within DA in the subdivision of the surfaces. The projection of the equatorial steps of both Janus spheres onto a common plane, normal to the axis connecting the colloids, results in two half-ellipses corresponding to each configuration. The surface ring with radius
Rs intersects the projections of the equatorial steps of both Janus spheres in a single point. Thus, the scaled radius
rs is defined as
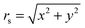
, with the intersection point (
x,
y) of the two ellipses determined by a particular solution of a system of two equations. For details, we refer to Appendix B.
Certain configurations of the two Janus particle give rise to forces which consist of force contributions of the same strength, but of opposite signs. All these cases can be subsumed by eqn (32)via the common prefactor sign((cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos
ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2)) and via the sign picking function
ϑ2)) and via the sign picking function
| | 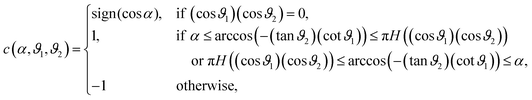 | (33) |
which assumes without the loss of generality that 0 ≤
α ≤ π; otherwise
α > π is replaced by
α → 2π −
α.
The scaling function  of the force (given by eqn (29)–(32)) is shown in Fig. 12 for various configurations with α = 0, i.e. ϕ1 = ϕ2, akin to Fig. 9 for parallel cylindrical Janus particles. In accordance with Fig. 11, α = 0 implies that the two orientation vectors n1 and n2 lie in the same plane, as for parallel cylinders, so that the corresponding equatorial planes are rotated with respect to each other (ϑ1 ≠ ϑ2), but not tilted (see Fig. 8). At first sight, the scaling functions of the force for Janus spheres and for Janus cylinders appear to be qualitatively very similar. Quantitatively, the force between spheres appears to be stronger than the force between parallel cylinders. However, one has to take into account that the force between two Janus cylinders is proportional to their length. A fair comparison of the strengths of the forces requires to consider a cylinder length which is comparable with the size of the sphere, i.e. L ≈ 2R. In this case the force between two parallel cylinders is stronger. Additionally, the scaling function for Janus spheres decays slightly faster as a function of Θ. Generally, the scaling function of the force between two Janus spheres is slightly more sensitive to small rotations of one particle than the one for cylinders.
of the force (given by eqn (29)–(32)) is shown in Fig. 12 for various configurations with α = 0, i.e. ϕ1 = ϕ2, akin to Fig. 9 for parallel cylindrical Janus particles. In accordance with Fig. 11, α = 0 implies that the two orientation vectors n1 and n2 lie in the same plane, as for parallel cylinders, so that the corresponding equatorial planes are rotated with respect to each other (ϑ1 ≠ ϑ2), but not tilted (see Fig. 8). At first sight, the scaling functions of the force for Janus spheres and for Janus cylinders appear to be qualitatively very similar. Quantitatively, the force between spheres appears to be stronger than the force between parallel cylinders. However, one has to take into account that the force between two Janus cylinders is proportional to their length. A fair comparison of the strengths of the forces requires to consider a cylinder length which is comparable with the size of the sphere, i.e. L ≈ 2R. In this case the force between two parallel cylinders is stronger. Additionally, the scaling function for Janus spheres decays slightly faster as a function of Θ. Generally, the scaling function of the force between two Janus spheres is slightly more sensitive to small rotations of one particle than the one for cylinders.
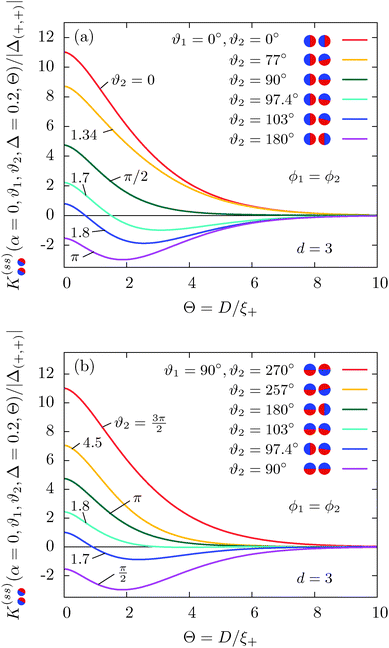 |
| | Fig. 12 The normalized scaling function of the force 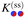 between two Janus spheres within DA in d = 3, as a function of Θ = D/ξ+ for the same orientations as in Fig. 9. (a) Configurations with ϑ1 = 0 for the orientation of the left particle ① for various orientation angles ϑ2 of the right particle ②, as visualized in the legend. (b) The case of ϑ1 = π/2 for various orientations ϑ2 of the second particle. In order to facilitate a transparent comparison with Fig. 8, the azimuthal angle α is set to α = 0, i.e. ϕ1 = ϕ2, which restricts the orientation vectors n1 and n2 to lie in a common plane, as it is the case in our analysis of parallel cylinders. between two Janus spheres within DA in d = 3, as a function of Θ = D/ξ+ for the same orientations as in Fig. 9. (a) Configurations with ϑ1 = 0 for the orientation of the left particle ① for various orientation angles ϑ2 of the right particle ②, as visualized in the legend. (b) The case of ϑ1 = π/2 for various orientations ϑ2 of the second particle. In order to facilitate a transparent comparison with Fig. 8, the azimuthal angle α is set to α = 0, i.e. ϕ1 = ϕ2, which restricts the orientation vectors n1 and n2 to lie in a common plane, as it is the case in our analysis of parallel cylinders. | |
B. Scaling function of the effective pair potential
As in the case of the Janus cylinders, the effective potential between two Janus spheres of radius R can be determined from the critical Casimir force in the relative coordinate system according to| | 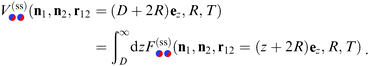 | (34) |
After inserting eqn (28), this can be cast into the scaling form| | 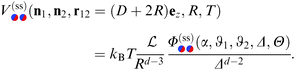 | (35) |
Following eqn (30), the scaling function 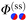 of the potential is divided into the two contributions
of the potential is divided into the two contributions| | 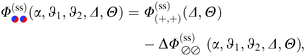 | (36) |
where| | 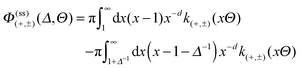 | (37) |
is the scaling function of the potential between two homogeneous spheres, and ΔΦ(ss)⊘⊘ is the Janus-induced excess scaling function. In view of the known expression for Φ(ss)(+,±)(Δ → 0,Θ),16,22 we again retain the explicit dependence on Δ in the scaling function of the homogeneous case for reasons of consistency with the orientation dependent excess scaling function in eqn (36). The previous caveats regarding the dependence on Δ within DA apply here, too.
Upon inserting the scaling function of the force (eqn (32)) into eqn (34)–(37), the excess scaling function of the potential is given by (see Appendix C)
| | ΔΦ(ss)⊘⊘(α,ϑ1,ϑ2,Δ,Θ) = πH((cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2))Δu(ss)(rs2,0,Δ,Θ) − sign((cos ϑ2))Δu(ss)(rs2,0,Δ,Θ) − sign((cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2))[Δv(ss)(rs2,ϑ1,Δ,Θ) + c(α,ϑ1,ϑ2)Δv(ss)(rs2,ϑ2,Δ,Θ)] + αΔu(ss)(1,rs2,Δ,Θ) ϑ2))[Δv(ss)(rs2,ϑ1,Δ,Θ) + c(α,ϑ1,ϑ2)Δv(ss)(rs2,ϑ2,Δ,Θ)] + αΔu(ss)(1,rs2,Δ,Θ) | (38) |
with
c(
α,
ϑ1,
ϑ2) defined by
eqn (33) and where
| | 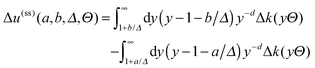 | (39) |
and (see
eqn (B8) concerning
rs)
| | 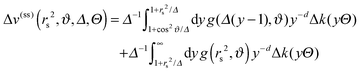 | (40) |
are excess scaling functions of Janus spheres (vaguely analogous to the chemical step-like scaling functions for Janus cylinders). The integrand of the latter scaling function Δ
v(ss) contains a geometry specific expression
| | 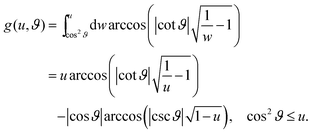 | (41) |
The free energy landscape of the scaling function

of the pair potential between two Janus spheres can be presented in a single plot only as a function of two variables, but not for the full set
α,
ϑ1,
ϑ2 of three variables. Accordingly, in
Fig. 13 we choose to show the scaling function of the pair potential between Janus spheres for the two values
α = 0 and
α = π. For
α = 0, in the range
ϑ1 > 0 the scaling function of the potential is very similar to the one for cylinders shown in
Fig. 10. On the other hand, for Janus spheres, the case of
α = π in
Fig. 13 is similar to the one of
ϑ1 < 0 for Janus cylinders. Obviously, in spherical coordinates an orientation vector with
α = π and
ϑ1 ∈ [0,π] lies in the same plane as an orientation vector with
α = 0, and can be mapped to a cylindrical angle
ϑ1 ∈ [−π,0]. The scaling function of the pair potential between Janus spheres is also dominated by the attractive minima and the repulsive plateaus of interaction (
Fig. 13(a)). The variation of the relative azimuthal angle
α affects the potential only locally around
ϑ1 =
ϑ2 = π/2. Upon increasing
α, the potential energy smoothly changes from having the potential minima connected by a valley to having the plateaus bridged.
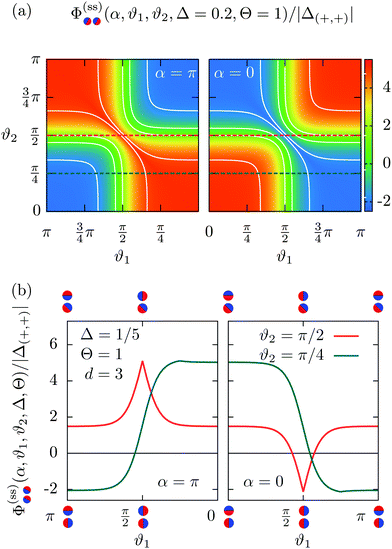 |
| | Fig. 13 The scaling function 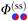 of the effective pair potential between two Janus spheres in d = 3 for α = π and α = 0 presented (a) as a free energy landscape in terms of ϑ1 and ϑ2 for a fixed scaled temperature Θ = 1, and (b) as a function of ϑ1 along the two paths ϑ2 = π/2 (red dashed line) and ϑ2 = π/4 (green dashed line). At the top of the panel, the geometric configurations indicate those which correspond to points of the green curve; configurations corresponding to the red curve are indicated at the bottom. The comparison with Fig. 10 tells that the free energy landscapes for cylinders and spheres are qualitatively very similar. Note that for α = π in (a) and (b) the horizontal axes are inverted in order to emphasize the geometric correspondence of α = π and ϑ1 > 0 in spherical coordinates to ϑ1 < 0 in cylindrical coordinates. An increase of α affects the potential only within a limited angular range around ϑ1 = ϑ2 = π/2, changing the potential in that range from being attractive (α = 0) to being repulsive (α = π). This means that upon increasing α the potential gradually develops a potential barrier (see the red curve in (b)). of the effective pair potential between two Janus spheres in d = 3 for α = π and α = 0 presented (a) as a free energy landscape in terms of ϑ1 and ϑ2 for a fixed scaled temperature Θ = 1, and (b) as a function of ϑ1 along the two paths ϑ2 = π/2 (red dashed line) and ϑ2 = π/4 (green dashed line). At the top of the panel, the geometric configurations indicate those which correspond to points of the green curve; configurations corresponding to the red curve are indicated at the bottom. The comparison with Fig. 10 tells that the free energy landscapes for cylinders and spheres are qualitatively very similar. Note that for α = π in (a) and (b) the horizontal axes are inverted in order to emphasize the geometric correspondence of α = π and ϑ1 > 0 in spherical coordinates to ϑ1 < 0 in cylindrical coordinates. An increase of α affects the potential only within a limited angular range around ϑ1 = ϑ2 = π/2, changing the potential in that range from being attractive (α = 0) to being repulsive (α = π). This means that upon increasing α the potential gradually develops a potential barrier (see the red curve in (b)). | |
With the scaling function of the potential at our disposal, inter alia we are able to elucidate a certain experimental aspect. A general issue concerning experimental studies of colloidal aggregation consists of the influence of the unavoidable presence of a substrate. It can be used deliberately, e.g., for the gravity induced formation of a monolayer of homogeneous particles on the bottom wall of the sample. Experimentally, the particles can be prevented from sticking to the substrate by applying a surface treatment of the substrate such that it becomes repulsive at small distances between the particles and the wall. For Janus particles, the experimental situation can be more intricate. Typically, the interaction with the wall is biased towards favoring one side of the colloid over the other. If the attractive interaction with the wall dominates over the inter-particle interaction (or similarly, if the substrate is repulsive towards only one of the two sides of the Janus particle), a scenario can prevail according to which all Janus particles orientate with one and the same side towards the substrate.
Within this line of reasoning, let us suppose that the interaction with the substrate has been reduced substantially, but is still present, resulting in a small biased tilt of all Janus particles relative to the substrate normal. Depending on the setup, this tilt might be barely noticeable, but would still affect the experimental determination of the effective pair potential between the particles.
In Fig. 14, we show the scaling function of the effective potential between two Janus spheres, which are tilted by a common angle γ relative to the axis connecting the centers of the two particles, due to the effects of a hypothetical substrate below the particles and parallel to the axis. Within this model, the horizontal components of the orientations n1 and n2 of the two Janus spheres are distributed isotropically in a plane parallel to the substrate; but the tilt γ is fixed to a given value, corresponding to an equilibrium configuration of the Janus colloids relative to the substrate. Thus, the tips of n1 and n2 fluctuate on circles in a plane parallel to the substrate. Note that for γ > 0 a rotation of the whole configuration around the normal of the plane corresponds to a non-trivial trajectory in the three-dimensional space of the relative spherical coordinates α, ϑ1, ϑ2, so that determining the average  requires knowledge of the full scaling function of the potential. Due to problems associated with the multivalued nature of the transformation functions, we refrain from providing an explicit parametrization of the orientations n1 and n2 in terms of the new coordinates which would include γ. Instead, for a fixed value of the tilt angle γ, we evaluate the scaling function
requires knowledge of the full scaling function of the potential. Due to problems associated with the multivalued nature of the transformation functions, we refrain from providing an explicit parametrization of the orientations n1 and n2 in terms of the new coordinates which would include γ. Instead, for a fixed value of the tilt angle γ, we evaluate the scaling function 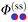 numerically on a discretized set of 64 × 64 orientations n1 and n2, each of them describing a circular path on the unit sphere. The set is expressed in terms of Cartesian coordinates and then transformed into spherical coordinates determining α, ϑ1, and ϑ2.81 The average
numerically on a discretized set of 64 × 64 orientations n1 and n2, each of them describing a circular path on the unit sphere. The set is expressed in terms of Cartesian coordinates and then transformed into spherical coordinates determining α, ϑ1, and ϑ2.81 The average  of the scaling function
of the scaling function  of the effective potential, i.e. the arithmetic mean of the dataset, is plotted as a function of the tilt angle γ, together with the standard deviation
of the effective potential, i.e. the arithmetic mean of the dataset, is plotted as a function of the tilt angle γ, together with the standard deviation  relative to the averaged scaling function for γ = 0. For γ = 0, the average is taken such that both n1 and n2 describe a great circle on each sphere. They can be parameterized unambiguously by the relative coordinates α = 0, 0 ≤ ϑ1,2 ≤ π, and α = π, 0 < ϑ1,2 < π (i.e. both free energy landscapes shown in Fig. 13(a) enter into the mean value), resulting within DA in the average (Φ(ss)(+,+) + Φ(ss)(+,−))/2 due to the symmetry of the potential.
relative to the averaged scaling function for γ = 0. For γ = 0, the average is taken such that both n1 and n2 describe a great circle on each sphere. They can be parameterized unambiguously by the relative coordinates α = 0, 0 ≤ ϑ1,2 ≤ π, and α = π, 0 < ϑ1,2 < π (i.e. both free energy landscapes shown in Fig. 13(a) enter into the mean value), resulting within DA in the average (Φ(ss)(+,+) + Φ(ss)(+,−))/2 due to the symmetry of the potential.
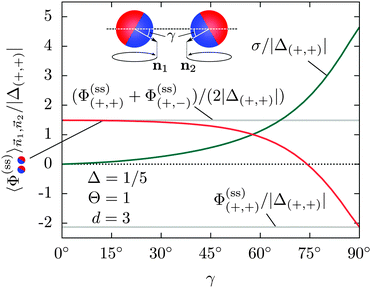 |
| | Fig. 14 Angularly averaged and normalized scaling function  of the effective pair potential for two Janus particles, which are considered to be at equal height above a substrate (not depicted), but far enough so that the influence of the substrate is weaker than that of the pair interaction between the particles. The orientations n1 and n2 are tilted by a common angle γ towards the substrate and out of the plane which contains both particle centers and is parallel to the substrate. However, the influence of the substrate is taken to be isotropic in the remaining lateral directions. This is supposed to mimic a typical experimental setup. Thus, we consider the average of the effective pair potential for two Janus particles, which are considered to be at equal height above a substrate (not depicted), but far enough so that the influence of the substrate is weaker than that of the pair interaction between the particles. The orientations n1 and n2 are tilted by a common angle γ towards the substrate and out of the plane which contains both particle centers and is parallel to the substrate. However, the influence of the substrate is taken to be isotropic in the remaining lateral directions. This is supposed to mimic a typical experimental setup. Thus, we consider the average  taken over n1 and n2 (see the main text), such that the tips of n1 and n2 form circles lying in a common plane parallel to the substrate surface (see the inset). The influence of the externally imposed tilt γ on the effective pair potential is visualized by the dependence on γ of the averaged scaling function taken over n1 and n2 (see the main text), such that the tips of n1 and n2 form circles lying in a common plane parallel to the substrate surface (see the inset). The influence of the externally imposed tilt γ on the effective pair potential is visualized by the dependence on γ of the averaged scaling function  (red curve) and its standard deviation σ with respect to the scaling function for γ = 0 (green curve; see the main text). For γ → 0 the average approaches the simple mean (Φ(ss)(+,+) + Φ(ss)(+,−))/2 of attraction and repulsion of homogeneous spheres (upper gray curve). For γ = 90° the Janus equators are tilted such that they are parallel to the substrate and thus unaffected by rotations around the normal of the substrate, leading to an average Φ(ss)(+,+) (lower gray curve). All quantities are normalized by |Δ(+,+)|. (red curve) and its standard deviation σ with respect to the scaling function for γ = 0 (green curve; see the main text). For γ → 0 the average approaches the simple mean (Φ(ss)(+,+) + Φ(ss)(+,−))/2 of attraction and repulsion of homogeneous spheres (upper gray curve). For γ = 90° the Janus equators are tilted such that they are parallel to the substrate and thus unaffected by rotations around the normal of the substrate, leading to an average Φ(ss)(+,+) (lower gray curve). All quantities are normalized by |Δ(+,+)|. | |
The presence of a planar substrate effectively leads to a tilt γ > 0. In the extreme case of a strongly dominant substrate force, a tilt of γ = 90° towards the substrate rotates the two Janus equators into a configuration in which both of them are parallel to the substrate surface. In this case, the rotation around the normal of the substrate does not affect the pair interaction, so that always equal boundary conditions face each other. Accordingly, within DA, the average is simply given by Φ(ss)(+,+). Fig. 14 shows that even intermediate tilt angles γ do not alter the effective interaction drastically. Up to γ ≈ 30° the mean value and the standard deviation remain rather constant and small, respectively. The deviations become significant only above γ ≈ 45°, which can be expected to be an experimentally detectable tilt. For smaller angles γ, ignoring the tilt entirely turns out to be a safe approximation.
The weak influence of small tilt angles on the appearance of the effective pair potential is associated with the flat plateaus in the energy landscape of the scaling function of the potential (see, e.g., Fig. 13(a)). However, the proper average takes fully into account the trough- and ridge-like extrema occurring for orthogonal orientations (see, e.g., Fig. 13(b)). This shows that the critical Casimir interaction is not only rather insensitive to small tilts for specific configurations, but even for a statistical ensemble of orientations. However, experimentally observed aggregation structures may be driven by additional effects not captured by the DA-based effective pair potential, such as the occurrence of order parameter bridges between the particles (see ref. 77) or non-additive many-body effects.79,82 Thus, the aggregation of Janus particles into a complex spatial structure should still be analyzed carefully by taking into account the relevance of substrate induced tilting beyond the DA.
VI. Summary, conclusions, and outlook
The aim of this study has been to determine theoretically the effective pair interaction between Janus particles immersed in a near-critical solvent and thus interacting via critical Casimir forces. The Janus particles under study are the ones with an opposing BC such as possessing a hydrophilic and hydrophobic half, which exhibit both repulsive and attractive forces at the same time. First, we have calculated the critical Casimir force acting on a single cylindrical Janus particle in the presence of a homogeneous substrate (Section IIIA) both by using the Derjaguin approximation (DA), and by applying mean field theory (MFT), which is valid in d = 4 spatial dimensions.
The DA implies a close relation between the critical Casimir forces for distinct geometries. Indeed, a comparison of DA with results from full MFT in d = 4 reveals that, in the limit Δ = D/R → 0 of the ratio of the distance D and radius R, the DA holds equally both for the force between a Janus cylinder and a substrate and for the force between a homogeneous cylinder and a substrate with a chemical step (see Fig. 1 and 2). However, as shown in Fig. 3, the MFT scaling functions for the two geometries are distinct for nonzero Δ. This caused us to address the question of whether the relation between these two geometries has any merit beyond the limit Δ → 0 in which DA holds.
In the case of nonzero Δ, for a homogeneous cylinder above a homogeneous substrate with opposing BCs it is known that the MFT scaling function deviates quantitatively from the DA scaling function.71 In ref. 71, the deficiencies of the DA for Δ > 0 have been traced back to an implicit assumption of the DA about the location and the shape of the interface which appears in this system for t = (T − Tc)/Tc < Tc, i.e. in the demixed phase. Following this argument, in Section IIIB we have inspected the MFT order parameter (OP) profiles shown in Fig. 4 for both aforementioned types of configurations and for two scaled temperatures Θ = D/ξ+(t) = tνD/ξ+0 for t > 0, i.e. in the mixed phase. Thus, there is no interface present and the OP profile ϕ(r,t) is mostly small. Still, the opposing BC of ϕ → +∞ and ϕ → −∞ on the surface of the (Janus) particle and of the (stepped) substrate imposes the occurrence of a line at which ϕ(r) crosses zero. DA makes implicit assumptions about the OP profile based on the one between a homogeneous particle and a homogeneous substrate with the opposing BC and at the same temperature. We have found that the isoline ϕ(r) = 0 indeed follows closely the profile for homogeneous surfaces, however it smoothly bends towards the particle or the substrate, which is unaccounted for within DA. In Fig. 4, one can compare visually examples of the order parameter profiles for these two configurations, each of which gives rise to a force equal in strength to that in the other case for the same temperature Θ. For the MFT results one can find systematically via interpolation for each scaled position 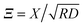 of the substrate step a certain rotational orientation ϑ of a Janus cylinder close to a homogeneous substrate which results in the same strength of the critical Casimir force, yielding numerically a discrete set {Ξ,ϑ}. Visually, it appears that the forces are equal in strength whenever the bending and the extension of the isolines ϕ(r) = 0 are similar for both configurations. An improved model has been introduced by applying the DA for a fictional, larger colloid, scaled by a parameter p, in order to incorporate the bending of the isoline into DA by fiat (see Fig. 5). This translates to a relation
of the substrate step a certain rotational orientation ϑ of a Janus cylinder close to a homogeneous substrate which results in the same strength of the critical Casimir force, yielding numerically a discrete set {Ξ,ϑ}. Visually, it appears that the forces are equal in strength whenever the bending and the extension of the isolines ϕ(r) = 0 are similar for both configurations. An improved model has been introduced by applying the DA for a fictional, larger colloid, scaled by a parameter p, in order to incorporate the bending of the isoline into DA by fiat (see Fig. 5). This translates to a relation 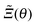 in eqn (10) for the rescaled step position
in eqn (10) for the rescaled step position 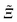 , with p as the only parameter. The model fits well to the discrete set {Ξ,ϑ} determined from the MFT results for p ≈ 1/4, roughly independent of temperature. This corresponds to placing the fictional, rescaled colloid surface halfway between the physical surface and the isoline ϕ(r) = 0 as depicted in Fig. 5. The improvement achieved using the relation
, with p as the only parameter. The model fits well to the discrete set {Ξ,ϑ} determined from the MFT results for p ≈ 1/4, roughly independent of temperature. This corresponds to placing the fictional, rescaled colloid surface halfway between the physical surface and the isoline ϕ(r) = 0 as depicted in Fig. 5. The improvement achieved using the relation 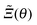 in eqn (10) with p = 1/4 is demonstrated in Fig. 6, where the two scaling functions
in eqn (10) with p = 1/4 is demonstrated in Fig. 6, where the two scaling functions  and
and  for a homogeneous cylinder close to a chemically stepped substrate and a Janus cylinder close to a homogeneous substrate, respectively, coincide even for Δ = 1, far away from the DA limit Δ → 0. Thus, the correspondence between these two configurations holds also within MFT, albeit this is based on a relation
for a homogeneous cylinder close to a chemically stepped substrate and a Janus cylinder close to a homogeneous substrate, respectively, coincide even for Δ = 1, far away from the DA limit Δ → 0. Thus, the correspondence between these two configurations holds also within MFT, albeit this is based on a relation 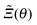 which differs from the one obtained by using the original, unmodified DA.
which differs from the one obtained by using the original, unmodified DA.
The correspondence of Janus particles and chemical steps on a substrate is also relevant for Section IIIC which discusses the scaling function of the force between a Janus cylinder and a substrate with a chemical step. The MFT scaling function in Fig. 7 for a Janus cylinder and a step at a lateral position X = 0 is qualitatively similar to the dependence of the scaling function of the force between two patterned substrates on a lateral shift.76 This configuration reveals a deficiency of DA due to the assumption of additivity: for an orthogonal orientation of the Janus particle, i.e. when the Janus equator faces the substrate at ϑ = ±π/2, within DA the scaling function of the force exhibits cusplike extrema of attraction or repulsion as a function of the particle orientation, whereas the MFT results are smooth. However, for Δ = 1/5, i.e. close to the DA limit Δ → 0, the agreement between DA and full MFT is surprisingly good even for this pathological case (see Fig. 7(b)).
In Section IV we have used DA in order to obtain the scaling function of the force between two parallel Janus cylinders (eqn (18)–(21)). With a view on the experimental interest in Janus particles, in Fig. 9 the results for the corresponding scaling function of the force are given in d = 3 spatial dimensions. We find that the force between two Janus cylinders can be attractive and repulsive, depending on their orientations. The strongest attraction is found in the case of the two Janus cylinders facing each other with the same face, whereas the strongest repulsion occurs when they are orientated in line. The force is rather insensitive against tilts out of these two configurations. Based on the scaling function of the force we have also determined the scaling function of the effective pair potential between two Janus cylinders (eqn (24)–(27)). In Fig. 10 we present it as an energy landscape in terms of the particle orientations ϑ1 and ϑ2. There are two shallow and stable minima in the potential energy, which are connected by a narrow trough representing counter-rotating orientations of the Janus particles. The large plateaus of repulsive orientational states corresponding to opposing BCs yield a checkerboard landscape pattern.
Similarly, in Section V we have derived the scaling function of the force between two Janus spheres in a relative coordinate system as a function of three spherical coordinates α = ϕ2 − ϕ1, ϑ1, and ϑ2 (Fig. 11 and eqn (30)–(32)). The details of this derivation, accounting for all possible orientations, are provided in Appendix B. The result is shown in Fig. 12, which is rather similar to the case of two Janus cylinders. The scaling function of the force between two Janus spheres decays faster as a function of Θ and, for the same tilt out of the attractive (repulsive) configuration of the particles facing each other (orientated in line), the force is less attractive (less repulsive) compared to the same configuration for two cylinders. Also here, the force has been integrated in order to determine the scaling function of the effective pair potential between two Janus spheres. Since it is a function of three spherical coordinates, one cannot visualize, within a single plot, the full dependencies of the potential. In Fig. 13, we show the energy landscape for the two cases α = 0 and α = π. The free energy landscape is qualitatively similar to that in Fig. 10 for two Janus cylinders. For spheres and α = π, the two orientation vectors (and the axis connecting the centers of the particles) form the same plane as in the case of α = 0, and thus the two configurations α = 0 and α = π correspond to ϑ1 > 0 and ϑ1 < 0 for cylinders, respectively. For 0 < α < π the scaling function of the effective potential varies primarily only around orientations ϑi = π/2 for the two particles i = {1,2} (Fig. 13). However, the pronounced plateau structure is largely unaffected by the changes of α.
We have used the scaling function of the effective potential in order to address the special experimental situation in which the particle positions and orientations are confined to a plane parallel to the planar surface of a substrate, however such that the substrate does not alter the pair interaction among the particles. Using the full pair interaction potential, we have analyzed how the effective influence of the substrate, incorporated as an externally imposed common tilt γ of all Janus particles, changes the effective pair interaction among the Janus particles. The deviations turn out to be small for tilts γ ≲ 30° and still acceptable for γ ≲ 45° (Fig. 14). Under this condition, concerning the interaction among the particles the substrate induced interaction can be discarded. Note that this holds for the direct two-body interaction; contributions at the level of three-body interactions and higher are likely relevant.79,82
It is evident that for Janus particles, the most attractive configuration is the one with the same BC on both particles facing each other. Interestingly, the strength of the attraction is quite insensitive to tilts of the particles. Thus our findings are to a certain extent compatible with the on–off “bond-like” interaction underlying the popular Kern–Frenkel model.44 However, so far we have discussed only the orientational part of the interaction at a fixed spatial distance between the particles. Whereas the Kern–Frenkel model is based on a short-ranged square-well potential, close to Tc the critical Casimir interaction is long-ranged, which is more on a par with van der Waals forces or dipole–dipole interactions. Furthermore, the critical Casimir potential carries both attractive and repulsive contributions. Since the repulsion is stronger than the attraction, less than half of all configurations are actually attractive (see Fig. 13), despite the overall Janus character. All these aspects contribute to the thermodynamic properties of suspensions of Janus particles with a critical solvent via integrals of the effective potential over both orientations and the radial distance.
Future studies could focus more on identifying those features of the effective interactions which are unique to the critical Casimir effect. Upon approaching the critical point (T → Tc), the scaling function of the critical Casimir force increases non-monotonically (see Fig. 9 and 12), and close to Tc the repulsive contributions become much stronger than the attractive ones. Additionally, the range of interactions increases significantly near Tc and diverges at Tc. Considering an actual suspension of Janus particles, the critical Casimir interaction competes with other effects such as electrostatic repulsion and van der Waals attraction. However, only the critical Casimir part is singular as a function of t = (T − Tc)/Tc.84 The tuneable range of the critical Casimir interaction has profound effects on the aggregation behavior of chemically homogeneous colloids.85–88 It is expected that this holds also, maybe a fortiori, for Janus particles, deserving both experimental and theoretical investigations. On the other hand, for simulations such as molecular dynamics, in practice, it would be beneficial to employ a computationally more efficient model of the pair interaction than the one provided here. However, reducing the complexity of the pair interaction between Janus particles while keeping its distinguishing features intact poses a significant challenge. It is natural to extend the present study along these lines.
Appendix A: special cases for the force between two Janus cylinders
(i) In the limit of both ϑ1 → 0 and ϑ2 → 0, one has Ξ1 = Ξ2 = Δ−1/2, so that in eqn (21) both terms involving Δk(cc) have the same values of their arguments and according to eqn (20) one finds Δk(cc)(Δ−1/2, Δ, Θ) = 0, so that| | | ΔK(cc)⊘⊘(ϑ1 = 0, ϑ2 = 0, Δ, Θ) = 0. | (A1) |
This correctly resolves the issue that sign(ϑ1ϑ2) in eqn (21) depends on the direction of the limit, i.e. whether ϑ1,2 → 0+ or ϑ1,2 → 0−, but the resulting force should not. With this, the scaling function of the force is given by (see eqn (15) and (18))| | 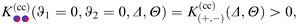 | (A2) |
as expected.
If instead ϑ1 = 0 and ϑ2 = π, one has Ξ1 = Δ−1/2 = −Ξ2. Similarly, this leads to Δk(cc)(±Δ−1/2,Δ,Θ) = 0 (eqn (20)) and ΔK(cc)⊘⊘(ϑ1 = 0, ϑ2 = π,Δ,Θ) = 0. According to eqn (15), the scaling function in eqn (18) has to be evaluated for the second case of Ξ(ϑ1)Ξ(ϑ2) < 0, which reduces to K(cc)⊘⊘(ϑ1 = 0, ϑ2 = π,Δ,Θ) = K(cc)(+,+)(Δ,Θ) < 0.
(ii) The case ϑ1 = ϑ2 = π/2 corresponds to Ξ1,2 = 0 and eqn (21) reduces to (see eqn (20))
| | 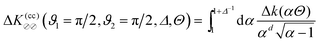 | (A3) |
In this case, a careful analysis of
Ξ(
ϑ1)
Ξ(
ϑ2) ≷ 0, which appears in
eqn (15), is required. If both
ϑ1 → π/2 and
ϑ2 → π/2 approach the limit from the same direction (both from above, or both from below), one has
Ξ(
ϑ1)
Ξ(
ϑ2) → 0
+ and the total scaling function in
eqn (18) between such Janus cylinders reduces to (compare
eqn (A3), where Δ
k =
k(+,+) −
k(+,−), with
eqn (19))
| | 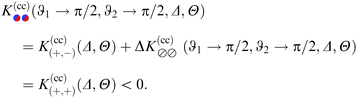 | (A4) |
If, however,
ϑ1 → π/2
+ and
ϑ2 → π/2
−, or
vice versa, one has
Ξ(
ϑ1)
Ξ(
ϑ2) → 0
−; thus the second case in
eqn (15) maps
ϑ1 = π/2 +
ε (where
ε → 0
+) to
. The excess scaling function of the force Δ
K(cc)⊘⊘(
Θ,
Δ,
ϑ1 = −π/2,
ϑ2 = π/2) in
eqn (21) vanishes because sign(
ϑ1ϑ2) = −1 and one finds
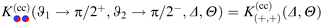
as in
eqn (A4). Therefore, the two sided limit exists and the force in this configuration is attractive for all temperatures
t > 0.
(iii) Similarly, for ϑ1 → −π/2+ and ϑ2 → π/2−, one also has Ξ(ϑ1)Ξ(ϑ2) → 0+ and ΔK(cc)⊘⊘(−π/2,π/2,Δ,Θ) = 0. Thus, the scaling function between the Janus cylinders in this case is
| | 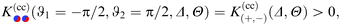 | (A5) |
i.e. the force in this configuration is repulsive for all temperatures
t > 0.
(iv) The last limit we discuss is ϑ1 = ±π/2 and ϑ2 = 0, which implies Ξ1 = 0 and Ξ2 = Δ−1/2. Note that in this case, the numbering of the particles ① and ② is not interchangeable due to the restriction |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1| < |cos
ϑ1| < |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2|. Since Δk(cc)(Ξ2 = Δ−1/2, Δ, Θ) = 0, only the first term in eqn (21) contributes, thus with Δk = k(+,+) − k(+,−) resulting in
ϑ2|. Since Δk(cc)(Ξ2 = Δ−1/2, Δ, Θ) = 0, only the first term in eqn (21) contributes, thus with Δk = k(+,+) − k(+,−) resulting in
| | 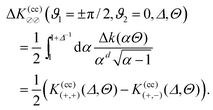 | (A6) |
Regardless of the sign of
ϑ1 = ±π/2 as well as whether
Ξ(
ϑ1)
Ξ(
ϑ2) → 0
±, for these orientations due to
eqn (15) and (18) the scaling function of the force between two Janus cylinders reduces to the mean value of the attractive and the repulsive force between homogeneous cylinders:
| | 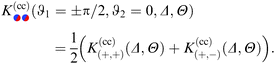 | (A7) |
Appendix B: Derjaguin approximation for the force between two Janus spheres
Concerning the geometry of two homogeneous, i.e. isotropic spheres, the Derjaguin approximation consists of subdividing their surfaces into infinitesimal thin rings of area 2πρ dρ, parameterized by their radius ρ.16 This has been used successfully in several studies, such as ref. 16, 22 and 57, generally in conjunction with the so-called “parabolic distance approximation” for the local distance L(ρ) between surface elements of the two colloids:| | 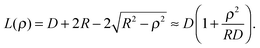 | (B1) |
Building on that, for Janus spheres the corresponding step in the BC has to be incorporated additionally, depending on the particle orientations. Within DA, the overlap of pairs of surface elements on both spheres is determined after the projection along the vector r12 connecting the centers of the two spheres. We choose to express this geometry in terms of a local coordinate system, the z axis of which passes through the centers of the two colloids, so that r12 = (D + 2R) ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 with
12 with ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 = (0,0,1) (see Fig. 11). The orientations of the colloids can be represented by orientation vectors n1 and n2, which can be chosen to point either into the direction of the (+) (red) or the (−) (blue) side. As far as the figures in the main text are concerned, the orientation vector is chosen to point towards the (−) (blue) cap. However, regarding the general approach in the present appendix, we shall use the more abstract notions of “north” and “south”, which are supposed to underscore the arbitrariness of this choice.
12 = (0,0,1) (see Fig. 11). The orientations of the colloids can be represented by orientation vectors n1 and n2, which can be chosen to point either into the direction of the (+) (red) or the (−) (blue) side. As far as the figures in the main text are concerned, the orientation vector is chosen to point towards the (−) (blue) cap. However, regarding the general approach in the present appendix, we shall use the more abstract notions of “north” and “south”, which are supposed to underscore the arbitrariness of this choice.
Without the loss of generality, we define the coordinate system such that the orientation of the first particle has an azimuthal angle ϕ1 = 0 and a polar angle ϑ1; the orientation (α, ϑ2) of the second particle is taken relative to the “prime meridian” of the first (i.e. α = ϕ2 − ϕ1). Rotations of the coordinate system while keeping (α,ϑ1,ϑ2) fixed do not change the interaction between the particles. Still, there remains a choice in the numbering of the particles. We implement this such that |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1| < |cos
ϑ1| < |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2|, as it shortens the notation below; otherwise one can exchange the labels (1) and (2) and rotate the frame of reference around the y axis by 180° (see Fig. 11).
ϑ2|, as it shortens the notation below; otherwise one can exchange the labels (1) and (2) and rotate the frame of reference around the y axis by 180° (see Fig. 11).
The orientations n1,2 and two mirror points r1 and r2 on the surface of colloids 1 and 2, respectively, are parameterized within the relative coordinate system by
| | 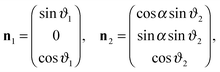 | (B2) |
| | 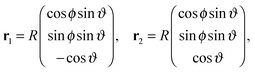 | (B3) |
where
ϑ1 is the polar angle of the first particle, (
α,
ϑ2) are the azimuthal and polar angle of the second particle, and (
ϕ,
ϑ) are the spherical coordinates of the vectors
r1 and
r2 of a pair of surface elements, where
r1 and
r2 are mirror images of each other with respect to the midplane orthogonal to
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12
12 =
ez, such that (
r1)
z = −(
r2)
z (see
Fig. 15). After the projection into the midplane by using the orthogonal projection matrix
| |  | (B4) |
surface elements with equal distance from their mirror element on the other particle form a ring with polar coordinates (
ρ =
R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ,
ϕ) and a fixed value of
ϑ.
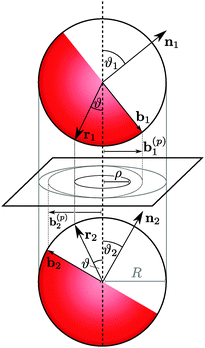 |
| | Fig. 15 Two Janus spheres within the Derjaguin approximation. The two orientations of the two particles are given by the direction vectors n1 and n2 which are normals of the respective equatorial planes. In the relative coordinate system, given by the axis through the centers of both particles, the orientations can be represented by the two polar angles ϑ1 and ϑ2 and the relative azimuthal angle α; for simplicity, here we depict the case α = 0 in which the two equatorial planes are rotated with respect to each other but not tilted (see Fig. 11 for a reduced schematic drawing with α ≠ 0). A pair of surface elements at r1(ϕ, ϑ) and r2(ϕ, ϑ) on the two Janus spheres, such that they are mirror images of each other, i.e. (r1)z = −(r2)z, share the same “northern” BC if r1·n1 > 0 and r2·n2 > 0. Likewise, two surface elements share the same “southern” BC if r1·n1 < 0 and r2·n2 < 0; otherwise for the selected pair of surface elements the BC on the two Janus spheres differs. Surface elements at r1 and r2 with equal distance between them (dotted line parallel to the axis through the centers of both particles and connecting the tips of r1 and r2) form a ring with radius ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ (here, the inner black circle) which is shown in the midplane between the particles. The equatorial steps of the Janus spheres ① and ② form half-ellipses when projected onto the same midplane. The vectors b1 and b2 lie in the equatorial plane of the corresponding particles and thus are orthogonal to n1 and n2, respectively. Their direction is chosen to point to that point on each equator which is closest in the sight of the opposite particle. The projections b(p)1 and b(p)2 of the vectors b1 and b2, respectively, onto the midplane render the semi-minor axes of the half-ellipses. ϑ (here, the inner black circle) which is shown in the midplane between the particles. The equatorial steps of the Janus spheres ① and ② form half-ellipses when projected onto the same midplane. The vectors b1 and b2 lie in the equatorial plane of the corresponding particles and thus are orthogonal to n1 and n2, respectively. Their direction is chosen to point to that point on each equator which is closest in the sight of the opposite particle. The projections b(p)1 and b(p)2 of the vectors b1 and b2, respectively, onto the midplane render the semi-minor axes of the half-ellipses. | |
The force between the Janus spheres, as constructed within DA, depends on the combination of the BC for a pair of surface elements. A selected pair of surface elements will share the “northern” BC if r1·n1 > 0 and r2·n2 > 0. Likewise, they will both have the “southern” BC if r1·n1 < 0 and r2·n2 < 0, otherwise the surface elements have different BCs.
In our parameterization and with f1(ϕ) := r1·n1 = −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1 + cos
ϑ1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1 and f2(ϕ) := r2·n2 = cos
ϑ1 and f2(ϕ) := r2·n2 = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2 + cos(α − ϕ)
ϑ2 + cos(α − ϕ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2, the two conditions above read
ϑ2, the two conditions above read
| | | same BC (“north”) ⇔ f1(ϕ) > 0 ∧ f2(ϕ) > 0 | (B5a) |
or
| | | same BC (“south”) ⇔ f1(ϕ) < 0 ∧ f2(ϕ) < 0. | (B5b) |
There are two more conditions representing the opposing BC, with opposite signs of
f1(
ϕ) ≷ 0 and
f2(
ϕ) ≶ 0. For any value of
ϕ, one and only one of these four conditions is fulfilled. Thus, these four conditions hold in four intervals. Determining the zeroes of
f1 and
f2 as a function of
ϕ renders four possible values, separating the intervals (note that four points naturally enclose three closed intervals, and one more interval due to the periodicity in
ϕ):
Strictly speaking,
eqn (B5) has an infinite number of solutions, because any solution shifted by ±2π is also a solution. With (+2π) we indicate that
ϕ2 and
ϕ3 may need to be shifted such that all four given solutions are the relevant ones within the principal interval [0,2π].
Fig. 16 puts the meaning of these four values of ϕ given by eqn (B6) into proper perspectives. Fig. 16 shows a schematic (top-down) plan view of the geometry shown in Fig. 15 which is rendered by the projection matrix Pz for four different values of α and with additional details, visualizing how the projected surface elements entering the DA are partitioned by eqn (B6) (compare also Fig. 11). The spherical colloids are drawn with non-occluding outlines and the equatorial step is indicated only partially. The projection of the equatorial steps between the “north” and the “south” Janus BC on each sphere results in two ellipses. This follows from noting that the two equators can be parameterized as circles pi = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi,sin
ϕi,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi,0), tilted by a rotation matrix
ϕi,0), tilted by a rotation matrix
| | 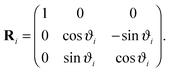 | (B7) |
One finds that
Pz·
Ri·
pi = (cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi
ϕi,cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi
ϑi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi
ϕi,0) fulfills the ellipse equation
for
a = 1 and
b = |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi
ϑi|. Of the two elliptical projections, we draw only that half facing the other colloid, resulting in two half-elliptical curves, which are intersecting for 0 <
α < π (
i.e. they do not intersect for
α = 0 and
α = π). The semi-minor axes of the half-ellipses are indicated by the projections
b(p)1 and
b(p)2 of the vectors
b1 and
b2, respectively, which have a projected length of
R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2
ϑ1,2 and form the angle π −
α between them. The projected Janus steps divide the circular area of radius
R into four regions (blue, white, red, white); a selected ring of fixed radius
ρ =
R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ (corresponding to the color colored circle in
Fig. 16) is divided into four arcs by points with the polar coordinates (
ρ,
ϕ1) to (
ρ,
ϕ4). In the case of small
α as shown in
Fig. 16(a), the numbering of the values
ϕ1 to
ϕ4 given in eqn (B6) corresponds to a clockwise counting of the intersections of the ring with the projected Janus steps (
i.e. the half-ellipses). However, the order of their occurrence changes upon increasing
α towards π (see
Fig. 16(a)–(d)).
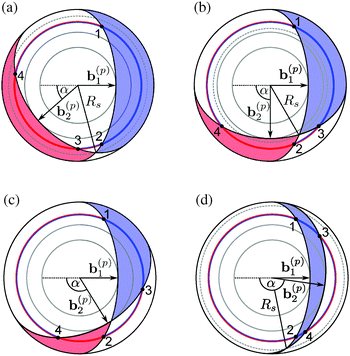 |
| | Fig. 16 A top-down plan view, as rendered by the projection matrix Pz, of the geometry of two Janus spheres, which is the same as in Fig. 15, but highlights the significance of the angles ϕ1 to ϕ4 of the DA procedure given in eqn (B6). The two half-elliptical curves running through 1 and 2 and through 3 and 4, respectively, represent the projection of the Janus equators onto the midplane. Their semi-minor axes are given by the projections b(p)1 and b(p)2 of the vectors b1 and b2, respectively, shown in Fig. 15, which enclose the angle π − α. The full gray circles have radii |b(p)i|. Here, the parameters of the particle orientations n1,2 (⊥b1,2) are ϑ1 = π/3 and ϑ2 = π/4, and α is varied from (a) α = 0.7, (b) α = π/2, and (c) α = 2.1 to (d) α = 3.0. In this projection, two surface elements forming a pair at r1 and r2 lie on top of each other, rendering a single point within the circular area. The projected area, indicated in blue, corresponds to those pairs of surface elements which share the “northern” BC. Likewise, the projected area within which both surface elements feature the “southern” BC is indicated in red. The white areas correspond to pairs of surface elements with opposite BCs. As a function of ϕ and for a fixed value of ϑ, in projection the pairs of surface elements form a ring of radius ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϑ) (see Fig. 15). We depict the case ϑ = 1 so that ρ = 0.84R (color-coded ring). The points 1 to 4 mark the intersections of the color-coded ring with the projected equatorial steps of the BC, which are given by the polar coordinates (ρ, ϕ1) through (ρ, ϕ4). Both the thick red and the thick blue arcs of this ring represent equal BCs on both particle surfaces, whereas those arcs being half blue and half red correspond to opposite BCs. Additional explanations, such as the meaning of Rs, are given in the main text. sin(ϑ) (see Fig. 15). We depict the case ϑ = 1 so that ρ = 0.84R (color-coded ring). The points 1 to 4 mark the intersections of the color-coded ring with the projected equatorial steps of the BC, which are given by the polar coordinates (ρ, ϕ1) through (ρ, ϕ4). Both the thick red and the thick blue arcs of this ring represent equal BCs on both particle surfaces, whereas those arcs being half blue and half red correspond to opposite BCs. Additional explanations, such as the meaning of Rs, are given in the main text. | |
Within DA, the force due to each ring of surface elements of equal distance between them is proportional to its arc length and to the force between parallel walls corresponding to the respective combination of the BC. In Fig. 16(a), the blue curve, representing a common “northern” BC, has an arc length of (ϕ2 − ϕ1)ρ, whereas the red arc represents a common “southern” BC with an arc length of (ϕ4 − ϕ3)ρ. In this case, using the relation arccos(−x) = π − arccos(x), the total arc length of equal BCs amounts to [2π − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arccos(cot
arccos(cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot
cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1) − 2
ϑ1) − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arccos(cot
arccos(cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot
cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2)]ρ.
ϑ2)]ρ.
The number and the order of intersections between a ring of equidistant surface element pairs and the projected Janus equators depend on the radius of the ring. For ρ < R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1 (the inner gray circle in Fig. 16 indicates ρ = R
ϑ1 (the inner gray circle in Fig. 16 indicates ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1), the ring does not cross the projected steps in the BC at all. For R
ϑ1), the ring does not cross the projected steps in the BC at all. For R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1 < ρ < R
ϑ1 < ρ < R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2, there are two points of intersection (we recall that the labels ① and ② are chosen such that |cos
ϑ2, there are two points of intersection (we recall that the labels ① and ② are chosen such that |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1| < |cos
ϑ1| < |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2|). Starting from ρ = R
ϑ2|). Starting from ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2 (indicated by the outer gray circle), for ρ > R
ϑ2 (indicated by the outer gray circle), for ρ > R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2 there are four points of intersection. However, at a specific radius ρ = Rs (gray dashed line in Fig. 16), the two half-ellipses intersect and the order of the values ϕ1,…,ϕ4 changes (e.g. compare the order of the intersections in Fig. 16(a) and (b)).
ϑ2 there are four points of intersection. However, at a specific radius ρ = Rs (gray dashed line in Fig. 16), the two half-ellipses intersect and the order of the values ϕ1,…,ϕ4 changes (e.g. compare the order of the intersections in Fig. 16(a) and (b)).
The dimensionless radius 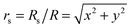 is determined by the intersection point (x, y) of the two semi-ellipses, which is found from a solution of the general problem of the intersection between two co-centric ellipses: the first ellipse (x/a1)2 + (y/b1)2 = 1 and the second ellipse (x/a2)2 + (y/b2)2 = 1 rotated by an angle α. Within their parametric representations the intersections follow from
is determined by the intersection point (x, y) of the two semi-ellipses, which is found from a solution of the general problem of the intersection between two co-centric ellipses: the first ellipse (x/a1)2 + (y/b1)2 = 1 and the second ellipse (x/a2)2 + (y/b2)2 = 1 rotated by an angle α. Within their parametric representations the intersections follow from
| | 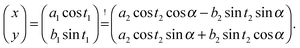 | (B8) |
Eqn (B8) is a system of two equations for the two unknowns
t1 and
t2, which become functions of
a1,
b1,
a2,
b2, and
α. For the present situation, and with
x and
y giving rise to a dimensionless factor
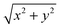
of the radius
R, the problem reduces to the special case in which the semi-major axes are
a1 =
a2 = 1 (
i.e. the semi-major axes are touching the circle of radius
R) and the semi-minor axes are the projected lengths
b1 = |
b(p)1|/
R = |cos(
ϑ1)| and
b2 = |
b(p)2|/
R = |cos(
ϑ2)|. While in principle this system of equations can be solved analytically, it is not guaranteed that all solutions are real, because in degenerate cases (
e.g. for
α = 0 or
α = π and
b1 =
b2, or
b1 =
b2 = 1, or
b1 =
b2 = 0) the number of physically acceptable solutions can be less than four. In the non-degenerate cases, out of these four general solutions of the intersection of two ellipses, only one gives the intersection of two half-ellipses. We have followed a pragmatic approach by solving
eqn (B8) numerically within an
a priori chosen interval of
t2 in order to preselect the appropriate solution for the half-ellipses.
83 We note that our definition enforces the relation |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1| < |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2|, so that the dimensionless radius
rs corresponding to the point of intersection between the two half-ellipses is bound by |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2| ≤
rs ≤ 1, because any point on the second ellipse has a radial distance from its center, the value of which lies between the semi-minor axis
b2 = cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2 and the semi-major axis
a2 = 1, and so does the point of intersection.
Using this procedure, we have constructed the force between two Janus spheres within DA by integrating the force between the rings of surface elements of radius ρ, with attractive and repulsive contributions proportional to the respective four arc lengths determined by ϕ1,…,ϕ4 in eqn (B6), and using the numerically determined radius Rs = Rs(α,ϑ1,ϑ2) for each configuration, which governs the occurrence of the attractive and repulsive force contributions (depending on ρ ≶ Rs) by interchanging the order of ϕ1,…,ϕ4. A thorough investigation of all geometric configurations reveals that the excess force takes the following form
| | 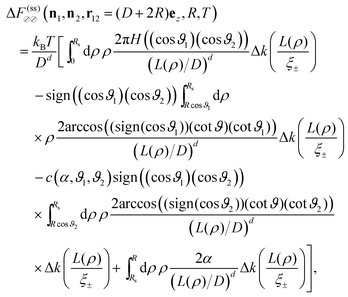 | (B9) |
with
ρ =
R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ and
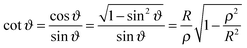
, for
r12 = (
D + 2
R)
ez and
n1,2 in relative coordinates (see
eqn (B2)). The occurrence of various expressions in
eqn (B9) can be rationalized as follows: the combined arclength of equal BCs is generally of the form ±
ϕ4 ∓
ϕ3 ±
ϕ2 ∓
ϕ1 (
i.e. different combinations of the signs). According to eqn (B6), additional shifts of 2π might be required to ensure
ϕi ∈ [0,2π]. In fact the term 2π occurs only for rings of surface elements with radii
ρ <
Rs, provided (cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1)(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2) ≥ 0, which is expressed by the limits of integration of the first term in
eqn (B9) (see below also the note regarding the second and third term). Similarly, the azimuthal angle
α contributes in total as 2
α to the arclength if
ρ >
Rs, but it does not contribute if
ρ <
Rs, leading to the fourth and last term in
eqn (B9). The second and third term reproduce the functional dependence of the arclength on
ϑ(
ρ) and
ϑ1,2. The changes of the sign of the argument in the arccos functions in eqn (B6) generalize to sign(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2
ϑ1,2) in
eqn (B9) due to the relation 2arccos(−
x) = 2π − 2arccos(
x). Note that the shift of 2π re-enters the first term; in
eqn (B9) the first term reflects the notation in the second and third term. Analogous to the geometry of two Janus cylinders, we find a dependence of the sign of the second and third term on the sign of (cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1)(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2). Furthermore, the sign picking function
c(
α,
ϑ1,
ϑ2) is given by
| | 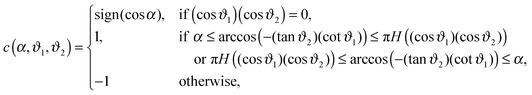 | (B10) |
with the restriction that
α is replaced by 2π −
α if
α > π.
Finally, the scaling function of the excess force is found from eqn (B9) by using the distance function L(ρ) within the “parabolic distance approximation” 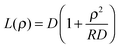 and by applying the substitution
and by applying the substitution 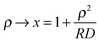 with
with 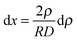 , which leads to L(x) = Dx,
, which leads to L(x) = Dx, 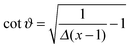 , and
, and
| | 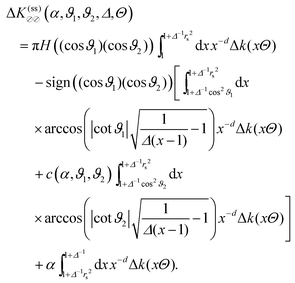 | (B11) |
with the abbreviation
rs =
Rs/
R, and the replacement of (sign(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2
ϑ1,2))cot
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2
ϑ1,2 = |cot
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2
ϑ1,2|, which holds in the domain of the definition of the polar angles,
i.e. for
ϑ1,2 ∈ [0,π].
Appendix C: scaling function of the effective potential for two Janus spheres
The effective potential can be determined from the force in the relative coordinate system according to| | 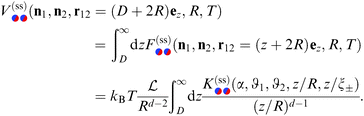 | (C1) |
Substitution of z = D ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) with dz = D d
with dz = D d![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) yields
yields| | 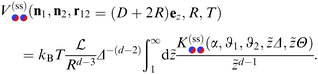 | (C2) |
This can be cast into the scaling form| | 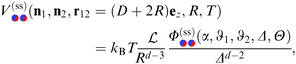 | (C3) |
with the scaling function 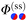 of the effective potential,
of the effective potential,| | 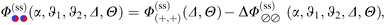 | (C4) |
where| | 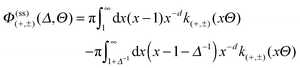 | (C5) |
is the scaling function of the potential between two homogeneous spheres,16 with an explicit dependence on Δ retained (in spite of the underlying DA limit Δ → 0) for consistency with the dependence on Δ of the orientation dependent term ΔΦ(ss)⊘⊘.
In order to obtain the excess scaling function ΔΦ(ss)⊘⊘ one has to integrate ΔK(ss)⊘⊘ from eqn (B11) in accordance with eqn (C2). The integral of ΔK(ss)⊘⊘ features two generic types of integrals (here, omitting the tilde of the integration variable):
| | 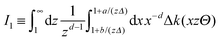 | (C6) |
with the first and last contribution to this integral [compare
eqn (B11) and (C2)] being described by
a =
rs2,
b = 0 and
a = 1,
b =
rs2, respectively, and
| | 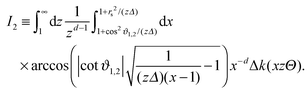 | (C7) |
We represent integral
I1 by the function
| | 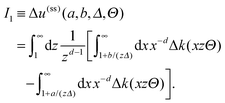 | (C8) |
With the substitution
x →
w =
zΔ(
x − 1) so that d
w =
zΔd
x one has
| | 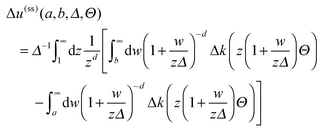 | (C9) |
and with the substitution
z →
y =
z +
w/
Δ with d
y = d
z one finds
| | 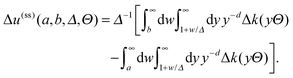 | (C10) |
After switching the order of the integrations according to
| | 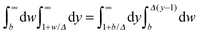 | (C11) |
the integration over
w can be carried out, resulting in
| | 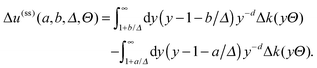 | (C12) |
Integral
I2 is represented by the function
| |  | (C13) |
As before, we first use the substitution
x →
w =
zΔ(
x − 1) with d
w =
zΔd
x, followed by the substitution
z →
y =
z +
w/
Δ with d
y = d
z. This renders
| | 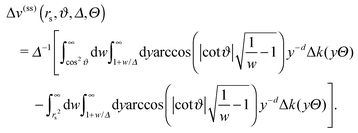 | (C14) |
We recall that the semi-minor axes of the two half-ellipses are given by
b1,2 = |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2
ϑ1,2| and that
rs denotes the distance of the intersection point between the half-ellipses from the symmetry axis of the two particles. Obviously, the intersection point cannot be closer to the common origin than any semi-minor axis, so that |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1| ≤
rs and |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2| ≤
rs. Based on
eqn (B11), we need to evaluate Δ
v(ss)(
rs,
ϑ,
Δ,
Θ) for
ϑ =
ϑ1 and
ϑ =
ϑ2. For that reason, we consider only the case |cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ| <
rs and reorder the integrals:
| | 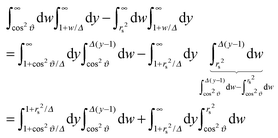 | (C15) |
so that finally
| | 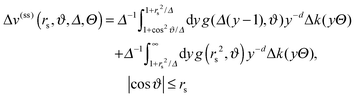 | (C16) |
and
| | 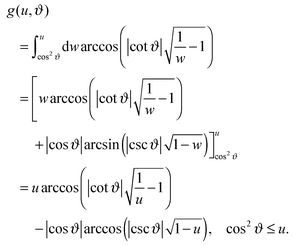 | (C17) |
Note that
g(
u = cos
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ,
ϑ) = 0. Concerning the derivation of
eqn (C17) we leave out the detailed case analysis for the sign of cot
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ, which in the end, can be subsumed by taking the absolute values as stated in
eqn (C17). Putting the results together, the excess scaling function of the potential is given by
| | ΔΦ(ss)⊘⊘(α,ϑ1,ϑ2,Δ,Θ) = πH((cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2))Δu(ss)(rs2,0,Δ,Θ) − sign((cos ϑ2))Δu(ss)(rs2,0,Δ,Θ) − sign((cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2))[Δv(ss)(rs2,ϑ1,Δ,Θ) + c(α,ϑ1,ϑ2)Δv(ss)(rs2,ϑ2,Δ,Θ)] + αΔu(ss)(1,rs2,Δ,Θ). ϑ2))[Δv(ss)(rs2,ϑ1,Δ,Θ) + c(α,ϑ1,ϑ2)Δv(ss)(rs2,ϑ2,Δ,Θ)] + αΔu(ss)(1,rs2,Δ,Θ). | (C18) |
Acknowledgements
M. L. L. would like to thank Ludger Harnau and Matthias Tröndle for helpful discussions.
References
- M. E. Fisher and P. G. de Gennes, C. R. Seances Acad. Sci., Ser. B, 1978, 287, 207 CAS.
- H. G. B. Casimir, Proc. K. Ned. Akad. Wet., 1948, 51, 793 Search PubMed.
- M. Fukuto, Y. F. Yano and P. S. Pershan, Phys. Rev. Lett., 2005, 94, 135702 CrossRef PubMed.
- S. Rafai, D. Bonn and J. Meunier, Physica A, 2007, 386, 31 CrossRef.
- R. Garcia and M. H. W. Chan, Phys. Rev. Lett., 2002, 88, 086101 CrossRef CAS PubMed.
- T. Ueno, S. Balibar, T. Mizusaki, F. Caupin and E. Rolley, Phys. Rev. Lett., 2003, 90, 116102 CrossRef CAS PubMed.
- R. Garcia and M. H. W. Chan, Phys. Rev. Lett., 1999, 83, 1187 CrossRef CAS.
- A. Ganshin, S. Scheidemantel, R. Garcia and M. H. W. Chan, Phys. Rev. Lett., 2006, 97, 075301 CrossRef CAS PubMed.
- A. Hucht, Phys. Rev. Lett., 2007, 99, 185301 CrossRef PubMed.
- O. Vasilyev, A. Gambassi, A. Maciołek and S. Dietrich, EPL, 2007, 80, 60009 CrossRef.
- O. Vasilyev, A. Gambassi, A. Maciołek and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 041142 CrossRef CAS PubMed; O. Vasilyev, A. Gambassi, A. Maciołek and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 039902(E) CrossRef.
- M. Hasenbusch, J. Stat. Mech.: Theory Exp., 2009, P07031 Search PubMed.
- M. Hasenbusch, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 174434 CrossRef.
- M. Hasenbusch, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 104425 CrossRef.
- C. Hertlein, L. Helden, A. Gambassi, S. Dietrich and C. Bechinger, Nature, 2008, 451, 172 CrossRef CAS PubMed.
- A. Gambassi, A. Maciołek, C. Hertlein, U. Nellen, L. Helden, C. Bechinger and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061143 CrossRef CAS PubMed.
- F. Pousaneh, A. Ciach and A. Maciolek, Soft Matter, 2012, 8, 7567 RSC.
- B. Derjaguin, Kolloid Z., 1934, 69, 155 CrossRef.
- M. Hasenbusch, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022130 CrossRef PubMed.
- T. W. Burkhardt and E. Eisenriegler, Phys. Rev. Lett., 1995, 74, 3189 CrossRef CAS PubMed; W. Burkhardt and E. Eisenriegler, Phys. Rev. Lett., 1997, 78, 2867 CrossRef.
- E. Eisenriegler and U. Ritschel, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 13717 CrossRef CAS.
- A. Hanke, F. Schlesener, E. Eisenriegler and S. Dietrich, Phys. Rev. Lett., 1998, 81, 1885 CrossRef CAS.
- F. Schlesener, A. Hanke and S. Dietrich, J. Stat. Phys., 2003, 110, 981 CrossRef CAS.
- E. Eisenriegler, J. Chem. Phys., 2004, 121, 3299 CrossRef CAS PubMed.
- P. G. de Gennes, Rev. Mod. Phys., 1992, 64, 645 CrossRef.
- Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381 CrossRef CAS PubMed.
- F. Romano and F. Sciortino, Soft Matter, 2011, 7, 5799 RSC.
- S. N. Fejer and D. J. Wales, Soft Matter, 2015, 11, 6663 RSC.
- A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150 CrossRef CAS PubMed.
- E. Bianchi, R. Blaak and C. N. Likos, Phys. Chem. Chem. Phys., 2011, 13, 6397 RSC.
- N. Prasad, J. Perumal, C.-H. Choi, C.-S. Lee and D.-P. Kim, Adv. Funct. Mater., 2009, 19, 1656 CrossRef CAS.
- A. Walther, M. Drechsler, S. Rosenfeldt, L. Harnau, M. Ballauff, V. Abetz and A. H. E. Müller, J. Am. Chem. Soc., 2009, 131, 4720 CrossRef CAS PubMed.
- G.-R. Yi, D. J. Pine and S. Sacanna, J. Phys.: Condens. Matter, 2013, 25, 193101 CrossRef PubMed.
- J. Zhang, E. Luijten and S. Granick, Annu. Rev. Phys. Chem., 2015, 66, 581 CrossRef CAS PubMed.
- C. Yu, J. Zhang and S. Granick, Angew. Chem., Int. Ed., 2014, 53, 4364 CrossRef CAS PubMed.
- L. Hong, A. Cacciuto, E. Luijten and S. Granick, Nano Lett., 2006, 6, 2510 CrossRef CAS PubMed.
- E. Bianchi, G. Kahl and C. N. Likos, Soft Matter, 2011, 7, 8313 RSC.
- F. Soyka, O. Zvyagolskaya, C. Hertlein, L. Helden and C. Bechinger, Phys. Rev. Lett., 2008, 101, 208301 CrossRef PubMed.
- M. Tröndle, O. Zvyagolskaya, A. Gambassi, D. Vogt, L. Harnau, C. Bechinger and S. Dietrich, Mol. Phys., 2011, 109, 1169 CrossRef.
- M. Tröndle, S. Kondrat, A. Gambassi, L. Harnau and S. Dietrich, EPL, 2009, 88, 40004 CrossRef.
- Y. Iwashita and Y. Kimura, Soft Matter, 2013, 9, 10694 RSC.
- Y. Iwashita and Y. Kimura, Soft Matter, 2014, 10, 7170 RSC.
- T. F. Mohry, A. Maciołek and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 061117 CrossRef CAS PubMed.
- N. Kern and D. Frenkel, J. Chem. Phys., 2003, 118, 9882 CrossRef CAS.
- Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407 CrossRef CAS.
- F. Sciortino, A. Giacometti and G. Pastore, Phys. Rev. Lett., 2009, 103, 237801 CrossRef PubMed.
- F. Sciortino, A. Giacometti and G. Pastore, Phys. Chem. Chem. Phys., 2010, 12, 11869 RSC.
- Z. Preisler, T. Vissers, G. Munao, F. Smallenburg and F. Sciortino, Soft Matter, 2014, 10, 5121 RSC.
- T. Vissers, Z. Preisler, F. Smallenburg, M. Dijkstra and F. Sciortino, J. Chem. Phys., 2013, 138, 164505 CrossRef PubMed.
- R. Fantoni, A. Giacometti, F. Sciortino and G. Pastore, Soft Matter, 2011, 7, 2419 RSC.
- B. D. Marshall, D. Ballal and W. G. Chapman, J. Chem. Phys., 2012, 137, 104909 CrossRef PubMed.
- A. Giacometti, C. Gögelein, F. Lado, F. Sciortino, S. Ferrari and G. Pastore, J. Chem. Phys., 2014, 140, 094104 CrossRef PubMed.
- H. Shin and K. S. Schweizer, Soft Matter, 2014, 10, 262 RSC.
- F. Parisen Toldin and S. Dietrich, J. Stat. Mech.: Theory Exp., 2010, P11003 CrossRef.
- F. Parisen Toldin, M. Tröndle and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052110 CrossRef PubMed.
- F. Parisen Toldin, M. Tröndle and S. Dietrich, J. Phys.: Condens. Matter, 2015, 27, 214010 CrossRef PubMed.
- M. Tröndle, S. Kondrat, A. Gambassi, L. Harnau and S. Dietrich, J. Chem. Phys., 2010, 133, 074702 CrossRef PubMed.
- A. Pelissetto and E. Vicari, Phys. Rep., 2002, 368, 549 CrossRef CAS.
-
K. Binder, in Phase Transitions and Critical Phenomena, ed. C. Domb and J. L. Lebowitz, Academic, London, 1983, vol. 8, p. 1 Search PubMed.
-
H. W. Diehl, in Phase Transitions and Critical Phenomena, ed. C. Domb and J. L. Lebowitz, Academic, London, 1986, vol. 10, p. 75 Search PubMed.
-
M. Krech, The Casimir Effect in Critical Systems, World Scientific, Singapore, 1994 Search PubMed.
-
J. M. Brankov, D. M. Danchev and N. S. Tonchev, Theory of critical phenomena in finite-size systems, World Scientific, Singapore, 2000 Search PubMed.
- A. Gambassi, J. Phys.: Conf. Ser., 2009, 161, 012037 CrossRef.
- M. Krech and S. Dietrich, Phys. Rev. Lett., 1991, 66, 345 CrossRef CAS PubMed; M. Krech and S. Dietrich, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 1886 CrossRef; M. Krech and S. Dietrich, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 1922 CrossRef.
- M. Krech, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 1642 CrossRef CAS.
- A. Hanke and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 5081 CrossRef CAS.
- S. Kondrat, L. Harnau and S. Dietrich, J. Chem. Phys., 2007, 126, 174902 CrossRef CAS PubMed.
- S. Kondrat, L. Harnau and S. Dietrich, J. Chem. Phys., 2009, 131, 204902 CrossRef CAS PubMed.
- H. B. Tarko and M. E. Fisher, Phys. Rev. Lett., 1973, 31, 926 CrossRef; H. B. Tarko and M. E. Fisher, Phys. Rev. B: Solid State, 1975, 11, 1217 CrossRef.
- D. Bonn, J. Otwinowski, S. Sacanna, H. Guo, G. Wegdam and P. Schall, Phys. Rev. Lett., 2009, 103, 156101 CrossRef PubMed; A. Gambassi and S. Dietrich, Phys. Rev. Lett., 2010, 105, 059601 CrossRef PubMed.
- M. Labbe-Laurent, M. Tröndle, L. Harnau and S. Dietrich, Soft Matter, 2014, 10, 2270 RSC.
- D. Dantchev and M. Krech, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 046119 CrossRef PubMed.
- M. Hasenbusch, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174421 CrossRef.
- Another definition of the volume of a hypercylinder would be x2 + y2 + z2 ≤ R2, 0 ≤ w ≤ L4, which we dismiss for formal reasons: the projection of this object onto three dimensions renders a sphere instead of a cylinder. Thus this object does not fulfill the expectation for a basic extension of a cylinder from three to four dimensions.
- D. Dantchev and G. Valchev, J. Colloid Interface Sci., 2012, 372, 148 CrossRef CAS PubMed.
- M. Sprenger, F. Schlesener and S. Dietrich, J. Chem. Phys., 2006, 124, 134703 CrossRef PubMed.
-
A. D. Law, M. Labbe-Laurent and S. Dietrich, to be published.
- The one-sided limit is required not because of any discontinuities in the scaling function, but for consistency with the discontinuous definition
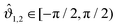 . The two-sided limit does exist and the scaling function is continuous, see Appendix A. Concerning the numerical evaluation,
. The two-sided limit does exist and the scaling function is continuous, see Appendix A. Concerning the numerical evaluation, 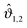 can be equally defined as the remainder of the division of x = ϑ1,2 + π/2 (dividend) by y = π (divisor) minus π/2. The remainder is obtained from the floating point version of the modulo operation, provided by most programming languages. However, care has to be taken as the floating point modulus is ambiguous for negative numbers. The right-sided limit is compatible only with the definition of the modulo
operation by “floored division”
can be equally defined as the remainder of the division of x = ϑ1,2 + π/2 (dividend) by y = π (divisor) minus π/2. The remainder is obtained from the floating point version of the modulo operation, provided by most programming languages. However, care has to be taken as the floating point modulus is ambiguous for negative numbers. The right-sided limit is compatible only with the definition of the modulo
operation by “floored division” 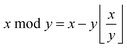 , where the integer quotient is given by the floor function
, where the integer quotient is given by the floor function 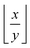 , ensuring that 0 ≤ x mod π < π ∀x; see
D. Knuth, The Art of Computer Programming, Addison-Wesley, Reading, 1997, vol. 1, p. 39 Search PubMed.
, ensuring that 0 ≤ x mod π < π ∀x; see
D. Knuth, The Art of Computer Programming, Addison-Wesley, Reading, 1997, vol. 1, p. 39 Search PubMed.
- S. Paladugu, A. Callegari, Y. Tuna, L. Barth, S. Dietrich, A. Gambassi and G. Volpe, Nat. Commun., 2016, 7, 11403 CrossRef CAS PubMed.
- We only consider orientations of the Janus spheres in d = 3 and disregard the possible, but contrived case of orientations in d = 4 which would violate the invariance in the extra dimension.
- Although the transformation (x, y, z) → (α, ϑ1, ϑ2) also involves inverse trigonometric functions, which are multivalued within the principal domains α ∈ [0, 2π] and ϑi ∈ [0, π] the only points which give rise to ambiguities are the “north” and “south” pole at ϑi = 0 and ϑi = π, for which the value of α is completely arbitrary. However, for tilt angles γ > 0 these poles do not lie on the circular paths of n1 and n2 and therefore are avoidable by this transformation.
- T. G. Mattos, L. Harnau and S. Dietrich, J. Chem. Phys., 2013, 138, 074704 CrossRef CAS PubMed.
- This also allows us to use optimized numerical root finding algorithms operating within an interval in which the function changes sign. We have chosen Brent's root finding method, http://mathworld.wolfram.com/BrentsMethod.html, which is implemented in the SciPy library http://docs.scipy.org/doc/scipy-0.16.0/reference/generated/scipy.optimize.brentq.html.
- D. Dantchev, F. Schlesener and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011121 CrossRef PubMed.
- T. F. Mohry, A. Maciołek and S. Dietrich, J. Chem. Phys., 2012, 136, 224902 CrossRef CAS PubMed; T. F. Mohry, A. Maciołek and S. Dietrich, J. Chem. Phys., 2012, 136, 224903 CrossRef PubMed.
- H. Hobrecht and A. Hucht, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 042315 CrossRef PubMed.
- J. R. Edison, N. Tasios, S. Belli, R. Evans, R. van Roij and M. Dijkstra, Phys. Rev. Lett., 2015, 114, 038301 CrossRef CAS PubMed; J. R. Edison, S. Belli, R. Evans, R. van Roij and M. Dijkstra, Mol. Phys., 2015, 113, 2546 CrossRef.
- V. D. Nguyen, M. T. Dang, T. A. Nguyen and P. Schall, J. Phys.: Condens. Matter, 2016, 28, 043001 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article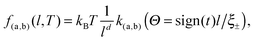
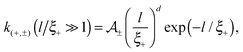
 are universal amplitudes.16
are universal amplitudes.16
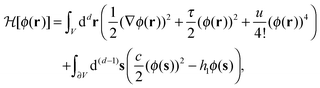
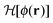 for t < 0 in the demixed phase; u is dimensionless in d = 4. In order to treat off-critical concentrations, the expression in eqn (4) can be extended to contain a term proportional to a bulk field h. The surface enhancement c and the symmetry breaking surface field h1 determine the BC. We focus on the so-called normal surface universality class, which is generic for liquids, with c = 0 and the two fixed point values h1 = ±∞. This leads to a divergence of ϕ → ±∞ at the surface of the colloids corresponding to what is denoted as the (+) and (−) BC.60 Concerning the numerical implementation, the divergence is realized by a short distance expansion close to the surface.66,67 Within MFT, only the order parameter configuration with the largest statistical weight
for t < 0 in the demixed phase; u is dimensionless in d = 4. In order to treat off-critical concentrations, the expression in eqn (4) can be extended to contain a term proportional to a bulk field h. The surface enhancement c and the symmetry breaking surface field h1 determine the BC. We focus on the so-called normal surface universality class, which is generic for liquids, with c = 0 and the two fixed point values h1 = ±∞. This leads to a divergence of ϕ → ±∞ at the surface of the colloids corresponding to what is denoted as the (+) and (−) BC.60 Concerning the numerical implementation, the divergence is realized by a short distance expansion close to the surface.66,67 Within MFT, only the order parameter configuration with the largest statistical weight 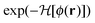 is considered and fluctuations of the order parameter are neglected. Within this approximation the free energy follows from
is considered and fluctuations of the order parameter are neglected. Within this approximation the free energy follows from 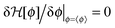 . The MFT order parameter profile defined as m = 〈ϕ〉/ϕt minimizes the Hamiltonian
. The MFT order parameter profile defined as m = 〈ϕ〉/ϕt minimizes the Hamiltonian 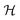 , where
, where 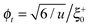 is the non-universal amplitude of the bulk order parameter ϕb = ϕt|t|β, β = 1/2 in d = 4 and β ≃ 0.33 in d = 3. MFT captures correctly the critical behavior above the upper critical dimension dc = 4, with logarithmic corrections in d = 4. In the context of renormalization group theory, the MFT results represent also the leading order contribution within an expansion in terms of ε = 4 − d. There are only two independent non-universal bulk amplitudes,59,60 such as ϕt and ξ+0.
is the non-universal amplitude of the bulk order parameter ϕb = ϕt|t|β, β = 1/2 in d = 4 and β ≃ 0.33 in d = 3. MFT captures correctly the critical behavior above the upper critical dimension dc = 4, with logarithmic corrections in d = 4. In the context of renormalization group theory, the MFT results represent also the leading order contribution within an expansion in terms of ε = 4 − d. There are only two independent non-universal bulk amplitudes,59,60 such as ϕt and ξ+0.
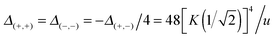 , where K is the complete elliptic integral of the first kind.
, where K is the complete elliptic integral of the first kind. has been minimized numerically using a three-dimensional finite element method in order to obtain the order parameter profiles. The system is assumed to be translationally invariant along an extra dimension in d = 4. The critical Casimir forces are determined directly from the order parameter profile using the stress-tensor method.23,65,68
has been minimized numerically using a three-dimensional finite element method in order to obtain the order parameter profiles. The system is assumed to be translationally invariant along an extra dimension in d = 4. The critical Casimir forces are determined directly from the order parameter profile using the stress-tensor method.23,65,68![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) with Θ < 0 for t < 0 and Θ > 0 for t > 0, respectively. We note that the scaling variable Θ = sign(t)l/ξ± contains distinct denominators ξ±0 for t ≷ 0 in accordance with the universal ratio Rξ = ξ+0/ξ−0 = 1.96 in d = 358 and
with Θ < 0 for t < 0 and Θ > 0 for t > 0, respectively. We note that the scaling variable Θ = sign(t)l/ξ± contains distinct denominators ξ±0 for t ≷ 0 in accordance with the universal ratio Rξ = ξ+0/ξ−0 = 1.96 in d = 358 and 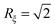 in d = 4.69 Here, we focus on t ≥ 0, for which the solvent is in the homogeneous, mixed phase. This relates to the common experimental situation in which the critical behavior near the lower critical point of a binary liquid mixture is studied upon approaching Tc along a thermodynamic path from below (e.g.ref. 15, 38, 40–42 and 70).
in d = 4.69 Here, we focus on t ≥ 0, for which the solvent is in the homogeneous, mixed phase. This relates to the common experimental situation in which the critical behavior near the lower critical point of a binary liquid mixture is studied upon approaching Tc along a thermodynamic path from below (e.g.ref. 15, 38, 40–42 and 70).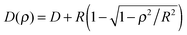 , where D is the closest distance between the particle surface with radius R and the planar wall. Since the DA holds only in the limit of large particle radii R, i.e. Δ = D/R → 0, it is often16,22,57 used in conjunction with the further “parabolic distance approximation” D(ρ) ≈ D(1 + ρ2/(2RD)). For comparison, the surface-to-surface distance
, where D is the closest distance between the particle surface with radius R and the planar wall. Since the DA holds only in the limit of large particle radii R, i.e. Δ = D/R → 0, it is often16,22,57 used in conjunction with the further “parabolic distance approximation” D(ρ) ≈ D(1 + ρ2/(2RD)). For comparison, the surface-to-surface distance 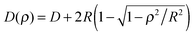 either between two spheres or between two cylinders increases twice as fast with ρ; correspondingly, within the “parabolic distance approximation” one has in these two cases D(ρ) ≈ D(1 + ρ2/(RD)).
either between two spheres or between two cylinders increases twice as fast with ρ; correspondingly, within the “parabolic distance approximation” one has in these two cases D(ρ) ≈ D(1 + ρ2/(RD)).

 in order to denote
in order to denote  in d = 3 and
in d = 3 and 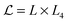 in d = 4.
in d = 4.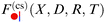 between a homogeneous cylindrical particle of length L and radius R, and a substrate with a step, at a lateral position X, has the scaling form (see eqn (D1) in Appendix D of ref. 57)
between a homogeneous cylindrical particle of length L and radius R, and a substrate with a step, at a lateral position X, has the scaling form (see eqn (D1) in Appendix D of ref. 57)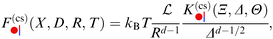
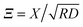 , Δ = D/R, and Θ = ±D/ξ±(T) (with sign(Θ) = sign(t)) in d dimensions. The scaling function
, Δ = D/R, and Θ = ±D/ξ±(T) (with sign(Θ) = sign(t)) in d dimensions. The scaling function 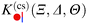 of the force
of the force  can be decomposed as57
can be decomposed as57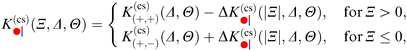
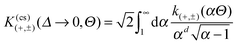
 involving the step position X is given within DA by (see eqn (D6) in ref. 57)
involving the step position X is given within DA by (see eqn (D6) in ref. 57)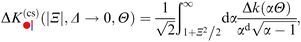
 depends only on the absolute value of the scaled distance Ξ, because the inverted position is equivalent to a switch of the BC of the step, which is covered by eqn (6).
depends only on the absolute value of the scaled distance Ξ, because the inverted position is equivalent to a switch of the BC of the step, which is covered by eqn (6).
 obtained within DA for d = 4 viaeqn (6)–(8) (dashed curves) with the corresponding full MFT results (solid lines) determined by numerical minimization of the Hamiltonian. As expected from ref. 57, in Fig. 2(a) the DA scaling function approximates the full MFT results well for the geometry of a homogeneous cylinder above a substrate step, shown for various scaled step positions Ξ on both sides of the step.
obtained within DA for d = 4 viaeqn (6)–(8) (dashed curves) with the corresponding full MFT results (solid lines) determined by numerical minimization of the Hamiltonian. As expected from ref. 57, in Fig. 2(a) the DA scaling function approximates the full MFT results well for the geometry of a homogeneous cylinder above a substrate step, shown for various scaled step positions Ξ on both sides of the step.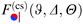 depends on the orientation angle ϑ (Fig. 1(b)) of the Janus cylinder. The scaling form remains the same as in the previous case, i.e.,
depends on the orientation angle ϑ (Fig. 1(b)) of the Janus cylinder. The scaling form remains the same as in the previous case, i.e.,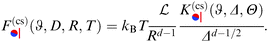
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ between the (left) edge of the projection and the projection of the cylinder axis (Fig. 1(b)). Conversely, the projection of the axis of a homogeneous cylinder onto a substrate with a chemical step renders a distance X between them (Fig. 1(b)). Choosing X = XJ = R
ϑ between the (left) edge of the projection and the projection of the cylinder axis (Fig. 1(b)). Conversely, the projection of the axis of a homogeneous cylinder onto a substrate with a chemical step renders a distance X between them (Fig. 1(b)). Choosing X = XJ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, within DA the sums of the surface elements vis-à-vis for these two configurations are the same and thus yield the same force. In terms of the present scaling function the relation X = XJ translates into
ϑ, within DA the sums of the surface elements vis-à-vis for these two configurations are the same and thus yield the same force. In terms of the present scaling function the relation X = XJ translates into 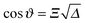 . This implies that within DA the scaling function
. This implies that within DA the scaling function  of the force between a Janus cylinder and a homogeneous substrate follows from eqn (6)–(8) upon substituting X = R
of the force between a Janus cylinder and a homogeneous substrate follows from eqn (6)–(8) upon substituting X = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ therein. Fig. 2(b) shows for a Janus cylinder next to a homogeneous wall as a function of the scaled temperature Θ the full MFT results (solid lines) for various orientations ϑ (chosen independently from Fig. 2(a)). The corresponding DA scaling functions are shown as dashed lines. In Fig. 2(b), for the same distance Δ = 1/5, the DA scaling functions appear to deviate slightly more from the corresponding full MFT results than those in Fig. 2(a).
ϑ therein. Fig. 2(b) shows for a Janus cylinder next to a homogeneous wall as a function of the scaled temperature Θ the full MFT results (solid lines) for various orientations ϑ (chosen independently from Fig. 2(a)). The corresponding DA scaling functions are shown as dashed lines. In Fig. 2(b), for the same distance Δ = 1/5, the DA scaling functions appear to deviate slightly more from the corresponding full MFT results than those in Fig. 2(a).
 and
and 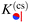 of the force for fixed scaled temperature Θ as a function of the scaling variable
of the force for fixed scaled temperature Θ as a function of the scaling variable 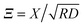 , which either corresponds to the lateral position X of the axis of a homogeneous cylinder relative to a chemical step on the substrate, or to the orientation
, which either corresponds to the lateral position X of the axis of a homogeneous cylinder relative to a chemical step on the substrate, or to the orientation 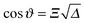 of a Janus cylinder above a homogeneous substrate. Accordingly, for the two scaled temperatures Θ = 1 and Θ = 5.65 in Fig. 3 we show the full MFT scaling function
of a Janus cylinder above a homogeneous substrate. Accordingly, for the two scaled temperatures Θ = 1 and Θ = 5.65 in Fig. 3 we show the full MFT scaling function 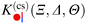 of the force for the homogeneous cylinder-step geometry [eqn (5)] as solid lines and the full MFT scaling function
of the force for the homogeneous cylinder-step geometry [eqn (5)] as solid lines and the full MFT scaling function 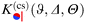 of a Janus cylinder next to a homogeneous substrate [eqn (9)] as dashed lines. The two values of Θ, here and in subsequent figures, are chosen to represent on the one hand values very close to Tc, and on the other hand those approaching Tc, but within the range of the monotonic decay of the scaling function (see also Fig. 2). In the spirit of the aforementioned equivalence within DA, the orientation angle ϑ of the Janus cylinder is related to the distance X between the projected axis of a homogeneous cylinder and the chemical step at the wall via the DA relation Ξ = Δ−1/2
of a Janus cylinder next to a homogeneous substrate [eqn (9)] as dashed lines. The two values of Θ, here and in subsequent figures, are chosen to represent on the one hand values very close to Tc, and on the other hand those approaching Tc, but within the range of the monotonic decay of the scaling function (see also Fig. 2). In the spirit of the aforementioned equivalence within DA, the orientation angle ϑ of the Janus cylinder is related to the distance X between the projected axis of a homogeneous cylinder and the chemical step at the wall via the DA relation Ξ = Δ−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ. For Δ = 1 in Fig. 3(a), there is a visible difference between the two scaling functions. However, for Δ = 1/5 in Fig. 3(b), which is closer to the DA limit Δ ≪ 1, the difference is considerably smaller. For comparison, in gray the scaling function of the force within DA is shown, which approximates both MFT scaling functions for Δ ≪ 1.
ϑ. For Δ = 1 in Fig. 3(a), there is a visible difference between the two scaling functions. However, for Δ = 1/5 in Fig. 3(b), which is closer to the DA limit Δ ≪ 1, the difference is considerably smaller. For comparison, in gray the scaling function of the force within DA is shown, which approximates both MFT scaling functions for Δ ≪ 1.
 between a homogeneous cylinder above a chemical step on the substrate (solid lines) and
between a homogeneous cylinder above a chemical step on the substrate (solid lines) and  for a Janus cylinder above a homogeneous substrate (dashed lines). The DA (valid for Δ ≪ 1) implies the same scaling function in both cases (gray lines), provided the tilt angle ϑ of the Janus cylinder (see Fig. 1(b)) is related to the scaled step position on the substrate as Ξ = Δ−1/2
for a Janus cylinder above a homogeneous substrate (dashed lines). The DA (valid for Δ ≪ 1) implies the same scaling function in both cases (gray lines), provided the tilt angle ϑ of the Janus cylinder (see Fig. 1(b)) is related to the scaled step position on the substrate as Ξ = Δ−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ. The full mean field results for
ϑ. The full mean field results for  (step) and
(step) and 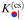 (Janus) are shown for Δ = 1 in (a) and Δ = 1/5 in (b), each for the two scaled temperatures Θ = 1 (red; close to Tc) and Θ = 5.65 (green; within the monotonic decay of
(Janus) are shown for Δ = 1 in (a) and Δ = 1/5 in (b), each for the two scaled temperatures Θ = 1 (red; close to Tc) and Θ = 5.65 (green; within the monotonic decay of  as a function of Θ). From (a) it can be seen that within full MFT the correspondence between the case of a homogeneous cylinder above a chemical step on the substrate and a Janus particle above a homogeneous substrate does not hold in general. It holds roughly for Θ = 5.65 and further away from Tc, but not close to Tc (such as for Θ = 1). However, for Δ = 1/5 in (b), i.e. close to the DA limit of Δ ≪ 1, the correspondence of the two scaling functions within DA carries over to the MFT results. As a guide to the eye, visualizations of the geometry corresponding to certain values of Ξ are provided at the top of the panels.
as a function of Θ). From (a) it can be seen that within full MFT the correspondence between the case of a homogeneous cylinder above a chemical step on the substrate and a Janus particle above a homogeneous substrate does not hold in general. It holds roughly for Θ = 5.65 and further away from Tc, but not close to Tc (such as for Θ = 1). However, for Δ = 1/5 in (b), i.e. close to the DA limit of Δ ≪ 1, the correspondence of the two scaling functions within DA carries over to the MFT results. As a guide to the eye, visualizations of the geometry corresponding to certain values of Ξ are provided at the top of the panels.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ = −0.64. We have included certain isolines of the profile as a guide to the eye. The green line represents the zero crossing of the profiles, which has a special significance discussed in the main text. The gray curve indicates the zero crossing expected (at the same temperate) for the profile in the case that both the particle and the substrate are homogeneous, but with opposite BCs.
ϑ = −0.64. We have included certain isolines of the profile as a guide to the eye. The green line represents the zero crossing of the profiles, which has a special significance discussed in the main text. The gray curve indicates the zero crossing expected (at the same temperate) for the profile in the case that both the particle and the substrate are homogeneous, but with opposite BCs.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, which seeks to incorporate the bending of the zero crossing line. The base of this idea follows from ref. 71, where a similar principle was used successfully in order to reconcile DA with MFT results.
ϑ, which seeks to incorporate the bending of the zero crossing line. The base of this idea follows from ref. 71, where a similar principle was used successfully in order to reconcile DA with MFT results.![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) = R + pD and an effective surface-to-surface distance
= R + pD and an effective surface-to-surface distance ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = (1 − p)D, so that the zero crossing line follows the solid light gray line. This yields an improved scaled position (dotted, vertical light gray line)
= (1 − p)D, so that the zero crossing line follows the solid light gray line. This yields an improved scaled position (dotted, vertical light gray line)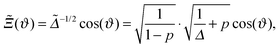

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ of the step in the BC of the Janus particle, projected onto the substrate along the normal of the substrate (dark gray dotted line). The improved DA relation
ϑ of the step in the BC of the Janus particle, projected onto the substrate along the normal of the substrate (dark gray dotted line). The improved DA relation 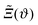 in eqn (10) follows the same principle, but applied to a fictitious particle of increased radius R + pD, with the rescaling parameter p, resulting in the solid light gray zero crossing line and the light gray vertical dotted line. The inset provides a magnified view of the relevant features.
in eqn (10) follows the same principle, but applied to a fictitious particle of increased radius R + pD, with the rescaling parameter p, resulting in the solid light gray zero crossing line and the light gray vertical dotted line. The inset provides a magnified view of the relevant features.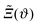 in eqn (10) can be checked against this discrete set {Ξ,ϑ}. We note that the projected, scaled step position
in eqn (10) can be checked against this discrete set {Ξ,ϑ}. We note that the projected, scaled step position 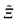 is proportional to
is proportional to ![[capital Delta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10b.gif) −1/2 > Δ−1/2 for p > 0, i.e. for the same orientation ϑ, the scaled step position
−1/2 > Δ−1/2 for p > 0, i.e. for the same orientation ϑ, the scaled step position 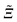 is larger than Ξ. However, for values of Ξ ≫ 1, the scaling function of the force saturates (see Fig. 3) and relating Ξ and ϑ numerically via the force within MFT becomes rather error-prone. This discredits fitting assumptions beyond the linear order. However, the relation in eqn (10), linearized around
is larger than Ξ. However, for values of Ξ ≫ 1, the scaling function of the force saturates (see Fig. 3) and relating Ξ and ϑ numerically via the force within MFT becomes rather error-prone. This discredits fitting assumptions beyond the linear order. However, the relation in eqn (10), linearized around 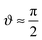 by using
by using 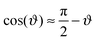 , results in a reasonable fit for p ≈ 1/4. Within fitting errors, the fit parameter p does not depend noticeably on the scaled temperature Θ and the scaling variable Δ. The value of the rescaling parameter p = 1/4 is in line with the presentation in Fig. 5, as it places the surface of the fictitious colloid halfway between the physical particle and the zero crossing line.
, results in a reasonable fit for p ≈ 1/4. Within fitting errors, the fit parameter p does not depend noticeably on the scaled temperature Θ and the scaling variable Δ. The value of the rescaling parameter p = 1/4 is in line with the presentation in Fig. 5, as it places the surface of the fictitious colloid halfway between the physical particle and the zero crossing line.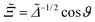 in eqn (10) with p = 1/4 compared with that of the approach used in Fig. 3, even for Δ = 1.
in eqn (10) with p = 1/4 compared with that of the approach used in Fig. 3, even for Δ = 1.
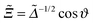 (eqn (10) with p = 1/4) for
(eqn (10) with p = 1/4) for  . In this case, the correspondence between the scaling functions of the two configurations
. In this case, the correspondence between the scaling functions of the two configurations  and
and  holds within full MFT, for values of Δ outside the DA limit Δ ≪ 1.
holds within full MFT, for values of Δ outside the DA limit Δ ≪ 1.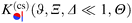 between a chemical step on the substrate and a Janus particle with orientation ϑ and its center shifted by
between a chemical step on the substrate and a Janus particle with orientation ϑ and its center shifted by 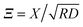 from the substrate step attains certain limiting expressions. For an upright orientation ϑ = 0 it has the same value as the scaling function
from the substrate step attains certain limiting expressions. For an upright orientation ϑ = 0 it has the same value as the scaling function 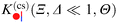 of the force between a homogeneous cylinder and a stepped substrate. If the Janus cylinder is positioned far away from the step, i.e. Ξ ≫ 1,
of the force between a homogeneous cylinder and a stepped substrate. If the Janus cylinder is positioned far away from the step, i.e. Ξ ≫ 1, 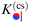 reduces to the scaling function of a Janus cylinder above a homogeneous substrate, then
reduces to the scaling function of a Janus cylinder above a homogeneous substrate, then 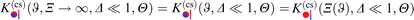 (where Ξ(ϑ) = Δ−1/2cos
(where Ξ(ϑ) = Δ−1/2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ or is given by eqn (10); analogously for Ξ → −∞).
ϑ or is given by eqn (10); analogously for Ξ → −∞).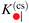 in eqn (6) and (7), the scaling function
in eqn (6) and (7), the scaling function 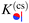 can be decomposed as
can be decomposed as 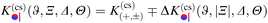 , where K(cs)(+,±) again refers to the scaling function of the force between a homogeneous cylinder and a homogeneous substrate (the rules when to use the upper and lower signs depend on ϑ and Ξ; see below):
, where K(cs)(+,±) again refers to the scaling function of the force between a homogeneous cylinder and a homogeneous substrate (the rules when to use the upper and lower signs depend on ϑ and Ξ; see below):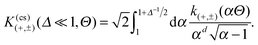
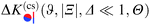 . The latter depends on the position of the Janus cylinder relative to the substrate step (again only via the scaled absolute value |Ξ| of the distance) and on the orientation ϑ ∈ [−π,π]. The sign of the position Ξ and the sign of the orientation ϑ can be chosen according to different conventions. Here, the coordinates are chosen such that ϑ > 0 rotates the normal of the equatorial plane of the Janus particle towards that side of the substrate which has the same BC, i.e. here, the rotation is counter-clockwise towards the side Ξ < 0 (see Fig. 1(b)). We note that the force is invariant under reflection at the plane normal to the substrate and containing the cylinder axis (ϑ → −ϑ, Ξ → −Ξ and exchange of the BC on the substrate), i.e.
. The latter depends on the position of the Janus cylinder relative to the substrate step (again only via the scaled absolute value |Ξ| of the distance) and on the orientation ϑ ∈ [−π,π]. The sign of the position Ξ and the sign of the orientation ϑ can be chosen according to different conventions. Here, the coordinates are chosen such that ϑ > 0 rotates the normal of the equatorial plane of the Janus particle towards that side of the substrate which has the same BC, i.e. here, the rotation is counter-clockwise towards the side Ξ < 0 (see Fig. 1(b)). We note that the force is invariant under reflection at the plane normal to the substrate and containing the cylinder axis (ϑ → −ϑ, Ξ → −Ξ and exchange of the BC on the substrate), i.e.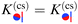 . Utilizing this symmetry, the decomposition reads
. Utilizing this symmetry, the decomposition reads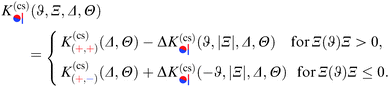
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ or, alternatively, by eqn (10).) The condition Ξ(ϑ) Ξ ≷ 0 considers in which direction the Janus cylinder is tilting (e.g. Ξ(ϑ) ∝ cos
ϑ or, alternatively, by eqn (10).) The condition Ξ(ϑ) Ξ ≷ 0 considers in which direction the Janus cylinder is tilting (e.g. Ξ(ϑ) ∝ cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ > 0 ⇒ upwards) and over which side of the step it levitates (via Ξ). Additionally, the equivalences k(+,+) = k(−,−) and k(+,−) = k(−,+) of the interaction between homogeneous, planar, and parallel walls lead to an invariance of the scaling function
ϑ > 0 ⇒ upwards) and over which side of the step it levitates (via Ξ). Additionally, the equivalences k(+,+) = k(−,−) and k(+,−) = k(−,+) of the interaction between homogeneous, planar, and parallel walls lead to an invariance of the scaling function  upon inverting the normal of the particle, i.e. ϑ → ϑ ± π (such that ϑ ∈ [−π,π]) and exchanging the BC of the substrate step (but without changing the position Ξ), so that
upon inverting the normal of the particle, i.e. ϑ → ϑ ± π (such that ϑ ∈ [−π,π]) and exchanging the BC of the substrate step (but without changing the position Ξ), so that 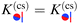 .
.
 is obtained from the careful DA summation of the corresponding surface elements:
is obtained from the careful DA summation of the corresponding surface elements: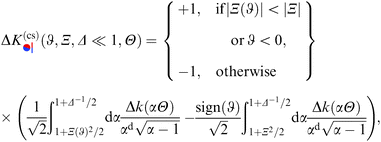
 depends on ϑ only via the sign and via |Ξ(ϑ)| ∝ |cos
depends on ϑ only via the sign and via |Ξ(ϑ)| ∝ |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ|. One can verify that both the symmetry operations of reflection (ϑ → −ϑ) as well as inversion (ϑ → ϑ ± π such that ϑ ∈ [−π,π]) yield the same result for the excess scaling function, i.e.
ϑ|. One can verify that both the symmetry operations of reflection (ϑ → −ϑ) as well as inversion (ϑ → ϑ ± π such that ϑ ∈ [−π,π]) yield the same result for the excess scaling function, i.e.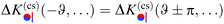 . Note that neither reflecting the position Ξ → −Ξ nor exchanging the BC affects
. Note that neither reflecting the position Ξ → −Ξ nor exchanging the BC affects  , but only
, but only 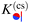 .
.
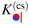 for two separations Δ = 1 in (a) and Δ = 1/5 in (b), with the step on the substrate fixed at Ξ = 0 (red sets of squares and lines). Within DA, this represents a peculiar configuration in that the orientations ϑ = ±π/2 of the Janus particle correspond to configurations in which both the step on the particle and the one on the substrate share a common vertical plane (see the sketches below the horizontal axis). At ϑ = −π/2, due to the opposing BC between all DA surface elements, the force (red lines) is repulsive (>0). For Δ = 1, around ϑ = −π/2 the DA result slightly overestimates the MFT result. Similarly, the special orientation at ϑ = π/2 leads to an attractive force (<0); here, however, for Δ = 1, DA clearly underestimates the MFT results. The cusplike shape of the scaling function around the maximum and minimum is an artifact of the DA; MFT renders a smooth and broader curve. In general, the MFT results are slightly more attractive and less repulsive than those predicted by DA. Nonetheless, for Δ ≪ 1 [Fig. 7(b)] DA and MFT agree rather well, even at ϑ = ±π/2. This is reassuring because for these orientations the shortcomings of the DA are particularly pronounced. As implied by the DA and in view of its reliability, the overall shape of the scaling function
for two separations Δ = 1 in (a) and Δ = 1/5 in (b), with the step on the substrate fixed at Ξ = 0 (red sets of squares and lines). Within DA, this represents a peculiar configuration in that the orientations ϑ = ±π/2 of the Janus particle correspond to configurations in which both the step on the particle and the one on the substrate share a common vertical plane (see the sketches below the horizontal axis). At ϑ = −π/2, due to the opposing BC between all DA surface elements, the force (red lines) is repulsive (>0). For Δ = 1, around ϑ = −π/2 the DA result slightly overestimates the MFT result. Similarly, the special orientation at ϑ = π/2 leads to an attractive force (<0); here, however, for Δ = 1, DA clearly underestimates the MFT results. The cusplike shape of the scaling function around the maximum and minimum is an artifact of the DA; MFT renders a smooth and broader curve. In general, the MFT results are slightly more attractive and less repulsive than those predicted by DA. Nonetheless, for Δ ≪ 1 [Fig. 7(b)] DA and MFT agree rather well, even at ϑ = ±π/2. This is reassuring because for these orientations the shortcomings of the DA are particularly pronounced. As implied by the DA and in view of its reliability, the overall shape of the scaling function 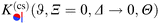 , within MFT and as a function of ϑ, is consistent with the dependence of the scaling function of the force between two patterned, planar substrates on a lateral shift (see ref. 76).
, within MFT and as a function of ϑ, is consistent with the dependence of the scaling function of the force between two patterned, planar substrates on a lateral shift (see ref. 76).
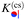 of the force between a Janus cylinder and a step on the substrate (in red), as a function of the particle orientation ϑ for Ξ = 0. The solid lines represent the results within DA, whereas the squares correspond to numerical MFT results for a separation Δ = D/R = 1. The green lines and triangles represent the scaling function
of the force between a Janus cylinder and a step on the substrate (in red), as a function of the particle orientation ϑ for Ξ = 0. The solid lines represent the results within DA, whereas the squares correspond to numerical MFT results for a separation Δ = D/R = 1. The green lines and triangles represent the scaling function  of the force which corresponds to the case of a homogeneous substrate, or equally, to the case of a step that is far away from the particle, i.e. |Ξ| ≫ 1 [see eqn (6)]. (b) The same, but for Δ = 1/5. Both in (a) and (b), the MFT values of the scaling functions K(cs)(+,+) and K(cs)(+,−) [eqn (11)] for the fully attractive (<0) and repulsive (>0) cases, respectively, of a homogeneous cylinder and a homogeneous substrate are indicated by dotted golden lines. At the top of the panels, we indicate configurations with the Janus cylinder above a homogeneous substrate corresponding to certain points of the green curve for Ξ ≫ 1. Similarly, at the bottom of the panels, configurations are shown with the Janus particle directly above the step corresponding to the red curve, i.e. Ξ = 0.
of the force which corresponds to the case of a homogeneous substrate, or equally, to the case of a step that is far away from the particle, i.e. |Ξ| ≫ 1 [see eqn (6)]. (b) The same, but for Δ = 1/5. Both in (a) and (b), the MFT values of the scaling functions K(cs)(+,+) and K(cs)(+,−) [eqn (11)] for the fully attractive (<0) and repulsive (>0) cases, respectively, of a homogeneous cylinder and a homogeneous substrate are indicated by dotted golden lines. At the top of the panels, we indicate configurations with the Janus cylinder above a homogeneous substrate corresponding to certain points of the green curve for Ξ ≫ 1. Similarly, at the bottom of the panels, configurations are shown with the Janus particle directly above the step corresponding to the red curve, i.e. Ξ = 0.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, the agreement between DA and MFT turns out to be poorer in Fig. 7(a), i.e. for Δ = 1, but remains comparable to the good agreement evident in Fig. 7(b), i.e. for Δ = 1/5 (see also Fig. 3). We find that the explicit dependence on Δ introduced by eqn (10) and (11) does not improve the agreement between DA and MFT for the strongly attractive or repulsive configurations: in Fig. 7(a) see the difference between the green line and the green symbols as well as the dotted golden lines which refer to MFT results for K(cs)(+,+) < 0 and K(cs)(+,−) > 0. However, the dependence on Δ of the MFT scaling functions for the case of a homogeneous cylinder and substrate has a different cause.71 Within DA, a dependence on Δ has been introduced via the DA relation Ξ(ϑ) = Δ−1/2cos
ϑ, the agreement between DA and MFT turns out to be poorer in Fig. 7(a), i.e. for Δ = 1, but remains comparable to the good agreement evident in Fig. 7(b), i.e. for Δ = 1/5 (see also Fig. 3). We find that the explicit dependence on Δ introduced by eqn (10) and (11) does not improve the agreement between DA and MFT for the strongly attractive or repulsive configurations: in Fig. 7(a) see the difference between the green line and the green symbols as well as the dotted golden lines which refer to MFT results for K(cs)(+,+) < 0 and K(cs)(+,−) > 0. However, the dependence on Δ of the MFT scaling functions for the case of a homogeneous cylinder and substrate has a different cause.71 Within DA, a dependence on Δ has been introduced via the DA relation Ξ(ϑ) = Δ−1/2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ or viaeqn (10) along with the dependence on ϑ. Thus, the good agreement between the slopes of the DA and MFT scaling functions shown in Fig. 7 as a function of ϑ for different Δ values indicates the consistency of these relations beyond the DA limit.
ϑ or viaeqn (10) along with the dependence on ϑ. Thus, the good agreement between the slopes of the DA and MFT scaling functions shown in Fig. 7 as a function of ϑ for different Δ values indicates the consistency of these relations beyond the DA limit.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ. The modified scaling variable
ϑ. The modified scaling variable 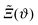 (eqn (10)) improves quantitatively the agreement with the full MFT results. We consider these properties as a justification to study below two Janus particles based on DA only.
(eqn (10)) improves quantitatively the agreement with the full MFT results. We consider these properties as a justification to study below two Janus particles based on DA only.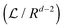 and a dimensionless scaling function
and a dimensionless scaling function 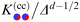 , as in the case of two homogeneous cylinders:77
, as in the case of two homogeneous cylinders:77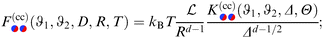
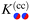 is the universal scaling function of the force between two Janus cylinders with equal radius R, ϑ1 and ϑ2 are the orientations of the two Janus particles, and Δ = D/R and Θ = ±D/ξ±(T) are dimensionless scaling variables for the surface-to-surface distance and the temperature, respectively. This scaling form is of the same type as the one in eqn (5) for a homogeneous cylindrical particle above a stepped substrate and to the one in eqn (9) for a Janus cylinder above a homogeneous substrate; however, the corresponding scaling functions are distinct. Within DA, for certain configurations
is the universal scaling function of the force between two Janus cylinders with equal radius R, ϑ1 and ϑ2 are the orientations of the two Janus particles, and Δ = D/R and Θ = ±D/ξ±(T) are dimensionless scaling variables for the surface-to-surface distance and the temperature, respectively. This scaling form is of the same type as the one in eqn (5) for a homogeneous cylindrical particle above a stepped substrate and to the one in eqn (9) for a Janus cylinder above a homogeneous substrate; however, the corresponding scaling functions are distinct. Within DA, for certain configurations 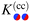 and, e.g.,
and, e.g., 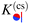 can attain the same values as the corresponding scaling functions for homogeneous particles. Within the corresponding expressions (see eqn (12)), K(cs)(+,±) for a homogeneous cylindrical particle and a homogeneous substrate is stronger by a factor of
can attain the same values as the corresponding scaling functions for homogeneous particles. Within the corresponding expressions (see eqn (12)), K(cs)(+,±) for a homogeneous cylindrical particle and a homogeneous substrate is stronger by a factor of 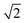 compared with K(cc)(+,±) for two homogeneous cylinders.
compared with K(cc)(+,±) for two homogeneous cylinders.
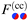 between two Janus cylinders orientated top-to-bottom [(ϑ1,ϑ2) = (0,0) and (±π,±π)], bottom-to-bottom [(0,±π)], or top-to-top [(±π,0)] is identical to the force between two homogeneous cylinders F(cc)(a,b)77 with (a,b) as the BC of the sides facing each other (compare Fig. 7). Upon construction this follows from the fact that for these configurations, the equatorial planes are orthogonal to the axis connecting the centers of the particles. Analogously as in eqn (12), we express the force between two Janus cylinders
between two Janus cylinders orientated top-to-bottom [(ϑ1,ϑ2) = (0,0) and (±π,±π)], bottom-to-bottom [(0,±π)], or top-to-top [(±π,0)] is identical to the force between two homogeneous cylinders F(cc)(a,b)77 with (a,b) as the BC of the sides facing each other (compare Fig. 7). Upon construction this follows from the fact that for these configurations, the equatorial planes are orthogonal to the axis connecting the centers of the particles. Analogously as in eqn (12), we express the force between two Janus cylinders  relative to the force F(cc)(+,±) between two homogeneous cylinders, yielding
relative to the force F(cc)(+,±) between two homogeneous cylinders, yielding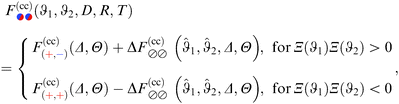
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi and where, without the loss of generality, we introduced the reduced angles
ϑi and where, without the loss of generality, we introduced the reduced angles 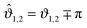 such that
such that 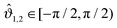 . Note that a shift of ±π amounts to reflecting the normals n1 and n2 at the corresponding equatorial plane of particles ① and ②, respectively. The subscript of the excess scaling function
. Note that a shift of ±π amounts to reflecting the normals n1 and n2 at the corresponding equatorial plane of particles ① and ②, respectively. The subscript of the excess scaling function 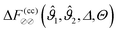 is not colored in order to emphasize that only the reduced angles enter. As in the previous case, the form given by eqn (15) is manifestly invariant against that reflection while also exchanging the BCs of the particles. For instance, for any configuration with ϑ1,2 ∈ [−π/2,π/2], i.e. Ξ(ϑ1) Ξ(ϑ2) > 0, one has
is not colored in order to emphasize that only the reduced angles enter. As in the previous case, the form given by eqn (15) is manifestly invariant against that reflection while also exchanging the BCs of the particles. For instance, for any configuration with ϑ1,2 ∈ [−π/2,π/2], i.e. Ξ(ϑ1) Ξ(ϑ2) > 0, one has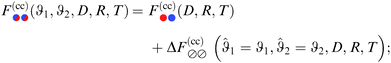
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2′ < 0, leading to
ϑ2′ < 0, leading to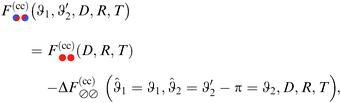
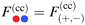 and
and 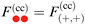 between homogeneous particles has been colored in order to visualize the BC. We additionally enforce
between homogeneous particles has been colored in order to visualize the BC. We additionally enforce 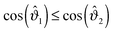 . The expressions for
. The expressions for  for all other configurations can be reduced to those in eqn (15) by exchanging the BC (a,b), by appropriately setting
for all other configurations can be reduced to those in eqn (15) by exchanging the BC (a,b), by appropriately setting 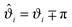 with i = {1,2}, and by switching the labeling
with i = {1,2}, and by switching the labeling 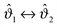 . In this sense, in the following we drop the hat of
. In this sense, in the following we drop the hat of 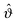 in favor of a lighter notation. Note that Ξ(ϑ1) Ξ(ϑ2) = 0 is exempted from the cases considered in eqn (15); in this limiting case the conditions should be read as abbreviations for
in favor of a lighter notation. Note that Ξ(ϑ1) Ξ(ϑ2) = 0 is exempted from the cases considered in eqn (15); in this limiting case the conditions should be read as abbreviations for 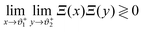 , i.e. the right-sided limit from above.78
, i.e. the right-sided limit from above.78
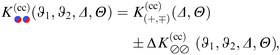
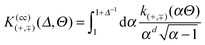
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2 within DA. In order for the separation in eqn (18) to be consistent, both scaling functions K(cc)(+,∓) and ΔK(cc)⊘⊘ need to retain their dependence on Δ. Nonetheless, the scaling functions within DA are expected to hold only for small but nonzero Δ; keeping the dependence on Δ is not necessarily a refinement (see Section III).
ϑ1,2 within DA. In order for the separation in eqn (18) to be consistent, both scaling functions K(cc)(+,∓) and ΔK(cc)⊘⊘ need to retain their dependence on Δ. Nonetheless, the scaling functions within DA are expected to hold only for small but nonzero Δ; keeping the dependence on Δ is not necessarily a refinement (see Section III).
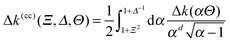
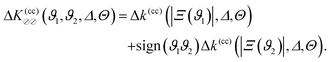
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1| ≤ |cos
ϑ1| ≤ |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2|. Moreover, the factor −sign(ϑ1) is replaced by sign(ϑ1ϑ2); a configuration ϑ1 > 0 and ϑ2 > 0 results in a projected step–step configuration with opposite signs for the step positions Ξ(ϑ1) and Ξ(ϑ2) (see Fig. 8(a)), thus, compared to eqn (13), changing the sign of the term. This concise representation of ΔK(cc)⊘⊘ in terms of the sign function is possible only for the reduced domain
ϑ2|. Moreover, the factor −sign(ϑ1) is replaced by sign(ϑ1ϑ2); a configuration ϑ1 > 0 and ϑ2 > 0 results in a projected step–step configuration with opposite signs for the step positions Ξ(ϑ1) and Ξ(ϑ2) (see Fig. 8(a)), thus, compared to eqn (13), changing the sign of the term. This concise representation of ΔK(cc)⊘⊘ in terms of the sign function is possible only for the reduced domain  . Special configurations of the two Janus cylinders, for which the scaling functions of the force require explicit considerations, are analyzed analytically in Appendix A.
. Special configurations of the two Janus cylinders, for which the scaling functions of the force require explicit considerations, are analyzed analytically in Appendix A.

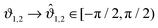 . The middle parts show the unrolled surfaces of the Janus cylinders opposing each other. The construction of the DA for two Janus cylinders is akin to the interaction between two structured substrates interacting,54,76 considering, however, only the portion of the chemical structure that ranges from −R to +R, i.e. from −Δ−1/2 to +Δ−1/2 in terms of the scaling variable, and using the appropriate local surface-to-surface distance. In its straightforward version, the DA projects the Janus equators to step positions at Ξ1,2 ≡ Ξ(ϑ1,2) = Δ−1/2
. The middle parts show the unrolled surfaces of the Janus cylinders opposing each other. The construction of the DA for two Janus cylinders is akin to the interaction between two structured substrates interacting,54,76 considering, however, only the portion of the chemical structure that ranges from −R to +R, i.e. from −Δ−1/2 to +Δ−1/2 in terms of the scaling variable, and using the appropriate local surface-to-surface distance. In its straightforward version, the DA projects the Janus equators to step positions at Ξ1,2 ≡ Ξ(ϑ1,2) = Δ−1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϑ1,2). Additionally, depending on sign(ϑ1ϑ2), either the left or the right edge of the equatorial plane enters into the projection, leading to opposite step positions ±Ξ1,2.
cos(ϑ1,2). Additionally, depending on sign(ϑ1ϑ2), either the left or the right edge of the equatorial plane enters into the projection, leading to opposite step positions ±Ξ1,2.
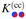 of the force between two Janus cylinders, within DA in d = 3, as a function of scaled temperature Θ = D/ξ+ for various orientations. The scaling function is normalized by the absolute value of the universal critical Casimir amplitude Δ(+,+). The wall–wall scaling function k(a,b)(L/ξ±), which, inter alia, determines Δ(+,+), is taken from MC results for the film geometry in ref. 11. (a) Configurations with ϑ1 = 0 for the orientation of particle ① for various orientation angles ϑ2 of particle ②, as visualized in the legend. (b) The case of ϑ1 = π/2 for various orientations ϑ2 of particle ②. The scaling function for the configuration ϑ1 = ϑ2 = 0 matches (repulsive) one of the two homogeneous cylindrical particles with the opposing BC, whereas the scaling function for the configuration ϑ1 = 0, ϑ2 = π equals the (attractive) one between two homogeneous cylinders with the same BC. The orientation angles belonging to the other curves have been chosen in order to visualize the particular sensitivity and insensitivity of the scaling function around the top-to-bottom, top-to-top, and bottom-to-bottom configurations, respectively. The angle ϑi is the one between the axis connecting the centers of the particles and the normal of the equatorial plane of particle i (see Fig. 8).
of the force between two Janus cylinders, within DA in d = 3, as a function of scaled temperature Θ = D/ξ+ for various orientations. The scaling function is normalized by the absolute value of the universal critical Casimir amplitude Δ(+,+). The wall–wall scaling function k(a,b)(L/ξ±), which, inter alia, determines Δ(+,+), is taken from MC results for the film geometry in ref. 11. (a) Configurations with ϑ1 = 0 for the orientation of particle ① for various orientation angles ϑ2 of particle ②, as visualized in the legend. (b) The case of ϑ1 = π/2 for various orientations ϑ2 of particle ②. The scaling function for the configuration ϑ1 = ϑ2 = 0 matches (repulsive) one of the two homogeneous cylindrical particles with the opposing BC, whereas the scaling function for the configuration ϑ1 = 0, ϑ2 = π equals the (attractive) one between two homogeneous cylinders with the same BC. The orientation angles belonging to the other curves have been chosen in order to visualize the particular sensitivity and insensitivity of the scaling function around the top-to-bottom, top-to-top, and bottom-to-bottom configurations, respectively. The angle ϑi is the one between the axis connecting the centers of the particles and the normal of the equatorial plane of particle i (see Fig. 8). between two parallel Janus cylinders can be determined from the force F according to
between two parallel Janus cylinders can be determined from the force F according to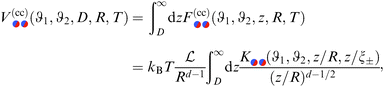
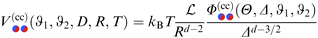
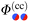 of the potential follows the same partition as the force in eqn (15) so that
of the potential follows the same partition as the force in eqn (15) so that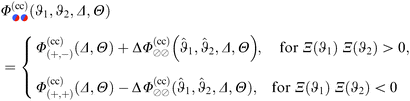
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi and where
ϑi and where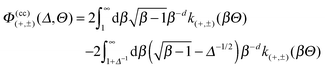
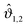 (see the previous subsection) follows from integrating eqn (20) and (21). This keeps the general structure of the force scaling function, leading to
(see the previous subsection) follows from integrating eqn (20) and (21). This keeps the general structure of the force scaling function, leading to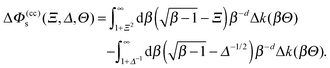
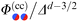 of the potential describes an energy in units of kBT and per reduced length
of the potential describes an energy in units of kBT and per reduced length  of the cylinders, it is useful to present it as an energy landscape in terms of the orientation angles ϑ1 and ϑ2, for a fixed scaled temperature Θ and a fixed reduced distance Δ = D/R (see Fig. 10). This facilitates a thermodynamic interpretation. For example, it relates to the typical experimental setup in which the temperature is fixed and the formation of clusters is attributed to a minimum of the effective interaction potential. Invoking the critical Casimir effect alone, which leads to an irreversible aggregation, is insufficient to describe the distance dependence of effective interactions between colloids in suspension. Typically, in addition to the critical Casimir effect, there are repulsive electrostatic interactions due to counterions, which are short-ranged and prevent coagulation of the colloids. If, however, these additional interactions are basically isotropic (e.g. due to a more or less homogeneous charge distribution on the colloid surface), the critical Casimir potential considered here is the only orientation dependent interaction and thus fully responsible for any orientation dependent behavior during the clustering of Janus particles close to Tc.
of the cylinders, it is useful to present it as an energy landscape in terms of the orientation angles ϑ1 and ϑ2, for a fixed scaled temperature Θ and a fixed reduced distance Δ = D/R (see Fig. 10). This facilitates a thermodynamic interpretation. For example, it relates to the typical experimental setup in which the temperature is fixed and the formation of clusters is attributed to a minimum of the effective interaction potential. Invoking the critical Casimir effect alone, which leads to an irreversible aggregation, is insufficient to describe the distance dependence of effective interactions between colloids in suspension. Typically, in addition to the critical Casimir effect, there are repulsive electrostatic interactions due to counterions, which are short-ranged and prevent coagulation of the colloids. If, however, these additional interactions are basically isotropic (e.g. due to a more or less homogeneous charge distribution on the colloid surface), the critical Casimir potential considered here is the only orientation dependent interaction and thus fully responsible for any orientation dependent behavior during the clustering of Janus particles close to Tc.
 denotes
denotes 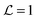 in d = 3 and
in d = 3 and 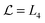 in d = 4.
in d = 4.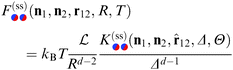
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 = R(Δ + 2)
12 = R(Δ + 2)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 is expressed in terms of the surface-to-surface distance D along the direction
12 is expressed in terms of the surface-to-surface distance D along the direction ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 = r12/|r12|. Note that in the case of two spheres, at Tc the force decays as Δ−(d−1) with distance,16 compared to Δ−(d−1/2) for the force between two cylinders (see eqn (14)). As in the case of Janus cylinders, we decompose the scaling function
12 = r12/|r12|. Note that in the case of two spheres, at Tc the force decays as Δ−(d−1) with distance,16 compared to Δ−(d−1/2) for the force between two cylinders (see eqn (14)). As in the case of Janus cylinders, we decompose the scaling function 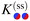 of the force into a part given by the scaling function K(ss)(+,±) between two homogeneous spheres16
of the force into a part given by the scaling function K(ss)(+,±) between two homogeneous spheres16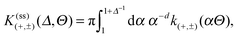
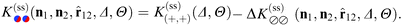
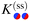 . Instead we divide them into ΔK(ss)⊘⊘, because the underlying symmetries are less intuitive and transparent. This leaves one with the arbitrary choice of whether to relate ΔK(ss)⊘⊘ to K(ss)(+,+)(Δ, Θ) or K(ss)(+,−)(Δ, Θ); we follow the definition in eqn (30). Note that it is not necessary to express ΔK(ss)⊘⊘ in terms of reduced angles, because as a spherical coordinate ϑ1,2 ∈ [0,π] is a reduced angle by definition. Again, the uncolored subscript emphasizes invariance with respect to the shift ϑi → ϑi ± π.
. Instead we divide them into ΔK(ss)⊘⊘, because the underlying symmetries are less intuitive and transparent. This leaves one with the arbitrary choice of whether to relate ΔK(ss)⊘⊘ to K(ss)(+,+)(Δ, Θ) or K(ss)(+,−)(Δ, Θ); we follow the definition in eqn (30). Note that it is not necessary to express ΔK(ss)⊘⊘ in terms of reduced angles, because as a spherical coordinate ϑ1,2 ∈ [0,π] is a reduced angle by definition. Again, the uncolored subscript emphasizes invariance with respect to the shift ϑi → ϑi ± π.
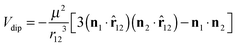
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi and n1·n2 = cos
ϑi and n1·n2 = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2 + sin
ϑ2 + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1
ϑ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2
ϑ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ1 − ϕ2). Thus, concerning the dependence on the orientations, the critical Casimir interaction between two Janus spheres exhibits the same level of complexity as the dipole–dipole interaction.
cos(ϕ1 − ϕ2). Thus, concerning the dependence on the orientations, the critical Casimir interaction between two Janus spheres exhibits the same level of complexity as the dipole–dipole interaction.
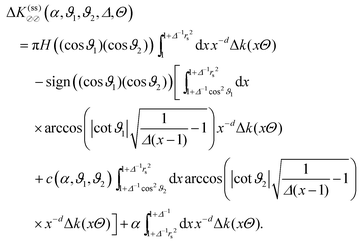
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos
ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2)) as a prefactor effectively serves the same purpose as the case analysis within the scaling functions of previous geometries (see, e.g., eqn (15), with Ξ(ϑ1)Ξ(ϑ2) ∝ (cos
ϑ2)) as a prefactor effectively serves the same purpose as the case analysis within the scaling functions of previous geometries (see, e.g., eqn (15), with Ξ(ϑ1)Ξ(ϑ2) ∝ (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos
ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2)). Additionally, ΔK(ss)⊘⊘ depends non-trivially on α, ϑ1, and ϑ2, inter alia, via the dimensionless radius rs = Rs(α,ϑ1,ϑ2)/R (see eqn (B8)) of a particular ring of surface elements occurring within DA in the subdivision of the surfaces. The projection of the equatorial steps of both Janus spheres onto a common plane, normal to the axis connecting the colloids, results in two half-ellipses corresponding to each configuration. The surface ring with radius Rs intersects the projections of the equatorial steps of both Janus spheres in a single point. Thus, the scaled radius rs is defined as
ϑ2)). Additionally, ΔK(ss)⊘⊘ depends non-trivially on α, ϑ1, and ϑ2, inter alia, via the dimensionless radius rs = Rs(α,ϑ1,ϑ2)/R (see eqn (B8)) of a particular ring of surface elements occurring within DA in the subdivision of the surfaces. The projection of the equatorial steps of both Janus spheres onto a common plane, normal to the axis connecting the colloids, results in two half-ellipses corresponding to each configuration. The surface ring with radius Rs intersects the projections of the equatorial steps of both Janus spheres in a single point. Thus, the scaled radius rs is defined as 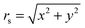 , with the intersection point (x, y) of the two ellipses determined by a particular solution of a system of two equations. For details, we refer to Appendix B.
, with the intersection point (x, y) of the two ellipses determined by a particular solution of a system of two equations. For details, we refer to Appendix B.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos
ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2)) and via the sign picking function
ϑ2)) and via the sign picking function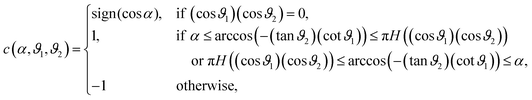
 of the force (given by eqn (29)–(32)) is shown in Fig. 12 for various configurations with α = 0, i.e. ϕ1 = ϕ2, akin to Fig. 9 for parallel cylindrical Janus particles. In accordance with Fig. 11, α = 0 implies that the two orientation vectors n1 and n2 lie in the same plane, as for parallel cylinders, so that the corresponding equatorial planes are rotated with respect to each other (ϑ1 ≠ ϑ2), but not tilted (see Fig. 8). At first sight, the scaling functions of the force for Janus spheres and for Janus cylinders appear to be qualitatively very similar. Quantitatively, the force between spheres appears to be stronger than the force between parallel cylinders. However, one has to take into account that the force between two Janus cylinders is proportional to their length. A fair comparison of the strengths of the forces requires to consider a cylinder length which is comparable with the size of the sphere, i.e. L ≈ 2R. In this case the force between two parallel cylinders is stronger. Additionally, the scaling function for Janus spheres decays slightly faster as a function of Θ. Generally, the scaling function of the force between two Janus spheres is slightly more sensitive to small rotations of one particle than the one for cylinders.
of the force (given by eqn (29)–(32)) is shown in Fig. 12 for various configurations with α = 0, i.e. ϕ1 = ϕ2, akin to Fig. 9 for parallel cylindrical Janus particles. In accordance with Fig. 11, α = 0 implies that the two orientation vectors n1 and n2 lie in the same plane, as for parallel cylinders, so that the corresponding equatorial planes are rotated with respect to each other (ϑ1 ≠ ϑ2), but not tilted (see Fig. 8). At first sight, the scaling functions of the force for Janus spheres and for Janus cylinders appear to be qualitatively very similar. Quantitatively, the force between spheres appears to be stronger than the force between parallel cylinders. However, one has to take into account that the force between two Janus cylinders is proportional to their length. A fair comparison of the strengths of the forces requires to consider a cylinder length which is comparable with the size of the sphere, i.e. L ≈ 2R. In this case the force between two parallel cylinders is stronger. Additionally, the scaling function for Janus spheres decays slightly faster as a function of Θ. Generally, the scaling function of the force between two Janus spheres is slightly more sensitive to small rotations of one particle than the one for cylinders.
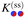 between two Janus spheres within DA in d = 3, as a function of Θ = D/ξ+ for the same orientations as in Fig. 9. (a) Configurations with ϑ1 = 0 for the orientation of the left particle ① for various orientation angles ϑ2 of the right particle ②, as visualized in the legend. (b) The case of ϑ1 = π/2 for various orientations ϑ2 of the second particle. In order to facilitate a transparent comparison with Fig. 8, the azimuthal angle α is set to α = 0, i.e. ϕ1 = ϕ2, which restricts the orientation vectors n1 and n2 to lie in a common plane, as it is the case in our analysis of parallel cylinders.
between two Janus spheres within DA in d = 3, as a function of Θ = D/ξ+ for the same orientations as in Fig. 9. (a) Configurations with ϑ1 = 0 for the orientation of the left particle ① for various orientation angles ϑ2 of the right particle ②, as visualized in the legend. (b) The case of ϑ1 = π/2 for various orientations ϑ2 of the second particle. In order to facilitate a transparent comparison with Fig. 8, the azimuthal angle α is set to α = 0, i.e. ϕ1 = ϕ2, which restricts the orientation vectors n1 and n2 to lie in a common plane, as it is the case in our analysis of parallel cylinders.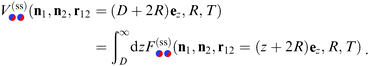
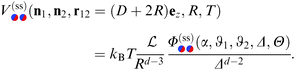
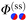 of the potential is divided into the two contributions
of the potential is divided into the two contributions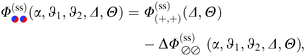
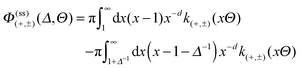
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos
ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2))Δu(ss)(rs2,0,Δ,Θ) − sign((cos
ϑ2))Δu(ss)(rs2,0,Δ,Θ) − sign((cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos
ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2))[Δv(ss)(rs2,ϑ1,Δ,Θ) + c(α,ϑ1,ϑ2)Δv(ss)(rs2,ϑ2,Δ,Θ)] + αΔu(ss)(1,rs2,Δ,Θ)
ϑ2))[Δv(ss)(rs2,ϑ1,Δ,Θ) + c(α,ϑ1,ϑ2)Δv(ss)(rs2,ϑ2,Δ,Θ)] + αΔu(ss)(1,rs2,Δ,Θ)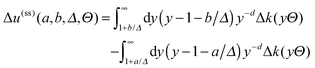
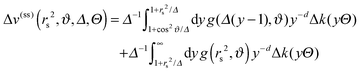
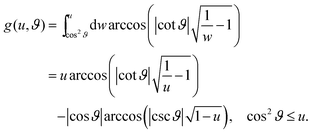
 of the pair potential between two Janus spheres can be presented in a single plot only as a function of two variables, but not for the full set α, ϑ1, ϑ2 of three variables. Accordingly, in Fig. 13 we choose to show the scaling function of the pair potential between Janus spheres for the two values α = 0 and α = π. For α = 0, in the range ϑ1 > 0 the scaling function of the potential is very similar to the one for cylinders shown in Fig. 10. On the other hand, for Janus spheres, the case of α = π in Fig. 13 is similar to the one of ϑ1 < 0 for Janus cylinders. Obviously, in spherical coordinates an orientation vector with α = π and ϑ1 ∈ [0,π] lies in the same plane as an orientation vector with α = 0, and can be mapped to a cylindrical angle ϑ1 ∈ [−π,0]. The scaling function of the pair potential between Janus spheres is also dominated by the attractive minima and the repulsive plateaus of interaction (Fig. 13(a)). The variation of the relative azimuthal angle α affects the potential only locally around ϑ1 = ϑ2 = π/2. Upon increasing α, the potential energy smoothly changes from having the potential minima connected by a valley to having the plateaus bridged.
of the pair potential between two Janus spheres can be presented in a single plot only as a function of two variables, but not for the full set α, ϑ1, ϑ2 of three variables. Accordingly, in Fig. 13 we choose to show the scaling function of the pair potential between Janus spheres for the two values α = 0 and α = π. For α = 0, in the range ϑ1 > 0 the scaling function of the potential is very similar to the one for cylinders shown in Fig. 10. On the other hand, for Janus spheres, the case of α = π in Fig. 13 is similar to the one of ϑ1 < 0 for Janus cylinders. Obviously, in spherical coordinates an orientation vector with α = π and ϑ1 ∈ [0,π] lies in the same plane as an orientation vector with α = 0, and can be mapped to a cylindrical angle ϑ1 ∈ [−π,0]. The scaling function of the pair potential between Janus spheres is also dominated by the attractive minima and the repulsive plateaus of interaction (Fig. 13(a)). The variation of the relative azimuthal angle α affects the potential only locally around ϑ1 = ϑ2 = π/2. Upon increasing α, the potential energy smoothly changes from having the potential minima connected by a valley to having the plateaus bridged.

 of the effective pair potential between two Janus spheres in d = 3 for α = π and α = 0 presented (a) as a free energy landscape in terms of ϑ1 and ϑ2 for a fixed scaled temperature Θ = 1, and (b) as a function of ϑ1 along the two paths ϑ2 = π/2 (red dashed line) and ϑ2 = π/4 (green dashed line). At the top of the panel, the geometric configurations indicate those which correspond to points of the green curve; configurations corresponding to the red curve are indicated at the bottom. The comparison with Fig. 10 tells that the free energy landscapes for cylinders and spheres are qualitatively very similar. Note that for α = π in (a) and (b) the horizontal axes are inverted in order to emphasize the geometric correspondence of α = π and ϑ1 > 0 in spherical coordinates to ϑ1 < 0 in cylindrical coordinates. An increase of α affects the potential only within a limited angular range around ϑ1 = ϑ2 = π/2, changing the potential in that range from being attractive (α = 0) to being repulsive (α = π). This means that upon increasing α the potential gradually develops a potential barrier (see the red curve in (b)).
of the effective pair potential between two Janus spheres in d = 3 for α = π and α = 0 presented (a) as a free energy landscape in terms of ϑ1 and ϑ2 for a fixed scaled temperature Θ = 1, and (b) as a function of ϑ1 along the two paths ϑ2 = π/2 (red dashed line) and ϑ2 = π/4 (green dashed line). At the top of the panel, the geometric configurations indicate those which correspond to points of the green curve; configurations corresponding to the red curve are indicated at the bottom. The comparison with Fig. 10 tells that the free energy landscapes for cylinders and spheres are qualitatively very similar. Note that for α = π in (a) and (b) the horizontal axes are inverted in order to emphasize the geometric correspondence of α = π and ϑ1 > 0 in spherical coordinates to ϑ1 < 0 in cylindrical coordinates. An increase of α affects the potential only within a limited angular range around ϑ1 = ϑ2 = π/2, changing the potential in that range from being attractive (α = 0) to being repulsive (α = π). This means that upon increasing α the potential gradually develops a potential barrier (see the red curve in (b)). requires knowledge of the full scaling function of the potential. Due to problems associated with the multivalued nature of the transformation functions, we refrain from providing an explicit parametrization of the orientations n1 and n2 in terms of the new coordinates which would include γ. Instead, for a fixed value of the tilt angle γ, we evaluate the scaling function
requires knowledge of the full scaling function of the potential. Due to problems associated with the multivalued nature of the transformation functions, we refrain from providing an explicit parametrization of the orientations n1 and n2 in terms of the new coordinates which would include γ. Instead, for a fixed value of the tilt angle γ, we evaluate the scaling function  numerically on a discretized set of 64 × 64 orientations n1 and n2, each of them describing a circular path on the unit sphere. The set is expressed in terms of Cartesian coordinates and then transformed into spherical coordinates determining α, ϑ1, and ϑ2.81 The average
numerically on a discretized set of 64 × 64 orientations n1 and n2, each of them describing a circular path on the unit sphere. The set is expressed in terms of Cartesian coordinates and then transformed into spherical coordinates determining α, ϑ1, and ϑ2.81 The average  of the scaling function
of the scaling function  of the effective potential, i.e. the arithmetic mean of the dataset, is plotted as a function of the tilt angle γ, together with the standard deviation
of the effective potential, i.e. the arithmetic mean of the dataset, is plotted as a function of the tilt angle γ, together with the standard deviation  relative to the averaged scaling function for γ = 0. For γ = 0, the average is taken such that both n1 and n2 describe a great circle on each sphere. They can be parameterized unambiguously by the relative coordinates α = 0, 0 ≤ ϑ1,2 ≤ π, and α = π, 0 < ϑ1,2 < π (i.e. both free energy landscapes shown in Fig. 13(a) enter into the mean value), resulting within DA in the average (Φ(ss)(+,+) + Φ(ss)(+,−))/2 due to the symmetry of the potential.
relative to the averaged scaling function for γ = 0. For γ = 0, the average is taken such that both n1 and n2 describe a great circle on each sphere. They can be parameterized unambiguously by the relative coordinates α = 0, 0 ≤ ϑ1,2 ≤ π, and α = π, 0 < ϑ1,2 < π (i.e. both free energy landscapes shown in Fig. 13(a) enter into the mean value), resulting within DA in the average (Φ(ss)(+,+) + Φ(ss)(+,−))/2 due to the symmetry of the potential.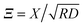 of the substrate step a certain rotational orientation ϑ of a Janus cylinder close to a homogeneous substrate which results in the same strength of the critical Casimir force, yielding numerically a discrete set {Ξ,ϑ}. Visually, it appears that the forces are equal in strength whenever the bending and the extension of the isolines ϕ(r) = 0 are similar for both configurations. An improved model has been introduced by applying the DA for a fictional, larger colloid, scaled by a parameter p, in order to incorporate the bending of the isoline into DA by fiat (see Fig. 5). This translates to a relation
of the substrate step a certain rotational orientation ϑ of a Janus cylinder close to a homogeneous substrate which results in the same strength of the critical Casimir force, yielding numerically a discrete set {Ξ,ϑ}. Visually, it appears that the forces are equal in strength whenever the bending and the extension of the isolines ϕ(r) = 0 are similar for both configurations. An improved model has been introduced by applying the DA for a fictional, larger colloid, scaled by a parameter p, in order to incorporate the bending of the isoline into DA by fiat (see Fig. 5). This translates to a relation 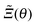 in eqn (10) for the rescaled step position
in eqn (10) for the rescaled step position 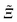 , with p as the only parameter. The model fits well to the discrete set {Ξ,ϑ} determined from the MFT results for p ≈ 1/4, roughly independent of temperature. This corresponds to placing the fictional, rescaled colloid surface halfway between the physical surface and the isoline ϕ(r) = 0 as depicted in Fig. 5. The improvement achieved using the relation
, with p as the only parameter. The model fits well to the discrete set {Ξ,ϑ} determined from the MFT results for p ≈ 1/4, roughly independent of temperature. This corresponds to placing the fictional, rescaled colloid surface halfway between the physical surface and the isoline ϕ(r) = 0 as depicted in Fig. 5. The improvement achieved using the relation 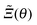 in eqn (10) with p = 1/4 is demonstrated in Fig. 6, where the two scaling functions
in eqn (10) with p = 1/4 is demonstrated in Fig. 6, where the two scaling functions  and
and  for a homogeneous cylinder close to a chemically stepped substrate and a Janus cylinder close to a homogeneous substrate, respectively, coincide even for Δ = 1, far away from the DA limit Δ → 0. Thus, the correspondence between these two configurations holds also within MFT, albeit this is based on a relation
for a homogeneous cylinder close to a chemically stepped substrate and a Janus cylinder close to a homogeneous substrate, respectively, coincide even for Δ = 1, far away from the DA limit Δ → 0. Thus, the correspondence between these two configurations holds also within MFT, albeit this is based on a relation 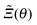 which differs from the one obtained by using the original, unmodified DA.
which differs from the one obtained by using the original, unmodified DA.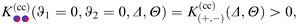
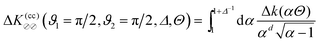
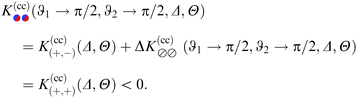
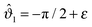 . The excess scaling function of the force ΔK(cc)⊘⊘(Θ, Δ, ϑ1 = −π/2, ϑ2 = π/2) in eqn (21) vanishes because sign(ϑ1ϑ2) = −1 and one finds
. The excess scaling function of the force ΔK(cc)⊘⊘(Θ, Δ, ϑ1 = −π/2, ϑ2 = π/2) in eqn (21) vanishes because sign(ϑ1ϑ2) = −1 and one finds 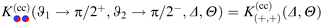 as in eqn (A4). Therefore, the two sided limit exists and the force in this configuration is attractive for all temperatures t > 0.
as in eqn (A4). Therefore, the two sided limit exists and the force in this configuration is attractive for all temperatures t > 0.
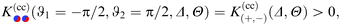
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1| < |cos
ϑ1| < |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2|. Since Δk(cc)(Ξ2 = Δ−1/2, Δ, Θ) = 0, only the first term in eqn (21) contributes, thus with Δk = k(+,+) − k(+,−) resulting in
ϑ2|. Since Δk(cc)(Ξ2 = Δ−1/2, Δ, Θ) = 0, only the first term in eqn (21) contributes, thus with Δk = k(+,+) − k(+,−) resulting in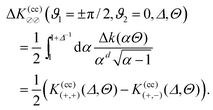
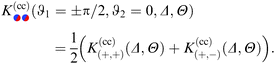
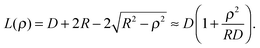
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 with
12 with ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 = (0,0,1) (see Fig. 11). The orientations of the colloids can be represented by orientation vectors n1 and n2, which can be chosen to point either into the direction of the (+) (red) or the (−) (blue) side. As far as the figures in the main text are concerned, the orientation vector is chosen to point towards the (−) (blue) cap. However, regarding the general approach in the present appendix, we shall use the more abstract notions of “north” and “south”, which are supposed to underscore the arbitrariness of this choice.
12 = (0,0,1) (see Fig. 11). The orientations of the colloids can be represented by orientation vectors n1 and n2, which can be chosen to point either into the direction of the (+) (red) or the (−) (blue) side. As far as the figures in the main text are concerned, the orientation vector is chosen to point towards the (−) (blue) cap. However, regarding the general approach in the present appendix, we shall use the more abstract notions of “north” and “south”, which are supposed to underscore the arbitrariness of this choice.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1| < |cos
ϑ1| < |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2|, as it shortens the notation below; otherwise one can exchange the labels (1) and (2) and rotate the frame of reference around the y axis by 180° (see Fig. 11).
ϑ2|, as it shortens the notation below; otherwise one can exchange the labels (1) and (2) and rotate the frame of reference around the y axis by 180° (see Fig. 11).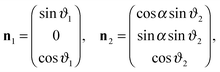
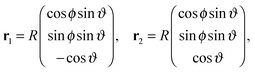
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 = ez, such that (r1)z = −(r2)z (see Fig. 15). After the projection into the midplane by using the orthogonal projection matrix
12 = ez, such that (r1)z = −(r2)z (see Fig. 15). After the projection into the midplane by using the orthogonal projection matrix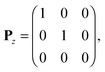
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ,ϕ) and a fixed value of ϑ.
ϑ,ϕ) and a fixed value of ϑ.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ (here, the inner black circle) which is shown in the midplane between the particles. The equatorial steps of the Janus spheres ① and ② form half-ellipses when projected onto the same midplane. The vectors b1 and b2 lie in the equatorial plane of the corresponding particles and thus are orthogonal to n1 and n2, respectively. Their direction is chosen to point to that point on each equator which is closest in the sight of the opposite particle. The projections b(p)1 and b(p)2 of the vectors b1 and b2, respectively, onto the midplane render the semi-minor axes of the half-ellipses.
ϑ (here, the inner black circle) which is shown in the midplane between the particles. The equatorial steps of the Janus spheres ① and ② form half-ellipses when projected onto the same midplane. The vectors b1 and b2 lie in the equatorial plane of the corresponding particles and thus are orthogonal to n1 and n2, respectively. Their direction is chosen to point to that point on each equator which is closest in the sight of the opposite particle. The projections b(p)1 and b(p)2 of the vectors b1 and b2, respectively, onto the midplane render the semi-minor axes of the half-ellipses.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1 + cos
ϑ1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1 and f2(ϕ) := r2·n2 = cos
ϑ1 and f2(ϕ) := r2·n2 = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2 + cos(α − ϕ)
ϑ2 + cos(α − ϕ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2, the two conditions above read
ϑ2, the two conditions above read![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi,sin
ϕi,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi,0), tilted by a rotation matrix
ϕi,0), tilted by a rotation matrix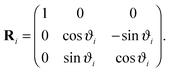
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi,cos
ϕi,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi
ϑi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕi,0) fulfills the ellipse equation
ϕi,0) fulfills the ellipse equation  for a = 1 and b = |cos
for a = 1 and b = |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi|. Of the two elliptical projections, we draw only that half facing the other colloid, resulting in two half-elliptical curves, which are intersecting for 0 < α < π (i.e. they do not intersect for α = 0 and α = π). The semi-minor axes of the half-ellipses are indicated by the projections b(p)1 and b(p)2 of the vectors b1 and b2, respectively, which have a projected length of R
ϑi|. Of the two elliptical projections, we draw only that half facing the other colloid, resulting in two half-elliptical curves, which are intersecting for 0 < α < π (i.e. they do not intersect for α = 0 and α = π). The semi-minor axes of the half-ellipses are indicated by the projections b(p)1 and b(p)2 of the vectors b1 and b2, respectively, which have a projected length of R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2 and form the angle π − α between them. The projected Janus steps divide the circular area of radius R into four regions (blue, white, red, white); a selected ring of fixed radius ρ = R
ϑ1,2 and form the angle π − α between them. The projected Janus steps divide the circular area of radius R into four regions (blue, white, red, white); a selected ring of fixed radius ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ (corresponding to the color colored circle in Fig. 16) is divided into four arcs by points with the polar coordinates (ρ,ϕ1) to (ρ,ϕ4). In the case of small α as shown in Fig. 16(a), the numbering of the values ϕ1 to ϕ4 given in eqn (B6) corresponds to a clockwise counting of the intersections of the ring with the projected Janus steps (i.e. the half-ellipses). However, the order of their occurrence changes upon increasing α towards π (see Fig. 16(a)–(d)).
ϑ (corresponding to the color colored circle in Fig. 16) is divided into four arcs by points with the polar coordinates (ρ,ϕ1) to (ρ,ϕ4). In the case of small α as shown in Fig. 16(a), the numbering of the values ϕ1 to ϕ4 given in eqn (B6) corresponds to a clockwise counting of the intersections of the ring with the projected Janus steps (i.e. the half-ellipses). However, the order of their occurrence changes upon increasing α towards π (see Fig. 16(a)–(d)).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϑ) (see Fig. 15). We depict the case ϑ = 1 so that ρ = 0.84R (color-coded ring). The points 1 to 4 mark the intersections of the color-coded ring with the projected equatorial steps of the BC, which are given by the polar coordinates (ρ, ϕ1) through (ρ, ϕ4). Both the thick red and the thick blue arcs of this ring represent equal BCs on both particle surfaces, whereas those arcs being half blue and half red correspond to opposite BCs. Additional explanations, such as the meaning of Rs, are given in the main text.
sin(ϑ) (see Fig. 15). We depict the case ϑ = 1 so that ρ = 0.84R (color-coded ring). The points 1 to 4 mark the intersections of the color-coded ring with the projected equatorial steps of the BC, which are given by the polar coordinates (ρ, ϕ1) through (ρ, ϕ4). Both the thick red and the thick blue arcs of this ring represent equal BCs on both particle surfaces, whereas those arcs being half blue and half red correspond to opposite BCs. Additional explanations, such as the meaning of Rs, are given in the main text.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arccos(cot
arccos(cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot
cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1) − 2
ϑ1) − 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arccos(cot
arccos(cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ
ϑ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot
cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2)]ρ.
ϑ2)]ρ.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1 (the inner gray circle in Fig. 16 indicates ρ = R
ϑ1 (the inner gray circle in Fig. 16 indicates ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1), the ring does not cross the projected steps in the BC at all. For R
ϑ1), the ring does not cross the projected steps in the BC at all. For R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1 < ρ < R
ϑ1 < ρ < R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2, there are two points of intersection (we recall that the labels ① and ② are chosen such that |cos
ϑ2, there are two points of intersection (we recall that the labels ① and ② are chosen such that |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1| < |cos
ϑ1| < |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2|). Starting from ρ = R
ϑ2|). Starting from ρ = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2 (indicated by the outer gray circle), for ρ > R
ϑ2 (indicated by the outer gray circle), for ρ > R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2 there are four points of intersection. However, at a specific radius ρ = Rs (gray dashed line in Fig. 16), the two half-ellipses intersect and the order of the values ϕ1,…,ϕ4 changes (e.g. compare the order of the intersections in Fig. 16(a) and (b)).
ϑ2 there are four points of intersection. However, at a specific radius ρ = Rs (gray dashed line in Fig. 16), the two half-ellipses intersect and the order of the values ϕ1,…,ϕ4 changes (e.g. compare the order of the intersections in Fig. 16(a) and (b)).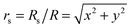 is determined by the intersection point (x, y) of the two semi-ellipses, which is found from a solution of the general problem of the intersection between two co-centric ellipses: the first ellipse (x/a1)2 + (y/b1)2 = 1 and the second ellipse (x/a2)2 + (y/b2)2 = 1 rotated by an angle α. Within their parametric representations the intersections follow from
is determined by the intersection point (x, y) of the two semi-ellipses, which is found from a solution of the general problem of the intersection between two co-centric ellipses: the first ellipse (x/a1)2 + (y/b1)2 = 1 and the second ellipse (x/a2)2 + (y/b2)2 = 1 rotated by an angle α. Within their parametric representations the intersections follow from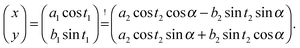
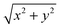 of the radius R, the problem reduces to the special case in which the semi-major axes are a1 = a2 = 1 (i.e. the semi-major axes are touching the circle of radius R) and the semi-minor axes are the projected lengths b1 = |b(p)1|/R = |cos(ϑ1)| and b2 = |b(p)2|/R = |cos(ϑ2)|. While in principle this system of equations can be solved analytically, it is not guaranteed that all solutions are real, because in degenerate cases (e.g. for α = 0 or α = π and b1 = b2, or b1 = b2 = 1, or b1 = b2 = 0) the number of physically acceptable solutions can be less than four. In the non-degenerate cases, out of these four general solutions of the intersection of two ellipses, only one gives the intersection of two half-ellipses. We have followed a pragmatic approach by solving eqn (B8) numerically within an a priori chosen interval of t2 in order to preselect the appropriate solution for the half-ellipses.83 We note that our definition enforces the relation |cos
of the radius R, the problem reduces to the special case in which the semi-major axes are a1 = a2 = 1 (i.e. the semi-major axes are touching the circle of radius R) and the semi-minor axes are the projected lengths b1 = |b(p)1|/R = |cos(ϑ1)| and b2 = |b(p)2|/R = |cos(ϑ2)|. While in principle this system of equations can be solved analytically, it is not guaranteed that all solutions are real, because in degenerate cases (e.g. for α = 0 or α = π and b1 = b2, or b1 = b2 = 1, or b1 = b2 = 0) the number of physically acceptable solutions can be less than four. In the non-degenerate cases, out of these four general solutions of the intersection of two ellipses, only one gives the intersection of two half-ellipses. We have followed a pragmatic approach by solving eqn (B8) numerically within an a priori chosen interval of t2 in order to preselect the appropriate solution for the half-ellipses.83 We note that our definition enforces the relation |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1| < |cos
ϑ1| < |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2|, so that the dimensionless radius rs corresponding to the point of intersection between the two half-ellipses is bound by |cos
ϑ2|, so that the dimensionless radius rs corresponding to the point of intersection between the two half-ellipses is bound by |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2| ≤ rs ≤ 1, because any point on the second ellipse has a radial distance from its center, the value of which lies between the semi-minor axis b2 = cos
ϑ2| ≤ rs ≤ 1, because any point on the second ellipse has a radial distance from its center, the value of which lies between the semi-minor axis b2 = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2 and the semi-major axis a2 = 1, and so does the point of intersection.
ϑ2 and the semi-major axis a2 = 1, and so does the point of intersection.
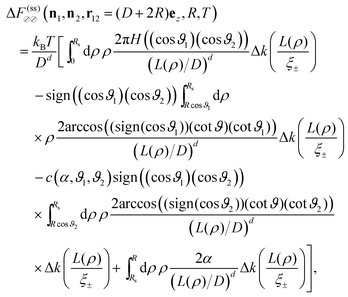
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ and
ϑ and 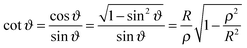 , for r12 = (D + 2R)ez and n1,2 in relative coordinates (see eqn (B2)). The occurrence of various expressions in eqn (B9) can be rationalized as follows: the combined arclength of equal BCs is generally of the form ±ϕ4 ∓ ϕ3 ± ϕ2 ∓ ϕ1 (i.e. different combinations of the signs). According to eqn (B6), additional shifts of 2π might be required to ensure ϕi ∈ [0,2π]. In fact the term 2π occurs only for rings of surface elements with radii ρ < Rs, provided (cos
, for r12 = (D + 2R)ez and n1,2 in relative coordinates (see eqn (B2)). The occurrence of various expressions in eqn (B9) can be rationalized as follows: the combined arclength of equal BCs is generally of the form ±ϕ4 ∓ ϕ3 ± ϕ2 ∓ ϕ1 (i.e. different combinations of the signs). According to eqn (B6), additional shifts of 2π might be required to ensure ϕi ∈ [0,2π]. In fact the term 2π occurs only for rings of surface elements with radii ρ < Rs, provided (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos
ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2) ≥ 0, which is expressed by the limits of integration of the first term in eqn (B9) (see below also the note regarding the second and third term). Similarly, the azimuthal angle α contributes in total as 2α to the arclength if ρ > Rs, but it does not contribute if ρ < Rs, leading to the fourth and last term in eqn (B9). The second and third term reproduce the functional dependence of the arclength on ϑ(ρ) and ϑ1,2. The changes of the sign of the argument in the arccos functions in eqn (B6) generalize to sign(cos
ϑ2) ≥ 0, which is expressed by the limits of integration of the first term in eqn (B9) (see below also the note regarding the second and third term). Similarly, the azimuthal angle α contributes in total as 2α to the arclength if ρ > Rs, but it does not contribute if ρ < Rs, leading to the fourth and last term in eqn (B9). The second and third term reproduce the functional dependence of the arclength on ϑ(ρ) and ϑ1,2. The changes of the sign of the argument in the arccos functions in eqn (B6) generalize to sign(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2) in eqn (B9) due to the relation 2arccos(−x) = 2π − 2arccos(x). Note that the shift of 2π re-enters the first term; in eqn (B9) the first term reflects the notation in the second and third term. Analogous to the geometry of two Janus cylinders, we find a dependence of the sign of the second and third term on the sign of (cos
ϑ1,2) in eqn (B9) due to the relation 2arccos(−x) = 2π − 2arccos(x). Note that the shift of 2π re-enters the first term; in eqn (B9) the first term reflects the notation in the second and third term. Analogous to the geometry of two Janus cylinders, we find a dependence of the sign of the second and third term on the sign of (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos
ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2). Furthermore, the sign picking function c(α,ϑ1,ϑ2) is given by
ϑ2). Furthermore, the sign picking function c(α,ϑ1,ϑ2) is given by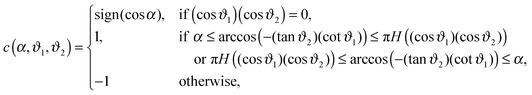
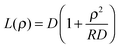 and by applying the substitution
and by applying the substitution 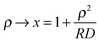 with
with 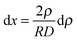 , which leads to L(x) = Dx,
, which leads to L(x) = Dx, 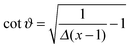 , and
, and 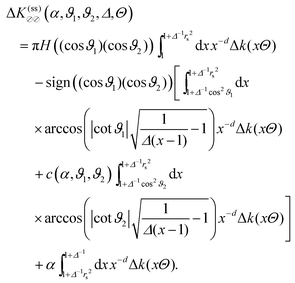
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2))cot
ϑ1,2))cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2 = |cot
ϑ1,2 = |cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2|, which holds in the domain of the definition of the polar angles, i.e. for ϑ1,2 ∈ [0,π].
ϑ1,2|, which holds in the domain of the definition of the polar angles, i.e. for ϑ1,2 ∈ [0,π].
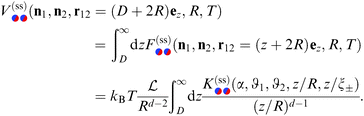
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) with dz = D d
with dz = D d![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) yields
yields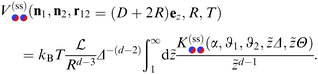
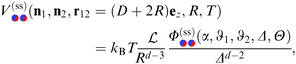
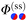 of the effective potential,
of the effective potential,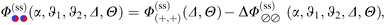
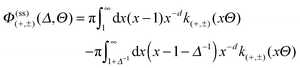
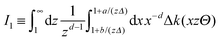
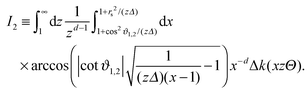
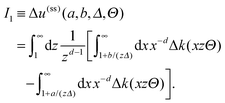
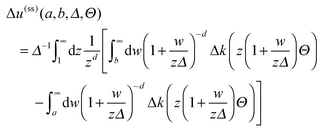
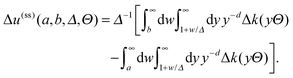
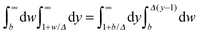
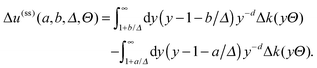

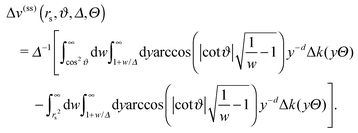
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1,2| and that rs denotes the distance of the intersection point between the half-ellipses from the symmetry axis of the two particles. Obviously, the intersection point cannot be closer to the common origin than any semi-minor axis, so that |cos
ϑ1,2| and that rs denotes the distance of the intersection point between the half-ellipses from the symmetry axis of the two particles. Obviously, the intersection point cannot be closer to the common origin than any semi-minor axis, so that |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1| ≤ rs and |cos
ϑ1| ≤ rs and |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2| ≤ rs. Based on eqn (B11), we need to evaluate Δv(ss)(rs,ϑ,Δ,Θ) for ϑ = ϑ1 and ϑ = ϑ2. For that reason, we consider only the case |cos
ϑ2| ≤ rs. Based on eqn (B11), we need to evaluate Δv(ss)(rs,ϑ,Δ,Θ) for ϑ = ϑ1 and ϑ = ϑ2. For that reason, we consider only the case |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ| < rs and reorder the integrals:
ϑ| < rs and reorder the integrals: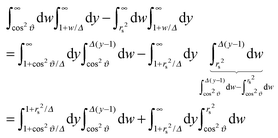
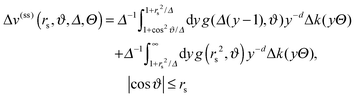
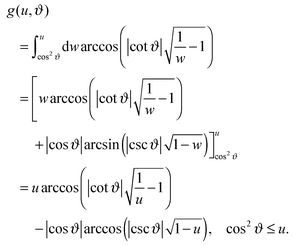
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ,ϑ) = 0. Concerning the derivation of eqn (C17) we leave out the detailed case analysis for the sign of cot
ϑ,ϑ) = 0. Concerning the derivation of eqn (C17) we leave out the detailed case analysis for the sign of cot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ, which in the end, can be subsumed by taking the absolute values as stated in eqn (C17). Putting the results together, the excess scaling function of the potential is given by
ϑ, which in the end, can be subsumed by taking the absolute values as stated in eqn (C17). Putting the results together, the excess scaling function of the potential is given by![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos
ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2))Δu(ss)(rs2,0,Δ,Θ) − sign((cos
ϑ2))Δu(ss)(rs2,0,Δ,Θ) − sign((cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ1)(cos
ϑ1)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑ2))[Δv(ss)(rs2,ϑ1,Δ,Θ) + c(α,ϑ1,ϑ2)Δv(ss)(rs2,ϑ2,Δ,Θ)] + αΔu(ss)(1,rs2,Δ,Θ).
ϑ2))[Δv(ss)(rs2,ϑ1,Δ,Θ) + c(α,ϑ1,ϑ2)Δv(ss)(rs2,ϑ2,Δ,Θ)] + αΔu(ss)(1,rs2,Δ,Θ). . The two-sided limit does exist and the scaling function is continuous, see Appendix A. Concerning the numerical evaluation,
. The two-sided limit does exist and the scaling function is continuous, see Appendix A. Concerning the numerical evaluation, 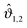 can be equally defined as the remainder of the division of x = ϑ1,2 + π/2 (dividend) by y = π (divisor) minus π/2. The remainder is obtained from the floating point version of the modulo operation, provided by most programming languages. However, care has to be taken as the floating point modulus is ambiguous for negative numbers. The right-sided limit is compatible only with the definition of the modulo
operation by “floored division”
can be equally defined as the remainder of the division of x = ϑ1,2 + π/2 (dividend) by y = π (divisor) minus π/2. The remainder is obtained from the floating point version of the modulo operation, provided by most programming languages. However, care has to be taken as the floating point modulus is ambiguous for negative numbers. The right-sided limit is compatible only with the definition of the modulo
operation by “floored division” 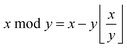 , where the integer quotient is given by the floor function
, where the integer quotient is given by the floor function 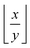 , ensuring that 0 ≤ x mod π < π ∀x; see
D. Knuth, The Art of Computer Programming, Addison-Wesley, Reading, 1997, vol. 1, p. 39 Search PubMed.
, ensuring that 0 ≤ x mod π < π ∀x; see
D. Knuth, The Art of Computer Programming, Addison-Wesley, Reading, 1997, vol. 1, p. 39 Search PubMed.