 Open Access Article
Open Access ArticleInfluence of polymer shape on depletion potentials and crowding in colloid–polymer mixtures
Wei Kang
Lim
and
Alan R.
Denton
*
Department of Physics, North Dakota State University, Fargo, ND 58108-6050, USA. E-mail: alan.denton@ndsu.edu
First published on 15th December 2015
Abstract
Depletion-induced interactions between colloids in colloid–polymer mixtures depend in range and strength on size, shape, and concentration of depletants. Crowding by colloids in turn affects shapes of polymer coils, such as biopolymers in biological cells. By simulating hard-sphere colloids and random-walk polymers, modeled as fluctuating ellipsoids, we compute depletion-induced potentials and polymer shape distributions. Comparing results with exact density-functional theory calculations, molecular simulations, and experiments, we show that polymer shape fluctuations play an important role in depletion and crowding phenomena.
1 Introduction
Depletion forces are ubiquitous in soft materials that contain hard particles and flexible macromolecules,1 such as colloid–polymer and colloid–surfactant mixtures. Over 60 years ago, Asakura and Oosawa2 recognized that the exclusion of one species (depletant) from the space between two particles of another species creates an osmotic pressure imbalance that induces an entropy-driven attraction between the particles and can drive demixing into colloid-rich and colloid-poor phases.3,4 Practical applications of depletion forces are in initiating flocculation of impurities in water treatment and winemaking, promoting aggregation of DNA and crystallization of proteins,5 and controlling stability and dynamical properties of many consumer products, including paints, foods, and pharmaceuticals.1 Depletion forces have been measured by several experimental methods, including total internal reflection microscopy,6 atomic force microscopy,7 neutron scattering,8 and optical trapping.9–11 Modeling efforts have invoked force-balance theory,12,13 perturbation theory,14,15 polymer field theory,16–21 density-functional theory,22,23 adsorption theory,24,25 integral-equation theory,26–28 Monte Carlo simulation methods,29–41 and free-volume theories for thermodynamic phase behavior.42–44Complementary to depletion is the phenomenon of crowding upon mixing polymers or other flexible macromolecules with impenetrable obstacles. When colloids, nanoparticles, or other crowding agents are dispersed in a polymer solution or blend, flexible chains adjust their size and shape to conform to the accessible volume.45 The prevalence and importance of macromolecular crowding in biology was recognized over three decades ago.46 In the congested environment of a cell's cytoplasm or nucleoplasm, conformations of proteins, RNA, and DNA are constrained by the presence of other macromolecules, affecting biopolymer function.47–49 Crowding of polymers has been studied experimentally by neutron scattering,50,51 computationally via Langevin dynamics52–54 and Monte Carlo simulations of coarse-grained models,55–57 and by free-volume theories.45,56–58
Attempts to interpret experimental or simulation data for depletion forces in colloid–polymer mixtures typically assume the spherical polymer model and treat the polymer size and concentration as free parameters.6–10 The fitted parameters invariably differ from measured values. Dependences on particle curvature and depletant concentration have been partially accounted for by introducing an effective polymer size or depletion layer thickness.19,36,38,43 The influence of depletant shape on interactions has been studied in mixtures of colloidal spheres and rods10,15 or ellipsoids,13,59 but only of fixed size and shape. Other workers have explored the impact of polymer conformations on relative stabilities of hard-sphere colloidal crystals60–62 and of crowding on polymer size50–58 (but not shape). Despite ample evidence that random-walk polymers exhibit significant asphericity,63–66 however, no studies have yet related shape fluctuations to depletion interactions and crowding. This paper presents the first consistent analysis of the role of depletant shape in mixtures of colloids and nonadsorbing polymers. By comparing results with exact theoretical calculations and with data from molecular simulations and experiments, we demonstrate the importance of polymer shape fluctuations for depletion and crowding.
2 Model
Our model generalizes the widely-studied Asakura–Oosawa–Vrij (AOV) model of colloid–polymer mixtures,2,3 which represents the colloids as hard spheres and the polymers as effective spheres of fixed size that are mutually noninteracting, but impenetrable to the colloids. The assumption of hard colloid–polymer interactions is reasonable for colloids larger than the polymers. However, the effective-sphere approximation ignores conformational fluctuations of polymer coils. Here we go beyond previous coarse-grained models of polymer-induced depletion interactions by representing the polymers as soft ellipsoids that fluctuate in size and shape.A polymer coil of N segments has size and shape characterized by its gyration tensor, 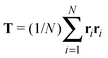 , where ri is the position vector of segment i relative to the center of mass. A conformation with gyration tensor eigenvalues Λ1, Λ2, Λ3 has instantaneous radius of gyration
, where ri is the position vector of segment i relative to the center of mass. A conformation with gyration tensor eigenvalues Λ1, Λ2, Λ3 has instantaneous radius of gyration 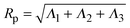 . The experimentally measurable (root-mean-square) radius of gyration is an ensemble average over polymer conformations, Rg ≡ 〈Rp2〉1/2. If the average is defined relative to the polymer's principal-axis frame, the coordinate axes being labelled to preserve the eigenvalue order (Λ1 > Λ2 > Λ3), then the average gyration tensor describes an aspherical object, whose average shape is an elongated (prolate), flattened ellipsoid.63–65 Each eigenvalue is proportional to the square of a principal radius of the general ellipsoid that best fits the shape of the polymer coil: x2/Λ1 + y2/Λ2 + z2/Λ3 = 3.
. The experimentally measurable (root-mean-square) radius of gyration is an ensemble average over polymer conformations, Rg ≡ 〈Rp2〉1/2. If the average is defined relative to the polymer's principal-axis frame, the coordinate axes being labelled to preserve the eigenvalue order (Λ1 > Λ2 > Λ3), then the average gyration tensor describes an aspherical object, whose average shape is an elongated (prolate), flattened ellipsoid.63–65 Each eigenvalue is proportional to the square of a principal radius of the general ellipsoid that best fits the shape of the polymer coil: x2/Λ1 + y2/Λ2 + z2/Λ3 = 3.
Ideal, freely-jointed (random-walk) polymer coils can be modeled as soft Gaussian ellipsoids.67 For coils sufficiently long that extensions in orthogonal directions are essentially independent, the shape probability distribution is well approximated by the factorized form68
| P(λ1,λ2,λ3) = P1(λ1)P2(λ2)P3(λ3), | (1) |
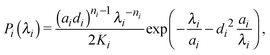 | (2) |
The deviation of a polymer's average shape from a sphere is quantified by the asphericity65
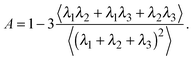 | (3) |
3 Methods
To explore the influence of polymer shape on depletion-induced interactions between colloids, and of crowding on polymer conformations, we developed a Monte Carlo (MC) algorithm for simulating mixtures of hard colloidal spheres and ideal polymers, whose shape distribution follows eqn (1). At fixed temperature T and volume, trial displacements of colloids and displacements and rotations of polymers are accepted with the Metropolis probability69 min{e−βΔU,1}, where β = 1/(kBT) and ΔU is the associated change in potential energy. Colloid–colloid and colloid–polymer overlaps yield infinite energy and so are always rejected. To detect intersection of a polymer with a colloid, we implemented an overlap algorithm that determines the shortest distance between the surfaces of a sphere and a general ellipsoid by numerically evaluating the root of a 6th-order polynomial.70 For trial rotations, we define the orientation of a polymer by a unit vector u, aligned with the long axis of the ellipsoid, and generate a new (trial) direction u′ = (u + τv)/|u + τv|, where v is a randomly oriented unit vector and τ is a tolerance determining the magnitude of the rotation.69 In addition, we perform trial changes in shape of a polymer coil, from gyration tensor eigenvalues λ ≡ (λ1,λ2,λ3) to new eigenvalues λ′ ≡ (λ1′,λ2′,λ3′). Such trial moves, which entail a change in internal free energy of the coil,71Fc = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P0(λ), are accepted with probability
P0(λ), are accepted with probability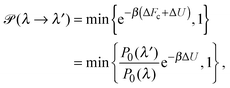 | (4) |
Depletion of polymers induces an effective interaction between colloids that reduces, in the dilute limit, to the potential of mean force (PMF), vmf(r) = Ω(r) − Ω(∞), defined as the change in grand potential Ω(r) upon bringing two colloids from infinite to finite (center-to-center) separation r by working against the polymer osmotic pressure, Πp = npkBT (for ideal polymers). If we make the choice Ω(∞) = 0, then vmf(r) = −ΠpVo(r), where Vo(r) is the intersection of the excluded-volume regions surrounding the colloids. For spherical polymers (AOV model),
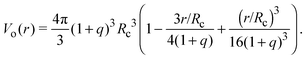 | (5) |
Accurate calculation of the PMF requires calibrating the ellipsoidal polymer model to consistently match the polymer radius to the depletion layer thickness and to account for deformation of a polymer coil near a curved surface.29 A rational criterion for choosing the effective size ratio qeff is based on equating the free energy to insert a hard sphere into a bath of ideal polymers, as predicted by polymer field theory,16 with the work required to inflate a sphere in the model polymer solution.36,38,43 For nonspherical polymers, we generalize this criterion to
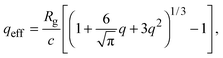 | (6) |
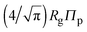 .
.
4 Results
As a first test of the ellipsoidal polymer model, we computed the PMF in the dilute colloid limit by performing simulations over a sequence of colloid pair separations for the same size ratios as used by Forsman and Woodward23 in their exact density-functional theory (DFT) calculations for a continuum-chain polymer model (q = 0.125) and by Meijer and Frenkel29 (q = 0.7776) in their MC simulations of random-walk polymer chains on a cubic lattice. In each comparison, we used appropriate effective size ratios computed from eqn (6) with c/Rg = 1 for spheres and c/Rg = 0.93254 for ellipsoids, and averaged over five independent runs, each of 2 × 107 polymer insertions. Fig. 1 shows that the PMFs resulting from the ellipsoidal polymer model are in excellent agreement with the corresponding PMFs from both of the explicit polymer models. Thus, calibration of the effective polymer size near hard, flat plates (q = 0) proves accurate also for polymers near hard spheres (q > 0). In contrast, the AOV model [eqn (5)] predicts a shorter-ranged (and, for q = 0.7776, also deeper) potential, reflecting lack of freedom of a spherical polymer to deform to avoid obstacles.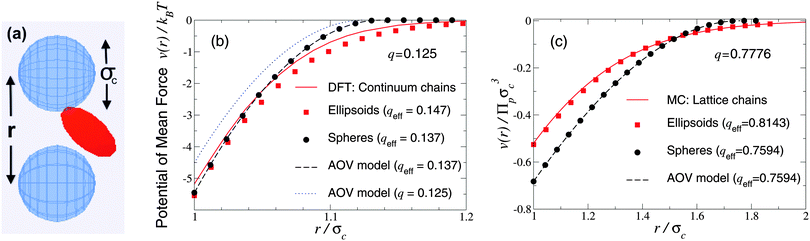 | ||
| Fig. 1 Simulation snapshot (a) depicts colloids (blue spheres) and polymer (red ellipsoid), which induces potential of mean force v(r) at center–center distance r (units of colloid diameter σc) for polymer-to-colloid size ratios (b) q = 0.125, (c) q = 0.7776. Our MC simulation data for the fluctuating ellipsoidal polymer model (squares), and predictions of the spherical polymer (AOV) model (circles, dashed curves), are compared with (b) density-functional theory (DFT) predictions (solid curve) for continuum-chain polymers23 and (c) MC simulation data (solid curve) for lattice-chain polymers29 at corresponding effective size ratios qeff [eqn (6)]. Also shown in (b) is the AOV model prediction for the bare size ratio q (dotted curve). Error bars are smaller than symbols. | ||
We turn next to the experiments of Verma et al.,9 who used an optical tweezer to measure interactions between silica microspheres of diameter σc = 1.25 ± 0.05 μm in aqueous solutions of λ-DNA (contour length 16 μm, radius of gyration Rg ≃ 500 nm), whose conformations are known to be random walks of ∼160 Kuhn segments.66 Taking the nominal size ratio of q = 0.8, we computed the PMF in both the ellipsoidal and spherical polymer models and here compare our results with data for a dilute DNA solution of concentration 25 μg ml−1 (np = 0.5 μm−3), in which polymer interactions should be negligible (Fig. 2 and 3 of ref. 9). Since the experiments cannot accurately resolve the vertical offset of the potential, we varied the offset to most closely fit our simulation data. With this single fit parameter, the ellipsoidal polymer model, with effective size ratio qeff = 0.8351 [from eqn (6)], is in close agreement with the measured interaction potential (Fig. 2), as is seen by comparing the least-squares fit to the experimental data with our simulation data (solid curve and squares in Fig. 2). In contrast, the AOV model, with qeff = 0.7788, significantly overestimates the depth, and underestimates the range, of the potential. From visual inspection, it is clear that no vertical shift of the experimental data will yield close alignment with the AOV model (solid and dashed curves in Fig. 2).
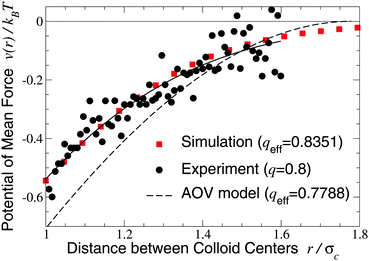 | ||
| Fig. 2 Potential of mean force between a pair of silica microspheres (diameter σc = 1.25 μm) induced by λ-DNA in water with Rg = 0.5 μm (q = 2Rg/σc = 0.8). Our MC simulation data for the fluctuating ellipsoidal polymer model (squares) at effective size ratio qeff = 0.8351 [eqn (6)] are compared with both experimental data9 (circles) and predictions of the AOV model (dashed curve) [eqn (5)] for qeff = 0.7788 [eqn (6)]. The solid curve is a least-squares fit to the experimental (not simulation) data of the function −exp(a0 + a1r + a2r2) with a0 = 0.817, a1 = −0.167, a2 = −1.269. | ||
The close agreement of depletion potentials from our simulations of the ellipsoidal polymer model with, on the one hand, DFT calculations and simulations for explicit polymer models and, on the other hand, experimental data from optical tweezer measurements of colloid–DNA mixtures is strong evidence that aspherical polymer shapes play a significant role in depletion. Contrary to previous studies,1,19,25 we conclude that depletion interactions between hard-sphere colloids are not fully captured by modeling polymers simply as penetrable spheres of an effective size or, equivalently, with an effective depletion layer thickness. Moreover, our approach consistently accounts for fluctuations in polymer shape, in contrast to models of spheroidal depletants.13,59
Our approach may be compared with the powerful and elegant method of Bolhuis and Louis et al.32–38 that models polymers as “soft colloids” by replacing a polymer coil with a single particle at the center of mass. These authors determined the effective pair potential between two polymers and between a polymer and a hard sphere by first computing the respective radial distribution function g(r) between the centers of mass, via MC simulation of explicit segmented polymers on a lattice, and then inverting g(r) via the Ornstein–Zernike integral equation. From subsequent simulations of a coarse-grained model of colloid–polymer mixtures governed by such effective pair potentials, they extracted polymer depletion-induced interactions between hard-sphere colloids. For polymers in a good solvent, whose excluded-volume interactions were modeled via self-avoiding walks, comparisons of effective pair potentials derived from simulations of the explicit and coarse-grained models were in close agreement for q ≃ 1 and in the dilute polymer concentration regime, with deviations emerging abruptly at higher concentrations. Moreover, a computationally practical superposition approximation that expresses two-body depletion interactions in terms of the radially symmetric density profile of a polymer around a single colloidal sphere, which for ideal depletants can be implemented as a simple convolution integral,75 proves nearly as accurate as simulations. Our analysis of polymer shape fluctuations, although here limited to ideal polymers, would suggest that the soft-colloid approach succeeds largely by capturing, in the effective colloid–polymer potential, an accurate representation of the distortion of a polymer coil near a hard, curved surface.
Our restriction thus far to the dilute limit, while intended to highlight the role of polymer shape fluctuations in depletion interactions, raises the important question of how such shape fluctuations may be modified in more crowded environments, as in concentrated suspensions and biological cells. As a first step toward assessing the impact of crowding on polymer shapes, we simulated polymers amidst many mobile colloids, now including trial displacements of both species. Previously, we computed polymer shape distributions, radii of gyration, and asphericities in the protein limit (q ≫ 1), using a coated-ellipsoid approximation for the excluded volume.57 By applying the exact overlap algorithm, we can now extend this analysis to the colloid limit (q < 1). Fig. 3 shows results from simulations of 216 colloids and one polymer at q = 0.8 in a cubic box with periodic boundary conditions, along with predictions of a free-volume theory based on a mean-field approximation for the average volume accessible to an ellipsoid in a hard-sphere fluid.57 Upon increasing the colloid volume fraction, ϕc ≡ (4π/3)ncRc3, the polymer eigenvalue distributions shift toward contraction of the polymer along all three principal axes, while the radius of gyration and asphericity decrease, reflecting compactification of the polymer. These trends imply a decreasing range of pair attraction with increasing colloid concentration.
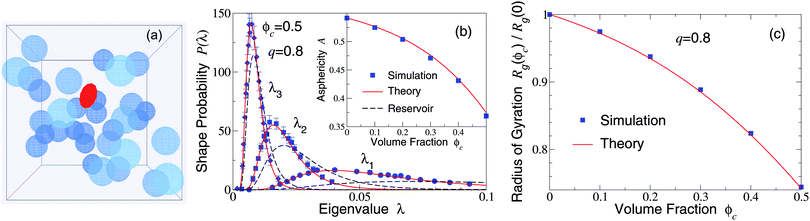 | ||
| Fig. 3 (a) Simulation snapshot depicts colloids (blue spheres) and polymer (red ellipsoid) in a cubic simulation cell with periodic boundary conditions. (b) Probability distributions for eigenvalues (λ1, λ2, λ3) of the gyration tensor of an ideal polymer coil with random-walk segment statistics. Simulation data (symbols) are compared with predictions of free-volume theory57 (solid curves) for an ellipsoidal polymer with uncrowded size ratio q = 0.8 amidst 216 colloids of volume fraction ϕc = 0.5. Dashed curves: uncrowded (ϕc = 0) distributions [eqn (1)]. Inset: Polymer asphericity A vs. ϕc [eqn (3)]. (c) Polymer radius of gyration Rgvs. ϕc. | ||
5 Conclusions
In summary, we computed depletion potentials between hard, spherical colloidal particles induced by ideal polymers, modeled as fluctuating ellipsoids with random-walk segment statistics. Comparisons with exact theoretical calculations and data from both molecular simulations and experiments demonstrate that shape-fluctuating polymers induce significantly weaker and longer-ranged interactions than spherical depletants, even after accounting for particle curvature via an effective depletion layer thickness. While the depletion potentials computed here in the dilute limit are not expected to directly transfer to concentrated colloid–polymer mixtures, in which many-body effective interactions may be significant, the ellipsoidal polymer model should be applicable at nonzero concentrations. When progressively crowded by colloids, polymer coils remain aspherical, but become more compact in size and shape.Our approach provides a new conceptual framework for interpreting experiments, is computationally more efficient than explicit polymer models, and may be adapted to model depletion and crowding in mixtures of colloids and excluded-volume polymers,35–40,43 represented as self-avoiding random walks64 in good solvents. It may be further extended to the protein limit of polymer–nanoparticle mixtures, by incorporating an appropriate penetration free energy.57,76 Models of shape-fluctuating particles also may be useful for exploring phase behavior in polymer nanocomposites and in dispersions of soft colloids, e.g., microgels, whose shapes deform at high concentrations.77
Acknowledgements
This research was supported by the National Science Foundation (Grant No. DMR-1106331).References
- H. N. W. Lekkerkerker and R. Tuinier, Colloids and the Depletion Interaction, Springer, Heidelberg, 2011 Search PubMed.
- S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255 CAS.
- A. Vrij, Pure Appl. Chem., 1976, 48, 471–483 CrossRef CAS.
- P. N. Pusey, in Colloidal Suspensions, ed. J. -P. Hansen, D. Levesque and J. Zinn-Justin, North-Holland, Amsterdam, 1991, vol. 2, pp. 763–931 Search PubMed.
- A. Kulkarni and C. Zukoski, J. Cryst. Growth, 2001, 232, 156–164 CrossRef CAS.
- D. Rudhardt, C. Bechinger and P. Leiderer, Phys. Rev. Lett., 1998, 81, 1330–1333 CrossRef CAS.
- A. Milling and S. Biggs, J. Colloid Interface Sci., 1995, 170, 604–606 CrossRef CAS.
- X. Ye, T. Narayanan, P. Tong and J. S. Huang, Phys. Rev. Lett., 1996, 76, 4640–4643 CrossRef CAS PubMed.
- R. Verma, J. C. Crocker, T. C. Lubensky and A. G. Yodh, Phys. Rev. Lett., 1998, 81, 4004–4007 CrossRef CAS.
- K. H. Lin, J. C. Crocker, A. C. Zeri and A. G. Yodh, Phys. Rev. Lett., 2001, 87, 088301 CrossRef CAS PubMed.
- F. Hilitski, A. R. Ward, L. Cajamarca, M. F. Hagan, G. M. Grason and Z. Dogic, Phys. Rev. Lett., 2015, 114, 138102 CrossRef PubMed.
- J. Y. Walz and A. Sharma, J. Colloid Interface Sci., 1994, 168, 485–496 CrossRef CAS.
- M. Piech and J. Y. Walz, J. Colloid Interface Sci., 2000, 232, 86–101 CrossRef CAS PubMed.
- Y. Mao, M. E. Cates and H. N. W. Lekkerkerker, Physica A, 1995, 222, 10–24 CrossRef CAS.
- Y. Mao, M. E. Cates and H. N. W. Lekkerkerker, J. Chem. Phys., 1997, 106, 3721–3729 CrossRef CAS.
- E. Eisenriegler, A. Hanke and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 1134–1152 CrossRef CAS.
- A. Hanke, E. Eisenriegler and S. Dietrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 6853–6878 CrossRef CAS.
- T. Odijk, Physica A, 2000, 278, 347–355 CrossRef CAS.
- G. J. Fleer, A. M. Skvortsov and R. Tuinier, Macromolecules, 2003, 36, 7857–7872 CrossRef CAS.
- E. Eisenriegler, A. Bringer and R. Maassen, J. Chem. Phys., 2003, 118, 8093–8105 CrossRef CAS.
- H. Wang, C. E. Woodward and J. Forsman, J. Chem. Phys., 2014, 140, 194903 CrossRef PubMed.
- C. Bechinger, D. Rudhardt, P. Leiderer, R. Roth and S. Dietrich, Phys. Rev. Lett., 1999, 83, 3960–3963 CrossRef CAS.
- J. Forsman and C. E. Woodward, J. Chem. Phys., 2009, 131, 044903 CrossRef PubMed.
- R. Tuinier, G. A. Vliegenthart and H. N. W. Lekkerkerker, J. Chem. Phys., 2000, 113, 10768–10775 CrossRef CAS.
- R. Tuinier and A. V. Petukhov, Macromol. Theory Simul., 2002, 11, 975–984 CrossRef CAS.
- A. P. Chatterjee and K. S. Schweizer, J. Chem. Phys., 1998, 109, 10464–10476 CrossRef CAS.
- S. Ramakrishnan, M. Fuchs, K. S. Schweizer and C. F. Zukoski, J. Chem. Phys., 2002, 116, 2201–2212 CrossRef CAS.
- A. Moncho-Jordá, A. A. Louis, P. G. Bolhuis and R. Roth, J. Phys.: Condens. Matter, 2003, 15, S3429–S3442 CrossRef.
- E. J. Meijer and D. Frenkel, J. Chem. Phys., 1994, 100, 6873–6887 CrossRef CAS.
- E. J. Meijer and D. Frenkel, Phys. Rev. Lett., 1991, 67, 1110–1113 CrossRef CAS PubMed.
- R. Dickman and A. Yethiraj, J. Chem. Phys., 1994, 100, 4683–4689 CrossRef CAS.
- A. A. Louis, P. G. Bolhuis, J.-P. Hansen and E. J. Meijer, Phys. Rev. Lett., 2000, 85, 2522–2525 CrossRef CAS PubMed.
- P. G. Bolhuis, A. A. Louis, J.-P. Hansen and E. J. Meijer, J. Chem. Phys., 2001, 114, 4296–4311 CrossRef CAS.
- P. G. Bolhuis, A. A. Louis and J.-P. Hansen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 021801 CrossRef CAS PubMed.
- P. G. Bolhuis, A. A. Louis and J.-P. Hansen, Phys. Rev. Lett., 2002, 89, 128302 CrossRef CAS PubMed.
- A. A. Louis, P. G. Bolhuis, E. J. Meijer and J.-P. Hansen, J. Chem. Phys., 2002, 116, 10547–10556 CrossRef CAS.
- P. G. Bolhuis and A. A. Louis, Macromolecules, 2002, 35, 1860–1869 CrossRef CAS.
- A. A. Louis, P. G. Bolhuis, E. J. Meijer and J.-P. Hansen, J. Chem. Phys., 2002, 117, 1893–1907 CrossRef CAS.
- P. G. Bolhuis, E. J. Meijer and A. A. Louis, Phys. Rev. Lett., 2003, 90, 068304 CrossRef PubMed.
- M. Doxastakis, Y. L. Chen and J. J. de Pablo, J. Chem. Phys., 2005, 123, 34901 CrossRef CAS PubMed.
- M. Camargo and C. N. Likos, Phys. Rev. Lett., 2010, 104, 078301 CrossRef PubMed.
- H. N. W. Lekkerkerker, W. C. K. Poon, P. N. Pusey, A. Stroobants and P. B. Warren, Europhys. Lett., 1992, 20, 559–564 CrossRef CAS.
- D. G. A. L. Aarts, R. Tuinier and H. N. W. Lekkerkerker, J. Phys.: Condens. Matter, 2002, 14, 7551–7561 CrossRef CAS.
- G. J. Fleer and R. Tuinier, Adv. Colloid Interface Sci., 2008, 143, 1–47 CrossRef CAS PubMed.
- A. R. Denton, in New Models of the Cell Nucleus: Crowding and Entropic Forces and Phase Separation and Fractals, ed. R. Hancock and K. W. Jeon, Academic Press, UK, 2013, pp. 27–72 Search PubMed.
- A. P. Minton, Biopolymers, 1981, 20, 2093–2120 CrossRef CAS.
- R. J. Ellis, Trends Biochem. Sci., 2001, 26, 597–604 CrossRef CAS PubMed.
- M. S. Cheung, Curr. Opin. Struct. Biol., 2013, 23, 1–6 CrossRef PubMed.
- N. A. Denesyuk and D. Thirumalai, Biophys. Rev., 2013, 5, 225–232 CrossRef CAS.
- T. Kramer, R. Schweins and K. Huber, J. Chem. Phys., 2005, 123, 014903 CrossRef PubMed.
- C. Le Coeur, B. Demé and S. Longeville, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 031910 CrossRef CAS PubMed.
- M. Cheung, D. Klimov and D. Thirumalai, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 4753–4758 CrossRef CAS PubMed.
- E. Chen, A. Christiansen, Q. Wang, M. S. Cheung, D. S. Kliger and P. Wittung-Stafshede, Biochemistry, 2012, 51, 9836–9845 CrossRef CAS PubMed.
- N. A. Denesyuk and D. Thirumalai, J. Phys. Chem. B, 2013, 117, 4901–4911 CrossRef CAS PubMed.
- T. Hoppe and J.-M. Yuan, J. Phys. Chem. B, 2011, 115, 2006–2013 CrossRef CAS PubMed.
- B. Lu and A. R. Denton, J. Phys.: Condens. Matter, 2011, 23, 285102 CrossRef PubMed.
- W. K. Lim and A. R. Denton, J. Chem. Phys., 2014, 141, 114909 CrossRef PubMed.
- A. P. Minton, Biophys. J., 2005, 88, 971–985 CrossRef CAS PubMed.
- M. Triantafillou and R. D. Kamien, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 5621–5624 CrossRef CAS.
- N. A. Mahynski, S. K. Kumar and A. Z. Panagiotopoulos, Nat. Commun., 2014, 5, 4472 CAS.
- N. A. Mahynski, S. K. Kumar and A. Z. Panagiotopoulos, Soft Matter, 2015, 11, 280–289 RSC.
- N. A. Mahynski, S. K. Kumar and A. Z. Panagiotopoulos, Soft Matter, 2015, 11, 5146–5153 RSC.
- W. Kuhn, Kolloid-Z., 1934, 68, 2–15 CrossRef CAS.
- K. Šolc, J. Chem. Phys., 1971, 55, 335–344 CrossRef.
- J. Rudnick and G. Gaspari, Science, 1987, 237, 384–389 CAS.
- C. Haber, S. A. Ruiz and D. Wirtz, PNAS, 2000, 97, 10792–10795 CrossRef CAS PubMed.
- M. Murat and K. Kremer, J. Chem. Phys., 1998, 108, 4340–4348 CrossRef CAS.
- F. Eurich and P. Maass, J. Chem. Phys., 2001, 114, 7655–7668 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic, London, 2nd edn, 2001 Search PubMed.
- J. C. Hart, in Graphics Gems IV, ed. P. S. Heckbert, Academic, San Diego, 1994, pp. 113–119 Search PubMed.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon, Oxford, 1986 Search PubMed.
- A. R. Denton and M. Schmidt, J. Phys.: Condens. Matter, 2002, 14, 12051–12062 CrossRef CAS.
- B. Widom, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- S. M. Oversteegen and R. Roth, J. Chem. Phys., 2005, 122, 214502 CrossRef CAS PubMed.
- L. Rovigatti, N. Gnan, A. Parola and E. Zaccarelli, Soft Matter, 2015, 11, 692–700 RSC.
- W. K. Lim and A. R. Denton, 2015, unpublished.
- M. Pelaez-Fernandez, A. Souslov, L. A. Lyon, P. M. Goldbart and A. Fernández-Nieves, Phys. Rev. Lett., 2015, 114, 098303 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |
