Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Crack patterns over uneven substrates†
Pawan
Nandakishore
and
Lucas
Goehring
*
Max Planck Institute for Dynamics and Self-Organization (MPIDS), 37077 Göttingen, Germany. E-mail: lucas.goehring@ds.mpg.de; Fax: +49-551-5176-202; Tel: +49-551-5176-507
First published on 6th January 2016
Abstract
Cracks in thin layers are influenced by what lies beneath them. From buried craters to crocodile skin, crack patterns are found over an enormous range of length scales. Regardless of absolute size, their substrates can dramatically influence how cracks form, guiding them in some cases, or shielding regions from them in others. Here we investigate how a substrate's shape affects the appearance of cracks above it, by preparing mud cracks over sinusoidally varying surfaces. We find that as the thickness of the cracking layer increases, the observed crack patterns change from wavy to ladder-like to isotropic. Two order parameters are introduced to measure the relative alignment of these crack networks, and, along with Fourier methods, are used to characterise the transitions between crack pattern types. Finally, we explain these results with a model, based on the Griffith criteria of fracture, that identifies the conditions for which straight or wavy cracks will be seen, and predicts how well-ordered the cracks will be. Our metrics and results can be applied to any situation where connected networks of cracks are expected, or found.
1 Introduction
From networks of cracks across the surfaces of planets1–4 to artistic craquelure in pottery glazes and paintings,5–7 or bespoke fracture textures in thin films,8,9 crack patterns naturally occur on a wide variety of lengths. They are even implicated in the formation of scales on crocodiles.10 All these structures represent the outcome of failure processes that occur in a brittle medium supported by an uneven substrate. Here we show how the shape of the substrate plays an important role in determining the geometry of the resulting cracks. We will demonstrate how to use the substrate to template fractures, explore the conditions necessary to generate a variety of patterns, and introduce general metrics to quantify the orientational ordering of any set of connected cracks.To introduce the concerns of our work we will first briefly present three examples of cracks on the scales of kilometres, centimetres, and micrometres. These motivational examples, and those shown additionally in Fig. 1, also aim to highlight the need for quantitative approaches to the analysis of fracture patterns.
 | ||
| Fig. 1 Examples of crack networks, oriented by different effects. (a) Cracks in lava over a buried crater in Goethe Basin, Mercury.11 (b) Craquelure pattern of traditional oil-on-wood technique. (c) Paint cracks on a beam, reflecting the growth rings of the underlying wood. (d) Cracks in dried blood droplets, in a range of humidities, are affected by the way the droplets dry (courtesy of D. Brutin, adapted from ref. 12, Fig. 6). (e) Skin cracks on embryonic crocodiles are the result of differential growth of the skin layers, and form tiles that mature into scales (courtesy of M. Milinkovitch, adapted from ref. 10, Fig. 1b). (f) Desiccation cracks in pastes are influenced by any vibration or flow prior to drying (courtesy of A. Nakahara, adapted from ref. 13, Fig. 3b). | ||
On large length scales, radial graben are associated with buried craters on Mercury3,4 and Mars.1,2 These features are due to the repeated filling and cooling of lava in impact craters. The uneven stresses caused by the edge of a crater are believed to lead to wrinkle ridges above the crater rim.4 Contraction cracks also form within the interior of the crater, leading to a mixture of polygonal and circular graben patterns.3,4 The radial symmetry of the substrate imposes a characteristic structure to the such cracks, as in Fig. 1(a).
On a more intermediate length scale, craquelure (Fig. 1(b and c)) is the result of differential strains between a coating and its substrate.5–7,14 This may be due to tension in the framing of a painted canvas,5 for example, or changes in the relative humidity at which a painting has been stored.14 Alternatively, it may result from an artist's choice of a pottery glaze with a higher coefficient of thermal contraction than the clay it covers. Such craquelure patterns are extremely hard to forge, and can thus aid in the attribution of paintings.6 They have been shown to be influenced by local painting style and choice of substrate, including, for paint on wood, even the species of wood used.6,15 The analysis of similar patterns, in dried blood (Fig. 1(d)), is also being developed as a forensic tool, for example to help determine the relative humidity when the blood was spilt.12,16
On the micrometre scale, recent attention has focussed on controlling cracks. For example, Nam et al.8 showed how to selectively initiate, refract, and stop both straight and wavy cracks in silicon nitride thin films, vapour-deposited on silicon wafers, by adding notches, cutting stairs, or introducing interfacial layers between the wafer and film. Kim et al.9 instead looked at soft substrates, with crack formation guided by strategically placed notches along grooves; their work aims to control failure in situations, such as flexible electronics, where it must be expected. They find the most regular results when they design for crack spacings that are near the natural crack spacing of the brittle film.
A common feature of all these situations is that the cracking layer is thin, compared to its lateral extent. Nonetheless, the layer thickness imposes the natural length-scale of such problems, and the spacing of the cracks in each case reflects this thickness.9,17–19 Here we study the model problem of contraction cracks in ‘thin’ elastic layers adhered to rigid substrates and show how the shape of the substrate also plays an important role in determining the geometry of the crack pattern.
For this end we choose the system of desiccation cracks in drying clays as a simple, yet representative, experiment. As clays dry they tend to shrink, uniformly. So-called channel cracks open in the film, to relieve its growing strain energy (see e.g. in ref. 20–22). The appropriate physical model for stress in a wet clay, poroelasticity, has an exact mathematical analogy with the thermoelastic model of how most solids shrink as they cool.23–25 In biology, comparable conditions can also result from the differential growth of layered tissues.26–28 This is known to lead to the formation of scales on the heads of Nile crocodiles10 (Fig. 1(e)), for example, while a similar mechanism has been proposed to account for leaf venation patterns.26,27
2 Materials and methods
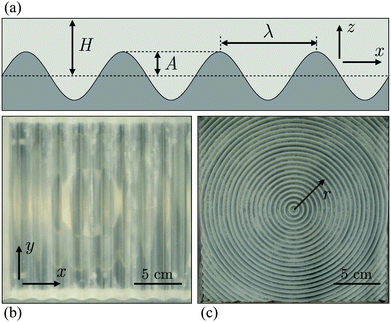
Briefly, bentonite clay was dried over rigid patterned substrates, where it cracked; a schematic summary of the experiment is given in Fig. 2(a). Compared to the wet clay, the substrate is undeformable and unbreakable.Each substrate consisted of a 20 × 20 cm2 plate. Five sinusoidal plates were cut from acrylic blocks by computer-numerical-control (CNC) milling, with a resolution of 200–400 μm. These plates were corrugated; their surface z varied sinusoidally along one direction, x, with a constant profile along the other, y, direction such that z = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πx/λ). The wavelengths λ and amplitudes A of the plates are given in Table 1. Two pairs of plates had the same dimensionless ratios a = A/λ, in order to check the scale-independence of the fracture patterns. Two additional plates were prepared by 3D printing from acrylic photopolymer, with a vertical resolution of 30 μm, and a contour resolution of 5 μm (4D Concepts). These plates had radial wave patterns, with surface profiles (see Table 1) that varied periodically in the radial direction, r, away from the centre of the plate, such that z = A
sin(2πx/λ). The wavelengths λ and amplitudes A of the plates are given in Table 1. Two pairs of plates had the same dimensionless ratios a = A/λ, in order to check the scale-independence of the fracture patterns. Two additional plates were prepared by 3D printing from acrylic photopolymer, with a vertical resolution of 30 μm, and a contour resolution of 5 μm (4D Concepts). These plates had radial wave patterns, with surface profiles (see Table 1) that varied periodically in the radial direction, r, away from the centre of the plate, such that z = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πr/λ). Finally, a flat acrylic plate was used for control experiments. All plates were smooth to the touch. For each plate 10 cm high acrylic walls were glued to each edge, to make a waterproof container.
cos(2πr/λ). Finally, a flat acrylic plate was used for control experiments. All plates were smooth to the touch. For each plate 10 cm high acrylic walls were glued to each edge, to make a waterproof container.
| Plate | A (cm) | λ (cm) | a = A/λ |
|---|---|---|---|
| 1 | 0.25 | 2 | 0.125 |
| 2 | 0.25 | 1 | 0.25 |
| 3 | 0.5 | 2 | 0.25 |
| 4 | 0.25 | 0.5 | 0.5 |
| 5 | 0.5 | 1 | 0.5 |
| 1r | 0.25 | 1 | 0.25 |
| 2r | 0.25 | 0.5 | 0.5 |
Slurries of potassium bentonite (Acros Organics K-10 montmorillonite) were prepared by mixing a set weight of bentonite powder with twice as much water, by mass. Slurries were then stirred until smooth and immediately poured evenly into a container, over a substrate. At this concentration the slurries behaved as fluids, rather than pastes. These conditions avoid the memory effect,29,30 whereby the flow or vibration of a yield-stress paste can affect the way it cracks (see Fig. 1(f)). We checked that this effect was absent by drying slurries over flat substrates, and finding isotropic crack patterns.
After pouring, the bentonite settled slightly, separating into a dense clay covered by a thin water layer. We measured the thicknesses of these submerged clay layers in flat-bottomed containers after 6 hours of settling, without significant evaporation, and found that the consolidated wet clay consistently contained 0.49 grams of bentonite per cubic centimetre. For slurries poured over the sinusoidal substrates we therefore used the total mass of the bentonite as a proxy for the average layer thickness H of the wet clay layer. All experiments were performed in the range of H from 3 to 15 mm.
Once a slurry had been poured, it was left to dry in a quiet, warm environment for 6–48 hours, depending on the amount of clay used. When drying is complete, the bentonite becomes lighter in colour; no further cracks appear after this time. For the linear wave plates, drying was accelerated by halogen heat lamps, which raised the surface temperature of the clay to ∼50 °C. As elevated temperatures would melt the printed plates, drying over the radial plates was enhanced by raising the room temperature to about 30 °C. During drying, the appearance and evolution of the cracks were imaged every 5 minutes using a digital SLR camera (Nikon D5000 series), mounted above the drying container. By comparing the initial wet height H to the dry height of various layers, we estimate a total vertical strain of 0.27, during drying.
2.1 Image processing
Images were pre-processed using ImageJ and Matlab, as shown in Fig. 3. Each image was cropped to isolate the cracked clay, then converted to grayscale by averaging across all colour channels, and contrast-enhanced. Next, a band-pass filter was applied to remove high-frequency noise (3-pixel cutoff to reduce single-pixel noise) and low-frequency variations in lighting intensity (40-pixel cutoff, comparable to the width of the largest cracks). Finally, each image was thresholded to give a black-and-white representation of the crack network, as in Fig. 3(b).To characterise the crack patterns we will focus on the shape of the crack network, and on the relative positions and orientations of features such as the vertices between cracks. For some measurements, we thus chose to eliminate unconnected cracks and spurs from the binary images. Isolated cracks, and other noise, were removed by deleting objects below a threshold size. Every image was then thickened, by 3 pixels, to ensure that small breaks in the crack network, or en-passant cracks,31 were filled in. The result was then eroded to leave a skeleton consisting of one-pixel-wide cracks that connected various vertices or nodes, and which delimited isolated patches, or peds. Cracks that branched off the main network, but stopped without connecting to anything, were then removed. Both the binary images and the skeletons were used as the basis for further analyses.
Finally, we note here that the error bars given throughout this work are estimated by subdividing the processed images into quarters, analysing each subsection separately, and then calculating the standard deviation of the four different results.
3 Results and discussion
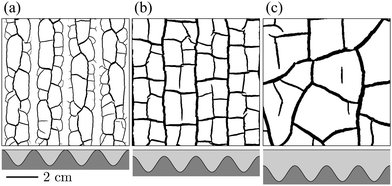
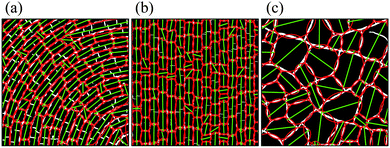
We found that as the thickness of the brittle layer increases, its contraction cracks slowly lose information about their substrate. However, in order to understand the effect of an uneven substrate, we must first briefly summarise the base case of cracks in flat bentonite layers. For the flat control plate, isotropic crack patterns were seen for all layer thicknesses (H from 4–15 mm). Cracks appeared one by one, sequentially breaking the clay into smaller and smaller pieces, as in ref. 32 and 33. This process stops at some finite spacing, when the pattern saturates18,25 – further drying increases the widths of the cracks in these ‘mature’ networks, as in ref. 34 and 35, rather than creating new ones. We confirmed that the natural crack spacing over the flat plate is between 2–3 times the wet layer thickness H, using the line-dropping method.36 The results are compatible with the crack spacings reported in ref. 36, but consistently smaller, as the dry heights of bentonite layers were reported in that study.For clays dried over the sinusoidally varying substrates the typical sequence of crack patterns, after drying is complete, is shown in Fig. 4. A wavy pattern developed in thin layers, with the first cracks meandering back and forth as they travelled along the troughs of the underlying substrate. Various shorter cracks then filled in the pattern, as in Fig. 4(a). For intermediate thicknesses of clay regular straight cracks appeared over each ridge, followed by cracks between these primary cracks, and at right angles to them, like the rungs of a ladder. As in Fig. 4(b), additional short cracks also often formed along the troughs of the pattern, especially in the later stages of drying. Both variants – with parallel cracks appearing only over ridges, or on both ridges and troughs – are described here as ‘ladder-like’ patterns. For thick layers, as in Fig. 4(c), there was no obvious effect of the substrate on the crack pattern, which was essentially isotropic. Time-lapse movies showing the development of representative cases of wavy, ladder-like and isotropic cracks are provided as online ESI.†
Linear elastic fracture mechanics has no inherent length-scales, other than those set by the geometry of the system under study. If this assumption holds, then the dependence of the fracture pattern on the shape of our substrates can be entirely captured by considering two dimensionless parameters, such as a dimensionless layer thickness, h = H/λ, and a dimensionless amplitude, a = A/λ, of the substrate's relief. Since in many situations, including ours, the spacing of thin-film cracks scales with the thickness of the cracking layer,9,17–19 the parameter h should describe the relative match between the natural spacing of any cracks and the wavelength of the perturbations affecting their pattern. The dimensionless amplitude a describes the sharpness of the peaks on the substrate.
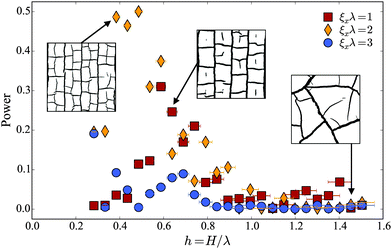
For the linear wave plates we categorised each fully-dried crack pattern by visual inspection as either wavy, straight or isotropic. As summarised in Fig. 5, the different patterns divide up the expected dimensionless phase space into well-defined regions. At the boundaries between the different patterns were small areas of coexistence, for example between wavy and straight cracks. This coexistence represents two scenarios – either both patterns were observed within different regions of a single experiment, or were seen for the same h, but on different plates. For dimensionless layer heights in excess of about h = 1, only isotropic patterns were ever seen.
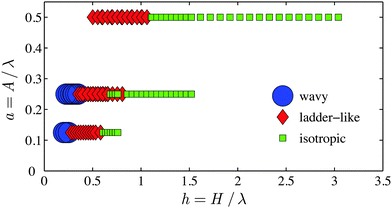 | ||
| Fig. 5 A phase diagram showing where wavy, ladder-like and isotropic crack patterns were seen, for the linear wave plates. | ||
Although there are clear visual differences between the patterns shown in Fig. 4, there are no well-established methods by which they can be characterised. In order to analyse our patterns quantitatively we therefore need to develop new order parameters similar to, for example, the orientational order parameter of liquid crystals.37 We present three such measurements next, based on Fourier methods, the relative orientation of the regions outlined by the crack network and the positions of neighbouring crack vertices.
3.1 Fourier analysis of crack patterns
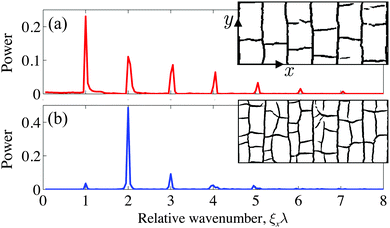
The presence of evenly spaced cracks that are well-aligned with the substrate's features suggests the use of Fourier methods to quantify our crack patterns. Although a two-dimensional transform could be used to measure crack spacings, we focus here on a one-dimensional approach, which allows us to measure the relative alignment and periodicity of the cracks with respect to the linear substrates. To this end, we first collapse each binary image to find the average density of cracks at each position along the x-direction. This is done by summing over the y-direction of the images, where cracks are represented by ones and uncracked material by zeros. We then find the power spectrum of the crack density as the absolute value of the square of its Fourier transform, normalised to have an integrated power of one.In cases where cracks are aligned with the substrate there are sharp peaks in the power spectrum of the crack density when the wavenumber ξx is an integer multiple of the wavelength λ of the substrate, as in Fig. 6. In other words, the substrate prefers there to be an integer number of cracks, per wavelength. The responses of all five linear wave plates were very similar: typically, most power was found in the first or the second mode, i.e. when ξxλ = 1 or 2, and higher order peaks were consistent with harmonics of this main peak. Furthermore, there was a change in the dominant mode of the power spectra around h = 0.5–0.75. Below this, most power was in the ξxλ = 2 peak, while above this the ξxλ = 1 peak was also strong. Visually, the point where these intensities cross over coincides with the transition between patterns with cracks along every ridge (Fig. 6(a), ξxλ = 1), and patterns with cracks along both the ridges and troughs (Fig. 6(b), ξxλ = 2). The appearance of wavy cracks, at very small h, are associated with a decline in the power of the ξxλ = 2 mode. Since they meander, their crack density is not as strongly localised as the ladder-like cracks, and the Fourier analysis reflects this. The isotropic cracks, around h = 1 or thicker, show no significant coupling to their substrate's periodicity.
An example of all of the above behaviour is given in Fig. 7 for plate 2, where a = 0.25. The results for plate 3 are consistent with this, and extend the range of suppressed ξxλ = 2 down to h = 0.2. For plates 4 and 5, where the substrate is relatively sharper (a = 0.5), the sequence of responses is identical, but shifted to slightly higher values of h: the transition from one to two cracks per wavelength is at h = 0.75, for example. For plate 1, with shallow relief, this transition is shifted down to about 0.4–0.5, but the Fourier analysis does not produce very clear results, otherwise. These variations in the conditions leading to the different types of crack patterns are consistent with the visual classifications given in Fig. 5.
Thus, Fourier methods capture the regularity of the observed crack patterns, and quantify how the transition from one to two cracks per wavelength occurs when the periodicity of the substrate is about 1.5 to 2 times the thickness of the cracking layer – i.e. approaching the natural crack spacing of the clay over a flat substrate. However, it does not provide a good indication of the alignment of the various crack features with the substrate. The absolute intensity of the power spectral peaks, which could be such a measure, is too easily affected by noise to serve in this way. The next two sections aim to provide more robust measures of alignment.
3.2 An orientational order parameter
As the clay dries in our experiments, its cracks subdivide and isolate individual regions of material, whose shapes are then determined by their sets of final bounding cracks. For example, in Fig. 4(b) the cracks around the dried peds are mostly parallel or perpendicular to the substrate relief. The cracked regions therefore have rectangular shapes, and tile the plane like rows of bricks. In contrast, the cracks in Fig. 4(c) are only weakly influenced by the substrate and define cracked regions with more arbitrary shapes and orientations. This section aims to measure the degree of alignment of these regions, with respect to the ripples along their substrate.From each image we extracted a binary skeleton of the crack network (see Section 2.1). Each connected region in this image is identified and its orientation is measured by the direction that minimises the second moment of area of the region, with respect to a line passing through its centroid. In practice, this measurement was made by fitting an ellipse to each region: the area of the ellipse matches the area of the region, while its major axis goes through the region's centroid with an orientation, θ, that minimises the region's second moment of area. The average eccentricity of the ellipses, while not used here, could serve as an additional metric characterizing square vs. elongated regions (e.g. for craquelure on paintings6 or blood plaques16). Fig. 8 shows examples of elliptical fits of cracked regions with three different patterns.
To characterise the crack-bounded regions, through their best-fit ellipses, we use an orientational order parameter that measures the relative alignment of rod-like particles, or any objects that are invariant after rotation by 180°. This parameter is well-known in the physics of liquid crystals (e.g. in ref. 37), where it is used to describe the transition from an isotropic to a nematic (orientational order without positional order) phase, for example. In our case, for dimension d = 2, the general definition38 of this nematic order parameter simplifies to
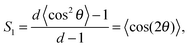 | (1) |
The orientational ordering for all our experiments is shown in Fig. 9. For each dimensionless amplitude a there is good agreement between the different experiments, although the radial plates give slightly higher values of S1 than the linear plates. For small enough h, in particular around h = 0.5 and below, the peds are very strongly aligned with the relief of the substrate, and this alignment slowly decreases as the layer thickness increases, until S1 becomes statistically equivalent to its value over the flat plate above a relative thickness of at most h = 1.25. Furthermore, the intensity of the ordering decreases with the relative sharpness of the plates, a, for experiments with the same h. However, unlike the Fourier analysis, or the order parameter we introduce in the next section to describe the relative alignment of the individual cracks, S1 remains high for very low h. It is a sensitive measure of the straight-to-isotropic transition, but because it averages over the entire shape of a cracked region, it does not detect the meandering of the cracks.
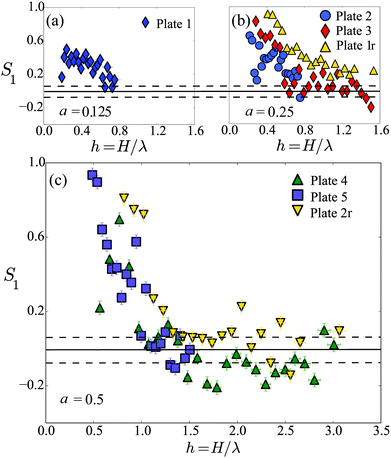 | ||
| Fig. 9 The orientational order parameter S1 (eqn (1)) describes how well-aligned individual peds (continuous regions, entirely bounded by cracks) are with the orientation of their substrate. Results are given for wave plates with dimensionless amplitudes (a) a = 0.125, (b) a = 0.25 and (c) a = 0.5. The solid and dashed lines represent the mean and standard deviation of measurements of S1 on flat plates. | ||
3.3 Crack alignment order parameter
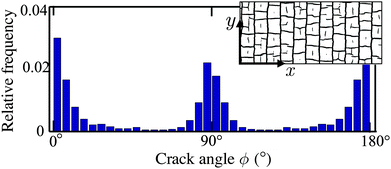
A second order parameter is introduced to describe the relative alignment of the cracks with their substrate. Working from the skeletons of the cracks, we first find the coordinates of all vertices, or intersections between cracks. These skeletons form closed networks, where all isolated features and spurs have been removed. The vertices are therefore points along the skeleton that touch at least three different cracked regions, and this property is used to identify them. Crack segments are then defined by the paths between any two neighbouring, connected vertices, and their orientations ϕ by the vectors connecting these two endpoints. Since one end of a crack cannot be effectively distinguished from the other, the distribution of crack angles is collapsed onto the range from 0–180°. These angles are referenced to the y or radial directions, for the linear or radial wave plates, respectively.It should be emphasised that this method creates a very local definition of the orientation of a crack, and splits long cracks into many individual segments, between adjacent intersections with other cracks. This is different from some other network analyses of cracks,33,39,40 which focus instead on the entire length of a crack, regardless of any intersections it has with other features. An example of a crack pattern, and the relative abundance of crack orientations in it, is given in Fig. 10.
In our more well-ordered experiments, as in Fig. 10, there are typically prominent cracks along the ridges of the substrate, and shorter perpendicular cracks that join these together. Their measure must reflect this symmetry. In analogy with S1, it should take a value of +1 for cracks that are either parallel or perpendicular to some reference direction, 0 for random patterns, and −1 for cracks that are completely mis-aligned with the reference (here, cracks at ±45° to the substrate features). The simplest such definition is for a crack alignment order parameter
| S2 = 〈cos(4ϕ)〉. | (2) |
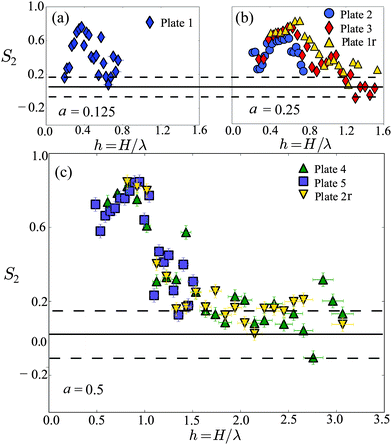 | ||
| Fig. 11 The crack alignment order parameter S2 (eqn (2)) measures the relative alignment of cracks with their substrate, and takes large values for networks with cracks that are parallel or perpendicular to the underlying relief. Shown are the results for (a) a = 0.125, (b) a = 0.25, and (c) a = 0.5. The solid and dashed lines represent the mean and standard deviation of S2 for cracks over the flat plate. | ||
We found that the crack alignment order parameter, S2, matches the orientational order parameter of the cracked regions, S1, in most situations. There is also good data collapse between the linear and radial wave plates, and between all plates of the same relative amplitude a, confirming that our results do not depend on the absolute scale of the drying experiments. There is a loss of ordering around h = 1, again at slightly higher values of h for the sharper substrate ridges, and slightly lower values for the shallower relief. However, unlike S1, there is a clear downturn in S2 at low layer thicknesses – the cracks become less aligned for very thin layers. As it is a local measure, the crack orientation is more sensitive than our other metrics to any curvature of the cracks, and some of the decrease in S2 for very low h is due to the wavy cracks. Nevertheless, in all cases S2 starts to fall well before we can see wavy cracks by eye. In Section 4 we will show how this effect, and the other transitions in the crack pattern, can be explained by the relative forcing of the uneven substrate, which will be shown to be strongest at the intermediate layer thicknesses where both order parameters are largest.
3.4 Extension to other crack networks
The two order parameters S1 and S2 introduced above describe, respectively, the relative alignment of crack-bounded areas, or individual cracks, with respect to some known angle. In our experiments there was an obvious direction to choose for this angle, based on the substrates used – either the local radial vector, or one of the Cartesian axes. However these metrics can also be used to determine whether a crack network is aligned or not without knowing, in advance, any such preferred direction. By extending the liquid-crystal analogy of the order parameter S1, one may use the local director, or average local orientation of the relevant objects, as the reference direction. In other words, one may first calculate the average θ or ϕ, either over all cracks or areas in a region of interest, or locally over neighbourhoods that are large enough to provide good statistical averaging. These neighbourhoods could be defined, for example, by all objects within a given radius of each point in the image, allowing one to map the director field, and to search for domains of different orientation. Then, in calculating the order parameters through eqn (1) and (2), all angles can be referenced to this local director orientation. This would allow one to compare the relative degree of alignment of natural crack patterns like polygonal terrain41,42 and the hydraulic channels of heavily fractured rock,39,43 for example. It would also allow one to better measure manufactured patterns such as craquelure,6,15 or custom-designed micro-cracks.8,94 Modelling the crack pattern transitions
When a crack opens, it releases stored strain energy from its environment. In Griffith's model of fracture this energy is used to create the new surface area of the crack, as it grows.44,45 In this section we consider a finite element model of a channel crack opening over a sinusoidal surface, and use the Griffith criteria for fracture to predict where the first cracks will appear. We will show how the observed transitions from wavy to straight to isotropic cracks can be explained in terms of the relative strain energy released by a crack opening at different locations in a thin elastic layer drying – or cooling, or with some other misfit strain – over such a rippled substrate.In particular, we consider a linear poroelastic46 model for cracks in drying clay. The total stress ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) in the clay is a sum of the elastic stress σ supported by the network of clay particles and the capillary pressure p of the interstitial liquid, such that
in the clay is a sum of the elastic stress σ supported by the network of clay particles and the capillary pressure p of the interstitial liquid, such that
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) ij = σij − pδij. ij = σij − pδij. | (3) |
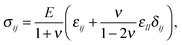 | (4) |
| εij = (∂iuj + ∂jui)/2. | (5) |
We solved eqn (3)–(5) using Matlab's finite-element routines, on domains like those shown in Fig. 12, namely semi-rectangular regions with straight edges at the top (z = 1, dimensionless units, scaled so that the average film thickness H = 1), left (x = 0) and right (x = 10) sides, and a corrugated base where z = 1 − ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = A
= A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πx/λ + ψ). Here ψ is an offset phase, allowing us to examine the strain energy released by fracture at various positions along the substrate, and
cos(2πx/λ + ψ). Here ψ is an offset phase, allowing us to examine the strain energy released by fracture at various positions along the substrate, and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) is the local film thickness. Plane strain conditions, with no displacements allowed in the y-direction, were used to model a channel crack advancing with a constant profile along the sinusoidal plate. The upper surface was taken to be traction free (σxz = σzz = 0 on z = 1), while the lower surface was treated as no-slip, such that u = 0 there, and only vertical displacements were allowed (ux = 0) along the right boundary. The left-face boundary was either treated like the right one, for an intact film, or as a traction-free boundary, for a cracked film. Finally, the pressure p was taken to be constant everywhere, as appropriate for quasi-static fracture.
is the local film thickness. Plane strain conditions, with no displacements allowed in the y-direction, were used to model a channel crack advancing with a constant profile along the sinusoidal plate. The upper surface was taken to be traction free (σxz = σzz = 0 on z = 1), while the lower surface was treated as no-slip, such that u = 0 there, and only vertical displacements were allowed (ux = 0) along the right boundary. The left-face boundary was either treated like the right one, for an intact film, or as a traction-free boundary, for a cracked film. Finally, the pressure p was taken to be constant everywhere, as appropriate for quasi-static fracture.
The work done by the growth of the channeling crack can be measured by integrating the product of the pre-crack stress, σ*, and the opening displacements of the crack, δ, as in ref. 21 and 45. This is, essentially, the sum of the forces on the incipient crack surfaces, acting over the distance they travel as the crack opens. The strain energy released, per unit area of new crack, is thus
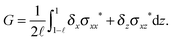 | (6) |
For a flat substrate, this problem has been studied in detail by Beuth,21 Xia and Hutchinson22 and Yin et al.47,48 They showed that G scales as
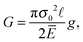 | (7) |
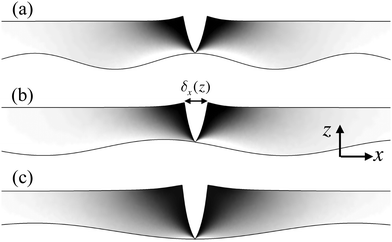
For an uneven substrate G depends on location, measured here by the offset ψ. As the clay dries the relative shape of G(ψ) will not change, but rather its magnitude will simply increase along with the capillary pressure. The Griffith criteria predict that fractures can only grow once G reaches some critical value, Gc, which is a material parameter (see e.g. in ref. 45). The first cracks in the brittle drying layer should therefore form at the positions where the strain energy released by these cracks, i.e. G, would be a maximum, as these are the first places where G = Gc. For a Poisson ratio of ν = 1/3, we calculated how G varies with position for a wide range of experimental conditions, from A = 0.01–0.90 and λ = 0.5–8.0. To focus only on geometric effects we used eqn (7) to rescale G by the relative stiffness 2Ē/πσ02, so that Ḡ = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) g. The results are summarised in Fig. 13(a), which shows the values of ψ that maximise G for various A and λ. Depending on the shape of the substrate and the thickness of the clay, the preferred positions of the earliest cracks can be either (i) over the peaks of the substrate, (ii) over the troughs or (iii) at pairs of points displaced to either side of each peak. Examples of the displacement field and energy release rate of all three cases are shown in Fig. 12.
g. The results are summarised in Fig. 13(a), which shows the values of ψ that maximise G for various A and λ. Depending on the shape of the substrate and the thickness of the clay, the preferred positions of the earliest cracks can be either (i) over the peaks of the substrate, (ii) over the troughs or (iii) at pairs of points displaced to either side of each peak. Examples of the displacement field and energy release rate of all three cases are shown in Fig. 12.
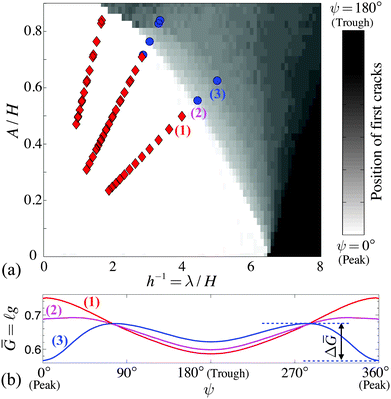 | ||
| Fig. 13 Modelling the straight-to-wavy transition. (a) Predicted positions of the first cracks, based on the offset ψ where the energy release rate G is maximised. Red diamonds and blue circles show the experimental parameters where ladder-like or wavy cracks were seen, respectively (from Fig. 5). (b) Energy landscapes of Ḡ(ϕ) for three conditions, indicated by (1–3) in (a), which cross over the straight-to-wavy transition. Under these conditions there is a bifurcation from one energy maximum for a crack on the top of a ridge, to two preferred locations, on either side of the ridge. | ||
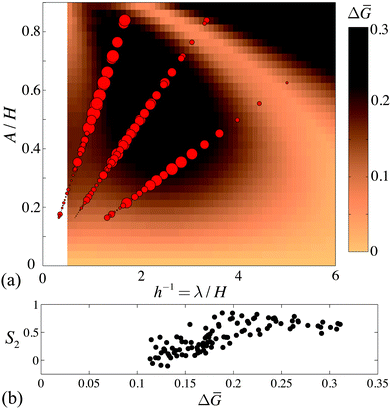
Fig. 13(a) also replots the observations from Fig. 5, corresponding to the conditions where wavy and ladder-like cracks are found; the new axes here highlight the low-h region of interest. For all experiments where straight cracks were seen the model correctly predicts that the first cracks should appear over the ridges of the substrate. Where wavy cracks are seen, the model instead generally predicts two stable positions for cracks, along the sides of the ridges. Although our model has no dynamic component, this empirical agreement of the division of phase-space suggests that the wavy cracks result from cracks moving back and forth between their two bistable positions. The boundary between the straight and wavy cases corresponds to a forward pitchfork bifurcation, as sketched in Fig. 13(b).
To consider the more gradual transition from ladder-like to isotropic cracks, we looked at the relative variations in Ḡ, defining ΔḠ as the difference between the maximum and minimum values of Ḡ(ψ), for each value of A and λ studied. If ΔḠ is small, then there is only weak guidance for the cracks, and they should appear more random than in cases of larger variation of energy release rate. We tested this hypothesis by comparing ΔḠ with the crack alignment order parameter of our experiments. First, we calculated ΔḠ for each point in our simulation, mapping the results in Fig. 14 alongside the data showing S2 for our various experiments with linear wave plates. This figure shows that there is a neighbourhood of driving parameters, centred around λ/H = 2.2 and A/H = 0.6, where ΔḠ is large. There is another area of strong contrast at high A/H and λ/H, and the lower values of ΔḠ between these two regions corresponds to the straight-to-wavy transition of Fig. 13. Our experiments pass through the central region, and show their most well-ordered patterns as they do so. To quantify this agreement, we then calculated ΔḠ for the conditions corresponding to each experiment where ladder-like or isotropic cracks were seen. As shown in Fig. 14(b), there is indeed a good correlation between the range of energy release rates allowed for any particular geometry, and the relative alignment of the cracks that formed over it.
Finally, we note that some insight into the limits of our results can be gained through a qualitative comparison to channel cracks in flat films and coatings. Here the stresses relaxed by the crack will decay away over a length comparable to the thickness of the film.20,22 This effect can also be seen in Fig. 12. For a wavy substrate this limit is approached when the amplitude of the relief goes to zero, and under such conditions isotropic cracks with a spacing ∼H are clearly expected. However, for finite A/H the limit can still offer insight. For very long wavelength ripples, large λ/H, each crack will see a local environment, of size ∼H, that is approximately flat. Since, for a perfectly flat film, the critical cracking stress will scale as 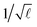 (see ref. 21 and 22 or invert eqn (7)), the cracks in this limit should form first over the troughs of the pattern, as the layer is deepest there, and will break at the lowest stress. This intuitive result matches our model predictions for conditions of large enough relative wavelength (i.e. see the lower right corner of Fig. 13). Although these conditions were not probed by our experiments, we would also expect an isotropic pattern in this case, but one with a local modulation of the crack spacing reflecting the changes in local thickness. For the opposite limit, of very sharp features where λ/H ≪ 1, the region around any crack will sample many ridges and troughs, and these local variations will tend to cancel each other out (see Saint-Venant's principle e.g. in ref. 49); again, isotropic cracks would be expected. In other words, for finite-amplitude relief a brittle layer must filter out the high and low-frequency information of its substrate, and any contraction cracks that form should reflect this.
(see ref. 21 and 22 or invert eqn (7)), the cracks in this limit should form first over the troughs of the pattern, as the layer is deepest there, and will break at the lowest stress. This intuitive result matches our model predictions for conditions of large enough relative wavelength (i.e. see the lower right corner of Fig. 13). Although these conditions were not probed by our experiments, we would also expect an isotropic pattern in this case, but one with a local modulation of the crack spacing reflecting the changes in local thickness. For the opposite limit, of very sharp features where λ/H ≪ 1, the region around any crack will sample many ridges and troughs, and these local variations will tend to cancel each other out (see Saint-Venant's principle e.g. in ref. 49); again, isotropic cracks would be expected. In other words, for finite-amplitude relief a brittle layer must filter out the high and low-frequency information of its substrate, and any contraction cracks that form should reflect this.
5 Conclusions
Our results explore the effects of an uneven substrate on the development of contraction cracks in thin films, and are inspired by natural patterns of cracks around buried craters, paintings, and vapour-deposited thin films. We showed that the wavy, periodic undulation of a substrate can cause the ordering of a crack pattern that forms above it, and has the strongest influence on this pattern when the thickness of the cracking layer is comparable to, or slightly smaller than, the periodicity of the substrate.Generally we found that for increasing layer thickness the crack pattern changed from one with wavy cracks running along the troughs of the substrate, to straight cracks appearing over each peak and trough of the substrate, to straight cracks on only the peaks of the substrate, and finally to a disordered or isotropic pattern. The wavy-to-straight transition was the most abrupt change, as evidenced by examples of single experiments that were wavy on one side of the plate, and straight on the other. All these patterns were quantified by Fourier methods and orientational order parameters, similar to the nematic order parameter of liquid crystals, which are easily adaptable to other types of crack networks. Finally, we showed how the transitions between pattern type could be explained by a simple finite-element model of channeling cracks advancing over uneven relief, regardless of whether those cracks were driven by drying, cooling or the differential growth of crocodilian skin.
Acknowledgements
We thank U. Schminke and M. Wolff for assistance with the design and manufacture of our plates; LG thanks P. Keen and A. Chetwood for their contributions to an early version of this experiment; PN thanks A. Fourrière for helpful discussions.References
- G. E. McGill and L. S. Hills, J. Geophys. Res., 1992, 97, 2633–2647 CrossRef.
- M. Cooke, F. Islam and G. McGill, J. Geophys. Res., 2011, 116, E09003 Search PubMed.
- A. M. Freed, D. M. Blair, T. R. Watters, C. Klimczak, P. K. Byrne, S. C. Solomon, M. T. Zuber and H. Melosh, J. Geophys. Res., 2012, 117, E00L06 Search PubMed.
- D. M. Blair, A. M. Freed, P. K. Byrne, C. Klimczak, L. M. Prockter, C. M. Ernst, S. C. Solomon, H. J. Melosh and M. T. Zuber, J. Geophys. Res., 2013, 118, 47–58 Search PubMed.
- A. Karpowicz, J. Am. Inst. Conserv., 1990, 29, 169–180 CrossRef.
- S. L. Bucklow, Comput. Hum., 1998, 31, 503–521 CrossRef.
- L. Pauchard, V. Lazarus, B. Abou, K. Sekimoto, G. Aitken and C. Lahanier, Reflets Phys., 2007, 3, 5–9 CrossRef.
- K. H. Nam, I. H. Park and S. H. Ko, Nature, 2012, 485, 221–224 CrossRef CAS PubMed.
- B. C. Kim, T. Matsuoka, C. Moraes, J. Huang, M. Thouless and S. Takayama, Sci. Rep., 2013, 3, 221–224 Search PubMed.
- M. C. Milinkovitch, L. Manukyan, A. Debry, N. Di-Poï, S. Martin, D. Singh, D. Lambert and M. Zwicker, Science, 2013, 339, 78–81 CrossRef CAS PubMed.
- MESSENGER, Goethe Basin, 2012, NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.
- W. B. Zeid and D. Brutin, Colloids Surf., A, 2013, 430, 1–7 CrossRef.
- H. Nakayama, Y. Matsuo, O. Takeshi and A. Nakahara, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 13001–13008 Search PubMed.
- G. A. Berger and W. H. Russell, J. Am. Inst. Conserv., 1990, 29, 45–76 CrossRef.
- I. Crisologo, C. Monterola and M. Soriano, Int. J. Mod. Phys. C, 2011, 22, 1191–1209 CrossRef.
- W. B. Zeid, J. Vicente and D. Brutin, Colloids Surf., A, 2013, 432, 139–146 CrossRef.
- C. Allain and L. Limat, Phys. Rev. Lett., 1995, 74, 2981–2984 CrossRef CAS PubMed.
- T. Bai, D. D. Pollard and H. Gao, Nature, 2000, 403, 753–756 CrossRef CAS PubMed.
- K. A. Shorlin, J. R. de Bruyn, M. Graham and S. W. Morris, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 6950 CrossRef CAS.
- J. W. Hutchinson and Z. Suo, Adv. Appl. Mech., 1992, 29, 63–191 Search PubMed.
- J. L. Beuth Jr, Int. J. Solids Struct., 1992, 29, 1657–1675 CrossRef.
- Z. C. Xia and J. W. Hutchinson, J. Mech. Phys. Solids, 2000, 48, 1107–1131 CrossRef CAS.
- M. A. Biot, J. Appl. Phys., 1956, 27, 240–253 CrossRef.
- A. Norris, J. Appl. Phys., 1992, 71, 1138–1141 CrossRef.
- L. Goehring, A. Nakahara, T. Dutta, S. Kitsunezaki and S. Tarafdar, Desiccation cracks and their patterns: Formation and Modelling in Science and Nature, Wiley-VCH, Singapore, 2015, p. 349 Search PubMed.
- Y. Couder, L. Pauchard, C. Allain and S. Douady, Eur. Phys. J. B, 2002, 28, 135–138 CrossRef CAS.
- M. F. Laguna, S. Bohn and E. A. Jagla, PLoS Comput. Biol., 2008, 4, e1000055 Search PubMed.
- A. Boudaoud, Trends Plant Sci., 2010, 15, 353–360 CrossRef CAS PubMed.
- A. Nakahara and Y. Matsuo, J. Phys. Soc. Jpn., 2005, 74, 1362–1365 CrossRef CAS.
- Y. Matsuo and A. Nakahara, J. Phys. Soc. Jpn., 2012, 81, 024801 CrossRef.
- M. Fender, F. Lechenault and K. Daniels, Phys. Rev. Lett., 2010, 105, 125505 CrossRef PubMed.
- S. Bohn, L. Pauchard and Y. Couder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 046214 CrossRef CAS PubMed.
- S. Bohn, J. Platkiewicz, B. Andreotti, M. Addabedia and Y. Couder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 046215 CrossRef CAS PubMed.
- D. Mal, S. Sinha, S. Mitra and S. Tarafdar, Physica A, 2005, 346, 110–115 CrossRef.
- D. Mal, S. Sinha, T. Dutta, S. Mitra and S. Tarafdar, J. Phys. Soc. Jpn., 2007, 76, 014801 CrossRef.
- L. Goehring, R. Conroy, A. Akhter, W. J. Clegg and A. F. Routh, Soft Matter, 2010, 6, 3562–3567 RSC.
- P.-G. de Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, Oxford, 1993, 2nd edn, p. 597 Search PubMed.
- A. A. Mercurieva and T. M. Birshtein, Makromol. Chem., Theory Simul., 1992, 1, 205–214 CrossRef.
- C. Andresen, A. Hansen, R. Goc, P. Davy and S. Hope, Front. Phys., 2013, 1, 1–5 Search PubMed.
- A. Hafver, E. Jettestuen, M. Kobchenko, D. K. Dysthe, P. Meakin and A. Malthe-Sørenssen, EPL, 2014, 105, 56004 CrossRef.
- R. S. Sletten, B. Hallet and R. C. Fletcher, J. Geophys. Res., 2003, 108, 8044 CrossRef.
- P. Pina, J. Saraiva, L. Bandeira and J. Antunes, Planet. Space Sci., 2008, 56, 1919–1924 CrossRef.
- L. Valentini, D. Perugini and G. Polil, Physica A, 2007, 377, 323–328 CrossRef.
- A. A. Griffith, Philos. Trans. R. Soc. London, Ser. A, 1921, 221, 163–198 CrossRef.
- B. R. Lawn, Fracture of Brittle Solids, Cambridge University Press, Cambridge, UK, 1993, 2nd edn, p. 378 Search PubMed.
- M. A. Biot, J. Appl. Phys., 1941, 12, 155–164 CrossRef.
- H. M. Yin, G. H. Paulino and W. G. Buttlar, Int. J. Fract., 2008, 153, 39–52 CrossRef.
- H. M. Yin, Int. J. Solids Struct., 2010, 47, 1007–1015 CrossRef.
- M. H. Sadd, Elasticity theory, applications, and numerics, Elsevier, 2005, p. 461 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Time-lapse movies of fracture patterns. See DOI: 10.1039/c5sm02389k |
| This journal is © The Royal Society of Chemistry 2016 |