Trapping, entrainment and synchronization of semiflexible polymers in narrow, asymmetric confinements

Abstract

The physical properties of polymeric actin facilitate many mechanical processes within the cell, including cellular deformation and locomotion, whereby the polymers can be confined to a range of different geometries. As actin polymers often form entangled solutions in the cell, we have investigated the effect of confinement on the evolution of entangled semiflexible polymer solutions. Using a microfluidic platform, we examined the physical dynamics of actin polymers confined within narrow (2–4 μm) rectangular channels. Focusing on the entanglement process of two actin polymers, we found that their prolonged entrainment leads to synchronized horizontal undulations and decreased translational diffusion. In the absence of cross-linking molecules or proteins, the long-range entrainment interactions are predominantly controlled by the geometric boundaries. We directly measure the deflection length Λ for an individual polymer, either solitarily confined within a channel or confined in the presence of a second filament, enabling the determination of the change in free energy associated with polymer entanglement. Our results indicate that geometrical confinement can serve as a solitary variable influencing the physical dynamics of entangled semiflexible polymers.

---

Introduction

Entangled solutions and networks of semiflexible polymers underlie the remarkable active and passive mechanical performance of the cellular cytoskeleton, an entity that is highly dynamic in space and time and closely connected with numerous biological processes.¹ The heterogeneous behavior of biopolymer systems generally diverges from their synthetic counterparts, which provides another interesting motivation on the level of fundamental physics.² Many studies have focused on the statistical mechanical properties of single biopolymers confined to tube-like geometries,^3–7 however, the effect of asymmetrical boundaries on the dynamic formation of entangled polymer solutions remains poorly studied. In vitro assays have shown that geometric confinement, independent of accessory binding proteins, can influence the organization of actin polymers.^8,9 Still a complete physical understanding of confined polymers, including inter-polymer long-range interactions, could help explain the diverse arrangement of biopolymers in motile and shape-changing cells, as well as in micro-scale chip devices. In this study we not only look at the dynamics of semiflexible polymers confined in rectangular microfluidic channels, but we also observe the effects of incorporating more than one polymer in the confinement area.

We concentrate on the entanglement process of polymers in narrow (d = 2–4 μm) asymmetric channels, by studying the dynamics of two entangling actin polymers in narrow confinements. We find that when two polymers within a rectangular channel diffuse into the same vicinity, they can become trapped together indefinitely if their crossover length is above a certain critical length L*. Upon entrapment, the horizontal movement of one polymer is entrained by the second, resulting in correlated fluctuations, accompanied by dampened translational motion. Furthermore, we are able to measure the deflection length for both the one- and two-polymer cases, exhibiting that a polymer also undergoes a conformational rearrangement upon entrapment with another polymer.

Materials and methods

Microfluidics platform

Using standard lithography methods, we have fabricated microfluidic devices that consist of primary flow channels (height h₁ = 5 μm) connected with diffusion-controlled rectangular channels (h₂ = 0.5 μm, width = 2–4 μm, length = 120 μm).¹⁰ Silicon wafers coated with SU-8 negative photoresist are used to create the design, which is then embossed in polydimethylsiloxane (PDMS) to create complementary channels that are then plasma-sealed to glass slides. Experiments are conducted by continuously pumping monomeric actin solution (3 μM) through the main channel of the microfluidic device (Fig. 1). The actin polymers are visualized using an Atto488-tagged monomeric actin, which is combined with monomeric actin in a 1 : 5 ratio. In order to prevent the actin adsorption to the walls of the PDMS device, we first flush the device with bovine serum albumin (BSA 1 mg mL⁻¹, Sigma Aldrich, Switzerland). The device is submerged in water before and during the experiments to avoid permeation-driven flow through the PDMS walls.

Fig. 1 (a) Sketch of the microfluidics system consisting of a main channel with height h₁ = 5 μm connected via a diffusion interface (blue) to narrow confinements with a height h₂ = 0.5 μm and width d = 2–4 μm. A solution of actin is flowed through the main channel, but only actin monomers can diffuse into the confinement areas where they then polymerize into filaments. (b) Inverted images of fluorescent actin polymers inside a narrow channel (i) a single polymer, (ii) two short entangled polymers, (iii) two long entrapped polymers, and (iv) many entrapped polymers.

Actin polymerization

Monomeric actin derived from rabbit skeletal muscle is purchased as a lyophilized powder (Hypermol EK, Germany). It is dissolved in Millipore water to produce a stock solution of 4 mg mL⁻¹. The stock solution consists of 95.2 μM actin, 8 mM Tris-Cl (pH 8.2), 1.6 mM ATP, 2 mM dithioreitol (DTT), 0.4 mM CaCl₂ and 0.8% disaccharides. Fluorescence microscopy is used to visualize the actin filaments, thus fluorescently labeled Atto488 G-actin (Hypermol EK, Germany) is mixed with non-fluorescent actin in a 1 : 5 ratio. A monomix dilution buffer (Hypermol EK, Germany), containing 2 mM Tris-Cl (pH 8.2), 0.4 mM ATP, 0.1 mM CaCl₂ and 0.5 mM DTT, is used to obtain an overall actin concentration of 3 μM. To instigate the polymerization process of G-actin into filamentous actin, Polymix buffer (Hypermol EK, Germany), containing 1 M KCl, 0.1 M imidazole (pH 7.4), 10 mM ATP and 20 mM MgCl₂, is added to the actin solution in a 1 : 9 ratio, according to the protocol recommended by Hypermol. The actin solution is pumped at a constant rate into the main channel using syringe pumps (neMESYs low pressure syringe pump, Cetoni GmbH, Germany) through a 100 μL syringe (Hamilton, Switzerland), which is connected with the microfluidic device via appropriate tubing (polytetrafluoroethylene (PTFE) microtube).

Microscopy and image analysis

Actin polymerization and dynamics are observed with an Olympus IX81 inverted microscope equipped with fluorescence illumination (X-Cite Series 120 Q). A 100× (N.A. 1.49) UApo N oil immersion objective is used for all experiments. Images of actin polymers are recorded with a PCO Edge SensiCam (PCO AG, Germany) at frame rates up to 200 Hz and exposure times ranging from 4 to 25 ms. We observe the projection of the actin polymers in the focal plane of the microscope. For a single polymer, the fluctuations occurring in the focal plane are decoupled from the ones occurring in the perpendicular plane, thus we can treat them independently and analyze the polymer projection in a two-dimensional manner.^11,12 As the number of polymers within the channel increases, it is possible that the fluctuations in the z-direction of one polymer could be coupled with fluctuations occurring in the perpendicular plane due to the increasing density of polymers. However, since we have focused on analyzing either one or two polymer(s), we have analyzed their 2D projections for consistent comparison between the two cases. Furthermore, when two polymers are observed crossing over one another, their 2D projections have the same coordinates at the crossover positions, but in reality they are less likely to be directly interacting (Δz < 0.5 μm, actin filament diameter = 8 nm^13,14). All actin image sequences are analyzed using Matlab (R2012a, The MathWorks Inc., USA).

Results and discussions

Evolution of entangled solutions

To study the dynamics of entangled actin solutions in a flow-free and diffusion-controlled environment we have designed and fabricated a multi-height microfluidics device. The microfluidics system consists of a main channel with a height h₁ = 5 μm, connected with confinement areas that are considerably smaller in height h₂ = 0.5 μm. Since the height of the main channel is ten-fold larger than that of the connecting confinements, we create a diffusion interface between the two (Fig. 1a), due to the large hydraulic resistance of the connecting confinements. Therefore, we are able to flow a solution of monomeric actin, including the cations and ATP necessary for in vitro polymerization (but not for bundling), through the main channel, whereby they will diffuse into the connecting confinements and polymerize into filaments. Previous work has validated that the confinements are flow-free.^10,15

In the beginning, the confinement areas are completely filled with only monomeric actin, which over time polymerizes to form filaments (Fig. 1b(i)). Interestingly, in many circumstances when two polymers are present in the channel and reptate into the same vicinity, they can become trapped together and continue polymerizing (Fig. 1b(ii–iii)). As more polymers nucleate and grow they are also incorporated into the entangled solution, forming a densely packed polymeric arrangement (Fig. 1b(iv)). In general, when a continuous supply of G-actin is flowed through the main channel, most connecting narrow channels are filled with entangled actin solutions (>3 filaments) after 4–5 hours, as seen in Fig. 1b(iv). In this study, we have chosen to focus on the preceding time periods where we can capture the movement of one or two actin filaments within the same channel. From these fluorescence images we are able to accurately track the 2D projections of either a single polymer or two polymers and correlate these projections over time.

Entrapment of two polymers

To follow the entrapment process of two polymers in a narrow channel, we record their movement at a frame rate of 0.15 Hz as they become trapped together (Video S1, ESI†). By plotting the y-coordinates along the length of each polymer and the overlap length between the two, we notice that as the polymers are trapped their translational motion appears to dampen (Fig. 2a). It is important to note that we have captured a dynamic process and the actin filaments are continuously polymerizing throughout the time lapse. At a certain time, the polymers' overlap length exceeds a critical length L* and they can no longer completely separate from each other. If the length L of either of the polymers is less than L*, then they can move completely past one another without becoming permanently trapped together. We find that L* increases with the channel width d (Fig. 2b). The existence of a threshold crossover length presumes that there could be a weak attractive force between the polymers that augments with greater overlap, eventually leading to their indefinite entrainment.

Fig. 2 (a) Kymograph showing the end-to-end length of two entrapping polymers (red and blue) versus time. y_i represents every y position along the channel occupied by a polymer, thus at a given time t, the difference between the maximum y_i and minimum y_i for a given polymer (red or blue) is equal to the end-to-end length. The overlap length L_o between the two polymers is shown in green. At a certain time the overlap length exceeds a critical length L* and the polymers remain entrapped indefinitely. The inlaid plot shows the length of each polymer over the time lapse of the kymograph. (b) A plot of the critical length versus the channel width d. (c) The linear fits for the MSD of a polymers center of mass in the lateral direction versus time for the one- (red, triangles) and two-polymer (blue, circles) cases (d = 2 μm); the data is averaged from five separate experiments in each case.

Decreased translational diffusion

In separate experiments, we have recorded the motion of a single polymer and two trapped polymers, each with a contour length L ≃ 10 μm, at a faster frame rate (25 Hz), enabling the determination of a translational diffusion. For each case the center of mass of a single polymer only in the lateral direction was considered. Motion in the perpendicular direction is a reflection of wriggling between the confining boundaries and can be neglected. Several data sets showing the mean squared displacement (MSD) of the polymer's center of mass in a narrow channel confirm that the lateral diffusion is significantly decreased for the two-polymer case (Fig. 2c). Given the relation for one-dimensional diffusion 〈(y_t)²〉 = 2Dt, where y is the step size, and D is the diffusion constant, we can calculate the diffusion constant for each scenario. We find that the diffusion constant for the one-polymer case D₁ ≃ 0.9 μm² s⁻¹ (L = 10 μm, d = 2 μm), which is on the same scale as values measured for actin polymers in semi-dilute entangled solutions.¹⁶ On the other hand, the diffusion constant calculated for the two-polymer case, D₂ ≃ 0.37 μm² s⁻¹ (L = 10 μm, d = 2 μm), is approximately half of the value in the one-polymer case. It is possible that the raw MSD data, especially in the two-polymer case could also be described with slightly sub-diffusive behavior, though we have chosen to fit each data set as if it follows classical Brownian motion, primarily to show the difference between the diffusion for each of the two cases. That way, the polymer's lateral diffusion can also be compared to previous studies, which have measured the lateral diffusion of a polymer within entangled solutions.^16,17 If we take into account the relation, ξD = k_BT,^18,19 where ξ is the friction coefficient and k_B is Boltzmann's constant, we see that there could be a virtual increase in friction to account for the decreased diffusion constant in the two-polymer case (when we refer to the one- and two-polymer cases, we are always considering a single confined polymer, either solitary or in the presence of a second entangled polymer, respectively). We can estimate the ratio of the friction coefficients ξ₂ : ξ₁ ≃ 2.4 for the two-versus the one-polymer case, respectively. Two entangled polymers in a narrow channel display a mesh size similar to that of a highly concentrated entangled solution. For instance, if a single polymer within a channel mimics the tube model for a polymer within a semi-dilute solution, then two polymers within the same channel would decrease the polymers' effective tube diameter, relating to a more concentrated entangled solution. In polymer theory, concentrated solutions of semiflexible polymers can be described using rigid rod models, however, it is interesting to note that the opposite effect is seen for stiff rods, which display increased diffusion with increasing concentration.^20,21 Thus the phenomena we observe must be unique to semiflexible polymers.

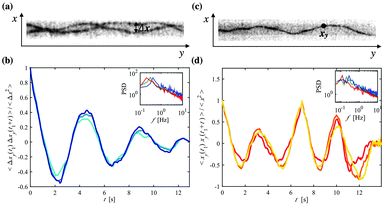
Correlated horizontal undulations

A decreased translational motion of two trapped polymers in a narrow asymmetric confinement is accompanied by a synchronization of their wriggling movement. The distance separating two trapped polymers Δx (Fig. 3a and Video S2, ESI†) is a measure that quantifies their positional correlation over time. We have chosen to measure Δx as a function of y because it is a value that can be accurately determined for a large number of images. Furthermore, as all polymers are tagged with the same fluorescent dye, it is often difficult to distinguish which polymer is crossing over which in a 2D fluorescent image, making Δx an ideal measure because it does not depend on the z position of either polymer. Specifically, we define Δx as the difference between the x positions of two entrapped polymers at a given position y along the channel. We have calculated the autocorrelation function of Δx for two trapped polymers with L > 20 μm, 〈Δx_y(t₁) Δx_y(t₁ + t)〉/〈Δx²〉 [averaged over t₁] and have seen that Δx oscillates from being highly correlated to highly anti-correlated during a time frame of several seconds (Fig. 3b). As the polymers wriggle between the confining channel walls, Δx is cyclically increasing and then decreasing, which explains why we see a periodicity in the autocorrelation function.

Fig. 3 (a) A fluorescent image of two entangled polymers in a narrow channel (d = 4 μm), denoting the distance between the two polymers Δx. (b) The autocorrelation function of Δx at three different y positions: y_i, y_i + 2 μm, and y_i + 5 μm (d = 4 μm). An inlaid plot shows the power spectra for three separate data sets on a log–log scale. (c) A fluorescent image of a single polymer confined in a narrow channel (d = 4 μm), denoting one position x_y. (d) The autocorrelation function of x at three different y positions: y_i, y_i + 2 μm, and y_i + 5 μm (d = 4 μm), averaged over t₁. An inlaid plot shows the power spectra for three separate data sets on a log–log scale.

For different lateral positions y_i the period of the autocorrelation function of Δx is nearly constant for a given experiment; here we have shown a few examples within the range of actin's persistence length (∼10–15 μm^22,23). The power spectra show the peaks that correspond to the dominant frequency of the oscillations of 〈Δx_y(t₁) Δx_y(t₁ + t)〉/〈Δx²〉 (Fig. 3b inlay), which reveal an average frequency around 0.5 Hz and have no significant dependency on the channel width. Upon looking at the autocorrelation of the x position over time for a single polymer, 〈x_y(t₁) x_y(t₁ + t)〉/〈x²〉 [averaged over t₁] (Fig. 3c and d and Video S3, ESI†), we find that the frequency of the undulations of x show a normal distribution centered around 0.5 Hz, almost similar to the frequency distribution found for Δx.

Conformational rearrangement

Not only does the entrapment of two polymers lead to an entrainment of one polymer by the other, but it also causes a change in their organization. A parameter that characterizes the conformation of a confined polymer is the deflection length λ, a measure describing the interplay between the bending and the confinement free energies. Odijk defines λ as the distance along a polymer between two points of contact with a surrounding tube with a radius D, and has shown that it scales in the following way with D and the persistence length P, λ ≃ D^2/3P^1/3.²⁴ The polymers in our system are confined within a rectangular channel of width d rather than a circular tube, though we will show that Odijk's predicted scaling can be applied to our measured deflection length that we will call Λ.

If we consider the cross-correlation function of the polymer's x position between position y_i and a subsequent position y_i + Δy, 〈x_y(t₁) x_y+Δy(t₁ + t)〉/〈Δx²〉, we see a shift τ_shift in time where the maximum value occurs. As Δy increases, τ_shift, or the time at which the cross-correlation function reaches a maximum, will continue to increase until reaching a maximum when the two x positions are separated by a distance Δy = Λ (Fig. 4a and c). On the other hand, Λ can be determined for two trapped polymers by calculating the cross-correlation function of Δx between y_i and y_i + Δy, 〈Δx_y(t₁) Δx_y+Δy(t₁ + t)〉/〈Δx²〉. In this case, when τ_shift falls back to a minimum, Δy is equal to Λ (Fig. 4b and d). Thus, contrary to the single polymer case, Δy = Λ/2 when τ_shift reaches a maximum, and the lag time of the cross-correlation function is at a maximum. It is important to note that this method depends on the correlation of the polymers' movement, otherwise Λ would approach infinity. For a number of data sets, for both the one- and the two-polymer cases, we can see a distribution of τ_shift as we increase the distance Δy (Fig. 4e and f) and we find that the maximum τ_shift and consequently Λ are shifted to the right with increasing channel width. Considering first a single confined polymer, we find that Λ follows the same scaling predicted by Odijk with the inclusion of a numerical prefactor, Λ₁ ≃ Cd^2/3P^1/3, where C ≃ 2.2. The Λ values measured in the two-polymer case again follow Odijk's scaling, however they are always a factor greater than Λ₁, leading to the incorporation of another prefactor, Λ₂ ≃ αCd^2/3P^1/3, where α ≃ 1.2 (Fig. 5). An increased Λ value upon the entanglement of two polymers could be interpreted as an augmented polymer rigidity or a virtual increase in P since the enclosing boundary dimensions (d) remain constant.

Fig. 4 (a) Sketch of a single confined polymer, noting the deflection length Λ. The cross-correlation function of the polymer's x position will show a maximum value at the greatest time lag τ_shift for the two y positions denoted by red and green dots where Δy = Λ; whereas, τ_shift will be at a minimum for the two y positions denoted by red dots, where Δy = Λ. (b) Sketch of two entangled confined polymers, pointing out that the cross-correlation of Δx reaches a maximum τ_shift when Δy = Λ/2, corresponding to the red and green dots; and τ_shift will be at a minimum when Δy reaches Λ, corresponding to the two red dots. (c) The normalized cross-correlation function of x between the position y_i and the following positions: y_i + 2 μm (green), y_i + 5 μm (red), y_i + 7 μm (blue), y_i + 12 μm (yellow), y_i + 15 μm (dashed blue), y_i + 20 μm (dashed red), and y_i + 25 μm (dashed green), for d = 4 μm. The peaks corresponding to the time lag τ_shift are noted. (d) The normalized cross-correlation function of Δx between the position y_i and the following positions: y_i + 1 μm (green), y_i + 3 μm (red), y_i + 5 μm (blue), y_i + 7 μm (yellow), and y_i + 9 μm (dashed blue), y_i + 11 μm (dashed red), y_i + 13 μm (dashed green), for d = 4 μm. (e) The distribution of τ_shift for different Δy, for d = 2 μm (red, squares), d = 3 μm (blue, circles), and d = 4 μm (green, triangles), for the single polymer case, where the maximum occurs when Δy = Λ. (f) The same distribution of τ_shift, but for the two-polymer case, where the maximum τ_shift occurs when Δy = Λ/2.

Fig. 5 (a) A double logarithmic plot of the measured deflection length Λ versus the channel width d, exhibiting Odijk's predicted scaling, Λ ∼ d^2/3, for the one- (blue) and the two-polymer (red) cases. (b) Sketch showing the extension of Λ when a polymer is entrapped with a second polymer.

Nonetheless, the transition from the one- to the two-polymer case can be quantified in terms of a change in free energy. Following the scaling arguments of Odijk, the free energy ΔF_c per unit length of confinement is given by ΔF_c ≃ k_BT/d^2/3P^1/3.^6,24,25 Expressing this equation in terms of Λ enables us to estimate that the free energy of confinement would decrease upon the entrapment of two polymers by a factor of 1/α. It should be noted that in both cases we are considering the free energy of a single polymer, either alone or in the presence of a second trapped polymer. According to the formulations made by Odijk,²⁴ we can approximate the cost of free energy per length segment λ of a confined polymer as approximately k_BT. The presence of a second polymer in narrow confinement leads to an increase in the deflection length Λ, thereby decreasing the overall free energy per unit length of the polymer. Thus we can infer that the polymer adopts an extended configuration in the presence of a second trapped polymer in order to minimize its overall free energy of confinement. Furthermore, given the decrease in free energy it is plausible that weak attractive forces play a role in favoring the entrainment of two polymers above critical overlap length scales within confining boundaries. Hydrodynamic and van der Waals interactions offer possible sources for the weak attraction observed. Contrary to our results, the entrapment of two polymers should lead to a decrease in their effective tube diameters, which is associated with a decrease in Λ. Although we are able to show that the two-polymer entrapment scenario yields deflection lengths that follow Odijk's scaling, our results are counterintuitive when considering the effective entropic diameter of the polymers. If however, we consider that weak interactions occur between the two polymers, then the deflection length is found to increase for reasons other than the tube diameter; and therefore, it is possible that our results cannot be entirely explained by previous theories, which had not taken these interactions into account.

Conclusions

Our findings demonstrate that strong asymmetric confinement can significantly affect the motion and conformation of entangled polymer solutions. Interestingly, we find that the entrapment interactions between two polymers are caused by long-range interactions, thus only the geometric boundaries, rather than bundling agents or cross-linking proteins, can lead to the synchronized motion and the arrangement of the polymers. On that account, we suggest that the entropic limitations imposed on two interacting polymers leads to stiffening, through an increased deflection length, and weak attractive forces give rise to a decrease in free energy and to prolonged entrapment interactions. While we have alluded to the presence of long-range interactions, future experiments or rather simulations are necessary to explore the exact nature of the long-range interactions. Furthermore, we have examined the entrainment process between two polymers, though more work is required to uncover the changing dynamics when multiple polymers or additional actin binding proteins are incorporated into the entangled solution. In the scope of in vitro reconstituted biological systems, we conclude that semiflexible polymers can behave alone as dynamical signaling elements, responding exclusively to changes in their geometrical boundaries.

Acknowledgements

We thank Thomas Kampmann and Jan Kierfeld for fruitful discussions. Financial support by the Swiss National Science Foundation (SNF_ 200020_141270) is gratefully acknowledged.

References

1. A. R. Bausch and K. Kroy, Nat. Phys., 2006, 2, 231.
2. C. P. Broederz and F. C. MacKintosh, Rev. Mod. Phys., 2014, 86, 995.
3. P. G. de Gennes, Macromolecules, 1976, 9, 587.
4. S. Köster, J. Kierfeld and T. Pfohl, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 25, 439.
5. W. Reisner, K. J. Morton, R. Riehn, Y. M. Wang, Z. Yu, M. Rosen, J. C. Sturm, S. Y. Chou, E. Frey and R. H. Austin, Phys. Rev. Lett., 2005, 94, 196101.
6. T. W. Burkhardt, Y. Yang and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041801.
7. A. Muralidhar, D. R. Tree and K. D. Dorfman, Macromolecules, 2014, 47, 8446.
8. A. Liu, D. L. Richmond, L. Maibaum, S. Pronk, P. L. Geissler and D. A. Fletcher, Nat. Phys., 2008, 4, 789–793.
9. A. Reymann, J. Martiel, T. Cambier, L. Blanchoin, R. Boujemaa-Paterski and M. Théry, Nat. Mater., 2010, 9, 827.
10. S. Deshpande and T. Pfohl, Biomicrofluidics, 2012, 6, 034120.
11. S. Köster and T. Pfohl, Cell Motil. Cytoskeleton, 2009, 66, 771.
12. B. Nöding and S. Köster, Phys. Rev. Lett., 2012, 108, 088101.
13. R. A. Milligan, M. Whittaker and D. Safer, Nature, 1990, 348, 217.
14. E. Grazi, C. Schweinbacher and E. Magri, Biochem. Biophys. Res. Commun., 1993, 197, 1377.
15. S. Deshpande and T. Pfohl, PLoS One, 2015, 10, e0116521.
16. J. Käs, H. Strey and E. Sackmann, Nature, 1994, 368, 226.
17. J. Käs, H. Strey, J. X. Tang, D. Finger, R. Ezzell, E. Sackmann and P. A. Janmey, Biophys. J., 1996, 70, 609.
18. M. von Smoluchowski, Ann. Phys., 1906, 326, 756.
19. A. Einstein, Ann. Phys., 1905, 322, 549.
20. M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, Oxford, 1986.
21. M. P. Lettinga, J. K. G. Dhont, Z. Zhang, S. Messlinger and G. Gomper, Soft Matter, 2010, 6, 4556.
22. L. Blanchoin, R. Boujemaa-Paterski, C. Sykes and J. Plastino, Physiol. Rev., 2014, 94, 235.
23. M. Harasim, B. Wunderlich, O. Peleg, M. Kröger and A. Bausch, Phys. Rev. Lett., 2013, 110, 108302.
24. T. Odijk, Macromolecules, 1983, 16, 1340.
25. L. Auvray, J. Phys. (Orsay Fr.), 1981, 42, 473–477.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of any supplementary information available should be included here. See DOI: 10.1039/c5sm02304a

‡ Present address: Laboratory of Biological Network Characterization, EPFL, 1015 Lausanne, Switzerland.

§ Present address: Department of Bionanoscience, Delft University of Technology, 2628 CJ Delft, The Netherlands.

---