Mechanism for the stabilization of protein clusters above the solubility curve†
James F.
Lutsko
* and
Grégoire
Nicolis
Center for Nonlinear Phenomena and Complex Systems, Université Libre de Bruxelles, Code Postal 231, Blvd. du Triomphe, 1050 Brussels, Belgium. E-mail: jlutsko@ulb.ac.be
First published on 21st September 2015
Abstract
Pan, Vekilov and Lubchenko [J. Phys. Chem. B, 2010, 114, 7620] have proposed that dense stable protein clusters appearing in weak protein solutions above the solubility curve are composed of protein oligomers. The hypothesis is that a weak solution of oligomer species is unstable with respect to condensation causing the formation of dense, oligomer-rich droplets which are stabilized against growth by the monomer–oligomer reaction. Here, we show that such a combination of processes can be understood using a simple capillary model yielding analytic expressions for the cluster properties which can be used to interpret experimental data. We also construct a microscopic Dynamic Density Functional Theory model and show that it is consistent with the predictions of the capillary model. The viability of the mechanism is thus confirmed and it is shown how the radius of the stable clusters is related to physically interesting quantities such as the monomer–oligomer rate constants.
1 Introduction
Proteins in solution demonstrate a surprisingly rich variety of phenomena, many of which have biological implications. These include liquid–liquid separation (e.g. protein rich droplets forming in a weak solution), crystallization and gelation.1 Perhaps most surprising is the relatively recent discovery of the existence of protein clusters having a typical, stable size and long lifetime that have been found to exist under a wide variety of conditions including those for which no condensed phases are stable.2–4 There is abundant evidence that these clusters play an important role in protein crystallization5–7 and it has been suggested that they play a similar role in the formation of protein aggregates that are actors in pathologies such as hemoglobin polymers in sickle cell anemia and fibrils of misfolded proteins that underlie various neurological disorders.8 Thus, understanding their origin and nature is of importance for both fundamental and practical reasons.The existence of stable clusters at some place in the phase diagram is intriguing. A subcritical droplet of a condensed phase should, by definition, evaporate whereas a supercritical droplet should grow until all available material is incorporated. Multiple droplets can compete with one another for the available material slowing down the growth process during the so-called ripening stage, until only very large droplets remain. Coalescence of droplets can also contribute to this outcome. However, the experimental evidence indicates that for the protein clusters whatever ripening is occuring is not consistent with the predictions of the classical theories.9 While there are possible mechanisms for the stabilization of clusters, e.g. a competition between short-ranged dispersion forces and long-ranged screened-Coulomb repulsion as seen in colloids10 or micelle formation, these seem to be ruled out by experiment.8 Furthermore, a mechanism involving impurities – such as Kohler theory – would require that the dense-protein phase be thermodynamically favored and this is specifically not the case for the conditions of interest here.
Recently, Vekilov and co-workers proposed that the stable protein clusters might not be composed of the native protein but, rather, of some complex formed from them such as an oligomer or a mis-folded monomer.8,9,11 Their idea was that in the original, weak protein solution the new species is in equilibrium with the protein monomer but that the phase diagram of the new species is such that a condensed phase is favored so that super-critical clusters (e.g. oligomer-rich droplets) can form. However, since the density of the secondary species within the clusters would be well above the concentration for chemical equilibrium with the monomer, there would be a tendency for the secondary species to convert back to monomers within the cluster thus impeding its growth. If one adds the assumption that excluded volume effects prevent a high monomer concentration within the droplet (which could also lead to a stable chemical equilibrium between the two species) then a possible mechanism for stabilization is apparent. Although this idea has motivated further experimental work, little has been done to formalize it theoretically. The goal of this paper is to do so at two levels. First, the stabilization problem will be considered phenomenologically using concepts from Classical Nucleation Theory (CNT).12 This will result in simple analytic expressions for the size of the stable clusters as a function of the properties of the original solution and of the concentration and pressure of the secondary species. This analytic relation opens up the door to the determination of these properties from the experiment. Our second contribution is the formulation of a detailed Dynamic Density Functional Theory (DDFT) model based on the same assumptions and is used to confirm the phenomenological predictions while providing a more fundamental means of investigating the nature of the clusters.
2 Phenomenology
For the sake of concreteness, we will assume that the secondary population is composed of dimers. All of the subsequent development can be trivially adapted to other possibilities. We then begin by postulating a simple mass-balance reaction model for the conversion of monomers into dimers and vice versa. Denoting the monomer number density n1 and the dimer density n2 this takes the form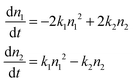 | (1) |
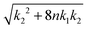 .
.
Now, let us consider a pure solution of dimers and we assume that conditions are such that the fluid nucleates a dense phase. In the capillary approximation used in CNT, it is assumed that the density inside a cluster having radius R is constant, n2(r < R) = n(0)2 and equal to the density of the homogeneous, condensed phase, while the density outside the cluster n2(r > R) = n(∞)2 is also constant. In this case, the rate of growth of a sufficiently large supercritical cluster is, under the diffusion-limited conditions expected to dominate for macromolecules in solution, given by ref. 13
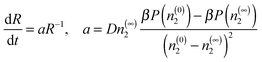 | (2) |
Now, let us consider the effect of adding monomers to the picture. Outside the cluster, the monomers and dimers will reach equilibrium so we have that k1n(∞)21 = k2n(∞)2. We assume that the monomers and dimers have no interaction aside from excluded volume effects. In this case adding monomers to the cluster increases its free energy so that one expects the monomers to be expelled by diffusion leading to the hypothesis that the monomer concentration inside the cluster is very low, n(0)1 ≃ 0. Clearly, the realization of this condition will depend on diffusion being sufficiently fast compared to the rate of production of the monomers. In terms of the dimer concentration within the cluster, the net effect (conversion of dimers into monomers and expulsion of the monomers) is a simple extinction reaction that lowers the total number of dimers, 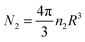 , according to dN2/dt = −k2N2. Since the free energy of the cluster will be minimized by maintaining a dimer density near that of the thermodynamically stable condensed phase, this leads to a reduction in the size of the cluster given by dR/dt = −k2R/3.
, according to dN2/dt = −k2N2. Since the free energy of the cluster will be minimized by maintaining a dimer density near that of the thermodynamically stable condensed phase, this leads to a reduction in the size of the cluster given by dR/dt = −k2R/3.
The combined effect of the reaction and of diffusion gives an evolution equation for the radius of the form
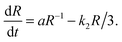 | (3) |
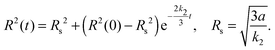 | (4) |
These expressions link accessible experimental quantities such as the cluster size and the rate of relaxation of the system to the parameters governing the model. In particular, they in principle give experimental access to the rate constants since one expects the exterior dimer concentration, n(∞)2, to be in equilibrium with the monomer concentration outside the droplet (k1n(∞)21 = k2n(∞)2) so that the measurement of the respective concentrations, together with knowledge of k2, allows the determination of k1 and thus complete characterization of the reaction between the two species.
3 Microscopic model
To test these ideas, we now describe a microscopic model that incorporates the growth of a super-critical droplet and the excluded volume interaction of the monomer and dimer species. Our approach is based on Dynamic Density Functional Theory (DDFT) which is commonly used to describe the dynamics of over-damped systems (such as colloids and macromolecules in solution) under conditions such that thermal fluctuations may be ignored.14–16 In DDFT, the fundamental quantity is the time-dependent local density (or equivalently, concentration) n(r;t). The diffusion-limited growth of a super-critical droplet in a pure solution of dimers (i.e. with no monomers present) is governed by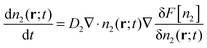 | (5) |
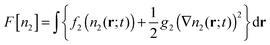 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n2Λ3 − n2 so that the left hand side of the DDFT equation reduces to D2∇2n2, i.e. it becomes the diffusion equation. Thus, one may think of DDFT as a generalization of the diffusion equation that accounts for particle interactions.
n2Λ3 − n2 so that the left hand side of the DDFT equation reduces to D2∇2n2, i.e. it becomes the diffusion equation. Thus, one may think of DDFT as a generalization of the diffusion equation that accounts for particle interactions.
To generalize to two species, the free energy functional is replaced by one depending on the local densities of both species, F[n1,n2], and a second DDFT equation is included for n1. In the present case, we must also include the chemical reactions thus giving
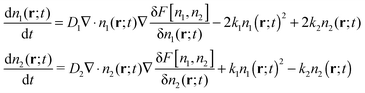 | (7) |
Finally, the form of the free energy functional must be specified. Since the monomers are supposed to be above their critical point, we simply treat them as hard spheres with hard-sphere diameter d so as to account for excluded volume effects. The final form we employ is
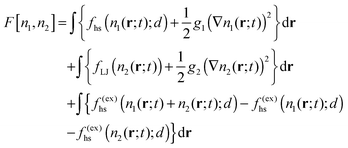 | (8) |
The third line accounts for the mutual excluded volume interaction of the two species: we treat both as hard spheres of diameter d and replace their individual hard-sphere contributions to the excess free energy by one dependent on the sum of the local densities. (Note that the excess part of the free energy is just f(ex) = f − f(id): we only replace the excess part because the ideal contributions are already accounted for.) If either density is zero, this interaction term vanishes. Of course, a dimer with twice the mass of a monomer and the same density would have a diameter about 25% larger but for simplicity we ignore this relatively small difference. Similarly, we take g1 = g2 = gLJ and D1 = D2 since we expect the differences in these coefficients to be of no physical importance. A final simplification is that we do not include a cross term involving the gradients. This model is a generalization of the model used by Huberman to discuss the appearance of striations in a reacting system.20 Huberman's model was constructed in the approximation of a single active reactant with an autocatalytic chemical reaction out of equilibrium. Here, the presence of two species participating in an equilibrium reaction is fully accounted for. This necessarily requires adding an additional contribution to the free energy and, most importantly, the third line in eqn (8) which accounts for the most basic excluded-volume interaction of the two species. Note that in this setting the conservation condition n1 + 2n2 = const. no longer holds locally.
The Lennard-Jones potential introduces a length scale, σ, and an energy scale ε. In the following, temperature will be reported in the scaled units T* = kBT/ε and all lengths will be scaled by σ. We also take the hard-sphere diameter d = σ: typical prescriptions such as Barker–Henderson21 change this by a few percent but for present purposes this difference is unimportant. A time scale, τ, is introduced such that D2τ/σ2 = 1. After scaling, the available parameters are the monomer background density, the dimer supersaturation, the scaled temperature and the scaled reaction coefficient k1*. The dimer reaction constant is determined via the equilibrium condition 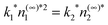 . We report the results here for T* = 0.8 and supersaturation n(∞)2/n(coex)2 = 2 where n(coex)2 is the vapor density coexisting at this temperature. Under these conditions the density in the vapor is
. We report the results here for T* = 0.8 and supersaturation n(∞)2/n(coex)2 = 2 where n(coex)2 is the vapor density coexisting at this temperature. Under these conditions the density in the vapor is 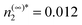 and in the condensed phase n2* = 0.85. The background monomer density is taken to be 5 times that of the dimer phase. In reality, this ratio is thought to be much greater8 but the computational cost of the calculation increases with this ratio so our choice represents a compromise. The only remaining parameter is k1* which is discussed below.
and in the condensed phase n2* = 0.85. The background monomer density is taken to be 5 times that of the dimer phase. In reality, this ratio is thought to be much greater8 but the computational cost of the calculation increases with this ratio so our choice represents a compromise. The only remaining parameter is k1* which is discussed below.
Our calculations were performed assuming spherical symmetry with boundary conditions appropriate for an open system (see ESI† for technical details). We began by locating the critical cluster for the pure dimer system. With the chosen parameters, this has radius Rc* = 5.2. We then make this supercritical by increasing its radius, an amount ΔR, and then adding in the monomers. Further details are given in the ESI† of the numerical algorithms used to integrate the DDFT equations. Also discussed there are the question of the definition of the radius to be used for comparing the capillary model to the DDFT and the agreement between the two theories for the case of the growth of a super-critical droplet in a single-component system.
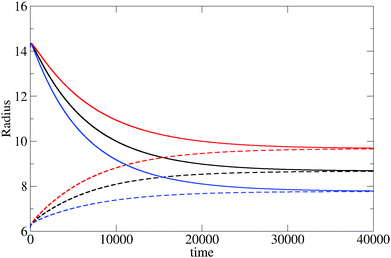
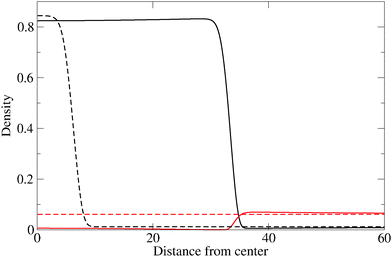
The evolution of the cluster radius for three different values of the reaction constant is shown in Fig. 1. In each case, two initial displacements are used: an “under” displacement of one unit (broken lines) and an “over” displacement of 9 units (full lines). The fact that the under- and over-displaced clusters evolve into the same final cluster is strong empirical evidence for the stability of the final cluster. The structure of the stable cluster is shown in Fig. 2 where it can be seen that most of the monomer species is expelled from the cluster except in the interfacial region.
The scaling relationship between the stable radius and the reaction constant k2* predicted by the capillary model, eqn (4), is tested against the numerical DFT results in Fig. 3. For lower values of the dimensionless reaction coordinate, there are significant deviations as is to be expected since the capillary model is only accurate for large clusters. As the reaction rate decreases, and the size of the stable cluster increases, convergence to the prediction is evident.
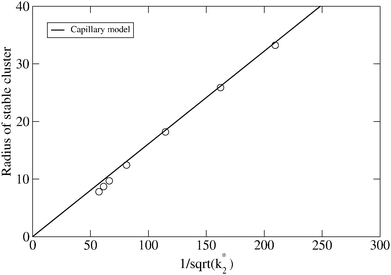 | ||
Fig. 3 Predicted stable radius from the capillary model, eqn (4), compared to the results of numerical integration of the DFT model (symbols) as a function of 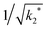 . With these variables, the prediction is simply a straight line. . With these variables, the prediction is simply a straight line. | ||
4 Conclusions
We have shown that super-critical clusters, which would otherwise be unstable with respect to growth, can be stabilized by means of the combined effect of diffusion and a chemical reaction. Diffusion – driven by thermodynamics – leads to the purification of the cluster so as to lower its free energy. The purified cluster is then in turn subjected to degradation due to the conversion of the dimer species to monomers. This dynamic process can be successfully described by a simple capillary model as well as more systematically investigated by means of a microscopic Dynamic Density Functional Theory model. The two approaches were shown to be in agreement. While these results were necessarily achieved for specific choices of molecular interactions and, particularly, for a specific chemical reaction, it is clear that the arguments may be trivially adapted to other choices. We also note that we used relatively simple squared-gradient free energy functionals and that, while more complex functionals that more fully incorporate the molecular potentials are available,16 we do not believe that their use would change the results in any qualitative manner.The microscopic DDFT model presented here is a natural generalization of the standard reaction-diffusion model used to describe chemical reactions in spatially extended systems. The crucial element in our formulation of this generalization is the free energy functional and particularly the interaction term given in the third line of eqn (8). The free energy contribution can be viewed as giving rise to a density-dependent diffusion constant which, for the condensed phase, is negative thus driving growth of a cluster rather than its diffusive evaporation as in ordinary diffusion. The interaction term in the free energy is critical in that it leads to a monomer diffusion constant that increases with increasing density of dimers thus causing expulsion of the monomers from the dimer cluster. This leads to a locally frozen nonequilibrium steady state in which a current of dimers flows into the cluster where they are converted into monomers and expelled in the form of a corresponding outward current. In this state growth of the droplet and the conversion of species are mutually quenched. Since such a nonequilibrium state cannot persist indefinitely without a driving force (due e.g., to mode-coupling effects not considered in the over-damped limit used here ref. 13), the clusters are not expected to be stable indefinitely. Furthermore, shape fluctuations are also likely to prove destabilizing since any deviation from a spherical shape will lower the thermodynamic driving force for growth and potentially lead to irreversible shrinking of the cluster to a size below the critical radius. Finally, as mentioned earlier, in the results presented here the system is actually treated as an open system spatially infinite, continually replenished by monomers and coupled implicitly to an infinite solvent13 that acts as a reservoir. This further postpones the establishment of a global equilibrium throughout.
We conclude with several observations concerning this mechanism. First, there is no constraint on the free energy of the stable droplet since the only requirement is that it should be larger than the critical cluster. It could therefore have a free energy nearly as high as that of the critical cluster (leading to a relatively low number of such droplets in equilibrium) or it could have an arbitrarily low free energy (leading to a large population).
Second, we have assumed that when the reaction removes dimers the density of the cluster remains constant so that the net effect is that the cluster shrinks in size. This only makes physical sense if the reaction is in some sense slow compared to the process of removing monomers from the cluster (i.e. diffusion). When this is not the case, monomers would quickly build up within the cluster and poison it leading to its collapse. In this context, it is also worth noting that this differs slightly from the original proposal in ref. 8, 9 and 11. There, it is stated that there will be an influx of monomers which are then preferentially converted into dimers thus leading to a depleted monomer density. However, we believe that this neglects to take into account that the effect of the excluded volume will produce a diffusive tendency to reduce the densities to their background values. For the dimers, this is counter-acted by the thermodynamic tendency of the cluster to grow but for the monomers, lacking this element, the effect can only be to lower their density as confirmed by the DDFT calculations (see also ESI†).
Third, we note the generality of the mechanism leading to a stable cluster with a characteristic size: a force driving growth that scales more slowly than a force opposing growth. Regardless of the mechanisms giving rise to the forces, these are the required elements. Clusters in other systems could be stabilized by some other combination of growth-promoting and -opposing forces provided the relative scaling satisfies this rule.
Fourth, one can contrast this mechanism to that of the stabilizing vesicles. The latter consist of a volume with amphiphilic molecules arranged on their surface so that their hydrophobic parts are inside the volume, shielded from water, while their hydrophilic parts are on the outside of the surface, exposed to the water. Within the vesicle could be void, more of the amphiphilic molecules or some other substance. If the interior has a higher free energy than the solution, the vesicle can be stabilized in the same manner as proposed above: the surface dominates the free energy of small vesicles leading to growth while the volume dominates large vesicles leading to dissolution. However, in the case of vesicles there is another factor: such a system can increase its surface to volume ratio, and hence decrease its free energy, by becoming non-spherical (by becoming flat, in the extreme limit). In our case, the free energy is minimized by a spherical shape so that the mechanism favors the formation of spherical clusters.
Fifth, there is no scope within this model for ripening: i.e. the growth of larger clusters at the expense of smaller ones. Something like ripening has in fact been reported by Li et al.9 albeit with the unusual feature that the ripening stops while there is still a finite population of clusters. If the present model were correct, this “ripening” would have to be reinterpreted: perhaps as a slowly relaxing transient. As stated above, the reaction must be slow compared to diffusion, as is reflected in the small dimensionless reaction constants used in our work, and this could simply result in very slow dynamics for the entire system. Alternatively, it is possible that the dimer to monomer reaction is suppressed within the cluster (due to the high free energy barrier involved in removing a dimer from the condensed phase) and that the reaction is most productive only in the boundary of the cluster (where the dimer is in an energetically unfavorable state). In this case, the reaction term in eqn (3) would be a constant rather than scaling as R (in fact, R would be replaced by the characteristic width of the boundary region) and this would lead to algebraic rather than exponential relaxation of the cluster to its stable size. To capture this, the model could be modified by replacing the concentrations in the rate equations with more general expressions involving the chemical affinities. Such an algebraic dynamics combined with small reaction constants could well give transients that decay very slowly and could therefore be interpreted as a transient ripening.
This is related to our sixth and final point. We mentioned above that for consistency, we should replace the concentrations appearing in the chemical reaction kinetics by the corresponding activities, ni(r,t) → n(0)i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(βμi(r,t) − βμi) where the local chemical potential is
exp(βμi(r,t) − βμi) where the local chemical potential is 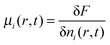 and where μi is the chemical potential for species i in the homogeneous system in which ni(r,t) = n(0)i. This has not been used in the present work in order to explore the consistency of the simple capillary model with the microscopic model in the case that the relationship between the two is most straightforward. We conjecture that the effect of the use of the activities will be a suppression of the dimer to monomer reaction within the cluster and an enhancement of the importance of the reaction in the interfacial region, therefore possibly leading to the scenario alluded to above of an algebraic rather than exponential relaxation. Preliminary calculations using the activities support this and this issue will be discussed fully in a future publication.
and where μi is the chemical potential for species i in the homogeneous system in which ni(r,t) = n(0)i. This has not been used in the present work in order to explore the consistency of the simple capillary model with the microscopic model in the case that the relationship between the two is most straightforward. We conjecture that the effect of the use of the activities will be a suppression of the dimer to monomer reaction within the cluster and an enhancement of the importance of the reaction in the interfacial region, therefore possibly leading to the scenario alluded to above of an algebraic rather than exponential relaxation. Preliminary calculations using the activities support this and this issue will be discussed fully in a future publication.
Acknowledgements
This work was supported in part by the European Space Agency under contract number ESA AO-2004-070. The authors thank Peter Vekilov for numerous conversations on this subject and Pierre Gaspard for useful comments concerning the model.References
- J. D. Gunton, A. Shiryayev and D. L. Pagan, Protein Condensation: Kinetic Pathways to Crystallization and Disease, Cambridge University Press, Cambridge, 2007, p. 376 Search PubMed.
- W. Pan, O. Galkin, L. Fibobelo, R. L. Nagel and P. G. Vekilov, Biophys. J., 2007, 92, 267–277 CrossRef CAS PubMed.
- O. Gliko, N. Neumaier, W. Pan, I. Haase, M. Fischer, A. Bacher, S. Weinkauf and P. G. Vekilov, J. Am. Chem. Soc., 2005, 127, 3433–3438 CrossRef CAS PubMed.
- O. Gliko, W. Pan, P. Katsonis, N. Neumaier, O. Galkin, S. Weinkauf and P. G. Vekilov, J. Phys. Chem. B, 2007, 111, 3106–3114 CrossRef CAS PubMed.
- P. G. Vekilov, Cryst. Growth Des., 2004, 4, 671 CAS.
- J. F. Lutsko and G. Nicolis, Phys. Rev. Lett., 2006, 96, 046102 CrossRef PubMed.
- M. Sleutel and A. E. S. V. Driessche, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E546–E553 CrossRef CAS PubMed.
- W. Pan, P. G. Vekilov and V. Lubchenko, J. Phys. Chem. B, 2010, 114, 7620–7630 CrossRef CAS PubMed.
- Y. Li, V. Lubchenko, M. A. Vorontsova, L. Filobelo and P. G. Vekilov, J. Phys. Chem. B, 2012, 116, 10657 CrossRef CAS PubMed.
- A. Stradner, H. Sedgwick, F. Cardinaux, W. C. K. Poon and S. U. Egelhaaf, Nature, 2004, 432, 492 CrossRef CAS PubMed.
- Y. Li, V. Lubchenko and P. G. Vekilov, Rev. Sci. Instrum., 2011, 82, 053106 CrossRef PubMed.
- D. Kashchiev, Nucleation: basic theory with applications, Butterworth-Heinemann, Oxford, 2000 Search PubMed.
- J. F. Lutsko, J. Chem. Phys., 2012, 136, 034509 CrossRef PubMed.
- U. M. B. Marconi and P. Tarazona, J. Chem. Phys., 1999, 110, 8032 CrossRef CAS.
- A. J. Archer and R. Evans, J. Chem. Phys., 2004, 121, 4246 CrossRef CAS PubMed.
- J. F. Lutsko, Adv. Chem. Phys., 2010, 144, 1–92 CrossRef CAS.
- R. Evans, Adv. Phys., 1979, 28, 143 CrossRef CAS.
- J. F. Lutsko, J. Chem. Phys., 2011, 134, 164501 CrossRef PubMed.
- J. K. Johnson, J. A. Zollweg and K. E. Gubbins, Mol. Phys., 1993, 78, 591–618 CrossRef CAS.
- B. A. Huberman, J. Chem. Phys., 1976, 65, 2013–2019 CrossRef CAS.
- J. A. Barker and D. Henderson, J. Chem. Phys., 1967, 47, 4714 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm02234g |
| This journal is © The Royal Society of Chemistry 2016 |