A master dynamic flow diagram for the shear thickening transition in micellar solutions

Abstract

The shear thickening behavior of dilute micellar solutions of hexadecyltrimethylammonium-type surfactants with different counterions (tosylate, 3- and 4-fluorobenzoate, vinylbenzoate and salicylate) and of n-alkyltetradecylammonium bromide (C_nTAB), with n = 14, 16 and 18, is examined here. These solutions undergo a shear thickening transition due to the formation of shear-induced structures (SISs) in the shear range studied. Here we report a relationship between the shear thickening intensity and the differences in the hydrophobicity of counterions according to the Hofmeister-like anion series, which leads to a master flow diagram. This master flow diagram is produced by plotting a normalized shear thickening intensity (I_η − 1)/(I_max − 1) versus C_D/C_D,max, where I_η is the shear-thickening intensity, defined as the largest viscosity obtained in the shear-thickening transition (STT) at a given surfactant concentration C_D divided by the Newtonian viscosity η₀, and I_max is the largest intensity value obtained in the STT at a surfactant concentration C_D,max. The master flow diagram is built using several cetyltrimethylammonium-type surfactants with different counterions, according to a Hofmeister-like series, and by n-alkyltetradecylammonium bromide surfactants with different alkyl chain lengths.

---

Introduction

Micellar solutions are complex fluids that exhibit a fascinating rheological behavior in the dilute, semi-dilute and concentrated regimes.^1,2 In the dilute regime, shear thickening develops above a critical shear rate ([small gamma, Greek, dot above]_c) after an induction time (t_i); this induction time lasts from seconds to minutes and becomes shorter as the applied shear rate departs from [small gamma, Greek, dot above]_c.³ In the semi-dilute and concentrated regimes in which polymer-like (or wormlike) micelles form, the rheological response is controlled by either reptation (slow-breaking regime) or by breaking-and-recombination (fast-breaking regime).⁴ In the last case, Maxwell behavior with a single relaxation time is commonly observed in linear viscoelastic measurements, whereas shear-banding flow appears between two critical shear rates in nonlinear rheological measurements.^1,2

Most of the research on shear thickening behavior has been performed with cationic surfactants in the presence of inorganic electrolytes^5–9 or of salts containing strongly binding counterions such as salicylate or tosylate.^5,10–13 The reason is that micellar growth in ionic surfactant solutions is promoted by electrostatic screening that reduces the repulsion between the charged polar heads upon addition of electrolytes¹⁴ or by the reduction of the micellar surface charge-density by adding salts with strongly binding counterions.^15,16 As a consequence, the presence of electrolytes decreases the concentration at which rod-like micelles develop, cmc₂, and the overlap concentration, c*, which have a strong effect on the shear thickening transition (STT) in dilute micellar solutions.^17,18

Few works have been reported on electrolyte-free ionic micellar solutions. The early work of Hoffmann and co-workers with hexadecylpyridinium salicylate (CPyS)¹⁹ and tetradecyltrimethylammonium salicylate (TTAS)²⁰ demonstrated that these micellar solutions showed shear thickening behavior and viscoelasticity at low concentrations in the absence of electrolytes or other additives. Several reports on the STT of electrolyte-free cationic surfactants micellar solutions have appeared.^21–26

Sometime ago, Berret et al.²⁷ proposed a generalized flow phase diagram for micellar solutions for which shear-banding flow develops. In this diagram, in which the shear-stress divided by the plateau modulus (σ/G₀) is plotted against the shear-rate times the main relaxation time ([small gamma, Greek, dot above]τ_R), the flow curves overlap at low normalized shear rates, i.e., [small gamma, Greek, dot above]τ_R < 1; at higher normalized shear rates, a stress plateau forms that shifts to larger values of the normalized shear stress with increasing temperature or surfactant concentration. This generalized flow diagram has been reported for other micellar solutions as a function of surfactant concentration or temperature.^25,28,29

For shear thickening micellar systems, however, few attempts to describe a generalized relationship have been presented in the literature. Hu et al. reported kinetic studies of micellar solutions of tetradecyldimethylammonium oxide (TMADO) mixed with sodium dodecyl sulfate (SDS) that exhibit slow viscosity build-up and follow time-dependent stress growth upon application of a shear stress, probing changes in the microstructure with optical methods. They found that the unusually slow stress build-up occurs only when the applied shear rate exceeded a critical value above which shear thickening occurs.³⁰ Prötzl and Springer reported that three stages conformed the SIS formation: induction, aggregations and orientation and, more interestingly, that the time needed to reach the orientation stage minus the induction time (t_o − t_i) was independent of the applied shear-rate to induce shear-thickening.³¹ Oda et al. observed that γ_c strongly depended on the gap distance of the Couette cell employed, which ruled out the SIS phenomenon as a phase transition.³²

More recently, we examined the shear thickening behavior of cetyltrimethylammonium tosylate (CTAT) micellar solutions as a function of surfactant concentration and ionic strength using electrolytes with different counterion valence, and found that the shear thickening diminishes with increasing surfactant concentration and ionic strength.³³ From those results we proposed a generalized master flow-diagram that indicated two controlling regimes: one in which electrostatic screening dominates and induces micellar growth, and another at higher surfactant and electrolyte concentration, where chemical equilibrium among surfactant counterions and electrolyte ions controls the rheology by altering micellar breaking and recombination. More interestingly, in that paper we proposed a Hofmeister-like series of headgroups together with a predictive theory of interactions between different types of ions and head-groups.³³

In this paper, a master flow diagram for shear thickening micellar solutions is obtained by plotting the normalized shear intensity, (I_η − 1)/(I_max − 1), versus the normalized surfactant concentration, C_D/C_D,max, for surfactants with the same hydrophobic tail (C₁₆) and head (trimethylammonium) but different counterions (tosylate, vinylbenzoate, salicylate and fluorobenzoate) as well as for surfactants of n-alkyltetradecylammonium bromide (C_nTAB), with n = 14, 16 and 18; all of them were examined at several surfactant concentrations. Here I_η = η/η₀, I_max being the largest intensity value obtained in the STT at a surfactant concentration, C_D,max.

Experimental section

Hexadecyltrimethylammonium tosylate (CTAT), 99% pure from Sigma, was re-crystallized from a chloroform (Aldrich) solution prior to experiments. Hexadecyltrimethylammonium salycilate (CTAS), hexadecyltrimethylammonium vinylbenzoate (CTAVB), hexadecyltrimethylammonium 3-fluorobenzoate (CTA3FB) and hexadecyltrimethylammonium 4-fluorobenzoate (CTA4FB) were synthesized as reported elsewhere.^25,34,35 Samples were prepared by weighing the appropriate amounts of surfactant and water in 20 ml glass vials, homogenized and placed in a temperature-controlled chamber at 30 °C for a week before performing the rheological tests. Diluting a 0.1 wt% stock surfactant solution produced samples with smaller concentrations.

Steady and transient shear rate measurements were performed at 30 °C in an ARES strain-controlled rheometer, using a double wall Couette geometry with bob internal and outer diameters of 29.5 and 32 mm, respectively; cup: D_i = 27.94 cm, D_o = 34 cm, and a humidification chamber to minimize water losses by evaporation. For CTA3FB, steady and transient rheological measurements were carried out in a stress-controlled ARG2 rheometer from TA Instruments with a parallel plate geometry of 60 mm in diameter. The rheological data of the n-alkyltetradecylammonium bromide (C_nTAB) surfactants with an equimolar ratio of sodium salicylate added were taken from Dehmoune et al.^36,37

Results and discussion

Fig. 1 depicts the apparent shear viscosity as a function of [small gamma, Greek, dot above] for CTAT and CTAVB; in this figure three concentrations of these two surfactants were included. The plots are similar but shear thickening occurs at lower shear rates in CTAVB solutions compared to the CTAT ones, which (as shown below) is the consequence of the ordering of the counterions according to the Hofmeister series proposed by us elsewhere.³³ The plots exhibit similar characteristics, mainly that (1) the zero-shear rate viscosity, η₀, increases with surfactant concentration, (2) when the applied shear rate becomes equal or exceeds γ_c, η begins to increase after an induction time, t_i, has elapsed, and (3) the rise ends in another plateau that decreases at larger shear rates, signaling the onset of the shear thinning regime.

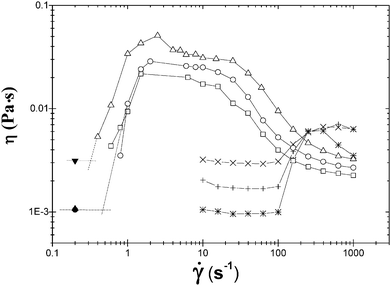Fig. 1 Apparent shear viscosity versus shear rate measured at 30 °C at different surfactant concentrations for CTAT: (*) 0.2, (+) 0.6 and (×) 0.8 wt%; CTAVB: (□) 0.03, (○) 0.05 and (△) 0.1 wt%.

It has been documented for several cationic surfactant micellar systems, which exhibit the STT, that their induction time, t_i, obeys a power law-dependence with the shear rate of the form [small gamma, Greek, dot above] ∼ t_i^−m, where 1 ≤ m ≤ 2;^2,3,30,35 however, no dependence of t_i with the normalized alkyl chain length of the surfactants, |l| = l_n/l_C14, has been reported as far as we know; here, we choose the tail length of the C₁₄ surfactant l_C14 for the normalization procedure. Fig. 2 depicts a plot of t_iversus the normalized alkyl chain length of the alkyltetradecylammonium bromide surfactants examined. This figure reveals that the induction time increases almost linearly with tail length, although dispersion of data is apparent. Only three surfactants were examined because the C₁₂ surfactant does not form rod like micelles and it does not exhibit shear-thickening;^36,37 and the C₂₀ surfactant cannot exhibit the shear thickening transition probably because this surfactant tends to form hexagonal liquid crystals instead of wormlike micelles and, in fact, no reports on SISs using this surfactant have appeared in the current literature a far as we know.

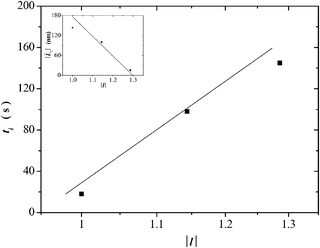Fig. 2 Induction-time versus normalized alkyl chain-length for the C_nTAB surfactants. Inset: Estimated average micellar length versus the normalized alkyl chain-length of the C_nTAB surfactants.

To understand the growth behavior from short to large wormlike micelles, we invoke the mean-field theory of the micellar growth process for neutral or highly screened micelles. This theory predicts the average contour-length of the wormlike micelles (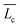) in terms of surfactant concentration (c) and the scission energy required to produce two hemispherical end caps (E_c) as 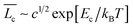.³⁸ For charged micelles in the absence of electrolytes, the scission energy has an additional electrostatic component, E_e, due to the repulsion of the charges along the backbone that favors shorter cylindrical micelles. For this situation, the mean size in the semi-dilute regime is 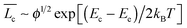with E_e expressed as E_e ∼ k_BTl_Br_csν²ϕ^1/2. Here, l_B is the Bjerrum length, r_cs the radius of the cylindrical micelles, ν the effective charge per unit length, and ϕ the micellar volume-fraction. For the series of alkyltetradecylammonium bromide surfactants examined, the tail length of the alkyl chain is related to r_csvia the electrostatic contribution to E_c since all of them have the same head. Hence, following the arguments given by Schubert et al.,³⁹ as the surfactant tail length increases, E_e augments as well, diminishing the net contribution of E_c and thus reducing the micellar length 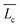. This tendency is observed in the inset of Fig. 2 where the estimated average micellar length (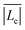) versus the normalized alkyl chain length of the C_nTAB surfactants is depicted. This inset reveals that the average length of the wormlike micelles decreases almost linearly with tail length. Furthermore, according to the kinetics of breaking and recombination of wormlike micelles developed by Cates,⁴⁰ the times for breaking and recombination in our systems are expected to be similar and inversely proportional to the average length of the micelles; hence, such times can be related to t_i. A further examination of Fig. 2 and its inset reveals that indeed, t_i diminishes with the average micellar length.

Fig. 3 depicts the shear thickening intensity, I_η, versus surfactant concentration, C_D, for all surfactants examined here, i.e., CTAT, CTAS, CTAVB, CTA3FB, CTA4Fb and C_nTAB (with n = 14, 16 and 18). For each surfactant, I_η first increases, reaches a maximum and then it decreases at larger surfactant concentrations, attaining values of one for some of the systems, indicating the disappearance of the STT.

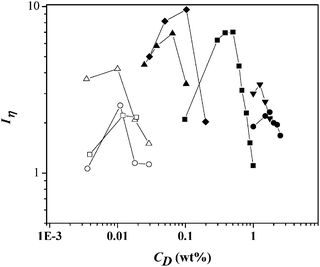Fig. 3 Shear-thickening intensity as a function of surfactant concentration for micellar solutions containing: CTAT (closed square), CTAVB (closed diamond), CTA3FB (closed inverted triangle), CTA4FB (closed circle), CTASal (closed triangle), and data adapted from Dehmoune et al.:^36,37 C₁₄TAB (open triangle), C₁₆TAB (open circle), and C₁₈TAB (open square).

The concentration range where the shear thickening region appears largely depends on the surfactant type (see Fig. 3). Depending on the counterion structure for the hexadecyltrimethylammonium-type surfactants, the I_η curves shift to larger concentrations in the counterions' order: S⁻ < VB⁻ < T⁻ < 3FB⁻ < 4FB⁻, which suggest that 4FB⁻ and 3FB⁻ are hydrophobic anions according to the Hofmeister series and that they only promote the growth of the surfactant aggregates by reducing the electrostatic repulsion among the surfactant head-groups. These hydrophobic anions stay at the surface of the surfactant aggregates rather than penetrating into the hydrophobic core, allowing strong electrostatic repulsions between the surfactant headgroups at the interface and consequently increasing the curvature of the micelle surface and the cmc values.^9,34 At the other end of the series, S⁻, VB⁻ and T⁻ bind very strongly, i.e., they penetrate into the hydrophobic core, which results in smaller cmc values and in a larger micellar surface curvature, inducing micellar growth and the formation of long wormlike micelles at substantially lower surfactant concentrations.^25,34 It is noteworthy the screening effect of the sodium salicylate added to the alkyltetradecylammonium bromide (C_nTAB) surfactants that shifts the I_η curves to lower concentration than the one exhibited by CTAS.

The trend of the surfactant counterions of hexadecyltrimethylammonium-type surfactants reported in Fig. 3 can be explained by applying the concept of matching water affinities proposed by Collins⁴¹ and the surfactant head group's Hoffmeister series reported by Vlachy et al.⁴² Following the Hofmeister's approach, ions have been classified according to their relative abilities to change the structure of surrounding water molecules into kosmotropes (structure makers) or chaotropes (structure breakers). Vlachy and co-workers propose the same classification for the surfactant head groups and the counterions.⁴² Following Collins' concept, chaotrope head groups can form direct ion pairs with other chaotrope counterions, similar to kosmotrope head-groups with other kosmotrope counterions. But chaotropes do not come into close contact with kosmotropes counterions. According to matching water affinities, the surfactant head group CTA⁺ is considered chaotrope, the counterions S⁻, VB⁻, and T⁻ can also be classified as chaotropes, whereas the counterions 3FB⁻ and 4FB⁻ can be considered as kosmotropes.⁴² Israelachvilli's packing parameters were calculated for the surfactants reported in Fig. 3 according to v/l_ca₀, where v is the volume of the hydrocarbon chain in the surfactant, l_c is the critical chain length and a₀ is optimal surface area per molecule.³⁸ Values of the packing parameters obtained for the CTA-counterion surfactants were 0.49, 0.46, 0.38, and 0.37, for CTASal, CTAVB, CTAT, CTA3FB, respectively; and for all the C_nTAB were 0.37. The packing parameters fall in the range 1/3 < v/l_ca₀ < 1/2 that corresponds to the formation of cylindrical micelles. Since large packing parameters correspond to small optimal surface area for surfactants of the same chain length, Fig. 3 reveals that for surfactants with smaller a₀, higher concentrations are required for the SIS to occur. Once again, the screening effect of the sodium salicylate added to the alkyltetradecylammonium bromide (C_nTAB) surfactants is evident from the shifting to smaller I_ηs; however, the I_η curves for C_nTAB are shifted to lower concentration than the one exhibited by CTASal.

Data shown in Fig. 3 for the different surfactants and concentrations employed can be comprised in a master flow diagram (Fig. 4) by plotting the normalized shear intensity, (I_η − 1)/(I_max − 1), versus the normalized surfactant concentration, C_D/C_D,max. Within experimental error, all data collapse in the shear thickening region where C_D/C_D,max ≤ 1. A similar plot was reported elsewhere for CTAT solutions with several electrolytes.³³Fig. 4 was built accordingly because it allows defining the mechanism that controls the shear thickening transition, i.e., micellar growth by electrostatic screening or micellar scission or branching and/or scission-reformation due to chemical equilibrium among surfactant molecules, as detailed elsewhere.³³ Notice that smaller surfactant concentrations of the chaotrope counterions are needed compared to those of the kosmotrope counterions, as a consequence of the arguments given above.

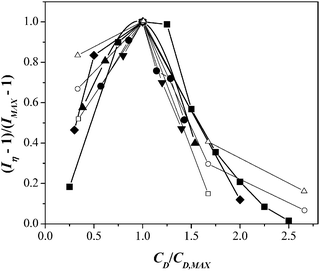Fig. 4 Generalized diagram of normalized shear-thickening intensity as a function of normalized surfactant concentration for micellar solutions containing CTAT (closed square), CTAVB (closed diamond), CTA3FB (closed inverted triangle), CTA4FB (closed circle), CTASal (closed triangle), and data adapted from Dehmoune et al.:^32,33 C₁₄TAB (open triangle), C₁₆TAB (open circle), and C₁₈TAB (open square).

Conclusions

Here we report the shear thickening behavior of electrolyte-free micellar solutions of hexadecyltrimethylammonium-type surfactants with different counterions (tosylate, vinylbenzoate, salicylate, and 3- and 4-fluorobenzoate) to examine the effect of the counterion as well as of n-alkyltetradecylammonium bromide with different alkyl chain length to elucidate the influence of the alkyl chain length upon the shear thickening development in the dilute regime. The STT induction time and the magnitude of the viscosity growth as a function of shear rate depend strongly on the surfactant concentration, counterion type and alkyl chain length. Moreover, the critical shear rate for the viscosity growth can be correlated with surfactant concentration. The induction time decreases strongly with the shear rate when the surfactant concentration is fixed, according to a power law. The induction time of the C_nTAB surfactants increases almost linearly with surfactant tail length and diminishes with the average wormlike micellar length. This behavior is expected according to the mean field theory and the kinetics of breaking and recombination of the micellar growth process. According to the intensity of shear thickening, we propose that the hydrophobicity of the counterions can be qualitatively determined by rheological measurements and by the fact that the counterions studied here follow a Hofmeister-like sequence. Furthermore, shear-thickening data for all the systems reported here fall into a single curve in a master flow diagram of normalized shear thickening intensity as a function of normalized surfactant concentration.

Acknowledgements

We thank the support of CONACYT (grants no. CB-2014-235880, 25463, 38681E/9869 and 25463).

References

1. J. F. Berret, Rheology of wormlike micelles: Equilibrium properties and shear banding transitions, in Molecular gelsm, ed. R. Weiss and P. Terech, Springer, Netherlands, 2006, pp. 667–720 DOI:10.1007/1-4020-3689-2_20.
2. J. Puig, F. Bautista, J. Soltero and O. Manero, Nonlinear rheology of giant micelles, in Gigant miceles, ed. E. W. Kaler and R. Zana, CRC Press, 2007, pp. 289–322 DOI:10.1201/9781420007121.ch9.
3. J. Puig, J. Escalante, J. Soltero, F. Bautista and O. Manero, Rheological behavior of dilute micellar solutions, in Encyclopedia of surface and colloid sciencein, ed. P. Somasundaran, Taylor & Francis, 2012 DOI:10.1081/E-ESCS-120047408.
4. M. Cates and S. Fielding, Theoretical rheology of gigant miceles, in Gigant miceles, ed. E. W. Kaler and R. Zana, CRC Press, 2007, pp. 109–162. DOI:10.1201/9781420007121.ch4.
5. V. Hartmann and R. Cressely, Simple salts effects on the characteristics of the shear thickening exhibited by an aqueous micellar solution of ctab/nasal, Europhys. Lett., 1997, 40, 691,  DOI:10.1209/epl/i1997-00524-7.
6. Y. Hu, C. Rajaram, S. Wang and A. Jamieson, Shear thickening behavior of a rheopectic micellar solution: Salt effects, Langmuir, 1994, 10, 80–85,  DOI:10.1021/la00013a012.
7. E. Macías, F. Bautista, J. Pérez-López, P. Schulz, M. Gradzielski, O. Manero, J. Puig and J. Escalante, Effect of ionic strength on rheological behavior of polymer-like cetyltrimethylammonium tosylate micellar solutions, Soft Matter, 2011, 7, 2094–2102,  10.1039/C0SM00739K.
8. C. Oelschlaeger, G. Waton, E. Buhler, S. Candau and M. Cates, Rheological and light scattering studies of cationic fluorocarbon surfactant solutions at low ionic strength, Langmuir, 2002, 18, 3076–3085,  DOI:10.1021/la015687v.
9. M. Truong and L. Walker, Controlling the shear-induced structural transition of rodlike micelles using nonionic polymer, Langmuir, 2000, 16, 7991–7998,  DOI:10.1021/la0006263.
10. V. Hartmann and R. Cressely, Influence of sodium salicylate on the rheological behaviour of an aqueous ctab solution, Colloids Surf., A, 1997, 121, 151–162,  DOI:10.1016/S0927-7757(96)03773-9.
11. V. Hartmann and R. Cressely, Shear thickening of an aqueous micellar solution of cetyltrimethylammonium bromide and sodium tosylate, J. Phys. II, 1997, 7, 1087–1098,  DOI:10.1051/jp2:1997173.
12. V. Hartmann and R. Cressely, Occurrence of shear thickening in aqueous micellar solutions of ctab with some added organic counterions, Colloid Polym. Sci., 1998, 276, 169–175,  DOI:10.1007/s003960050225.
13. W. J. Kim and S.-M. Yang, Microstructures and rheological responses of aqueous ctab solutions in the presence of benzyl additives, Langmuir, 2000, 16, 6084–6093,  DOI:10.1021/la991086g.
14. J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, Theory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568,  10.1039/F29767201525.
15. P. Hassan, S. R. Raghavan and E. W. Kaler, Microstructural changes in sds micelles induced by hydrotropic salt, Langmuir, 2002, 18, 2543–2548,  DOI:10.1021/la011435i.
16. P. Hassan and J. Yakhmi, Growth of cationic micelles in the presence of organic additives, Langmuir, 2000, 16, 7187–7191,  DOI:10.1021/la000517o.
17. C. Oelschlaeger, G. Waton, S. Candau and M. Cates, Structural, kinetics, and rheological properties of low ionic strength dilute solutions of a dimeric (gemini) surfactant, Langmuir, 2002, 18, 7265–7271,  DOI:10.1021/la025645m.
18. M. F. Torres, J. M. González, M. R. Rojas, A. J. Müller, A. E. Sáez, D. Löf and K. Schillén, Effect of ionic strength on the rheological behavior of aqueous cetyltrimethylammonium p-toluene sulfonate solutions, J. Colloid Interface Sci., 2007, 307, 221–228,  DOI:10.1016/j.jcis.2006.11.002.
19. D.-C. H. Rehage and H. Hoffmann, Shear induced phase transitions in highly dilute aqueous detergent solutions, Progress and trends in rheology, Springer, 1982, pp. 207–209 DOI:10.1007/BF01534347.
20. I. Wunderlich, H. Hoffmann and H. Rehage, Flow birefringence and rheological measurements on shear induced micellar structures, Rheol. Acta, 1987, 26, 532–542,  DOI:10.1007/BF01333737.
21. J. F. Berret, R. Gamez-Corrales, S. Lerouge and J. P. Decruppe, Shear-thickening transition in surfactant solutions* New experimental features from rheology and flow birefringence, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 2, 343–350,  DOI:10.1007/s101890050016.
22. J. F. Berret, S. Lerouge and J. P. Decruppe, Kinetics of the shear-thickening transition observed in dilute surfactant solutions and investigated by flow birefringence, Langmuir, 2002, 18, 7279–7286,  DOI:10.1021/la011471h.
23. R. Gamez-Corrales, J. F. Berret, L. Walker and J. Oberdisse, Shear-thickening dilute surfactant solutions* Equilibrium structure as studied by small-angle neutron scattering, Langmuir, 1999, 15, 6755–6763,  DOI:10.1021/la990187b.
24. E. Mac&inodot;as, F. Bautista, J. Soltero, J. Puig, P. Attané and O. Manero, On the shear thickening flow of dilute ctat worm-like micellar solutions, J. Rheol., 2003, 47, 643–658,  DOI:10.1122/1.1562479.
25. J. Soltero, J. Alvarez-Ramirez, V. Fernández, N. Tepale, F. Bautista, E. Macías, J. Pérez-López, P. Schulz, O. Manero and C. Solans, Phase and rheological behavior of the polymerizable surfactant CTAVB and water, J. Colloid Interface Sci., 2007, 312, 130–138,  DOI:10.1016/j.jcis.2006.08.001.
26. V. Weber and F. Schosseler, Shear-thickening in salt-free aqueous solutions of a gemini cationic surfactant: A study by small angle light scattering, Langmuir, 2002, 18, 9705–9712,  DOI:10.1021/la026253i.
27. J. F. Berret, G. Porte and J.-P. Decruppe, Inhomogeneous shear flows of wormlike micelles: A master dynamic phase diagram, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 1668,  DOI:10.1103/PhysRevE.55.1668.
28. J. Escalante, E. Macias, F. Bautista, J. Pérez-López, J. Soltero, J. Puig and O. Manero, Shear-banded flow and transient rheology of cationic wormlike micellar solutions, Langmuir, 2003, 19, 6620–6626,  DOI:10.1021/la034052o.
29. V. Fernández, N. Tepale, J. Alvarez, J. Pérez-López, F. Bautista, F. Pignon, Y. Rharbi, R. Gámez-Corrales, O. Manero and J. Puig, Rheology of the Pluronic 103/water system in a semidilute regime: Evidence of nonequilibrium critical behavior, J. Colloid Interface Sci., 2009, 336, 842–849,  DOI:10.1016/j.jcis.2009.02.064.
30. Y. Hu, S.-Q. Wang and A. H. Jamienson, Kinetics Studies of a Shear Thickening Micellar Solution, J. Colloid Interface Sci., 1993, 156, 31–37.
31. B. Prötzl and J. Springer, Light Scattering Experiments on Shear Induced Sturctures of Micellar Solutions, J. Colloid Interface Sci., 1997, 190, 327–333.
32. R. Oda, P. Panniza, M. Schmutz and F. Lequeux, Direct Evidence of the Shear-Induced Structure of Wormlike Micelles: Gemini Surfactant 12 – 2 – 12, Langmuir, 1997, 13, 6407–6413.
33. N. Tepale, E. Macías, F. Bautista, J. Puig, O. Manero, M. Gradzielski and J. Escalante, Effects of electrolyte concentration and counterion valence on the microstructural flow regimes in dilute cetyltrimethylammonium tosylate micellar solutions, J. Colloid Interface Sci., 2011, 363, 595–600,  DOI:10.1016/j.jcis.2011.07.051.
34. J. Alfaro, G. Landázuri, A. González-Álvarez, E. Macías, V. Fernandez, P. Schulz, J. Rodríguez and J. Soltero, Phase and rheological behavior of the hexadecyl (trimethyl) azanium; 2-hydroxybenzoate/water system, J. Colloid Interface Sci., 2010, 351, 171–179,  DOI:10.1016/j.jcis.2010.07.038.
35. G. Landazuri, E. Macias, V. Fernandez, J. Escalante, L. Perez-Carrillo, J. Alvarez, P. Schulz, Y. Rharbi, J. Puig and J. Soltero, On the shear thickening behavior of micellar aqueous solutions of cetyltrimethylammonium fluorobenzoates: Effect of the fluor position, Colloids Surf., A, 2013, 436, 10–17,  DOI:10.1016/j.colsurfa.2013.05.076.
36. J. Dehmonue, J.-P. Decruppe, O. Greffier and H. Xu, Rheometric and rheo-optical investigation of the effect of the aliphatic chain length of the surfactant on the shear thickening of dilute worm-like micellar solutions, Rheol. Acta, 2006, 46, 1121–1129,  DOI:10.1007/s00397-007-0206-7.
37. J. Dehmonue, J.-P. Decruppe, O. Greffier and H. Xu, Rheometric investigation of the temporal shear thickening of dilute micellar solutions of C₁₄-, C₁₆- and C₁₈TAB/NaSal, J. Rheol., 2007, 52, 923–940,  DOI:10.1122/1.2933352.
38. J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, London, 1991.
39. B. A. Schubert, E. W. Kaler and N. J. Wagner, The Microestructure and Rheology of Mixed Cationic/Anionic Wormlike Micelles, Langmuir, 2003, 19, 4079–4089.
40. M. E. Cates, Reptation of Living Polymers: Dynamics of Entangled Polymers in the Presence of Reversible Chain-Scission Reactions, Macromolecules, 1987, 20, 2289–2296.
41. K. D. Collins, Ions from the hofmeister series and osmolytes: Effects on proteins in solution and in the crystallization process, Methods, 2004, 34, 300–311,  DOI:10.1016/j.ymeth.2004.03.021.
42. N. Vlachy, B. Jagoda-Cwiklik, R. Vácha, D. Touraud, P. Jungwirth and W. Kunz, Hofmeister series and specific interactions of charged headgroups with aqueous ions, Adv. Colloid Interface Sci., 2009, 146, 42–47,  DOI:10.1016/j.cis.2008.09.010.

---