Open Access Article
Open Access ArticleMultitechnique investigation of Dy3 – implications for coupled lanthanide clusters†
Maren
Gysler
a,
Fadi
El Hallak
b,
Liviu
Ungur
 c,
Raphael
Marx
a,
Michael
Hakl
d,
Petr
Neugebauer
a,
Yvonne
Rechkemmer
a,
Yanhua
Lan
e,
Ilya
Sheikin
d,
Milan
Orlita
d,
Christopher E.
Anson
e,
Annie K.
Powell
ef,
Roberta
Sessoli
g,
Liviu F.
Chibotaru
c and
Joris
van Slageren
*a
c,
Raphael
Marx
a,
Michael
Hakl
d,
Petr
Neugebauer
a,
Yvonne
Rechkemmer
a,
Yanhua
Lan
e,
Ilya
Sheikin
d,
Milan
Orlita
d,
Christopher E.
Anson
e,
Annie K.
Powell
ef,
Roberta
Sessoli
g,
Liviu F.
Chibotaru
c and
Joris
van Slageren
*a
aInstitut für Physikalische Chemie, Universität Stuttgart, Pfaffenwaldring 55, 70569 Stuttgart, Germany. E-mail: slageren@ipc.uni-stuttgart.de
b1. Physikalisches Institut, Universität Stuttgart, Pfaffenwaldring 57, 70569 Stuttgart, Germany
cTheory of Nanomaterials Group, Katholieke Universiteit Leuven, Celestijnenlaan 220F, 3001 Leuven, Belgium
dLaboratoire National des Champs Magnétiques Intenses (LNCMI-EMFL), CNRS, UGA, 38042 Grenoble, France
eInstitut für Anorganische Chemie, Karlsruhe Institute of Technology (KIT), Engesserstr. 15, 76131 Karlsruhe, Germany
fInstitut für Nanotechnologie, Karlsruhe Institute of Technology (KIT), Postfach 3640, D-76021 Karlsruhe, Germany
gDipartimento di Chimica Ugo Schiff, Università degli Studi di Firenze, Via della Lastruccia 3-13, 50019 Sesto Fiorentino, Italy
First published on 16th March 2016
Abstract
In-depth investigations of the low energy electronic structures of mononuclear lanthanide complexes, including single molecule magnets, are challenging at the best of times. For magnetically coupled polynuclear systems, the task seems well nigh impossible. However, without detailed understanding of the electronic structure, there is no hope of understanding their static and dynamic magnetic properties in detail. We have been interested in assessing which techniques are most appropriate for studying lanthanide single-molecule magnets. Here we present a wide ranging theoretical and experimental study of the archetypal polynuclear lanthanide single-molecule magnet Dy3 and derive the simplest model to describe the results from each experimental method, including high-frequency electron paramagnetic resonance and far-infrared spectroscopies and cantilever torque magnetometry. We conclude that a combination of these methods together with ab initio calculations is required to arrive at a full understanding of the properties of this complex, and potentially of other magnetically coupled lanthanide complexes.
Introduction
In recent years, lanthanide-based molecular nanomagnets (MNMs) have become of great interest due to their large angular momenta and their huge anisotropies.1 The magnetic anisotropy is a consequence of the crystal field (CF) splitting of the ground multiplet of the lanthanide ion.2 These properties engender slow relaxation of the magnetic moment to give single molecule magnet (SMM) behaviour, making them suitable for use in novel ultrahigh-density magnetic data storage devices. Most of the research has focussed on compounds where the magnetic relaxation properties can be assigned to the single ion processes of the individual lanthanide ions even for situations where the compound is chemically speaking polynuclear.3,4 For such polynuclear 4f compounds the magnetic interactions between the ions are typically dipolar in nature, rather than exchange coupled, and this typically leads to enhancement of the relaxation rates with a concomitant deterioration in the SMM properties of the compounds.5 Clearly, improving the understanding of the electronic structure and its relation to the static and dynamic magnetic properties of lanthanide-based SMMs is essential in order to make rational progress towards improved SMMs. The majority of studies on polynuclear 4f systems combine bulk magnetic susceptibility investigations with results from ab initio calculations, but comprehensive understanding is not usually achieved. Increasingly, spectroscopic methods are being used to assist in unravelling the details of the electronic and magnetic structure.6 Recently, a full experimental determination of the CF splitting of a lanthanide-based SMM has proven to be possible combining several spectroscopic techniques like far infrared (FIR), electron paramagnetic resonance (EPR), luminescence and magnetic circular dichroism (MCD) spectroscopy.7Given that it is recognised that the main challenge in improving SMM behaviour in lanthanide containing systems is eliminating efficient tunnelling of the magnetic moment near zero magnetic field, arguably the most viable approach to this end is the development of polynuclear systems with strong magnetic couplings. However, the number of systems where the magnetic properties are substantially determined by magnetic couplings is limited. An early example of such a system is provided by lanthanide-radical 4f-np systems.8 In terms of pure 4f polynuclear systems, exchange bias has been observed in dysprosium dimers.9 Importantly for this work, compounds based on manipulation of the archetypal triangular motif first reported in 200610 formed with ortho-vanillin-derived ligands show a variety of exotic phenomena,3,10–18 and the archetypal triangular systems have essentially nonmagnetic ground states.10 In their paramagnetic excited states, the Dy3 triangles show clear SMM behaviour. The nonmagnetic ground state originates from the fact that the magnetic moments of the individual dysprosium ions are all located in the plane of the triangle at low temperatures,12 as confirmed by ab initio calculations.11,13 The almost perpendicular angle between the magnetic moment and the line from the triangle centre through the dysprosium ion leads to a so-called toroidal magnetic moment.11 The two degenerate (Kramers doublet, KD) states with all moments arranged clockwise or anticlockwise are chiral. Even though the Dy3 molecule occupies a general site within the crystal unit cell, such that all three dysprosium ions are crystallographically distinct, the available experimental data could be fitted with astonishingly simple models.12 The simplest of these is the model where only the ground KD of each ion, assumed to be purely mJ = ±15/2 is taken into account by means of pseudo spins ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) = 1/2, and all local anisotropy axes are assumed to be related by 120° rotations around the molecular x-axis perpendicular to the triangle plane. The magnetic coupling was taken to be of the Ising type only. This model could quantitatively explain the single crystal magnetisation curve with the exception of a slight increase of the magnetic moment towards higher fields in the experiment. An enhanced model, able to describe all details of the magnetisation curve included isotropic exchange interactions, as well as mJ = ±13/2 excited doublets for each of the ions at an energy of 71 cm−1. However, CASSCF calculations suggested that the energy gap between ground and first excited Kramers doublets of the ions is at least twice this value.
= 1/2, and all local anisotropy axes are assumed to be related by 120° rotations around the molecular x-axis perpendicular to the triangle plane. The magnetic coupling was taken to be of the Ising type only. This model could quantitatively explain the single crystal magnetisation curve with the exception of a slight increase of the magnetic moment towards higher fields in the experiment. An enhanced model, able to describe all details of the magnetisation curve included isotropic exchange interactions, as well as mJ = ±13/2 excited doublets for each of the ions at an energy of 71 cm−1. However, CASSCF calculations suggested that the energy gap between ground and first excited Kramers doublets of the ions is at least twice this value.
In order to investigate this discrepancy in more detail we have embarked on a more stringent experimental test of the model required to describe the electronic structure of Dy3. A complete model within the 4f9 configuration of all dysprosium ions would have to take into account 27 CF- and 20 free ion parameters for each dysprosium (in C1 symmetry).19 These parameters determine the composition of the low-lying CF multiplets on each Dy ion as linear combinations of corresponding |JM〉 wave functions.19 The magnetic coupling between Dy ions includes two basic interactions, the magnetic dipolar and the exchange interaction.20 The magnetic dipolar interaction is completely determined by magnetic properties of individual Dy ions and does not require additional parameters for its description. On the contrary, the complete exchange interaction between the CF multiplets originating from the ground atomic J = 15/2 multiplets on the dysprosium sites is described by 2058 parameters per pairwise magnetic coupling in the absence of symmetry.21 This is in sharp contrast with the exchange coupling between two isotropic spins described by one single Heisenberg exchange parameter. However, if the ground KDs on the Dy sites are strongly separated from the excited KDs compared to the energy of the exchange coupling, then only the exchange coupling between individual KDs is relevant. This requires a maximum of 9 exchange parameters per dysprosium pair in the absence of symmetry.20 Together with CF and free ion parameters for each dysprosium this gives a staggering total of 168 parameters. In the case of strong axiality of the ground KDs on lanthanide sites, the exchange interaction between them becomes of non-collinear Ising type, described by one single Ising parameter.20 This was found to be the case in previous ab initio calculations of Dy3 triangle,11 for which the exchange coupling included three Ising exchange parameters – one per each pair of non-equivalent Dy ions.
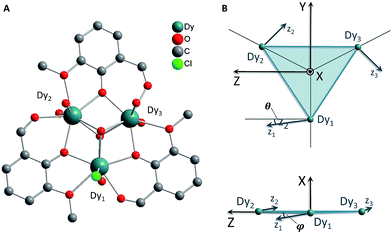
Here we present experimental studies of the compound [Dy3(μ3-OH)2L3Cl(H2O)5]Cl3 (where L is the anion of o-vanillin), hereafter abbreviated Dy3 (Fig. 1 and S1†). Dy3 crystallises in the monoclinic space group C2/c with Z = 8.9 The molecule thus has no crystallographically-imposed point group symmetry beyond C1. Two of the dysprosium ions have very similar coordination geometries, while the third is slightly different and bears a chloride ligand. As a result of the symmetry elements present in the monoclinic unit cell, the Dy3 molecules are divided into two sets. Within each set, the triangles are oriented with their planes exactly co-parallel, but molecules from one set have no symmetry requirement to be parallel to those from the other set. Very conveniently, however, the dihedral angle between triangles from different sets is only 5.2°; the crystal b-axis thus makes an angle of only 2.7° to each Dy3 triangle in the crystal (Fig. S1†).
We have used a combination of high-field electron paramagnetic resonance (HFEPR) and far-infrared (FIR) spectroscopies, as well as cantilever torque magnetometry (CTM). We have also revisited the ab initio calculations. In all cases we have established the minimal model that explains the experimental results of a given method and we thus assess which method provides the most stringent interrogation of the electronic structure.
Results and discussion
Ab initio calculations
Some of us have shown that in order to obtain a reliable description of the crystal field splitting of low-symmetry molecular lanthanide complexes from experiment, a combination of HFEPR, FIR, but also various optical spectroscopies (UV/Vis/NIR, magnetic circular dichroism, luminescence) is necessary.7 Unfortunately, extensive optical spectroscopic measurements on the Dy3 system (Fig. S2–S4†) did not produce very informative results. Therefore, we have instead carried out accurate ab initio calculations to determine the electronic structure of the lanthanide ions. The calculations follow the familiar CASSCF/RASSI-SO recipe.22 In contrast to previous calculations,11 the entire experimental structure was taken into account for the investigation of local electronic structure at individual dysprosium sites, while the “fragmentation” was limited to the replacements of the other two Dy ions with diamagnetic Lu3+. The calculations show that the ground KDs of each of the ions along its anisotropy axis (see Fig. 1B) essentially (>95%) consist of mJ = ±15/2, with minor contributions of mJ = ±11/2 (Table S1–S3†). All other contributions lie below 0.4%. The g tensors for the lowest KDs of the ions upon projection onto a![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) = 1/2 pseudo spin are all highly axial, with the transverse components for Dy(1) an order of magnitude higher than for the other ions (Table 1). The first excited KDs indeed feature main contributions from mJ = ±13/2 (ranging from ca. 50% for Dy(1) to ca. 85% for Dy(3)) with minor contributions from mJ = ±9/2 (Dy(2) and Dy(3)). The first excited KD in Dy(1) presents a more mixed character, importantly including substantial contributions from mJ functions with opposite projection of the magnetic moment (Table S1†). The energy gaps between ground and first excited KDs are calculated to range from ca. 143 to ca. 187 cm−1 (Table 1). These energies are smaller than previously calculated and, as shown below, much closer to experimentally extracted values. At the same time the magnetic anisotropy on individual Dy sites, in particular, the directions of the local main magnetic axes in the ground KDs of the three dysprosium ions were modified to a much smaller extent compared to reported calculations.11 As previously calculated, the single ion anisotropy axes are almost perpendicular to the line connecting the triangle centre with the relevant dysprosium ion, leading to a maximised toroidal moment.11,13 Importantly, the quantisation axes are calculated to make small but significant angles with the triangle plane (Table 1). Finally, considering Ising exchange interactions between local
= 1/2 pseudo spin are all highly axial, with the transverse components for Dy(1) an order of magnitude higher than for the other ions (Table 1). The first excited KDs indeed feature main contributions from mJ = ±13/2 (ranging from ca. 50% for Dy(1) to ca. 85% for Dy(3)) with minor contributions from mJ = ±9/2 (Dy(2) and Dy(3)). The first excited KD in Dy(1) presents a more mixed character, importantly including substantial contributions from mJ functions with opposite projection of the magnetic moment (Table S1†). The energy gaps between ground and first excited KDs are calculated to range from ca. 143 to ca. 187 cm−1 (Table 1). These energies are smaller than previously calculated and, as shown below, much closer to experimentally extracted values. At the same time the magnetic anisotropy on individual Dy sites, in particular, the directions of the local main magnetic axes in the ground KDs of the three dysprosium ions were modified to a much smaller extent compared to reported calculations.11 As previously calculated, the single ion anisotropy axes are almost perpendicular to the line connecting the triangle centre with the relevant dysprosium ion, leading to a maximised toroidal moment.11,13 Importantly, the quantisation axes are calculated to make small but significant angles with the triangle plane (Table 1). Finally, considering Ising exchange interactions between local ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) = 1/2 pseudo spins as well as the dipolar interactions, the exchange interactions were calculated to be between −7 and −8 cm−1 (
= 1/2 pseudo spins as well as the dipolar interactions, the exchange interactions were calculated to be between −7 and −8 cm−1 (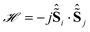 formulation, Table 1), comparable to that previously found.11,13 The first three exchange coupled excited states are calculated to lie at 7.24 to 7.39 cm−1.
formulation, Table 1), comparable to that previously found.11,13 The first three exchange coupled excited states are calculated to lie at 7.24 to 7.39 cm−1.
| Dy(1) | Dy(2) | Dy(3) | |
|---|---|---|---|
| KD1 | 0.00 | 0.00 | 0.00 |
| KD2 | 142.90 | 186.13 | 187.26 |
| KD3 | 174.27 | 281.35 | 294.45 |
| KD4 | 239.96 | 344.49 | 365.05 |
| KD5 | 296.38 | 376.11 | 423.39 |
| KD6 | 337.42 | 425.39 | 455.69 |
| KD7 | 380.00 | 499.62 | 486.35 |
| KD8 | 417.82 | 531.91 | 586.80 |
| g 1 | 0.0316 | 0.006 | 0.004 |
| g 2 | 0.0369 | 0.007 | 0.006 |
| g 3 | 19.742 | 19.640 | 19.698 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Tilting angle of anisotropy axis with tangential direction (θ) | |||
| 9.05° | 7.99° | 11.21° | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Tilting angle of anisotropy axis with Dy 3 plane (φ) | |||
| 3.01° | 0.68° | −5.57° | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Exchange interaction (cm −1 ) | |||
| Dy(1)–Dy(2), −7.45 | Dy(1)–Dy(3), −7.36 | Dy(2)–Dy(3), −7.69 | |
High-frequency electron paramagnetic resonance spectroscopy
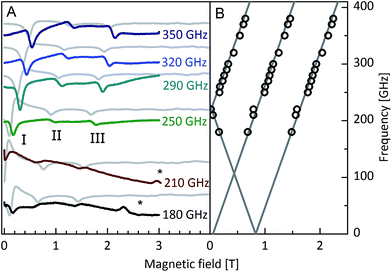
The first experimental method that we have employed to test the minimal model required to describe the results is high-frequency electron paramagnetic resonance (HFEPR). Some of us have recently shown that HFEPR spectra were essential in arriving at a satisfactory description of the electronic structure of an erbium SMM.7 Therefore, HFEPR spectra were recorded on immobilised powder samples of Dy3 at 4.2 K between 180 and 350 GHz (Fig. 2A, S5 and S6†). In all spectra, three peaks can be clearly observed (I–III). No resonances were observed at higher fields. Extrapolation of the resonance frequencies to zero field (Fig. 2B) reveals that peak II has a zero intercept and is thus assigned to an intra-KD transition. Peaks I and III have nonzero intercepts and can be assigned to excitations between the ground and first excited KDs of the coupled system. Peak I is attributed to the transition from the nonmagnetic ground state to the first excited KD (Fig. 2B and S7†). Peak III is the counterpart to peak I where the order of the levels has been reversed due to the field-induced level crossing at ca. 0.8 T. The zero field gap of 215 GHz = 7.17 cm−1 corresponds very well to that derived from ab initio calculations (7.24 cm−1).The minimal model to accurately reproduce these spectra turns out to be surprisingly simple. In it, each of the ions is modelled as a ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) = 1/2 pseudo spin corresponding to its ground KD. Furthermore, the magnetic coupling is considered in the pure Ising limit:
= 1/2 pseudo spin corresponding to its ground KD. Furthermore, the magnetic coupling is considered in the pure Ising limit:
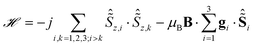 | (1) |
The local anisotropy axes are taken to lie in the plane of the triangle at exactly 120° from each other, and the local coordinate systems were rotated into the molecular one by appropriate rotation matrices. This model corresponds exactly to the simplest model used for fitting the magnetic data.12 The only adaptation required is to introduce nonzero perpendicular components of the g tensor for just one of the ions (Dy(1)). Fits (Fig. 2) gave the g tensor values reported in Table 2, which correspond astoundingly well with ab initio calculated ones (Table 1). In addition, the exchange coupling value of j = −7.3 ± 0.5 cm−1 corresponds very well to coupling values derived from ab initio calculations (−7.36 to −7.69 cm−1, Table 1). In conclusion, the interpretation of HFEPR does not provide a very strict test of the electronic structure of Dy3 and models used to describe it, since a rudimentary model, excluding excited CF levels suffices to fit the results.
| Dy(1) | Dy(2) | Dy(3) |
|---|---|---|
| 0.03 | 0.0 | 0.0 |
| 0.04 | 0.0 | 0.0 |
| 19.5 | 19.5 | 19.5 |
Far-infrared spectroscopy
The energies of the first excited crystal field levels of lanthanide SMMs can be determined with great precision by means of far-infrared (FIR) spectroscopy.7,23,24 Thus we have recorded FIR spectra on a pressed powder sample of Dy3 at 4.2 K and different applied magnetic fields up to 10 T (Fig. S8†). The transmission spectra are not very informative, because electric-dipole transitions such as vibrational transitions are much more intense than CF transitions. The latter are made visible by normalising the spectra through division by the zero-field spectrum (Fig. 3A). Four distinct field dependent features at 150, 170, 198 and 229 cm−1 can be observed (peak I–IV). Note that the relative transmission changes are very small, of the order of 1%, due to the necessary trade-off between sample amount and absolute transmission. Attributing the observed features to transitions from the ground KDs to the first excited KDs of the ions leads to the conclusion that the energy splittings lie in the range previously calculated by ab initio means. The main mJ components of the ground and first excited KDs of the dysprosium ions differ by ΔmJ = 1, thereby fulfilling the magnetic resonance selection rule. The rudimentary model that was used to fit the HFEPR results cannot work here, because it does not include excited CF levels. Therefore, we have attempted to use the model previously employed by some of us,12 which is based on three pseudo-spins![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) = 15/2, that are isotropically coupled, in addition to a local energy gap δi between the mJ = ±15/2 ground and ±13/2 excited states:
= 15/2, that are isotropically coupled, in addition to a local energy gap δi between the mJ = ±15/2 ground and ±13/2 excited states: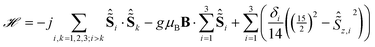 | (2) |
 | ||
| Fig. 3 (A) Experimental FIR spectra recorded on a powder sample of Dy3 in eicosane at 4.2 K and different magnetic fields. (B) Simulations using the model of eqn (2). (C) Simulations using the model derived in this work (B) based on ab initio results of the lowest eigenstates. | ||
Cantilever torque magnetometry
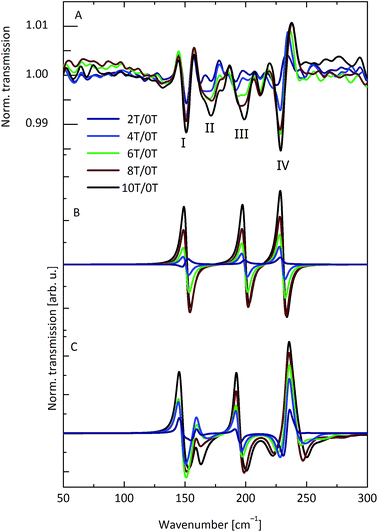
Torque magnetometry is based on measuring the magnetic torque τ that is experienced by a magnetically anisotropic sample in an applied magnetic field (τ = M × B).25 The torque is usually determined by measuring the deflection of a cantilever and is thus named cantilever torque magnetometry (CTM). Some of us have recently used CTM to investigate the magnetic anisotropy and CF splitting of lanthanide based SMMs.26,27 These studies have shown that CTM is much more sensitive to the CF splitting than standard magnetisation and magnetic susceptibility techniques.Thus, we have recorded single crystal CTM curves at different angles at temperatures down to T = 50 mK and fields up to 32 T. The b-axis of the crystal, which is almost parallel to the line connecting Dy(1) and Dy(3) of both molecules (i.e. almost in the planes of the molecules, Fig. 1C), was chosen as the rotation axis. Fig. 4A and S9† display averaged (±α) torque curves at different small angles α with the plane of the triangle (α close to 0°). The crystal was oriented in such a manner that the field is almost parallel to the line connecting the centre of the triangle with the Dy(2) ion. At small fields, the torque is negligible, but at 0.8 T a sharp step occurs, followed by a near linear increase in the torque. No saturation occurs. The step is also found in magnetisation measurements12 and is due to the field-induced crossing of the paramagnetic excited state of the magnetically coupled system with the nonmagnetic ground state. The torque is proportional to the susceptibility anisotropy. This in turn is related to the CF splitting energy, which is huge compared to the Zeeman energy even at 32 T. Hence no saturation of the torque occurs, in contrast to what is found in the magnetisation measurements.12
 | ||
| Fig. 4 (A) Averaged torque signals at 50 mK and different angles between the triangle plane and the magnetic field. (B) Simulated torque curves, based on eqn (1). All curves are normalised to the high-field torque value at 5.2°. | ||
The torque curves were simulated on the basis of eqn (1) (Fig. 4B). Simulation and experiment agree very well in terms of the step position and the behaviour at higher fields. The experimental step is slightly more rounded, suggesting a slight distribution of parameters smearing out the step. More elaborate models (see below) do not improve the simulation. Hence, in-plane torque measurements are also not a sensitive test of the model used for the description of the electronic structure of Dy3.
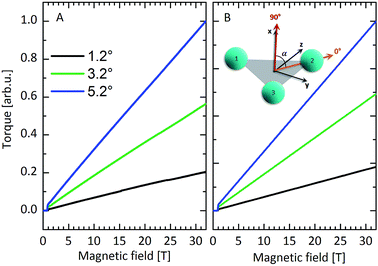
In contrast, averaged (90° ± α) CTM measurements at angles close to 90° with the triangle plane (out-of-plane) show a very different behaviour (Fig. 5 and S10†). Again the magnetic torque is negligible at small fields due to the nonmagnetic nature of the ground state. At around 8 T the torque starts to increase, reaching a maximum at ca. 28 T, before decreasing again. Applying the field out of the Dy3 plane forces the magnetic moments out of their easy direction, i.e. excited states of the CF multiplet are mixed into the ground state by the field. Eqn (1), which neglects excited KDs, is therefore unable to model these data. Simulations based on eqn (2), which takes the excited KDs of the single dysprosium ions into account, gave completely unsatisfactory results (Fig. 5B). Clearly the model of eqn (2) is insufficient to explain either FIR or out-of-plane CTM. We have therefore taken the experimental FIR and out-of-plane CTM data and aimed to improve the model that describes the electronic structure of Dy3.
 | ||
| Fig. 5 (A) Experimental averaged torque signals at different angles close to 90° at 50 mK. (B) Simulated torque curves based on eqn (2). (C) Definitive torque simulation based on the most elaborate model taking into account mJ mixing and CF quantisation axis tilting. | ||
Improvement of the description of the electronic structure
HFEPR and in-plane CTM data could be simulated very well on the basis of a rudimentary model considering Ising-type coupling between three![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) = 1/2 pseudo spins (eqn (1)). The FIR data could be qualitatively modelled assuming pure mJ = ±15/2 and pure mJ = ±13/2 excited doublets with different gaps for each of the three dysprosium ions. In both cases the local anisotropy axes were assumed to rigorously lie in the plane of the triangle (φ = 0°, Fig. 1B), and perpendicular to the line connecting the centre of the triangle with the relevant dysprosium ion (θ = 0°, Fig. 1B). There are many avenues along which more elaborate models can be explored. The ab initio calculations showed that the angles θ and φ of the three dysprosium ions have values of up to 11°. Furthermore they revealed that the KDs, especially of Dy(1), do not have pure ±mJ character. The magnetic resonance transition dipole moments can be very sensitive to the nature of the wavefunctions. Therefore, in a first step, we have taken the mJ compositions of the ground and first excited KD for each dysprosium ion, as derived from ab initio calculations, as the basis for the simulations. Thus we have set up 4 × 4 matrices (eqn (3)) for each of the three ions. The total spin Hamiltonian matrix was constructed using the tensor product formalism. In addition, we have used the tilting angles of the anisotropy axis for each of the dysprosium ions θ and φ as calculated by ab initio methods (Table 1).
= 1/2 pseudo spins (eqn (1)). The FIR data could be qualitatively modelled assuming pure mJ = ±15/2 and pure mJ = ±13/2 excited doublets with different gaps for each of the three dysprosium ions. In both cases the local anisotropy axes were assumed to rigorously lie in the plane of the triangle (φ = 0°, Fig. 1B), and perpendicular to the line connecting the centre of the triangle with the relevant dysprosium ion (θ = 0°, Fig. 1B). There are many avenues along which more elaborate models can be explored. The ab initio calculations showed that the angles θ and φ of the three dysprosium ions have values of up to 11°. Furthermore they revealed that the KDs, especially of Dy(1), do not have pure ±mJ character. The magnetic resonance transition dipole moments can be very sensitive to the nature of the wavefunctions. Therefore, in a first step, we have taken the mJ compositions of the ground and first excited KD for each dysprosium ion, as derived from ab initio calculations, as the basis for the simulations. Thus we have set up 4 × 4 matrices (eqn (3)) for each of the three ions. The total spin Hamiltonian matrix was constructed using the tensor product formalism. In addition, we have used the tilting angles of the anisotropy axis for each of the dysprosium ions θ and φ as calculated by ab initio methods (Table 1).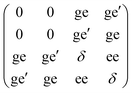 | (3) |
In eqn (3), the off diagonal elements ge and ge′ mix ground and excited KDs, which parametrises effects due to possible imperfections of the ab initio description of the wavefunctions. The factor ee parametrises additional excited state splitting, due to the magnetic coupling between the excited KDs being possibly different from that between the ground KDs. Finally, δ is the CF gap between ground and excited KD.
Simulations of the FIR spectra, considering nonzero values only for the CF gaps δ, revealed some improvement, especially when changing the order of the CF gaps δi of the ions. The compositions of the wavefunctions of the lowest KDs of the single ions given by ab initio results strongly influence the shape of the transitions. The best agreement in lineshape is obtained for (in cm−1): δ1 = 229, δ2 = 147, δ3 = 192 (Fig. S11†). The exchange interaction is again found to be j = −0.064 cm−1, which is kept fixed for further simulations. The simulated out-of-plane torque curves (Fig. S12†) are still very far away from those measured.
In a second step, we considered improvements of the ab initio wavefunctions and the ab initio description of the magnetic coupling. The former we have attempted to simulate by mixing the ground and excited KDs of the ions by incorporating ad hoc off-diagonal elements ge and ge′ in eqn (3). This gives us a handle to explore the effect of KD composition on the simulations. Clearly, free variation of the KD wavefunctions would create a vast parameter space, in which finding a point that allows simulation of the data would be impossible. The latter takes into account the fact that the exchange coupling between the KD, assumed equal and isotropic in the POLY_ANISO routine, may be KD-dependent. In this manner improved fits of the FIR spectra could be obtained by inclusion of only 4 out of 9 possible nonzero off-diagonal parameter values (Table 3, Fig. 3 and S11†). The discrepancy that still exists may be due to the imperfect description of the composition of the KDs as well as of the exchange interaction, even after considering eqn (3). Here we have no way to improve these descriptions either by further experiments (because optical data cannot be obtained) or by further theory (because the molecule is too large for more detailed consideration of dynamical electron correlation or configuration interaction). The simulated out-of-plane torque curves are also improved, but still not satisfactory (Fig. S12†).
| Dy(1) | Dy(2) | Dy(3) | |
|---|---|---|---|
| ge | 0 | 4 | 1 |
| ge′ | −8 | 0 | 0 |
| ee | 0 | 2 | 0 |
| δ | 229 | 147 | 192 |
In the final step, we have varied the tilting angles θ and φ. To limit the number of free parameters, we have only scaled the values for these angles as φi = aφab initio,i, θi = bθab initio,i (Fig. S13 and S14†). It turns out that only a 10% change of the out-of-plane tilting angle φ (a = 0.9) suffices to finally arrive at very satisfactory simulations of the out-of-plane torque curves (Fig. 5C). Beyond this model, one could also envision including further KDs of the dysprosium ions. We have not pursued this road, because we have no experimental evidence of the energetic positions of these states. Hence their inclusion would lead to a large number of additional free fit parameters.
Conclusions
We have tested the informative value of high-frequency electron paramagnetic resonance (HFEPR) and far-infrared (FIR) spectroscopies, as well as cantilever torque magnetometry (CTM) to interrogate the electronic structure of the archetypal polynuclear lanthanide-based single-molecule magnet Dy3. These researches were complicated by the fact that no informative UV/Vis/NIR optical data could be obtained for this compound, as well as the vast number of parameters required in a complete model. The interplay between ab initio calculations and advanced experimental techniques was essential in this study. We have demonstrated that both HFEPR and in-plane torque measurements can be simulated well by means of a rudimentary model and thus do not allow in depth elucidation of the electronic structure. In contrast FIR and CTM turned out to be very sensitive both to the crystal field splitting of the individual ions and to details of the magnetic coupling. The out-of-plane torque measurements were also very sensitive to the exact tilting angles of the local anisotropy axes from the plane of the Dy3 molecule. Thus, we have presented one of the first comprehensive spectroscopic and magnetometric studies in the area of polynuclear lanthanide based SMMs. It appears that the most appropriate tools for advancement in this area may be very different from those best suitable for mononuclear lanthanide complexes.Experimental
[Dy3(μ3-OH)2L3Cl(H2O)5]Cl3 (where L is the anion of o-vanillin) was synthesised as previously published and characterised by standard chemical analytical techniques.10Ab initio calculations on mononuclear fragments were performed by using MOLCAS 7.8 employing the CASSCF/RASSI-SO/SINGLE_ANISO routines. Magnetic coupling constants were obtained by using the POLY_ANISO routine in combination with experimental magnetic data.11,13,22
High-frequency EPR spectra (180–380 GHz) were recorded on a home-built induction mode spectrometer with a VDI synthesizer source and multipliers, a Thomas Keating quasi optical bridge, an Oxford Instruments 15/17 T solenoid magnet and a QMC InSb bolometer detector. The sample was measured as a 5 mm pressed pellet (34 mg). A magnetic field modulation amplitude of approximately 150 G was used. EPR spectra were simulated by means of the Weihe program.
FIR transmission spectra (30–600 cm−1) were recorded at the Laboratoire National des Champs Magnétiques Intenses in Grenoble on a sample of Dy3 diluted (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) in eicosane on a Bruker IFS 66v/s FTIR spectrometer with globar source, where the sample was placed inside an 11 T solenoid magnet, with a composite bolometer detector element located inside the magnet. The spectra were simulated by means of the Easyspin toolbox, modified for our purposes.24,28
20) in eicosane on a Bruker IFS 66v/s FTIR spectrometer with globar source, where the sample was placed inside an 11 T solenoid magnet, with a composite bolometer detector element located inside the magnet. The spectra were simulated by means of the Easyspin toolbox, modified for our purposes.24,28
Cantilever torque measurements were recorded at Laboratoire National des Champs Magnétiques Intenses in Grenoble and at the National High Magnetic Field Laboratory in Tallahassee using home-made CuBe cantilevers. Torque curves were simulated by taking the numerical derivative of the energy with respect to the rotation angle.
Luminescence spectra were recorded at the University of Copenhagen in collaboration with Dr S. Piligkos and Dr T. Brock-Nannestad. Samples of Dy3 dispersed into Baysilone vacuum grease were measured on a Horiba FluoroLog3 luminescence spectrometer equipped with an Oxford Instruments helium flow optical cryostat and photomultiplier.
MCD spectra on a frozen solution of Dy3 in 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 EtOH/MeOH were recorded on a home-built spectrometer based on an Aviv 42 CD spectrometer, with an Oxford instruments Spectromag 10 T optical cryomagnet and PMT and InGaAs detectors.
1 EtOH/MeOH were recorded on a home-built spectrometer based on an Aviv 42 CD spectrometer, with an Oxford instruments Spectromag 10 T optical cryomagnet and PMT and InGaAs detectors.
Acknowledgements
We thank Høgni Weihe (University of Copenhagen) for his EPR simulation program and useful discussions. We are grateful to Mael Etienne, Kevin Bernot, Lapo Bogani, Lena Friedrich, Eric C. Palm, Stergios Piligkos and Theis Brock-Nannestad for experimental contributions. We thank Martin Dressel for useful discussions. We thank the following for funding: Deutsche Forschungsgemeinschaft (SFB/TRR88 “3MET”, GRK 448, INST 41/863-1, 41/864-1, SPP1601, SL104/5-1), COST CM1006 Eufen, Methusalem and GOA grants from the KU Leuven, as well as LNCMI-CNRS, member of the European Magnetic Field Laboratory (EMFL).References
- Lanthanides and Actinides in Molecular Magnetism, ed. R. Layfield and M. Murugesu, Wiley-VCH, Weinheim, 2015 Search PubMed.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- S.-D. Jiang, B.-W. Wang and S. Gao, in Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer, Berlin Heidelberg, 2015, vol. 164, ch. 153, pp. 111–141 Search PubMed.
- E. Moreno Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243 CrossRef CAS PubMed.
- K. S. Pedersen, D. N. Woodruff, J. Bendix and R. Clérac, in Lanthanides and Actinides in Molecular Magnetism, ed. R. A. Layfield and M. Murugesu, Wiley-VCH, Weinheim, 2015 Search PubMed.
- Y. Rechkemmer, J. E. Fischer, R. Marx, M. Dörfel, P. Neugebauer, S. Horvath, M. Gysler, T. Brock-Nannestad, W. Frey, M. F. Reid and J. van Slageren, J. Am. Chem. Soc., 2015, 137, 13114–13120 CrossRef CAS PubMed.
- S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176 CrossRef CAS.
- J. Long, F. Habib, P. H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 5319–5328 CrossRef CAS PubMed.
- J. K. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733 CrossRef CAS PubMed.
- L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126–4128 CrossRef CAS PubMed.
- J. Luzon, K. Bernot, I. J. Hewitt, C. E. Anson, A. K. Powell and R. Sessoli, Phys. Rev. Lett., 2008, 100, 247205 CrossRef PubMed.
- L. Ungur, W. Van den Heuvel and L. F. Chibotaru, New J. Chem., 2009, 33, 1224–1230 RSC.
- S. Xue, X.-H. Chen, L. Zhao, Y.-N. Guo and J. Tang, Inorg. Chem., 2012, 51, 13264–13270 CrossRef CAS PubMed.
- I. J. Hewitt, Y. H. Lan, C. E. Anson, J. Luzon, R. Sessoli and A. K. Powell, Chem. Commun., 2009, 6765–6767 RSC.
- I. J. Hewitt, J. Tang, N. T. Madhu, C. E. Anson, Y. Lan, J. Luzon, M. Etienne, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 6352–6356 CrossRef CAS PubMed.
- Z. Salman, S. R. Giblin, Y. Lan, A. K. Powell, R. Scheuermann, R. Tingle and R. Sessoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 174427 CrossRef.
- G. Novitchi, G. Pilet, L. Ungur, V. V. Moshchalkov, W. Wernsdorfer, L. F. Chibotaru, D. Luneau and A. K. Powell, Chem. Sci., 2012, 3, 1169–1176 RSC.
- C. Görller-Walrand and K. Binnemans, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner and L. Eyring, Elsevier, Amsterdam, 1996, vol. 23 Search PubMed.
- L. F. Chibotaru, in Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer, Berlin, 2015, vol. 164, pp. 185–230 Search PubMed.
- N. Iwahara and L. F. Chibotaru, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 174438 CrossRef.
- L. Ungur and L. F. Chibotaru, in Lanthanides and Actinides in Molecular Magnetism, Wiley-VCH Verlag GmbH & Co. KGaA, 2015, pp. 153–184 Search PubMed.
- S. Haas, E. Heintze, S. Zapf, B. Gorshunov, M. Dressel and L. Bogani, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 174409 CrossRef.
- R. Marx, F. Moro, M. Dörfel, L. Ungur, M. Waters, S. D. Jiang, M. Orlita, J. Taylor, W. Frey, L. F. Chibotaru and J. van Slageren, Chem. Sci., 2014, 5, 3287–3293 RSC.
- A. Cornia, D. Gatteschi and R. Sessoli, Coord. Chem. Rev., 2001, 219–221, 573–604 CrossRef CAS.
- M. Perfetti, G. Cucinotta, M.-E. Boulon, F. El Hallak, S. Gao and R. Sessoli, Chem.–Eur. J., 2014, 20, 14051–14056 CrossRef CAS PubMed.
- M. Perfetti, E. Lucaccini, L. Sorace, J. P. Costes and R. Sessoli, Inorg. Chem., 2015, 54, 3090–3092 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details and extended results. Further experimental results. See DOI: 10.1039/c6sc00318d |
| This journal is © The Royal Society of Chemistry 2016 |