Adsorption and decarbonylation of furfural over H-ZSM-5 zeolite: a DFT study

Abstract

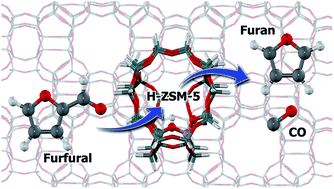
The conversion of low cost biomass and its derivatives is receiving considerable and growing attention as an alternative feedstock for fuel and chemicals production. Herein, the furfural adsorption and decarbonylation to furan on H-ZSM-5 zeolite are studied by density functional theory calculations. The furfural interacts with the zeolite active site through its three sites of methine carbon atoms, ring's oxygen and carbonyl group with the adsorption Gibbs free energies of −5.5, −8.3 and −15.7 kcal mol⁻¹, respectively. Three pathways are considered for the decarbonylation of furfural. In the first pathway, the reaction starts with the protonation of a alpha-carbon leading to the arenium-ion like intermediate. This intermediate then eliminated the CO group to form the furan product. The earlier step is considered to be the rate-determining step of this pathway with an activation energy of 22.1 kcal mol⁻¹. In the second pathway, it commences by protonation of furfural at the beta-carbon to produce the arenium-ion like intermediate. This intermediate then undergoes a 1,2-hydride shift and is subsequently decarbonated to eliminate the CO molecule and form the furan product. The first step of the furfural protonation has the highest activation energy, 27.7 kcal mol⁻¹, and is therefore rate-determining. For the last path, the protonation at the furfural carbonyl group to the surface hydroxyalkyl species formation is the first step of this pathway. The reaction then proceeds through the migration of H to form the tertiary carbocation intermediates followed by the 1,2-hydride shift to form the secondary carbocation species. Finally the CO molecule is eliminated to generate the furan product. The rate-determining step of this pathway is the second step of the H migration with the activation energy of 45.8 kcal mol⁻¹. Since the first pathway requires a lower rate-determining step activation barrier compared with the second and third pathways, the first pathway is therefore preferred for the furfural decarbonylation on H-ZSM-5 zeolite. The effect of the zeolite framework is also highlighted to greater stability of the intermediates and also transition state complexes.

---

1. Introduction

At the present time, the conversion of low cost biomass into fuel and fine chemicals is important for the development of clean technology for the chemical industry.^1–3 Furfural is a mutual intermediate acquired from the dehydration of carbohydrate resources and is also a significant component contained in bio-oils. It is considered to be a promising platform molecule used to produce various valuable chemicals.^4,5 Furan is one of the important chemicals obtained from furfural via the well-known process of decarbonylation.^4,6 It is a useful chemical used generally in the production of tetrahydrofuran. Transition metals^7–12 e.g., Cu, Pd, Ni Pt and Rh have been used as the catalysts and found to be active for the furfural decarbonylation to furan.

Different kinds of zeolites have been utilized for biomass upgrading that involves oxygen elimination via a series of dehydration, decarboxylation, and decarboxylation reactions.^13–21 Among these, ZSM-5 is found to be an efficient catalyst for this conversion. From literatures, the H-ZSM-5 zeolite can catalyse the conversion of oxygenated model compounds including furfural.^13–17 W. Fanchiang and Y. Lin²¹ investigated catalytic pyrolysis furfural over the ZSM-5 zeolite. It was found that furfural conversion over H-ZSM-5 at 500 °C was 100%. With reducing contact time, products excepting furan, decreased. The obtained result suggests that the beginning of furfural conversion is the decarbonylation process to produce furan and CO as the products. Afterward, generated furans inside pores of zeolite are further converted to intermediates (e.g., cyclohexene and 3,4-dimethylbenzaldehyde), which are subsequently converted to higher aromatics.²¹ As result, the initial formation of furan from the furfural decarbonylation is the most important step for the deoxygenations process of biomass-derived compounds to hydrocarbons. To the best of our knowledge, the reaction mechanisms of the furfural decarbonylation to furan over acidic zeolite have never been investigated theoretically in atomistic detail. We therefore investigate the reaction mechanisms of furfural decarbonylation to furan over H-ZSM-5 zeolite in order that analyzing its mechanistic, energetic and electronic features might reveal directions for improving or designing efficient zeolite catalysts.

To understand the hydrocarbon reactions inside zeolite catalysts, investigation by using the theoretical calculations are found to be a simple tool that can provide useful information in deep detail. The van der Waals interactions are well-known as an important effect for such accurate investigation, particularly for the structures and energies of the intermediates, products as well as transition state complexes.^22–26 Previously, the Minnesota density functional (M06 series)^27,28 was found to be a well-organized method for studying several reactions in zeolites. In it, the van der Waals interactions are is taken into account in the parameterization. We have demonstrated earlier the efficient use of these methods for investigating the adsorption and reaction mechanisms over zeolites^29–41 and over metals–organic frameworks.^42–46

In this work, we study the decarbonylation of the furfural on H-ZSM-5 with the M06-2X density functional. We discussed the reaction mechanisms and their relative energies and structures of intermediates and transition states. This was to predict the possible reaction pathway for the furfural decarbonylation on H-ZSM-5 zeolite. The studied results of this could be related for predicting and developing catalysts for the decarbonylation of furfural and also other biomass-derived carboxylic acid.

2. Models and method

The ZSM-5 zeolite is represented by the 34T cluster model as illustrated in Fig. 1. It was generated from its crystallographic structures.⁴⁷ One of the silicon atoms at the T12 site was replaced with an aluminium atom to generate the Brønsted acid site. This site is the most stable Al substitution site and has been generally used to model the active site of H-ZSM-5 zeolite.⁴⁸

Fig. 1 34T cluster model of H-ZSM-5 zeolite.

The M06-2X density functional^27,28 with the 6-31G (d,p) basis set was used in all structure optimizations. From literature, the M06-2X/6-31G(d,p) with the 34T cluster model of ZSM-5 zeolite was shown to be a sufficient method and model for studying the adsorption of various molecules and the reactions inside the pore of zeolites.^30,31 During geometry optimizations, only the 5T cluster of the active region, [(≡SiO)₃Al(OH)Si≡] and the adsorbed molecules are allowed to relax, while the remaining atoms were fixed at the crystallographic coordinates. For the convergence criteria in calculations, the self-consistent field (SCF) cycle was set to 10⁻⁸ hartrees and gradients of maximum force, rms force, and maximum displacement and rms displacement were 0.000450, 0.000300, 0.001800, and 0.001200, respectively. Transition states were located with the “Berny Algorithm”.⁴⁹ Frequency calculations were performed at the same level of theory to identify the nature of all the stationary points and to obtain thermodynamic properties. IRC calculations^50,51 was used to ensure that the reaction minima connected appropriate reactants and products. The relative energies reported in this work are the Gibbs free energies (ΔG) at 298 K. All calculations were performed with the Gaussian 09 code.⁵² The relative energy in the reaction energy profiles was calculated by:

ΔG²⁹⁸_ads = G²⁹⁸_complex − (G²⁹⁸_zeolite + G²⁹⁸_adsorbate) (1)

where G²⁹⁸_complex, G²⁹⁸_zeolite and G²⁹⁸_adsorbate are Gibbs free energies at 298 K of the H-ZSM-5–adsorbate complex, the isolated H-ZSM-5 and the furfural molecule, respectively.

3. Results and discussion

3.1 Furfural adsorption on H-ZSM-5 zeolite

Optimized structures of furfural adsorption on H-ZSM-5 zeolite obtained from the M06-2X/6-31G(d,p) calculations are shown in Fig. 2. Selected geometrical structures for the adsorption complexes are tabulated in Table 1. It can be seen that the furfural can absorb on the Brønsted acid site in three different configurations. In the first configuration (Ads_1), the furfural weakly interacts on zeolite through interactions between the π-bond of two methine carbon atoms (=CH–) and the Brønsted acid site (cf. Fig. 2a). The interatomic H1⋯C2 and H1⋯C3 distances are 2.61 and 2.32 Å, respectively. The internal geometries of furfural are not significantly changed because the adsorption interactions are weak. The bond distances of the O–H2 and the C1–C2 of furfural change slightly from the isolated molecules. The positive partial atomic charge analysed by Mulliken of the H1 atom is decreased from 0.419e to 0.399e. This result shows slightly electron transfer from π-bond of furfural to Brønsted proton of zeolite. The calculated adsorption free energy is −5.5 kcal mol⁻¹. In the second configuration (Ads_2), the furfural's ring oxygen interacts with the Brønsted acid site via a lone pair of O atom to form a hydrogen bond with the interatomic H1⋯Or distance of 1.64 Å (see Fig. 2b). This adsorption structure is in agreement with previous the theoretical studies for the furan adsorption on acidic zeolite.⁵³ The interaction induces the lengthening of the O1–H1 bond distance from 0.97 to 1.00 Å. In addition, the Mulliken population analysis reveals an electron transfer from the furfural to the zeolite, which leads to an increased positive charge of the furfural molecule (0.065e). However, the partial charge of Or compared to the isolated molecule is more negative (from −0.350e to −0.558e) by reason of the electrons induced from ring carbons to Or. The calculated adsorption free energy is −8.3 kcal mol⁻¹. For the last configuration (Ads_3), the furfural is adsorbed on H-ZSM-5 zeolite via two hydrogen bonding interactions: one is the carbonyl oxygen (O) of furfural interacted with the Brønsted acid site (H1) and another one is the furfural hydrogen (H2) interacted with the zeolite oxygen bridging (O2) as displayed in Fig. 2c. The adsorption influences both the structures of H-ZSM-5 and furfural. In H-ZSM-5, the O1⋯H1 bond distance is stretched from 0.97 to 1.07 Å. In furfural, the C–O bond of carbonyl group lengthens from 1.21 to 1.24 Å due to the electron transfer from O to H1. The negative charge of the O atom is reduced from −0.721e to −0.524e. The adsorption free energy of this is −15.7 kcal mol⁻¹, which is the most stable one among the three configurations.

Fig. 2 Optimized structures and adsorption energies of furfural interacted over H-ZSM-5 zeolite (a) Ads_1, (b) Ads_2 and (c) Ads_3.

Table 1 The optimized geometric parameters of the isolated zeolite clusters and furfural adsorption on H-ZSM-5 zeolite

Parameters	Isolate	Ads_1	Ads_2	Ads_3
Distances (Å)
O1–H1	0.97	0.98	1.00	1.07
Al–O1	1.82	1.82	1.80	1.78
Al–O2	1.68	1.68	1.68	1.69
C1–C2	1.46	1.47	1.46	1.43
C2–C3	1.36	1.37	1.36	1.37
O–C1	1.21	1.20	1.21	1.24
Or–C2	1.36	1.35	1.37	1.36
H1–C2	—	2.61	2.58	3.61
H1–C3	—	2.32	3.64	4.35
H1–Or	—	3.38	1.64	4.68
H1–O	—	4.11	4.23	1.37
∠Angles (°)
O1–Al–O2	90.4	90.5	90.9	92.0
O1–H1–Or	—	—	170.9	—
O1–H1–O	—	—	—	168.1

---

3.2 Furfural decarbonylation on H-ZSM-5 zeolite

The furfural decarbonylation on H-ZSM-5 is systematically investigated in three possible mechanisms via the protonation of zeolite proton to the adsorbed furfural at different positions of the alpha-carbon (C2), the beta-carbon (C3) and the carbonyl group oxygen (O). These reaction pathways are proposed to occur via the arenium-ion like intermediate. It is similar to the furfuran decarbonylation into furan in acid media that reported this arenium ion intermediate to be a key species in the process.¹⁴ Selected geometrical parameters for these reaction pathways are shown in Table 2 and optimized structures of intermediates and transition states along the reaction coordinates are shown in Fig. 3–5.

Table 2 Optimized geometrical parameters of the species involved in the furfural decarbonylation on H-ZSM-5 zeolite

Parameter	TS1_a	Int_a	TS2_a	Prod	TS1_b	Int1_b	TS2_b	TS1_c	Int1_c	TS2_c
Distances (Å)
Al–O1	1.76	1.71	1.71	1.68	1.65	1.71	1.71	1.70	1.68	1.71
Al–O2	1.69	1.71	1.73	1.82	1.71	1.72	1.71	1.77	1.82	1.72
O1–H1	1.31	3.56	2.77	2.42	1.65	2.24	3.11	1.78	1.93	4.24
O2–H2	2.83	3.00	1.63	0.99	2.60	2.66	2.56	2.73	2.70	2.56
C1–C2	1.55	1.64	2.04	3.43	1.51	1.52	1.54	1.46	1.50	1.49
C2–C3	1.42	1.46	1.39	1.36	1.43	1.47	1.42	1.36	1.36	1.41
O–C1	1.19	1.18	1.15	1.13	1.20	1.20	1.20	1.30	1.34	1.23
Or–C2	1.40	1.42	1.37	1.36	1.28	1.28	1.35	1.35	1.35	1.31
H1–C2	1.32	1.09	1.08	1.08	1.98	2.11	1.29	2.46	2.44	1.73
H1–C3	2.26	2.20	2.24	2.24	1.17	1.10	1.38	2.77	2.88	1.37
H2–C1	1.10	1.10	1.13	2.00	1.10	1.10	1.10	1.08	1.08	1.09
H1–Or	2.24	2.09	2.10	2.08	2.88	3.04	2.15	3.71	3.50	2.71
H1–O	—	—	—	—	—	—	—	0.98	0.97	1.41
C1–O1	3.10	2.78	3.38	3.95	3.20	2.56	2.61	1.30	2.71	2.74
C1–O2	2.67	3.34	2.62	2.92	3.04	2.95	3.04	1.85	1.58	2.49
Angles (°)
O1–Al–O2	93.3	95.4	96.0	92.0	94.4	93.4	94.4	93.8	93.2	93.4
O1–H1–C2	166.5	64.0	114.8	111.8	152.8	79.6	—	—	—	—
O1–H1–C3	149.0	53.4	90.5	94.4	152.9	109.8	—	—	—	—
O–C1–H2	124.6	128.2	158.8	175.8	125.4	127.1	126.1	112.6	107.3	125.8
O1–H1–O	—	—	—	—	—	—	—	133.4	126.5	—

---

In the first pathway (cf. Fig. 3), the decarbonylation of furfural proceeds via two steps: the protonation of furfural to produce the secondary carbocation intermediate and the elimination of the CO group to the furan product. In this process, the decarboxylation takes place via the protonation at the double bond of the furfural molecule. Therefore, this process would start with the adsorption of furfural molecule via the Ads_1 configuration with the adsorption energy of −5.5 kcal mol⁻¹.

Fig. 3 Energy profile and structures of reactants, intermediates and transition states for the first pathway for the furfural decarbonylation on H-ZSM-5 zeolite.

The adsorbed furfural is then protonated by acidic zeolite at the alpha-carbon (C2) and then the arenium-ion like intermediate is formed. A late transition state is expected according to Hammond's postulate.⁵⁴ The transition state of this step (TS1_a) is characterized by H1 being transferred from the zeolite bridging oxygen (O1) to the carbon (C2) of the furfural. As for the results, the O1–H1 bond distance of the Brønsted is lengthened from 0.98 to 1.31 Å. The C1–C2 bond distance is also increased to 1.55 Å. This transition state has one imaginary frequency at 1084.2i cm⁻¹ and is also confirmed by intrinsic reaction coordinate (IRC) calculation. From IRC's result (see Fig. S1 in ESI†), it was found that the O1–H1 bond of zeolite is broken and the H1 is concurrently transferred to the C2, leading to the formation of arenium-ion like intermediate. The activation energy of this step is 22.1 kcal mol⁻¹. This value is in the range of the calculated activation energy for the protonation of the corresponding furfural molecule on H-ZSM-5.⁵⁵ The arenium-ion like intermediate is then formed with the C2 carbon of the ring no longer presented as a conjugated π orbital (Int_a). It is adsorbed on the zeolite surface with the complexation energy of 11.0 kcal mol⁻¹. The last step of the reaction path is the formation of furan and CO molecules via the decarbonylation transition state (TS2_a). At the transition state, the H2 proton is back-transferred to the oxygen of the zeolite framework and the C1–C2 bond of the intermediate is simultaneously broken. The H2–C1 and C1–C2 distances increase to 1.13 and 2.04 Å while the O2–H2 distance decreases to 1.63 Å leading to form a new bond. Normal mode analysis reveals one imaginary frequency at 392.8i cm⁻¹ linked with this transition state in which the H2 moves to O2 and the C1–C2 bond breaks simultaneously. This TS2_a is also confirmed by the IRC calculations as showed in Fig. S2 in ESI.† The activation energy of this step is 12.3 kcal mol⁻¹. The furan product is formed and adsorbed on the acidic site of the zeolite nearby the CO molecule after back-migration of the proton to the zeolite framework. The adsorption energy with respect to the isolated is −5.5 kcal mol⁻¹. Finally, the furan and CO molecules are desorbed with a required energy of 3.0 kcal mol⁻¹.

In the second possible pathway (Fig. 4), the reaction starts with the protonation of the adsorbed furfural at the beta-carbon (C3) to form the tertiary carbocation intermediates. At the transition state (TS1_b), the proton (H1) transfers to the C3 leading to the lengthening of the Brønsted O1–H1 bond distance from 0.98 to 1.65 Å and decreasing of the H1–C3 distance to 1.17 Å. One imaginary frequency at 155.9i cm⁻¹ matches to the movement of the H1 to C3. The activation energy of 27.7 kcal mol⁻¹ is higher than the activation energy of the protonation of the zeolite proton to the alpha-carbon (C2) in the first pathway reported above. The arenium-ion like intermediate with two hydrogen atoms bonded to the beta-carbon (C3) is then produced and stabilized in the zeolite nano-cavity (Int1_b). The complexation energy of this intermediate compared to the isolate molecule is 20.8 kcal mol⁻¹. Then, this arenium species is converted to another one via the 1,2-hydride shift transition state TS2_b in which the H1–C3 bond is broken and the H1 proton is transferred to the oxygen atom C2. In this TS, the H1–C3 bond distance increases from 1.01 to 1.38 Å, while the H1⋯C2 distance decreases to 1.29 Å. The Mulliken population analysis for the partial atomic charge of the H1 atom is 0.260e, which indicates a hydride character of this proton. The transition state has one imaginary frequency of 777.8i cm⁻¹. The activation energy of this step is 16.4 kcal mol⁻¹. This barrier is also close to the previously calculated activation for the 1,2-hydride shift step in the propene oxide isomerization on H-ZSM-5.²⁵ The carbocation intermediate stays adsorbed in the zeolite with the energy of the adsorption complex compared to the isolated molecules of 11.0 kcal mol⁻¹. The next step is the decarbonylation of the CO group of the intermediate to form the product of furan via the transition state TS2_a (see Fig. 3), which is identical with the first pathway. The activation energy of this step is 12.3 kcal mol⁻¹. The products, furan and CO molecules, are co-adsorbed on the zeolite acidic site with an energy of −5.5 kcal mol⁻¹ in respect of the isolate and again is then desorbed with an energy of 3.0 kcal mol⁻¹.

Fig. 4 Energy profile and structures of reactants, intermediates and transition states for the second pathway for the furfural decarbonylation on H-ZSM-5 zeolite.

In the last reaction pathway, the reaction occurs via a four-step process (Fig. 5). It initials by the most stable adsorbed form of furfural on the Brønsted acid site with an adsorption energy of −15.7 kcal mol⁻¹ as discussed above. This adduct reacts to form the surface hydroxyalkyl species via the transition state TS1_c shown in Fig. 5. In this transition state, the Brønsted proton H1 is moved to the furfural carbonyl oxygen and the carbon C1 is adjusted to the bridging oxygen O2 of the zeolite. This results in an elongation of the Brønsted O1–H1 bond distance from 1.07 to 1.78 Å. The C1–O2 bond distance is decreased to 1.85 Å. The activation energy for this transition state is 16.8 kcal mol⁻¹. This transition state has one imaginary frequency at 155.9i cm⁻¹ related to the movement of H1 from O1 to O and the formation of the C1–O2 bond. The surface hydroxyalkyl species is formed in the zeolite pore with the relative energy of 1.0 kcal mol⁻¹. The H1 of the intermediate then migrates to the beta-carbon (C2) via the transition state TS2_c that involves the concerted bond breaking of the H1–O bond and the simultaneous formation of the H1–C2 bond. The H1–O bond distance increases from 0.97 to 1.41 Å, while the H1–C3 bond contracts to 1.37 Å. The vibrational mode of the transition state with an imaginary frequency at 1466.0i cm⁻¹ corresponds to the movement of H1 from O to C3. The activation energy is 45.8 kcal mol⁻¹. After the transition state migration, the arenium-ion intermediate (Int1_b) is formed with the relative energy of 20.8 kcal mol⁻¹. The following step is the same as in the second pathway in which the arenium-ion like intermediate (Int1_b) re-arranges via a hydride shift into another arenium intermediate (Int_a) and subsequently the Int_a intermediate is decarbonylated to produce the furan and CO molecule. The activation energies are calculated to be 16.4 and 12.3 kcal mol⁻¹, respectively.

Fig. 5 Energy profile and structures of reactants, intermediates and transition states for the third pathway for the furfural decarbonylation on H-ZSM-5 zeolite.

Fig. 6 shows the energetic profiles for all reaction pathways on H-ZSM-5 zeolite. It can be seen that the protonation step at the carbonyl group of furfural in the third pathway needs the smallest activation barrier compared to the first and second pathways. The activation energy is 16.8 kcal mol⁻¹. The reason is that the O of the furfural C=O group of contains more electrons density than the C2 and C3 carbon atoms. However, this protonation forms the low thermodynamic stability of the intermediate. It can be converted back to adsorbed furfural with a very small activation barrier of only 0.2 kcal mol⁻¹. Moreover, the step following the H transfer from O to beta-carbon, which is the rate determining step of this pathway, also requires a very high activation barrier (45.8 kcal mol⁻¹). This indicates that the continual steps from the protonation step to form the furan product are very difficult to occur. For the first and the second pathways, the protonation step is considered to be the rate-determining step. The activation energies are 22.1 and 27.7 kcal mol⁻¹ for the protonation at the alpha-carbon (C2) of the first pathway and at the beta-carbon (C3) of the second pathway, respectively. This indicates that the protonation at the C2 carbon of furfural occurs more easily than the C3 one which might be due to more electron density located C2 carbon. The subsequent reaction steps of these pathways are more facile than the protonation steps. In the first pathway, the activation barrier for the decarbonylation is 12.3 kcal mol⁻¹. For the second pathway, the 1,2 hydride shift and the decarbonylation of the subsequent reaction require activation energies of 16.4 and 12.3 kcal mol⁻¹, respectively. Altogether, the first pathway is the more favorable one because of the lower activation barrier in its rate-determining step.

Fig. 6 Comparison of all energy profiles for the furfural decarbonylation mechanisms over zeolites (energies are in kcal mol⁻¹).

We also consider the effect of the zeolite's framework by investigating the preferred reaction pathway on the small 12T cluster model (cf. Fig. S3†) by using the same level of theory. The 5T portion of active region and the reacting molecule are allowed to relax during geometry optimizations. The Table 3 shows the relative energies involved in the reaction on the 12T cluster compared to the 34T cluster models. The calculated adsorption free energy of furfural on the 12T is endothermic of −2.3 kcal mol⁻¹ which is 3.2 kcal mol⁻¹ less stable than the 34T zeolite cluster. This shows the contribution of the zeolite framework to be around of 40% in the furfural adsorption. Moreover, the relative energies of all reaction intermediates and the transition state calculated on the 12T cluster are also 5–13 kcal mol⁻¹ lower than those stationary points on the 34T cluster. The apparent activation barrier is contributed by the framework by 34 and 18%, for the first and second steps, respectively. These results show that the zeolite framework has an important role on the reaction studied in this work and cannot be ignored in a correct energy profile. This finding is in good agreement with our previous work, tungsten-methylidene formation on W/ZSM-5 zeolite.⁴¹

Table 3 Relative energies with respect to the reactants for the first pathway of the furfural decarbonylation on 12T and 34T clusters of H-ZSM-5 zeolite

Reaction coordinates	H-ZSM-5 clusters
	12T	34T
Ads_3	−2.3	−5.5
TS1_a	25.2 (Ea1 = 27.5)	16.6 (Ea1 = 22.1)
Int_a	24.3	11.0
TS2_a	28.5 (Ea2 = 4.2)	23.3 (Ea2 = 12.3)
Prod	−1.2	−5.5
Desorption	0.2	3.0

---

4. Conclusions

The reaction mechanism of the furfural decarbonylation over H-ZSM-5 zeolite has been investigated by using the M06-2X density functional. The adsorption energies of furfural are −5.5, −8.3 and −15.7 kcal mol⁻¹ for the interacting sites of the methine carbon atoms, ring's oxygen and hydroxyl group, respectively. The hydroxyl group site is the preferred one due to the strong hydrogen bonds interaction. After the adsorption, the furfural is decarbonated through three proposed possible pathways. In the first one, the furfural is protonated at the alpha-carbon leading to form an arenium-ion like intermediate which is then converted into furan via the decarbonylation process. The activation barriers are 22.1 and 12.3 kcal mol⁻¹, respectively. The rate-determining step is therefore the protonation. In the second pathway, the protonation of the beta-carbon furfural leads to an arenium-ion like intermediate species with C2 bonded by two hydrogen atoms. Then, the intermediate is re-arranged into another arenium-ion intermediate via the 1,2-hydride shift and subsequently the furan and CO molecules are created through decarbonylation reaction. The first step is rate-determining with an activation energy of 27.7 kcal mol⁻¹. The activation barriers of two subsequent steps are 16.4 and 12.3 kcal mol⁻¹, respectively. For the last pathway, furfural protonates and the surface hydroxyalkyl species is formed. The activation barrier is 16.8 kcal mol⁻¹. The reaction follows by the migration of hydrogen to form an arenium-ion like intermediate with the activation energy of 45.8 kcal mol⁻¹, which is considered to be a rate-determining step of this pathway. Then, the intermediate is re-arranged into another arenium-ion intermediate via a hydride shift and subsequently the furan and CO molecules are created which is the same as in the second step. With a smaller activation energy in the rate-determining step, the first pathway is the more favorable one. The zeolite framework is also found to play a role in stabilizing all of the species in the reaction coordinate as well as the transition state complexes.

Acknowledgements

This work was partially supported by grants from the National Science and Technology Development Agency (NANOTEC Center for Nanoscale Materials Design for Green Nanotechnology funded by the National Nanotechnology Center), the PTT group (PTT Public Company Limited, PTT Exploration & Production, PTT Global Chemical, IRPC Thaioil), the Commission on Higher Education, Ministry of Education (the “National Research University Project of Thailand (NRU)”), Kasetsart University Research and Development Institute (KURDI) and the Thailand Research Fund (TRF) to TM (TRG5880248).

References

1. A. J. Ragauskas, C. K. Williams, B. H. Davison, G. Britovsek, J. Cairney, C. A. Eckert, W. J. Frederick Jr, J. P. Hallett, D. J. Leak, C. L. Liotta, J. R. Mielenz, R. Murphy, R. Templer and T. Tschaplinski, Science, 2006, 311, 484.
2. G. W. Huber, S. Iborra and A. Corma, Chem. Rev., 2006, 106, 4044.
3. Y.-C. Lin and G. W. Huber, Energy Environ. Sci., 2009, 2, 68.
4. K. J. Zeitsch, The Chemistry and Technology of Furfural and Its Many Byproducts, Elsevier, Amsterdam, 1^st edn, 2000, vol. 13.
5. D. C. Elliott and T. R. Hart, Energy Fuels, 2009, 23, 631.
6. A. Corma, S. lborra and A. Velty, Chem. Rev., 2007, 107, 2411.
7. P. Lejemble, A. Gaset and P. Kalck, Biomass, 1984, 4, 263.
8. K. J. Jung and A. Gaset, Biomass, 1988, 16, 89.
9. W. Zhang, Y. Zhu, S. Niu and Y. Li, J. Mol. Catal. A: Chem., 2011, 335, 71.
10. J. Kijenski, P. Winiarek, T. Paryjczak, A. Lewicki and A. Mikołajska, Appl. Catal., A, 2002, 233, 171.
11. S. Sitthisa and D. E. Resasco, Catal. Lett., 2011, 141, 784.
12. V. V. Pushkarev, N. Musselwhite, K. An, S. Alayoglu and G. A. Somorjai, Nano Lett., 2012, 12, 5196.
13. J.-L. Grandmaison, P. D. Chantal and S. C. Kaliaguine, Fuel, 1990, 1058.
14. P. A. Horne and P. T. Williams, Fuel, 1996, 75, 1043.
15. P. A. Horne and P. T. Williams, Fuel, 1996, 75, 1051.
16. P. A. Horne and P. T. Williams, Renewable Energy, 1996, 7, 131.
17. M. I. Haniff and L. H. Dao, Appl. Catal., 1988, 39, 33.
18. T. R. Carlson, J. Jae, Y. C. Lin, G. A. Tompsett and G. W. Huber, J. Catal., 2010, 270, 110.
19. T. R. Carlson, Y. T. Cheng, J. Jae and G. W. Huber, Energy Environ. Sci., 2011, 4, 145.
20. Y. T. Cheng and G. W. Huber, ACS Catal., 2011, 1, 611.
21. W. L. Fanchiang and Y. C. Lin, Appl. Catal., A, 2012, 419–420, 102.
22. S. Namuangruk, P. Pantu and J. Limtrakul, J. Catal., 2004, 225, 523.
23. S. Namuangruk, P. Pantu and J. Limtrakul, ChemPhysChem, 2005, 6(7), 1333.
24. B. Jansang, T. Nanok and J. Limtrakul, J. Phys. Chem. B, 2006, 110, 12626.
25. S. Namuangruk, P. Khongpracha, P. Pantu and J. Limtrakul, J. Phys. Chem. B, 2006, 110(51), 25950.
26. N. Hansen, T. Brüggemann, A. T. Bell and F. J. Keil, J. Phys. Chem. C, 2008, 112, 15402.
27. Y. Zhao and D. G. Truhlar, J. Phys. Chem. C, 2008, 112, 6860.
28. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157.
29. B. Boekfa, S. Choomwattana, P. Khongpracha and J. Limtrakul, Langmuir, 2009, 25(22), 12990.
30. T. Maihom, B. Boekfa, J. Sirijaraensre, T. Nanok, M. Probst and J. Limtrakul, J. Phys. Chem. C, 2009, 113, 6654.
31. T. Maihom, P. Pantu, C. Tachakritikul, M. Probst and J. Limtrakul, J. Phys. Chem. C, 2010, 114, 7850.
32. B. Boekfa, P. Pantu, M. Probst and J. Limtrakul, J. Phys. Chem. C, 2010, 114, 15061.
33. S. Wannakao, B. Boekfa, P. Khongpracha, M. Probst and J. Limtrakul, ChemPhysChem, 2010, 11, 3432.
34. K. Bobuatong, M. Probst and J. Limtrakul, J. Phys. Chem. C, 2010, 114, 21611.
35. S. Wannakao, P. Khongpracha and J. Limtrakul, J. Phys. Chem. A, 2011, 115, 12486.
36. T. Maihom, P. Khongpracha, J. Sirijaraensre and J. Limtrakul, ChemPhysChem, 2013, 14, 101.
37. S. Wannakao, C. Warakulwit, K. Kongpatpanich, M. Probst and J. Limtrakul, ACS Catal., 2012, 2, 986.
38. W. Panjan, J. Sirijaraensre, C. Warakulwit, P. Pantu and J. Limtrakul, Phys. Chem. Chem. Phys., 2012, 14, 16588.
39. T. Maihom, S. Wannakao, B. Boekfa and J. Limtrakul, Chem. Phys. Lett., 2013, 556, 217.
40. T. Maihom, M. Probst and J. Limtrakul, J. Phys. Chem. C, 2014, 118(32), 18564.
41. T. Maihom, M. Probst and J. Limtrakul, ChemPhysChem, 2015, 16(15), 3334.
42. R. B. Getman, J. H. Miller, K. Wang and R. Q. Snurr, J. Phys. Chem. C, 2011, 115, 2066.
43. T. Maihom, S. Choomwattana, P. Khongpracha, M. Probst and J. Limtrakul, ChemPhysChem, 2012, 13, 245.
44. T. Maihom, S. Wannakao, B. Boekfa and J. Limtrakul, J. Phys. Chem. C, 2013, 117(34), 17650.
45. K. Lee, W. C. Isley, A. L. Dzubak, P. Verma, S. J. Stoneburner, L. C. Lin, J. D. Howe, E. D. Bloch, D. A. Reed, M. R. Hudson, C. M. Brown, J. R. Long, J. B. Neaton, B. Smit, C. J. Cramer, D. G. Truhlar and L. Gagliardi, J. Am. Chem. Soc., 2014, 136(2), 698.
46. C. Raksakoon, T. Maihom, M. Probst and J. Limtrakul, J. Phys. Chem. C, 2015, 119(7), 3564.
47. H. van Koningsveld, H. van Bekkum and J. C. Jansen, Acta Crystallogr., Sect. B: Struct. Sci., 1987, 43, 127.
48. W. Ding, G. D. Meitzner, D. O. Marler and E. Iglesia, J. Phys. Chem. B, 2001, 105, 3928.
49. H. B. Schlegel, J. Comput. Chem., 1982, 3, 214.
50. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1989, 90, 2154.
51. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523.
52. M. J. T. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision C01, Gaussian, Inc., Wallingford CT, 2010.
53. S. Vaitheeswaran, S. K. Green, P. Dauenhauer and S. M. Auerbach, ACS Catal., 2013, 3, 2012.
54. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334.
55. K. Seonah, J. E. Tabitha, M. Calvin, B. Lintao, T. B. Gregg, R. N. Mark, S. P. Robert and J. R. David, ACS Sustainable Chem. Eng., 2016, 4, 2615.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1 and S2: IRC calculation for the furfural protonation to the secondary carbocation and the elimination of the CO group to the furan. Fig. S3: the 12T cluster model of H-ZSM-5 zeolite. Tables S1–S3: relative energies from ΔE, ΔE_zero, ΔH and ΔG values at 298.15 K for the furfural decarbonylation. See DOI: 10.1039/c6ra24631a

---