Ultrashort-laser-pulse-induced thermal lensing effect in pure H2O and a NaCl–H2O solution†
Yi-Ci Lia,
Yu-Ting Kuoa,
Po-Yuan Huanga,
Cheng-I. Leeb and
Tai-Huei Wei*a
aDepartment of Physics, National Chung Cheng University, Min-Hsiung, Chia-Yi 621, Taiwan. E-mail: twei@ccu.edu.tw; Fax: +886-05-272-0587; Tel: +886-05-272-0411 ext. 66324
bDepartment of Life Science, National Chung Cheng University, Min-Hsiung, Chia-Yi 621, Taiwan
First published on 14th November 2016
Abstract
Using the Z-scan technique with 82 MHz 18 femtosecond (fs) laser pulses at 820 nm, we explore the thermal lensing effect induced in pure H2O and a NaCl–H2O solution. We verify that linear absorption dominates over both two-photon absorption and stimulated light scattering (SLS) in heating of pure H2O. This differs from the situation wherein SLS dominates heating of CS2. In addition, when dissolution of NaCl into H2O at a concentration of 1 M incorporates thermal and mass diffusions into the mechanisms of the thermal lensing effect, we find that this effect is enhanced and thus determine that the sign of the Soret coefficient of NaCl is positive. Notably, use of 820 nm 18 fs laser pulses in this study, in contrast to visible continuous light commonly used in the thermal diffusion forced Rayleigh scattering technique embedded with the optical heterodyne detection scheme, eliminates the need to add inert dyes into NaCl–H2O to enhance the absorption. This avoids the artefact caused by the dyes.
Introduction
Water is an essential substance in living systems. The biological importance of water has been recognized for its chemical and physical properties. For example, due to the polarity, water dissolves ionic compounds and polar molecules such as salts, carbohydrates, proteins and amino acids; however, it does not dissolve nonpolar molecules such as oils and fats. Due to hydrogen bonding, water facilitates specific inter-molecular interactions in aqueous solutions. As a result, water's polarity and hydrogen bonding drive the biological self-assembly processes, e.g., folding of proteins and nucleic acids, membrane formation of biomolecular complexes and lipids, etc.1 When these self-assembly processes underlie the construction of biologic macromolecular assemblies in living organisms, they are crucial to the multiple interdependent functions of cells.1,2 Another example is water's large heat capacity. When water is involved in many metabolic reactions, such as ATP syntheses, this thermal property helps organisms resist temperature rise and hence ensures enzymes to catalyse biochemical metabolic reactions.3,4 More unambiguous studies demonstrated that water plays a central role in biological processes rather than just being a solvent modelled as a homogeneous dielectric medium.5 Up to date, many diseases are not curable due to the lack of deep understanding of the mechanisms of biological processes. Therefore, for the biological importance of water, it is essential to further study the role of water in explicit molecular participation in various processes such as solvation, diffusion and transport, biomolecular interactions, etc. Notably, all of these processes are influenced by the properties of water interfaces.Several techniques have been used to study the chemical and physical properties of water interface with biomolecules or free space from the microscopic view point, such as scanning tunneling microscopy,6 atomic force microscopy,7 optical second-harmonic generation and sum-frequency generation,8 ultrafast optical techniques, infrared and terahertz spectroscopies,9–11 electron and nuclear magnetic resonance,12 X-ray spectroscopy and neutron reflectivity.13,14 Besides, the explicit influences of the dynamics, polarity and hydrogen bonding of the interfacial water to the biomolecules have been numerically simulated.15
In this work we investigate, using the Z-scan technique with 82 MHz 18 femtosecond (fs) laser pulses at 820 nm, the thermal lensing effect induced in pure H2O and a NaCl–H2O solution, the most commonly used electrolyte solution. For pure H2O, we quantitatively explain this effect in terms of temperature change Δθ (≡θ − θe with θ being the sample temperature and θe being the equilibrium sample temperature), induced by laser heating and thermal diffusivity, as well as temperature-gradient (∇θ)-driven density change Δρ (≡ρ − ρe with ρ being the sample density and ρe being the equilibrium sample density). In particular, we compare the heating mechanisms of H2O with those of CS2 which have been previously verified with fs laser pulses delivered at repetition rates of tens of MHz.16–20 It is worth noting that when individual 820 nm 18 fs laser pulses excite CS2 via the stimulated light scattering [SLS, Fig. 1(a)] processes,20 a category of third-order nonlinear optical processes, this work shows that the same pulses do not effectively excite H2O via the SLS processes. Instead, they promote H2O molecules, via one-photon absorption (OPA) [Fig. 1(b)], from the vibrational ground state to a Raman combination of the first overtone of O–H symmetric stretching, bending, and O–H asymmetric stretching fundamental.21–23 Since population density reduction of the vibrational ground state due to OPA is negligible (vide infra), OPA is regarded as linear absorption (LA). In contrast to CS2, a benchmark simple liquid, H2O has a strong polarity and hydrogen bonding network which give it the peculiar chemical and physical properties as mentioned in the preceding paragraph. For NaCl–H2O, a binary system, we additionally involve thermal diffusion, namely, the Ludwig–Soret effect, and mass diffusion as the mechanisms of thermal lensing effect. Accordingly, we further consider the contribution of mass fraction changes of NaCl (Δw) and H2O (−Δw) to the thermal lensing effect. As a result, we find that dissolution of NaCl into H2O at 1 M strengthens the thermal lensing effect of pure H2O. This indicates that the Soret coefficient of NaCl is positive and that of H2O is negative. The behaviors of thermal and mass diffusions relate to inter-molecular interaction between interfacial H2O and NaCl. Understanding of these behaviors at the molecular level is not fully clear yet and can be pursued by molecular dynamics (MD) simulation methods in the future (vide infra).
 | ||
| Fig. 1 The schemes of simple liquid excitation from the ground states to the excited states by (a) SLS, (b) OPA and (c) TPA. Ω's and ΔΩ's denote the band center energies and band widths. | ||
With regard to the application potential of this work, we expect our interpretation of the thermal lensing effect, particularly the thermal acoustic wave (also referred to as photoacoustic wave) generation, helps the development of photoacoustic wave tomography.24,25 In connection with drug delivery, we further anticipate that it helps to clarify the mechanisms of cell membrane permeabilization by a laser-induced photoacoustic wave.26,27 As to the understanding of photo-thermal properties of the interfacial water, this work may serve as a reference. For example, by executing the same measurements on aqueous solutions of biomolecules and comparing the results with those of this work, we expect to learn more about the properties of water interface with the biomolecules.28,29
Experimental
Z-Scan is a single-beam technique for investigating various materials' nonlinear absorption (NLA) and nonlinear refraction (NLR) properties.20,30 As shown in Fig. 2, this technique measures a sample's total transmittance and axial transmittance (the transmitted powers, P2 and P3, detected by detector D2 and detector D3 placed behind an aperture in the far field, divided by the input power P1 monitored by detector D1) of a focused Gaussian beam as functions of the sample position z (more strictly speaking, the sample's front surface position) relative to the beam waist. The open aperture Z-scan curve, the plot of the total transmittance D2/D1 as a function of z, reveals NLA alone. The closed aperture Z-scan curve, the plot of the axial transmittance D3/D1 as a function of z, contains NLR in combination with NLA (if present). When NLA is evident, division of the closed aperture Z-scan curve by the corresponding open aperture Z-scan curve yields a curve with NLA effectively eliminated and NLR retained. This curve, referred to as the divided Z-scan curve, shows the sign of NLR. When NLA is absent or unapparent, the closed aperture Z-scan curve itself reveals the sign of NLR. Because NLA is unapparent for both H2O and NaCl–H2O (vide infra), we present in this study the open aperture and closed aperture Z-scan curves with their transmittances normalized with those in the linear regime (regions of large |z| in which linear absorption and linear refraction prevail). We refer to these Z-scan curves as the normalized ones. | ||
| Fig. 2 The Z-scan setup which records the total and axial transmittances as functions of the sample position z. | ||
For pure H2O, the light source is a self-mode locked Ti:Al2O3 laser operated in the TEM00 mode to generate laser pulses with a central wavelength of λc = 820 nm (equivalently a central angular frequency of ωc = 2.3 × 1015 s−1), a duration of τ = 18 fs measured at half-width at e−1 maximum (HWe−1M) and a repetition rate of 82 MHz (equivalently a pulse-to-pulse separation of τp–p = 12.2 ns). A shutter is placed in the light path before the beam splitter BS1 to chop the laser pulses into trains with a train width of τt = 41 ms and a train-to-train separation of τt–t = 0.18 s (Fig. 3). The major portion (∼96%) of the incident pulse trains passing BS1 is tightly focused to the waist at z = 0 of radius w0 ≡ w(0) = 14.0 μm half-width at e−2 maximum (HWe−2M). The rest (∼4%) of the incident pulse trains is reflected to D1 by BS1. The total and axial transmittances (D2/D1 and D3/D1) are recorded for each sample position z relative to the beam waist at 10 different times relative to the leading pulse of the train: T ≡ t − t0 = 1, 2, 3, 5, 7, 9, 11, 21, 31 and 41 ms. Here t denotes the time in the laboratory reference frame and t0 specifies the arrival time of the leading pulse (i = 0) at a certain sample position z. The sample was contained in a quartz cuvette with a thickness of L = 0.1 cm. The aperture before D3 (0.3 cm in radius) was placed at 22.5 cm after the beam waist. This allows 67% of the power at the aperture plane to reach D3 given the sample placed in the linear regime.
Referring to ref. 20 and 31 for z and r (the lateral distance) dependence of a monochromatic TEM00 mode laser beam, we write the frequency-domain electric field strength of a pulse, say the ith one (0 ≤ i ≤ iend with iend = 41 ms/τp–p) in a train, as
 | (1) |
 is the frequency-domain on-axis electric field strength of the ith pulse at z = 0 and ω = ωc. The term
is the frequency-domain on-axis electric field strength of the ith pulse at z = 0 and ω = ωc. The term 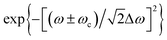 is introduced to reflect the experimentally measured Gaussian distributed spectrum of a pulse. Here the “+” and “−” signs before ωc are employed when ω is negative and positive, respectively. Δω is the spectrum width of a 18 fs laser pulse, measured at half-width at e−1 maximum (HWe−1M). k = ω/c denotes the wave propagation number. The following term is the phase slowly varying with z in contrast to e−ikz:
is introduced to reflect the experimentally measured Gaussian distributed spectrum of a pulse. Here the “+” and “−” signs before ωc are employed when ω is negative and positive, respectively. Δω is the spectrum width of a 18 fs laser pulse, measured at half-width at e−1 maximum (HWe−1M). k = ω/c denotes the wave propagation number. The following term is the phase slowly varying with z in contrast to e−ikz:
 | (2) |
 is a Hermitian complex quantity, i.e., its real and imaginary parts are respectively symmetrical and anti-symmetrical about ω = 0, the Fourier transform of it gives the time-domain electric field strength32
is a Hermitian complex quantity, i.e., its real and imaginary parts are respectively symmetrical and anti-symmetrical about ω = 0, the Fourier transform of it gives the time-domain electric field strength32
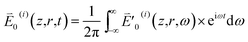 | (3) |
 equals
equals  . This indicates that each pulse in a train is identical. According to ref. 20, each pulse represented by eqn (1) and (3) is transform limited with Δω = 1/τ.20,33 We confirmed this relation by respectively conducting autocorrelation and spectrum measurements immediately before BS1 and obtained τ = 18 fs and Δω = 5.5 × 1013 s−1 whose product equals one. By ignoring chirping induced in BS1 and the lens by nonzero second-order derivative of k with respect to ω (d2k/dω2), we assume that the pulses remain transform limited until the sample at z and then derive the electric field strength at z from eqn (1) or (3).
. This indicates that each pulse in a train is identical. According to ref. 20, each pulse represented by eqn (1) and (3) is transform limited with Δω = 1/τ.20,33 We confirmed this relation by respectively conducting autocorrelation and spectrum measurements immediately before BS1 and obtained τ = 18 fs and Δω = 5.5 × 1013 s−1 whose product equals one. By ignoring chirping induced in BS1 and the lens by nonzero second-order derivative of k with respect to ω (d2k/dω2), we assume that the pulses remain transform limited until the sample at z and then derive the electric field strength at z from eqn (1) or (3).
By integrating the magnitude of the Poynting vector [ with ε0 = 8.85 × 10−14 C2 (N m2)−1 denoting the electric permittivity of free space] of the ith pulse over its duration, we obtain, according to eqn (1) and (3), the fluence (energy per unit area)
with ε0 = 8.85 × 10−14 C2 (N m2)−1 denoting the electric permittivity of free space] of the ith pulse over its duration, we obtain, according to eqn (1) and (3), the fluence (energy per unit area)
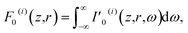 | (4) |
 | (5) |
 denotes the frequency-domain on-axis intensity of the ith pulse at z = 0 and ω = ωc.
denotes the frequency-domain on-axis intensity of the ith pulse at z = 0 and ω = ωc.  represents the amplitude of
represents the amplitude of 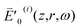 which slowly varies with z in contrast to e−ikz. Since
which slowly varies with z in contrast to e−ikz. Since  is Hermitian, similar to
is Hermitian, similar to 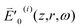 , I′0(i)(z,r,ω) equals I′0(i)(z,r,−ω) and thus eqn (4) can be rewritten as
, I′0(i)(z,r,ω) equals I′0(i)(z,r,−ω) and thus eqn (4) can be rewritten as
 | (6) |
| ε0(i) = π3/2w02ΔωI′0(i)(0,0,ωc). | (7) |
 | (8) |
For NaCl–H2O at 1 M, the experimental setup is the same as the one used for pure H2O except that the major portion of the incident pulse trains passing BS1 is focused more tightly to the waist at z = 0 of radius w0 = 12.0 μm. The sample was contained in a quartz cuvette with a thickness of L = 0.1 cm. Additionally, when the sample was placed in the linear regime, the transmittance D3/D1 through the aperture was reduced to 40% from 67%.
Theoretical model
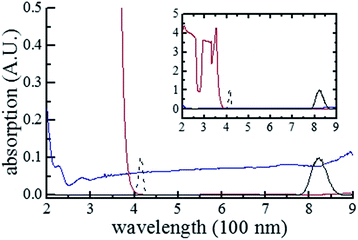
For pure H2O, we first describe in this section the formation of a thermal lens in terms of temperature change Δθ, induced by individual-pulse heat generation, cross-pulse heat accumulation and thermal diffusivity, as well as density change Δρ, stemming from ∇θ-driven thermal acoustic wave. Secondly, we elucidate how the intensity and phase of each pulse are changed by absorption and refraction. Finally, we simulate the Z-scan curves to be compared with the experimentally obtained ones. For NaCl–H2O, we follow the procedures for pure H2O except that we involve the contributions of mass fraction changes of NaCl (Δw) and H2O (−Δw) to the thermal lensing effect.Fig. 4 shows the absorption spectra of pure H2O and CS2. From the full linear absorption spectra of them (see the inset), we might think that both samples are transparent at 410 and 820 nm. However, by expanding the weak absorption in the ranges [209 nm, 900 nm] for H2O and [382 nm, 900 nm] for CS2, we find that H2O is absorptive at both 410 and 820 nm when CS2 is transparent at these two wavelengths (see the main figure). This means that H2O shows stronger OPA and two-photon absorption [a third-order nonlinear optical process other than SLS, dubbed TPA, Fig. 1(c)] of 820 nm 18 fs laser pulses than CS2. According to ref. 21, OPA by H2O may excite its molecular motion from the vibrational ground state to a Raman combination of the first overtone of O–H symmetric stretching, bending, and O–H asymmetric stretching fundamental, referred to as 2Ωv(ss) + Ωv(b) + Ωv(as), by absorbing a photon at ω ∼ ωc (2.3 × 1015 s−1). Here Ωv(ss) denotes the fundamental symmetric stretching energy and equals 6.2 × 1014 s−1 (3280 cm−1), Ωv(b) denotes the fundamental bending energy and equals 3.1 × 1014 s−1 (1645 cm−1), and Ωv(as) denotes the fundamental asymmetric stretching energy and equals 6.6 × 1014 s−1 (3490 cm−1).21 In addition, TPA by H2O may excite its molecular motion from the vibrational ground state to aΩv(ss) + bΩv(as) with a + b = 8, via an intermediate virtual state, by absorbing two photons, one at ω1 and the other at ω2 with ω1 + ω2 ∼ 2ωc. Henceforth, we denote the vibrational ground state by |0)v, the state 2Ωv(ss) + Ωv(b) + Ωv(as) by |1)O, and the state aΩv(ss) + bΩv(as) with a + b = 8 by |1)T for short. In this study, the occurrence of OPA requires overlap of its spectrum range [ΩO − ΔΩO/2, ΩO + ΔΩO/2] with the spectrum range of a pulse [ωc − Δω, ωc + Δω] [see Fig. 1(b)]. Here ΩO and ΔΩO respectively denote the band center energy, relative to |0)v, and band width of |1)O with Planck's constant ħ divided out. The occurrence of TPA demands overlap of its spectrum range [ΩT − ΔΩT/2, ΩT + ΔΩT/2] with the spectrum range [2ωc − 2Δω, 2ωc + 2Δω] pertaining to self-frequency summation of a pulse [see Fig. 1(c)]. Here ΩT and ΔΩT respectively denote the band center energy, relative to |0)v, and band width of |1)T with ħ divided out.
Besides OPA and TPA, we consider the SLS processes as possible mechanisms for H2O's molecular motion excitation. This is because they have been used to quantitatively explain the thermal lensing effect induced in CS2 by 820 nm 18 fs laser pulses delivered at a repetition rate of 82 MHz.20 Indeed, excitation of molecular motions in various simple liquids, including H2O and CS2, via the SLS processes has been verified with time-resolved optical Kerr effect (OKE) measurements.34–40 When molecular motions of simple liquids can be categorized into vibration (v), libration (l), diffusive reorientation (d) and polarizability distortion (p), the SLS processes responsible for excitation of vibration and libration are called the stimulated Raman scattering (SRS) and those for excitation of diffusive reorientation and polarizability distortion are called the stimulated Rayleigh-wing scattering (SRWS).41 SLS of H2O may excite its molecular motions from the ground states |0)m's to the excited states |1)m's, via an intermediate virtual state, by absorbing a photon at a higher angular frequency (ω1) and emitting a photon at a lower angular frequency (ω2) with ω1 − ω2 ∼ Ωm [see Fig. 1(a)]. Here Ωm denotes the band center energy of |1)m relative to |0)m with ħ divided out and m denotes v, l, d or p. In this study, the occurrence of a SLS process requires overlap of its spectrum range [Ωm − ΔΩm/2, Ωm + ΔΩm/2] with the spectrum range [0, 2Δω] pertaining to self-frequency subtraction of a pulse [see Fig. 1(a)].20 This indicates that a pulse should have a spectrum width (Δω) wider or comparable with the energy Ωm to fulfill a SLS process. Here ΔΩm denotes the band width of |1)m with ħ divided out. Since Δω for a 18 fs laser pulse used in this study [5.5 × 1013 s−1 (292 cm−1)] is smaller than Ωv [3.1 × 1014 s−1 (1645 cm−1)] and Ωl [5.7 × 1013 to 1.9 × 1014 s−1 (300 to 1000 cm−1)]42 but much larger than Ωd and Ωp estimated in the range of 5 to 200 cm−1,43 the pulses can more likely excite diffusive reorientation and polarizability distortion of H2O by SRWS but not vibration and libration by SRS. Relaxation of these two excited molecular motions may contribute to the thermal lensing effect, the main concern of this study. In the following, we consider the diffusive reorientation and polarizability distortion in combination and use Ωd+p and ΔΩd+p to denote the effective band center energy and band width.
Absorption of a TEM00 mode 820 nm 18 fs pulse, by H2O via OPA, TPA or SLS, excites its molecular motions. Relaxation of these excited molecular motions causes a laterally non-uniform temperature change (Δθ) and hence a temperature gradient (∇θ) which drives in the sample an acoustic wave, namely, the thermal acoustic wave, propagating in the lateral direction at a speed of vs = 1497 m s−1.44 This wave renders a sample density change Δρ which predominantly contributes to the thermal lensing effect.45 Since Δρ becomes noticeable after the acoustic wave propagates across the beam cross section in the transit time τac (≡w0/vs with w0 denoting the beam radius at the waist) estimated in 10 ns order (vide infra),46 an 18 fs pulse with its duration much shorter than τac does not experience the thermal lensing effect induced by itself. However, it experiences the thermal lensing effect induced by the preceding pulses in the same train because the pulse-to-pulse separation of τp–p = 12.2 ns is comparable with τac. Because the train width τt = 41 ms is considerably longer than the thermal diffusivity time τth of the sample [341 μs (vide infra)], the thermal lensing effect built up across neighboring pulses is gradually suppressed and balanced by thermal diffusivity. On the other hand, because τt–t is significantly longer than τth, the sample thermally perturbed by a certain pulse train returns to thermodynamic (thermal, mechanical and chemical) equilibrium before the next pulse train arrives.
To calculate the absorption and refraction of a pulse in H2O (say the ith one in a train), we start with the electromagnetic wave equation driven by the third-order polarization pertaining to an SLS process20
 | (9) |
 equals
equals  defined in eqn (1). μ is the magnetic permeability of the sample, which is nearly equal to that of the vacuum (μ0) since the sample is nonmagnetic.
defined in eqn (1). μ is the magnetic permeability of the sample, which is nearly equal to that of the vacuum (μ0) since the sample is nonmagnetic. 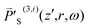 is the third-order nonlinear polarization pertaining to an SLS process and can be related to the frequency-domain electric field strength as20
is the third-order nonlinear polarization pertaining to an SLS process and can be related to the frequency-domain electric field strength as20
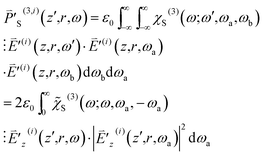 | (10) |
 are both Hermitian, we restrict ourselves to the situation that ω is positive without loss of generality. Here the third-order susceptibility χS(3)(ω;ω,ωa,ωb) is represented by the product of
are both Hermitian, we restrict ourselves to the situation that ω is positive without loss of generality. Here the third-order susceptibility χS(3)(ω;ω,ωa,ωb) is represented by the product of ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) S(3)(ω;ω,ωa,ωb) and the delta function δ(ωa + ωb) because ωa + ωb is required to be zero.
S(3)(ω;ω,ωa,ωb) and the delta function δ(ωa + ωb) because ωa + ωb is required to be zero. ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) S(3)(ω;ω,ωa,−ωa) (=
S(3)(ω;ω,ωa,−ωa) (=![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) SRe(3) + i
SRe(3) + i![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) SIm(3)) depends on ω − ωa explicitly and is nonzero only when |ω − ωa| falls in the SLS spectrum range [Ωm − ΔΩm/2, Ωm + ΔΩm/2]. That is,
SIm(3)) depends on ω − ωa explicitly and is nonzero only when |ω − ωa| falls in the SLS spectrum range [Ωm − ΔΩm/2, Ωm + ΔΩm/2]. That is, ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) S(3) is nonzero only when ωa falls in the range [ω − Ωm − ΔΩm/2, ω − Ωm + ΔΩm/2] or [ω + Ωm − ΔΩm/2, ω + Ωm + ΔΩm/2]. In order for
S(3) is nonzero only when ωa falls in the range [ω − Ωm − ΔΩm/2, ω − Ωm + ΔΩm/2] or [ω + Ωm − ΔΩm/2, ω + Ωm + ΔΩm/2]. In order for  to be nonzero, ωa in the range [ω − Ωm − ΔΩm/2, ω − Ωm + ΔΩm/2] needs to be covered in the spectrum of
to be nonzero, ωa in the range [ω − Ωm − ΔΩm/2, ω − Ωm + ΔΩm/2] needs to be covered in the spectrum of  with ω, and ωa in the range [ω + Ωm − ΔΩm/2, ω + Ωm + ΔΩm/2] needs to be covered in the spectrum of
with ω, and ωa in the range [ω + Ωm − ΔΩm/2, ω + Ωm + ΔΩm/2] needs to be covered in the spectrum of 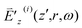 with ω. This demands overlap of [Ωm − ΔΩm/2, Ωm + ΔΩm/2] with [0, 2Δω].
with ω. This demands overlap of [Ωm − ΔΩm/2, Ωm + ΔΩm/2] with [0, 2Δω].
In the following, we incorporate into the right hand side of eqn (9) the first- and third-order polarizations pertaining to the OPA and TPA processes
 | (11) |
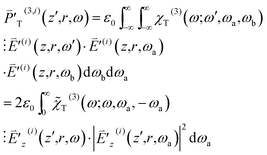 | (12) |
 to be nonzero, ω needs to fall in the spectrum range of OPA [ΩO − ΔΩO/2, ΩO + ΔΩO/2] and that of a pulse [ωc − Δω, ωc + Δω]. This demands overlap of [ΩO − ΔΩO/2, ΩO + ΔΩO/2] with [ωc − Δω, ωc + Δω]. The third-order susceptibility χT(3)(ω;ω,ωa,ωb) is represented by the product of
to be nonzero, ω needs to fall in the spectrum range of OPA [ΩO − ΔΩO/2, ΩO + ΔΩO/2] and that of a pulse [ωc − Δω, ωc + Δω]. This demands overlap of [ΩO − ΔΩO/2, ΩO + ΔΩO/2] with [ωc − Δω, ωc + Δω]. The third-order susceptibility χT(3)(ω;ω,ωa,ωb) is represented by the product of ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) T(3)(ω;ω,ωa,ωb) and δ(ωa + ωb) because ωa + ωb is required to be zero.
T(3)(ω;ω,ωa,ωb) and δ(ωa + ωb) because ωa + ωb is required to be zero. ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) T(3)(ω;ω,ωa,−ωa) (=
T(3)(ω;ω,ωa,−ωa) (=![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) TRe(3) + i
TRe(3) + i![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) TIm(3)) depends on ω + ωa explicitly and is nonzero only when ω + ωa falls in the TPA spectrum range [ΩT − ΔΩT/2, ΩT + ΔΩT/2]. That is,
TIm(3)) depends on ω + ωa explicitly and is nonzero only when ω + ωa falls in the TPA spectrum range [ΩT − ΔΩT/2, ΩT + ΔΩT/2]. That is, ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) T(3) is nonzero only when ωa falls in the range [ΩT − ω − ΔΩT/2, ΩT − ω + ΔΩT/2]. In order for
T(3) is nonzero only when ωa falls in the range [ΩT − ω − ΔΩT/2, ΩT − ω + ΔΩT/2]. In order for 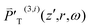 to be nonzero, ωa in the range [ΩT − ω − ΔΩT/2, ΩT − ω + ΔΩT/2] needs to be covered in the spectrum of a pulse [ωc − Δω, ωc + Δω] with ω. This demands overlap of [ΩT − ΔΩT/2, ΩT + ΔΩT/2] with [2ωc − 2Δω, 2ωc + 2Δω].
to be nonzero, ωa in the range [ΩT − ω − ΔΩT/2, ΩT − ω + ΔΩT/2] needs to be covered in the spectrum of a pulse [ωc − Δω, ωc + Δω] with ω. This demands overlap of [ΩT − ΔΩT/2, ΩT + ΔΩT/2] with [2ωc − 2Δω, 2ωc + 2Δω].
Since (i)  is a quasi-plane wave disturbance with
is a quasi-plane wave disturbance with  , (ii)
, (ii)  varies with (z + z′) much more slowly than e−ik(z+z′), and (iii) the sample satisfies the thin sample condition with its thickness 0.1 cm equal to the diffraction length of the ωc component of the pulse in it [n × z0(ωc) = 0.1 cm with n = 1.33 being H2O's refractive index44 and z0(ωc) = 7.5 × 10−2 cm being the diffraction length of the ωc component of the pulse in free space], we eventually arrive at the Beer's law equation and phase change equation by following the procedures to derive eqn (17) and (18) in ref. 20
varies with (z + z′) much more slowly than e−ik(z+z′), and (iii) the sample satisfies the thin sample condition with its thickness 0.1 cm equal to the diffraction length of the ωc component of the pulse in it [n × z0(ωc) = 0.1 cm with n = 1.33 being H2O's refractive index44 and z0(ωc) = 7.5 × 10−2 cm being the diffraction length of the ωc component of the pulse in free space], we eventually arrive at the Beer's law equation and phase change equation by following the procedures to derive eqn (17) and (18) in ref. 20
 | (13) |
 | (14) |
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) TIm(3)(ω;ω,ωa,−ωa), βSl = −
TIm(3)(ω;ω,ωa,−ωa), βSl = −![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) SIm(3)(ω;ω,ωl,−ωl), βSh = −
SIm(3)(ω;ω,ωl,−ωl), βSh = −![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) SIm(3)(ω;ω,ωh,−ωh), nT2 =
SIm(3)(ω;ω,ωh,−ωh), nT2 = ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) TRe(3)(ω;ω,ωa,−ωa), nS2l =
TRe(3)(ω;ω,ωa,−ωa), nS2l = ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) SRe(3)(ω;ω,ωl,−ωl) and nS2h =
SRe(3)(ω;ω,ωl,−ωl) and nS2h = ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) SRe(3)(ω;ω,ωh,−ωh), all multiplied by 2π/cε0. Note that when (ω − ωl) equals −(ω − ωh), βSl equals −βSh and nS2l equals nS2h.20 At z′ = 0, I′z(i)(z′,r,ω) and ϕz(i)(z′,r,ω) equal I′0(i)(z,r,ω) and ϕ0(i)(z,r,ω) defined in eqn (5) and (2), respectively. From eqn (13) and (14) we learn that χOIm(1)(ω),
SRe(3)(ω;ω,ωh,−ωh), all multiplied by 2π/cε0. Note that when (ω − ωl) equals −(ω − ωh), βSl equals −βSh and nS2l equals nS2h.20 At z′ = 0, I′z(i)(z′,r,ω) and ϕz(i)(z′,r,ω) equal I′0(i)(z,r,ω) and ϕ0(i)(z,r,ω) defined in eqn (5) and (2), respectively. From eqn (13) and (14) we learn that χOIm(1)(ω), ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) TIm(3) and
TIm(3) and ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) SIm(3) are responsible for the sample's absorption; χORe(1),
SIm(3) are responsible for the sample's absorption; χORe(1), ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) TRe(3) and
TRe(3) and ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) SRe(3) are responsible for the sample's refraction.
SRe(3) are responsible for the sample's refraction.
From Fig. 4, we find that the spectra ranges of OPA and TPA, [ΩO − ΔΩO/2, ΩO + ΔΩO/2] and [ΩT − ΔΩT/2, ΩT + ΔΩT/2], fully cover the spectrum range of a 820 nm 18 fs laser pulse [ωc − Δω, ωc + Δω] and that pertaining to a self-frequency summation of a 820 nm 18 fs laser pulse [2ωc − 2Δω, 2ωc + 2Δω], respectively. In addition, OPA and TPA spectra exhibit no discernable variation within the ranges [ωc − Δω, ωc + Δω] and [2ωc − 2Δω, 2ωc + 2Δω], respectively. Accordingly, we can ignore the dispersions of χO(1)(ω) and ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) T(3)(ω;ω,ωa,−ωa) and approximate them as χO(1)(ωc) and
T(3)(ω;ω,ωa,−ωa) and approximate them as χO(1)(ωc) and ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) T(3)(ωc;ωc,ωa,−ωa). Moreover, we can reduce the integration range [0, ∞] for the second terms on the right hand sides of eqn (13) and (14) to several times of Δω centered at ωc. On the other hand, when a 820 nm 18 fs laser pulse has its spectrum width Δω (5.5 × 1013 s−1) larger than Ωd+p and ΔΩd+p, both being in the order of 1012 s−1 (tens of cm−1), we can reduce the integration range [0, ω] for the third terms on the right hand sides of eqn (13) and (14) to a few times of ΔΩd+p/2 centered at ω − Ωd+p. Similarly, we can reduce the integration range [ω, ∞] for the fourth terms on the right hand sides of eqn (13) and (14) to a few times of ΔΩd+p/2 centered at ω + Ωd+p. For a specific z, we can integrate eqn (13) and (14) over the sample thickness z′ from 0 to L = 0.1 cm, with the initial conditions I′z(i)(0,r,ω) = I′0(i)(z,r,ω) and ϕz(i)(z′,r,ω) = ϕ0(i)(z,r,ω), to obtain I′z(i)(L,r,ω) and ϕ′z(i)(L,r,ω) [equivalently
T(3)(ωc;ωc,ωa,−ωa). Moreover, we can reduce the integration range [0, ∞] for the second terms on the right hand sides of eqn (13) and (14) to several times of Δω centered at ωc. On the other hand, when a 820 nm 18 fs laser pulse has its spectrum width Δω (5.5 × 1013 s−1) larger than Ωd+p and ΔΩd+p, both being in the order of 1012 s−1 (tens of cm−1), we can reduce the integration range [0, ω] for the third terms on the right hand sides of eqn (13) and (14) to a few times of ΔΩd+p/2 centered at ω − Ωd+p. Similarly, we can reduce the integration range [ω, ∞] for the fourth terms on the right hand sides of eqn (13) and (14) to a few times of ΔΩd+p/2 centered at ω + Ωd+p. For a specific z, we can integrate eqn (13) and (14) over the sample thickness z′ from 0 to L = 0.1 cm, with the initial conditions I′z(i)(0,r,ω) = I′0(i)(z,r,ω) and ϕz(i)(z′,r,ω) = ϕ0(i)(z,r,ω), to obtain I′z(i)(L,r,ω) and ϕ′z(i)(L,r,ω) [equivalently  ] at the exit surface of the sample (pure H2O).
] at the exit surface of the sample (pure H2O).
On the right hand side of eqn (14), we additionally introduce the term kΔnz(i) to cope with the possible situation that after being perturbed by the 0th through the (i − 1)th pulses (i > 0), the sample does not fully restore thermodynamic equilibrium when the ith pulse arrives. Considering that absorption of individual 18 fs pulses by the sample induces the thermal lensing effect, this effect is sustained across neighboring pulses because the thermal diffusivity time constant of τth = 341 μs (vide infra) for H2O is much longer than the pulse-to-pulse separation of τp–p = 12.2 ns. Hence the term kΔnz(i) represents the thermal lensing effect. Here Δnz(i) denotes the thermally induced refractive index change by the 0th through the (i − 1)th pulses and experienced by the ith pulse. Note that Δn(0)z equals 0 because the sample is in full thermodynamic equilibrium when the leading pulse (i = 0) starts to interact with the sample.
To derive Δnz(i) for i > 0, we first recede the superscript i in eqn (13) to (i − 1) and then evaluate the heat generated in a unit volume of the sample by the (i − 1)th pulse
 | (15) |
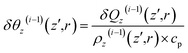 | (16) |
 | (17) |
Subsequent to temperature change by non-radiative relaxation and thermal diffusivity [see eqn (17)], sample density ρz(z′,r,t) changes with t in response to the ∇θ-driven thermal acoustic wave46
 | (18) |
 | (19) |
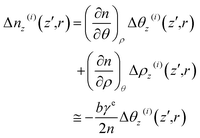 | (20) |
For NaCl–H2O, a binary system, we incorporate thermal and mass diffusions into the mechanisms of the thermal lensing effect. This demands a modification of eqn (20) as47
 | (21) |
 | (22) |
 | (23) |
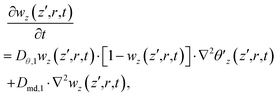 | (24) |
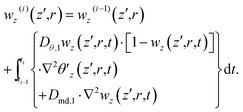 | (25) |
By subtracting θ′z(i), ρ′z(i) and wz(i) from their equilibrium values θ′(0)z(z′,r) = θ′e, ρ′(0)z(z′,r) = ρ′e and w(0)z(z′,r) = we (estimated 5.6%), we can derive Δθz(i)(z′,r), Δρ′z(i)(z′,r) and Δwz(i)(z′,r) and then substitute them into eqn (21) to evaluate Δn′z(i)(z′,r).
Computational detail
For pure H2O, to simulate both the open aperture and closed aperture Z-scan curves measured at each of the 10 times relative to the leading pulse (T's), ranging between 1 and 41 ms, we numerically integrate eqn (13) and (14), for all the sample positions z′s and all the i's sequentially advanced from 0 to iend, over z′ from 0 to L to derive the frequency-domain intensity I′z(i)(L,r,ω) and phase ϕz(i)(L,r,ω) [equivalently ] at the exit surface of the sample. Note that when we advance from one pulse to the next one, we deal with the effects accumulated over the time between them. For i > 0, we need to conduct integration or calculation in eqn (15)–(17), (19) and (20) beforehand. This yields Δnz(i) involved in eqn (14). However, for the leading pulse (i = 0), we simply substitute Δn(0)z = 0 into eqn (14) before the numerical integrations of eqn (13) and (14).
] at the exit surface of the sample. Note that when we advance from one pulse to the next one, we deal with the effects accumulated over the time between them. For i > 0, we need to conduct integration or calculation in eqn (15)–(17), (19) and (20) beforehand. This yields Δnz(i) involved in eqn (14). However, for the leading pulse (i = 0), we simply substitute Δn(0)z = 0 into eqn (14) before the numerical integrations of eqn (13) and (14).
By invoking Huygens–Fresnel propagation formalism,49 we deduce the frequency-domain intensity at the aperture I′a(i) from  . By respectively integrating 2I′z(i)(L,r,ω) over the spectrum width and the cross section of the ith pulse, we obtain the total transmitted pulse energy εt(i) [see eqn (6) and (7) for the integration detail]. By respectively integrating 2I′a(i) over the spectrum width of the ith pulse and the aperture area, we obtain the axial transmitted pulse energy εa(i). Given the response function of the detectors [output of an incident delta function δ(T)] h(T) = 0 for T ≤ 0 and e−T/20 μs for T > 0, we further simulate the powers
. By respectively integrating 2I′z(i)(L,r,ω) over the spectrum width and the cross section of the ith pulse, we obtain the total transmitted pulse energy εt(i) [see eqn (6) and (7) for the integration detail]. By respectively integrating 2I′a(i) over the spectrum width of the ith pulse and the aperture area, we obtain the axial transmitted pulse energy εa(i). Given the response function of the detectors [output of an incident delta function δ(T)] h(T) = 0 for T ≤ 0 and e−T/20 μs for T > 0, we further simulate the powers  ,
,  and
and  to be compared with the experimentally measured D1, D2 and D3. Here “*” denotes the convolution operation, Ti ≡ (i − 1) × τp–p is the arrival time of the ith pulse, relative to the leading pulse, at the sample and T is sequentially set to be the data measuring times: 1, 2, 3, 5, 7, 9, 11, 21, 31 and 41 ms. Plots of P2(T)/P1(T) and P3(T)/P1(T), after being normalized with those in the linear regime, as functions of z yield the simulated normalized open aperture and closed aperture Z-scan curves.
to be compared with the experimentally measured D1, D2 and D3. Here “*” denotes the convolution operation, Ti ≡ (i − 1) × τp–p is the arrival time of the ith pulse, relative to the leading pulse, at the sample and T is sequentially set to be the data measuring times: 1, 2, 3, 5, 7, 9, 11, 21, 31 and 41 ms. Plots of P2(T)/P1(T) and P3(T)/P1(T), after being normalized with those in the linear regime, as functions of z yield the simulated normalized open aperture and closed aperture Z-scan curves.
Given the Avogadro constant Na = 6.02 × 1023 mol−1 as well as equilibrium density ρe = 1.0 g cm−3 and molecular weight M = 18.02 g mol−1 for pure H2O, we obtain the equilibrium molecular concentration 3.3 × 1022 cm−3 for H2O residing on |0)v. On the other hand, division of δQz=0(i)(z′ = 0,r = 0), pertaining to Pavg = 270 mW, by ħΩO yields the maximum possible molecular concentration of 6.6 × 1014 cm−3 for H2O promoted to the |1)O state. Since it is much smaller than the equilibrium one on |0)v, population density decrease of |1)O is negligible. Accordingly, we regard OPA as LA in this study.
For NaCl–H2O, we can simulate its Z-scan results by simply following the procedures for pure H2O with the parameters replaced by those for NaCl–H2O and eqn (20) replaced by eqn (21). However, in this study, we only show the experimental Z-scan result of NaCl–H2O accompanied by that for pure H2O, both taken at the train end (T = τt = 41 ms), for qualitative comparison.
Results and discussion
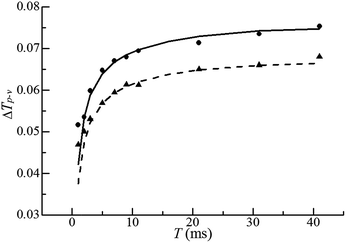
For H2O, the normalized open aperture Z-scan curve obtained with un-modulated 18 fs pulses at Pavg = 270 mW [equivalently ε0(i) = 3.3 × 10−9 J] is shown by dots in Fig. 5(a), in which NT denotes the normalized total transmittance. Exhibiting no discernable structures at around z = 0, this curve suggests that H2O does not show noticeable NLA (TPA or SLS). Since the open aperture Z-scan measurements are insensitive to linear absorption, this curve does not involve any information of χOIm(1). The dots in Fig. 5(b)–(h) show the normalized closed aperture Z-scan curves measured with 82 MHz 18 fs pulses (at Pavg = 270 mW) chopped into trains with a train-width of τt = 41 ms and a train-to-train separation of τt–t = 0.18 s. Each of the 7 frames correlates to a measuring time relative to the leading pulse of the train: T = 1, 3, 7, 11, 21, 31, and 41 ms, respectively. The measurements conducted at T = 2, 5, and 9 ms are omitted in this figure. Appearance of a peak and a valley on the −z and +z sides in each curve indicates a negative lensing effect of H2O. When the magnitude of the lensing effect is reflected by the difference between the peak and valley values of NTa (the normalized axial transmittance) in a normalized closed aperture Z-scan curve, which is denoted by ΔTp–v, we exhibit ΔTp–v's, extracted from Fig. 5(b)–(h), by dots in Fig. 6 as a function of time relative to the leading pulse (T). It is evident that ΔTp–v's increase with increasing T within τth = 341 μs and gradually steadies after T exceeds τth. This suggests that the contribution of thermal lensing effect to the dotted curves in Fig. 5(b)–(h). As depicted by eqn (15)–(17), (19) and (20), this effect is accumulated across neighboring pulses and is gradually balanced by thermal diffusivity. Since the closed aperture Z-scan measurements are insensitive to linear refraction (LR) but sensitive to the thermal lensing effect, these curves do not reflect any information of χORe(1) but may reveal the information of χOIm(1) provided that the thermal lensing effect involves the contribution of LA.The best fits to the dotted curves in Fig. 5(b)–(h), shown by the continuous line curves, are acquired using χOIm(1)(ω) = 6.5 × 10−7 cm (V s)−1, βT = βSl = βSh = 0, and nT2 = nS2l = nS2h = 0. This indicates that the thermal lensing effect is predominantly contributed by LA rather than TPA or SLS. The peak–valley separation (zp–v) of each dotted curve in Fig. 5(b)–(h) is nearly 1.3 mm, 1.7 times of the diffraction length z0. This agrees with the reasoning in ref. 18 that the LA-induced thermal lensing effect yields the closed aperture Z-scan curves with zp–v = 1.7z0. The line curve in Fig. 6 is extracted from the line curves in Fig. 5(b)–(h). The triangles and the dashed line curve shown in Fig. 6 are the experimental and theoretical results, corresponding to an average incident laser power of Pavg = 240 mW (equivalently ε0(i) = 3.3 × 10−9 J), obtained in the same manner as the dots and the solid line curve. Since the ratio of ΔTp–v for the dots to that for the triangles at any time T is proportional to the first power of the power ratio (270 mW/240 mW)1, this further confirms that heat is primarily generated by LA.18 It is worth noting that the heating mechanism of H2O differs from that of CS2, a benchmark simple liquid. As reported in ref. 20, zp–v for CS2 equals 1.2z0 and the ratios of ΔTp–v's measured at any two of the three employed incident powers are proportional to the second power of the corresponding power ratios. This indicates that heating of CS2 is induced by third order NLA. In particular, since CS2 is transparent in the frequency range of a frequency doubled 820 nm 18 fs laser pulse (see Fig. 4), NLA due to SLS is considered as the dominant heating mechanism of CS2.20
For 1 M NaCl–H2O, the normalized closed aperture Z-scan curve measured at the train end (T = τt = 41 ms) with Pavg = 281 mW (equivalently ε0(i) = 3.4 × 10−9 J) is presented by the red dotted curve in Fig. 7. The accompanying black crossed curve shows the result of pure H2O obtained under the same experimental condition. Since the mass diffusion time constant τmd = w02/4Dmd is longer than the train width τt = 41 ms by (typically) three orders of magnitude,50 the thermal and mass diffusions contributed to the thermal lensing effect in the red dotted curve is activated at the early stage. On the other hand, since LA of an 820 nm laser is weaker in NaCl–H2O than in pure H2O,51 the temperature gradient and hence the density change in NaCl–H2O (∇θ′ and Δρ′) are expected to be smaller than those in pure H2O. Thus, the actual thermal lensing effect of NaCl–H2O is expected to be less than that of pure H2O before thermal and mass diffusions are activated. Accordingly, the fact that ΔTp–v of the red dotted curve is larger than that of the black crossed curve indicates an enhancement of the thermal lensing effect in NaCl–H2O by thermal and mass diffusions. That is, the thermal and mass diffusions of NaCl–H2O cause a negative lensing effect cooperatively. Also, by extending the train width τt from 41 ms to τmd, we expect ΔTp–v of the red dotted curve will be significantly increased but that of the black crossed curve will remain nearly unchanged.
 | ||
| Fig. 7 Z-Scan results of a NaCl–H2O solution at 1 M and pure H2O represented by red dots and black crosses, respectively. | ||
Given that (∂n′/∂w)ρ′,θ′ in eqn (21) is positive,52 we learn, by comparing the two curves in Fig. 7, that Δwz(i)(z′,r) is negative and less at the beam center (warmer region) than at the peripheral (cooler region) in the course of the pulse train irradiation. This means that, according to eqn (24) and (25), Dθ,1 and hence the Soret coefficient ST,1 (≡Dθ,1/Dmd,1) of NaCl are positive so that ∇θ drives NaCl to migrate from the warmer region to the cooler region, with respect to the center of mass of NaCl–H2O. On the contrary, since the Soret coefficient of H2O ST,2 (≡Dθ,2/Dmd,2 = −ST,1) is negative,53 ∇θ drives H2O to migrate from the cooler region to the warmer region, relative to the center of mass.
In the future we will study, in more depth, the thermal and mass diffusions of NaCl–H2O at various mass fractions of NaCl (w's). Firstly, we will conduct the Z-scan measurements on NaCl–H2O in the same way as executed on pure H2O in this study except that the train width τt and train-to-train separation τt–t are extended to surpass the mass diffusion time constant τmd = w02/4Dmd. Here the extension of τt and τt–t is to allow the binary system to carry out thermal and mass diffusions sufficiently and then to restore thermodynamic equilibrium fully. Secondly, we will quantitatively fit the experimental results, in the manner described in Sec. IV, to extract the signs and magnitudes of Dθ,1(2), Dmd,1(2) and ST,1(2). In particular, we will see if the signs of ST,1(2) change with w. Finally, we will pursue an explanation of both diffusions at the microscopic level.
In the ESI,† we comprehensively review the completed work and on-going tasks of thermal and mass diffusions. From the reviewed references, we learn that most of the first measurements of both diffusions in various binary systems were conducted with the thermal diffusion forced Rayleigh scattering (TDFRS) technique embedded with a heterodyne detection (OHD) scheme. In comparison with this technique (OHD-TDFRS), Z-scan has the advantage of ease of operation and the disadvantage of higher sensitivity to convection-induced artifact. Besides, use of the 820 nm 18 fs laser pulses in this study, in contrast to visible continuous light commonly used in OHD-TDFRS, eliminates the need to add inert dyes into NaCl–H2O to enhance absorption. This avoids artifact caused by the dyes.
To understand more fully the OHD-TDFRS results of various systems at the molecular level, molecular dynamics (MD) simulation methods have been developed to compute the Soret coefficients ST's to be compared with the ones obtained by quantitatively fitting the experimental results. Up to now, molecular understanding of thermal and mass diffusions is still in progress.
Based on the ESI,† we will specifically deal with the following points in our future Z-scan study of both diffusions induced in NaCl–H2O and other binary systems. Firstly, we will make efforts to rule out the influence of convection. Secondly, we will pursue, with MD simulation methods, a deeper understanding of inter-molecular interaction at the molecular level, particularly the effects of hydrogen bonding and molecular polarity. Finally, we will apply our knowhow to aqueous solutions of various biological molecules in order to unravel the properties of H2O interfaces with these molecules.
Conclusions
In this study, we have quantitatively studied the thermal lensing effect induced in pure H2O by 820 nm 18 fs laser pulses at a repetition rate of 82 MHz. As a result, we found that the heating mechanism of H2O is OPA rather than SLS, the dominant heating mechanism of CS2. Also, we have qualitatively studied the thermal lensing effect induced in NaCl–H2O at 1 M. Consequently, we learned that dissolution of NaCl into H2O incorporates thermal and mass diffusions into the mechanisms of the thermal lensing effect. In addition, we noted that these two diffusions cooperatively enhance the thermal lensing effect. Accordingly, given that the derivative of the refractive index n′ with respect to the mass fraction of NaCl [(∂n′/∂w)ρ′,θ′, see eqn (21)] is positive, the Soret coefficient of NaCl ST,1 is positive. This indicates that NaCl migrates from the warmer region to the cooler region with respect to the center of mass of NaCl–H2O.Continuous light at 980 nm has been used in ref. 54 to avoid adding inert dyes to the investigated aqueous and non-aqueous mixtures which are absorptive at 980 nm. In this study, we further used 820 nm 18 fs laser pulses delivered at 82 MHz as the light source. Not only does this avoid using inert dyes because H2O is absorptive at 820 nm, it also enables nonlinear absorption of binary systems transparent at 820 nm, e.g., CS2 mixed with another liquid transparent therein.
Considering heating mechanisms of CS2 (SLS) and pure H2O (OPA) are at two extremes, we will take, in the future, the same approach to compare the contributions of OPA and SLS to the heating effects of 1,2-dichloroethane and 1,2-dibromoethane which show non-negligible OPA at ∼820 nm and relevant SLS.38 Hopefully, we can find out a way to quantitatively compare the contributions of OPA and SLS to the heating effects of various simple liquids.
Acknowledgements
T. H. Wei gratefully acknowledges financial support from National Science Council grant MOST 105-2112-M-194-003. T. H. Wei also thanks E. W. Van Stryland of CREOL, University of Central Florida, for helpful discussions. C. I. Lee is grateful to the Ministry of Science and Technology for financial support (MOST 104-2113-M-194-006).References
- G. Hummer and A. Tokmakoff, J. Chem. Phys., 2014, 141, 22D101 CrossRef PubMed.
- A. V. Martinez, E. Malolepsza, E. Rivera, Q. Lu and J. E. Straub, J. Chem. Phys., 2014, 141, 22D530 CrossRef PubMed.
- D. Nelson and M. Cox, Lehninger Principles of Biochemistry, W. H. Freeman, New York, 5th edn, 2008, ISBM: 978-071-677108-1 Search PubMed.
- T. Engel, G. Drobny and P. Reid, Physical Chemistry for the Life Sciences, Pearson Prentice Hall, Upper Saddle River, N. J., 2008, ISBM: 9780-321-50449-4 Search PubMed.
- K. Karhan, R. Z. Khaliullin and T. D. Kuhne, J. Chem. Phys., 2014, 141, 22D528 CrossRef PubMed.
- T. Mitsui, M. K. Rose, E. Fomin, D. F. Ogletree and M. Salmeron, Science, 2002, 297, 1850 CrossRef CAS PubMed.
- J. W. G. Tyrrell and P. Attard, Phys. Rev. Lett., 2001, 87, 176104 CrossRef CAS PubMed.
- N. Ji, V. Ostroverkhov, C. S. Tian and Y. R. Shen, Phys. Rev. Lett., 2008, 100, 096102 CrossRef CAS PubMed.
- S. A. Waldauer, B. S. Buchli, L. Frey and P. Hamm, J. Chem. Phys., 2014, 141, 22D514 CrossRef PubMed.
- S. Wolf, E. Freier, Q. Cui and K. Gerwert, J. Chem. Phys., 2014, 141, 22D524 CrossRef PubMed.
- H. Vondracek, J. D. Gessner, W. Lubitz, M. Knipp and M. Havenith, J. Chem. Phys., 2014, 141, 22D534 CrossRef PubMed.
- I. V. Sergeyev, S. Bahri, L. A. Day and A. E. McDermott, J. Chem. Phys., 2014, 141, 22D533 CrossRef PubMed.
- S. Ghosal, J. C. Hemminger, H. Bluhm, B. S. Mun, E. L. D. Hebenstreit, G. Ketteler, D. F. Ogletree, F. G. Requejo and M. Salmeron, Science, 2005, 307, 563 CrossRef CAS PubMed.
- D. Schwendel, T. Hayashi, R. Dahint, A. Pertsin, M. Grunze, R. Steitz and F. Schreiber, Langmuir, 2003, 19, 2284 CrossRef CAS.
- S. Roy, S. M. Gruenbaum and J. L. Skinner, J. Chem. Phys., 2014, 141, 22D505 CrossRef CAS PubMed.
- M. Falconieri and G. Salvetti, Appl. Phys. B, 1999, 69, 133 CrossRef CAS.
- K. Kamada, K. Matsunaga, A. Yoshino and K. Ohta, J. Opt. Soc. Am. B, 2003, 20, 529 CrossRef CAS.
- A. Gnoli, L. Razzari and M. Righini, Opt. Express, 2005, 13, 7976–7981 CrossRef CAS PubMed.
- Y.-C. Li, S.-Z. Kuo, T. H. Wei, J.-N. Wang, S. S. Yang and J.-L. Tang, Jpn. J. Appl. Phys., 2009, 48, 09LF06 Search PubMed.
- Y.-C. Li, Y.-T. Kuo, P.-Y. Huang, S. S. Yang, C.-I. Lee and T.-H. Wei, Phys. Chem. Chem. Phys., 2015, 17, 24738 RSC.
- R. M. Pope and E. S. Fry, Appl. Opt., 1997, 36, 8710 CrossRef CAS PubMed.
- R. N. Tolchenov, O. Naumenko, N. F. Zobov, S. V. Shirin, O. L. Polyansky, J. Tennyson, M. Carleer, P.-F. Coheur, S. Fally, A. Jenouvrier and A. C. Vandaele, J. Mol. Spectrosc., 2005, 233, 68 CrossRef CAS.
- N. F. Zobov, S. V. Shirin, R. I. Ovsyannikov, O. L. Polyansky, R. J. Barber, J. Tennyson, P. F. Bernath, M. Carleer, R. Colin and P.-F. Coheur, Mon. Not. R. Astron. Soc., 2008, 387, 1093 CrossRef CAS.
- X. Wang, Y. Pang, G. Ku, X. Xie, G. Stoica and L. V. Wang, Nat. Biotechnol., 2003, 21, 803 CrossRef CAS PubMed.
- Z. Xu, C. Li and L. V. Wang, J. Biomed. Opt., 2010, 15, 036019 CrossRef PubMed.
- P. Soman, W. Zhang, A. Umeda, Z. Jonathan and S. Chen, J. Biomed. Nanotechnol., 2011, 7, 1 CrossRef.
- M. Waleed, S.-U. Hwang, J.-D. Kim, I. Shabbir, S.-M. Shin and Y.-G. Lee, Biomed. Opt. Express, 2013, 4, 1533 CrossRef PubMed.
- B.-J. de Gans, R. Kita, B. Muller and S. Wiegand, J. Chem. Phys., 2003, 118, 8073 CrossRef CAS.
- G. A. Orozco, O. A. Moultos, H. Jiang, I. G. Economou and A. Z. Panagiotopoulos, J. Chem. Phys., 2014, 141, 234507 CrossRef PubMed.
- M. Sheik-Bahae, A. A. Said, T. H. Wei, D. J. Hagan and E. W. Van Stryland, IEEE J. Quantum Electron., 1990, 26, 760 CrossRef CAS.
- A. Yariv, Optical Electronics, Oxford University Press, New York, 1990, ch. 2 Search PubMed.
- M. Schubert and B. Wilhelmi, Nonlinear Optics and Quantum Electronics, Wiley, 1986, p. 107 Search PubMed.
- J.-C. M. Diels, J. J. Fontaine, I. C. McMichael and F. Simoni, Appl. Opt., 1985, 24, 1270 CrossRef CAS PubMed.
- Y. X. Yan and K. A. Nelson, J. Chem. Phys., 1987, 87, 6240 CrossRef CAS.
- W. Lotshaw, D. McMorrow, C. Kalpouzos and G. A. Kenney-Wallace, Chem. Phys. Lett., 1987, 136, 323 CrossRef CAS.
- S. J. Rosenthal, N. F. Scherer, M. Cho, X. Xie, M. E. Schmidt and G. R. Fleming, in Ultrafast Phenomena, ed. J. L. Martin, A. Migus, G. A. Mourou and A. H. Zewail, Springer, Berlin, 1993, vol. 8, p. 616 Search PubMed.
- T. H. Huang, C. C. Hsu, T. H. Wei, M. J. Chen, S. Chang, W. S. Tse, H. P. Chiang and C. T. Kuo, Mol. Phys., 1999, 96, 389 CrossRef CAS.
- J. L. Tang, C. W. Chen, J. Y. Lin, Y. D. Lin, C. C. Hsu, T. H. Wei and T. H. Huang, Opt. Commun., 2006, 266, 669 CrossRef CAS.
- N. A. Smith and S. R. Meech, Int. Rev. Phys. Chem., 2002, 21, 75 CrossRef CAS.
- S. Ruhman, B. Kohler, A. G. Joly and K. A. Nelson, IEEE J. Quantum Electron., 1988, 24, 470 CrossRef.
- Y. R. Shen, The Principles of Nonlinear Optics, Wiley-Interscience, 1984, p. 187 Search PubMed.
- F. N. Keutsch, R. S. Fellers, M. G. Brown, M. R. Viant, P. B. Petersen and R. J. Saykally, J. Am. Chem. Soc., 2001, 123, 5938 CrossRef CAS PubMed.
- P. A. Madden, Chem. Phys. Lett., 1986, 123, 502 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 83rd edn, 1996 Search PubMed.
- D. I. Kovsh, S. Yang, D. J. Hagan and E. W. Van Stryland, Appl. Opt., 1999, 38, 5168 CrossRef CAS PubMed.
- D. I. Kovsh, D. J. Hagan and E. W. Van Stryland, Opt. Express, 1999, 4, 315 CAS.
- W. Kohler and R. Schafer, Adv. Polym. Sci., 2000, 151, 1 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Pergamon Press, 2nd edn, 1987, p. 233 Search PubMed.
- M. Born and E. Wolf, Principles of Optics, Pergamon, 5th edn, 1975, p. 383 Search PubMed.
- J. Rauch and W. Kohler, Phys. Rev. Lett., 2002, 88, 185901 CrossRef CAS PubMed.
- R. Rottgers, D. McKee and C. Utschig, Opt. Express, 2014, 22, 25093 Search PubMed.
- D. Malarde, Z. Y. Wu, P. Grosso, J.-L. de Bougrenet de la Tocnaye and M. Le Menn, Meas. Sci. Technol., 2009, 20, 015204 CrossRef.
- M. M. Bou-Ali, A. Ahadi, D. A. de Mezquia, Q. Galand, M. Gebhardt, O. Khlybov, W. Kohler, M. Larranga, J. C. Legros, T. Lyubimova, A. Mialdun, I. Ryzhkov, M. Z. Saghir, V. Shevtsova and S. Van Vaerenbergh, Eur. Phys. J. E, 2015, 38, 15030 CrossRef PubMed.
- P. Polyakov and S. Wiegand, Phys. Chem. Chem. Phys., 2009, 11, 864 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra24361d |
| This journal is © The Royal Society of Chemistry 2016 |