Associated relationship between ventilation rates and indoor air quality
Abstract
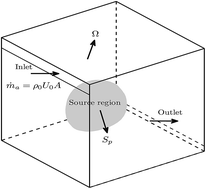
Ventilation represents a significant portion of building energy consumption. Current codes and standards do not offer adequate guidance with respect to energy efficiency and to the relationship between the ventilation rate and the degree of indoor hazard. For the sake of energy savings, it is of great importance to study the associations between ventilation rates and indoor air quality (IAQ). Hence, in this work we aimed to investigate the influence of ventilation rates on IAQ for an indoor ventilated enclosure. Herein, ventilation efficiency is represented by the maximal local volume-averaged concentration and recirculation rate. In the present study, computation fluid dynamics (CFD) was applied and the low-Re-number k–ε model (verified by experiments) was selected for Reynolds-averaged Navier–Stokes (RANS) simulations, with buoyancy effects considered due to density differences. We found that when increasing the inlet ventilation rates, the impact on indoor pollutant concentration was considerable due to the increase in the turbulent diffusion effects. Moreover, this was less dependent on the larger range of slot Reynolds numbers (for the current study, Res ≥ 3000) and it ultimately tends to show an asymptotic behavior, which refutes the common working hypothesis of “the larger the ventilation rates, the better the IAQ”. These findings should further play an important role in the design of energy-efficient ventilation systems.

 Please wait while we load your content...
Please wait while we load your content...