Hyperfine interaction vs. spin–orbit coupling in organic semiconductors

Abstract

Organic semiconductors have shown magnetic field responses in electrical currents. This phenomenon has been generally attributed to hyperfine interaction (HFI) and spin–orbit coupling (SOC). For the first time, we report the experimental and theoretical studies on hyperfine interaction vs. spin–orbit coupling in one thin film of organic semiconductor poly [9,9-di-n-hexyl-fluorenyl-2,7-diyl] and the dramatic influence of doping the PFO with complexes of bis [2-(2′-benzothienyl)-pyridinato-N, C3′] iridium (acetyl-acetonate). The intra-molecular HFI and SOC are only dependent on the intra-molecular interaction among electrons, nuclei and orbital field in a given molecule. Phosphorescence and fluorescence spectroscopies were used to measure the spin–orbit coupling strength. Furthermore, HFI is a short-range interaction and inter-molecular HFI is negligible. Inter-molecular SOC depends not only on molecular structure but also distance between adjacent molecules. Inter-molecular SOC strength increases strongly when the distance between adjacent molecules is decreased.

---

1 Introduction

Spintronics uses electron spins as quantum information carriers. Remarkable progress has been observed in the field of organic spintronics using polymers and small molecules.^1–10 The report of a magnetic field influencing the emission of an organic semiconducting material was first introduced by Johnson for an anthracene crystal.¹¹ Recently, polyfluorene has been shown to have a large magnetoresistance of over 10% at room temperature with magnetic fields of only a few mT.¹⁰ As a result, interest in the science behind this intrinsic magnetic field effects has risen sharply. Even though the exact mechanism behind magnetic field effects is still debated,¹² it is widely believed to be related to hyperfine interaction (HFI) and spin–orbit coupling (SOC). HFI is the spin–spin interaction between the nucleus spin and the electron spin. As an example, in a typical organic semiconductors tris-(8-hydroxyquinoline) gallium, HFI is predominantly due to the H atoms and other nuclear atoms, such as Ga and N in tris-(8-hydroxyquinoline) gallium. SOC is the coupling between the electron orbital angle momentum and its spin momentum. Many studies suggest that HFI in simple π-conjugated molecules is dominated.^13,14 On the contrary, the heavy-metal complex molecule always exhibit strong spin–orbital coupling.¹⁵ Obviously, HFI and SOC are two major contributions to magnetic field responses in organic semiconductors. However, they were investigated separately in the most published papers. To date, many experiments have been carried out to measure the HFI using the nuclear magnetic resonance and electron spin resonance (ESR) between ITO and metal electrodes.^16,17 However, the SOC is not directly measurable, so there is little quantification of SOC in individual organic semiconductor. It prevents the direct understanding of spin mechanism in organic materials. It is therefore necessary to investigate hyperfine interaction and spin–orbit coupling in the same system. In the present work, intra-molecular and inter-molecular hyperfine interaction vs. spin–orbit coupling competed on the same platform. Fluorescence and phosphorescence spectroscopies were used to measure the spin–orbit coupling strength. We give the report for the first time, the theoretical and experimental studies on hyperfine interaction vs. spin–orbit coupling in one thin film of organic semiconductor poly [9,9-di-n-hexyl-fluorenyl-2,7-diyl] (PFO) and the dramatically influence of doping the PFO with complexes of bis [2-(2′-benzothienyl)-pyridinato-N, C3′] iridium (acetyl-acetonate) (BtpIr) that introduce tuning hyperfine interaction and spin–orbit coupling.

2 Experimental

The polymer PFO and the phosphorescent dye BtpIr were purchased from Aldrich Chemical Company and used them as purchased without further purification. The structural formulas of these compounds are illustrated in Fig. 1(a). The BtpIr was mixed with the polymer PFO in chloroform keeping the polymer PFO concentration constant (10 mg ml⁻¹) and altering the dye concentration. A schematic diagram of the device fabricated is shown in Fig. 1(b). The pre-patterned ITO glass substrates were cleaned ultra-sonically (sequentially) with acetone, de-ionize water, and chloroform. A PEDOT : PSS layer was spin coated over the ITO (having sheet resistance 12 Ω per square) keeping the spin rate at 3000 rpm for 15 s. Next, different concentration (100 : 0.1, 100 : 1, 100 : 2 w/w) of PFO : BtpIr solutions were spin cast on the top of PEDOT : PSS layer. All of these organic films were prepared under the nitrogen atmosphere protection. The samples were then baked in vacuum at 120 °C. Finally, the aluminum electrode was deposited by thermal evaporation equipment under a base pressure of 2 × 10⁻⁴ Pa at a rate of 2.0 Å s⁻¹. The active device area was roughly 2 × 2 mm². The magnetic field effects were measured by recording the change of the device current using a Keithley 2400 Source Meter under a parallel magnetic field to the device plane. The samples were immersed in liquid nitrogen condition which is to be taken to avoid oxygen and can keep constant temperature. The thin films for the photoluminescence (PL) measurements were characterized by a Hitachi 2700 spectrophotometer.

Fig. 1 (a) The structural formulas of dopant and host materials that have been used in control experiments. (b) Schematic diagram of the devices fabricated for the MR measurements.

3 Results and discussion

The magnetic field response, magnetoresistance (MR) is determined by measuring the change in current at a constant applied voltage with different magnetic field.where I_B and I₀ are the injection current with and without an applied magnetic field.

Fig. 2 shows the magnetic field response on MR for all devices with various doping ratio. The MR was measured at constant voltage model with 0–320 mT magnetic field. It can be seen that all the MR is negative and the magnitude of MR rapidly increases with increasing magnetic field in the low field range and then slowly saturates in the range from 45 mT to 130 mT. It is well known that the carrier density is usually low for an organic semiconductor device. So the devices were operating in the space-charge-limited current (SCLC) regime when an electric field was applied. A series of current–voltage measurements were undertaken to experimentally verify this regime, as is shown in Fig. 2. The current density can be shown as:¹⁸

here, b is the thickness of the organic semiconductor film, V is the voltage across that film, ε₀ is the dielectric constant of space, ε_r is the relative dielectric constant of the organic semiconductor, and μ_e (h) is the mobility of the electrons (holes) in the organic semiconductor. The term μ_r is the e–h recombination mobility,

μ_r = ε₀ε_rβ/2e (3)

where β is the recombination coefficient.¹⁹ The magnetic field can influence the injected current by means of impacting the recombination of the system. If μ_r increases, the current density decreases. However, in the presence of a magnetic field, the energy band degeneracy of the triplet states is changed by Zeeman splitting, and inter-system crossing (ISC) only occurs between the m₀ states, while the singlet no longer interconvert with the long-lived triplets in the m_±1 states and has a reasonable possibility of dissociation.¹⁸ HFI will benefit from triplets to convert into singlets when the energy states degenerate. As a result, the MR signal exhibit negative in these devices.

Fig. 2 Typical magnetoresistance (MR) traces for a constant applied voltage for PFO : BtpIr with the different doping concentration (100 : 0.1, 100 : 1, 100 : 2 w/w) as compared to pure PFO and BtpIr molecules. The experimental error for magnetocurrent is about 0.01%. Inset: the current–voltage characteristics of the devices studied (measured without an applied magnetic field).

On the other hand, it is seen that MR typically decreases in magnitude with the BtpIr increasing ratio of PFO : BtpIr in the Fig. 2. The overall MR is motivated by the SOC and HFI in the organic blend of PFO : BtpIr (eqn (4)),

where Ĥ_SOC,HFI is SOC and HFI Hamiltonian. S₁ and S₂ are the intra-molecular and inter-molecular SOC strength, respectively. ℏ is planck's constant. S and L are the spin angular momentum and the electronic orbital, respectively. f₁ and f₂ are the intra-molecular and inter-molecular HFI strength, respectively. is the proton spin. g_L and g_S are the orbital and spin g-factors, respectively. μ_B is the electronic Bohr magneton.²⁰

The Ĥ_SOC,HFI Hamiltonian can be written²⁰ as:

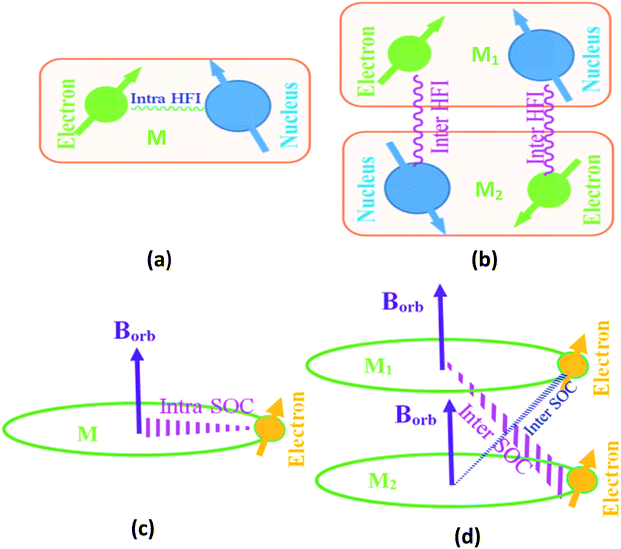
We use the first order perturbation theory (time dependent) to study the spin-dynamics.²⁰ In our studied organic semiconductor, the electronic structure is derived from sp₂ hybridization of the C atoms with the p_z orbitals forming π bonds. The electrical transport properties are essentially determined by the π electrons. SOC is the coupling between the electron orbital angle momentum and its spin momentum. SOC is long-range interaction; it can be divided inter-molecular SOC (S₁) and intra-molecular SOC (S₂), as schematically described in eqn (4) and shown in Fig. 3. However, HFI is the spin–spin interaction between the nucleus spin and the electron spin. It is well known that the intra-molecular HFI and SOC are only dependent of intra-molecular interaction [shown in Fig. 3(a)] among electrons, nucleus and orbital field in a given molecule. HFI belongs to short-range interaction and its strength is weak, so inter-molecular HFI [shown in Fig. 3(b)] exhibits negligible, f₁ ≫ f₂. SOC operator is then proportional to Z⁴ (Z is atomic charge).²⁰ Thus, once molecular structure is arranged, the intra-molecular HFI and SOC [shown in Fig. 3(c)] becomes a fixed quantity. However, the inter-molecular SOC [shown in Fig. 3(d)] depends not only on molecular structure but also distance between different molecules.

Fig. 3 (a) Intra-molecular HFI generated by interaction between the nucleus spin and the electron spin within a single molecule M. (b) Inter-molecular HFI generated by interaction between the nucleus spin and the electron spin within adjacent molecules M₁ and M₂. (c) Intra-molecular SOC generated by interaction between the electron spin and the orbital magnetic field B_Orb located within a single molecule M. (d) Inter-molecular SOC generated by interaction between the electron spin and the orbital magnetic field B_Orb located on adjacent molecules M₁ and M₂.

Inter-molecular SOC strength increases strongly when the distance between different molecules is decreased. The pure PFO only contains light atoms and consequently has the very weak SOC strength. MR effect contributes mainly from HFI. However, SOC is dominated for the pure BtpIr. External magnetic field cannot compete with the strong internal magnetic field generated by SOC. In other word, applied magnetic field cannot effectively change the recombination coefficient β under a condition controlled by SOC. As a result, the pure BtpIr shows negligible MR because of its strong SOC.

The average distance of PFO and BtpIr molecules can be calculated approximately by assuming an organic amorphous film is composed of packed cubic molecules. The average volume for a molecule occupies in an organic amorphous film can be treated as a cube by

where M is the molar mass of the constituent molecules, ρ is the density of the film, and N_A is Avogadro constant, respectively.

The ρ and M values for PFO and BtpIr are 1.22 g cm⁻³, 20 000 g mol⁻¹ (M_PFO), and 1.19 g cm⁻³, 711.87 g mol⁻¹ (M_BtpIr). Thus the average distance of PFO^21,22 and BtpIr molecules can be expressed as eqn (6)⁵ in PFO : BtpIr (c wt%) films.

where L_PFO (L_BtpIr) is the average distance of a pure PFO (BtpIr) film. M_PFO (M_BtpIr) is the molar mass of the constituent PFO (BtpIr) molecule. c is guest concentration. The calculated d values corresponding to different concentration in PFO : BtpIr films are given in Table 1.

Table 1 Calculated d values corresponding to different concentration

PFO : BtpIr (w/w)	100 : 0.1	100 : 1	100 : 2
d (nm)	8.622	7.583	7.740

---

Notably, the average distance decreases when guest concentration increases. That is to say, the heavy metal atom Ir becomes more and more close PFO. As a result, inter-molecular SOC strength increases with guest concentration increased.

On the basis of competing between HFI and SOC. HFI is much larger than SOC in the pure PFO thin film. So its MR response shows as large as −6.5%. On the contrary, HFI is much less than SOC in the pure BtpIr thin film and PFO : BtpIr (100 : 1) system. Therefore, theirs MR signs exhibit zero. The MR response for other architectures shows between zero and −6.5%.

Now we further measure the inter-molecular SOC of the PFO : BtpIr thin films with different doping concentration on the basis of the spectral overlap between the phosphorescent and fluorescent emission spectra. Fig. 4 shows PL spectrum of the thin films (excitation wavelength = 370 nm). As the doping ratio increases, the value of the phosphorescence intensity (I_Ph) compared to the fluorescence intensity (I_F) increases. For the sake of comparison, the PL spectra of neat PFO (10 mg ml⁻¹) and neat BtpIr (1.2 mg ml⁻¹) thin films has been shown in the inset of the Fig. 4. All the photoluminescence spectra were excited in the same condition. As in the inset, the pure PFO film PL intensity (peak) is 10⁷ CPS (420 nm) and the pure BtpIr film PL intensity (peak) is 9 × 10³ CPS (616 nm). As in the Fig. 4, the 420 nm PL intensity (peak) is 10⁶ CPS and the 616 nm PL intensities (peak) are 4 × 10⁴ CPS (100 : 0.1), 3.7 × 10⁵ CPS (100 : 1) and 3.9 × 10⁵ CPS (100 : 2), respectively. Although BtpIr has its own chromophore and the same emission spectrum, only a weak 616 nm PL emission was observed for the pure BtpIr film. BtpIr has a significantly higher PL intensity for the PFO : BtpIr with the different doping concentration (100 : 0.1, 100 : 1, 100 : 2 w/w). At the same time, PFO film PL intensity shows a slight decrease for this doped system. It is well known that only singlet excitons are generated in the polymers and small molecules when they are excited optically. The triplet state can become populated through intersystem crossing. For the PFO : BtpIr blend system, the emission with a peak at 420 nm originates from the radiative recombination of singlet excitons from PFO host. The emission with a peak at 616 nm, to a large extent, belongs to recombination of triplet excitons by intersystem crossing on BtpIr guest molecules for these doped films.

Fig. 4 The photoluminescence spectra (excitation wavelength = 370 nm) for PFO : BtpIr with the different doping concentration (100 : 0.1, 100 : 1, 100 : 2 w/w). Inset: (a) the photoluminescence spectra for pure PFO film. (b) The photoluminescence spectra for pure BtpIr film.

The ISC rate can be written as²⁰

In other words, the ISC rate mainly depends on the strength of the spin–orbit coupling. Therefore, quite generally, the relative strength of the fluorescence and phosphorescence bands is intimately related to the spin–orbit coupling strength T_so.

Furthermore,

where I_F and I_ph are the fluorescence and phosphorescence intensity, respectively; E₁ and E₂ are the phosphorescence and fluorescence photon energy, respectively; τ is the singlet lifetime; η₁ and η₂ are the triplet and singlet emission quantum efficiencies, respectively.

Eqn (9) therefore allows a straightforward calculation of K_ISC from the (spectrally integrated) phosphorescence and fluorescence intensities.²⁰ The K_ISC values can be extracted using spectrally integrated method from the photoluminescence spectra (fluorescence and phosphorescence intensity) in Fig. 4 are shown in Table 2.

Table 2 Calculated values for K_ISC

PFO : BtpIr (w/w)	100 : 0.1	100 : 1	100 : 2
KISC (s^−1)	2.6 × 10^−10	7.8 × 10^−10	8.1 × 10^−10

---

So the spin–orbit coupling strength increases with increasing the doping ratio.

4 Conclusions

In summary, we have studied the magnetic field response in one doped organic polymer PFO : BtpIr solid film. From these systematic studies, the result indicates that MR attributed to hyperfine interaction and spin–orbit coupling in organic semiconductors. Intra-molecular and inter-molecular hyperfine interaction vs. spin–orbit coupling competed on the same platform. HFI belongs to short-range interaction. However, SOC is long–range interaction. The magnetic field is capable of impacting the injected current by means of influencing the recombination of the PFO : BtpIr system. Fluorescence and phosphorescence spectroscopes were used to measure the spin–orbit coupling strength. Clearly, our experimental studies confirmed that inter-molecular SOC strength increases strongly when the distance between adjacent molecules is decreased.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 60806047, 11504036, 11504300 and 61475126), the Natural Science Foundation Project of CQ CSTC (Grant No CSTC2015jcyjA70001 and CSTC2015jcyjBX0032), the Chongqing science and technology personnel training program (Grant No. cstc2013kjrc-qnrc90003), and the Research Programs for Science and Technology of Chongqing Municipal Education Commission (Grant No. KJ1400509, KJ1600327 and KJ1500318) and the Foundation for the Creative Research Groups of Higher Education of Chongqing (No. CXTDX201601016). We acknowledge assistance from Dr L. Yan (University of North Carolina at Chapel Hill) and fruitful discussions with Dr H. D. Zang (Los Alamos National Laboratory).

References

1. H. Malissa, M. Kavand, D. P. Waters, K. J. Schooten, P. L. Burn, Z. V. Vardeny, B. Saam, J. M. Lupton and C. Boehme, Science, 2014, 345, 1487–1489.
2. D. Yuan, L. B. Niu, Q. S. Chen, W. Y. Jia, P. Chen and Z. H. Xiong, Phys. Chem. Chem. Phys., 2015, 17, 27609–27614.
3. L. Yan, M. Wang, N. P. Raju, A. Epstein, L. S. Tan, A. Urbas, L. Y. Chiang and B. Hu, J. Am. Chem. Soc., 2012, 134, 3549–3554.
4. P. Chen, Y. L. Lei, Q. L. Song, Y. Zhang, R. Liu, Q. M. Zhang and Z. H. Xiong, Appl. Phys. Lett., 2009, 95, 213304.
5. W. Y. Jia, Q. S. Chen, L. X. Chen, D. Yuan, J. Xiang, Y. B. Chen and Z. H. Xiong, J. Phys. Chem. C, 2016, 120, 8380–8386.
6. J. Devkota, R. G. Geng, R. C. Subedi and T. D. Nguyen, Adv. Funct. Mater., 2016, 26, 3881–3898.
7. Y. F. Wang, K. S. Tiras, N. J. Harmon, M. Wohlgenannt and M. E. Flatté, Phys. Rev. X, 2016, 6, 011011.
8. B. Hu and Y. Wu, Nat. Mater., 2007, 6, 985–991.
9. F. Maciá, F. Wang, N. J. Harmon, M. Wohlgenannt, A. D. Kent and M. E. Flatté, Nat. Commun., 2014, 5, 3069.
10. O. Mermer, G. Veeraraghavan, T. L. Francis, Y. Sheng, D. T. Nguyen, M. Wohlgenannt, A. Kohler, M. K. A. Suti and M. S. Khan, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 205202.
11. R. C. Johnson and R. E. Merrifield, Phys. Rev. B: Solid State, 1970, 1, 896–902.
12. C. Boehme and J. M. Lupton, Nat. Nanotechnol., 2013, 8, 612–615.
13. P. A. Bobbert, T. D. Nguyen, F. W. A. van Oost, B. Koopmans and M. Wohlgenannt, Phys. Rev. Lett., 2007, 99, 216801.
14. Y. Wu, Z. Xu, B. Hu and J. Howe, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 035214.
15. Z. G. Yu, Phys. Rev. Lett., 2011, 106, 106602.
16. E. Shikoh, K. Ando, K. Kubo, E. Saitoh, T. Shinjo and M. Shiraishi, Phys. Rev. Lett., 2013, 110, 127201.
17. L. Yan, M. Shao, C. F. O. Graeff, I. Hummelgen, D. G Ma and B. Hu, Appl. Phys. Lett., 2012, 100, 013301.
18. J. D. Bergeson, V. N. Prigodin, D. M. Lincoln and A. J. Epstein, Phys. Rev. Lett., 2008, 100, 067201.
19. V. N. Prigodin, J. D. Bergeson, D. M. Lincoln and A. J. Epstein, Synth. Met., 2006, 156, 757–761.
20. Y. G. Sheng, University of Iowa, Ph.D. Dissertations, 2008.
21. S. Kilina, E. R. Batista, P. Yang, S. Tretiak, A. Saxena, R. L. Martin and D. L. Smith, ACS Nano, 2008, 2, 1381–1388.
22. P. A. Lane, L. C. Palilis, D. F. O'Brien, C. Giebeler, A. J. Cadby, D. G. Lidzey, A. J. Campbell, W. Blau and D. D. C. Bradley, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 235206.

---