Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fractional molecular charge studied via molecular vibrational properties. Specific aspects in Jahn–Teller active molecular species†
Ioan Bâldea‡
*
Theoretische Chemie, Universität Heidelberg, Im Neuenheimer Feld 229, D-69120 Heidelberg, Germany
First published on 22nd September 2016
Abstract
In this paper, we report results obtained within the density functional theory (DFT) demonstrating that information on the fractional (non-integral) charge of a single molecule can be extracted from its vibrational properties. This is important because, unlike the former, the latter can be measured experimentally, e.g., via surface enhanced Raman spectroscopy (SERS). As a concrete example, we choose a benzene molecule and consider changes brought about by continuously varying the fractional charge from q = 0 to q = 1 corresponding to neutral and radical cation species. Molecular electronics or electrochemical platforms may offer experimental realizations of continuously tuning non-integral molecular charges. We found that changes in the vibrational frequencies ωv(q) can be substantially larger than those recently measured by varying applied bias in molecular junctions. Our results indicate important qualitative and quantitative differences between the dependence ωv = ωv(q) exhibited by vibrational modes that are JT active and those that are JT inactive; typically, the former is stronger and nonlinear, while the latter is weaker and linear.
1 Introduction
Understanding the interplay between electronic and vibrational degrees of freedom represents a key issue of chemical/molecular physics. Interactions between charge carriers and molecular vibration degrees of freedom are important to understand electron transfer at interfaces and electron transport through molecules embedded in molecular junctions.1–7 By monitoring changes in vibrational properties brought about by the oxidation or reduction of a given neutral molecular species, valuable insight on the impact of local electronic density on various vibrational modes can be gained. However interesting, investigations done on molecular charge species existing in the natural form or easily prepared via ionization or electron attachment inherently suffer from an important limitation: only molecular species having an integral charge can be targeted. Thanks to recent advances in nano-/molecular electronics8–13 and electrochemistry,14,15 this limitation could be overcome. An excess charge transferred to fullerene molecules embedded in electromigrated molecular junctions of up to one tenth of an electron under an applied bias has been claimed from concurrent transport-SERS (surface enhanced Raman spectroscopy) measurements.16 The fraction of the electron charge transfer has been estimated from changes in the vibrational properties. The latter can be measured via SERS or SEIRAS (surface enhanced infrared absorption spectroscopy) in nanojunctions consisting of one or a few molecules, because sharp electrodes act as plasmonic antennas and enormously enhance the local electric field.17 Furthermore, our recent theoretical calculations,18 which employed parameters extracted from experiments on EC-STM junctions based on viologen,9 indicated the possibility that an entire electron can be transferred. By continuously varying the overpotential—which is the counterpart of the gate potential of conventional electronics—, the LUMO occupancy of a molecule embedded in an EC-STM three terminal device based on an STM (scanning tunneling microscope) junction under EC (electrochemical control) can be smoothly tuned between zero for a neutral species and unity for a completely reduced species.18The largest changes in vibrational frequencies deduced in ref. 16 are of the order of ∼10 cm−1. These changes are comparable to those measured in much older SERS studies19 on pyzarine molecules adsorbed on a macroscopic metallic silver electrode whose potential was varied in a certain range, wherein the main focus was on determining the orientation of the molecules on the metallic surface. Further theoretical work20 elaborated the effect of the electrode potential in terms of an effective molecular charge.
Substantially larger changes in molecular vibrational properties upon charge transfer can be expected in cases of molecules where the geometry of the charged species is qualitatively different from that of the neutral molecules. A benzene molecule is best suited to this purpose. Removing an electron from the ground state of the neutral D6h-symmetric benzene molecule yields a state that is twofold degenerate (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1g21) at the D6h geometry. According to the Jahn–Teller (JT) theorem,22,23 this is a degenerate state of a nonlinear molecule, and its degeneracy is lifted by a JT distortion yielding a lowering of the symmetry; D6h → D2h in the case of benzene.24,25 Over decades, the Jahn–Teller distortion of a benzene radical cation has been the subject of detailed investigations.21,24,26–30
2E1g21) at the D6h geometry. According to the Jahn–Teller (JT) theorem,22,23 this is a degenerate state of a nonlinear molecule, and its degeneracy is lifted by a JT distortion yielding a lowering of the symmetry; D6h → D2h in the case of benzene.24,25 Over decades, the Jahn–Teller distortion of a benzene radical cation has been the subject of detailed investigations.21,24,26–30
In the present work, we present results for a benzene molecule demonstrating that changes in vibrational frequencies driven by varying the fractional molecular charge of benzene can indeed be substantially larger that those observed so far in experiments.16 Furthermore, these results demonstrate that JT-active vibrational modes are qualitatively differently affected by charge removal compared to the JT-inactive ones. The latter are found to behave similarly to those reported recently31 for 1,4-benzenedithiol, a molecule that does not possess JT-active vibrational modes. From a molecular electronics perspective, considering below positively charged species—fractional charges 0 < q < + 1 ranging from the neutral (q = 0) to the radical cation (q = +1) species—is also motivated: charge transport through benzene-based molecular junctions is often of the p-type, i.e., mediated by the highest occupied molecular orbital (HOMO).5,32–34
2 Computational details
Most calculations done in this study have been performed running the SIESTA35 trunk-462 package36 in parallel.37 Unlike most quantum chemical packages available, such as the GAUSSIAN 09 package38 also partially employed in this study, SIESTA allows us to compute molecular vibrational properties for non-integer charge states. For calculations of the fractional charge states SIESTA uses a DFT (density functional theory) implementation developed in ref. 39. Similar to ref. 31, in our SIESTA-based calculations, we used the generalized gradient exchange correlation functional of Perdew, Burke, and Ernzerhof (GGA-PBE)40 and split-valence TZP (split triple zeta polarized) basis sets for all atoms. Below we presented numerical results obtained using cubic 30 × 30 × 30 Å cells and three dimensional real-space grids characterized by an energy cutoff of 800 Ry. The latter defines the maximum kinetic energy of the electronic plane wave basis set utilized; following SIESTA’s manual,36 it will be referred to as the mesh cutoff below.Employing cubic cells for a planar molecule like benzene is less common. It is motivated by the specific character of calculations to a charged system treated within an infinite periodic scheme utilized in the present paper, whose total energy converges very slowly with respect to the cell size. For cubic cells and only for these, a Madelung correction can be/is applied to the total energy, and this substantially improves convergence.
To obtain vibrational properties, SIESTA computes the dynamical matrix with a finite difference calculation of the forces41 via the VIBRA utility, which is part of the SIESTA package distribution.36 This method represents an alternative to the more popular method of obtaining phonons based on linear response DFT schemes.42
Table S1 of the ESI† comparatively presents the benzene vibrational frequencies computed via the presently adopted SIESTA/PBE/TZP method and other DFT as well as ab initio (CCSD, MP2) methods. Albeit not dramatic, certain differences between the SIESTA values and those of the other methods—including those obtained employing GAUSSIAN 09 with keywords PBEPBE/TZVP—exist. They trace back to SIESTA’s specific manner of numerically constructing localized orbitals; SIESTA’s TZVP orbitals and GAUSSIAN’s TZVP orbitals are not the same. However, we note that neither these differences nor the specific theoretical method producing the closest frequency values to experimental values represent the main issue in the present paper. What we want to emphasize is that, upon a nearly complete electron transfer, as it turned out to be possible by using three-terminal setups based on electrolyte gating18 or asymmetric two terminal setups,43 bias-driven changes in vibrational frequencies can be substantially larger than what has been experimentally observed so far16 and, hence, are easier to be measured by means of SERS or SEIRAS.
3 Results and discussion
3.1 Preliminary remarks
The calculations done for all fractional molecular charges (0 ≤ q ≤ 1) investigated in the present paper refer to the lowest (ground) electronic state. A series of precautions has been taken in order to diminish as much as possible spurious numerical effects on the calculated vibrational properties, which—as delineated below and also encountered recently31—is a challenging task for SIESTA.We relaxed the molecular geometries until the forces on all atoms were less than 0.1 meV Å−1. This is a much more severe condition than typical default force tolerances (0.04 eV Å−1 in SIESTA and ∼0.023 eV Å−1 in GAUSSIAN 09). The latter are often sufficient for relaxation studies, but the calculations of vibrational properties are usually much more demanding than those for relaxation.
Attention was paid to reduce egg-box effects. It might be helpful to remember that, to calculate various integrals, SIESTA uses a finite three-dimensional spatial grid. Because the relevant quantities (e.g., density or potential) have plane wave components beyond the finite mesh cutoff utilized, the translational invariance is broken (egg-box effect). This numerical effect disappears for infinitely fine grids (infinite mesh cutoff). For mesh cutoff values of ∼200–300 eV, egg-box effects on the total energy or relaxed geometry are normally completely insignificant; see Fig. 1 and discussion below.
However, eliminating such effects on the vibrational properties is much more difficult. We checked that changes to the cutoff values in the range of 300–1000 eV do not conclusively reduce the degree of numerical noise exhibited by the vibrational properties. The results presented below have been obtained using a mesh cutoff of 800 eV.
The effect of the finite difference procedure for force computations has also been considered. We determined that there is no substantial improvement by varying the displacement used for the computation of the force constant matrix (SIESTA keyword MD.FCDispl) from 0.01 Å to 0.02 Å. For the results presented in this paper we used the value 0.01 Å.
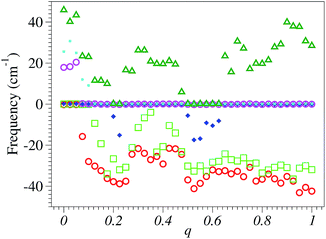
Neither the precautions delineated above nor playing around with pseudopotentials—that is, using others than those actually utilized, obtained from translating the ABINIT pseudo’s database available to download36—allowed us to eliminate some numerical inaccuracies/noise, which appear to be hardly avoidable in SIESTA calculations for vibrational properties while absent in considering more common electronic properties. The results depicted in Fig. 1 and 2, which were obtained by employing the same SIESTA settings/parameters, illustrate this contrast.
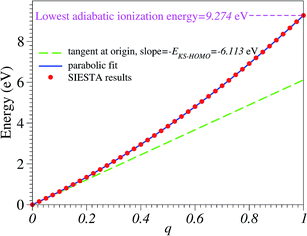
Numerical noise does not affect the total energy ε(q) computed for various fractional charge states. In Fig. 1 we present the results for the total energy ε(q) as a function of the oxidation degree q. The corresponding curve is a noise-free smooth curve, whose slope at the origin can be unambiguously extracted and yields a HOMO energy44–46
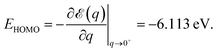 | (1) |
This value excellently agrees with the Kohn–Sham-(KS-) HOMO energy EHOMO|q=0 = −6.153 eV computed for the neutral molecule (q = 0), as extracted from the SIESTA *.EIG file. As is amply documented,47 although conceptually less problematic qualitatively than other KS “orbitals”, the quantitative description of the physical HOMO by the KS-HOMO is rather poor; the above value(s) differs by more than 3 eV from the value corresponding to the lowest adiabatic ionization energy obtained via Δ-DFT calculations48–50 IP = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (q = 1) −
(q = 1) − ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (q = 0) ≡
(q = 0) ≡ ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) equilibriumcation −
equilibriumcation − ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) equilibriumneutral = 9.274 eV. This value of adiabatic ionization energy excellently agrees with the experimental value of the lowest adiabatic one-electron binding energy (9.243 eV) measured by photoelectron spectroscopy.51 This agreement may not be taken too seriously, given the fact that more elaborate quantum chemical methods—like equation-of motion coupled cluster singles and doubles (EOM-CCSD),21,52 third-order algebraic diagrammatic construction (ADC(3)),53 and outer valence Green’s functions (OVGF)51,52—do not yield such a “perfect” agreement; still, this fact demonstrates that SIESTA results for charged molecules may be reasonably trusted.
equilibriumneutral = 9.274 eV. This value of adiabatic ionization energy excellently agrees with the experimental value of the lowest adiabatic one-electron binding energy (9.243 eV) measured by photoelectron spectroscopy.51 This agreement may not be taken too seriously, given the fact that more elaborate quantum chemical methods—like equation-of motion coupled cluster singles and doubles (EOM-CCSD),21,52 third-order algebraic diagrammatic construction (ADC(3)),53 and outer valence Green’s functions (OVGF)51,52—do not yield such a “perfect” agreement; still, this fact demonstrates that SIESTA results for charged molecules may be reasonably trusted.
On the other side, in Fig. 2 we present the six lowest SIESTA frequencies, which correspond to the three rigid translations and rotations of the entire molecule; these frequencies should be strictly zero but they are not; a numerical inaccuracy that one cannot easily avoid. In fact, the problem with these values of six “should-be-zero” frequencies is also encountered in other quantum chemical packages. For instance, these are designated as “low frequencies” in the output files of GAUSSIAN 09, and their negative values mean imaginary frequencies.
Due to the D6h symmetry of the neutral benzene molecule, certain vibrational modes are twofold degenerate. As a result of the JT distortion, the benzene radical cation has a symmetry lower than the D6h-symmetry of the neutral benzene. Consequently, the twofold degeneracy of the vibrational modes of E1,g/u- and E2,g/u-symmetries of the neutral species is lifted upon electron removal. Because the corresponding energy splittings are small, they cannot be distinguished at the noise level of SIESTA calculations.54 The mode symmetry indicated throughout this paper refers to the neutral benzene molecule.
However, in spite of the SIESTA limitations for phonon studies, the numerical noise more or less visible in all of the figures presented below does not prevent the formulation of clear conclusions on the relationship between the fractional electron charge and vibrational frequencies.
3.2 Impact of charge removal on vibrational frequencies
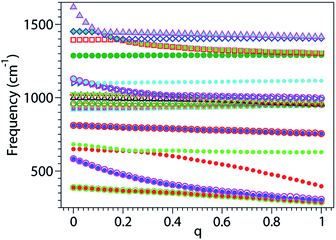
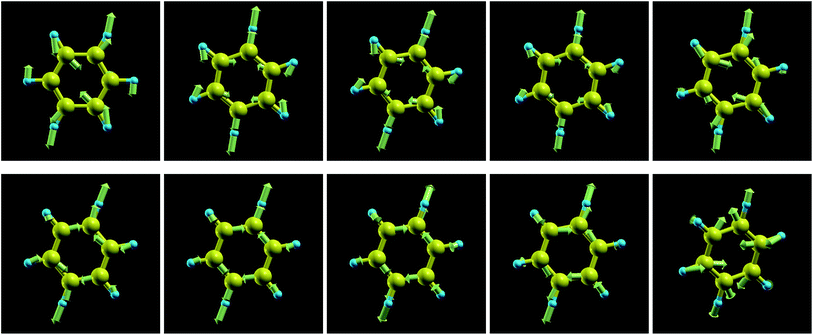
Our numerical results on the changes in the 24 relevant vibrational frequencies of the benzene molecule as a function of the electron deficit q are collected in Fig. 3. For convenience—since otherwise the drawing scale needed in Fig. 3 would be detrimental for visibility—, the six highest frequency modes corresponding to C–H stretching which are of lesser importance in the present context are not included in Fig. 3; their values are indicated in the last six lines of Table S1.†In the neutral benzene molecule, the lowest frequency mode is twofold degenerate and is denoted by 16a/16b in Wilson numbering55,56 and by 20 in Herzberg numbering.57 This mode has E2u-symmetry in the point group D6h and corresponds to an out-of-plane ring deformation (Fig. S4 of the ESI†). Its frequency decreases upon electron removal. The frequency reduction is nearly linear with the electron deficit q; at complete oxidation (q = 1) this reduction amounts to ∼100 cm−1 (Fig. 4a and S1a of the ESI†). The motion of the various atoms does not exhibit any spectacular change upon varying the oxidation degree q; compare the panels of Fig. S4 in the ESI.† This fact may be related to the linear q-dependence of the frequency, suggesting that electron removal basically acts as a first order perturbation.
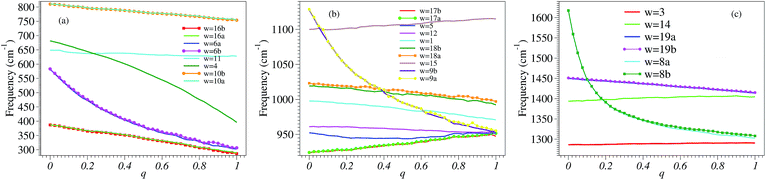 | ||
| Fig. 4 The three panels a–c of this figure were obtained by zooming in and splitting Fig. 3 in ranges of frequencies increasing from panel a to panel c, and joining the calculated points to build curves corresponding to well defined vibrational modes. | ||
Whether the frequencies decrease or increase by electron removal is not directly related to the mode’s symmetry. In Fig. 4b and S1c of the ESI,† we present results revealing that, in contrast with the above case, the frequencies of the vibrational modes denoted by 17a/17b in Wilson labeling or 19 in Herzberg labeling, which also have E2u-symmetry in the neutral benzene, linearly increase by electron removal. These modes correspond to out-of-plane CH bendings. The frequency increases amount to ∼30 cm−1 upon complete oxidation.
Wilson modes 16a/16b and 17a/17b are neither infrared (IR) nor Raman active but are of interest because they induce inter-state (pseudo-JT) vibronic couplings between a degenerate and a nondegenerate electronic state, e.g., between the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2E2g and
2E2g and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2A2u or between the
2A2u or between the ![[D with combining tilde]](https://www.rsc.org/images/entities/char_0044_0303.gif) 2E1u and Ẽ2B2u electronic excited states of the radical cation.27,29 They are important in understanding the overlapping
2E1u and Ẽ2B2u electronic excited states of the radical cation.27,29 They are important in understanding the overlapping ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) /
/![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) bands of the photoelectron spectrum and internal conversion dynamics.27,29
bands of the photoelectron spectrum and internal conversion dynamics.27,29
The frequencies of the modes 6a/6b in Wilson numbering or 18 in Herzberg numbering, known to produce a strong JT coupling within the electronic lowest energy manifold ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E1g, are more strongly affected by oxidation than the modes discussed above; see Fig. 4a and S2a of the ESI.† The various panels of Fig. 5 and 6 depict these modes for various values of oxidation degree 0 ≤ q ≤ 1. In contrast to Fig. S4 of the ESI,† the fact that the motion amplitudes and directions of the various atoms change with q is visible for these modes in Fig. 5 and 6. Wilson modes 6a/6b are Raman active. In neutral benzene they correspond to in-plane ring deformations (cf. Fig. 5 and 6); at higher q-values, SIESTA found that these vibrations exhibit certain deviations from planarity.
2E1g, are more strongly affected by oxidation than the modes discussed above; see Fig. 4a and S2a of the ESI.† The various panels of Fig. 5 and 6 depict these modes for various values of oxidation degree 0 ≤ q ≤ 1. In contrast to Fig. S4 of the ESI,† the fact that the motion amplitudes and directions of the various atoms change with q is visible for these modes in Fig. 5 and 6. Wilson modes 6a/6b are Raman active. In neutral benzene they correspond to in-plane ring deformations (cf. Fig. 5 and 6); at higher q-values, SIESTA found that these vibrations exhibit certain deviations from planarity.
The frequency that is most strongly affected by electron removal is that of Wilson mode 8a/8b, which is mode 16 in Herzberg numbering (Fig. S5 and S6 of the ESI†); complete oxidation yields a frequency decrease amounting to ∼315 cm−1 (Fig. 4c and S2c of the ESI†). This mode is Raman and JT active. As is visible in Fig. 4c, the curves for Wilson modes 8a/8b of E2g-symmetry cross the curves for Wilson modes 19a/19b (mode 12 in Herzberg labeling; E1u-symmetry) and Wilson mode 14 (Herzberg mode 10; B2u-symmetry). The crossing is possible due to the different symmetries of these modes.
From this standpoint, Wilson modes 9a/9b (or 17 in Herzberg notation) are even more interesting. Although the change in frequency upon complete oxidation (∼170 cm−1) is smaller than that for Wilson mode 8a/8b (Herzberg mode 16), the curves for these modes (again E2g symmetry) exhibit three crossings (cf. Fig. 4b and S2b of the ESI†) with those of Wilson mode 15 (9 in Herzberg notation; B2u symmetry), Wilson modes 18a/18b (13 in Herzberg notation; E1u symmetry), and the totally symmetric Wilson mode 1 (2 in Herzberg notation; A1g symmetry).
All the crossings discussed above involve at least a twofold degenerate mode. The last example presented in this section demonstrates that this is not necessarily the case. Here we show two nondegenerate modes: Wilson mode 11 (Herzberg mode 4; A1u symmetry) and Wilson mode 4 (Herzberg mode 8; B1g symmetry).
In neutral benzene, the frequency of Wilson mode 11 (mode 4 in Herzberg notation) is somewhat higher then that of Wilson mode 4 (mode 8 in Herzberg notation). The former is substantially decreased by oxidation while the latter is nearly constant (Fig. 4a). Having different symmetries (A1u and B2g, respectively), they do not mix; the corresponding curves can and do cross at q ≥ 0.2. However, because SIESTA does not use any symmetry in the calculations, a spurious mode mixing occurs at the crossing point; this is visible by comparing the panels corresponding for these two modes at q = 0.25 (i.e., close to the crossing point, cf. Fig. 4a) with the other panels of Fig. S7 and S8 of the ESI.†
4 Conclusion
In this paper, we have studied theoretically the impact of removing an amount 0 < q < 1 of electronic charge on the vibrational frequencies of a benzene molecule. We have determined that the changes in the phonon frequencies are substantially larger than found in recent experiments16 in nanojunctions based on fullerene.As an important result to be noted, we have demonstrated that vibrational frequencies ωv = ωv(q) are affected in a different manner by the charge deficit q, depending on whether the vibrational modes are Jahn–Teller active or not.
Basically, for JT-inactive modes, the dependence ωv vs. q is linear. This result gives microscopic support to our recent conjecture,18 amounting to considering the vibrational frequencies in a fractional charge state as a linear interpolation between the frequencies of the neutral and (in the concrete case investigated here) radical cation species with a weight determined by the charge deficit q. Rephrasing, the charge removal acts on the vibrational frequencies as a first-order perturbation. So, the conjecture of ref. 18 turned out to provide a reasonable framework for interpreting experimental data in nanojunctions based on mostly utilized molecules wherein charge transfer does not yield too strong perturbations, like the presently considered JT distortion. In assessing its operational utility for quantitative purposes one should take into account that, in order to make the DFT-computed values comparable with the measured vibrational frequencies, empirical scaling factors have to be applied,58 and these scaling factors may depend on the charge species.59
For JT-active modes, the dependence ωv vs. q has been found to be stronger and substantially deviates from linearity. This nonlinearity found, a qualitatively different aspect, is in agreement with the overall view on JT distortion as a source of qualitative different behavior.
Many vibrational modes in the ground state of the benzene radical cation have been found to have frequencies substantially different from those of the neutral benzene in the ground state. From the point of view of quantum dynamical simulations, this finding is also important. Ab initio quantum dynamical approaches to the benzene21,24,26–30 or halogen substituted benzene30,60,61 radical cation are often based on normal vibrational coordinates of the neutral species. In the language of those normal coordinates, the present result implies substantial quadratic couplings in the lowest energy manifold ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) E1g of the radical cation. From this perspective, augmenting quantum dynamical simulations done for the benzene radical cation21,24,26–30 by also including quadratic couplings, as done for halogen substituted counterparts,30,60,61 can be a meaningful next step.
E1g of the radical cation. From this perspective, augmenting quantum dynamical simulations done for the benzene radical cation21,24,26–30 by also including quadratic couplings, as done for halogen substituted counterparts,30,60,61 can be a meaningful next step.
Acknowledgements
Financial support for this research provided by the Deutsche Forschungsgemeinschaft (grant BA 1799/3-1) is gratefully acknowledged. This work was partially performed on the computational resources bwUniCluster and bwForCluster/JUSTUS-HPC facility funded by the Ministry of Science, Research and Arts Baden-Württemberg and the Universities of the State of Baden-Württemberg, Germany, within the framework program bwHPC.37Notes and references
- A. Nitzan, Annu. Rev. Phys. Chem., 2001, 52, 681–750 CrossRef CAS PubMed.
- J. Jiang, M. Kula, W. Lu and Y. Luo, Nano Lett., 2005, 5, 1551–1555 CrossRef CAS PubMed.
- M. Galperin, M. A. Ratner, A. Nitzan and A. Troisi, Science, 2008, 319, 1056–1060 CrossRef CAS PubMed.
- V. Coropceanu, R. S. Sánchez-Carrera, P. Paramonov, G. M. Day and J.-L. Brédas, J. Phys. Chem. C, 2009, 113, 4679–4686 CAS.
- H. Song, M. A. Reed and T. Lee, Adv. Mater., 2011, 23, 1583–1608 CrossRef CAS PubMed.
- R. Härtle and M. Thoss, in Molecular Electronics: An Experimental and Theoretical Approach, ed. I. Bâldea, Pan Stanford, 2015, ch. 5, pp. 155–221 Search PubMed.
- D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440 CrossRef CAS PubMed.
- A. Alessandrini, S. Corni and P. Facci, Phys. Chem. Chem. Phys., 2006, 8, 4383–4397 RSC.
- I. V. Pobelov, Z. Li and T. Wandlowski, J. Am. Chem. Soc., 2008, 130, 16045–16054 CrossRef CAS PubMed.
- S. Wang, M. Ha, M. Manno, C. D. Frisbie and C. Leighton, Nat. Commun., 2012, 3, 1210 CrossRef PubMed.
- W. Xie, S. Wang, X. Zhang, C. Leighton and C. D. Frisbie, Phys. Rev. Lett., 2014, 113, 246602 CrossRef PubMed.
- A. Alessandrini and P. Facci, in Molecular Electronics: An Experimental and Theoretical Approach, ed. I. Bâldea, Pan Stanford, 2015, ch. 9, pp. 325–352 Search PubMed.
- J. M. Artés-Vivancos, J. Hihath and I. Díez-Pérez, in Molecular Electronics: An Experimental and Theoretical Approach, ed. I. Bâldea, Pan Stanford, 2015, ch. 8, pp. 281–324 Search PubMed.
- A. Alessandrini and P. Facci, Eur. Polym. J., 2016 DOI:10.1016/j.eurpolymj.2016.03.028.
- J. Izquierdo and C. Kranz, Eur. Polym. J., 2016 DOI:10.1016/j.eurpolymj.2016.05.016.
- Y. Li, P. Doak, L. Kronik, J. B. Neaton and D. Natelson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1282–1287 CrossRef CAS PubMed.
- P. Mühlschlegel, H.-J. Eisler, O. J. F. Martin, B. Hecht and D. W. Pohl, Science, 2005, 308, 1607–1609 CrossRef PubMed.
- I. Bâldea, Phys. Chem. Chem. Phys., 2014, 16, 25942–25949 RSC.
- J. Soto, D. J. Fernández, S. P. Centeno, I. L. Tocón and J. C. Otero, Langmuir, 2002, 18, 3100–3104 CrossRef CAS.
- F. Avila, C. Ruano, I. López-Tocón, J. F. Arenas, J. Soto and J. C. Otero, Chem. Commun., 2011, 47, 4213–4215 RSC.
- M. Döscher, H. Köppel and P. G. Szalay, J. Chem. Phys., 2002, 117, 2645–2656 CrossRef.
- H. A. Jahn and E. Teller, Proc. R. Soc. London, Ser. A, 1937, 161, 220–235 CrossRef CAS.
- R. Englman, The Jahn–Teller effect in molecules and crystals, Wiley, New York, 1972 Search PubMed.
- H. Müller, H. Köppel and L. S. Cederbaum, New J. Chem., 1993, 17, 7–29 Search PubMed.
- K. Müller-Dethlefs and J. B. Peel, J. Chem. Phys., 1999, 111, 10550 CrossRef.
- M. Döscher and H. Köppel, Chem. Phys., 1997, 225, 93–105 CrossRef.
- H. Köppel, M. Döscher, I. Bâldea, H.-D. Meyer and P. G. Szalay, J. Chem. Phys., 2002, 117, 2657–2671 CrossRef.
- H. Köppel, I. Bâldea and P. Szalay, in Advances in Quantum Chemistry, ed. J. R. Sabin and E. J. Braendas, Academic Press, 2003, vol. 44, pp. 199–217 Search PubMed.
- I. Bâldea and H. Köppel, J. Chem. Phys., 2006, 124, 064101 CrossRef PubMed.
- I. Bâldea, J. Franz and H. Köppel, J. Mol. Struct., 2007, 838, 94–99 CrossRef.
- I. Bâldea, Chem. Phys., 2016 DOI:10.1016/j.chemphys.2016.08.024.
- H. Song, Y. Kim, Y. H. Jang, H. Jeong, M. A. Reed and T. Lee, Nature, 2009, 462, 1039–1043 CrossRef CAS PubMed.
- Z. Xie, I. Bâldea, C. Smith, Y. Wu and C. D. Frisbie, ACS Nano, 2015, 9, 8022–8036 CrossRef CAS PubMed.
- M. Tsutsui, T. Morikawa, Y. He, A. Arima and M. Taniguchi, Sci. Rep., 2015, 5, 11519 CrossRef CAS PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- Available at http://www.icmab.es/dmmis/leem/siesta/.
- bwHPC and bwHPC-C5, http://www.bwhpc-c5.de/, Computational resources funded by the Ministry of Science, Research and Arts Baden-Württemberg and the Universities of the State of Baden-Württemberg, Germany, and the German Research Foundation (DFG).
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. J. Ackland, M. C. Warren and S. J. Clark, J. Phys.: Condens. Matter, 1997, 9, 7861–7872 CrossRef CAS.
- S. Baroni, P. Giannozzi and A. Testa, Phys. Rev. Lett., 1987, 58, 1861–1864 CrossRef CAS PubMed.
- I. Bâldea, Phys. Chem. Chem. Phys., 2015, 17, 15756–15763 RSC.
- J. F. Janak, Phys. Rev. B: Solid State, 1978, 18, 7165–7168 CrossRef CAS.
- G. K.-L. Chan, J. Chem. Phys., 1999, 110, 4710–4723 CrossRef CAS.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115123 CrossRef.
- R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, Clarendon, Oxford, 1989 Search PubMed.
- R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746 CrossRef CAS.
- I. Bâldea, Europhys. Lett., 2012, 99, 47002 CrossRef.
- I. Bâldea, Faraday Discuss., 2014, 174, 37–56 Search PubMed.
- P. Baltzer, L. Karlsson, B. Wannberg, G. Öhrwall, D. Holland, M. MacDonald, M. Hayes and W. von Niessen, Chem. Phys., 1997, 224, 95–119 CrossRef CAS.
- I. Bâldea, Phys. Chem. Chem. Phys., 2015, 17, 20217–20230 RSC.
- M. S. Deleuze, A. B. Trofimov and L. S. Cederbaum, J. Chem. Phys., 2001, 115, 5859–5882 CrossRef CAS.
- For reader’s convenience, both Wilson55 and Herzberg57 labels of the various vibrational modes of benzene will be indicated.
- E. B. Wilson, Phys. Rev., 1934, 45, 706–714 CrossRef CAS.
- G. Varsanyi, in Assignments for Vibrational Spectra of Seven Hundred Benzene Derivatives, ed. I. Land, Adam Hilger, London, 1974, vol. 1, p. 1 Search PubMed.
- G. Herzberg, Molecular spectra and molecular structure, Infrared and Raman spectra of polyatomic molecules, Van Nostrand, Reinhold, New York, 1945, vol. 2 Search PubMed.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS.
- I. Bâldea, H. Köppel and W. Wenzel, Phys. Chem. Chem. Phys., 2013, 15, 1918–1928 RSC.
- I. Bâldea, J. Franz, P. G. Szalay and H. Köppel, Chem. Phys., 2006, 329, 65–75 CrossRef.
- E. Gindensperger, I. Bâldea, J. Franz and H. Köppel, Chem. Phys., 2007, 338, 207–219 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra21476b |
| ‡ Also at National Institute for Lasers, Plasmas, and Radiation Physics, Institute of Space Sciences, RO 077125, Bucharest-Măgurele, Romania, E-mail: E-mail: ioan.baldea@pci.uni-heidelberg.de |
| This journal is © The Royal Society of Chemistry 2016 |