Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optical in situ study of de-alloying kinetics in nanoporous gold sponges†
M. C. Tai,
A. Gentle,
M. D. Arnold and
M. B. Cortie *
*
Institute for Nanoscale Technology, University of Technology Sydney, PO Box 123, Broadway, NSW 2007, Australia. E-mail: michael.cortie@uts.edu.au
First published on 23rd August 2016
Abstract
Nanoporous gold sponges are useful for a variety of applications but the kinetics of the dissolution process used to make them is not well understood. Here we show how optical transmittance can be used to determine the rate at which sponges form from thin film precursors. The technique also provides a means by which de-alloying can be terminated at a target thickness. Analysis revealed three stages during the de-alloying process: initial depassivation, bulk dissolution and, finally, delamination. The dissolution rate is linear with hydroxide concentration, and exponential with temperature, with an activation energy of approximately 0.5 eV.
1 Introduction
Nanoporous gold sponges can be produced by de-alloying AuxAl precursors by selective corrosion of the Al.1–3 Sponges produced this way are often called “Raney” sponges by analogy with the widely used catalytic RANEY® nickel sponge produced by de-alloying NixAl alloys in NaOH solution. Although not commercially exploited, these types of gold sponges are effective catalysts for the oxidation of CO, and oxidation and reduction of NO, despite the generally unreactive nature of bulk gold. Presumably it is the very high specific surface area and abundant presence of lowly coordinated surface atoms that confers this attribute. Gold sponges produced from Au–Al alloys are a sub-set of the broader class of nanoporous gold sponges that can be produced by de-alloying precursors like Au–Ag, Au–Cu–Si or Au– Sn4–7 and, indeed, catalytic efficacy has been reported8,9 for these types of gold sponge too. Due to their good electrical conductivity,10 gold sponges may also find application in electrochemical capacitors,11,12 substrates for surface enhanced Raman scattering (SERS),13–15 plasmonic applications,16,17 electrodes for solar cells, and applications as sensors.18,19Understanding the kinetics and mechanism of dissolution in sponge formation is important for successful production. In order for de-alloying to begin, certain criteria must be met or else the alloy will be passivated.20 Overcoming this passivation state requires that the critical potential for the selective dissolution of one or more metals must be exceeded.21 Parameters such as the concentration of the electrolyte solution and of the reactive alloying element in the precursor alloy affect the dissolution rate.22 Although the basic conditions for de-alloying are known, there has been interest in acquiring further insights into the de-alloying kinetics of these sponges, with various models and simulations employed in an attempt to elucidate the mechanism further.4,23–27 Experimental observations reveal that de-alloying proceeds in the form of a reaction front that moves through the material, with considerable reorganization of the noble metal atoms taking place within the narrow width of the front. Once the front has passed, the remaining noble metal atoms are found to be organized into a skeleton of filaments or ligatures.20 This high-surface area structure may further coarsen with time and or by application of elevated temperatures. Selective dissolution is most commonly replicated using Monte Carlo simulations of either the kinetic20 or Metropolis types.23,24,26,28 These algorithms are effective in imitating both the movement of the de-alloying front and the morphology of the final product, however, the elapsed time taken to etch an alloy cannot be readily converted to physical units.
Several studies have tried to analyse the rates of dissolution when de-alloying parameters are altered.5,22,29–31 Parameters that have been studied include the composition and temperature of the electrolyte solution, and ratio of noble metal to reactive metal. There have been a very few in situ studies: Chen-Wiegart et al.,22 for example, used in situ synchrotron X-ray microscopy to probe the de-alloying of (Ag,Au) solid solutions and extract a velocity for the de-alloying front. Although the alloy compositions and electrolyte solution in that study differ from those used in the present investigation, the velocities recorded are still of interest as they provide one of the few comparators available in the literature. The rates of de-alloying in the Chen-Wiegart study were determined to be 319, 76, 16 and 9 nm s−1 for Ag contents of 80, 75, 70 and 65 at% respectively, in 10.9 M HNO3. When the concentration of acid was varied between 14.6 to 9.1 M it was found that the velocity of de-alloying in the 70 at% Ag sample declined from 79 to 8 nm s−1. No de-alloying occurred at Ag = 60 at% in agreement with the observation that the ‘parting limit’ of gold–silver alloys is of the order of 50 to 60 at% Ag32 (alloys with less than that content of active element do not readily de-alloy or ‘part’).
Rate kinetics for de-alloying may be modelled with an Arrhenius-type expression:20
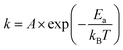 | (1) |
A synchrotron study is, however, a relatively expensive way of following a de-alloying front. Here we show how equivalent kinetic data for the rate of de-alloying may be more simply obtained by making in situ optical transmittance measurements of thin films undergoing de-alloying. The time-dependent position of the de-alloying front is then extracted from an optical stack model of the de-alloying film. In this case, only readily accessible laboratory equipment and software is used.
2 Materials and methods
AuAlx (x ≈ 2) thin films were deposited on glass slides or silicon wafers in a DC magnetron sputterer equipped with gold and aluminium targets. Glass substrates were cleaned in de-ionized water mixed with detergent and sonicated for 20 minutes whilst silicon substrates were sonicated in acetone then ethanol for 10 minutes each. All substrates were then rinsed with de-ionized water and dried with nitrogen. The glass/silicon wafers were placed on a rotating stage in the sputter chamber. The base pressures before deposition were better than 4 × 10−4 Pa (3 × 10−6 Torr). Sputtering was conducted in 2.7 × 10−1 Pa (2 mTorr) argon with 50 mm diameter gold and aluminium targets placed at a distance of approximately 100 mm from the substrate holder, with accelerating voltages of 460 and 357 V respectively. The substrates were at ambient temperature. Thin films produced on the glass slides were used for the in situ optical measurements during dissolution while the thin films on the silicon wafers were used for morphology characterization by scanning electron microscopy (SEM) and transmission electron microscopy (TEM).Glass samples were de-alloyed in cuvettes within a USB2000 Ocean Optics Spectrometer. The transmittance of light was repeatedly recorded from wavelengths of 300 to 1000 nm at 0.5 second intervals. The cuvettes were filled with NaOH at room temperature (concentrations 0.2 M, 0.15 M, 0.1 M, 0.05 M, 0.03 M and 0.01 M), which etched away the aluminium in the alloys. Experiments that investigated the effect of temperature on etch rate were performed with a quartz cuvette in contact with a Peltier temperature stage, set to 50 °C, 40 °C, 19 °C, 12 °C and at room temperature (∼23 °C) with 0.1 M NaOH. The temperature of the solution was monitored with a K-type thermocouple.
The compositions of the thin films were determined using energy dispersive X-ray spectroscopy (EDS) in a Zeiss Evo scanning electron microscope at 5 kV. Thin film samples were placed onto conductive carbon tape with additional copper tape used for earthing. Multiple areas were analyzed to confirm that films were consistent in composition. Deposited films were confirmed to be AuAl2 (approximately 69.2 at% Al and 30.8 at% Au for the first series of samples and 68.2 at% Al and 31.8 at% Au for the second series. Analysis error of the order of ±0.4 at%). The films displayed a distinctive33 bright purple colour indicating that they were substantially comprised of the AuAl2 phase (this compound is also known as ‘purple gold’ or ‘purple glory’34). TEM samples were made by floating fragments of sponge onto lacy carbon TEM grids.
Supplementary optical measurements were conducted on a PerkinElmer Lambda 950 and a J. A. Woollam VASE Ellipsometer. Samples of both the AuAl2 precursor and the nanoporous sponge were measured in both machines to verify instrument accuracy. An optical model was constructed to extract the thickness of the de-alloyed layer from the transmittance spectra. First, individual oscillator equations for each material were fitted using the WVASE32 software to the ellipsometer data for pure samples of glass, gold, as-deposited AuAl2 and completely de-alloyed Au nanosponge. From the oscillator equations, optical constants n(λ) and k(λ) were obtained. The refractive indices of pure H2O were also input into the model for the aqueous phase (a reasonable approximation as the NaOH concentration was less than 0.2 M). These optical constants were then used to build a composite thin film stack model using Griesmann's freely available Optical Thin Film Toolbox, (software available from https://www.sites.google.com/site/ulfgri/numerical/thin-films). The stack comprised of a back layer of water, followed by a 1 mm glass substrate, a variable thickness of AuAl2, a variable thickness of nanoporous Au and, finally, a top layer of water. The nanoporous Au layer was placed at the top of the stack since, as mentioned, the de-alloying front proceeds inwards from the corroding liquid phase into the solid alloy. The optical model was then iteratively fitted to the succession of measured transmission spectra to estimate the average time-dependent thicknesses of the AuAl2 and nanoporous Au layers in the stack. The mean squared error was generally better than 10−6 for most fits prior to the mesoporous gold layer eventually detaching from the glass. Certain constraints were placed onto the fitting algorithm to deter the software from producing impossible results. For example, at t = 0 the thickness of the nanoporous Au layer was set at 0 nm, and the starting thicknesses of the AuAl2 layer was set at 160 nm (which was the thickness of the as-deposited film measured by profilometry). The thickness was also not permitted to become negative or the AuAl2 layer to gain thickness after it had de-alloyed.
3 Results and discussion
The gold sponge produced in the present work had the so-called ‘foamy’ morphology,23 Fig. 1 and 2. Foamy sponges are comprised of interpenetrating metal ligaments that define roughly spherical pores, very much like a bathroom sponge. This is different from the nanoporous sponges produced by de-alloying (Au,Ag) solid solutions – these sponges consist of a bi-continuous, vermicular morphology of pores and ligaments.4 | ||
| Fig. 1 Transmission electron microscope images of fragments of the nanoporous gold film produced by de-alloying in 0.1 M NaOH. Contrast and brightness have been adjusted in these figures. | ||
 | ||
| Fig. 2 Scanning electron microscope image of surface of de-alloyed sponge (produced by de-alloying in 0.1 M NaOH). | ||
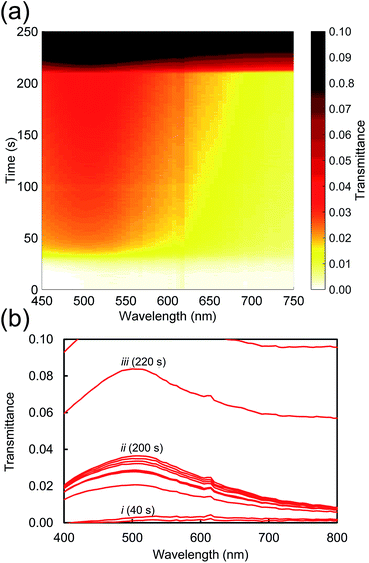
Next we consider the overall characteristics of the dynamic transmission spectra during dissolution: initially the transmittances of the films are close to zero due to the thickness of the opaque AuAl2 films, however the dissolution of Al renders the films more transparent as time passes. This is evident in a transmission peak forming at ∼500 nm corresponding to the formation nanoporous gold as presented in Fig. 3. Finally, there is an abrupt change at t > 200 s caused by the nanoporous gold film detaching from the substrate. An animation of the transmittance data is available in the ESI.†
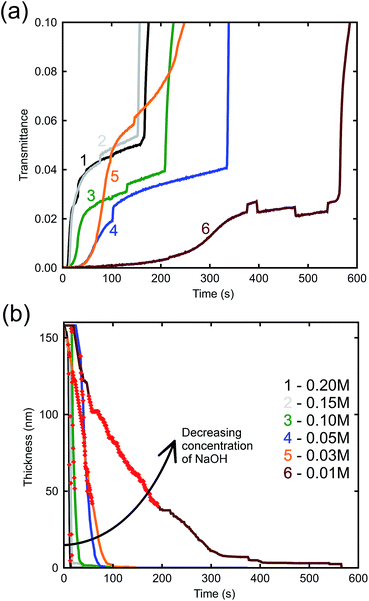
The effect of NaOH concentration on the dynamics of optical transmission at 500 nm can be seen in Fig. 4a. There is an initial incubation period before transmittance rises, saturates, and rises again. The initial delay is evidently associated the breakdown of initial surface passivation – presumably a film of Al2O3 – which evidently requires some time to occur, however, once the surface protective layer has been removed by the alkali, dissolution of the Al follows at a rapid rate. This is obviously the stage when the porous gold layer is created. Curve 5 is anomalous but the data are presented ‘as is’. In any case, it is mainly the initial slope that determines the thickness of the film. Finally, the film detaches from the glass substrate which causes a rapid increase in optical transmittance. In principle, availability of this data would allow the de-alloying process to be halted at any desired thickness of the nanoporous Au layer.
The arrow in the figure indicates bubble formation under the film as it begins to delaminate from the substrate. These abnormalities do not have a great effect on the thicknesses determined by the model as they occur after the sample has already completed de-alloying. Nevertheless, an attempt was made to minimize the formation of bubbles by placing the sample in the cuvette vertically, allowing bubbles that formed to rise up and escape. The etch rate can be derived from Fig. 4b, which illustrates the bulk dissolution rates of the alloy at the prescribed NaOH concentrations. The passivation-breakdown time is evidently concentration-dependent, but our main focus in understanding production of porous gold is the bulk etch rate, which requires further analysis.
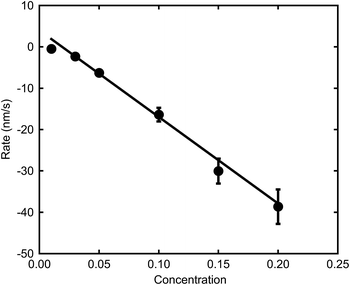
The relatively linear areas shown by red dots in Fig. 4b were used to determine the maximum rate of de-alloying. Fig. 5 illustrates that the maximum etch rates were approximately linear with concentration of NaOH and, therefore, that a first-order chemical reaction is occurring. The small deviations from linearity observed in Fig. 5 could be due to fitting inconsistencies and the random nature of de-alloying and morphology of sponges.
The effect of temperature (at a concentration of 0.1 M NaOH) is examined in Fig. 6a. In this case, an exponential increase in the dissolution rate with increase in temperature is found, as expected from eqn (1). An Arrhenius plot was made to obtain the activation energy graphically as depicted in Fig. 6b. The activation energy for the de-alloying process, as measured by the movement of the de-alloying interface, was calculated to be 46.5 ± 6.4 kJ mol−1 (0.48 ± 0.07 eV). This is a lower activation energy than that usually reported for the coarsening of the pores of the sponge after the de-alloying front has passed. In the latter case, values of the order of 60 kJ mol−1 (0.62 eV per atom) have been reported for Au alloys de-alloyed in either alkali31 or acid,30 which matches the value reported35 for the surface diffusion of Au in acidic solutions. The differences in the activation energies are due to the fact that two subtly different processes are being probed.
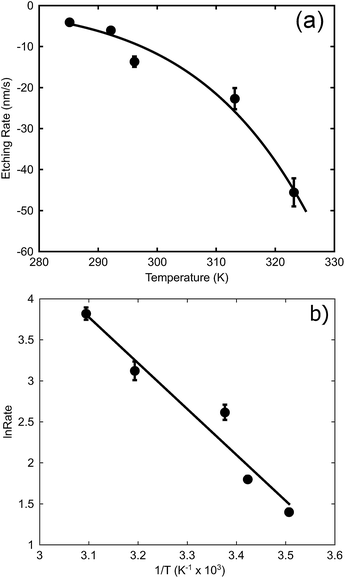 | ||
| Fig. 6 Effect of temperature on maximum de-alloying rate of AuAl2 (at 0.1 M NaOH). (a) The rates at various temperatures, (b) Arrhenius plot to determine activation energy. | ||
The activation energy for dimer diffusion of gold on aluminium surfaces has been estimated to be 0.82 eV for jumps and 0.24 eV for exchanges36 and so neither is a good match for the observed Ea. The activation energy for bulk diffusion of Au (1.74 eV per atom)35 is an even worse match. On the other hand, the Ea for dimer diffusion of aluminium on aluminium surfaces has been reported to be 0.54 eV and 0.40 eV for jumps and exchanges respectively.36 The activation energy dissolution of aluminium in sodium hydroxide can also be found in the literature, and is of the order of 0.59 eV.37 On balance, a better match of activation energy is found here for processes involving surface diffusion of Al atoms rather than those involving Au, suggesting that the rate limiting factors for the movement of the de-alloying front are the movement and dissolution of Al. Obviously, once the de-alloying front has passed, the actual coarsening of the sponge will be controlled by surface diffusion of Au atoms, with the higher value of activation energy of the prior literature being applicable.
4 Conclusions
An optical model based on in situ transmittance measurements made during the de-alloying process could be successfully used to monitor the de-alloying kinetics of AuAl2 in NaOH solutions. The resulting data provided a convenient means to extract the activation energy for the rate-controlling process. Etching rates showed a linear dependence on concentration of NaOH indicating a first-order chemical reaction. In contrast, etching rates were exponential when plotted against increasing temperature. A thermal activation energy of approximately 0.5 eV was determined. The available evidence indicates that the rate is limited by movement of Al atoms and not by surface diffusion or movement of the Au atoms.Acknowledgements
The authors thank the Australian Research Council for support under grant DP 140102003.References
- J. P. Candy, P. Fouilloux, M. Keddam and H. Takenouti, Electrochim. Acta, 1981, 26, 1029–1034 CrossRef CAS.
- M. B. Cortie, A. Maaroof, G. B. Smith and P. Ngoepe, Curr. Appl. Phys., 2006, 6, 440–443 CrossRef.
- X. Wang, Z. Zhang, H. Ji, J. Xu, X. Huang and Y. Ma, Appl. Surf. Sci., 2012, 258, 9073–9079 CrossRef CAS.
- J. Erlebacher, M. J. Aziz, A. Karma, N. Dimitrov and K. Sieradzki, Nature, 2001, 410, 450–453 CrossRef CAS PubMed.
- P. Rizzi, F. Scaglione and L. Battezzati, J. Alloys Compd., 2014, 586, S117–S120 CrossRef CAS.
- R. Li and K. Sieradzki, Phys. Rev. Lett., 1992, 68, 1168–1172 CrossRef CAS PubMed.
- S. Chen, Y. Chu, J. Zheng and Z. Li, Electrochim. Acta, 2009, 54, 1102–1108 CrossRef CAS.
- A. Wittstock, V. Zielasek, J. Biener, C. M. Friend and M. Bäumer, Science, 2010, 327, 319–322 CrossRef CAS PubMed.
- C. Xu, J. Su, X. Xu, P. Liu, H. Zhao, F. Tian and Y. Ding, J. Am. Chem. Soc., 2007, 129, 42–43 CrossRef CAS PubMed.
- G. B. Smith, A. I. Maaroof and A. Gentle, Opt. Commun., 2007, 271, 263–268 CrossRef CAS.
- M. B. Cortie, A. I. Maaroof and G. B. Smith, Gold Bull., 2005, 38, 15–23 CrossRef.
- X. Y. Lang, H. T. Yuan, Y. Iwasa and M. W. Chen, Scr. Mater., 2011, 64, 923–926 CrossRef CAS.
- S. Gao, H. Zhang, X. Wang, J. Yang, L. Zhou, C. Peng, D. Sun and M. Li, Nanotechnology, 2005, 16, 2530–2535 CrossRef CAS.
- J. Biener, G. W. Nyce, A. M. Hodge, M. M. Biener, A. V. Hamza and S. A. Maier, Adv. Mater., 2008, 9999, 1–7 Search PubMed.
- L. H. Qian, X. Q. Yan, T. Fujita, A. Inoue and M. W. Chen, Appl. Phys. Lett., 2007, 90, 153120 CrossRef.
- A. I. Maaroof, M. B. Cortie, A. Gentle and G. B. Smith, Phys. B, 2007, 394, 167–170 CrossRef CAS.
- H. A. Chen, J. L. Long, Y. H. Lin, C. J. Weng and H. N. Lin, J. Appl. Phys., 2011, 110, 6–11 Search PubMed.
- A. Mortari, A. Maaroof, D. Martin and M. B. Cortie, Sens. Actuators, B, 2007, 123, 262–268 CrossRef CAS.
- G. Ruffato, F. Romanato, D. Garoli and S. Cattarin, Opt. Express, 2011, 19, 13164–13170 CrossRef CAS PubMed.
- J. Erlebacher, J. Electrochem. Soc., 2004, 151, C614–C626 CrossRef CAS.
- K. Sieradzki, N. Dimitrov, D. Movrin, C. McCall, N. Vasiljevic and J. Erlebacher, J. Electrochem. Soc., 2002, 149, B370 CrossRef CAS.
- Y. C. K. Chen-Wiegart, S. Wang, I. McNulty and D. C. Dunand, Acta Mater., 2013, 61, 5561–5570 CrossRef CAS.
- S. Supansomboon, A. Porkovich, A. Dowd, M. D. Arnold and M. B. Cortie, ACS Appl. Mater. Interfaces, 2014, 6, 9411–9417 CAS.
- K. Sieradzki, R. R. Corderman, K. Shukla and R. C. Newman, Philos. Mag. A, 1989, 59, 713–746 CrossRef CAS.
- H. Shitamoto, M. Ema and T. Nagatani, J. Phys. D: Appl. Phys., 1998, 31, 781–789 CrossRef CAS.
- O. Zinchenko, H. A. D. Raedt, E. Detsi, P. R. Onck and J. T. M. D. Hosson, Comput. Phys. Commun., 2013, 184, 1562–1569 CrossRef CAS.
- S. A. Policastro, J. C. Carnahan, G. Zangari, H. Bart-Smith, E. Seker, M. R. Begley, M. L. Reed, P. F. Reynolds and R. G. Kelly, J. Electrochem. Soc., 2010, 157, C328–C337 CrossRef CAS.
- M. Tai, A. Gentle, K. S. de Silva, M. D. Arnold, E. van der Lingen and M. B. Cortie, Metals, 2015, 7, 1197–1211 CrossRef.
- A. A. El Mel, F. Boukli-Hacene, L. Molina-Luna, N. Bouts, A. Chauvin, D. Thiry, E. Gautron, N. Gautier and P. Y. Tessier, ACS Appl. Mater. Interfaces, 2015, 7, 2310–2321 CAS.
- L. H. Qian and M. W. Chen, Appl. Phys. Lett., 2007, 91, 083105 CrossRef.
- Z. Zhang, Y. Wang, Y. Wang, X. Wang, Z. Qi, H. Jia and C. Zhao, Scr. Mater., 2010, 62, 137–140 CrossRef CAS.
- H. W. Pickering, Corros. Sci., 1983, 23, 1107–1120 CrossRef CAS.
- W. C. Roberts-Austen, Proc. R. Soc. London, 1892, 50, 367–368 CrossRef.
- S. Supansomboon, A. Maaroof and M. B. Cortie, Gold Bull., 2008, 41, 296–304 CrossRef CAS.
- J. M. Doña and J. González-Velasco, J. Phys. Chem., 1993, 97, 4714–4719 CrossRef.
- G. Antczak and G. Ehrlich, Surface diffusion: Metals, metal atoms, and clusters, Cambridge University Press, 2010 Search PubMed.
- M. A. Streicher, J. Electrochem. Soc., 1948, 93, 285–316 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Video animation of transmittance during de-alloying. See DOI: 10.1039/c6ra18272k |
| This journal is © The Royal Society of Chemistry 2016 |