Scaling of mixing time for droplets of different sizes traveling through a serpentine microchannel†
Abstract
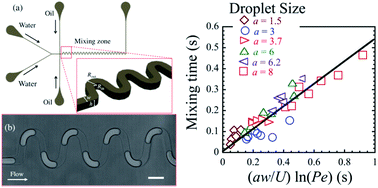
Here, we investigate separately the dependence of the mixing time on the size and velocity of micro-droplets moving through serpentine channels. We find that the mixing time scales linearly with droplet size. All experimental data collapse on a master-line, when the convective time scale is multiplied by the dimensionless droplet size.

 Please wait while we load your content...
Please wait while we load your content...