Molecular dynamics study on structure evolution of monocarboxylic acid intercalated layered double hydroxides

Abstract

Hydrotalcite derived materials are considered to be promising candidates for solid sorbents for carbon dioxide capture at intermediate temperatures (250–400 °C). The recently developed organically intercalated layered double hydroxide (LDH) shows a great improvement in carbon dioxide adsorption capacity compared to alternative sorbents. However, the molecular-scale structure of this new class of materials is yet to be understood, hindering the further development of high-capacity carbon dioxide adsorbents based on LDH. In the current study, classical molecular dynamics simulations were conducted to investigate the atomistic structures of monocarboxylic acid intercalated LDHs containing Mg and Al in the ratio 3 : 1. The replacement of carbonate anions by stearate anions (CH₃(CH₂)₁₆COO⁻) in LDH expanded the basal spacing from 7.8 Å to 19.6 Å. The presence of water molecules could further increase the basal spacing to up to 33.5 Å. In addition, the basal spacing of LDH could be expanded by other carboxylic anions (e.g., CH₃(CH₂)₁₁COO⁻, CH₃(CH₂)₅COO⁻), and the spacing was proportional to the length of the carbon chains. Water molecules inside interlayer galleries tend to bond firstly with the hydroxyl groups of hydroxide layers, and water molecules added subsequently then fill the gallery space. For comparison, LDHs intercalated by CH₃(CH₂)₁₆COO⁻ and CH₃(CH₂)₆COO⁻ were prepared by the acid-aided anion-exchange method and characterized by powder X-Ray Diffraction (XRD) analysis, thermogravimetry (TGA) and Differential Scanning Calorimetry (DSC). The basal spacing and XRD patterns observed in the simulations are in good agreement with experimental observations. The quantitative analyses in this work could provide guidelines for optimizing the lamellar structure of LDH to improve its capacity for CO₂ capture.

---

1 Introduction

Hydrotalcite is an abundant natural clay mineral and has been considered as a promising solid sorbent for pre-combustion carbon dioxide capture, which involves separating CO₂ from the hydrogen-rich shift gas from sweet/sour water–gas shift reactors at intermediate temperatures (250–400 °C).¹ Hydrotalcite is a layered double hydroxide (LDH) with a crystal structure similar to that of brucite.² The general form of hydrotalcite-like materials is [M_1−x²⁺M_x³⁺(OH)₂]^x+A_x/m^m−·nH₂O, where M²⁺ is a divalent metal cation (e.g., Mg, Fe, Co, Ga, etc.) and M³⁺ is a trivalent metal cation (e.g., Al, Cr, Mn, etc.). The replacement of divalent cations by trivalent cations makes the LDH positively charged, which can be neutralized by the anion A^m− in the interlayer gallery. The interlayer anions can be inorganic (e.g., CO₃²⁻, Cl⁻, CrO₄²⁻, etc.)³ or organic (stearate,⁴ DNA,⁵etc.), and can be incorporated by the anion-exchange method.⁶

To derive a carbon dioxide adsorbent from hydrotalcite, the divalent and trivalent cations are set as Mg²⁺ and Al³⁺ and carbonate is used as the interlayer anion (referred to as the Mg–Al–CO₃²⁻ system). Calcination of hydrotalcite at temperatures over 400–450 °C is usually applied to convert LDH into the layered double oxide (LDO), which is the final form for carbon dioxide adsorption at intermediate temperatures (250–400 °C). The capacity of the LDO derived from Mg–Al–CO₃²⁻ ranges from 0.2–0.7 mmol g⁻¹.¹ Given the difficulties of carbon dioxide capture at intermediate temperatures, this capacity is still lower than those of other adsorbents that are used at different temperature ranges. Great efforts have been made to improve the capacity of hydrotalcite-like materials by tuning particle size/shape, pore size, surface area, chemical components and intercalation anions.^7–11 The recent development of a stearate anion intercalated LDH (Mg–Al–stearate system) shows a promising capacity of 1.25 mmol g⁻¹,⁴ which is 2.5 times higher than that of the original Mg–Al–CO₃²⁻ system. Furthermore, a potassium-promoted stearate-pillared LDH derived CO₂ adsorbent shows a capacity of 1.93 mmol g⁻¹.¹² This class of organically intercalated LDH materials offers a new direction for the development of high temperature carbon dioxide adsorbents.

The intercalation of organic anions into hydrotalcites, on one hand, alters the crystal structures and hydrated states of LDH, and on the other hand, determines the intrinsic structure evolution during calcination, and consequently, the carbon dioxide adsorption capacity of the LDO. Various experimental studies have been carried out to investigate the particle sizes, surface areas and basal spacings (d) of organically intercalated LDHs. Wang et al.⁴ characterized the Mg₃–Al₁–stearate system (where 3 and 1 refer to the atomic ratio of Mg to Al) by powder X-ray diffraction (XRD) analysis and found that the interlayer distance was expanded to 35.4 Å by stearate chains. Li et al.¹² found that potassium-promoted Mg₃–Al₁–stearate has an interlayer of 38.7 Å using a similar characterization method. Kanoh et al.¹³ investigated the crystal structures of Mg₃–Al₁–stearate systems and found that stearate chains inside the LDH gallery have two interconvertible geometries, i.e., monolayer and bilayer geometries, at different treatment temperatures. The self-assembled bilayer geometry may expand the interlayer distance of LDH to 52.6 Å, when the stearate chains are tilted to around 61° from the hydroxide plane.¹⁴

However, it is still difficult to obtain molecular-scale insights into the crystal structures of organically intercalated layered minerals, and the distributions of carbon chains within interlayer galleries through currently available experimental technologies. Recent developments in molecular dynamics (MD) simulations and proper force fields make it possible to simulate clay–organic composites and investigate their atomic structures and even dynamics. Kirkpatrick and colleagues investigated the energy and structure of LDH intercalated with short chain carboxylic acids using MD simulations.^15,16 The hydrated interlayer galleries were found to be stabilized by an integrated hydrogen-bonding network among the anions, water molecules and hydroxyl groups of the LDH layers.¹⁷ Zhao and Burns investigated single chain quaternary ammonium cations (QAC) intercalated into montmorillonite using MD modelling and proposed a model to predict the QAC–clay microstructures.¹⁸ These studies have demonstrated the utility of MD methods to investigate the structure aspects of clay–organic composites and provided significant insights. However, to the authors' best knowledge, no MD investigations of the crystal structure evolution of stearate intercalated LDH exist.

In this study, MD simulations were employed to investigate the crystal structure and hydrated states of stearate (CH₃(CH₂)₁₆COO⁻) intercalated Mg₃–Al₁ LDH. CH₃(CH₂)₁₁COO⁻ and CH₃(CH₂)₆COO⁻ intercalated LDH models were also generated to investigate the effect of carbon chain length on the LDH crystal structure. Given the fact that most of the saturated fatty acids found in nature (i.e., in animals and plants) are straight hydrocarbon chains with an even number of carbon atoms, we used such readily available materials in our experiments; the use of them in our MD simulations was for comparison purposes. It is also well known that there is an alternation of melting points between fatty acids with odd and even numbers of carbon atoms (due to different alkyl chain packings in the bulk). Therefore, we also examined one chain with an odd number of carbon atoms to see whether such an alternation effect also exists in the packing within the confined interlayer galleries. For comparison, LDHs intercalated by CH₃(CH₂)₁₆COO⁻ and CH₃(CH₂)₆COO⁻ were prepared by the acid-aided method and characterized by XRD analysis, thermogravimetric analysis (TGA) and Differential Scanning Calorimetry (DSC). The basal spacing and XRD patterns of Mg₃–Al₁–stearate LDH obtained in MD simulations are in good agreement with those found in experiments carried out in this work. Further details of the carbon chains' orientations as well as the swelling patterns of Mg₃–Al₁–stearate LDH in hydrated environments are also provided in this study.

2 Methodology

2.1 Experimental

The acid-aided^2,12,19 anion-exchange method was employed to synthesize Mg–Al–carboxylic LDH from hydrotalcite. Since an Mg/Al mole ratio of 3 is considered optimal for CO₂ adsorption,⁴ PURAL MG70 with the Mg/Al mole ratio of 3 was used as the starting hydrotalcite in this study. Two representative carboxylic acids, CH₃(CH₂)₁₆COO⁻ and CH₃(CH₂)₆COO⁻, were inserted into the LDH interlayer galleries. Sodium carboxylic solution was added to 100 mL of hydrotalcite suspension in a flask at 80 °C, and diluted hydrochloric acid was added dropwise to adjust the pH of the mixed suspension to ∼4.0. The mixture was then stirred under N₂ protection for 4 hours at 80 °C to form Mg–Al–carboxylic LDH. The aged and stirred mixture was filtered and washed with deionized water at the same temperature until the pH was stabilized at ∼7.0. The mixture was then dried in an oven at 80 °C. Powder XRD was conducted on a Rigaku D-max 2500 X-ray diffractometer using Cu Kα radiation and a power of 40 KV at 40 mA. Signals were recorded with a step size of 0.02°. In order to quantitatively determine the water content, TG-DSC tests were performed using a TA Q600 thermal gravimetric analyzer. The CH₃(CH₂)₁₁COO⁻ and CH₃(CH₂)₆COO⁻ intercalated PURAL MG70 powder samples were gradually calcined from room temperature to 700 °C at a ramp rate of 5 K min⁻¹ in N₂.

2.2 Simulation details

In this study, atomic interactions in LDH were described by the CLAY force field (CLAYFF),²⁰ which is based on an ionic (non-bonded) description of the metal–oxygen interactions and has a flexible framework which can be combined with other potentials. CVFF²¹ was employed to simulate the organics intercalated inside the hydrotalcite galleries. Since CVFF has a similar framework to CLAYFF, these two force fields could be conveniently combined in MD simulations. A flexible single point charge (SPC) potential for water²⁰ was also integrated into current models to simulate hydrated LDH. To evaluate the total energy of the simulation models, non-bonded (van der Waals and Coulombic) and bonded (bond, angle, torsion and improper) interaction forces were evaluated. Detailed formulations of each interaction force have been described previously.^20,21 All MD simulations were conducted by LAMMPS²² and visualized by Ovito²³ and Materials Studio.

Hydrotalcite-like materials in general have a three-layer rhombohedral structure. To simulate the structure of carboxylic acid intercalated LDH, 3D orthogonal periodic models containing 11 × 8 × 3 lattice units were generated. The Mg : Al ratio was kept as 3 : 1 as this ratio is considered to be optimum for carbon dioxide capture.⁴ The lattice parameters in the x- and y-directions were initially set to be 3.05 Å, while the lattice parameter in the z-direction was initially set to be able to accommodate intercalated organic anions. The sizes of the model in the x- and y-directions were around 35 Å and 22 Å, respectively, while the size in the z-direction was controlled by the isothermal-isobaric (NPT) ensemble. The ratio of metal atoms to intercalated carboxyl anions was chosen to be 4 : 1 to ensure a neutral charge for the whole system, i.e., there were 22 carboxyl anions in each interlayer gallery. Initially, the carboxyl anions were positioned “vertically” to the basal plane and distributed evenly in the x–y plane (35 Å × 22 Å) in each interlayer gallery. In addition, half of the interlayer anions had the carboxylate anions closer to one side of gallery and the other half of the interlayer anions had the carboxylate anions closer to the other side of the interlayer gallery. In this study, three types of carboxyl acid anions were intercalated into the hydrotalcite materials, i.e., CH₃(CH₂)₁₆COO⁻, CH₃(CH₂)₁₁COO⁻ and CH₃(CH₂)₆COO⁻. To investigate the structure of the organically intercalated hydrotalcites in their hydrated states, water molecules were added into the interlayer galleries. The ratio of water molecules to intercalated anions ranged from 0 to 20.

After initial construction of the models, energy minimization using a conjugate gradient algorithm was conducted until the energy variance of the whole system was below 10 × 10⁻⁹ kcal mol⁻¹. An NPT ensemble with a Nose–Hoover thermostat and barostat^24,25 was then applied to the whole system. The temperature was fixed at 300 K and the pressure of the simulation box was fixed at 1 atm. The time step of MD simulations in this study was 0.5 femtoseconds (fs). These organic–inorganic systems all reached their energetic equilibrium states after around 200 picoseconds (ps). The basal spacing of each system was recorded and averaged from 400 ps to 1 nanosecond (ns). System configurations were recorded after 1 ns for carbon chain geometry analysis and powder XRD pattern simulation. The REFLEX module in Materials Studio was employed to simulate the powder XRD pattern of system configurations obtained in the MD simulations.

3 Results

3.1 Effect of carbon chain length

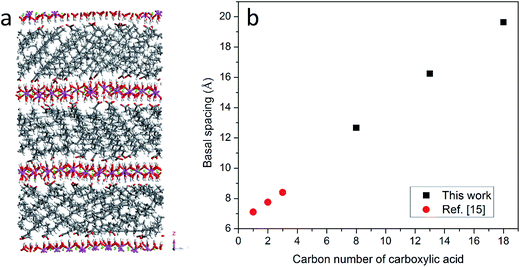
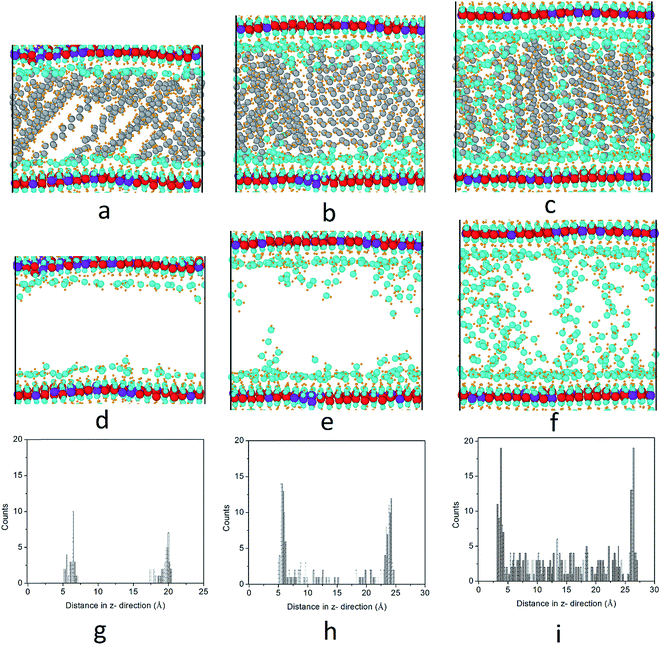
The organically intercalated systems show stable layered structures in the current study and the layered structure and hexagonal symmetry of hydrotalcite were well reproduced. The a- and b- unit cell dimensions in the current MD simulation are 3.19 Å, which are in good agreement with experimental data (3.14 Å).²Fig. 1(a) shows the atomic configuration of stearate intercalated LDH after 1 ns with the NPT ensemble. As expected, the stearate intercalated into the interlayer gallery expanded the basal spacing from the 7.8 Å of the original Mg–Al–CO₃²⁻ system to 19.6 Å. The stearate chains inside the gallery are neither perpendicular nor parallel to the hydroxide layer plane upon equilibration, even though initially the carboxylic chains were placed perpendicular to the hydroxide layer planes. The stearate carbon chains tilt in the gallery space with an average angle of 29.0° ± 4.8 with respect to the basal planes, as shown in Table 1. Recently, Naik et al.²⁶ reported the MD simulation of dodecyl sulfate (DDS) surfactant chains intercalated in an Mg–Al LDH, where a transition from monolayer surfactant chains to bilayer chains was observed, depending on the DDS density and the Al/Mg ratio. In that work,²⁶ a different ensemble was applied to obtain the equilibrium basal spacing, i.e., the NVT ensemble was performed when two single Mg–Al LDH sheets with anchored surfactant chains were brought closer together from infinite separation in incremental steps, and the LDH layers were kept rigid along all three directions. Therefore, a direct comparison between the current work and the results reported by Naik et al. is difficult to establish.

Fig. 1 (a) Atomic configuration of the hydrotalcite system intercalated by stearate after running the NPT ensemble for 1 ns. Atoms are displayed in stick mode; green is used for Mg, purple for Al, red for oxygen, white for hydrogen and grey for carbon atoms. (b) The relationship between the number of carbon atoms in the anions and the basal spacing of the hydrotalcites at room temperature without water molecules.

Table 1 Space angles of monocarboxylic acids intercalated in LDH with different water/anion ratios

Water/anion ratio	CH3(CH2)6COO^− (C8)		CH3(CH2)11COO^− (C13)		CH3(CH2)16COO^− (C18)
	Space angle (°)	Std. dev.	Space angle (°)	Std. dev.	Space angle (°)	Std. dev.
0	19.6	10.0	28.3	12.7	29.0	4.8
3	34.7	11.4	34.6	4.4	32.2	3.0
8	50.1	12.5	45.4	10.4	40.1	8.9
15	55.9	21.4	69.0	6.8	50.9	7.8
20	—	—	—	—	65.8	8.5

---

In addition to stearate carbon chains, CH₃(CH₂)₁₁COO⁻ and CH₃(CH₂)₆COO⁻ were inserted into the LDH system to investigate the effect of carbon chain length on the basal spacing of hydrotalcites. The basal spacings of CH₃(CH₂)₁₁COO⁻ and CH₃(CH₂)₆COO⁻ intercalated hydrotalcite are 16.2 and 12.7 Å, respectively. Combined with previous results from the literature,¹⁵ it is clear that the basal spacing of hydrotalcites is proportional to the length of the intercalated carbon chains, as shown in Fig. 1(b). The averaged space angles (the angles between the carbon chains and hydroxide layers) of CH₃(CH₂)₁₁COO⁻ and CH₃(CH₂)₆COO⁻ in the interlayer galleries are 28.3° ± 12.7 and 19.6° ± 10.0 respectively, as shown in Table 1. In addition, the standard deviation of the space angle of CH₃(CH₂)₆COO⁻ is larger than that of CH₃(CH₂)₁₆COO⁻, which indicates a more disordered distribution when the shorter carbon chains are intercalated in LDH.

3.2 Effect of the presence of water on the basal spacing

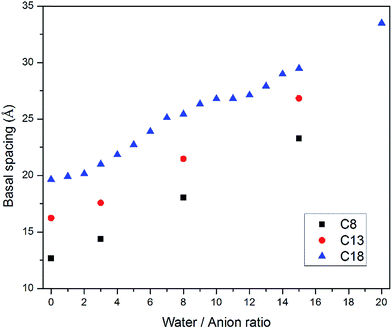
Water molecules are usually present in LDH interlayer galleries since anion exchanges are conducted in aqueous suspensions and carboxylic intercalated LDH has a strong tendency to adsorb water. To further investigate the swelling patterns of carboxylic intercalated LDH, water molecules were added into the interlayer galleries in the MD simulations. The ratio of water molecules to anions was varied from 0 to 20. The procedure used for investigating the hydrated states of carboxylic intercalated LDH was similar to that used for the system without water, as described in Section 2.2.

Taking stearate intercalated LDH as an example, the basal spacing was increased from 19.6 Å (without water) to 21.7 Å when the water/anion ratio was 3. In each system, after running NPT for 1 ns, the angles of all 66 stearate chains to the hydroxide plane were used to calculate the average of the space angles. The space angle between the stearate chain and hydroxide plane increased to 32.2° ± 3.0 with a water/anion ratio equal to 3. Further addition of water molecules continued the same trend, i.e., water molecules increased the basal spacing of LDH as well as the average angle between the stearate chains and hydroxide planes, as shown in Fig. 2. When the water/anion ratio reached 20, the basal spacing of LDH was 33.5 Å and the stearates' space angle was 65.8° ± 8.5. The averaged space angles of stearate chains with different amounts of water are listed in Table 1.

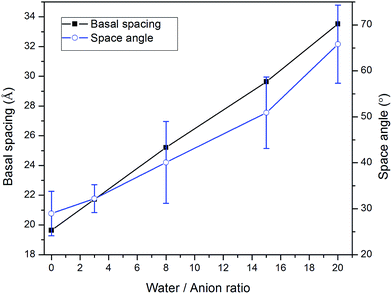Fig. 2 The correlation between the amount of water and both the basal spacing and the angle between the stearate chain (CH₃(CH₂)₁₆COO⁻) and basal plane in stearate intercalated hydrotalcite.

Water molecules were also inserted into the CH₃(CH₂)₁₁COO⁻ (C13) and CH₃(CH₂)₆COO⁻ (C8) intercalated LDH systems. The configurations after equilibration were similar to that of stearate intercalated LDH. As shown in Fig. 3, the LDH systems intercalated with relatively shorter carbon chains showed the same swelling pattern in their hydrated states as the stearate, i.e., more water molecules inside the interlayer galleries resulted in larger basal spacings. The trend observed in this study is consistent with previous computational work on short chain carboxylic acid intercalated hydrotalcites.¹⁵Fig. 3 also suggests that the layered structures could be delaminated in suspensions. For C8 carbon chains, the averaged space angle increased from 19.6° ± 10.0 (without water) to 55.9° ± 21.4 (water/anion ratio = 15), as shown in Table 1. The presence of water molecules could increase the space angle as well as the randomness of the intercalated carbon chains.

Fig. 3 Basal spacing of carboxylic acid intercalated hydrotalcites as functions of carbon chain length and water molecule amount. Carboxylic anions are referenced by their total carbon numbers, e.g., C8 refers to CH₃(CH₂)₆COO⁻, C13 refers to CH₃(CH₂)₁₁COO⁻ and C18 refers to CH₃(CH₂)₁₆COO⁻.

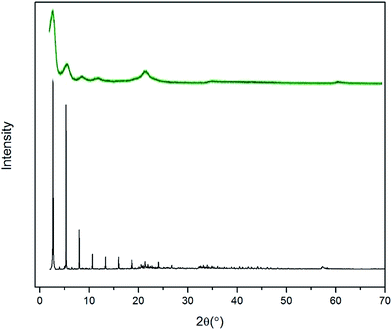
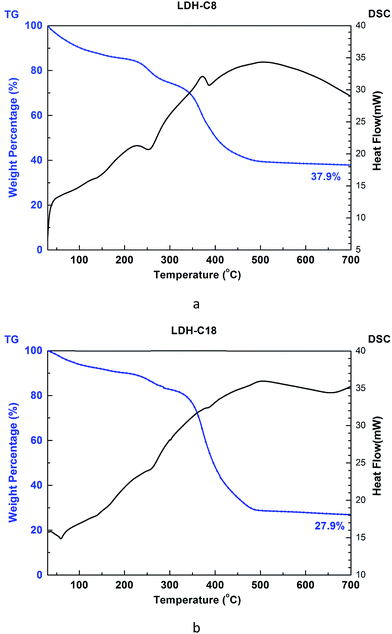
To validate the molecular-level crystal structures, an experimental study was carried out with the synthesis methods described in Section 2.1 to obtain powder XRD patterns of C8 and C18 intercalated LDH at room temperature. For stearate intercalated LDH, the stearate anions (with a length of 22.0 Å) expanded the basal spacing from the 7.7 Å of the original MG70 hydrotalcite to 34.0 Å, which is indicated by the (003) peak in the XRD pattern. Both experimental and computational XRD patterns show similar peak features for stearate intercalated LDH (see Fig. 4). We may observe that the peaks in the simulated XRD patterns shift slightly to the right compared to the experimental XRD patterns. The calculated basal spacing in the MD simulation (33.5 Å; water/anion ratio = 20) is about 1.25% smaller than that obtained from experiments (34.0 Å). It should be noted that the brucite-like layers in hydrotalcite occupy a thickness of about 4.8 Å and the stearate chain has a length of 22.0 Å. Clearly, the relatively large basal spacing observed in experiments (34.0 Å) is not simply due to the stearate chains vertically pillaring the interlayer galleries. One possible explanation is that during the anion-exchange process, an introduction of excess water in the interlayer gallery may physically expand the basal spacing and facilitate the formation of a complex long carbon chain network inside the gallery. The complex long carbon chain network may not collapse during the 80 °C drying step, leaving a relatively larger basal spacing. In addition, the uncertain amount of water in the experimentally synthesized Mg–Al–stearate LDH may contribute to the difference between experiments and simulations. Even though the Mg–Al–stearate LDH was dried in an oven at 80 °C, studies have demonstrated that interlayer water in hydrotalcite could remain in the galleries at temperature up to 190 °C as the interlayer water is “loosely held” by hydroxyl groups.²⁷ In the region 30–140 °C, the basal spacing remained relatively stable and there were still water molecules in the interlayer galleries. In order to quantitatively determine the water content, we performed TG-DSC tests. The CH₃(CH₂)₁₁COO⁻ and CH₃(CH₂)₆COO⁻ intercalated PURAL MG70 powder samples were gradually calcined from room temperature to 700 °C at a ramp rate of 5 K min⁻¹ in nitrogen. Fig. 5 shows the TG-DSC curves of both these samples. The remaining weight percentages of CH₃(CH₂)₁₁COO⁻ and CH₃(CH₂)₆COO⁻ were 27.9% and 37.9%, respectively. As shown in Fig. 5, two stages (from room temperature to about 250 °C, and from 250 °C to 450 °C) of weight loss were observed. A previous study²⁷ of Mg–Al–CO₃ LDH suggested that the first stage of weight loss is related to water loss and partial dehydroxylation while the second stage is caused by complete dehydroxylation. Since there is no evidence to show the decomposition temperature of intercalated anions, we assume that anion decomposition occurs throughout the calcination process. From the analysis above, it is confirmed that the first stage of weight loss will definitely include the separation of water molecules from LDH crystals (including surface adsorbed water molecules and interlayer crystal-bound water molecules), as well as the partial decomposition of OH⁻ and CH₃(CH₂)₁₁COO⁻ or CH₃(CH₂)₆COO⁻ anions.

Fig. 4 Experimental (green) and simulated (black) PXRD patterns of stearate intercalated LDH.

Fig. 5 TG-DSC curves of (a) CH₃(CH₂)₆COO⁻ (C8 LDH) and (b) CH₃(CH₂)₁₁COO⁻ (C18 LDH).

The amount of water in organically intercalated LDH structures is usually determined by the synthesis methods and drying temperature. The basal spacing of hydrotalcite was reported to decrease from 7.8 Å to 7.2 Å after heating at 200 °C.²⁸ Considering that the thickness of one layer of hydroxide is 4.8 Å, the space of the interlayer gallery has been decreased from 3.0 Å to 2.4 Å.²⁸ A similar trend was observed in the study by Yang et al., in which the interlayer distance was decreased from 2.8 Å to 1.8 Å upon heating at 190 °C.²⁷ Since the layered structure of LDH remains stable during heating up to 200 °C, it is actually the removal of water molecules that contributes to the difference in basal spacing. In a reaction to intercalate diphosphonates with aromatic bridging groups, [O₃P–(C₆H₄)_n–PO₃]⁴⁻, into hydrotalcite (Mg/Al ratio = 2), the temperature could affect the d-spacing values.²⁹ At a reaction temperature of 0 °C, the organically intercalated LDH has a basal spacing of 14.7 Å, while with a reaction temperature of 100–200 °C, the produced LDH has a basal spacing of 9.6 Å, which is 35% smaller. The difference between the basal spacings are attributed to the removal of water molecules in the interlayer galleries and of OH– groups connecting to the metal cations. Simulation results in this study have quantitatively demonstrated the different basal spacings of organically intercalated LDH in different hydration states.

For C8 intercalated LDH, the carbon chains expand the basal spacing to 21.2 Å as observed in XRD patterns. The experimental result matches well with simulated results (d = 23.2 Å with a water/anion ratio = 15).

The arrangement of organic anions in intercalated LDH has attracted great interest recently. A study by Iyi et al.³⁰ investigated the orientation of an anionic azobenzene derivative (AzAA) inside Mg–Al–LDH. Based on TEM and XRD results, they concluded that AzAA has horizontal orientation at low AzAA/LDH ratios and vertical orientation at higher ratios, while LDH with a horizontal orientation has a basal spacing of 8 Å and LDH with a vertical orientation has a basal spacing of 23 Å. The combination of horizontal and vertical orientation arrangements could possibly increase the basal spacing. For instance, the one-layer vertical one-layer horizontal stacking order may appear to form (003) peaks in XRD representing a larger basal spacing, i.e., 31 Å. Stearate-intercalated LDH composites have also been investigated by Li et al.,¹² and the orientation of the stearate chains was claimed to be vertical to the layered hydroxide planes, which was concluded from the relatively large basal spacing (34.0 Å). Itoh et al.¹⁴ proposed that stearate chains were neither vertically nor horizontally oriented. Instead, the carbon chains were tilted ∼61° from the hydroxide planes inside the interlayer galleries. The relatively large basal spacing in Itoh's study (53.7 Å) was attributed to the self-assembly behavior of intercalated stearate chains. In our current MD simulations, a highly ordered distribution of intercalated carbon chains was not observed, i.e., the carbon chains were neither vertical nor horizontal. Instead, the stearate chains were tilted inside the interlayer galleries, while the tilting angles were strongly correlated to the amount of water in the galleries. The tilting angle of 65.8° from LDH planes at the water/anion ratio of 20 in this study matches well with the experimental observations in Itoh's work.¹⁴ However, it should be noted that organics intercalated in LDH might have different geometries due to the different synthesis methods. The observation in the current study does not exclude the possibility of other distribution geometries.

3.3 Distribution of water molecules

We further investigated the water molecule distributions inside the interlayer gallery. Here, we illustrate the Mg₃–Al₁–stearate LDH as an example. The first row of Fig. 6 shows the atomic configurations of stearate intercalated LDH with water/anion ratios of 3, 8 and 15, while the second row shows the same configurations but with the stearate chains removed for clarity. To quantitatively characterize the water molecule distributions, a water count profile was performed through the interlayer gallery, as shown in Fig. 6g–i. When a small amount of water, (e.g., a water/anion ratio of 3) was added into the hydrotalcite, the formation of thin water layers bonded to the hydroxide layers may result, because water molecules can bond with the hydroxyl groups of LDH by forming hydrogen bonds.¹⁶ After the hydrogen bonding sites close to the hydroxide layers are saturated, further water added into the layer (i.e., when the water/anion ratio increases to 8 and 15) will be distributed in the interlayer gallery space. In this study, a longer simulation time (up to 2 ns) yielded a similar trend for water molecule distributions in the interlayer gallery.

Fig. 6 Distributions of water molecules in stearate intercalated hydrotalcites. Columns 1, 2 and 3 show the water distribution when the water/anion ratios are 3, 8 and 15, respectively. The first row shows the system atomic configurations (a–c); the second row shows the configurations without displaying the stearate anions (d–f); and the third row shows the water count profiling across the interlayer gallery (g–i). Atoms are displayed as spheres; purple spheres are used for Al, red spheres for Mg, blue spheres for oxygen, yellow spheres for hydrogen and grey spheres for carbon atoms.

LDHs intercalated with inorganic anions were found to have energetically favored hydration states due to local minima for hydration energy.^3,31 However, previous studies have demonstrated that LDH intercalated with carboxylate anions do not have energetically well-defined structural states at specific water contents.¹⁶ Instead, LDH intercalated with carboxylate anions prefer to adsorb water continuously in water-rich environments such as aqueous solutions and high relative humidity (R.H.) conditions.¹⁶ This behavior may lead to increased basal spacing or even delamination of the hydroxide layers. Li and Kirkpatrick³² have shown that citrate intercalated LDH has different basal spacings at different R.H. conditions. The basal spacing of citrate intercalated LDH changes from 8.9 Å at R.H. = 0% to 11.3 Å at R.H. = 75%, to 18.9 Å at 100% R.H., as shown by the XRD patterns. Fig. 6 also demonstrates the re-orientation of stearate chains from low water content to high water content.

Accurate molecular models are desirable to predict the structures and dynamics of LDH intercalated with organic and other mineral materials. The MD simulation and experimental characterization in the current study has demonstrated the feasibility of studying the structure of organic–clay composites by a computational approach. However, for a better understanding of the results, the limitations of MD simulations should be fully appreciated. First of all, accurate representations of atomic interactions in organic–clay composites are essential to obtain reasonable results. Secondly, the crystal structure and dynamics depend on the initial model construction for the MD simulation. For instance, different initial geometries of stearate-intercalated LDH could lead to slightly different basal spacings. In addition, MD simulations have limited time scales compared with experimental approaches. A typical simulation time is in the order of ns, while experimental synthesis of organic–clay composites may take hours or days. The energy minima reached within ns in MD simulations were interpreted as stable states of the organic–clay composites. However, we should not exclude the possibility of other stearate intercalated LDH crystal structures that may be reached during the synthesis process in experiments, over a much longer time scale. In experiments, the anion-exchange processes between stearate chains and carbonate anions in aqueous environments may determine the final crystal structures of organic–LDH composites.

4 Conclusions

In summary, MD simulations were conducted to investigate the structures of monocarboxylic acid intercalated LDHs. Stearate intercalated LDH without water molecules shows a basal spacing of around 19.7 Å. The stearate carbon chains inside hydrotalcite are tilted, with an average angle between the carbon chains and hydroxide layers of 29.0° ± 4.8. The basal spacings of carboxylic anion intercalated hydrotalcites have a linear relationship with the carbon chain length of the intercalated anions.

The presence of water molecules in the interlayer galleries increases the basal spacing. For instance, the basal spacing reaches 33.5 Å when the water/anion ratio is increased to 20 in the stearate intercalated system. The water molecules inside hydrotalcite firstly bond with the hydroxyl groups of hydroxide layers, forming water layers close to the LDH. Further addition of water fills the gallery space. An increased amount of water also facilitates the reorientation of the stearate chains and increases their tilt angle to around 65.8° ± 8.5. This trend is applicable to hydrotalcite intercalated with other carboxylic acids. Simulated powder XRD patterns show similar peaks positions to those obtained experimentally, which validates the effectiveness of the current models.

References

1. S. Choi, J. H. Drese and C. W. Jones, ChemSusChem, 2009, 2, 796–854.
2. Layered Double Hydroxides, ed. X. Duan and D. G. Evans, Springer-Verlag, Berlin, Heidelberg, 2006, vol. 119.
3. X. Hou, D. L. Bish, S.-L. Wang, C. T. Johnston and R. J. Kirkpatrick, Am. Mineral., 2003, 88, 167–179.
4. Q. Wang, H. H. Tay, Z. Zhong, J. Luo and A. Borgna, Energy Environ. Sci., 2012, 5, 7526.
5. H. Nakayama, A. Hatakeyama and M. Tsuhako, Int. J. Pharm., 2010, 393, 104–111.
6. S. Miyata, Clays Clay Miner., 1983, 31, 305–311.
7. K. B. Lee, a. Verdooren, H. S. Caram and S. Sircar, J. Colloid Interface Sci., 2007, 308, 30–39.
8. P. W. Xiao, J. Y. Jun, J. Cheng, P. H. Zheng and P. X. Zhi, Environ. Sci. Technol., 2008, 42, 614–618.
9. J. M. Oh, S. H. Hwang and J. H. Choy, Solid State Ionics, 2002, 151, 285–291.
10. C. V. Miguel, R. Trujillano, V. Rives, M. a. Vicente, a. F. P. Ferreira, a. E. Rodrigues, a. Mendes and L. M. Madeira, Sep. Purif. Technol., 2014, 127, 202–211.
11. Q. Wang, Y. Gao, J. Luo, Z. Zhong, A. Borgna, Z. Guo and D. O'Hare, RSC Adv., 2013, 3, 3414–3420.
12. S. Li, Y. Shi, Y. Yang, Y. Zheng and N. Cai, Energy Fuels, 2013, 27, 5352–5358.
13. T. Kanoh, T. Shichi and K. Takagi, Chem. Lett., 1999, 117–118.
14. T. Itoh, N. Ohta, T. Shichi, T. Yui and K. Takagi, Langmuir, 2003, 19, 9120–9126.
15. P. P. Kumar, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. C, 2007, 111, 13517–13523.
16. P. P. Kumar, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. B, 2006, 110, 3841–3844.
17. A. G. Kalinichev, P. Padma Kumar and R. James Kirkpatrick, Philos. Mag., 2010, 90, 2475–2488.
18. Q. Zhao and S. E. Burns, Environ. Sci. Technol., 2012, 46, 3999–4007.
19. F. Kooli, V. Rives and M. a. Ulibarri, Inorg. Chem., 1995, 34, 5114–5121.
20. R. T. Cygan, J.-J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266.
21. P. Dauber-Osguthorpe, V. A. Roberts, D. J. Osguthorpe, J. Wolff, M. Genest and A. T. Hagler, Proteins: Struct., Funct., Genet., 1988, 4, 31–47.
22. S. Plimpton, J. Comput. Phys., 1995, 117, 1–42.
23. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.
24. S. Nosé, J. Chem. Phys., 1984, 81, 511.
25. W. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
26. V. V. Naik, R. Chalasani and S. Vasudevan, Langmuir, 2011, 27, 2308–2316.
27. W. Yang, Y. Kim, P. K. T. Liu, M. Sahimi and T. T. Tsotsis, Chem. Eng. Sci., 2002, 57, 2945–2953.
28. N. D. Hutson, S. A. Speakman and E. A. Payzant, Chem. Mater., 2004, 16, 4135–4143.
29. J. D. Wang, G. Serrette, Y. Tian and A. Clearfield, Appl. Clay Sci., 1995, 10, 103–115.
30. N. Iyi, K. Kurashima and T. Fujita, Chem. Mater., 2002, 14, 583–589.
31. J. Wang, A. G. Kalinichev and R. J. Kirkpatrick, Geochim. Cosmochim. Acta, 2004, 68, 3351–3365.
32. Q. Li and R. J. Kirkpatrick, Am. Mineral., 2007, 92, 397–402.

---