Pressure effect on the structural, electronic, and elastic properties and Debye temperature of Rh3Nb: first-principles calculations
Chunyang Zhao,
Xueye Wang* and
Jiayun Peng
Key Laboratory of Environmentally Friendly Chemistry and Applications of Ministry of Education, College of Chemistry, Xiangtan University, Xiangtan, Hunan 411105, PR China. E-mail: wxueye@xtu.edu.cn; Fax: +86 0731 58292251; Tel: +86 0731 58292206
First published on 11th August 2016
Abstract
The structural, electronic, and elastic properties and Debye temperature (ΘD) of the L12-type intermetallic compound Rh3Nb ranging from 0 to 45 GPa have been systemically investigated using first-principles calculations. Lattice parameters, band structure and elastic constants of Rh3Nb are studied, which are used to evaluate the relationship between these properties and pressure from 0 to 45 GPa. With the increase of pressure, the lattice parameters and volume of Rh3Nb decrease, while the bulk modulus (B), Young's modulus (E), shear modulus (G) and Poisson's ratio (ν) of Rh3Nb increase. In addition, Mulliken charge and electron density difference imply that the ionicity increases between Rh and Nb with a rise in pressure. Finally, the Debye temperature (ΘD) is calculated along with the pressure.
1. Introduction
Nickel-based alloy is one of the main high-temperature materials, which has wide applications in aerospace fields, such as in turbine blades and aircraft engines.1 However, the operating temperature of aircraft engines has now become closer to their melting points,2 so it is urgent to find a new intermetallic compound. Recently, platinum metal-based alloys, such as Ir-and Rh-based alloys, have attracted great attention as ultra-high temperature materials due to their high-melting temperatures, favourable high-temperature strengths and good oxidation resistance.3–6 Compared with Ir-based alloys, Rh-based alloys possess lower density, lower thermal expansion coefficient, higher thermal conductivity and excellent oxidation resistance and many advantages. Therefore, the results of the detailed calculations on the structural, electronic, elastic properties and Debye temperature of Rh3Nb are not only considerable for academic interest but also serve as a valuable guide for high-temperature structural applications.There are only a few theoretical and experimental studies dealing with the structural, electronic and elastic properties of Rh3Nb in the literature. Y. Yamabe-Mitarai et al. studied the microstructure evolution and high-temperature strength properties of Rh-based alloys.6 M. Rajagopalan et al. reported the structural and electronic properties of Rh3Nb.7 Y. Terada et al. measured the thermal conductivity and thermal expansion as a function of the temperature for Rh3Nb in the temperature range of 300–1100 K.8 K. Chen et al. investigated the elastic and mechanical properties of Rh3Nb.9 S. Miura et al. studied experimentally the mechanical properties at various temperatures for Rh3Nb.2
However, all the researches mentioned above are analyzed at 0 GPa. The effect of pressure on the structural, electronic, elastic and thermodynamic properties of Rh3Nb has not been reported until now. As we all know, the pressure plays an important role in the mechanical, electronic and thermodynamic properties of alloy materials.10–12 Hence, it is necessary and meaningful to study the effect of pressure on Rh3Nb. In this work, the structural, electronic, elastic properties and Debye temperature of Rh3Nb under pressure (from 0 to 45 GPa) are investigated by first principles method, with the aim of having a profound and comprehensive comprehension about these properties.
2. Computational details
The calculations are performed within the frame of density function theory (DFT),13 which is implemented by the Cambridge Serial Total Energy Package (CASTEP).14 The ion–electron interaction is modeled by plane-wave ultrasoft pseudopotential.15,16 The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation function17–19 and local density approximation (LDA)20 with the form of Ceperley–Adler parameterized by Perdew and Zunger21 are both utilized. The kinetic cutoff energy for plane waves is set to be 380 eV. The Brillouin-zone integration is performed over the 10 × 10 × 10 grid sizes using the Monkhorst–Pack method.22 The Pulay scheme of density mixing is applied for the evaluation of energy and stress.23,24 The Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization scheme is used in the geometrical optimization.25,26 The tolerances of the geometrical optimization are set as follows: the difference of the total energy within 5.0 × 10−6 eV per atom, maximum ionic force within 0.01 eV Å−1, maximum ionic displacement within 5.0 × 10−4 Å, and maximum stress within 0.02 GPa. The Rh-4d85s1 and Nb-4s24p64d45s1 are considered as the valence atomic valence states, the other states are kept frozen as core and semi-core states.3. Results and discussion
3.1 Structural properties
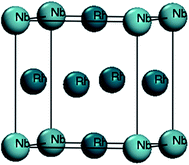
Fig. 1 shows the Rh3Nb compound with L12-type crystal structure (space group: Pm3m, no: 221). This unit cell contains three Rh and one Nb atoms, where the Rh and Nb atoms occupy the Wyckoff site of 3c (0, 0.5, 0.5) and 1a (0, 0, 0), respectively.We have discussed the lattice parameters a0, bulk modulus B0 and its pressure derivative B0′ of Rh3Nb from 0 to 45 GPa. In comparison to the experimental and theoretical results, both GGA and LDA method are performed to calculate the values of the lattice parameters a0, bulk modulus B0 and its pressure derivative B0′ at 0 GPa, which are listed in Table 1. It is shown that the equilibrium lattice parameter using GGA method is 1.76%, higher than the experimental value, while the LDA method deduced lattice parameter is 0.285%, lower than the experimental value. This is because GGA method overestimates the interaction of chemical bonds among atoms, leading to the lattice constant decrease when the lattice parameters are optimized. It is noticed that the calculated lattice parameters with LDA method show a better agreement with experimental value6 compared with GGA method. Therefore, for the equilibrium lattice parameters, the LDA method is believed to provide a more reasonable estimation. In order to understand the structural change with pressure in detail, Fig. 2 shows the relative the changes of (a) lattice parameters (a) and (b) unit cell volume (V) both GGA and LDA methods in the range from 0 to 45 GPa with a step of 5 GPa. It is identified that, as pressure increases, the a/a0 and V/V0 decrease and the GGA method decrease more rapidly than LDA method, respectively. The similar trend has also been observed in Rh3X (X = Ti, Hf and Zr) compounds.27–29
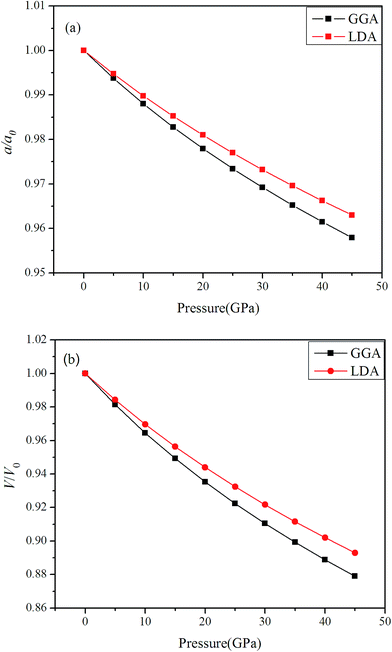 | ||
| Fig. 2 The relative changes of (a) lattice parameters (a); (b) unit cell volume (V) with the increase of external pressures. | ||
The values of pressure–volume in Fig. 2(b) are fitted to the third order Birch–Murnaghan equation30 using eqn (1):
 | (1) |
For the GGA method, the fitted bulk modulus B0 is 252.61 GPa, and its pressure derivative B0′ is 4.62 GPa. Correspondingly, for the LDA method, B0 and B0′ are 302.479 GPa and 4.61 GPa, respectively. The value of B0 is larger than the GGA calculated result. Meanwhile, the LDA calculations are in good compliance with the results reported by Chen et al.9
3.2 Electronic properties
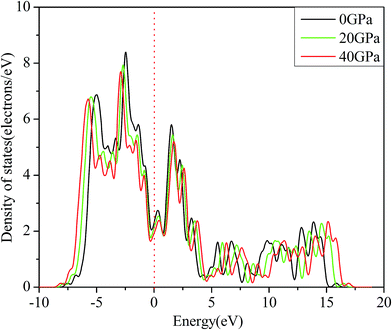
Electronic properties can reveal the bonding characteristics, mechanical properties and structural stability. Hence, it is essential to analyze the electronic properties of Rh3Nb compound. Fig. 3 gives the calculated band structures of Rh3Nb along high-symmetry directions included GGA and LDA methods at 0 GPa. There are two prominent features from Fig. 3. Firstly, compared with Fig. 3(a) and (b), it can be found that the calculated band structure with GGA method is almost the same as the LDA method. Therefore, in order to avoid calculating repeatedly, in this section, the following density of states (DOS) and the charge density difference are calculated only using LDA method. Secondly, it is clear that there is no energy gap near the Fermi level (horizontal dash line), so Rh3Nb compound is not only a conductor but also exhibits a metallic character at 0 GPa, which is consistent with other calculated result31 and other Rh3X (X = Hf, Ti and Zr) compounds also behave the identical properties7,29,31 by the first-principles calculations.To have a further insight into the bonding characteristics of Rh3Nb and reveal the mechanical properties and the fundamental structural stability mechanism, the total density of states (TDOS) and partial density of states (PDOS) of Rh3Nb have been calculated. Fig. 4 depicts the TDOS and PDOS of Rh3Nb in the vicinity of the Fermi level (vertical dash line) at 0 GPa with the energy interval from −10 eV to 20 eV, while Fig. 5 shows the TDOS as a function of variable pressure.
It can be seen that the density of states at the Fermi energy is non zero from Fig. 4, implying that Rh3Nb compound exhibits metallic characteristics, which is consistent with the previous analysis of band structure. The PDOS shows that the main bonding peaks near the Fermi level of Rh3Nb are dominated by the hybridization between Rh-3d orbital and Nb-4d orbital. Moreover, the hybridization between Rh and Nb atoms is obvious to form covalent bonding feature. The shape of TDOS curves presents that the structure of Rh3Nb compound has no structural phase transformation at 40 GPa in Fig. 5. Moreover, TDOS decreases with the increase of external pressure. It can be inferred that changes in the interaction potentials have occurred owing to the decrease of the distance between atoms under compression. The calculated N(Ef) (density of states at the Fermi level) under the pressure of 0, 20 and 40 GPa decreases successively, which indicates the depth of pseudogap increases. Therefore, the stability of Rh3Nb compound has been improved by the increasing pressure. For other Rh-based compound, such as Rh3Sc, the calculated N(Ef) also decreases continuously with pressure,32 so the changes of TDOS for Rh3Nb compound under high pressure can provide a significant reference for us to study more and more Rh-based compounds.
For the sake of insight into the chemical bonding characteristics of Rh3Nb under pressure, the Mulliken charge33 as well as bond length is analyzed to quantitatively evaluate the effect of the pressure on structural, elastic, thermodynamic and electronic properties. The calculated Mulliken charges, bond length and the overlap population at different pressures with GGA and LDA methods are listed in Table 2. It can be found that the charge transferred from Nb atom to Rh atom is 0.87 e (1.28 e) using GGA (LDA) method separately at 0 GPa, which means that Nb–Rh exists the ionic bonding and the LDA method has higher charge transferred value than the GGA method, so it can be concluded that LDA method can better present the charge transferred between Nb and Rh atom. Furthermore, the charge transferred from Nb atom to Rh atom increases with the ascending pressure, but bond length decreases with the increment of pressure. Additionally, the overlap population Nb–Rh increases, indicating that the ionic bonding between Nb and Rh is strengthened with increasing pressure.
| Method | Pressure (GPa) | Species | Charge (e) | Bond | Population | Length (Å) |
|---|---|---|---|---|---|---|
| GGA | 0 | Nb | 0.87 | Rh–Nb | −0.41 | 2.77542 |
| Rh | −0.29 | |||||
| 10 | Nb | 1.03 | Rh–Nb | −0.62 | 2.74218 | |
| Rh | −0.34 | |||||
| 20 | Nb | 1.18 | Rh–Nb | −0.83 | 2.71417 | |
| Rh | −0.39 | |||||
| 30 | Nb | 1.33 | Rh–Nb | −1.03 | 2.68993 | |
| Rh | −0.44 | |||||
| 40 | Nb | 1.47 | Rh–Nb | −1.24 | 2.66842 | |
| Rh | −0.49 | |||||
| LDA | 0 | Nb | 1.28 | Rh–Nb | −0.76 | 2.72018 |
| Rh | −0.43 | |||||
| 10 | Nb | 1.44 | Rh–Nb | −1.00 | 2.69194 | |
| Rh | −0.48 | |||||
| 20 | Nb | 1.59 | Rh–Nb | −1.21 | 2.66797 | |
| Rh | −0.53 | |||||
| 30 | Nb | 1.74 | Rh–Nb | −1.44 | 2.64675 | |
| Rh | −0.58 | |||||
| 40 | Nb | 1.88 | Rh–Nb | −1.65 | 2.62827 | |
| Rh | −0.63 |
The effect of pressure on the charge density distribution has been investigated. Fig. 6 shows the charge density difference in the (001) plane of Rh3Nb at 0 GPa and 40 GPa. Electron excess is drawn in red and electron deficiency in blue in units of number of electrons per Å3. From Fig. 6(a), it can be seen that the Rh and Rh atom in the slabs are held together by covalent bonding, and the bonding between Rh and Nb is mainly an ionic bonding. From the charge densities in Fig. 6(a) and (b), it is clear that the covalent bonding between Rh and Rh is enhanced with the increasing of pressure. The ionic bonding between Rh and Nb becomes stronger as pressure increases.
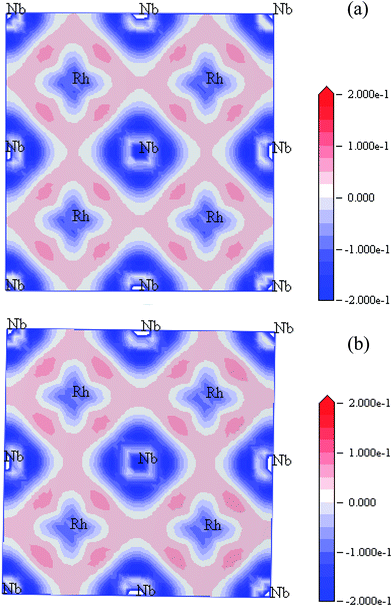 | ||
| Fig. 6 The charge density difference plotted in the (001) plane for Rh3Nb at 0 GPa (a) and 40 GPa (b). | ||
3.3 Elastic properties
Elastic constants can be used to measure the resistance of a crystal to an externally applied stress. For the cubic Rh3Nb crystals, there are three independent elastic constants: C11, C12, and C44. Table 3 gives the calculated elastic constants Cij at 0 GPa as well as other available theoretical calculations data. It is can be seen that the calculated results are in agreement with other theoretical calculations data.9,31As is known to all, the corresponding mechanical stability conditions of cubic crystal are calculated in eqn (2):34
| C11 − C12 > 0, C11 > 0, C44 > 0, C11 + 2C12 > 0 | (2) |
The calculated elastic constants using GGA and LDA methods are shown in Fig. 7, which indicates that the C11, C12 and C44 exhibit the linearly increasing relationships rising up to 45 GPa. Since C11 represents the elasticity in length, whereas C12 and C44 are on behave of the elasticity in shape. Therefore, it is found that Rh3Nb is mechanically stable up to 45 GPa via the eqn (2).
Cauchy pressure (C12 − C44) can describe the ductile/brittle nature of the given materials. According to Pettifor,35 if Cauchy pressure is positive, then the material has metallic bonding and is ductile. Moreover, the more positive the Cauchy pressure values are, the better the ductility will be. Contrarily, if the Cauchy pressure is negative, the material is brittle. Cauchy pressure is calculated with pressure ranging from 0 to 45 GPa through GGA and LDA methods in Fig. 8. It can be seen that Cauchy pressure is positive and the values are gradually increasing with the addition of the external pressure. Thus, the Rh3Nb compound presents metallic feature and the ductility becomes better and better as the pressure increases.
 | ||
| Fig. 8 Calculated Cauchy pressure with pressure range from 0 to 45 GPa through both GGA and LDA methods. | ||
According to Cij, the polycrystalline bulk modulus B and shear modulus G can be directly calculated on the basis of the Voigt–Reuss–Hill approximation.36 For cubic system, the calculation formulas are as follows.
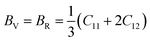 | (3) |
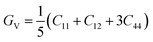 | (4) |
 | (5) |
 | (6) |
 | (7) |
Young's modulus (E) and Poisson's ratio (ν) are the major elasticity related parameters of materials, which can be calculated using the following formula:37
 | (8) |
 | (9) |
Typically, the bulk modulus B can represent the resistance to volume change and the Young's modulus E is often related to the stiffness of materials,38 while shear modulus G stands for the resistance to shape change under the applied pressure in materials. Polycrystalline bulk modulus B, shear modulus G and Young's modulus E as function of pressure (0–45 GPa) are depicted in Fig. 9. It can be seen that values of B, G and E increase with the enhancive pressure. Meanwhile, the LDA method has higher calculated values than the GGA method. Thus, the existence of an external pressure is of benefit to the hardness of the Rh3Nb compound.
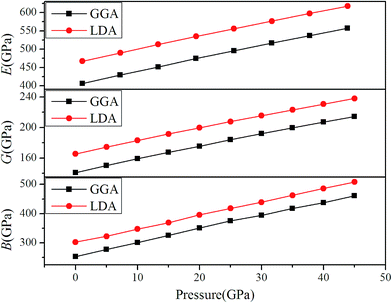 | ||
| Fig. 9 Pressure depends on bulk modulus B, shear modulus G and Young's modulus E for GGA and LDA methods. | ||
Pugh introduced that the ratio of bulk modulus to shear modulus (B/G) can predict the brittle and ductile behavior of materials.39 The critical value which separates ductile from brittle material is 1.75. If B/G > 1.75, the material behaves in a ductile manner. Otherwise, the material behaves in a brittle manner. Table 4 lists the values of B, G, E, B/G, ν and A at 0 GPa using GGA and LDA methods along with other theoretical calculations data. In view of Table 4, it is clear that our calculated values of B, G, E and A with the LDA method are larger than those obtained by K. Chen et al.9 and M. Ould Kada et al.,31 whereas the calculated values of B, B/G and ν with the GGA method is smaller than that reported in ref. 31. This discrepancy could be attributed to the different methods used to calculate the elastic properties.
| Method | B (GPa) | G (GPa) | E (GPa) | B/G | ν | A |
|---|---|---|---|---|---|---|
| GGA | 252.611 | 140.922 | 356.477 | 1.793 | 0.265 | 1.364 |
| LDA | 302.480 | 165.471 | 419.854 | 1.828 | 0.269 | 1.363 |
| Other cal.9,31 | 210.78 (ref. 9) | 146 (ref. 9) | 366 (ref. 9) | 1.44 (ref. 9) | 0.252 (ref. 9) | |
| 290.5 (ref. 31) | 132 (ref. 31) | 297.6 (ref. 31) | 2.22 (ref. 31) | 0.3 (ref. 31) | 1.02 (ref. 31) |
From Table 4, it can be found that the value of B/G is higher than 1.75, which means that the Rh3Nb compound is of ductile nature. Meanwhile, Fig. 10 depicts the ratio of bulk modulus to shear modulus B/G, Poisson's ratio ν and anisotropy index A as function of pressure. From Fig. 10(a), it can be seen that the values of B/G increase with the augment of external pressure, which suggests that higher pressure can improve the ductility.
 | ||
| Fig. 10 Dependence of (a) the ratio of shear modulus to bulk modulus (B/G), (b) Poisson's ratio (ν), and (c) the anisotropic index (A) on the pressure. | ||
In addition, Poisson's ratio ν (−1 < ν < 0.5) is usually used to quantify the stability of the crystal against shear, and the larger the Poisson's ratio, the better the plasticity.40 From Fig. 10(b), it can be observed that the Poisson's ratios of Rh3Nb increase with a raise of pressure, and the existence of an external pressure can improve the plasticity.
The Zener anisotropy factor (A) is an indicator of the degree of anisotropy in the solid structures. For a completely isotropic material, the factor A takes the value of 1. While a value larger or smaller than unity denotes the extent of this crystal's anisotropy. Thus, it is a measure of the degree of elastic anisotropy. For the cubic system, it can be obtained by the following formula:41
 | (10) |
From Fig. 10(c), it is known that the values of A increase with external pressure rising up to 45 GPa for Rh3Nb compound, which indicates that anisotropy can be enhanced. Moreover, in order to study the elastic properties of Rh-based compounds under high pressure, the elastic properties of Rh3Nb and the published Rh-based (Rh3Hf, Rh3Zr and Rh3Ti) compounds have been compared. For the elastic constants Cij, B, E, G, B/G, ν and A, these curves are very similar to the obtained for Rh3Zr compound29 with pressure increasing and the bulk modulus B of Rh3Hf and Rh3Ti compounds also present the same change trend as the pressure increases,27,28 which indicates that the elastic properties of Rh-based compounds have a high consistency.
3.4 Debye temperature
Debye temperature (ΘD) is a not only closely correlated with many physical properties of solids, such as specific heat and melting points but also it can be used to characterize the strength of covalent bonds in solids. With the purpose of having a further understanding of the thermodynamic behaviors and lattice stability under pressure, it is necessary to calculate the ΘD values under various pressures. The ΘD can be calculated from elastic constants by the following equations:42,43
 | (11) |
 | (12) |
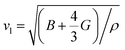 | (13) |
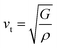 | (14) |
 | ||
| Fig. 11 Pressure dependence of vl (a), vt (b) and vm (c) of Rh3Nb calculated by GGA and LDA methods. | ||
 | ||
| Fig. 12 Pressure dependence of the ΘD of Rh3Nb for GGA and LDA methods along with other theoretical calculations data. | ||
From Fig. 11, it is shown that the sound velocities of vl, vt, and vm are increasing with the addition of the pressure for GGA and LDA methods. The values of vt, and vm for GGA method are smaller than that of the LDA method except vl, which indicates that the pressure has large impact on Rh3Nb. From Fig. 12, it can be observed that the ΘD increases with pressure for GGA and LDA methods and the LDA method is more close to the other calculated values.31 Thus, with the rising pressure, the covalent bonds become stronger between Rh and Rh atom for Rh3Nb, which is coherent with the analysis of electronic properties. Interestingly enough, the ΘD of Rh3Hf and Rh3Zr compounds28,31 increase with the enhancive pressure as well. Regrettably, there is no experimental data for the comparison. Therefore, it is difficult to evaluate the magnitude of errors between theory and experiments for Rh3Nb. However, the present results could be served as an effective prediction for the future experiment.
4. Conclusions
The effect of the structural, electronic, elastic properties and Debye temperature (ΘD) of Rh3Nb are studied using the first-principles with GGA and LDA methods under pressure from 0 to 45 GPa. The conclusions of this work are drawn specifically as following: the obtained structural parameters are consistent with the experimental data and other theoretical values. The DOS shows that the Rh3Nb compound exhibits metallic characteristics, and the structure of Rh3Nb compound has no dramatic changes under pressure up to 40 GPa. The difference charge densities and Mulliken charge analysis reveal the change of chemical bonds under high pressure. It is concluded that the bonding is a combination of covalent, ionic and metallic nature. The calculated elastic constants satisfy the stability criteria, which shows that Rh3Nb is mechanically stable. The results of elastic modulus under various pressure show that the hardness of Rh3Nb compound can be improved with elevated external pressure. The ΘD of Rh3Nb increases from 0 to 45 GPa, which provides an effective reference for the experimental and theoretical calculations in future. Besides, combined with the calculated results with both GGA and LDA methods, it can be found that the LDA method has many advantages of the GGA method on the geometrical optimization, Mulliken charge and Debye temperature, so the results demonstrate that the LDA method can be used firstly instead of GGA for lattice dynamical and thermodynamic properties of other Rh-based compounds.References
- J. R. Davis, ASM Specialty Handbook: Nickel, Cobalt and Their Alloys, ASM International, USA, 2000 Search PubMed.
- S. Miura, K. Honma, Y. Terada, J. Sanchez and T. Mohri, Intermetallics, 2000, 8, 785–791 CrossRef.
- J. Sha and Y. Yamabe-Mitarai, Intermetallics, 2013, 32, 145–150 CrossRef.
- J. Sha, Y. Yamabe-Mitarai and H. Harada, Intermetallics, 2006, 14, 1364–1369 CrossRef.
- Y. Yamabe, Y. Koizumi, H. Murakami, Y. Ro, T. Maruko and H. Harada, Scr. Mater., 1996, 35, 211–215 CrossRef.
- Y. Yamabe-Mitarai, Y. Koizumi, H. Murakami, Y. Ro, T. Maruko and H. Harada, Scr. Mater., 1997, 36, 393–398 CrossRef.
- M. Rajagopalan and M. Sundareswari, J. Alloys Compd., 2004, 379, 8–15 CrossRef.
- Y. Terada, K. Ohkubo, S. Miura, J. M. Sanchez and T. Mohri, J. Alloys Compd., 2003, 354, 202–207 CrossRef.
- K. Chen, L. Zhao, J. Tse and J. Rodgers, Phys. Lett. A, 2004, 331, 400–403 CrossRef.
- X. L. Yuan, M. A. Xue, W. Chen and T. Q. An, Comput. Mater. Sci., 2014, 82, 76–85 CrossRef.
- P. Mao, B. Yu, Z. Liu, F. Wang and Y. Ju, Comput. Mater. Sci., 2014, 88, 61–70 CrossRef.
- X. Li, W. Peng and H. Fu, J. Alloys Compd., 2013, 581, 867–872 CrossRef.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- M. Segall, P. J. Lindan, M. A. Probert, C. Pickard, P. Hasnip, S. Clark and M. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef.
- K. Laasonen, A. Pasquarello, R. Car, C. Lee and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 10142–10153 CrossRef.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- P. Pulay, J. Chem. Phys., 1983, 78, 5043–5051 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- D. F. Shanno, Math. Comput., 1970, 24, 647–656 CrossRef.
- T. H. Fischer and J. Almlof, J. Phys. Chem., 1992, 96, 9768–9774 CrossRef CAS.
- G. Surucu, K. Colakoglu, E. Deligoz and H. Ozisik, Intermetallics, 2010, 18, 286–291 CrossRef CAS.
- G. Surucu, K. Colakoglu, E. Deligoz, N. Korozlu and H. Ozisik, Comput. Mater. Sci., 2010, 48, 859–865 CrossRef CAS.
- S. Zhang, X. Zhang, Y. Zhu, M. Ma, J. Qin and R. Liu, Mater. Chem. Phys., 2015, 149–150, 553–558 CrossRef CAS.
- F. Birch, J. Geophys. Res.: Solid Earth, 1978, 83, 1257–1268 CrossRef CAS.
- M. Ould Kada, T. Seddik, A. Sayede, R. Khenata, A. Bouhemadou, E. Deligoz, Z. A. Alahmed, S. Bin Omran and D. Rached, Int. J. Mod. Phys. B, 2014, 28, 1450006 CrossRef.
- M. Sundareswari and M. Rajagopalan, Eur. Phys. J. B, 2006, 49, 67–75 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- G. Grimvall, Thermophysical properties of materials, Elsevier, Amsterdam, 1999 Search PubMed.
- D. Pettifor, J. Mater. Sci. Technol., 1992, 8, 345–349 CAS.
- R. Hill, J. Mech. Phys. Solids, 1963, 11, 357–372 CrossRef.
- B. Mayer, H. Anton, E. Bott, M. Methfessel, J. Sticht, J. Harris and P. Schmidt, Intermetallics, 2003, 11, 23–32 CrossRef CAS.
- Y. Liu, W. C. Hu, D. J. Li, X. Q. Zeng and C. S. Xu, Phys. Scr., 2013, 88, 045302 CrossRef.
- S. Pugh, Philos. Mag., 1954, 45, 823–843 CrossRef CAS.
- Y. Cao, J. Zhu, Y. Liu, Z. Nong and Z. Lai, Comput. Mater. Sci., 2013, 69, 40–45 CrossRef CAS.
- A. Every, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 1746–1760 CrossRef CAS.
- O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909–917 CrossRef CAS.
- Z. Huang, Y. Zhao, H. Hou and P. Han, Phys. B, 2012, 407, 1075–1081 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |