DOI:
10.1039/C6RA13836E
(Paper)
RSC Adv., 2016,
6, 78017-78027
Critical behavior study near the paramagnetic to ferromagnetic phase transition temperature in Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) manganites
Received
27th May 2016
, Accepted 10th August 2016
First published on 11th August 2016
Abstract
The aim of the present work is to study the critical behavior of Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) manganites, synthetized by the conventional solid-state reaction method, around the paramagnetic (PM)–ferromagnetic (FM) phase transition. The critical behavior is investigated through various techniques such as the modified Arrott plots, Kouvel–Fisher method, and critical isotherm analysis. The experimental results have revealed that our samples exhibit a second-order magnetic phase transition and the critical exponents β and γ are consistent with the prediction of the 3D-Ising model for x = 0 and x = 0.02, while, the estimated critical exponents of x = 0.06 are close to those found by the 3D-Heisenberg model. This proves the existence of a short-range ferromagnetic order in all our samples. The third exponent δ was determined independently from the critical magnetization isotherm satisfying the Widom scaling relationship for all our compounds. The validity of the calculated critical exponents using the various methods has been confirmed by the scaling equation of state. The obtained critical exponents are found to follow the scaling equation with the magnetization data scaled into two different curves below and above TC.
1. Introduction
Perovskite-type manganites RE1−xAxMnO3, where RE is a rare earth (La, Pr, Nd, Sm…) and A is a divalent element (Ca, Sr, Ba…) have attracted great interest since the discovery of colossal magnetoresistance (CMR)1–3 and magnetocaloric effect (MCE) phenomena.4–7 These oxides exhibit a rich variety of physical properties related, from a fundamental viewpoint, to the double-exchange interaction associated with Mn3+–Mn4+ pairs8 and to the strong electron–phonon interaction known as the Jahn–Teller effect.9 These properties can be controlled by doping suitable elements into the A-site or Mn to change the structural parameters and/or the Mn3+/Mn4+ ratio. In order to understand these mechanisms, extensive studies in structural, magnetic and transport properties of manganites have been investigated. To further elucidate the origin of these properties, more recent investigations have brought forward the nature of the ferromagnetic (FM)–paramagnetic (PM) transition. In manganites, two types of magnetic transition have been observed: a first order magnetic transition (FOMT) and a second-order magnetic transition (SOMT). It is clear that materials undergoing a FOMT transition exhibit a large magnetocaloric effect related to the existence of strong coupling between magnetism and structure in these materials. Two important questions about PM–FM transition should be clarified: one is the order of phase transition; the other is the common universality class based on the dimensionality of lattice (d) and the dimensionality of order parameter (n). Thus, it is necessary to investigate in details the critical exponents at the region of the PM–FM transition. Currently, four kinds of different theoretical models, which are mean field, 3D-Heisenberg, 3D-Ising, and tricritical mean field, are used to explain the critical behavior in manganites. Earlier studies on the critical behavior around the Curie temperature have indicated that the critical exponents play important roles in elucidating the interaction mechanisms near TC. Critical exponents for manganites show wide variation that almost covers all universality classes and different experimental tools are used for their determination.
In this paper, we focus on the critical behavior of Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) manganites using the isothermal magnetization around TC. In view of a sizable magnetic moment of Er3+ ion (9.58 μB), we think that a slight Er-substitution for Pr, as a fourth element in A-site, not only increases some extra magnetic interactions or influence magnetic disordering, but also do not remarkably change the double-exchange effect taken place on the B-site sublattices, which is mainly responsible for the magnetic interaction in this system. As an external magnetic field is applied on it, a large magnetic disordering–ordering transition maybe occurs and a considerable or large magnetic entropy change is possibly observed. Small contents of Er have been chosen to enhance the magnetocaloric properties and to not deviate the TC to low temperatures, which make our systems more suitable for magnetic refrigeration. In the present study, the critical exponents: β (related to the spontaneous magnetization Ms (μ0H = 0) below TC), γ (associated with the initial susceptibility χ = (∂M/∂(μ0H))μ0H=0 above TC) and δ (determined from the critical isotherm M (TC, μ0H) at TC) associated with the second order transition have been determined based on various approaches including the modified Arrott plots, the Kouvel–Fisher method and the critical isotherm analysis. Using these exponents, it has been also verified that the scaling hypothesis is perfectly obeyed indicating that they are reliable.
2. Experiment
Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) powder samples were synthetized using the conventional solid-state reaction method starting with Pr6O11, Er2O3, CaCO3, SrCO3 and MnO2 precursors with purity up to 99.9%. The starting powders were ground in an agate mortar, pressed into pellets and sintered at 800, 1000, 1100 and 1300 °C for 24 h for each cycle with intermediate regrinding and repelling to ensure a better crystallization. Finally, these pellets were cooled slowly to room temperature. Phase purity, homogeneity and cell dimensions were determined by X-ray powder diffraction (XRD) (diffractometer using Cu Kα radiation). Magnetic measurements were performed using a Physical Properties Measurement System PPMS (Quantum Design). Magnetization (M) as function of magnetic applied field (0 T ≤ μ0H ≤ 5 T) was recorded at several temperatures in intervals of 2 K.
3. Results and discussion
3.1. X-ray diffraction analysis
The X-ray diffraction (XRD) patterns of Pr0.6−xErxCa0.1Sr0.3MnO3 for x = 0, x = 0.02 and x = 0.06 samples are shown in Fig. 1a. The obtained results reveal that all our samples are single phase without any detectable secondary phase and crystallized in the orthorhombic structure with Pnma space group. The structural parameters were refined using the standard Rietveld technique. The quality of the refinement was evaluated though the goodness of the fit indicator χ2. A good fit between the observed and the calculated profiles was obtained. A rapid overview of the obtained structural results evidences a decrease of the unit cell volume with the increase of erbium content (Table 1). This is in agreement with the decrease of the average ionic radius of the perovskite A-site in which Er3+ cations substitute Pr3+ ones (r(Er3+) = 1.062 Å while r(Pr3+) = 1.179 Å), confirming the incorporation of Er ions and the formation of the desired solid solution.
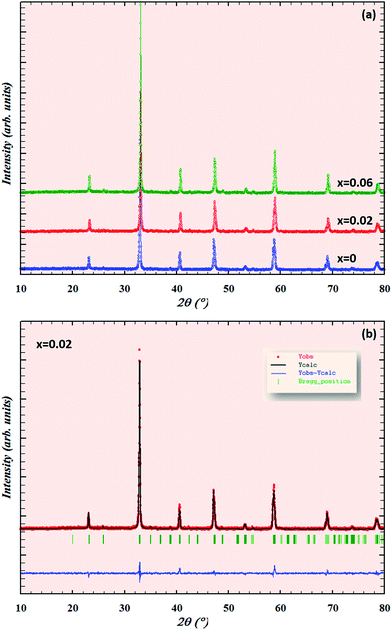 |
| | Fig. 1 (a) Observed X-ray diffraction data for Pr0.6−xErxCa0.1Sr0.3MnO3 for x = 0, x = 0.02 and x = 0.06. (b) Rietveld refinement for x = 0.02. | |
Table 1 Structural parameters for Pr0.6−xErxCa0.1Sr0.3MnO3 manganites determined from Rietveld analysis of X-ray powder diffraction data at room temperature
| Parameters |
X = 0 |
X = 0.02 |
X = 0.06 |
| Symmetry |
Orthorhombic |
Orthorhombic |
Orthorhombic |
| Space group |
Pnma |
Pnma |
Pnma |
| a (Å) |
5.4383(2) |
5.4390(3) |
5.4369(2) |
| b (Å) |
7.6795(3) |
7.6776(3) |
7.6764(3) |
| c (Å) |
5.4661(2) |
5.4624(2) |
5.4523(2) |
| V (Å3) |
228.28(1) |
228.10(2) |
227.55(2) |
| 〈rA〉 (Å) |
1.2184 |
1.2160 |
1.2113 |
| σ2 (10−3 Å2) |
3.59604 |
4.1946 |
5.1151 |
| χ2 |
1.74 |
1.78 |
1.63 |
3.2. Scaling analysis
To analyze the nature of the magnetic phase transition in details, we have carried out from the isothermal M (μ0H, T) data measured in different temperature ranges, a study of the critical exponents near TC for Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) samples. Fig. 3 shows the isothermal magnetization M (μ0H, T) curves for Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) samples at several temperatures in the vicinity of Curie temperature (275 K, 260 K and 216 K for x = 0, x = 0.02 and x = 0.06 respectively). The TC values were carried out from the inflection point of the temperature dependence of field-cooled (FC) magnetization measured at 0.05 T (Fig. 2). Characteristic M (μ0H, T) curves of manganites usually exhibit a very high increase in M at low fields and then a gradual saturation at high fields. The present samples also show a steep rise in the low field range; the magnetization still increases steadily with increasing magnetic field and does not show any sign of saturation as a consequence of the presence of a ferromagnetic short-range order. To confirm this suggestion, we have been based on the values of the critical exponents. The second-order magnetic phase transition near the Curie point is characterized by a set of the critical exponents β, γ and δ, which defined for the first-order transition since, in this case, the magnetic field can shift the transition, leading to a field-dependent phase boundary TC (μ0H).10 According to the scaling hypothesis, for a second-order phase transition around TC, the mathematical definitions of the exponents from magnetization measurements are given below:11,12| | |
Ms(T) = M0(−ε)−β; ε < 0, T < TC
| (1) |
where ε = (T − TC)/TC is the reduced temperature and  just below TC.
just below TC.
 |
| | Fig. 2 M (T) curves for Pr0.6−xErxCa0.1Sr0.3MnO3 for x = 0, x = 0.02 and x = 0.06. | |
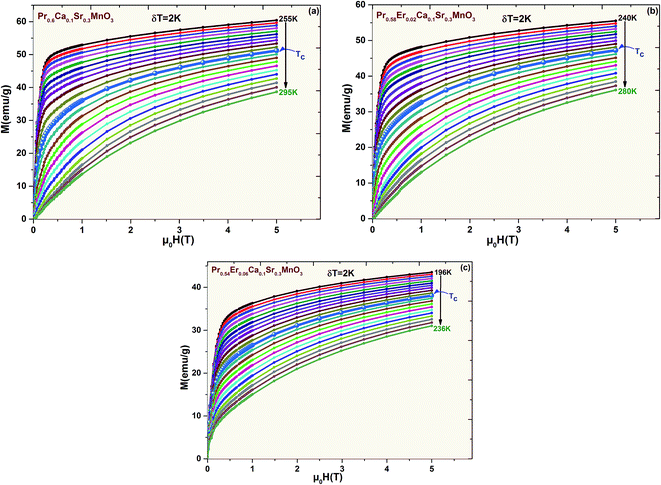 |
| | Fig. 3 Isothermal magnetization for Pr0.6−xErxCa0.1Sr0.3MnO3 for (a) x = 0 (b) x = 0.02 and (c) x = 0.06 measured at different temperatures around TC. | |
The exponent γ describes the temperature dependence of the zero-field susceptibility and is defined as:
| | |
χ0−1(T) = (h0/M0)εγ; ε > 0, T > TC
| (2) |
where

is the inverse zero-field susceptibility just above
TC.
The exponent δ describes the field dependence of the magnetization at the Curie temperature, TC:
| | |
M = D(μ0H)1/δ; ε = 0, T = TC
| (3) |
where
M0,
h0/
M0 and
D are the critical amplitudes.
Another way for determining the exponents β and γ is by using a scaling theory which predicts the existence of a reduced equation of state written as follow:
| | |
M (μ0H, ε) = εβf±(μ0H/εβ+γ)
| (4) |
where
f± are regular functions with
f+ and
f− for above and below
TC, respectively. The scaling relation claims that
M (
μ0H,
ε)|
ε|
−β vs. μ0H |
ε|
−(β+γ) should yield two universally different branches, one for
T >
TC and the other for
T <
TC, taking the values of
β,
γ and
TC determined according to the Kouvel–Fisher (KF) method.
3.2.1. Modified Arrott plots (MAP). Around the critical temperature for a second order transition, a generalized Arrott plots M1/β vs. (μ0H/M)1/γ (ref. 13) can be used to determine TC, spontaneous magnetization Ms (T, 0) below TC and the inverse of initial susceptibility χ0−1(T) above TC. In order to determine the type of the magnetic phase transition in the vicinity of Curie temperature, M2 vs. μ0H/M curves are firstly plotted (Fig. 4a and b), known as the standard Arrott plots. It is the simplest case; β and γ are given by their mean field values (0.5 and 1 respectively). In this case of FM long range interaction,14 M1/β vs. (μ0H/M)1/γ isotherms near TC of our samples should show a series of parallel lines and the line for T = TC passes through the origin. In the present case, the Arrott plots curves are not linear and show curvature downward even in the high field region, implying that the mean-field theory is not valid for our samples and suggesting magnetic short range ordering. The positive slope of the M2 vs. H/M plots indicates that the PM–FM transition is of second order for all compounds according to Banerjee's criteria.15 Hence, the modified Arrott plots should be employed to obtain correct critical parameters. The modified Arrott plots are based on the Arrott–Noakes equation of state:13| | |
(μ0H/M)1/γ = a(T − TC)/T + 4bM1/β
| (5) |
where a and b are considered to be constants.
 |
| | Fig. 4 Modified Arrott plots (MAP) for x = 0 and x = 0.06: isotherms of M1/β vs. (H/M)1/γ with (a) and (b) mean-field model (β = 0.5, γ = 1.0); (c) and (d) tricritical mean-field model (β = 0.25, γ = 1.0); (e) and (f) 3D-Heisenberg model (β = 0.365, γ = 1.336); (g) and (h) 3D-Ising model (β = 0.325, γ = 1.24) and as a function of temperature. | |
Fig. 4 shows the modified Arrott plots (MAP)13 at different temperatures by using four models of critical exponents for Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0 and 0.06) samples. Fig. 4a and b demonstrate the mean-field model (β = 0.5, γ = 1); Fig. 4c and d illustrate the tricritical mean-field model (β = 0.25, γ = 1), Fig. 4e and f show the 3D-Heisenberg model (β = 0.365, γ = 1.336) and Fig. 4g and h 3D-Ising model (β = 0.325, γ = 1.24).11,12,16 Based on these curves, the condition that the intercept of these lines on the (μ0H/M)1/γ axis is negative/positive below/above TC is shown. Most models render quasi-straight lines, nearly parallel to the high field region and the line of M1/β vs. (μ0H/M)1/γ at TC (∼275 K for x = 0, 260 K for x = 0.02 K and ∼216 K for x = 0.06) pass through the origin. Thus, it is somewhat difficult to distinguish which one of them is the best for determining the critical exponents. In order to compare these results and select the best model which describes this system, we calculated their relative slopes (RS) which are defined as RS = S(T)/S(TC), where S(T) and S(TC) are the slopes deduced from MAP around and at TC, respectively. Perfect parallel lines are described by RS equal to 1.36 The relative slopes for Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) samples is reported in Fig. 5. The results in Fig. 5a and b indicates that the relative slope (RS) for x = 0 and x = 0.02 compounds respectively, reported for 3D-Ising model are the closest to 1, meaning that this model can be suitable for proper choice to deduce the critical exponents. Fig. 5c indicate that the 3D-Heisenberg model is the best model to describe the critical behavior of x = 0.06. In Fig. 6, we plotted the temperature dependence of the spontaneous magnetization Ms (T, 0) below TC as well as the inverse of initial susceptibility χ0−1 (T) above TC for all our compounds. They were determined from the intersections of the linear extrapolation lines (for high-magnetic field parts) with the M1/β and the (μ0H/M)1/γ axes respectively. The curves in Fig. 6 denote the power law fitting of Ms (T, 0) vs. T and χ0−1 (T) vs. T according respectively to eqn (1) and (2). Thus, the optimum values of critical exponents β as well as γ and Curie temperature were determined and were noted in Table 2. These results are very close to the critical exponents of 3D-Ising model for x = 0 and x = 0.02 samples and they are closed to those of 3D-Heisenberg model for x = 0.06.
 |
| | Fig. 5 Relative slope (RS) as a function of temperature for (a) x = 0 (b) x = 0.02 and (c) x = 0.06. | |
 |
| | Fig. 6 Temperature dependence of spontaneous magnetization (Ms) and inverse initial susceptibility (χ−1) of Pr0.6−xErxCa0.1Sr0.3MnO3 for (a) x = 0 (b) x = 0.02 and (c) x = 0.06. | |
Table 2 Comparison of critical exponents of Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) compounds with earlier reported data, and with the various theoretical models. Abbreviations: CI, critical isotherm; MAP, modified Arrott plots and KF, Kouvel–Fisher
| Composition |
Method |
TC (K) |
β |
γ |
δ |
Reference |
| Mean field |
Theory |
|
0.5 |
1 |
3 |
12 |
| 3D-Heisenberg |
Theory |
|
0.365 |
1.336 |
4.80 |
19 |
| 3D-Ising |
Theory |
|
0.325 |
1.24 |
4.82 |
19 |
| Tricritical mean field |
Theory |
|
0.25 |
1 |
5 |
19 |
| Pr0.6Ca0.1Sr0.3MnO3 |
MAP |
275.10(16) |
0.317(9) |
1.197(9) |
4.532 |
This work |
| KF |
274.48(28) |
0.335(11) |
1.218(23) |
4.635 |
| CI |
|
|
|
4.347 |
| Pr0.58Er0.02Ca0.1Sr0.3MnO3 |
MAP |
258.11(5) |
0.337(9) |
1.189(28) |
4.528 |
This work |
| KF |
258.33(14) |
0.336(7) |
1.177(8) |
4.502 |
| CI |
|
|
|
4.216 |
| Pr0.54Er0.06Ca0.1Sr0.4MnO3 |
MAP |
214.71(7) |
0.355(8) |
1.294(12) |
4.645 |
This work |
| KF |
215.13(37) |
0.395(21) |
1.289(8) |
4.263 |
| CI |
|
|
|
4.484 |
| Pr0.6Sr0.4MnO3 |
|
301 |
0.365(4) |
1.309(3) |
4.586 |
20 |
| La0.67Ba0.22Sr0.11MnO3 |
|
342.73 |
0.386(6) |
1.393(4) |
4.730(3) |
21 |
| La0.7Sr0.25Na0.05Mn0.9Ti0.1O3 |
|
155.04 |
0.368(40) |
1.142(30) |
4.07(3) |
22 |
| La0.7Ca0.3Mn0.91Ni0.09O3 |
|
199.4 |
0.171(6) |
0.976(12) |
— |
23 |
| Pr0.4Eu0.2Sr0.4MnO3 |
|
238.4 |
0.310(3) |
1.261(4) |
5.065(1) |
24 |
| La0.7Ca0.05Sr0.25MnO3 |
|
344 |
0.42(2) |
1.14(2) |
3.7(2) |
25 |
| La0.7Ca0.1Sr0.2MnO3 |
|
326 |
0.36(1) |
1.22(1) |
4.4(2) |
25 |
| La0.7Ca0.2Sr0.1MnO3 |
|
289 |
0.26(1) |
1.06(2) |
5.1(2) |
25 |
| Nd0.7Sr0.1Ba0.1Ca0.1MnO3−δ |
|
117.4 |
0.355 |
1.329 |
4.743 |
26 |
| Sm0.25Pr0.3Sr0.45MnO3 |
|
226 |
0.255(21) |
0.957(14) |
5.10(15) |
27 |
3.2.2. Kouvel–Fisher plot (K–F). The critical exponents β and γ and Curie temperature TC can also be determined more accurately according to the Kouvel–Fisher (KF) method.17 This method is an alternative analytical expression of the power law defined as:| | |
Ms(T)(dMs/dT)−1 = (T − TC)/β
| (6) |
| | |
χ0−1(T)(dχ0−1/dT)−1 = (T − TC)/γ
| (7) |
According to these equations, plotting Ms(T)(dMs/dT)−1 and χ0−1(T)(dχ0−1/dT)−1 against temperature (Fig. 7) yields straight lines with slopes of 1/β and 1/γ, respectively, and the intercepts on the T axes are equal to TC. The linear curves confirm the applicability of Kouvel–Fisher formalism in the current investigation. From the fitted straight lines according respectively to eqn (6) and (7) we can carry out our parameters, the deduced exponents are summarized in Table 2. Obviously, the obtained values of the critical exponents β and γ and Curie temperature TC using the KF method are consistent with those obtained using the modified Arrott plots of 3D-Ising model for x = 0 and x = 0.02 samples and that of 3D-Heisenberg model for x = 0.06. This indicates the self-consistency of the values of the exponents.
 |
| | Fig. 7 Kouvel–Fisher plots of Ms(T)(dMs/dT)−1 and χ−1(T)(dχ−1/dT)−1 vs. T for (a) x = 0 (b) x = 0.02 and (c) x = 0.06. | |
3.2.3. Critical isotherm exponent. The third critical exponent δ can be determined according to eqn (3). As mentioned above, the critical points for Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) samples are 275 K, 260 K and 216 K, respectively. Fig. 8 shows critical isotherms M (TC) vs. μ0H plots for x = 0 and x = 0.06 respectively, and in the insets are the same plots presented in log–log scale. According to eqn (3), log(M(TC)) vs. log(μ0H) plots would give a straight line with a slope of 1/δ. From the linear fitting in the insets, we have obtained δ = 4.347, 4.216 and 4.484 for x = 0, 0.02 and 0.06, respectively. Furthermore, according to the statistical theory, the three critical exponents obey the Widom scaling relation:18| |
 | (8) |
 |
| | Fig. 8 Critical isotherm of M vs. μ0H close to the Curie temperature for (a) x = 0 and (b) x = 0.06. Insets shown the same on log–log scale and the straight line is the linear fit following eqn (3). The critical exponent δ are obtained from the slope of the linear fit. | |
Using this equation, δ values are calculated with γ and β values obtained from the modified Arrott plot and from the KF method. The values obtained from critical isotherms M (TC, μ0H) are close to those determined with the Widom scaling relation. We noted also that these values of δ are in good agreement with those given by 3D-Ising model for x = 0 and 0.02 and those given by 3D-Heisenberg for x = 0.06.
3.2.4. Reliability of the critical exponents. As a further test of the reliability of the obtained critical exponents values, we plotted in Fig. 9a and b M|ε|−β as a function of μ0H|ε|−(β+γ) for x = 0 and x = 0.06, respectively. Eqn (4) implies that M|ε|−β vs. μ0H|ε|−(β+γ) produces two universal curves, one for temperatures above TC and the other for temperatures below TC. It can be clearly seen that all data fall on two independent branches, one for temperatures T < TC and the other for temperatures T > TC. This result indicates that the obtained values of the critical exponents and Curie temperatures are reliable, reasonably accurate and unambiguous. In the insets of Fig. 9, we show the same plots of M|ε|−β vs. μ0H|ε|−(β+γ) in logarithmic scale and it is clearly observed that all the experimental curves at T < TC and T > TC coincided at higher magnetic fields further satisfying the criteria of scaling theory.12 We further confirm the reliability of the exponents and TC by the analysis m2 vs. h/m plot, where m = M (μ0H, ε)|ε|−β and h = μ0H|ε|−(β+γ).28 Fig. 10a and b show such plots for x = 0 and x = 0.06, respectively, with two functional behavior, one above TC and the other below TC. This clearly indicates that the interactions are properly renormalized in critical regime following scaling equation of state.
 |
| | Fig. 9 Scaled magnetization for (a) x = 0 and (b) x = 0.06 below and above TC, using β and γ mentioned in the text. This plot shows that all the data collapse onto two different curves: one below TC and another above TC. Insets shown the same plot on a log–log scale. | |
 |
| | Fig. 10 Scaling plots m2 vs. h/m for (a) x = 0 and (b) x = 0.06 below and above TC, using β and γ mentioned in the text. | |
3.2.5. Local exponent. In order to demonstrate the influence of critical exponent on magnetocaloric effect (MCE), the local exponent n, which depends on the magnetic state of the sample, was studied in terms of the field dependence of the magnetic entropy change. According to Oesterreicher and Parker,29 the field dependence of the magnetic entropy change of materials with second-order transition can be expressed as:where n depends upon the magnetic state of the compound and ‘a’ is a constant. Fig. 11 shows the fitting of the data of |ΔSmaxM| vs. μ0H at each temperature using eqn (9) for the two compounds x = 0 and x = 0.06 in order to determine n values. In another way, the local exponent n near the Curie temperature can be writing also as:| |
 | (10) |
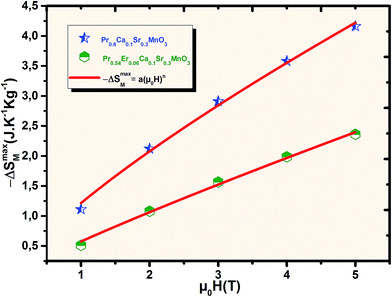 |
| | Fig. 11 The magnetic entropy change ΔSM versus applied magnetic field for x = 0 and x = 0.06. | |
According to eqn (10), n was calculated using the values of β and γ obtained from the modified Arrott plot and Kouvel–Fisher methods. Using the fitting of |ΔSmaxM| to eqn (9), the critical exponents from modified Arrott plots and Kouvel–Fisher methods, respectively, we have got n = 0.774, 0.548 and 0.571 for x = 0 and n = 0.887, 0.608 and 0.640 for x = 0.06. The values obtained from the fitting are different from those calculated from the exponent relation. This difference can be related to the instability of the |ΔSmaxM| position versus magnetic field, which is shifted when magnetic field increases, similar difference has been found by T. L. Phan et al.37 The deviation observed in the n values, from that predicted by the mean field model (n = 2/3)30 confirms the critical behavior studied previously for our samples and the invalidity of the mean field model in the description of the both samples near the Curie temperature. This deviation confirmed an existence of local inhomogeneities or superparamagnetic clusters in the vicinity of the Curie temperature of our samples.
3.2.6. Discussion. The values of the critical exponents for Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) samples, and the values based on different theoretical models12,19 as well as experimental values reported in the literature for other manganites20–27 are listed in Table 2 for comparison. From this table, the exponents values obtained from this analysis are very close to the values predicted by the 3D-Ising for x = 0 and x = 0.02 and by the 3D-Heisenberg model for x = 0.06 respectively. It means that there is an existence of FM short-range order (even above TC), caused by magnetic inhomogeneity and clusters, which is confirmed by the obtained values of local exponent calculated with several methods. The ferromagnetic behavior around the Curie temperature was properly renormalized following the scaling equation of state, indicating that the obtained values of β, γ and TC for these samples are reliable and in agreement with the scaling hypothesis. While the scaling is good at high fields, it becomes poor at low fields below TC. This could be attributed to the magnetic inhomogeneities and the effect due to the uncertainty in the calculation of the demagnetization factor, which becomes significant in this region.31 The change of the universality class and the effect of disorder on a system whose pure version undergoes a second order phase transition are understood based on the Harris criterion.32,24 If the critical exponent αpure is positive, disorder influence the critical exponents. While, if the αpure is negative, the disorder is irrelevant. Using the Rushbrooke scaling relation expressed as:24The exponent αpure is found to be positive (αpure = 0.151) for the pure system (Pr0.6Ca0.1Sr0.3MnO3), which implies that the disorder is relevant, and consequently influences the critical behavior. This disorder probably arises from dissimilar ions Pr3+, Er3+, Ca2+and Sr2+at A-site of perovskite structure and/or inhomogeneous phases above and below TC, and both properties are intrinsic to those systems.33 This fact explains the obtained 3D-Heisenberg class for Pr0.54 Er0.06Ca0.1Sr0.3MnO3 sample.
The obtained results can reflect the following useful informations: the critical exponents for the mentioned materials are governed by lattice dimension (3d), dimension of order parameter (n = 3, magnetization), and range of interaction (short-range, long range, or infinite). According to a renormalization-group analysis of systems performed by Fisher et al.,34 the universality class of the magnetic phase transition depends on the range of the exchange interaction J(r) ≈ r−(d+σ) where d is the dimension of the system and σ > 0 is the range of interaction. If σ ≥ 2, the 3D-Heisenberg exponents are valid (β = 0.365, γ = 1.336 and δ = 4.80) for the three-dimensional isotropic ferromagnet, and J(r) decreases faster than r−5. When σ ≤ 3/2, the mean field exponents (β = 0.5, γ = 1.0 and δ = 3.0) are valid, which indicates that J(r) decreases slower than r−4.5. For the intermediate range, meaning J(r) ≈ r−3−σ with 3/2 < σ < 2 the exponents belong to other universality classes, which depends on values of σ. A renormalization group analysis34,35 has suggested that the exponent of γ and the range of σ satisfy a mathematic relation as
| |
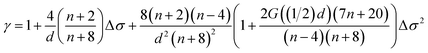 | (12) |
where

and

for a system with lattice dimensionality (
d) and spin (
n).
For our Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) samples, the values of the critical exponents for x = 0 and x = 0.02 are in agreement with 3D-Ising ferromagnet universality class which confirms that they are in the intermediate range. However, those of x = 0.06 are in agreement with 3D-Heisenberg ferromagnet universality class which confirms that J(r) decays slower than r−5.
4. Conclusion
In the present work, we have studied the effect of Er doping on the critical behavior of Pr0.6−xErxCa0.1Sr0.3MnO3 (x = 0, 0.02 and 0.06) manganites in the vicinity of the Curie temperature from FC magnetization measurements. The values of critical exponents for all our compounds were extracted using the modified Arrott plots method, Kouvel–Fisher method and critical isotherm analysis. The validity of the calculated critical exponents using various methods has been confirmed by the scaling equation of state. The obtained critical exponents are found to follow scaling equation with the magnetization data scaled into two different curves below and above TC. This confirms that the critical exponents and TC are reasonably accurate. The estimated critical exponents confirm that the experimental values agree well with the 3D-Ising model for x = 0 and x = 0.02 samples and with the 3D-Heisenberg model for x = 0.06.
Acknowledgements
The Tunisian Ministry of Higher Education and Scientific Research supported this work.
References
- J. M. D. Coey, M. Viret and S. von Molnar, Mixed-valence manganites, Adv. Phys., 1999, 48, 167 CrossRef CAS.
- M. B. Salamon and M. Jaime, The physics of manganites: Structure and transport, Rev. Mod. Phys., 2001, 73, 583 CrossRef CAS.
- C. N. R. Rao, A. Arulraj, A. K. Cheetham and B. Raveau, Charge ordering in the rare earth manganates: the experimental situation, J. Phys.: Condens. Matter, 2000, 12, R83 CrossRef CAS.
- A. Mleiki, S. Othmani, W. Cheikhrouhou-Koubaa, M. Koubaa, A. Cheikhrouhou and E. K. Hlil, Effect of praseodymium doping on the structural, magnetic and magnetocaloric properties of Sm0.55−xPrxSr0.45MnO3 (0.1 ≤ x ≤ 0.4) manganites, J. Alloys Compd., 2015, 645, 559 CrossRef CAS.
- J. Makni-Chakroun, W. Cheikhrouhou-Koubaa, M. Koubaa and A. Cheikhrouhou, Impact of a small amount of vacancy in both lanthanum and calcium on the physical properties of nanocrystalline La0.7Ca0.3MnO3 manganite, J. Alloys Compd., 2015, 650, 421 CrossRef CAS.
- A. Selmi, R. M'nassri, W. Cheikhrouhou-Koubaa, N. Chniba Boudjada and A. Cheikhrouhou, Effects of partial Mn-substitution on magnetic and magnetocaloric properties in Pr0.7Ca0.3Mn0.95X0.05O3 (Cr, Ni, Co and Fe) manganites, J. Alloys Compd., 2015, 619, 627 CrossRef CAS.
- M. Mansouri, H. Omrani, W. Cheikhrouhou-Koubaa, M. Koubaa, A. Madouri and A. Cheikhrouhou, Effect of vanadium doping on structural, magnetic and magnetocaloric properties of La0.5Ca0.5MnO3, J. Magn. Magn. Mater., 2016, 401, 593 CrossRef CAS.
- C. Zener, Interaction between the d-Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure, Phys. Rev., 1951, 82, 403 CrossRef CAS.
- A. J. Millis, P. B. little Wood and B. I. Shraiman, Double Exchange Alone Does Not Explain the Resistivity of La1−xSrxMnO3, Phys. Rev. Lett., 1995, 74, 5144 CrossRef CAS PubMed.
- D. Kim, B. Revaz, B. L. Zink, F. Hellman, J. J. Rhyne and J. F. Mitchell, Tricritical Point and the Doping Dependence of the Order of the Ferromagnetic Phase Transition of La1−xCaxMnO3, Phys. Rev. Lett., 2002, 89, 227202 CrossRef CAS PubMed.
- H. E. Stanley, Scaling, universality, and renormalization: Three pillars of modern critical phenomena, Rev. Mod. Phys., 1999, 71, S358 CrossRef CAS.
- H. E. Stanley, Introduction to Phase Transitions and Critical Phenomena, Oxford University Press, London, 1971, ch. 12.4, p. 200 Search PubMed.
- A. Arrott and J. E. Noakes, Approximate Equation of State For Nickel Near its Critical Temperature, Phys. Rev. Lett., 1967, 19, 786 CrossRef CAS.
- N. Moutis, I. Panagiotopoulos, M. Pissas and D. Niarchos, Structural and magnetic properties of La0.67 (BaxCa1−x)0.33MnO3 perovskites (0 < ∼x < ∼1), Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1129 CrossRef CAS.
- B. K. Banerjee, On a generalised approach to first and second order magnetic transitions, Phys. Lett., 1964, 12, 16 CrossRef.
- H. S. Shin, J. E. Lee, Y. S. Nam, H. L. Ju and C. W. Park, First-order-like magnetic transition in manganite oxide La0.7Ca0.3MnO3, Solid State Commun., 2001, 118, 377 CrossRef CAS.
- J. S. Kouvel and M. E. Fisher, Detailed Magnetic Behavior of Nickel Near its Curie Point, Phys. Rev., 1964, 136, A1626 CrossRef.
- B. Widom, Surface Tension and Molecular Correlations near the Critical Point, J. Chem. Phys., 1965, 43, 3892 CrossRef CAS.
- D. Ginting, D. Nanto, Y. D. Zhang, S. C. Yu and T. L. Phan, Influences of Ni-doping on critical behaviors of La0.7Sr0.3Mn1−xNixO3, Phys. B, 2013, 412, 17 CrossRef CAS.
- S. Rößler, H. S. Nair, U. K. Roessler, C. M. N. Kumar, S. Elizabeth and S. Wirth, Ferromagnetic transition and specific heat of Pr0.6Sr0.4MnO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 184422 CrossRef.
- F. Ben Jemaa, S. H. Mahmood, M. Ellouze, E. K. Hlil and F. Halouani, Structural, magnetic, magnetocaloric, and critical behavior of selected Ti-doped manganites, Ceram. Int., 2015, 41, 8191 CrossRef CAS.
- S. E. L. Kossi, S. Mnefgui, J. Dhahri and E. K. Hlil, Critical behavior and its correlation with magnetocaloric effect in La0.7Sr0.25Na0.05Mn(1−x)TixO3 (0 ≤ x ≤ 0.1) manganite oxide, Ceram. Int., 2015, 41, 8331 CrossRef CAS.
- A. Berger, G. Camopillo, P. Vivas, J. E. Pearson, S. D. Bader, E. Baca and P. Prieto, Critical exponents of inhomogeneous ferromagnets, J. Appl. Phys., 2002, 91, 8393 CrossRef CAS.
- R. M'nassri, N. Chniba-Boudjada and A. Cheikhrouhou, 3D-Ising ferromagnetic characteristics and magnetocaloric study in Pr0.4Eu0.2Sr0.4MnO3 manganite, J. Alloys Compd., 2015, 640, 183 CrossRef.
- M. H. Phan, V. Franco, N. S. Bingham, H. Srikanth, N. H. Hur and S. C. Yu, Tricritical point and critical exponents of La0.7Ca0.3−xSrxMnO3 (x = 0, 0.05, 0.1, 0.2, 0.25) single crystals, J. Alloys Compd., 2010, 508, 238 CrossRef CAS.
- N. Mtiraoui, M. Chennabasappa, R. Decourt, O. Toulemonde, J. Dhahri and M. Oumezine, Critical behavior and magnetic entropy change in Nd0.7Sr0.1Ba0.1Ca0.1MnO3−δ perovskite manganite, Ceram. Int., 2016, 42, 1036 CrossRef CAS.
- A. Mleiki, S. Othmani, W. Cheikhrouhou-Koubaa, M. Koubaa, A. Cheikhrouhou and E. K. Hlil, Critical behavior near the ferromagnetic–paramagnetic phase transition in compounds Sm0.55−xPrxSr0.45MnO3 (0.3 ≤ x ≤ 0.4), J. Alloys Compd., 2015, 648, 1043 CrossRef CAS.
- S. N. Kaul, Static critical phenomena in ferromagnets with quenched disorder, J. Magn. Magn. Mater., 1985, 53, 5 CrossRef CAS.
- H. Oesterreicher and F. T. Parker, Magnetic cooling near Curie temperatures above 300 K, J. Appl. Phys., 1984, 55, 4334 CrossRef CAS.
- V. Franco and A. Conde, Scaling laws for the magnetocaloric effect in second order phase transitions: From physics to applications for the characterization of materials, Int. J. Refrig., 2010, 33, 465 CrossRef CAS.
- R. Li, C. Zhang, L. Pi and Y. Zhang, Tricritical point in hole-doped manganite La0.5Ca0.4Li0.1MnO3, Europhys. Lett., 2014, 107, 47006 CrossRef.
- A. B. Harris, Effect of random defects on the critical behaviour of Ising models, J. Phys. C: Solid State Phys., 1974, 7, 1671 CrossRef.
- A. K. Pramanik and A. Banerjee, Phase separation and the effect of quenched disorder in Pr0.5 Sr0.5MnO3, J. Phys.: Condens. Matter, 2008, 20, 275207 CrossRef CAS PubMed.
- M. E. Fisher, S. K. Ma and B. G. Nickel, Critical Exponents for Long-Range Interactions, Phys. Rev. Lett., 1972, 29, 917 CrossRef.
- A. K. Pramanik and A. Banerjee, Critical behavior at paramagnetic to ferromagnetic phase transition in Pr0.5Sr0.5MnO3 A bulk magnetization study, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 214426 CrossRef.
- J. Fan, L. Ling, B. Hong, L. Zhang, L. Pi and Y. Zhang, Critical properties of the perovskite manganite La0.1Nd0.6Sr0.3MnO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 144426 CrossRef.
- T. L. Phan, N. T. Dang, T. A. Ho, T. V. Manh, T. D. Thanh, C. U. Jung, B. W. Lee, A. T. Le, A. D. Phan and S. C. Yu, First-to-second-order magnetic-phase transformation in La0.7Ca0.3−xBaxMnO3 exhibiting large magnetocaloric effect, J. Alloys Compd., 2016, 657, 818 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 
 just below TC.
just below TC.

 is the inverse zero-field susceptibility just above TC.
is the inverse zero-field susceptibility just above TC.





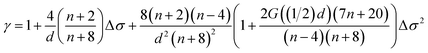
 and
and  for a system with lattice dimensionality (d) and spin (n).
for a system with lattice dimensionality (d) and spin (n).






