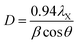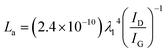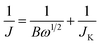The evolution of hierarchical porosity in self-templated nitrogen-doped carbons and its effect on oxygen reduction electrocatalysis

Abstract

Pyrolitic self-templating synthesis is an effective method for creating hierarchically porous N-doped carbons. We study the evolution of microstructure in self-templated carbons derived from magnesium nitrilotriacetate, in the 600–1000 °C temperature range. The materials are characterised using N₂ adsorption, Hg intrusion, X-ray diffraction, X-ray photoelectron spectroscopy, Raman spectroscopy, elemental analysis, scanning electron microscopy and transmission electron microscopy. The carbons display high specific surface areas (up to 1830 m² g⁻¹), and high pore volumes (up to 3.1 mL g⁻¹). Interestingly, each porosity type – micro, meso, and macro – evolves along its own route. Micropore growth is most significant between 600 and 700 °C, yet it slows down and stops around 800 °C; this indicates that micropores form by removal of tarry matter from the interstices between graphitic sheets, rather than by physical/chemical etching of these sheets. Mesopores, templated by spontaneously forming MgO nanoparticles, become dominant at 800 °C; further agglomeration of these particles leads to macropore templating at 900 °C. The porosity evolution is explained by the growth of MgO particles, as monitored by XRD broadening. Furthermore, the degree of disorder decreases with the pyrolysis temperature, most significantly between 700 and 800 °C, with the Raman I_D/I_G ratio dropping from 1.36 to 1.17. Correspondingly, the in-plane length of graphitic crystallites increases along the series, from 14 to 17 nm. Although the nitrogen content decreases with pyrolysis temperature, from 6.9 to 4.1 at%, the ratio between graphitic and pyridinic nitrogens remains constant. We then measure the performance of these carbons as electrocatalysts in the oxygen reduction reaction (ORR) at pH 13 using rotating disk electrode voltammetry and electrochemical impedance spectroscopy. Remarkably, the ORR activity trend is independent of nitrogen concentration or degree of disorder. Instead, it is governed by the microstructural parameters, most importantly surface area and microporosity.

---

1 Introduction

Activated carbon has been used as a dye and adsorbent for millennia,^1–4 and in catalysis for decades.^5,6 Lately, carbon has been hailed as a promising electrode material for electrochemical charge storage⁷ in batteries,^7–9 supercapacitors,^10–13 and fuel cells.^14–17 Specifically, carbons doped with heteroatoms such as nitrogen are a leading alternative to platinum as electrocatalysts in the oxygen reduction reaction (ORR) in alkaline solutions.^18–24

Both the elemental composition and the microstructure of carbon determine its catalytic performance.^15–31 Carbon comprises matter (sp³/sp² carbon ratio, doping, crystallinity) and voids (pore sizes, shapes and distribution). Micropores (d < 2 nm) provide most of the surface area of the material. This means that most catalytic active sites are located in micropores.³ Mesopores (d = 2–50 nm) contribute more to the internal volume of the carbon, serving as immediate reservoirs for reagents and enabling the transfer of reagents/products to/from the micropores.³² In some cases, the mesopores are small enough to affect reaction pathways by confinement effects.³³ Finally, macropore channels (d > 50 nm) are the highways for mass transfer through the carbon, contributing most to its internal volume.³⁴ The different pore levels must intersect, to enable the splitting of reagent/product flow; only then can porosity be termed ‘hierarchical’ (Fig. 1).^{21–23,35–37}

Fig. 1 Scheme of hierarchical porosity (type II),³⁷ showing intersecting pore types.

Yet carbon structure is easier described than designed. Carbon synthesis protocols come in two very different types: empirical and rational. In the former, abundant carbonaceous precursors (biomass-based or petro-based) are pyrolyzed in hope for serendipity.^38–43 The resulting carbons are easily made and cheap, but controlling their porosity and composition is difficult. In the latter, chemical precursors are transformed with various external templating methods. This allows a high degree of control over the material properties, but preparation is more complex and costly. External templating methods include hard templating^44–47 (e.g. on silica, which is then etched away by HF) and soft templating (based on organic self-assembly).^36,48,49 Other methods for controlling carbon structure include pyrolyzing preformed aerogels^50,51 and the etching of pores by chemical and physical means.³

Self-templating is a powerful route to hierarchical porous carbons.^52–59 In this approach, simple metal–organic salts such as magnesium citrate are used as both carbon precursor and templating agent. During pyrolysis, nano-sized metal oxide particles (e.g. MgO) form within the carbon matrix. Washing out these particles leaves behind mesopores (in case of single nanoparticles) and macropores (for nanoparticle agglomerates). Recently, we reported the discovery of a family of self-templating nitrogen-doped carbons, based on the pyrolysis of various magnesium nitrilotriacetates (MgNTA).^23,30 These carbons exhibit an interpenetrating network of micropores, mesopores and macropores, lined with graphitic shells. However, despite having advantages such as hierarchical porosity, graphitic network and high doping, the challenge of ‘designability’ remains open. To address it, we must first understand the mechanism of pyrolytic self-templating.

We now report a detailed study into the evolution of microstructure and composition in MgNTA-derived carbons, in the 600–1000 °C temperature range. Using a broad array of experimental techniques, we follow the surface area, internal volume, micro-/meso-/macro-pore distribution, size of templating MgO nanoparticles, degree of graphitization, and nitrogen content and distribution. The result is a step-by-step description of how micropores are formed, and how mesopore-templating nanoparticles of MgO grow and agglomerate. Finally, we test how the evolving microstructure and composition affect the carbons' ORR activity at pH 13, a reaction of rising importance due to the rise of alkaline exchange membranes for fuel cells.²⁰

2 Experimental

2.1 Procedure for synthesis of hierarchical porous carbons

This is a modification of a previously published procedure.²³ Briefly, magnesium nitrilotriacetate (MgNH(CH₂COO)₃(H₂O)₃) was precipitated from a 1 : 1 solution of basic magnesium carbonate (Strem) and nitrilotriacetic acid (Aldrich) at 85 °C. After drying and grinding, the salt was pyrolyzed at a range of temperatures (600–1000 °C) in Ar atmosphere for 1 h (heating rate 10°C min⁻¹). The resulting MgO@N:C composite was washed in citric acid (0.5 M) overnight, dried, and annealed in argon (1000 °C/1 h, heating rate of 5 °C min⁻¹).

2.2 Characterization of materials

Thermogravimetric analysis (TGA) was done on a Netzch Jupiter® STA 449F3 instrument, under argon (20 mL min⁻¹) between 30 and 800 °C. Transmission electron microscopy (TEM) was done on a Tecnai Osiris microscope at an accelerating voltage of 200 kV. Scanning electron microscopy (SEM) was done on a Zeiss EVO50 microscope operated at 15 kV. N₂ adsorption–desorption isotherms were measured on a Thermo Scientific Surfer instrument at 77 K, using vacuum dried samples (200 °C/3 h). Isotherms were analyzed by the ThermoFischer Advanced Data Processing 6.0 software. The isotherms were analyzed using the two-parameter Brunauer–Emmett–Teller (BET2) model for specific surface area, the Dubinin–Radushkevitch model for micropore volume, the Horvath–Kawazoe method for micropore size distribution, and non-local density functional theory (NLDFT) isotherm fitting for meso–macropore size distribution. In the latter, the model used was N₂/graphite at 77 K, with slit-shaped pores (giving a better fit than cylindrical pores). Helium density was measured on a Micromeritics Multivolume Pycnometer 1305. Mercury intrusion was carried out on a Pascal 440 Porosimeter (CE Instruments) up to 400 MPa, on the same pre-treated samples. X-Ray diffraction (XRD) patterns were obtained with a MiniFlex II diffractometer using Ni-filtered Cu-K_α radiation, at 30 kV and 15 mA. Approximate sizes of the coherently scattering domains (D) were calculated using the Scherrer equation:
where λ_X is the X-ray wavelength (1.54056 Å for Cu-Kα), β is the line broadening (in rad), and θ is the Bragg angle. This equation only accounts for size-dependent broadening, so it gives a lower limit for actual particle sizes.^60,61 No calibration was done to account for instrument broadening, so the calculated D values are limited to studying trends within the series.

Raman spectroscopy was performed on a Thermo Nicolet Almega XR Dispersive Raman microscope, with a ×50 lens and 10 exposures of 5 s. The laser wavelength is 532 nm (24 mW). First-order Raman spectra were fit iteratively with four Lorentzian components, based on literature assignments.^62–66 The in-plane (a direction) lengths of graphitic crystallites (L_a) were calculated from the intensity ratios of fitted D and G bands, according to the relation determined by Cançado et al.,⁶⁷

where λ_l is the laser wavelength (532 nm).

X-Ray photoelectron spectroscopy (XPS) measurements were carried out using a PHI VersaProbe II scanning XPS microprobe (Physical Instruments AG, Germany). Analysis was performed using a monochromatic Al Kα X-ray source of 24.8 W power with a beam size of 100 μm. The spherical capacitor analyzer was set at a 45° take-off angle with respect to the sample surface. The pass energy was 46.95 eV yielding a full width at half maximum of 0.91 eV for the Ag 3d_5/2 peak. Peaks were calibrated using the C 1s position. Curve fitting was done using XPSPeak 4.1.

2.3 Procedure for electrochemical measurements

Inks of the carbon powders (0.80 mL DI water, 0.20 mL ethanol, 10 μL Nafion® 5 wt% dispersion (Alfa Aesar), 1.0 mg carbon powder) were sonicated and dropcast (3 × 10 μL) on a polished ϕ = 5 mm (A = 0.196 cm²) glassy carbon electrode (Gamry), and dried at 50 °C. Total catalyst loading was 30 μg, or 153 μg cm⁻². Electrochemical experiments were performed in 0.1 M KOH at 25.0 ± 0.1 °C, using a Gamry Reference 600 potentiostat and a Gamry RDE710 Rotating Electrode setup. Saturated calomel electrode (SCE) separated by a 10 cm bridge was used as a reference electrode, and a graphite rod as a counter electrode. Potentials were reported vs. reversible hydrogen electrode (RHE) by adding 1.011 for pH 13. N₂ or O₂ (both 99.999%) were bubbled for >60 min to saturate the solution, and were flowed above the solution during the experiments. Voltammograms were collected from 1.01 to 0.31 V vs. RHE with a scan rate of 10 mV s⁻¹. RDE voltammograms were collected at rotating speeds of 2400, 2000, 1600, 1200, 900, 600 and 400 rpm. Reported current densities represent faradaic currents, after subtracting the capacitive charging background current. The solution resistance (typically 44–48 ohm) was measured prior to each measurement set. A positive feedback automatic iR correction of 90% was used. Before measurements, surface adsorbed oxygen was reduced and the wetting was improved by cycling the electrode between 0 and −0.7 V vs. SCE for 20 cycles at 50 mV s⁻¹. Electrochemical impedance spectroscopy (EIS) was measured potentiostatically at ±5 mV around the half-wave potential for ORR, while bubbling oxygen and rotating at 1600 rpm. The electrochemical impedance spectroscopy frequency range was 0.2–10⁶ Hz. The number of moles of electrons transferred per mol O₂ (n) was estimated by the Koutecký–Levich equation
where J is the measured current density (mA cm⁻²), J_K the kinetic (exchange) current density (mA cm⁻²), and ω is the electrode rotation rate (rpm). The term B is given by

B = 0.2nFC_OD_O^2/3ν^−1/6 (1)

where F is Faraday's constant (96 485 C mol⁻¹), C_O is the concentration of dissolved O₂ (1.2 mM at 25 °C in 0.1 M KOH), D_O is the diffusion coefficient of O₂ (1.9 × 10⁻⁵ cm² s⁻¹ at 25 °C in 0.1 M KOH), and ν is the kinematic viscosity of the 0.1 M KOH electrolyte at 25 °C (0.01 m² s⁻¹). By plotting 1/J versus 1/ω^1/2 at different potentials and fitting linear equations to the data, the number of electrons could be calculated from the 1/B slope.

3 Results and discussion

3.1 Microstructure of the carbons

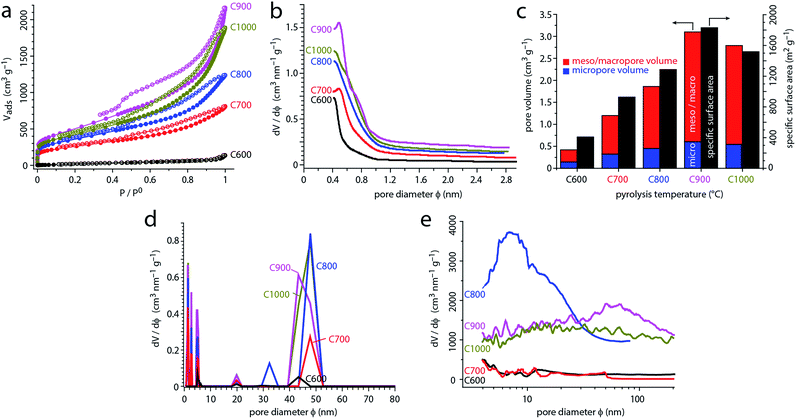
N-Doped carbons were prepared by pyrolyzing magnesium nitrilotriacetate at five different temperatures between 600 °C and 1000 °C (see Experimental section 2.1 for full procedure). Sample names denote the pyrolysis temperature in °C (C600, C700, C800, C900 and C1000). All of the MgO-free carbons were then annealed at the same temperature (1000 °C), removing any surface functionalities introduced during the acid wash step.^23,53,54 Carbonization of MgNTA is complete at 540 °C, according to the thermogravimetric analysis in argon (Fig. S1†). The reactions occurring during carbonization were described by Budkuley and Naik.⁶⁸ Here, we will focus on the subsequent microstructural changes.

The surface area and porosity of the carbons were studied using N₂ adsorption. Fig. 2a shows the N₂ adsorption–desorption isotherms at 77 K for carbons C600 to C1000, as a function of equilibrium relative pressure (P/P⁰, where P⁰ is the saturation pressure of N₂ at 77 K).⁶⁹ The initial sharp rise at P/P⁰ < 0.01 corresponds to micropore filling, a primary physisorption process distinct from surface adsorption. The magnitude of the rise in carbons C700–C1000 reflects abundant micropores. The consequent slope (P/P⁰ > 0.2) corresponds to the filling of mesopores with monolayers and multilayers of N₂. The ultimate rise (P/P⁰ > 0.8) and subsequent desorption hysteresis are characteristic for capillary condensation in the finite-volume of the mesopores. While C600 exhibits a type III isotherm (typical for nonporous solids), C700–C1000 show typical type IVa isotherms, characteristic for micro–mesoporous materials.⁶⁹ The hysteresis loops in the latter are type H4.⁶⁹ Such hysteresis may arise by different mechanisms, such as adsorption metastability (delayed condensation), pore blocking at narrow pore necks, and/or cavitation-induced evaporation.⁶⁹

Fig. 2 Porosimetry on carbons pyrolyzed at 600–1000 °C. (a) N₂ adsorption–desorption isotherms (filled and empty circles, respectively) at 77 K. (b) Micropore size distribution, calculated from the N₂ adsorption data by the Horvath–Kawazoe method. (c) Left axis: volumes of micropores (blue, calculated by the Dubinin–Radushkevich method from the N₂ adsorption data) and mesopores + macropores (red, obtained by subtracting the micropore volumes from the total nitrogen adsorbed at 0.99 relative pressure). Right axis (black): specific surface areas, calculated by the BET2 method. (d) Pore size distributions calculated by NLDFT from the N₂ adsorption–desorption isotherms. (e) Pore size distributions obtained by Hg intrusion, focusing on the pore diameter range which corresponds to intraparticulate pores.

The carbons exhibit specific surface areas (SSAs) as high as 1830 m² g⁻¹ (C900, Fig. 2b and Table 1) and total pore volumes as reaching 3.1 mL g⁻¹ (C900, at P/P⁰ = 0.99). While high SSAs are often observed in activated carbons, the high pore volumes reveal the predominance of mesopores and macropores. By quantifying the micropore volumes with the Dubinin–Radushkevitch model, we could separate the contributions of different pore types to the total volume (Fig. 2c and Table 1). The relative volume of mesopores and macropores is high – it rises from 65% in C600 to a stable 76–80% in C800–C1000. Moreover, while all pore types increase in volume as a function of the pyrolysis temperature, the micropore volume increases by a factor of 4, while the combined mesopore and macropore volume by as much as a factor of 9 (C600 vs. C900). When the pyrolysis temperature is further raised from 900 °C to 1000 °C, the surface area starts shrinking, probably due to pores collapsing.^70,71

Table 1 Microstructural, compositional, and electrocatalytic properties of the MgNTA-derived carbons^a

	aS (m^2 g^−1)	Vmicropore	Vmesopore	Vtotal	N wt% (EA)	O at% (XPS)	N at% (XPS)	Npy (%)	Ngr (%)	Nox (%)	MgO (220) FWHM (°)	MgO XRD ‘size’ (nm)	Raman ID/IG	La (nm)	E1/2 (V vs. RHE)	n
a aS is specific surface area, determined by N2 adsorption at 77 K with BET2 fitting. V = volume in cm^3 g^−1. EA = elemental analysis, XPS = X-ray photoelectron spectroscopy. La is the in-plane graphite crystalline length calculated from the ID/IG ratios. n is the electron transfer number, in mol e^− per mol O2.
C600	409	0.15; 35%	0.28; 65%	0.42	4.89	3.07	6.36	28	45	27	1.51	6.46	1.37	13.8	0.69	2.19
C700	928	0.33; 27%	0.87; 73%	1.20	5.59	2.15	6.87	31	52	17	1.23	7.88	1.36	14.0	0.74	3.04
C800	1286	0.45; 24%	1.41; 76%	1.86	5.69	2.42	6.16	34	51	15	1.22	7.94	1.17	16.2	0.75	3.06
C900	1831	0.61; 20%	2.49; 80%	3.10	4.61	2.72	5.86	36	51	14	1.10	8.81	1.09	17.4	0.77	3.64
C1000	1519	0.55; 20%	2.24; 80%	2.79	4.03	2.01	4.09	31	46	22	0.97	9.99	1.18	16.2	0.81	3.79

---

To follow and quantify the evolution of microporosity, we analyzed the N₂ monolayer formation using the Horvath–Kawazoe model (Fig. 2b).⁷² In all the carbons, micropores are smaller than 1 nm. Micropores grow as the pyrolysis temperature is increased, and the most significant increase in micropore sizes occurs between 600 and 700 °C. Further growth slows down and finally stops: there is barely any change in the microporosity from 800 °C to 1000 °C. Yet how do these micropores form? According to the TGA, the carbon loses 5.7% of its weight (0.84 percentage points in Fig. S1†) between 550 °C and 800 °C. This, together with the growth deceleration, suggests that micropores form between 600 °C and 800 °C due to the elimination of tar from the interstices between the carbon sheets.³ When this “tar supply” runs out (>800 °C), the pore growth decelerates and stops. This is the most plausible mechanism in the absence of external activation agents.³

The N₂ adsorption data can be further analyzed using NLDFT isotherm fitting, giving information about mesopores and macropores (Fig. 2d and S2†). According to Fig. 2d, all carbons contain small (∼5 nm), medium (∼20 nm) and large (∼40–50 nm) mesopores. All pore types become more abundant at higher pyrolysis temperatures. The NLDFT-derived pore size distributions are more qualitative, as they depend on a range of mathematical and physical assumptions for the fitting process.^3,72 However, this method does shed some light on pore growth, especially at the transition between C800 and C900–C1000. The former shows two separate pore sizes at ∼33 and ∼48 nm, while the latter show a broader pore cluster at ∼40–50 nm. This increase may reflect pore growth or convergence near the mesopore/macropore boundary.

We then studied the mesopore and macropore size distribution of carbons C600–C1000 by mercury intrusion (Fig. 2e). This method gives more reliable data on this type of porosity compared with simulation-based methods involving N₂ adsorption–desorption isotherms.^3,72 The measurement is robust and direct, and can also distinguish between pores inside particles and inter-particle volumes in particle agglomerates. At low pyrolysis temperatures (C600, C700), almost no intrusion occurs, reflecting the absence of intraparticulate pores (mesopores or small macropores). When heated to 800 °C, significant mesoporosity develops (C800), creating 5–20 nm pores. As the pyrolysis temperature is increased further, this peak broadens and shifts to larger pore sizes, all the way up to 150 nm. In this temperature range, the pore volume increases dramatically (by nearly 70%). Thus, the 700–800 °C temperature range spans the micropore/mesopore transition, while the 800–900 °C range spans the mesopore/macropore transition.

The evolution of the mesoporosity and macroporosity can be explained by the growth of MgO particles, which act as templates. Initially (≤700 °C), the MgO nanoparticles are too small and/or too few to give rise to significant volumes of mesopores. As they grow (C800), they become large enough to serve as templates in the small mesopore region (∼5–20 nm). The further broadening of pores, observed in C900, may result from particle growth and/or agglomeration; the two are hard to distinguish by N₂ adsorption alone. The consequent decrease in pore volume in C1000 may arise from further particle agglomeration, leading to segregation of the MgO from the carbon. Moreover, pore collapse becomes more significant at higher temperatures.^3,70,71,73

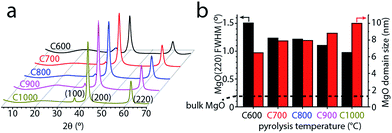
To understand the evolution of the MgO nanoparticle templates, we studied the XRD patterns of the MgO@carbon composites immediately after pyrolysis (before washing out the MgO particles). The diffractograms in Fig. 3 shows the typical broad carbon peak at ∼24°, corresponding to the (100) planes in carbon, and also three sharp peaks at 36.7°, 42.8° and 62.1°. These peaks are assigned to the (111), (200) and (220) planes of MgO, respectively (JCPDS card 45-0946). Control experiments showed that the MgO peaks in the MgO@carbon composites are broader than those in bulk MgO. This broadening proves that the MgO particles are indeed nanometric and allows following their growth on a semi-quantitative level. As the temperature is increased, the peaks' full widths at half maximum (FWHMs) are narrowed. For MgO(220), they decrease from 1.5 to 1.0, while the corresponding FWHM in bulk MgO(220) is just 0.2. The Scherrer equation allows us to compare the approximate sizes of the coherently scattering MgO domains, yielding values between 6.5 and 10 nm (Table 1). Thus, the drastic mesopore broadening between 800 and 900 °C cannot arise from the rapid growth of MgO nanoparticles, since their sizes increase only by several nanometers. Rather, the mesopore broadening and the disappearance of small mesopores, arise from MgO agglomeration at higher temperatures. Agglomeration decreases the number of MgO nanoparticles available for templating small mesopores, and the resultant agglomerates serve as templates for large mesopores and macropores.

Fig. 3 (a) X-ray diffractograms of the MgO@N:C powders after different pyrolysis temperatures. (b) Full widths at half-maximum (FWHMs) the MgO (220) plane (black) and approximate diameters of coherently scattering domains (red), calculated from the FWHMs using the Scherrer equation. The dashed line marks the bulk MgO (220) FWHM.

In addition to porosity, other structural parameters affect the electrocatalytic behavior of a carbon material. These include conductivity and dopant concentration. The electronic conductivity is linked with the degree of graphitization and the percolation of graphitic domains in the carbon.

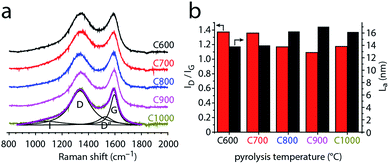
Raman spectroscopy affords more quantitative measures of the former, describing the degree of disorder and graphitization in the material by various descriptors. To study the degree of disorder in carbons C600–C1000, we measured their first-order Raman spectra (Fig. 4 and S3†). Two maxima occur near 1345 and 1595 cm⁻¹ for all samples. These were assigned to the D and G bands of graphite, respectively. The G band appears in all sp² carbon Raman spectra, arising from E_2g in-plane bond-stretching motions of pairs of sp² carbons. The D band is a breathing mode of sp² carbons in rings; this A_1g vibration is forbidden in perfect graphite yet is activated by symmetry reduction near defects, crystal edges, or impurities. Thus, the D band is often used as an indicator of disorder.^63–66,74 Fitting the spectra with just two Lorentzian functions proved impossible, revealing another peak between the two major bands, as well as a shoulder in the low wavenumber side of D band. The former is assigned to the D′′ band, typically associated with turbostratic defects (graphene layers slipping out of alignment).^63–65 The latter shoulder is assigned to the I band,^63–65 arising from impurity-induced disorder; it has been observed only in disordered carbons.^62–64

The mixed graphitic/disordered nature of the carbons is thus revealed by the presence of the D, D′′ and I Raman bands, as well as the relatively high I_D/I_G ratios (1.1–1.4, Fig. 4b). This mixed nature is typical for many N-doped carbons,^{15,16,64–66} in which the nitrogen doping induces structural defects and contributes to local symmetry breaking.

Fig. 4 (a) First-order Raman spectra of carbons C600–C1000, normalized by the G band intensity. The spectrum of C1000 is fitted with the I, D, D′′ and G bands (see text for details). (b) Intensity ratio of the fitted D and G bands (red, left axis), and the in-plane graphite crystalline length (L_a) calculated from the I_D/I_G ratios.

To study how the disorder in the carbon changes with pyrolysis temperature, we followed the I_D/I_G ratio. Fig. 4b shows that this ratio generally decreases with pyrolysis temperature. Thus, the carbons become more ordered when heated above 600 °C. This change reflects the in-plane growth of graphitic crystallites, whose lengths (L_a) can be calculated from the I_D/I_G ratios. The crystallite lengths range from 13.8 nm for C600 up to 17.4 nm for C900 (Fig. 4c). The slight decrease in L_a between C900 and C1000 (16.2 nm) may reflect shrinking and curving of the graphene layers.⁷⁵ Such shrinking was suggested also by the N₂ adsorption porosimetry (Fig. 2c). Interestingly, the I_D/I_G ratio drops sharply from 1.36–1.37 (C600, C700) to 1.09–1.18 (C800, C900, C1000). This step is not correlated with nitrogen loss, which would have explained an increase in order.^64–66 Rather, the increasing order shows that the 700–800 °C temperature range is critical for graphitization catalysis using this particular carbon feedstock (graphitization occurs at different temperatures with different carbon feedstocks, even when using similar MgO catalysts^76–78).

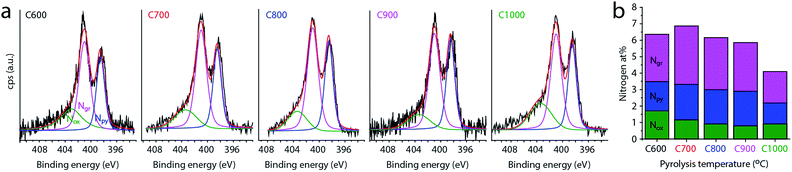
Finally, the concentration and distribution of nitrogen dopants in the carbon matrix plays an important role in its electrocatalytic activity. The bulk concentration of nitrogen was determined by elemental analysis to be 4.0–5.7 wt% (Table 1). All carbons contained 0.21–0.35 wt% of residual magnesium, and 1.60–1.85 wt% of hydrogen (Table S1†). We then used XPS to further study the surface and near-surface composition of the carbons, as most relevant for catalysis (Table 1 and Fig. 5). All the carbons contain some surface oxygen (typically 2–3 at%), with the O 1s peak constant at 532.1 ± 0.1 eV (see Fig. S4, ESI†). The nitrogen concentration is close to 6 at% and relatively constant between 600 and 800 °C. At higher temperatures it decreases gradually, dropping to 4 at% at 1000 °C (Fig. 5b). This decrease corresponds to temperature-driven denitrogenation.^79,80 Nonetheless, the N content values are high for single-precursor carbons, without resorting to external nitrogen sources. Fig. 5b also shows the distribution of nitrogen functionalities, which is important to oxygen reduction activity.^{14–16,18,24} Most of the nitrogen is in graphitic form, with pyridinic nitrogens coming close behind. There is an ongoing debate in the literature as to their relative merits in ORR,^{14–16,18,24} so an abundance of both is expected to be beneficial for catalysis. Interestingly, the graphitic-to-pyridinic nitrogen ratio remains almost constant at 1.5 ± 0.1 throughout the temperature range, even decreasing slightly at higher temperatures. This supports our hypothesis that the micropores form via the interstice cleaning route. Were the micropores formed by etching, pyridinic nitrogens would have been etched away faster than graphitic ones.³⁰

Fig. 5 (a) X-ray photoelectron spectra of carbons C600–C1000 in the N 1s region, with best fits of three nitrogen functionalities: pyrinidic (N_py, 398.5 eV), graphitic (N_gr, 401.1 eV) and ‘oxidized’ (N_ox, 403.4 eV). (b) Distribution of nitrogen functionalities in each carbon sample.

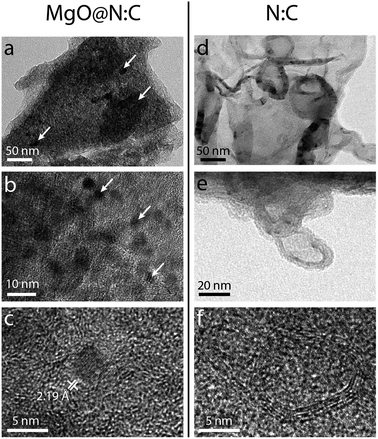
We also used high resolution transmission electron microscopy to obtain a qualitative picture of the material (Fig. 6). Pyrolysis at 900 °C, shows a composite of MgO nanoparticles in a carbon matrix (Fig. 6a–c). The particles themselves are either dispersed or agglomerated, and range between 5 and 10 nm in size. The final carbons show overlapping mesopores and macropores lined with graphitic shells (Fig. 6d–f). Moreover, a wormlike structure is seen in the high resolution micrographs (Fig. 6f). The black holes are about 3–6 Å in size, and are typically assigned to micropores.⁸¹ Scanning electron microscopy (SEM) studies of the carbon series shows that the macroscopic carbon particles become more fractured at higher pyrolysis temperatures (Fig. S5†). Mapping the elemental distribution in a small region using energy dispersive X-ray spectroscopy (EDS) reveals a homogeneous distribution of carbon and nitrogen (Fig. S5†). While these results (as in many SEM and TEM studies) are qualitative in nature, they complement the surface area, diffraction and spectroscopy measurements, confirming the hierarchical porosity and graphitic network in the carbon.

Fig. 6 High resolution transmission electron micrographs of C900, (a–c) before acid washing, and (d–f) after washing out the MgO with acid and annealing. Arrows mark MgO (a) agglomerates and (b) discrete nanoparticles.

3.2 Oxygen reduction electrocatalysis

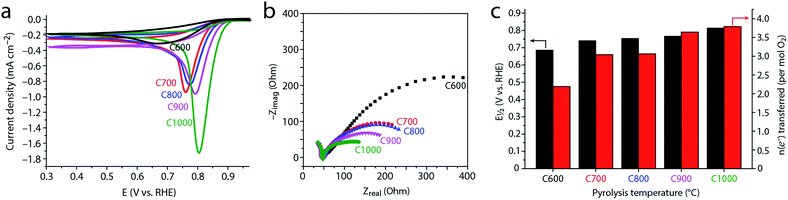
To study how the evolving microstructure and composition affect electrocatalytic activity, we tested the carbons as ORR electrocatalysts under basic conditions. Cyclic voltammetry (CV, Fig. 7a) in an O₂-saturated solution reveals that the activity improves with higher pyrolysis temperature (the onset and half-wave potentials for ORR shift positively). This finding is supported by potentiostatic EIS. The semicircle widths in the EIS-derived Nyquist plot (Fig. 7b) correspond to the charge-transfer resistance, and thus represent kinetic barriers during electrocatalysis.^21,82 These values decrease steadily as pyrolysis temperature is raised. Both the CV and EIS data reveal a significant jump in activity between 600 °C and 700 °C, and a further monotonous increase in activity as pyrolysis temperature is increased.

Fig. 7 Electrocatalytic oxygen reduction in 0.1 M KOH (pH = 13) at 25 °C on carbons C600–C1000. (a) Cyclic voltammograms (CV) in an O₂-saturated solution, scan rate 10 mV s⁻¹, after subtracting the capacitive currents measured in an O₂-free (N₂-saturated) solution. (b) Nyquist plots obtained by potentiostatic electrochemical impedance spectroscopy at E_1/2. (c) Half-wave potentials (E_1/2), obtained at a rotating speed of 1600 rpm (black, left axis); number of electrons transferred in the catalytic reactions (mol per mol O₂), obtained by Koutecký–Levich analysis at different rotation speeds (red, right axis).

This trend was quantified by voltammetry on a rotating disk; the Koutecký–Levich equation allows one to separate the mass-transfer component of the current (arising from controlled convection) from the kinetic (catalytic) current component. This yields the number of electrons transferred in the reaction per O₂ molecules consumed (Fig. 7c and S6†). The closer this value is to 2, the more H₂O₂ is produced and released without being reduced to OH⁻ nor decomposed. This is useful when H₂O₂ production is pursued,⁸³ and unwanted when complete (4e⁻) ORR is desired, e.g. in fuel cell or battery cathodes.^{14–16,18,24}

As Fig. 7c reveals, C600 catalyzes only the 2e⁻ reduction. Thus, despite containing over 6 at% nitrogen, its electrocatalytic activity is similar to that of an undoped carbon derived from magnesium citrate (the latter is similar enough to magnesium nitrilotriacetate so that one would expect the formation of similar carbon microstructures^15,23). This shows that a high nitrogen content is by itself insufficient for ORR activity. Rather, the nitrogen sites must also be sufficiently exposed, which requires a high surface area.

Conversely, carbons pyrolyzed at 700–800 °C perform the 2e⁻ and 4e⁻ reductions equally well, with an effective n = 3.04–3.06. Finally, the high temperature carbons C900 and C1000 show good performance towards full 4e⁻ ORR, with n = 3.64–3.79.

Deriving reliable structure–activity links is a challenge in the field of materials science in general, and electrocatalysis in particular. This is especially true in the case of N-doped carbons, because raising the pyrolysis temperature changes several properties of the material simultaneously: porosity, surface area, graphitization, nitrogen concentration and distribution. Nonetheless, we can identify some structure–activity trends:

(1) The ORR activity improves with the graphitization temperature, in line with the observations of Liang,²⁶ Müllen,⁸⁴ and others.^15–17 However, this improvement does not follow the concentration of nitrogen, which is depleted at higher pyrolysis temperatures. Thus, microstructural considerations play the deciding role over the entire 600–1000 °C temperature range.

(2) The dramatic increase in ORR activity at lower temperatures (600–700 °C) correlates with the increase in surface area. Although the chemical nature of active sites is determined by the bulk and surface composition of the doped carbons,^25–27 the number of exposed active sites is correlated with the surface area. Heating from 600 °C to 700 °C increases the surface area, and may expose many active sites, thus boosting electrocatalysis. Even at higher temperatures (up to 900 °C), the surface area may be behind the ORR activity rise.

(3) Several studies have shown a positive correlation between ORR activity and density of graphitic crystallite edges.³² This correlation was explained either in terms of exposing more (supposedly more active) pyridinic nitrogens, and/or by the intrinsic activity of graphene edges.^32,85,86 In carbons C600–C1000 we see the opposite trend: the degree of disorder decreases with pyrolysis temperature, yet electrocatalysis improves. This suggests that the benefits of graphitization (e.g. conductivity) may outweigh the loss of catalytic sites.

(4) The similar ORR activity of C700 and C800 suggests that the mesopore transition (700–800 °C) plays a smaller role in ORR electrocatalysis than the micropore transition (600–700 °C). However, it is possible that this “mesopore transition” is arbitrary, as it is defined by the ability of Hg intrusion to detect smaller pores. In this case, the beneficial effect of mesopores may be gradual, spreading over the entire temperature range.

(5) The second heat-treatment step at 1000 °C may play a separate role in determining the carbon properties. However, we expect the temperature of the first pyrolysis to determine most carbon properties,²⁶ since the MgO particles are then still present in the particles to act as graphitization catalysts and pore templates. Moreover, as all the carbons were annealed at the same temperature, most of the differences in their properties should arise from the first step.

4 Conclusions

The evolution of hierarchical porosity, as well as other microstructural and compositional properties of MgNTA-derived carbons, have been studied in the 600–1000 °C temperature range by a variety of experimental methods. As summarized in Fig. 8 and Table 1, the porosity may be divided in two main classes, evolving in parallel. The microporosity, on one hand, is derived mostly from the evacuation of tarry matter from interstices between aromatic sheets. The transition to microporosity occurs between 600 °C and 700 °C, and is accompanied by an increase in surface area, and a dramatic jump in ORR activity. Mesoporosity and macroporosity, on the other hand, are templated by spontaneously forming MgO nanoparticles. Discrete MgO particles give rise to small mesoporosity (>800 °C), whereas MgO agglomerates act as macropore templates (>900 °C). At a higher temperature (1000 °C), some pores collapse, decreasing surface area. The degree of order increases with pyrolysis temperature, suggesting an improved conductivity in the higher-temperature carbons. A significant graphitization step occurs between 700 and 800 °C, suggesting enhanced graphitization catalysis by MgO at this temperature.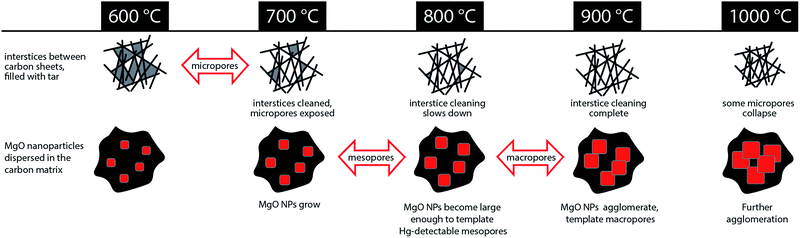

Fig. 8 Evolution of hierarchical porosity from 600 °C to 1000 °C in MgNTA-derived carbon. Red arrows mark significant transitions in porosity type.

Electrocatalytic ORR activity increases with pyrolysis temperature. It is not dictated by nitrogen content nor by edge plane density, both of which decrease along the series. In fact, ORR activity correlates best with microporosity (surface area and micropore volume), emphasizing the importance of active site exposure. Overall, understanding the evolution of microstructure in pyrolytic self-templating carbons can help in developing this important class of materials.

Acknowledgements

We thank Dr C. S. Sandu, P. Mettraux, Dr S. Mischler, Prof. N. Setter (EPFL) and the CIME-EPFL team for TEM and XPS measurements, and T. K. Slot for help with Raman fitting. This work is part of the Research Priority Area Sustainable Chemistry of the UvA, http://suschem.uva.nl.

Notes and references

1. W. Wreszinski, Der Papyrus Ebers, ed. J. C. Hinrichs, Leipzig, 1913.
2. C. A. Mitchell and T. C. Hepworth, Inks: their composition and manufacture, Griffin & Co., London, 1937.
3. R. C. Bansal, J.-B. Donnet and F. Stoeckli, Active Carbon, Marcel Dekker, New York, 1988.
4. M. C. Mittelmeijer-Hazeleger, PhD thesis, University of Amsterdam, 2006.
5. F. Rodríguez-Reinoso, Carbon, 1998, 36, 159–175.
6. E. Lam and J. H. T. Luong, ACS Catal., 2014, 4, 3393–3410.
7. M. Winter and R. J. Brodd, Chem. Rev., 2004, 104, 4245–4270.
8. F. Cheng and J. Chen, Chem. Soc. Rev., 2012, 41, 2172–2192.
9. I. Aldama, V. Barranco, T. A. Centeno, J. Ibañez and J. M. Rojo, J. Electrochem. Soc., 2016, 163, A758–A765.
10. A. G. Pandolfo and A. F. Hollenkamp, J. Power Sources, 2006, 157, 11–27.
11. T. Lin, I.-W. Chen, F. Liu, C. Yang, H. Bi, F. Xu and F. Huang, Science, 2015, 350, 1508–1513.
12. Q. Wang, J. Yan and Z. Fan, Energy Environ. Sci., 2016, 9, 729–762.
13. Y. Deng, Y. Xie, K. Zou and X. Ji, J. Mater. Chem. A, 2016, 4, 1144–1173.
14. Handbook of Fuel Cells, ed. W. Vielstich, A. Lamm and H. A. Gasteiger, John Wiley & Sons, 2003, vol. 2.
15. N. Daems, X. Sheng, I. F. J. Vankelecom and P. P. Pescarmona, J. Mater. Chem. A, 2014, 2, 4085–4110.
16. L. Dai, Y. Xue, L. Qu, H.-J. Choi and J.-B. Baek, Chem. Rev., 2015, 115, 4823–4892.
17. M. Shao, Q. Chang, J.-P. Dodelet and R. Chenitz, Chem. Rev., 2016, 116, 3594–3657.
18. Z. Yang, H. Nie, X. Chen, X. Chen and S. Huang, J. Power Sources, 2013, 236, 238–249.
19. J. R. Varcoe, P. Atanassov, D. R. Dekel, A. M. Herring, M. A. Hickner, P. A. Kohl, A. R. Kucernak, W. E. Mustain, K. Nijmeijer, K. Scott, T. Xu and L. Zhuang, Energy Environ. Sci., 2014, 7, 3135–3191.
20. Q. He and E. J. Cairns, J. Electrochem. Soc., 2015, 162, F1504–F1539.
21. H.-W. Liang, X. Zhuang, S. Brüller, X. Feng and K. Müllen, Nat. Commun., 2014, 5, 4973.
22. Z. Xu, X. Zhuang, C. Yang, J. Cao, Z. Yao, Y. Tang, J. Jiang, D. Wu and X. Feng, Adv. Mater., 2016, 28, 1981–1987.
23. D. Eisenberg, W. Stroek, N. J. Geels, C. S. Sandu, A. Heller, N. Yan and G. Rothenberg, Chem.–Eur. J., 2016, 22, 501–505.
24. D. Guo, R. Shibuya, C. Akiba, S. Saji, T. Kondo and J. Nakamura, Science, 2016, 351, 361–365.
25. K. Wan, Z. Yu, X. Li, M. Liu, G. Yang, J. Piao and Z. Liang, ACS Catal., 2015, 5, 4325–4332.
26. G. Long, K. Wan, M. Liu, X. Li, Z. Liang and J. Piao, Chin. J. Catal., 2015, 36, 1197–1204.
27. K. Wan, G.-F. Long, M.-Y. Liu, L. Du, Z.-X. Liang and P. Tsiakaras, Appl. Catal., B, 2015, 165, 566–571.
28. K. Wan, Z.-P. Yu and Z.-X. Liang, Catalysts, 2015, 5, 1034–1045.
29. J. Zhang, D. Liu, H. Song, Z. Liang, X. Guo, L. Du and S. Liao, RSC Adv., 2016, 6, 19515–19521.
30. D. Eisenberg, W. Stroek, N. J. Geels, S. Tanase, M. Ferbinteanu, S. J. Teat, P. Mettraux, N. Yan and G. Rothenberg, Phys. Chem. Chem. Phys., 2016, 18, 20778–20783.
31. T. K. Slot, D. Eisenberg, D. van Noordenne, P. Jungbacker and G. Rothenberg, Chem.–Eur. J., 2016, 22, 12307–12311.
32. W. He, Y. Wang, C. Jiang and L. Lu, Chem. Soc. Rev., 2016, 45, 2396–2409.
33. C. Li, H. Zhang, D. Jiang and Q. Yang, Chem. Commun., 2007, 547–558.
34. J. Liang, Y. Zheng, J. Chen, J. Liu, D. Hulicova-Jurcakova, M. Jaroniec and S. Z. Qiao, Angew. Chem., Int. Ed., 2012, 51, 3892–3896.
35. S. Israel, I. Gurevitch and M. S. Silverstein, Polymer, 2015, 72, 453–463.
36. N. López-Salas, D. Carriazo, M. C. Gutiérrez, M. L. Ferrer, C. O. Ania, F. Rubio, A. Tamayo, J. L. G. Fierro and F. del Monte, J. Mater. Chem. A, 2016, 4, 9146–9159.
37. W. Schwieger, A. G. Machoke, T. Weissenberger, A. Inayat, T. Selvam, M. Klumpp and A. Inayat, Chem. Soc. Rev., 2016, 45, 3353–3376.
38. R. J. White, in RSC Green Chemistry, ed. R. J. White, Royal Society of Chemistry, Cambridge, 2015, pp. 3–49.
39. M. Inagaki, M. Kato, T. Morishita, K. Morita and K. Mizuuchi, Carbon, 2007, 45, 1121–1124.
40. C. Zhang, M. Antonietti and T.-P. Fellinger, Adv. Funct. Mater., 2014, 24, 7655–7665.
41. S. Gao, X. Wei, H. Fan, L. Li, K. Geng and J. Wang, Nano Energy, 2015, 13, 518–526.
42. M. Wahid, G. Parte, D. Phase and S. Ogale, J. Mater. Chem. A, 2015, 3, 1208–1215.
43. L. Wei, H. E. Karahan, K. Goh, W. Jiang, D. Yu, Ö. Birer, R. Jiang and Y. Chen, J. Mater. Chem. A, 2015, 3, 7210–7214.
44. A. A. Zakhidov, R. H. Baughman, Z. Iqbal, C. Cui, I. Khayrullin, S. O. Dantas, J. Marti and V. G. Ralchenko, Science, 1998, 282, 897–901.
45. R. Ryoo, S. H. Joo and S. Jun, J. Phys. Chem. B, 1999, 103, 7743–7746.
46. H.-W. Liang, W. Wei, Z.-S. Wu, X. Feng and K. Müllen, J. Am. Chem. Soc., 2013, 135, 16002–16005.
47. D.-Y. Kang and J. H. Moon, Sci. Rep., 2014, 4, 5392.
48. Y. Meng, D. Gu, F. Zhang, Y. Shi, H. Yang, Z. Li, C. Yu, B. Tu and D. Zhao, Angew. Chem., 2005, 117, 7215–7221.
49. W. He, C. Jiang, J. Wang and L. Lu, Angew. Chem., Int. Ed., 2014, 53, 9503–9507.
50. H. Tamon, H. Ishizaka, T. Yamamoto and T. Suzuki, Carbon, 1999, 37, 2049–2055.
51. A. Allahbakhsh and A. R. Bahramian, Nanoscale, 2015, 7, 14139–14158.
52. T. Morishita, Y. Soneda, T. Tsumura and M. Inagaki, Carbon, 2006, 44, 2360–2367.
53. T. Morishita, T. Tsumura, M. Toyoda, J. Przepiórski, A. W. Morawski, H. Konno and M. Inagaki, Carbon, 2010, 48, 2690–2707.
54. M. Inagaki, H. Orikasa and T. Morishita, RSC Adv., 2011, 1, 1620–1640.
55. M. Sevilla and A. B. Fuertes, J. Mater. Chem. A, 2013, 1, 13738–13741.
56. B. Xu, H. Duan, M. Chu, G. Cao and Y. Yang, J. Mater. Chem. A, 2013, 1, 4565.
57. X. Y. Chen, Y. Y. He, H. Song and Z. J. Zhang, Carbon, 2014, 72, 410–420.
58. W. Jiang, Z. Luo, X. Jia and X. Wu, J. Solid State Electrochem., 2015, 19, 795–803.
59. G. A. Ferrero, M. Sevilla and A. B. Fuertes, Carbon, 2015, 88, 239–251.
60. P. Scherrer, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, 1918, pp. 98–100.
61. P. Scardi, M. Leoni and R. Delhez, J. Appl. Crystallogr., 2004, 381–390.
62. K. Angoni, Carbon, 1993, 31, 537–547.
63. A. Cuesta, P. Dhamelincourt, J. Laureyns, A. Martínez-Alonso and J. M. D. Tascón, Carbon, 1994, 32, 1523–1532.
64. S. Maldonado, S. Morin and K. J. Stevenson, Carbon, 2006, 44, 1429–1437.
65. S. Zhang, Z. Li, K. Ueno, R. Tatara, K. Dokko and M. Watanabe, J. Mater. Chem. A, 2015, 3, 17849–17857.
66. L. G. Bulusheva, A. V. Okotrub, I. A. Kinloch, I. P. Asanov, A. G. Kurenya, A. G. Kudashov, X. Chen and H. Song, Phys. Status Solidi B, 2008, 245, 1971–1974.
67. L. G. Cançado, K. Takai, T. Enoki, M. Endo, Y. A. Kim, H. Mizusaki, A. Jorio, L. N. Coelho, R. Magalhães-Paniago and M. A. Pimenta, Appl. Phys. Lett., 2006, 88, 163106.
68. J. S. Budkuley and G. K. Naik, Thermochim. Acta, 1998, 320, 115–120.
69. M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. W. Sing, Pure Appl. Chem., 2015, 87, 1051–1069.
70. R. H. Hurt, D. R. Dudek, J. P. Longwell and A. F. Sarofim, Carbon, 1988, 26, 433–449.
71. C. L. Burket, R. Rajagopalan, A. P. Marencic, K. Dronvajjala and H. C. Foley, Carbon, 2006, 44, 2957–2963.
72. F. Rouquerol, J. Rouquerol and K. Sing, Adsorption by powders & porous solids: principles, methodology and applications, 1st edn, 1999.
73. T. Kyotani, Carbon, 2000, 38, 269–286.
74. B. Hua, N. Yan, M. Li, Y.-F. Sun, J. Chen, Y.-Q. Zhang, J. Li, T. Etsell, P. Sarkar and J.-L. Luo, J. Mater. Chem. A, 2016, 4, 9080–9087.
75. Y. Li, Y.-S. Hu, H. Li, L. Chen and X. Huang, J. Mater. Chem. A, 2015, 4, 96–104.
76. M. H. Rümmeli, F. Schäffel, T. de los Arcos, D. Haberer, A. Bachmatiuk, C. Kramberger, P. Ayala, E. Borowiak-Palen, D. Adebimpe, T. Gemming, A. Leonhardt, B. Rellinghaus, L. Schultz, T. Pichler and B. Büchner, Phys. Status Solidi B, 2008, 245, 1939–1942.
77. M. H. Rümmeli, A. Bachmatiuk, A. Scott, F. Börrnert, J. H. Warner, V. Hoffman, J.-H. Lin, G. Cuniberti and B. Büchner, ACS Nano, 2010, 4, 4206–4210.
78. A. Bachmatiuk, R. G. Mendes, C. Hirsch, C. Jähne, M. R. Lohe, J. Grothe, S. Kaskel, L. Fu, R. Klingeler, J. Eckert, P. Wick and M. H. Rümmeli, ACS Nano, 2013, 7, 10552–10562.
79. A. Aijaz, N. Fujiwara and Q. Xu, J. Am. Chem. Soc., 2014, 136, 6790–6793.
80. G. Panomsuwan, N. Saito and T. Ishizaki, Phys. Chem. Chem. Phys., 2015, 17, 6227–6232.
81. T. Miyazaki, T. Oshida, T. Nakatsuka, H. Yamamoto, M. Okamoto and M. Endo, Mol. Cryst. Liq. Cryst., 2002, 388, 85–90.
82. P. Kichambare, J. Kumar, S. Rodrigues and B. Kumar, J. Power Sources, 2011, 196, 3310–3316.
83. Y. Liu, X. Quan, X. Fan, H. Wang and S. Chen, Angew. Chem., Int. Ed., 2015, 54, 6837–6841.
84. R. Liu, D. Wu, X. Feng and K. Müllen, Angew. Chem., Int. Ed., 2010, 49, 2565–2569.
85. P. Matter, L. Zhang and U. Ozkan, J. Catal., 2006, 239, 83–96.
86. R. Silva, J. Al-Sharab and T. Asefa, Angew. Chem., Int. Ed., 2012, 51, 7171–7175.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra16606g

---