Modeling study on the catalytic activities of 2-imino-1,10-phenanthrolinylmetal (Fe, Co, and Ni) precatalysts in ethylene oligomerization†
Wenhong Yang*ab,
Zhifeng Maab and
Wen-Hua Sun *ab
*ab
aKey Laboratory of Engineering Plastics, Beijing National Laboratory for Molecular Science, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China. E-mail: whyang@iccas.ac.cn; whsun@iccas.ac.cn
bUniversity of Chinese Academy of Sciences, Beijing 100049, China
First published on 16th August 2016
Abstract
In experiments, transition metal complex systems ligated with the same ligand showed significantly different catalytic activities towards ethylene oligo/polymerization. In this study, the variations of catalytic activities were investigated for series of 2-imino-1,10-phenanthrolinylmetal (Fe, Co and Ni) complexes. Their catalytic activities were evaluated by the multiple linear regression analysis (MLRA). The calculated activities are well consistent with the experimental data, reflecting by the correlation coefficient values (R2) for most of systems over 0.98. With regard to the influence of the analogue structure on the change of catalytic activities, the MLRA model was modified through using the variation of catalytic activities as response variable and the change of parameters as independent variable. The calculated variation of reaction activities present very good correlation with experimental results with R2 value closing to 1.0, whereas, the correlation results are relatively low for analogues with different metal atoms. Additionally, the contributions from electronic and steric effects were analyzed to explain the reason for variations of the activities.
Introduction
Ethylene oligomerization is one of the major industrial processes for producing linear alpha-olefin as substances for the preparation of detergents, lubricants and plasticizers.1 The transition metal complexes play an important role in the process of ethylene polymerization. Regarding the catalytic performance, reaction activity is one of the most important factors. For this purpose, considerable research efforts have been devoted to the design and synthesis of new catalyst with high activity. The significant progress is achieved in the probe of transition metal catalysts in ethylene oligomerization,2 for instance, from the chromium-based catalysts for the tetramerization of ethylene3 to the SHOP of nickel-based catalysts chelated by monoanionic [P^O],4 as well as its derivatives of P^N5 and N^N.6 In addition, on the basis of the bisiminopyridine,7 type of N^N^N iron, cobalt and nickel complex catalysts bearing phenanthroline backbone ligands showed higher catalytic activities toward ethylene oligomerization.8Although tremendous researches from experiments, the essential influence on the activity at molecular level is still unclear. Catalytic activity is mainly decided by catalyst's molecular structure, including two aspects such as electronic effect and steric effect. In our previous studies, from the view of electronic effect, the catalytic activities of late transition metal complex catalyst were investigated using the DFT combined with charge equilibration (QEq) method.9 It was found that effective net charge on metal center shows good correlation with catalytic activity for most of transition metal complex precatalysts. For iron complex catalysts, results presented that the catalytic activity decreased with the effective net charge on metal center increased,9a while for cobalt and nickel complex catalysts, the results were contrary.9b–d In addition to charge parameter, we found other electronic factors present correlation with catalytic activities, including the HOMO–LUMO orbital energy gaps and the energy difference among various spin states.9c
Coville and his coworkers reported that the activities of (CpR)2ZrCl2 catalysts were studied quantitatively by considering the influence of two parameters such as steric (θ) and electronic (F).10 Results show that catalytic activities elevate with increasing size of R substituents and electronic donating ability of the substituents. In our recent report, catalytic activities for the iron-, cobalt- and chromium-based 2-azacyclyl-6-aryliminopyridyl complex catalysts11 were investigated by the multiple linear regression analysis (MLRA) method through considering four parameters, using Hammett constants (F) and effective net charge (Q) to describe electronic effect, meanwhile open cone angle (θ) and bite angle (β) for steric effect. Results reveal that the correlation coefficient between calculated activities and experimental data ranged from 0.93 to 1.0, which provided a quantitative understanding of correlation between molecular structures and catalytic activities.12
From our experimental observations, it is found that the structures of some catalyst systems are very similar such as Fe–1, Fe–2 and Fe–3 as showed in Scheme 1. But their catalytic activities largely differ in the ethylene oligomerization. Moreover, for complex catalysts coordinated with different metal atoms, reaction activities generally decrease along with the Fe, Co and Ni analogue complexes; whereas for M–3 complex systems, the Co–3 and Ni–3 analogue complexes exhibit higher activities than Fe–3 complex. Presently, it is hard to explain the reason from molecular level. Herein, we intend to resolve the problem using the multiple linear regression analysis method proposed in our previous study,12 giving a quantitative understanding of the influence of ligands and metal center of analogues on reaction activities.
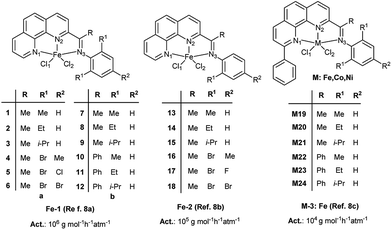 | ||
| Scheme 1 The structure of 2-imino-1,10-phenanthrolinyl Fe–1 complexes 1–12, Fe–2 complexes 13–18 and M–3 (Fe, Co and Ni) complexes M19–M24. | ||
In the present study, first, the catalytic activities for each series of 2-imino-1,10-phenanthrolinyl analogues Fe–1, Fe–2 and M–3 were investigated by MLRA method, respectively. The calculated activities were very close to experimental data with most of the correlation value over 0.98. Then, based on the variation of the four parameters in MLRA, the variations of catalytic activities for two series of complexes were accordingly studied. By analyzing the contribution, it shows that change of catalytic activities between Fe–1 and Fe–2 systems is mainly due to the electronic effect, while for Fe–1 and Fe–3 systems primarily by steric effect. For catalysts containing different metal centers (M–3), both steric and electronic effects attribute to the change of catalytic activities.
Computational details
From previous study, it showed that the calculated parameters (θ, β, Q) largely depend on the optimized structure.12 Thus, in this work, the selected catalysts were minimized by DFT and molecular mechanics (MM) methods. The obtained structures were compared with experiments crystal results in order to choose the more suitable method.The DFT calculations were performed by the Dmol3 program package.13 The basis set of double-numerical polarization (DNP)13 with effective core potentials (ECP)14 was used to describe electronic structures; the exchange-correlation functional is the GGA-type Becke–Perdew (BP).15 In the geometry optimization, the convergence value of optimized energy was 2.0 × 10−5 hartree, for maximum force and displacement it was 4.0 × 10−3 hartree per bohr and 5.0 × 10−3 Å, respectively. For self-consistent field (SCF) calculation, the convergence criterion was 1.0 × 10−5 hartree.
MM calculations were conducted by the Forcite program package. The geometry optimization and energy calculations were carried out using Dreiding force field,16 due to its advantage of reasonable prediction of structure. Unfortunately, there are no parameters for late transition metal elements, such as Fe, Co and Ni as well as the atom types which connect with metal elements. Based on previous reports,17 the crystal data for complexes Fe–1, Fe–2 and M–3 (Fe, Co, Ni) listed in Table 1 were added into the file of the Dreiding force field.
| Fe–1 | Fe–2 | Fe–3 | Co–3 | Ni–3 | |
|---|---|---|---|---|---|
| Bond length (Å) | |||||
| M–N1 | 2.271 | 2.223 | 2.391 | 2.313 | 2.300 |
| M–N2 | 2.110 | 2.107 | 2.100 | 2.035 | 1.961 |
| M–N3 | 2.275 | 2.303 | 2.298 | 2.279 | 2.238 |
| M–Cl1 | 2.281 | 2.275 | 2.341 | 2.292 | 2.274 |
| M–Cl2 | 2.305 | 2.304 | 2.249 | 2.236 | 2.217 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Bond angle (°) | |||||
| N1–M–N2 | 73.80 | 74.60 | 73.77 | 76.16 | 78.40 |
| N2–M–N3 | 71.86 | 71.90 | 73.18 | 74.00 | 76.00 |
| N1–M–N3 | 144.10 | 146.40 | 145.86 | 149.22 | 154.10 |
| N1–M–Cl1 | 97.95 | 95.90 | 93.70 | 97.95 | 95.46 |
| N2–M–Cl1 | 146.74 | 136.74 | 98.23 | 104.94 | 101.40 |
| N3–M–Cl1 | 104.97 | 106.24 | 99.19 | 96.80 | 93.11 |
| N1–M–Cl2 | 98.20 | 97.24 | 104.73 | 99.72 | 92.28 |
| N2–M–Cl2 | 103.06 | 110.84 | 141.53 | 133.77 | 120.90 |
| N3–M–Cl2 | 99.37 | 97.35 | 95.87 | 95.48 | 97.66 |
| Cl1–M–Cl2 | 110.04 | 112.21 | 120.09 | 121.12 | 137.71 |
The convergence tolerance was 0.001 kcal mol−1 for the energy, and convergence tolerance of force was 0.5 kcal mol−1. The maximum number of iterations was 500. To describe the electrostatic and van der Waals interaction, the atom based summation and truncation methods were used;18 the cutoff distance for cubic spline was 12.5 Å.
For MLRA, the describing parameters of steric effect and electronic effect were obtained based on the optimized structure of catalyst, including open core angle (θ),12 bite angle (β)19 and effective net charge (Q). Hammett constants (F) were taken from the literature.20
To analyze the variation of catalytic activities, the variation values of four parameters for two systems were calculated to correlate with the variation of activities for these two systems by the MLRA fitting showed in eqn (1):
| ΔA = w0 + w1Δθ + w2Δβ + w3ΔQ + w4ΔF | (1) |
 | (2) |
 | (3) |
Results and discussion
Predicted catalytic activity of Fe–1, Fe–2 and M–3 complexes
For Fe–1 complex system, there are twelve different substitutes in total. To compare with Fe–2 and Fe–3 respectively, the Fe–1 catalytic system was divided into two models Fe–1a and Fe–1b (as showed in Scheme 1). The calculated structure of complex 2 from MM and DFT methods was compared with the crystal structure from experimental data and the results were listed in Table 2. It can be seen that by MM method, the standard deviation δ for bond length and bond angle are 0.163 and 2.06, respectively, which are obviously lower than that from DFT calculations.| Complex 2 | Ex. | DFT | MM |
|---|---|---|---|
| Bond lengths (Å) | |||
| Fe–N1 | 2.271 | 2.059 | 2.272 |
| Fe–N2 | 2.110 | 1.831 | 2.115 |
| Fe–N3 | 2.275 | 2.018 | 2.270 |
| Fe–Cl1 | 2.281 | 2.218 | 2.281 |
| Fe–Cl2 | 2.305 | 2.229 | 2.305 |
| δ | 4.730 | 0.163 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Bond angles (°) | |||
| N1–Fe–N2 | 73.80 | 81.79 | 73.49 |
| N2–Fe–N3 | 71.86 | 80.17 | 71.25 |
| N1–Fe–N3 | 144.10 | 161.79 | 144.23 |
| N1–Fe–Cl1 | 97.95 | 88.61 | 102.89 |
| N2–Fe–Cl1 | 146.74 | 121.81 | 146.07 |
| N3–Fe–Cl1 | 104.97 | 98.79 | 102.90 |
| N1–Fe–Cl2 | 98.20 | 87.92 | 97.02 |
| N2–Fe–Cl2 | 103.06 | 98.80 | 103.94 |
| N3–Fe–Cl2 | 99.37 | 97.24 | 97.00 |
| Cl1–Fe–Cl2 | 110.04 | 138.24 | 109.37 |
| δ | 13.30 | 2.06 | |
From previous study, it was found that the obtained parameters for linear fitting, such as effective net charge (Q), open cone angle (θ), and bite angle (β), largely depend on the structures, so it is more reasonable to choose the optimized results by MM method in the present study. Accordingly, the calculated values of θ, β and Q were obtained and listed in Table 3 together with F taken from literature14 for complexes 1–12. Using LINEST function,15 the fitting coefficient values were calculated as showed in Table 4. Then reaction activity for each complex can be calculated and predicted. It exhibits very good relationship between calculated activities and experimental data in Fig. 1a and b for Fe–1a and Fe–1b systems, respectively. The obtained correlation results are very good with the R2 values of 1.0 and 0.983, respectively. It suggests that the calculated activities well accord with experimental results.
| Cat. | θ (°) | β (°) | Q (e) | F | Cat. | θ (°) | β (°) | Q (e) | F |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 95.42 | 144.4 | 0.712 | 0.05 | Fe19 | 62.74 | 144.8 | 0.700 | 0.05 |
| 2 | 93.20 | 144.3 | 0.700 | 0.03 | Fe20 | 62.24 | 144.8 | 0.692 | 0.03 |
| 3 | 85.79 | 142.5 | 0.682 | 0.11 | Fe21 | 62.27 | 145.4 | 0.698 | 0.11 |
| 4 | 93.23 | 144.5 | 0.786 | 0.91 | Fe22 | 65.59 | 145.0 | 0.658 | 0.05 |
| 5 | 94.57 | 144.5 | 0.796 | 1.32 | Fe23 | 63.54 | 145.3 | 0.705 | 0.03 |
| 6 | 94.13 | 144.5 | 0.795 | 1.35 | Fe24 | 49.94 | 143.7 | 0.685 | 0.11 |
| 7 | 95.42 | 144.5 | 0.712 | 0.05 | Co19 | 60.42 | 147.5 | 0.593 | 0.05 |
| 8 | 93.20 | 144.3 | 0.700 | 0.03 | Co20 | 59.22 | 147.8 | 0.590 | 0.03 |
| 9 | 85.79 | 142.5 | 0.682 | 0.11 | Co21 | 60.89 | 148.1 | 0.590 | 0.11 |
| 10 | 98.28 | 144.6 | 0.712 | 0.05 | Co22 | 63.44 | 147.7 | 0.603 | 0.05 |
| 11 | 94.58 | 143.9 | 0.689 | 0.03 | Co23 | 56.19 | 147.8 | 0.584 | 0.03 |
| 12 | 91.63 | 143.9 | 0.676 | 0.11 | Co24 | 46.57 | 146.3 | 0.578 | 0.11 |
| 13 | 93.72 | 145.2 | 0.721 | 0.07 | Ni19 | 56.04 | 150.9 | 0.497 | 0.05 |
| 14 | 94.91 | 145.2 | 0.702 | 0.06 | Ni20 | 51.93 | 151.0 | 0.492 | 0.03 |
| 15 | 92.32 | 144.7 | 0.691 | 0.10 | Ni21 | 58.11 | 151.6 | 0.497 | 0.11 |
| 16 | 93.43 | 145.2 | 0.667 | 0.49 | Ni22 | 59.19 | 151.2 | 0.508 | 0.05 |
| 17 | 94.34 | 145.3 | 0.680 | 0.93 | Ni23 | 49.14 | 151.3 | 0.486 | 0.03 |
| 18 | 92.95 | 145.2 | 0.681 | 0.93 | Ni24 | 42.86 | 149.9 | 0.484 | 0.11 |
| m0 | m1 | m2 | m3 | m4 | R2 | |
|---|---|---|---|---|---|---|
| Fe–1a | −711.81 | −0.78 | 5.50 | −5.54 | −2.08 | 1.00 |
| Fe–1b | −422.17 | −0.85 | 3.24 | 56.53 | −45.88 | 0.983 |
| Fe–2 | 1760.36 | 3.36 | −14.61 | 74.77 | 2.13 | 0.890 |
| Fe–3 | 367.43 | 0.75 | −0.53 | −474.81 | −29.78 | 0.902 |
| Co–3 | 467.41 | 0.69 | −2.24 | −288.58 | −25.77 | 1.00 |
| Ni–3 | 186.68 | −0.01 | −1.27 | 21.89 | 9.42 | 0.990 |
 | ||
| Fig. 1 The plot of calculated activities versus experimental activities for Fe–1a (a), Fe–1b (b), Fe–2 (c), Fe–3 (d), Co–3 (e) and Ni–3 (f) systems. | ||
In same manner, the catalytic activities of Fe–2 and M–3 (Fe, Co, Ni) complex systems were investigated (as showed in Scheme 1). The values of four parameters (θ, β, Q, F) were calculated and listed in Table 3, and then the fitting coefficients for each system were obtained and showed in Table 4. The calculated reaction activities present correlation with the experimental results as plotted in Fig. 1c–f, with the coefficient values of 0.890, 0.902, 1.0 and 0.990 for Fe–2, Fe–3, Co–3 and Ni–3 systems, respectively. These results indicate that the catalytic activities for model systems of Fe–1, Fe–2, and M–3 complexes are reasonably investigated by the MLRA through taking both electronic and steric effects into account.
Difference of catalytic activity between Fe–1a and Fe–2 systems
The Fe–1a and Fe–2 precatalysts have very similar skeleton structure, 2-imino-1,10-phenanthrolinyl ligands, containing same substituents. The only difference of structure lies in that the ortho-substituents of Fe–1a complex precatalysts are symmetrical, while that of Fe–2 are unsymmetrical (as showed in Scheme 1). However, their catalytic activities present great difference. Experimentally, it can be seen from the Table S1,† that the catalytic activities of Fe–1a system are higher about an order of magnitude than that of Fe–2 system. To illustrate the reason of the variation for catalytic activity, comparison of different catalytic activities was carried out to find out the essential mechanism.As discussed in above section, it is clear that the catalytic activities for these two series of complexes were modeled very well by MLRA method, respectively. However, the result of taking two complex systems together was relatively worse with the correlation coefficient only 0.6 as shown in Fig. S1 of ESI.† Herein, the MLRA approach was still used to clarify the impact of structure on the change of catalytic activity except that we use the variation of activities between Fe–1a and Fe–2 systems as response variable and the variation of four parameters as independent variable, aiming to establish the correlation between variation of structure and its change of catalytic activities. On the basis of the four parameters (θ, β, Q, F) of Fe–1a complexes 1–6 and Fe–2 complexes 13–18 (as showed in Table 3), the variation values of these four parameters (Δθ, Δβ, ΔQ and ΔF) were calculated and showed in Table 5. Meanwhile, the change values of activities (ΔAct.) were obtained and listed as well. The IFe1a–Fe2 system was defined as variation between Fe–1a and Fe–2 systems.
| Complex | Δθ (°) | Δβ (°) | ΔQ (e) | ΔF | ΔAct. |
|---|---|---|---|---|---|
| Original value IFe1a–Fe2 | |||||
| 1–13 | 1.698 | −0.731 | −0.009 | −0.020 | 295.70 |
| 2–14 | −1.705 | −0.930 | −0.002 | −0.030 | 400.00 |
| 3–15 | −6.536 | −2.154 | −0.009 | 0.010 | 7.00 |
| 4–16 | −0.193 | −0.703 | 0.119 | 0.420 | 347.90 |
| 5–17 | 0.229 | −0.702 | 0.116 | 0.390 | 103.60 |
| 6–18 | 1.181 | −0.699 | 0.114 | 0.420 | 195.70 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Standardized value IFe1a–Fe2 | |||||
| 1–13 | 0.859 | 0.441 | −0.947 | −0.939 | 0.47 |
| 2–14 | −0.272 | 0.098 | −0.843 | −0.982 | 1.16 |
| 3–15 | −1.877 | −2.017 | −0.946 | −0.810 | −1.44 |
| 4–16 | 0.231 | 0.490 | 0.951 | 0.953 | 0.81 |
| 5–17 | 0.371 | 0.491 | 0.907 | 0.824 | −0.80 |
| 6–18 | 0.687 | 0.497 | 0.877 | 0.953 | −0.19 |
From the difference values of the four parameters as a function of substituents, the variations of effective net charge and Hammett constants are evident with the ΔQ values of 0.119, 0.116 and 0.114, separately, and ΔF values range from 0.39 to 0.42 for complexes 4–16, 5–17 and 6–18 in IFe1a–Fe2 system (as showed in Table 5). While the variation values of steric effect, such as Δθ and Δβ, are not obvious.
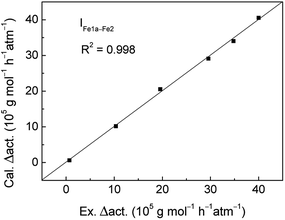
To quantitatively explain the change of catalytic activities caused by structure, the variation values of four parameters and activities were fitted by eqn (1) using LINEST function. The fitting coefficient values were obtained and showed in Table 6. Then calculated change values of activities were obtained and compared with experimental data. It can be seen from the Fig. 2 that the correlation presents very well with the coefficient value of 0.998. It means that the present model is reliable and can be used to predict the obvious change of catalytic activities caused by small variation of catalyst structure. In order to analyze the impact factors, the variation values of four parameters and activities were standardized by Z-score method and standardized values were showed in Table 5. Using eqn (2) and (3), the contributions of electronic and steric effects were calculated. It indicates that the contribution values of steric effect and electronic effect are 20.92 and 79.08%, respectively. Obviously, change of catalytic activities between Fe–1a and Fe–2 systems is mainly attributed to the electronic effect caused by the asymmetric substituent.
| w0 | w1 | w2 | w3 | w4 | ||
|---|---|---|---|---|---|---|
| IFe1a–Fe2 | Or. | 1721.90 | −215.40 | 1616.63 | −30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 893.54 893.54 |
8070.64 |
| St. | −9.12 × 10−16 | −4.30 | 6.20 | −13.81 | 12.44 | |
| IIFe1b–Fe3 | Or. | 3605.84 | −89.65 | 527.74 | −6427.73 | 0 |
| St. | −1.13 × 10−15 | −2.80 | 3.04 | −0.92 | 0 | |
| IIIFe3–Ni3 | Or. | −933.82 | −0.62 | 135.52 | −647.56 | 0 |
| St. | 2.53 × 10−15 | −0.14 | 0.78 | −0.95 | 0 | |
| IVNi3–Co3 | Or. | −1047.53 | −21.25 | 154.12 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832.83 832.83 |
0 |
| St. | −4.12 × 10−14 | −1.61 | 0.88 | 1.52 | 0 | |
Difference of catalytic activity between Fe–1b and Fe–3 systems
Regarding the Fe–1b and Fe–3 complexes (showed in Scheme 1), the structures are also very similar except that there is a phenyl substituent on the 9-position within Fe–3 complexes. While the catalytic activities present tremendous decrease from 106 g mol−1 (Fe) per h per atm for Fe–1b complex systems to 104 g mol−1 (Fe) per h per atm for Fe–3 complex systems.To explore the reason, the variation of four parameters was calculated and listed in Table 7. The IIFe1b–Fe3 system was defined as the change between Fe–1b and Fe–3 systems. It is clear that there is no variation for Hammett constants, and the ΔQ and Δβ values are also small. Only the variation of open cone angle (Δθ) is obvious with the values ranged from 23.5° to 41.6°. So it can be speculated that the reason of the decreasing of catalytic activities for Fe–3 system may be the reduction of open cone angle for each complex, making the space to accommodate the ethylene smaller.
| Complex | Δθ (°) | Δβ (°) | ΔQ (e) | ΔF | ΔAct. |
|---|---|---|---|---|---|
| Original value IIFe1b–Fe3 | |||||
| 7–Fe19 | 32.679 | −0.393 | 0.012 | 0 | 384.22 |
| 8–Fe20 | 30.965 | −0.551 | 0.008 | 0 | 489.37 |
| 9–Fe21 | 23.523 | −2.844 | −0.016 | 0 | 94.00 |
| 10–Fe22 | 32.689 | −0.436 | 0.054 | 0 | 100.60 |
| 11–Fe23 | 31.048 | −1.347 | −0.016 | 0 | 224.87 |
| 12–Fe24 | 41.687 | 0.169 | −0.009 | 0 | 12.83 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Standardized value IIFe1b–Fe3 | |||||
| 7–Fe19 | 0.010 | 0.475 | 0.244 | 0 | 0.90 |
| 8–Fe20 | −0.195 | 0.327 | 0.094 | 0 | 1.46 |
| 9–Fe21 | −1.477 | −1.818 | −0.808 | 0 | −0.67 |
| 10–Fe22 | 0.102 | 0.434 | 1.824 | 0 | −0.63 |
| 11–Fe23 | −0.181 | −0.418 | −0.809 | 0 | 0.04 |
| 12–Fe24 | 1.651 | 1.000 | −0.545 | 0 | −1.10 |
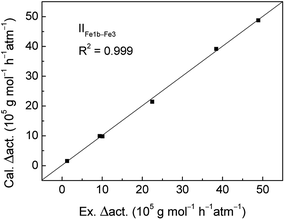
The MLRA method was conducted for IIFe1b–Fe3 system to quantitatively analyze the change of catalytic activities. The obtained fitting coefficients were showed in Table 6. The calculated change values of catalytic activities were almost the same as the variation values of experimental data seen in Fig. 3, with the correlation coefficient of 0.999. The result means that the modified MLAR model is reliable to explain the change of catalytic activities for analogues. Based on the standardized regression coefficient values in Table 6, the contribution values of steric effect and electronic effect are calculated with the value of 81.53% and 18.47%, respectively, showing that the steric effect is dominant in determining the change of catalytic activities for the IIFe1b–Fe3 system.
Difference of catalytic activity for Fe–3, Co–3 and Ni–3 systems
The discussion of previous section focused on the change of substituents or ligands. The emphasis of this section has been placed on the influence of different metal centers on the change of catalytic activities. The structures of the M–3 (Fe, Co, Ni) complexes bearing 2-imino-9-phenyl-1,10-phenanthrolinyl ligands are showed in Scheme 1. For most complexes coordinated with different late transition metals, the catalytic activities generally decrease from Fe-based to Co- and Ni-based complexes. However, in the present study, the activities for Fe–3, Ni–3 and Co–3 are gradually increased, with the values of 1.0 × 104, 3.0 × 105 and 5.0 × 105 g mol−1 (M) per h per atm, respectively. Thus, the variations were analyzed for the catalytic activities between Fe–3 and Ni–3 as well as Ni–3 and Co–3, which were defined as IIIFe3–Ni3 and IVNi3–Co3 systems, respectively. The variation values of the four parameters were calculated and listed in Table 8. It is clearly seen that for IIIFe3–Ni3 system, the variation of open cone angles (Δθ) and bite angle (Δβ) values are relatively similar, and ΔQ value is obvious from 0.150 to 0.219. It is assumed that steric effect and electronic effect may affect the change of catalytic activity both.| Complex | Δθ (°) | Δβ (°) | ΔQ (e) | ΔF | ΔAct. |
|---|---|---|---|---|---|
| Original value IIIFe3–Ni3 | |||||
| Fe19–Ni19 | 6.697 | −6.138 | 0.203 | 0 | −32.62 |
| Fe20–Ni20 | 10.305 | −6.191 | 0.200 | 0 | −31.27 |
| Fe21–Ni21 | 4.158 | −6.207 | 0.201 | 0 | −33.10 |
| Fe22–Ni22 | 6.405 | −6.201 | 0.150 | 0 | −8.30 |
| Fe23–Ni23 | 14.395 | −5.974 | 0.219 | 0 | −27.97 |
| Fe24–Ni24 | 7.083 | −6.216 | 0.201 | 0 | −58.53 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Standardized value IIIFe3–Ni3 | |||||
| Fe19–Ni19 | −0.407 | 0.178 | 0.312 | 0 | −0.04 |
| Fe20–Ni20 | 0.587 | −0.394 | 0.184 | 0 | 0.04 |
| Fe21–Ni21 | −1.106 | −0.567 | 0.227 | 0 | −0.07 |
| Fe22–Ni22 | −0.487 | −0.502 | −1.943 | 0 | 1.48 |
| Fe23–Ni23 | −1.714 | 1.949 | 0.993 | 0 | 0.25 |
| Fe24–Ni24 | −0.301 | −0.664 | 0.227 | 0 | −1.66 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Original value IVNi3–Co3 | |||||
| Ni19–Co19 | −4.377 | 3.474 | −0.096 | 0 | −31.10 |
| Ni20–Co20 | −7.287 | 3.248 | −0.098 | 0 | −34.20 |
| Ni21–Co21 | −2.787 | 3.517 | −0.093 | 0 | −19.00 |
| Ni22–Co22 | −4.255 | 3.509 | −0.095 | 0 | −21.10 |
| Ni23–Co23 | −7.053 | 3.458 | −0.098 | 0 | −31.10 |
| Ni24–Co24 | −3.709 | 3.677 | −0.094 | 0 | 30.30 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Standardized value IVNi3–Co3 | |||||
| Ni19–Co19 | 0.291 | −0.047 | −0.161 | 0 | −0.55 |
| Ni20–Co20 | −1.292 | −1.684 | −1.129 | 0 | −0.68 |
| Ni21–Co21 | 1.155 | 0.264 | 1.291 | 0 | −0.05 |
| Ni22–Co22 | 0.357 | 0.206 | 0.323 | 0 | −0.14 |
| Ni23–Co23 | −1.165 | −0.163 | −1.130 | 0 | −0.55 |
| Ni24–Co24 | 0.654 | 1.423 | 0.807 | 0 | 1.98 |
By linear fitting analysis, the regression coefficient values for eqn (1) were obtained and listed in Table 6. It can be seen that the relationships between calculated variation values of catalytic activities and that of experimental results are not very well; the value of correlation coefficient is 0.699 as showed in Fig. S2a of ESI.† It is assumed that the influences of electronic and steric effects for change of catalytic activities can be roughly investigated. By same manner, the standardized change values of four factors and activities were obtained as showed in Table 8. The calculated contributions of steric and electronic effects are 56.64 and 43.36%, respectively, meaning the electronic and steric effects play a simultaneous role for controlling change of catalytic activities.
For IVNi3–Co3 system, the calculated difference values of four parameters are also listed in Table 8. Comparing with IIIFe3–Ni3 system, the Δθ and Δβ values as well as ΔQ values are smaller which may be attributed to smaller variation of catalytic activities in IVNi3–Co3 system. In same manners, the obtained fitting coefficient values were listed in Table 6. The correlation between variation values of calculated activities and experimental data was a little higher than that of IIIFe3–Ni3 system with the value of 0.787 showed in Fig. S2b of ESI.† The rough contribution values of steric and electronic effects were estimated with the value of 61.10 and 38.90%, respectively. It suggests that similar with IIIFe3–Ni3 system, the change of catalytic activities is also simultaneously influenced by the steric and electronic effects for IVNi3–Co3 system. Meanwhile, compared with the results for IFe1a–Fe2 and IIFe1b–Fe3 systems, the ability to predict variation of catalytic activities for IIIFe3–Ni3 and IVNi3–Co3 systems seems relatively low.
Conclusions
In this work, several series of late transition metal complex analogues (Fe–1, Fe–2 and Fe–3) were investigated to establish the relationship between modification of structure in ligands and the corresponding variation of catalytic activities. First, the catalytic activities of each complex system were modeled by MLRA method proposed in our previous work. The open cone angle (θ), bite angle (β), effective net charge (Q) in fitting equation were obtained based on the optimized structures of precatalysts by molecular mechanics (MM). The calculated results indicate that for most of the complex systems, the activities can be predicted very well with the correlation coefficient value over 0.98. Then to explain the variation of catalytic activities between analogues, the modified MLRA method was adopted, using the variation of catalytic activities as response variable and the change of four parameters as independent variable. By this approach, the variation of catalytic activities for IFe1a–Fe2 and IIFe1b–Fe3 systems were investigated, showing very good fitting results with the correlation coefficient value over 0.99. By analyzing the contribution, it was found that for the IFe1a–Fe2 system, the change of catalytic activities is primarily due to the electronic effect, while for the IIFe1b–Fe3 system, it is predominantly ascribed to steric effect.Besides, analogue systems for the Fe–3, Co–3 and Ni–3 complexes were also investigated to explore the variation of catalytic activities caused by different central metals. The correlation coefficient values for IIIFe3–Ni3 and IVNi3–Co3 systems were around 0.7. The contributions were roughly estimated as the simultaneous role by electronic and steric effects.
This study explains the reason why smaller change of catalyst structure can induce tremendous variation of catalytic activities. The obtained results are expected to give guidance for the structure modification for transition metal complex catalyst with high activities.
Acknowledgements
This work was financially supported by National Natural Science Foundation of China (No. 2124092 and U1362204) and “One-Three-Five” Strategic Planning of ICCAS.Notes and references
- (a) J. Skupinska, Chem. Rev., 1991, 91, 613–648 CrossRef CAS; (b) M. Zhang, S. Zhang, P. Hao, S. Jie, W.-H. Sun, P. Li and X. Lu, Eur. J. Inorg. Chem., 2007, 3816–3826 CrossRef CAS.
- (a) S. A. Svejda and M. Brookhart, Organometallics, 1999, 18, 65–74 CrossRef CAS; (b) W.-H. Sun, Z. Li, H. Hu, B. Wu, H. Yang, N. Zhu, X. Leng and H. Wang, New J. Chem., 2002, 26, 1474–1478 RSC; (c) W.-H. Sun, W. Zhang, T. Gao, X. Tang, L. Chen, Y. Li and X. Jin, J. Organomet. Chem., 2004, 689, 9171–9929 Search PubMed; (d) W.-H. Sun, P. Hao, S. Zhang, Q. Shi, W. Zuo and X. Tang, Organometallics, 2007, 26, 2720–2734 CrossRef CAS.
- (a) A. Bollmann, K. Blann, J. T. Dixon, F. M. Hess, E. Killian, H. Maumela, D. S. McGuinness, D. H. Morgan, A. Neveling, S. Otto, M. Overett, A. M. Z. Slawin, P. Wasserscheid and S. Kuhlmann, J. Am. Chem. Soc., 2004, 126, 14712–14713 CrossRef CAS PubMed; (b) M. J. Overett, K. Blann, A. Bollmann, J. T. Dixon, F. Hess, E. Killian, H. Maumela, D. H. Morgan, A. Neveling and S. Otto, Chem. Commun., 2005, 622–624 RSC.
- (a) W. Keim, F. H. Kowaldt, R. Goddard and C. Krüger, Angew. Chem., Int. Ed. Engl., 1978, 17, 466–468 CrossRef; (b) W. Keim, A. Behr, B. Limbäcker and C. Krüger, Angew. Chem., Int. Ed. Engl., 1983, 22, 503 CrossRef; (c) W. Keim, Angew. Chem., 1990, 102, 251–260 CrossRef CAS; (d) W. Keim, Makromol. Chem., Macromol. Symp., 1993, 66, 225–230 CrossRef CAS; (e) J. Heinicke, M. He, A. Dal, H.-F. Klein, O. Hetche, W. Keim, U. Flörke and H.-J. Haupt, Eur. J. Inorg. Chem., 2000, 431–440 CrossRef CAS.
- (a) W. Keim, S. Killat, C. F. Nobile, G. P. Suranna, U. Englert, R. Wang, S. Mecking and D. L. Schröder, J. Organomet. Chem., 2002, 662, 150–171 CrossRef CAS; (b) W.-H. Sun, Z. Li, H. Hu, B. Wu, H. Yang, N. Zhu, X. Leng and H. Wang, New J. Chem., 2002, 26, 1474–1478 RSC; (c) F. Speiser and P. Braunstein, Organometallics, 2004, 23, 2625–2632 CrossRef CAS; (d) F. Speiser and P. Braunstein, Organometallics, 2004, 23, 2633–2640 CrossRef CAS; (e) Z. Weng, S. Teo and T. S. A. Hor, Organometallics, 2006, 25, 4878–4882 CrossRef CAS.
- (a) C. Shao, W.-H. Sun, Z. Li, Y. Hu and L. Han, Catal. Commun., 2002, 3, 405–410 CrossRef CAS; (b) X. Tang, W.-H. Sun, T. Gao, J. Hou, J. Chen and W. Chen, J. Organomet. Chem., 2005, 690, 1570–1580 CrossRef CAS; (c) S. Jie, D. Zhang, T. Zhang, W.-H. Sun, J. Chen, Q. Ren, D. Liu, G. Zheng and W. Chen, J. Organomet. Chem., 2005, 690, 1739–1749 CrossRef CAS; (d) J. M. Benito, E. Jesús, F. J. Mata, J. C. Flores, R. Gómez and P. Gómez-Sal, Organometallics, 2006, 25, 3876–3887 CrossRef CAS; (e) C. Zhang, W.-H. Sun and Z.-X. Wang, Eur. J. Inorg. Chem., 2006, 4895–4902 CrossRef CAS; (f) S. Du, X. Wang, W. Zhang, Z. Flisak, Y. Sun and W.-H. Sun, Polym. Chem., 2016, 7, 4188–4197 RSC.
- (a) B. L. Small and M. Brookhart, J. Am. Chem. Soc., 1998, 120, 7143–7144 CrossRef CAS; (b) Y. Chen, C. Qian and J. Sun, Organometallics, 2003, 22, 1231–1236 CrossRef CAS.
- (a) W.-H. Sun, S. Jie, S. Zhang, W. Zhang, Y. Song and H. Ma, Organometallics, 2006, 25, 666–677 CrossRef CAS; (b) S. Jie, S. Zhang, W.-H. Sun, X. Kuang, T. Liu and J. Guo, J. Mol. Catal. A: Chem., 2007, 269, 85–96 CrossRef CAS; (c) S. Jie, S. Zhang and W.-H. Sun, Eur. J. Inorg. Chem., 2007, 35, 5584–5598 CrossRef.
- (a) W. Yang, Y. Chen and W.-H. Sun, Macromol. Chem. Phys., 2014, 215, 1810–1817 CrossRef CAS; (b) Y. Chen, W. Yang, R. Sha, R.-D. Fu and W.-H. Sun, Inorg. Chim. Acta, 2014, 423, 450–453 CrossRef CAS; (c) W. Yang, J. Yi and W.-H. Sun, Macromol. Chem. Phys., 2015, 216, 1125–1133 CrossRef CAS; (d) W. Yang, Y. Chen and W.-H. Sun, Macromol. React. Eng., 2015, 9, 473–479 CrossRef CAS.
- (a) P. C. Möhring and N. J. Coville, J. Mol. Catal., 1992, 77, 41–50 CrossRef; (b) P. C. Möhring and N. J. Coville, J. Mol. Catal. A: Chem., 1995, 96, 181–195 CrossRef.
- (a) R. Gao, Y. Li, F. Wang, W.-H. Sun and M. Bochmann, Eur. J. Inorg. Chem., 2009, 4149–4156 CrossRef CAS; (b) L. Xiao, R. Gao, M. Zhang, Y. Li, X. Cao and W.-H. Sun, Organometallics, 2009, 28, 2225–2233 CrossRef CAS; (c) R. Gao, T. Liang, F. Wang and W.-H. Sun, J. Organomet. Chem., 2009, 694, 3701–3707 CrossRef CAS.
- J. Yi, W. Yang and W.-H. Sun, Macromol. Chem. Phys., 2016, 217, 757–764 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS.
- (a) J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249 CrossRef; (b) A. D. Becke, J. Chem. Phys., 1988, 88, 2547–2553 CrossRef CAS.
- (a) M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS; (b) A. Bergner, M. Dolg, W. Küechle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431–1441 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- T. Zhang, W.-H. Sun, T. Li and X. Yang, J. Mol. Catal. A: Chem., 2004, 218, 119–124 CrossRef CAS.
- P. C. Anderson and S. Mecozzi, J. Comput. Chem., 2006, 27, 1631–1640 CrossRef CAS PubMed.
- (a) C. P. Casey and G. T. Whiteker, Isr. J. Chem., 1990, 30, 299–304 CrossRef CAS; (b) P. W. N. M. van Leeuwen, P. C. J. Kamer, J. N. H. Reek and P. Dierkes, Chem. Rev., 2000, 100, 2741–2769 CrossRef CAS PubMed; (c) M.-N. Birkholz, Z. Freixa and P. W. N. M. van Leeuwen, Chem. Soc. Rev., 2009, 38, 1099–1118 RSC.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- L. E. Eberly, Multiple Linear Regressions, From: Methods in Molecular Biology, 2007, vol. 404 Search PubMed.
- Z. Li, K. Bian and M. Zhou, Excel for Windows 95 Encyclopaedia, Electronics Industry Press, Beijing, 1997 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: All coordinates of optimized structure, the values of experimental activities for each complex and correlation results for the combined system of Fe–1a and Fe–2. See DOI: 10.1039/c6ra15779c |
| This journal is © The Royal Society of Chemistry 2016 |