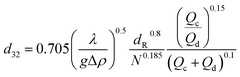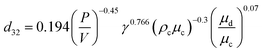A new model for prediction of drop size distribution in a liquid–liquid extraction column
Mehdi Asadollahzadeh*,
Meisam Torab-Mostaedi,
Rezvan Torkaman and
Jaber Safdari
Nuclear Fuel Cycle Research School, Nuclear Science and Technology Research Institute, P.O. Box: 11365-8486, Tehran, Iran. E-mail: masadollahzadeh@aeoi.org.ir; mehdiasadollahzadeh@alumni.iust.ac.ir; Fax: +98 2188221116; Tel: +98 2188221117
First published on 24th August 2016
Abstract
In this study, a new model for prediction of drop size distribution is proposed in the asymmetric rotating disc pilot plant column (ARDC) by the maximum entropy density approximation technique. The liquid extraction systems including toluene–water, n-butyl acetate–water and n-butanol–water were used with this column. An image analysis technique was applied to determine the drop size distribution as a function of operating parameters and physical properties. By applying abrupt changes of the operating parameters, the drop behaviors in the column were investigated. The results show that the agitation speed has a main effect on the drop size distribution in the column. However, the effects of phase flow rates are not significant. The empirical correlations are proposed to describe Lagrange multipliers in the maximum entropy function in terms of operating variables and physical properties of the systems. Except for these findings, an empirical correlation is proposed for estimation of the Sauter mean drop diameter in terms of operating variables, column geometry and physical properties. The proposed correlations are evaluated based on the goodness of fit statistics, namely, χ2, R2 and RMSE. The fitting results by the maximum entropy principle method seem to be fairly accurate and reasonable on the basis of the experimental data. These completed sets of data could be used for modeling approaches in the liquid–liquid extraction columns.
1. Introduction
Liquid–liquid extraction is a mass transfer operation in which a mixture of a solute and a carrier liquid is brought into intimate contact with a second immiscible liquid (solvent) in order to achieve transfer of the solutes from the feed to the solvent.1 Solvent extraction is now very well established, featuring extensively as a selective separation process.2In the process industry, a great variety of different equipment designs are used in extraction processes. This is due to the fact that the density difference between the two liquid phases is very small (Δρ < 100 kg m−3). The small density difference restricts the velocities of the phases to very small values and it reduces the rates of mass transfer.3 This problem is solved by using external motions such as pulsation or agitation in the system. Three types of solvent extractors can be distinguished such as static devices, pulsed devices and agitated devices.4,5
Rotary agitated extraction column consists of a tall column having a long rotating shaft fitted with a set of impellers. The column is divided into a number of compartments by a set of fixed partition plates. These extractors provide a pretty large number of theoretical plates in a single unit and have a low HETS.6,7
The rotating disc contactor developed in the 1950s by the Shell Company in the Netherlands, has been widely used in the chemical and petroleum industries. Nowadays, this is the best known agitated column extractor. The modification of RDC column is the asymmetric rotating disc contactor.8,9 In this equipment, the shaft with its agitating discs is placed asymmetrically away from the center-line in the column. Typical industrial applications are found in the different fields such as organic and petrochemical, inorganic and metallurgical and miscellaneous domains. The asymmetric rotating disc column extractors are currently in operation in more than 100 processes.4,10
The motion of droplets through liquid–liquid extraction equipment are influenced by several aspects such as agitation speed, temperature, physical properties or phase volume fractions of the systems. The power input to the agitated column extractors is thus transferred to the kinetic, surface, potential and heat energy of the droplets.11 The same mean drop size can be obtained from various drop size distributions which have different interfacial areas. Knowledge of the drop size distribution is used to process monitoring, to control or to characterize and to improve the product quality. Therefore, the change in the mean drop size and drop size distribution with agitation speed is very important in these extractors.12 Misek and Marek13 have shown that the maximum droplet diameter under mild agitation in the ARDC extraction column is independent of rotor speed and is given by:
 | (1) |
For intensive agitation, the expression was proposed for dmax in terms of column variables and physical properties, the transition rotor speed and the droplet size distribution. Kumar and Hartland14 reported that the equations for drop size proposed by Misek and Marek13 gave an average deviation of 54% in the case of rotating disc contactors. The unified correlations for prediction of the drop size in mechanically agitated columns are shown in Table 1.
The adequacies of various conventional probability density functions such as normal, log-normal, gamma, inverse Gaussian and Weibull functions were investigated by researchers for the prediction of drop size distribution in the liquid–liquid extraction column. There are many innovative and exciting statistical methods now being developed and applied to predict experimental data. The maximum entropy principle (MEP) has been successfully applied to many problems arising in a wide variety of fields such as physical, chemical, biological, computer science, etc.15–17 The maximum entropy method allows determining the least biased probability distribution function when the information available is limited by some macroscopic constraints.
There are a few literature data on the study of the drop size and drop size distribution in the pilot plant ARDC column, experimentally. In addition, a statistical approach with the maximum entropy method has not been attempted to derive the most probable drop size distribution in these columns.
In the present paper, the influence of operating conditions and physical properties of the three systems on drop size changes due to breakage and coalescence processes in the ARDC pilot plant column was investigated. The maximum entropy method according the previous research work in the multi-impeller extraction contactor18 were used for prediction of drop size distributions in the ARDC pilot plant column. The relevant Lagrange multipliers in the maximum entropy approach were correlated with effective variables such as operating parameters and physical properties of the three systems.
2. Fitting performance evaluation
The coefficient of determination (R2) is utilized to evaluate the performance of the maximum entropy distributions. This coefficient defined as a percentage indicate, show much of the total variation in the dependent variable can be accounted for by the experimental distribution. A higher R2 represents a better fit employing the theoretical or empirical function. The definition of the R2 is:19
 | (7) |
 | (8) |
 | (9) |
 | (10) |
 | (11) |
A smaller value of these parameters indicates a better fitting between the proposed probability distribution function and the experimental data. The values should be zero for these two parameters in the ideal case.
3. Experimental
3.1. Chemical systems
Three various systems with different interfacial tensions consisting of toluene–water (high interfacial tension), n-butyl acetate–water (medium interfacial tension) and n-butanol–water (low interfacial tension) were used for experiments without mass transfer. The European Federation of Chemical Engineering (E.F.C.E) has adopted these systems as Recommended Systems.20 The physical properties of the three systems are listed in Table 2. The organic phase solvents with 99.5% purity were used in the experiments.| Physical property | Toluene–water | n-Butyl acetate–water | n-Butanol–water |
|---|---|---|---|
| ρc [kg m−3] | 998.2 | 997.6 | 985.6 |
| ρd [kg m−3] | 865.2 | 880.9 | 846.0 |
| μc [mPa s] | 0.963 | 1.027 | 1.426 |
| μd [mPa s] | 0.854 | 0.734 | 3.364 |
| γ [mN m−1] | 36 | 14.1 | 1.75 |
3.2. Description of the ARDC pilot plant column
A pilot scale asymmetric rotating disc column consists of a cylindrical shell, a baffled stator, and a multistage agitator. The shell houses an extraction section and two settling zones. The extraction section consists of a 1430 mm long glass tube of 113 mm internal diameter, enclosing a stock of 36 discs mounted on a vertical shaft and driven by an electronic motor via a variable speed gearbox. The extraction section is divided by an asymmetrically positioned vertical stator baffle into a contact zone and a transportation zone. Both of these are subdivided by horizontal baffles into a series of staggered chambers that communicate with each other through openings on both sides of the vertical baffle. Disc impellers mounted on the agitator shaft and centered in each contact chamber provide mechanical agitation. The specific column geometries studied are summarized in Table 3 and the scheme of the ARDC pilot scale unit is shown in Fig. 1.| Column diameter (m) | 0.113 |
| Rotor diameter (m) | 0.042 |
| Stator diameter (m) | 0.11 |
| Column working height (m) | 1.43 |
| Compartment height (m) | 0.033 |
| No. of compartments (-) | 36 |
| Degree of asymmetry (-) | 120° |
A settler of 168 mm diameter at each end of the column permitted the liquids to coalesce and be decanted separately. Four stainless steel tanks with 85 L capacity were used to store the liquid feeds, and to collect the extract, and to the raffinate streams. The interface is maintained at the required level by means of an optical sensor as previously described by Torab-Mostaedi et al.21
3.3. Determination of drop size
A digital camera (Nikon D5000) was used to record successive pictures of drop size in the ARDC pilot plant extraction column. The photographs were analyzed with the software CAD for drop size determination. The real drop sizes were measured by comparing the size of the drops with the size-defined articles which were the thicknesses of stators in our investigation. The pictures of drop sizes for the three systems are shown in Fig. 2. | ||
| Fig. 2 The photos of drops for three systems (a) toluene–water, (b) n-butyl acetate–water, (c) n-butanol–water. | ||
It is found that the curved surface of the glass extraction column and significant differences between air and the glass refractive indices leads to a parallax deformation of the objects photographed in the extraction column. In order to omit this phenomenon, a container filled with water was attached to the extraction column and the photographic approach was used to calculate the size of the stator thickness served as the reference for drop size measurements.
The Sauter mean diameter is a popular representation of the mean drop size, defined as:
 | (12) |
To measure the number density and drop size distribution at each run, the size of drop is divided into several ranges (di ± 0.1 mm). The number of drops is then determined in each part and obtained according to the following equation:
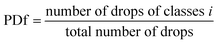 | (13) |
4. Results and discussion
Three vital operating parameters including aqueous and organic phase flow rates and rotor speed were chosen for the investigation of drop size distribution and the Sauter mean drop diameter in the pilot plant ARDC extraction column.4.1. The Sauter mean drop diameter
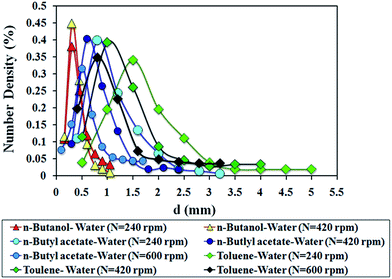
The Sauter mean drop diameters in the liquid–liquid systems are mainly a function of agitation speed, as well as the organic and aqueous phase velocities.The effects of agitation speed on the Sauter mean drop diameter for three different systems were analyzed (Fig. 3). For all systems, agitation had a strong effect on the Sauter mean drop diameter. The reason for this is that the energy input by the rotor blades increases with increasing agitation speed, so the dispersed phase is dispersed more easily. The droplet breakage is carried out with an increase in the energy supplied via agitation.
The difference in the physical properties of the liquid–liquid systems shows the different values of d32. The decrease in droplet size is expected with a decrease in the interfacial tension of systems.
Fig. 4 and 5 illustrate the effect of continuous and organic phase velocities in the Sauter mean drop size diameter. As depicted in Fig. 4, the mean drop diameter increases with an increase in dispersed phase velocity, while a slight increase occurred at low interfacial tension. This observation relates to the increasing drop collisions with the acceleration of the dispersed phase velocity and consequently, the coalescence frequency among the drops is increased. Fig. 5 shows that the continuous phase velocity has a negligible effect on the mean drop size. Therefore, the continuous phase velocity is not the main factor affecting the dispersed phase mean drop sizes.
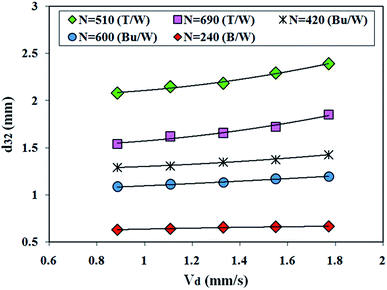 | ||
| Fig. 4 Effect of dispersed phase velocity on the Sauter mean drop diameter (toluene–water (T/W), n-butyl acetate–water (Bu/W), n-butanol–water (B/W)). | ||
 | ||
| Fig. 5 Effect of continuous phase velocity on the Sauter mean drop diameter (toluene–water (T/W), n-butyl acetate–water (Bu/W), n-butanol–water (B/W)). | ||
 | ||
| Fig. 6 Comparison of experimental values of Sauter mean drop diameter with previous correlations in Table 1. | ||
| Kumar and Hartland, 1985 | Kumar and Hartland, 1996 | Al-Rahawi et al., 2007 | Kadam et al., 2009 | Hemmati et al., 2015 | Present work (eqn (15)) | |
|---|---|---|---|---|---|---|
| χ2 | 0.135 | 0.168 | 0.194 | 0.031 | 0.033 | 0.024 |
| RMSE | 0.018 | 0.015 | 0.014 | 0.008 | 0.007 | 0.005 |
| R2 | 0.81 | 0.75 | 0.89 | 0.91 | 0.92 | 0.99 |
| d32 = f(dR, N, Vd, Vc, ρd, Δρ, μd, μc, γ) | (14) |
According to the dimensional analysis method, all the drop sizes obtained from this study have been correlated by the following equation:
 | (15) |
In the above equation, the geometric parameter was defined by the last dimensionless number. The experimental data by Moreira et al.22 (RDC column), Kadam et al.23 (ARDC column) and Hemmati et al.24 (PRDC column) were used for prediction of Sauter mean drop diameter.
The results obtained are shown in Fig. 7 and the statistical errors are summarized in Table 4. This figure and the statistical errors indicate that the suggested correlation can make highly accurate estimate for the Sauter mean drop diameter with the experimental data and the experimental works by other researchers.22–24
 | ||
| Fig. 7 Comparison between experimental data and the estimated values using eqn (15). | ||
4.2. Drop size distribution investigation
The drop size distributions in agitated systems are mainly a function of agitation speed, dispersed and continuous phase and the physical properties of the systems.According to these figures, the phase flow rates (continuous or dispersed) do not have any considerable effect on drop size distribution, hence they can be neglected. Thus, the drop size distribution is independent of both phase flow rates. Nevertheless, Moreira and co-workers observed that drop size distributions in the RDC column under low agitation were shifted to the larger drop by an increase in the phase flow rates.22
| Pi = exp(−α0 − α1f12(di) − α2f23(di)) | (16) |
 | (17) |
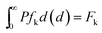 | (18) |
 | (19) |
 | (20) |
 | (21) |
To evaluate the Lagrange multipliers in the eqn (16), the above constraints (eqn (17)–(21)) are used and the probability drop size distribution is obtained by solving non-linear equations. A more complete description for maximum entropy approach in the multi-impeller extraction contactor was reported in a previous research work.18
These parameters were correlated as a function of operating variables and physical properties of the systems. The derived correlations are given below:
 | (22) |
The effects of physical properties and operating variables on the parameters in different probability distribution functions are shown by constant parameters, C1, to C6 in the above equations. The values of these parameters for Lagrange multipliers (α0, α1 and α2) are presented in Table 5.
| Lagrange multipliers | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|
| α0 | 2.68 | −0.08 | 0.51 | −0.44 | 0.27 | 0 |
| α1 | −10.25 | 0.39 | 2.29 | 0.59 | 0.91 | 0 |
| α2 | 58.85 | 0.45 | 2.14 | 0.29 | 1.47 | 1.76 |
In the latter equations, N, dR, ρc, μc, γ, Δρ, Vc, Vd and g denote the agitation speed, rotor diameter, density of the continuous phase, viscosity of the continuous phase, interfacial tension, density difference between continuous and dispersed phases, continuous velocity, dispersed velocity and gravity acceleration, respectively. It is observed from the above equations that the drop size distribution profiles are strongly affected by rotational speed.
The histogram data for the three systems and the comparative plots for probability distribution function from maximum entropy method is shown in Fig. 10.
 | ||
| Fig. 10 Comparison of maximum entropy distribution functions with a broad drop size distribution for (a) toluene–water, (b) n-butyl acetate–water. | ||
The fitting performance evaluation was implemented for the evaluation of proposed model, the obtained values are 0.99, 0.001 and 0.003 for coefficient of determination, root mean square error (RMSE) and χ2, respectively.
The result from fitting performance evaluation and Fig. 10 show that the maximum entropy method can be used as an alternative method to estimate the drop size distributions in ARDC pilot plant column.
Contribution of parametric uncertainty analysis was assessed by Monte Carlo simulation with program in Matlab software. In each run, the numerical solver executed 5000 Monte Carlo trails and the maximum entropy probability distributions were used for each uncertainty input parameter. A histogram of the probability size distribution for the toluene–water system is presented in Fig. 11.
The results of the uncertainty analysis of the drop size for toluene–water system show an expected mean value of 2.09 with a standard deviation of 0.5%. The results of the sensitivity analysis are described in a bar diagram (Fig. 12), which shows the six major contributors to the uncertainty of the mean drop size. The sensitivity analysis of the model parameters indicated that the rotor speed parameter is the major source of uncertainty in the modeling of drop size distribution with the maximum entropy method. The density and viscosity of the selected system have the least sensitivity on the drop size distribution.
5. Conclusion
This paper focuses on the study of the maximum entropy principle applied to fit the drop size distribution in the ARDC pilot plant column. A series of experiments have been performed to investigate the effect of operating parameters and physical properties on the drop size distributions and Sauter mean drop diameter. The drop size distributions predicted from the statistical approach are compared with the experimental data. The empirical correlations are proposed to describe Lagrange multipliers in the maximum entropy function in terms of operating variables and physical properties of the systems. Also, an empirical correlation is proposed for estimation of the Sauter mean drop diameter. The maximum entropy distribution is found to perform adequately and accurately in fitting the drop size distribution. Therefore, the maximum entropy probability distribution is more suitable for assessment of the drop size distribution and the performance of liquid–liquid extraction equipment.Nomenclature
| CII | Constant parameter in eqn (3) (-) |
| CΨ | Constant parameter in eqn (3) (-) |
| CΩ | Constant parameter in eqn (3) (-) |
| d30 | Volume drop diameter (m3) |
| d32 | Sauter mean drop diameter (m) |
| Dc | Column diameter (m) |
| Di | Droplet diameter (m) |
| dic | Value of drop size from calculated correlation (m) |
| dm | Mean value of drop size (m) |
| dmax | Maximum drop diameter (m) |
| dR | Rotor diameter (m) |
| e | Fractional cross sectional area (-) |
| g | Acceleration due to gravity (m s−2) |
| H | Effective height of the column (m) |
| hc | Compartment height (m) |
| m | Mass (kg) |
| N | Rotor speed (s−1) |
| ni | Number of droplets of mean diameter di (-) |
| P | Probability of number density (-) |
| P/V | Power per unit volume (W m−3) |
| Probability distribution function (-) | |
| Q | Flow rate of the continuous or dispersed phase (m3 s−1) |
| R2 | Coefficient of determination (-) |
| Re | Reynolds |
| RSME | Root mean square error for drop size (m) |
| S | Shannon entropy (-) |
| V | Superficial velocity (m s−1) |
Greek
| α | Lagrange multipliers of probability maximum entropy function |
| γ | Interfacial tension (N m−1) |
| Δρ | Density difference between phases (kg m−3) |
| ε | Power dissipated per unit mass (m2 s3) |
| μ | Viscosity (Pa s) |
| ρ | Density (kg m−3) |
| σ | Standard deviation of drop size (m) |
Subscripts
| c | Continuous phase |
| d | Dispersed phase |
Acknowledgements
The authors would like to thank Iran National Science Foundation (INSF) for providing the financial support for this project (Project No. 92038028).References
- M. Aguailar and J. L. Cortina, Solvent extraction and liquid membranes, CRC Press, New York, 2013 Search PubMed
.
- B. K. Dutta, Principles of mass transfer and separation processes, Wiley, New York, 2009 Search PubMed
.
- G. M. Ritcey and A. W. Ashbrook, Principles and applications to process metallurgy, Elsevier, New York, 1984 Search PubMed
.
- J. C. Godfrey and M. J. Slater, Liquid-Liquid Extraction Equipment, Wiley, New York, 1994 Search PubMed
.
- Martunus, Z. Helwani and M. R. Othman, Appl. Math. Model., 2010, 34, 2901–2909 Search PubMed
.
- J. D. Thornton, Science and practice of liquid- liquid extraction, Oxford University Press, Oxford, 1992 Search PubMed
.
- M. A. Morís, F. V. Díez and J. Coca, Sep. Purif. Technol., 1997, 11, 79–92 Search PubMed
.
- M. Torab-Mostaedi and M. Asadollahzadeh, Chem. Eng. Res. Des., 2015, 94, 90–97 Search PubMed
.
- T. Misek, Collect. Czech. Chem. Commun., 1963, 28, 1631–1645 Search PubMed
.
- S. Kalaivani and I. Regupathi, Sep. Sci. Technol., 2016, 146, 301–310 Search PubMed
.
- S. Sarker, C. J. Mumford and C. R. Phillips, Ind. Eng. Chem. Process Des. Dev., 1980, 19, 672–679 Search PubMed
.
- M. Asadollahzadeh, M. Torab-Mostaedi, S. Shahhosseini and A. Ghaemi, Chem. Eng. Res. Des., 2016, 105, 177–187 CrossRef CAS
.
- T. Misek and J. Marek, Brains Chem. Eng., 1970, 15, 202–207 Search PubMed
.
- A. Kumar and S. Hartland, Ind. Eng. Chem. Res., 1996, 35, 2682–2695 CrossRef CAS
.
- S. Akpinar and K. Akpinar, Energy Convers. Manage., 2007, 48, 1140–1149 CrossRef
.
- C. Sobrino, A. Acosta-Iborra, M. A. Izquierdo-Barrientos and M. D. Vega, Chem. Eng. J., 2015, 262, 628–639 CrossRef CAS
.
- L. M. Martyushev and V. D. Seleznev, Phys. Rep., 2006, 426, 1–45 CrossRef CAS
.
- M. Asadollahzadeh, M. Torab-Mostaedi, S. Shahhosseini and A. Ghaemia, RSC Adv., 2015, 5, 95967–95980 RSC
.
- J. Zhou, E. Erdem, G. Li and J. Shi, Energy Convers. Manage., 2010, 51, 1449–1458 CrossRef
.
- T. Míšek, R. Berger and J. Schroter, Standard test systems for liquid extraction studies, EFCE Publication Series, 1985 Search PubMed
.
- M. Torab-Mostaedi, A. Ghaemi and M. Asadollahzadeh, Can. J. Chem. Eng., 2012, 90, 1569–1577 CrossRef CAS
.
- E. Moreira, L. M. Pimenta, L. LCarneiro, R. C. L. Faria, M. B. Mansur and J. P. Ribiero, Chem. Eng. Commun., 2007, 192, 1017–1035 CrossRef
.
- B. D. Kadam, J. B. Joshi and R. N. Patil, Chem. Eng. Res. Des., 2009, 87, 756–769 CrossRef CAS
.
- A. Hemmati, M. Torab-Mostaedi, M. Shirvani and A. Ghaemi, Chem. Eng. Res. Des., 2015, 96, 54–62 CrossRef CAS
.
- A. Kumar, L. Steiner and S. Hartland, Ind. Eng. Chem. Process Des. Dev., 1986, 25, 728–733 CAS
.
- A. M. I. Al-Rahawi, Chem. Eng. Technol., 2007, 30, 184–187 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2016 |