Phonon transport in the ground state of two-dimensional silicon and germanium

Abstract

Large honeycomb dumbbell (LHD) silicene/germanene was recently found to be the ground state of two-dimensional (2D) silicon and germanium, which was much more stable than the well-known low buckled (LB) silicene/germanene (Matusalem et al., Phys. Rev. B, 92, 045436 (2015)). The existence of an intrinsic band gap of LHD silicene/germanene makes them prospective in future thermoelectric devices. In this work, lattice thermal conductivity (κ) of the LHD silicene/germanene is investigated systematically by solving the phonon Boltzmann transport equation with interatomic force constants extracted from first-principles calculations, and compared with that of low buckled (LB) silicene/germanene. It is intriguing to find that, as compared with LB silicene, although the much flatter structure of the LHD silicene/germanene leads to a significantly larger portion of the flexural modes to the overall thermal transport, the κ of the LHD silicene/germanene is only 5.9/1.6 W m⁻¹ K⁻¹, which is substantially lower than that of the LB silicene/germanene. We found that the volumetric specific heat, group velocity square and the phonon lifetime of the LB silicene are all larger than that of the LHD silicene/germanene, with group velocity playing the dominant role, which is further linked with the higher Young's modulus of LB silicene. Besides, the difference in phonon lifetime is further explained in terms of the potential energy change. The trend of the root mean-square displacement values and the phonon anharmonicity is opposite to that of the normalized mean lifetime, which is physically justified, as larger displacements will lead to stronger anharmonicity and reduced lifetimes. The intrinsic ultralow κ of the LHD silicene/germanene makes it prospective for thermoelectrics in the future.

---

1. Introduction

Research on two-dimensional (2D) materials such as graphene¹ and graphene-like group-IV materials^2,3 is of fundamental scientific interest from the view of the variety of applications. For example, graphene possesses extreme mechanical strength,^4,5 exceptionally high electrical⁶ and thermal conductivities,^7–9 as well as many other supreme properties,^10,11 all of which make it highly attractive for numerous applications.^12,13 Inspired by the prospective properties of graphene, there has been increasing interest in its “cousins”, i.e., two-dimensional honeycomb lattices composed of other group-IV elements, e.g. Si and Ge, which naturally have been considered to have a graphene-like hexagonal structure with similar exceptional properties.^2,3

Indeed, the analog 2D structures composed of group-IV elements, namely, silicene and germanene, have been predicted and studied theoretically and experimentally.^14–24 Unlike planar graphene, silicene and germanene naturally has buckled structure, which makes them partially sp³ hybridized.^14–17,25 Compared to graphene, silicene is more compatible with silicon-based semiconductor devices and therefore has greater potential in nanoelectronic applications. Besides, fabrication of these 2D materials has already been realized on different metal substrates in experiments.^18,26,27 For example, silicene and germanene were successfully synthesized on Ag¹⁸ and Au substrates,¹⁹ respectively.

As for silicene grown on Ag(111) surfaces, to explain some characteristics such as the √3 × √3 translational symmetry and the honeycomb images observed by the scanning tunneling microscopy (STM), some modifications of this graphene-like structure have been proposed.^28–30 It has been shown that the addition of Si adatoms to pristine silicene results in the formation of a dumbbell structure with a lower total energy per atom. Different from the situation of carbon with hexagonal structure (graphene) which was demonstrated to be the most stable form from previous first principles calculations, in the case of Si and Ge, the dumbbell structures, particularly the large honeycomb dumbbell (LHD) geometries, are the energetically favored geometries as compared with the sp²/sp³-bonded hexagonal lattice, i.e., low buckled (LB) silicene and germanene.²

Stability and electronic properties of these 2D allotropes of group-IV materials have been systematically investigated in previous theoretical work. It has been shown that, in contrast to graphene, the LHD sheet crystals of silicene and germanene are indirect semiconductors with a nonzero K → Γ energy gap of about 0.5 eV,² which may be very promising for enhancing Seebeck coefficient in thermoelectric devices, where the conduction of heat plays a critical role. Therefore, understanding thermal transport (mainly phonons) in these newly proposed LHD silicene and germanene is of great significance to emerging technologies.

In this work, lattice thermal conductivity (κ) of the LHD silicene/germanene is predicted by solving the phonon Boltzmann transport equation with interatomic force constants extracted from first principles calculations, and compared with that of the LB silicene/germanene. It is interesting to find that κ of the LHD silicene/germanene is 5.9/1.6 W m⁻¹ K⁻¹, which is substantially lower than that of silicene 21.1 W m⁻¹ K⁻¹ (25 (ref. 21)) and 19.34 W m⁻¹ K⁻¹ (ref. 3) and germanene (10.52 W m⁻¹ K⁻¹ (ref. 3)). The intrinsic ultralow κ of the LHD silicene/germanene make them be well suitable for serving as prospective thermoelectric materials.

2. Simulation model and computational method

The dumbbell structure is obtained by adding two extra silicon atoms at the two top sites of a 2 × 2 LB silicene supercell.^28,29 This Si adatom pushes down the original underneath Si atom to form a dumbbell-like structure with 3 + 1 coordination.²⁹ The optimized geometric structure of LHD silicene, which is a 2 × 2 LHD silicene with two dumbbell units,^2,30 is shown in Fig. 1. There are two kinds of Si atoms denoted by Si1 (on the top and bottom atomic layers) and Si2 (in the middle atomic layer). The Si1 and Si2 atoms have different bonding states. Si1 in the top layer is bonded with three neighbor Si2 atoms, but not bonded with the opposite Si1 in the bottom layer, which can be seen clearly from the electron localization function (ELF) values in xz plane across the center of the two opposite Si1 atoms in Fig. 1(d). ELF, with a value in the range from 0 to 1, can be used to manifest the bonding natures.³¹ ELF = 1 means highly localized and bounded electrons, while ELF = 0 means there is no electron. The value of ELF between two opposite Si1 atoms is ∼0.35, indicating that the electrons are quite delocalized and there is no bond connection between them. Besides, from the figure, we can see that the electrons of Si1 atom are mainly localized outside the two Si1 atoms in the out of plane direction, where ELF is red, suggesting the localization of electrons there and the existence of dangling bonds for Si1 atoms. In comparison, each Si2 atom is connected with two Si1 atoms and two Si2 atoms, and becomes fully saturated for its four 3s²3p² electrons. Different from the LB silicene where every atom has one dangling bond, the LHD silicene has a further lower cohesive energy (0.21 eV per atom difference) as compared with the LB silicene.² By substituting all Si atoms with Ge atoms in Fig. 1, the structure of LHD germanene can be obtained (not shown here for brevity).² Our calculated lattice constant and buckling distance (defined as the distance between the top and bottom Si (Ge) layers) of 2D LHD silicene (germanene) are L = 7.428 (7.872) Å, and d = 2.711 (2.957) Å, respectively. All these geometrical structure parameters are in good agreement with previously reported values.²

Fig. 1 (a) Top and (b) side view of large honeycomb dumbbell (LHD) silicene. The geometric structure parameter L and d are marked. Yellow and blue balls, denoted by Si1 and Si2, represent Si atoms on the top/bottom and middle layer, respectively. The black solid rhombus shows the periodic boundary. (c) The first Brillouin zone with high symmetry lines highlighted in red. (d) The electron localization function (ELF) values in xz plane across the center of two opposite Si1 atoms, which are rendered by VESTA.³²

We performed density functional theory (DFT) calculations in the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional,³³ as implemented in the Vienna Ab-initio Simulation Package (VASP),^34–37 in which the projected augmented wave method^38,39 is adopted. A kinetic energy cutoff of 600 eV for the plane-wave basis set is employed. The 3s²3p² orbitals of the Si atom and the 4s²3p² orbitals of the Ge atom are treated as valence ones. The 2D LHD silicene/germanene layer is placed in the xy-plane with a large enough vacuum region in the out-of-plane (z) direction (>20 Å) in order to avoid self-interaction due to the periodic boundary conditions used. We utilize a Monkhorst–Pack k-point mesh of 25 × 25 × 1 for the summation in the first Brillouin zone (BZ), in order to ensure energy convergence during the structure optimization and the total energy calculation. All atoms and the simulation box in x and y directions are fully relaxed. Geometric structure optimizations were performed by using the conjugate-gradient algorithm with a maximum residual force of 10⁻⁵ eV Å⁻¹ for each atom. The allowed stop criterion in total energy for the electron self-consistent loop is 10⁻⁸ eV. The layer thickness of LHD silicene (germanene), which are critical to thermal conductivity calculation, are taken as the distance between the top and bottom Si (Ge) atom layers (parameter “d” denoted in Fig. 1) plus the van der Waals diameter of the Si (Ge) atom.^22,24,40 The layer thickness of LHD silicene (germanene) are 6.911 Å and 7.177 Å, respectively.

By only considering phonon–phonon scattering processes, we calculated the intrinsic thermal conductivity of LHD silicene (germanene) by solving the semi-classical phonon Boltzmann transport equation (BTE) iteratively by the ShengBTE package,⁴¹ which is completely parameter-free and based only on the information of the atomic structure. Calculation of the thermal conductivity via iterative solution of the BTE requires anharmonic third-order interatomic force constants (IFCs) along with the harmonic second order IFCs. We used a 4 × 4 × 1 supercell containing 160 atoms for calculating the harmonic and anharmonic IFCs with only Γ point to sample the BZ. The second order harmonic IFCs are obtained within the linear response framework by employing density functional perturbation theory (DFPT), which calculates the dynamical matrix through the linear response of the electron density.⁴² The phonon dispersion is obtained by the Phonopy code, which is an open source package for phonon calculations at harmonic and quasi-harmonic levels, with the harmonic IFCs as input.^43,44 For anharmonic IFC calculations, interactions are taken into account up to the 4^th nearest neighbors to achieve convergence. Unless specified otherwise, all thermal conductivities are calculated at room temperature (300 K). For comparison, the κ of the LB silicene is also calculated. The geometrical structure is first obtained with a buckling distance of 0.45 Å, which is consistent with previous result.⁴⁵ A 5 × 5 × 1 supercell containing 50 atoms is used to obtain the harmonic and anharmonic IFCs with 2 × 2 × 1 to sample the BZ. Other parameters used to calculate κ are similar to those used for LHD silicene.

3. Results and discussions

3.1. Phonon dispersion

We first validate the phonon dispersion curves of the low buckled (LB) silicene and LHD silicene/germanene, which are done by solving the eigenvalues of the dynamical matrix constructed from the harmonic force constants. The phonon dispersions are depicted in Fig. 2. There are no imaginary frequencies in all phonon dispersions, confirming their mechanical stabilities. For the curves shown in Fig. 2(b) and (c), there are strong mixings between acoustic and optical phonon branches, leading to an intuitive expectation of strong acoustic–optical phonon couplings and scatterings, which thus results in low κ values as compared with that of LB silicene (Fig. 2(a)) and germanene without any mixing between acoustic and optical phonon branches.^3,21,23,24

Fig. 2 Phonon dispersion curves of (a) LB silicene, (b) LHD silicene and (c) LHD germanene.

Besides, it is worth noting that the phonon dispersion curves for the LHD silicene/germanene are very similar to each other due to their similar symmetry group (P6/mmm (191)) except their different frequency ranges, i.e. Debye cut-off frequencies (Fig. 2). Due to the stronger Si–Si bonds in LHD silicene, its Debye cutoff frequency is found to be ∼15.7 THz, which is comparable to that of the LB silicene ∼16.62 THz, but is nearly doubled that of LHD germanene (∼8.6 THz). In addition, two obvious gaps exist between optical phonon branches of LHD silicene/germanene, which are absent in that of LB silicene/germanene,^3,21 indicating that both of them have definite frequency channels for thermal transport.

Similar to the out-of-plane acoustic mode in graphene (i.e. flexural mode denoted by ZA or FA), there are also ZA modes in the LHD silicene/germanene. However, the ZA modes in LHD silicene/germanene are not perfectly perpendicular to the planes (i.e. not perfectly along the out-of-plane direction), because they have coupling with the in-plane longitudinal and transversal acoustic (LA and TA) modes due to the buckled structure. Physically, as long as the plane size is large enough, the coupling of the in- and out-of-plane atomic vibrations caused by the thickness (buckling) would vanish, due to that the ratio of thickness to size approaches zero, thus leading to disappearance of the buckling effect on the phonon dispersion. In fact, previous theoretical works showed that the group velocity of the ZA mode in the phonon dispersion of two dimensional structure should be zero at the Γ-point and the dispersion relation should be quadratic (ω ∼ q²), where ω is the angular frequency and q is the wave vector magnitude.^46,47 For LHD silicene/germanene, it can be observed from Fig. 2 that the ZA dispersions are quadratic-like but not purely quadratic. Numerical fitting gives an approximate relation of ω ∼ q^α (α is ∼1.9/1.8 for LHD silicene/germanene) in the frequency range near the Γ point (along Γ → M direction).

We further calculated the phonon group velocity from the relation 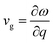. Correspondingly, the group velocity of the ZA modes gradually goes to zero with q decreasing, which are different from the linear phonon dispersion of the ZA branch of LB silicene near Γ point in the first BZ (along Γ → M), whose group velocity is ∼1.5 km s⁻¹ (1.08 km s⁻¹ (ref. 21)). For the LHD silicene, the group velocity of TA/LA branch near the Γ point is 5.03/8.88 km s⁻¹, which is slightly smaller than that of LB silicene 5.63/9.54 km s⁻¹ (5.63/9.55 km s⁻¹ (ref. 21)). The corresponding value for LHD germanene is 2.71/4.86 km s⁻¹, which is nearly half of that of LHD silicene, suggesting its further lower thermal conductivity.

3.2. Thermal conductivity and the relative contribution from the ZA mode

Firstly, the convergence of the lattice thermal conductivity (κ) with respect to the BZ sampling density N_K × N_K and the cutoff radius N_cutoff employed in the 3^rd IFC calculations are tested (the result is shown in Fig. S1 and S2 in the ESI†). In this work, the analysis of κ are all based on the converged k-grid N_K × N_K = 83 × 83 and N_cutoff = 4. The calculated κ from 200 to 600 K are shown in Fig. 3. It is noticed that κ diminishes with temperature increasing. The intrinsic κ of LHD silicene/germanene is 5.9/1.6 W m⁻¹ K⁻¹ at 300 K. These values are significantly smaller than that of LB silicene of 21.1 W m⁻¹ K⁻¹ calculated at k-grid N_K × N_K = 151 × 151 and N_cutoff = 4 (25 (ref. 21) and 19.34 W m⁻¹ K⁻¹ (ref. 3)) and germanene (10.52 W m⁻¹ K⁻¹ (ref. 3)). By fitting κ with the relation of κ ∼ 1/T^α, the parameter α for LB silicene, LHD silicene/germanene are 0.85, 0.98/0.93, respectively, which are almost equal to 1 as for that of phosphorene.⁴⁸

Fig. 3 Thermal conductivity (left axis, black solid) and the relative contribution from the out-of-plane ZA mode to the total thermal conductivity (right axis, red opened) as a function of temperature for LB silicene (squares), LHD silicene (circles) and LHD germanene (triangles). The black solid lines show the fitting result of κ ∼ 1/T^α.

To understand these κ differences between LB silicene/germanene and their LHD structures, more details have to be elaborated on the flexural branch. Different from graphene, the flexural modes of LB silicene/germanene and their LHD structures are all not purely out-of-plane vibrations.^23,24 The phonon transport in graphene is dominated by the flexural mode. For example, previous classical molecular dynamics simulations showed that the flexural mode of graphene contributes as large as 60% to the total κ.²² However, the behavior of LB silicene, the silicon-based counterpart of graphene with a 2D honeycomb lattice, is fundamentally different. Previous studies^29,39 revealed that as much as 80% of the total heat flux is caused by the in-plane lattice vibrations. Such difference in the mode-specific contribution is expected from the different atomic structures between LB silicene and graphene (buckled vs. planar), as the buckled structure of LB silicene implies that the ZA mode may behave differently in LB silicene than in graphene. Therefore, the negligible ZA contribution to the overall phonon transport in LB silicene is understandable. In our calculations, the ZA mode phonons in LB silicene only contribute 12% to the total κ.

An intuitive question that should be addressed is, whether the flexural ZA modes contribute significantly to κ for the case of LHD silicene/germanene. To this end, we quantify the relative contribution of the flexural ZA modes to the total phonon transport, as depicted in Fig. 3. The relative contribution of the flexural ZA mode of the LHD silicene/germanene to the total κ is found to be only 27.4%/21.9% at 300 K, respectively, both of which are much smaller than that of graphene (∼60% (ref. 22)), due to the buckled structure induced strong phonon scattering between ZA modes with other phonon modes. However, they are nearly twice as that in LB silicene (12.2%) due to the much more planar LHD structure (all Si2 atoms are in the same plane in Fig. 1) compared with LB silicene (the buckling distance is ∼0.45 Å). When temperature increases, such coupling will be enhanced, and therefore the ZA contribution to the total κ will be reduced.

3.3. Comparison of phonon transport between LB silicene and LHD silicene/germanene

We elaborately examined the underlying mechanism for phonon transport difference in the LB silicene and LHD silicene/germanene by calculating the phonon volumetric specific heat, group velocity and phonon lifetime, as shown in Fig. 4. Using the single-mode relaxation time approximation of the Boltzmann transport equation, the contribution of each phonon mode (κ_i) to the total thermal conductivity can be obtained by κ_i(q) = C_ph,i(q)V_g,i²(q)τ_i(q), where C_ph,i, V_g,i, and τ_i are the specific heat, group velocity and phonon relaxation time.

Fig. 4 Comparison of frequency dependent phonon volumetric specific heat C_ph (upper panel), group velocity square V_g² (middle panel) and phonon lifetime τ (lower panel) for LB silicene (black squares), LHD silicene (red balls) and LHD germanene (green uptriangles). The same legends are used in all panels.

Firstly, from the top panel of Fig. 4, it can be seen clearly that the volumetric specific heat of LB silicene is the largest among the three structures, and then C_ph,i of LHD silicene is a little bit larger than its germanene counterpart. Their order agrees with the Debye cutoff frequencies of the three structures (16.62 and 15.7/8.6 THz for LB silicene and LHD silicene/germanene, respectively). Secondly, the group velocities of each phonon mode (i, q) of the LB silicene, LHD silicene/germanene are shown in the middle panel of Fig. 4. An obvious uniform reduction of group velocities from the LB silicene to the LHD silicene and then to the LHD germanene reveals that group velocity is another critical factor to decide the higher (lower) κ of the LB silicene (LHD germanene). Moreover, the bottom panel of Fig. 4 tells that the lifetime of the three structures are not very distinctly different except in the smaller frequency range from 0 to ∼4 THz, in which the lifetime is in the similar order as those of specific heat and group velocity square, i.e. the lifetime decreases from the LB silicene to the LHD silicene and then to the LHD germanene. The analysis above indicates that the higher κ of LB silicene are possibly caused by the higher specific heat, group velocity square and lifetime.

To further verify this viewpoint and get a system-level measure of the mode scaling, we normalized the average specific heat C_ph,i, group velocity square V_g,i² and phonon lifetime τ_i of the LB silicene and LHD germanene in κ_i(q) = C_ph,i(q)V_g,i²(q)τ_i(q) by the corresponding values of LHD silicene. The results are reported in Fig. 5. We find that the average C_ph, V_g² and τ of LB silicene (LHD germanene) are all larger (smaller) than those of LHD silicene, confirming its higher (lower) κ. Remarkably, of these three physical quantities, we can easily find that V_g² plays the most important role in determining the higher (lower) κ of LB silicene (LHD germanene).

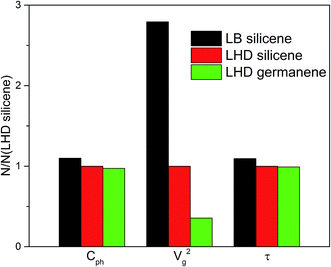Fig. 5 The specific heat capacity C_ph (black), group velocity square V_g² (red) and phonon lifetime τ (green) of the LB silicene and LHD germanene normalized by those values of LHD silicene.

3.3.1. Mechanical property. In order to further analyze why the differences among their group velocities are so large and explore the reason for their order from high to low from the LB silicene to the LHD silicene/germanene, the mechanical properties should be investigated in detail. Because similar results are obtained in y directions, here only the results in x directions are shown for brevity. We first calculated the Young's modulus (E) of the LB silicene and LHD silicene/germanene by linear fitting the strain–stress curve in the range of −0.5% < ε < 0.5%. The stress as a function of strain in x direction is presented in the top panel of Fig. 6(a). The layer thickness of LB silicene, i.e. 4.65 Å, is taken as the distance of Si–Si between the two layers plus van der Waals diameter of Si atom (4.2 Å).^22,24,40,49 The obtained Young's modulus values of the LB silicene and LHD silicene/germanene are E_x ≅ E_y = 133.1 and 100.9/68.2 GPa, respectively. 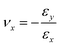Then the Poisson's ratio (ε_x and ε_y are strain, respectively, in the loaded and its perpendicular directions) is another fundamental mechanical property of materials. The Poisson's ratio of the LB silicene and LHD silicene/germanene are calculated to be ν_x = ν_y = 0.310 and 0.316/0.307, respectively.

Fig. 6 (a) Stress (upper panel) and strain energy (bottom panel) versus strain for the LB silicene (black squares), LHD silicene (red balls) and LHD germanene (green uptriangles). The negative (positive) strain represents the compressive (tensile) deformation. The strain energy is plotted as relative to the minimized energy after the structure optimization at ε = 0. Here, due to the similar results for strains in y direction, only the data for strains in x direction are shown for brevity. (b) Displacement energy and harmonic fit (upper panel) and anharmonic energy (bottom panel) for atom displacement in the out-of-plane (z) direction.

The quantities of Young's modulus, Poisson's ratio and mass density will be used to calculate the sound velocity in a solid. For the LB silicene and LHD silicene/germanene, we find that the order of their Young's modulus values (133.1 and 100.9/68.2 GPa) is in a similar trend with their normalized group velocity square N(V_g²) (2.79 and 1/0.36), meaning that the values for the LHD silicene is smaller than those for LB silicene, but larger than those for LHD germanene. In comparison, their Poisson's ratio values are almost the same (∼0.3). In addition, their corresponding mass density values are calculated to be 1.55 and 1.41/3.13 × 10³ kg m⁻³, which do not change monotonically from the LB silicene to LHD silicene/germanene.

The sound velocity propagating in a solid can be given by 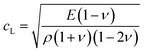, where E is the Young's modulus, ρ is the density, ν is Poisson's ratio.⁵⁰ c_L values for the LB silicene and LHD silicene/germanene through this formula are 10.9 and 10.0/5.5 km s⁻¹, respectively, which are comparable with their group velocities of the longitudinal acoustic branches near the Γ point in the first BZ (9.5, 8.9/4.9 km s⁻¹). All these analysis indicates that different Young's modulus values are the dominant reason for their group velocity square discrepancies.

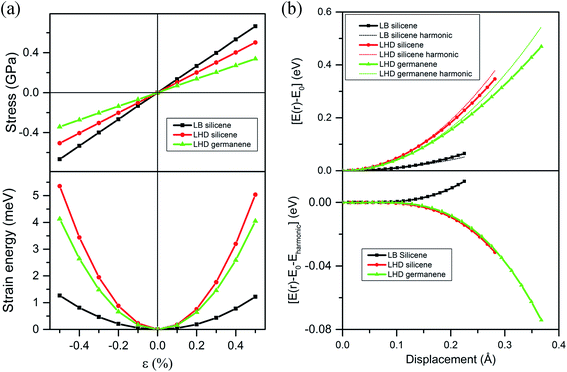
Besides, the in-plane stiffness, which is defined as 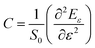, is also a good physical quantity to describe the mechanical properties of 2D materials, due to its irrelevance to thickness, which is tricky to define for 2D materials. Here, S₀ is the equilibrium area of the structure, E_ε is the strain energy defined as the energy difference between the strained and the relaxed (unstrained) structure, and ε is the uniaxial strain applied to the structure. In order to calculate the in-plane stiffness in different directions, we stretched the LB silicene and LHD silicene/germanene in either x or y direction and calculate the strain energy variation with applied strain. Then we fit the energy–strain curve by the 2^nd order polynomial in the range of −0.5% < ε < 0.5% to obtain the in-plane stiffness. The results are presented in the lower panel of Fig. 6(a). The calculated stiffness values of the LB silicene and LHD silicene/germanene are C_x ≈ C_y = 61.7 and 69.4/48.9 N m⁻¹, respectively, all of which are all much lower than that of graphene (340 N m⁻¹).⁴ The in-plane stiffness values in x and y directions are nearly the same, indicating the isotropy in the elastic mechanical property.

3.3.2. Potential well. To further explore the physical mechanism behind the phonon lifetime difference of the three structures, we analyzed the root mean-square (RMS) displacement which can be used to roughly quantify the anharmonic effect.⁵¹ Our calculated RMS values for LB silicene and LHD silicene/germanene are 0.23 and 0.28/0.37 Å, respectively, in a trend of RMS_{LB silicene} < RMS_{LHD silicene} < RMS_{LHD germanene}, which is exactly opposite to that of the normalized mean lifetime (N(τ)_{LB silicene} > N(τ)_{LHD silicene} > N(τ)_{LHD germanene}) (Fig. 5), suggesting that the anharmonicity trend is indeed consistent with that of the RMS.

Besides, the local potential energy well is mapped to decompose the potential energy into harmonic and anharmonic components. To further understand the difference in the lifetime trend, we performed statics (i.e., single-point energy) calculations for the three structures to map the potential energy surface experienced by an atom. A single atom (Si1 in LHD silicene) is displaced in small increments along the out-of-plane (z) direction and the total potential energy of the system is calculated. This analysis is performed up to the RMS displacement. In the upper panel of Fig. 6(b), the displacement energies for the three structures (i.e., the energy minus the zero-displacement energy) are plotted. To capture the harmonic part of the curve, a parabola is fit to the first six displacements and is plotted in the full range. We next subtract the harmonic fits from the potential wells and the results are plotted in the bottom panel of Fig. 6(b). For the LB silicene, the anharmonic contribution is positive for all strains, in comparison with the negative ones of the LHD structures. The anharmonicity at the RMS displacement (absolute value of [E(r) − E₀ − E_harmonic]) increases from LB silicene to LHD silicene and then to LHD germanene, thereby increasing phonon–phonon scattering and reducing their lifetimes.

3.4. Mode level phonon transport analysis

Acoustic branches with higher group velocity usually contribute more to the total κ than the optical ones with lower group velocities and higher frequencies. But if there are strong coupling between acoustic and optic phonons, the contribution to the total κ from acoustic phonons will be reduced. To verify this viewpoint, we plot the accumulative κ with respect to phonon frequency for LB silicene and LHD silicene/germanene in the left panel of Fig. 7. We can see that the main contribution (90%) to the total κ stems from phonons with frequencies below 13.0 and 5.6/4.7 THz (denoted as ν_0.9) for LB silicene and LHD silicene/germanene, respectively. It is noticed that ν_0.9 for LB silicene (13.0 THz) is much larger than its acoustic Debye cutoff frequency (∼5.8 THz), indicating significantly large contribution of optical phonon modes to the total κ.

Fig. 7 The frequency (left) and phonon mean free path (MFP) (right) accumulated thermal conductivity of LB silicene (black), LHD silicene (red) and LHD germanene (blue). The solid squares in the left (right) panel denote the frequencies (MFPs), below which the phonons contribute 90% (50%) to the overall thermal conductivity.

Besides, the accumulative κ with respect to the phonon mean free path (MFP) of the three structures are plotted in the right panel of Fig. 7. Phonons with MFPs smaller than 17.1 and 20.6/9.8 nm (MFP_0.5) contribute nearly half of the total κ for the LB silicene and LHD silicene/germanene, respectively. In other words, to get a better performance in thermoelectric devices (further decrease in thermal conductivity), nanostructures with characteristic lengths smaller than these values should be preferred.

3.5. Size effect and phonon-boundary scattering

It is well known that there are several phonon-scattering processes that lead to thermal resistivity in semiconductors. Phonon scattering mechanisms can be classified into either interactions with lattice imperfections or scattering by other phonons. The first one is collision of phonons with internal boundaries, impurity atoms, strain fields and precipitates, etc.; the second one relates to anharmonic lattice interactions which is divided into normal (N) and Umklapp (U) processes, in which the phonon momentum is not conserved.⁵² Each of these scattering mechanisms is characterized by its typical relaxation time τ_i, with i representing the different process, which is the inverse of the phonon scattering rate. Thus the overall effect of all processes is expressed by the Matthiessen rule: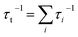 .⁵² Analytical and semi-empirical expressions for these τ_i values have been developed for different i processes.^53–55

At very low temperatures, the thermal conductivity can be very well explained on the basis of boundary scattering.⁵⁶ To quantify the possible effect of microstructure size, the phonon-boundary scattering rate is assumed to be independent of temperature and frequency, and can be estimated as 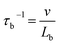, where L_b is characteristic length associated with the specimen under study and v is the phonon group velocity which is different for each mode. We believe that it is a better approximation if one uses the different phonon group velocities for different phonon branches. The characteristic length L_b is determined by the crystal dimensions and is assumed to be the same for all phonons. Here we treat L_b as an unknown parameter to which we assign a value in order to give the best fit to experimental results in the future.

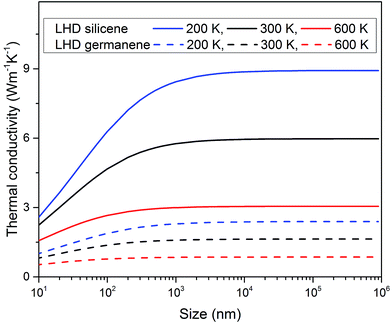
To quantify the possible effect of microstructure size, the thermal conductivities of LHD silicene and germanene with different grain boundary sizes ranging from 10 nm to 1 mm and for three typical temperatures (200 K, 300 K and 600 K) are shown in Fig. 8. Firstly, due to the presence of boundary, scattering rate of phonons is in reverse relationship with the grain boundary size, i.e. , and the thermal conductivity monotonically decreases when the grain boundary size is reduced, thus increasing the phonon-boundary scattering rate and lowering the phonon-boundary scattering phonon lifetime. Additionally from Fig. 8, we can see that the boundary effect at lower temperature (T = 200 K) is much stronger than that at higher temperature (T = 600 K). This is because the number of phonons at higher temperature (T = 600 K) is much larger than that at lower temperature (T = 200 K), so that phonon–phonon scattering will be the dominant process for the magnitude of κ at higher temperature. Therefore, the boundary scattering is remarkable only at lower temperature. The grain boundary size dependent thermal conductivity can provide direct reference size values for the LHD silicene/germanene based materials to be used in future nanoelectronic devices such as thermoelectrics.

Fig. 8 Thermal conductivities of LHD silicene (solid lines) and LHD germanene (dashed lines) with boundary sizes ranging from 10 nm to 1 mm at temperatures of 200 K (blue lines), 300 K (black lines) and 600 K (red lines).

4. Conclusions

In summary, we have studied the thermal transport of the LHD silicene/germanene systematically by first-principles calculations, which is compared with the case of LB silicene/germanene. It is interesting to find that the intrinsic κ of the LHD silicene/germanene is as low as 5.9/1.6 W m⁻¹ K⁻¹, which is substantially lower than that of LB silicene (∼20–25 W m⁻¹ K⁻¹) and germanene (∼10 W m⁻¹ K⁻¹). The relative contribution from the flexural ZA modes to the total κ of the LHD silicene/germanene is only 27.4%/21.9%, much smaller than that of perfectly planar graphene (∼60%), because the buckled structure induces an interaction between ZA modes with other phonon modes. However, this value is nearly twice as that of LB silicene (∼12.2%) because of the more planar LHD structure compared with the LB silicene. The detailed analysis shows that the volumetric specific heat, group velocity square and the phonon lifetime of LHD silicene/germanene are all lower than those of LB silicene. Among the three factors, the group velocity square is found to play the most dominant role in greatly reducing the intrinsic κ of the LHD silicene/germanene, which can be further correlated with their lower Young's modulus than that of LB silicene. Besides, the difference of phonon lifetimes among the LB silicene and LHD structures are further explained in-depth by examining the local potential well. The RMS values for LB silicene and LHD silicene/germanene are 0.23 and 0.28/0.37 Å, respectively, in a trend of RMS_{LB silicene} < RMS_{LHD silicene} < RMS_{LHD germanene}, which is exactly opposite to that of their normalized mean lifetime (N(τ)_{LB silicene} > N(τ)_{LHD silicene} > N(τ)_{LHD germanene}), justifying physically that the larger displacements will lead to stronger anharmonicity and reduced lifetimes. Finally, the boundary effect at lower temperature is found to be much stronger than that at higher temperature. Our results provide important insights into the thermal transport in the ground state of 2D Si and Ge, and offer guidelines for the use of LHD silicene/germanene in thermal management and thermoelectric devices.

Acknowledgements

This work is supported by the Deutsche Forschungsgemeinschaft (DFG) (Project No. HU 2269/2-1). Our numerical calculations were performed on the High Performance Computing Center of Nanjing University. Y. H. gratefully acknowledges technical support from Dr X. Zhang and Mr Y. G. Zhou at RWTH Aachen University.

References

1. K. S. Novoselov, A. K. Geim, S. Morozov, D. Jiang, Y. Zhang, S. A. Dubonos, I. Grigorieva and A. Firsov, Electric field effect in atomically thin carbon films, Science, 2004, 306, 666–669.
2. F. Matusalem, M. Marques, L. K. Teles and F. Bechstedt, Stability and electronic structure of two-dimensional allotropes of group-IV materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045436.
3. Y. Kuang, L. Lindsay, S. Shi and G.-P. Zheng, Tensile strains give rise to strong size effects for thermal conductivities of silicene, germanene and stanene, Nanoscale, 2016, 8, 3760–3767.
4. C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321, 385–388.
5. R. J. Young, I. A. Kinloch, L. Gong and K. S. Novoselov, The mechanics of graphene nanocomposites: a review, Compos. Sci. Technol., 2012, 72, 1459–1476.
6. S. Das Sarma, S. Adam, E. H. Hwang and E. Rossi, Electronic transport in two-dimensional graphene, Rev. Mod. Phys., 2011, 83, 407–470.
7. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Superior Thermal Conductivity of Single-Layer Graphene, Nano Lett., 2008, 8, 902–907.
8. S. Ghosh, I. Calizo, D. Teweldebrhan, E. P. Pokatilov, D. L. Nika, A. A. Balandin, W. Bao, F. Miao and C. N. Lau, Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits, Appl. Phys. Lett., 2008, 92, 151911.
9. A. A. Balandin, Thermal properties of graphene and nanostructured carbon materials, Nat. Mater., 2011, 10, 569–581.
10. K. S. Novoselov, V. Fal, L. Colombo, P. Gellert, M. Schwab and K. Kim, A roadmap for graphene, Nature, 2012, 490, 192–200.
11. A. Adán-Más and D. Wei, Photoelectrochemical properties of graphene and its derivatives, Nanomaterials, 2013, 3, 325–356.
12. Y. Shao, J. Wang, H. Wu, J. Liu, I. A. Aksay and Y. Lin, Graphene based electrochemical sensors and biosensors: a review, Electroanalysis, 2010, 22, 1027–1036.
13. W. Choi, I. Lahiri, R. Seelaboyina and Y. S. Kang, Synthesis of graphene and its applications: a review, Crit. Rev. Solid State Mater. Sci., 2010, 35, 52–71.
14. S. Cahangirov, M. Topsakal, E. Aktürk, H. Şahin and S. Ciraci, Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium, Phys. Rev. Lett., 2009, 102, 236804.
15. F. Bechstedt, L. Matthes, P. Gori and O. Pulci, Infrared absorbance of silicene and germanene, Appl. Phys. Lett., 2012, 100, 261906.
16. L. Matthes, P. Gori, O. Pulci and F. Bechstedt, Universal infrared absorbance of two-dimensional honeycomb group-IV crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035438.
17. M. Lars, P. Olivia and B. Friedhelm, Massive Dirac quasiparticles in the optical absorbance of graphene, silicene, germanene, and tinene, J. Phys.: Condens. Matter, 2013, 25, 395305.
18. L. Chun-Liang, A. Ryuichi, K. Kazuaki, T. Noriyuki, M. Emi, K. Yousoo, T. Noriaki and K. Maki, Structure of Silicene Grown on Ag(111), Appl. Phys. Express, 2012, 5, 045802.
19. M. E. Dávila, L. Xian, S. Cahangirov, A. Rubio and G. L. Lay, Germanene: a novel two-dimensional germanium allotrope akin to graphene and silicene, New J. Phys., 2014, 16, 095002.
20. X. Zhang, H. Bao and M. Hu, Bilateral substrate effect on the thermal conductivity of two-dimensional silicon, Nanoscale, 2015, 7, 6014–6022.
21. H. Xie, T. Ouyang, É. Germaneau, G. Qin, M. Hu and H. Bao, Large tunability of lattice thermal conductivity of monolayer silicene via mechanical strain, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 075404.
22. M. Hu, X. Zhang and D. Poulikakos, Anomalous thermal response of silicene to uniaxial stretching, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195417.
23. H. Xie, M. Hu and H. Bao, Thermal conductivity of silicene from first-principles, Appl. Phys. Lett., 2014, 104, 131906.
24. X. Zhang, H. Xie, M. Hu, H. Bao, S. Yue, G. Qin and G. Su, Thermal conductivity of silicene calculated using an optimized Stillinger–Weber potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 054310.
25. S. Balendhran, S. Walia, H. Nili, S. Sriram and M. Bhaskaran, Elemental analogues of graphene: silicene, germanene, stanene, and phosphorene, Small, 2015, 11, 640–652.
26. P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Silicene: Compelling Experimental Evidence for Graphenelike Two-Dimensional Silicon, Phys. Rev. Lett., 2012, 108, 155501.
27. A. Fleurence, R. Friedlein, T. Ozaki, H. Kawai, Y. Wang and Y. Yamada-Takamura, Experimental Evidence for Epitaxial Silicene on Diboride Thin Films, Phys. Rev. Lett., 2012, 108, 245501.
28. D. Kaltsas and L. Tsetseris, Stability and electronic properties of ultrathin films of silicon and germanium, Phys. Chem. Chem. Phys., 2013, 15, 9710–9715.
29. V. O. Özçelik and S. Ciraci, Local Reconstructions of Silicene Induced by Adatoms, J. Phys. Chem. C, 2013, 117, 26305–26315.
30. S. Cahangirov, V. O. Özçelik, L. Xian, J. Avila, S. Cho, M. C. Asensio, S. Ciraci and A. Rubio, Atomic structure of the √3 × √3 phase of silicene on Ag(111), Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035448.
31. B. Silvi and A. Savin, Classification of chemical bonds based on topological analysis of electron localization functions, Nature, 1994, 371, 683–686.
32. K. Momma and F. Izumi, VESTA: a three-dimensional visualization system for electronic and structural analysis, J. Appl. Crystallogr., 2008, 41, 653–658.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
34. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
35. G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid–metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
36. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
37. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
38. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
39. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
40. Y. Han and M. Hu, Ground state of bilayer hα-silica: mechanical and electronic properties, Nanotechnology, 2015, 26, 505702.
41. W. Li, J. Carrete, N. A. Katcho and N. Mingo, ShengBTE: A solver of the Boltzmann transport equation for phonons, Comput. Phys. Commun., 2014, 185, 1747–1758.
42. S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515.
43. A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl₂-type SiO₂ at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
44. A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5.
45. R. Li, J. Zhou, Y. Han, J. Dong and Y. Kawazoe, A new (2 × 1) reconstructed edge structure of zigzag Si nanoribbon: First principles study, J. Chem. Phys., 2013, 139, 104703.
46. L. N. Virgin, Vibration of axially-loaded structures, Cambridge University Press, Cambridge, United Kingdom, 2007.
47. J. Carrete, W. Li, L. Lindsay, D. A. Broido, L. J. Gallego and N. Mingo, Physically founded phonon dispersions of few-layer materials, and the case of borophene, arXiv preprint arXiv:1601.02884, 2016.
48. G. Qin, Q.-B. Yan, Z. Qin, S.-Y. Yue, M. Hu and G. Su, Anisotropic intrinsic lattice thermal conductivity of phosphorene from first principles, Phys. Chem. Chem. Phys., 2015, 17, 4854–4858.
49. H. Yang, Q. Guangzhao, J. Christoph and H. Ming, Strain-modulated electronic and thermal transport properties of two-dimensional O-silica, Nanotechnology, 2016, 27, 265706.
50. L. E. Kinsler, A. R. Frey, A. B. Coppens and J. V. Sanders, Fundamentals of Acoustics, ed. E. Kinsler, A. R. Frey, A. B. Coppens and J. V. Sanders, Wiley-VCH, John Wiley and sons Inc., New York, USA, 4th edn, 1999, p. 560, ISBN 0-471-84789-5.
51. K. D. Parrish, A. Jain, J. M. Larkin, W. A. Saidi and A. J. H. McGaughey, Origins of thermal conductivity changes in strained crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 235201.
52. C. Kittel, Introduction to solid state physics, Wiley, 2005.
53. M. Asen-Palmer, K. Bartkowski, E. Gmelin, M. Cardona, A. Zhernov, A. Inyushkin, A. Taldenkov, V. Ozhogin, K. Itoh and E. Haller, Thermal conductivity of germanium crystals with different isotopic compositions, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 9431.
54. D. Morelli, J. Heremans and G. Slack, Estimation of the isotope effect on the lattice thermal conductivity of group IV and group III–V semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 195304.
55. Y. Amouyal, Reducing Lattice Thermal Conductivity of the Thermoelectric Compound AgSbTe₂ (P4/mmm) by Lanthanum Substitution: Computational and Experimental Approaches, J. Electron. Mater., 2014, 43, 3772–3779.
56. P. Carruthers, Theory of Thermal Conductivity of Solids at Low Temperatures, Rev. Mod. Phys., 1961, 33, 92–138.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra14351b

---