The influence of protonation on the structure and spectral properties of porphine: UV-vis, 1H NMR and ab initio studies†
Abstract
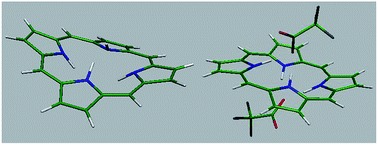
In this study, protonation of porphine (H2P) with a range of weak and strong acids was investigated. The dication of H2P was water soluble and therefore UV-vis and 1H NMR studies were performed in water and D2O as well as in dichloromethane and dimethylformamide. In contrast to the dication of other porphyrins, protonated species of H2P were completely decomposed upon evaporation of solvent at room temperature and therefore were studied in solution. Also, high level ab initio calculations were used to predict the structure, frontier molecular orbitals and transition energies of H2P dication. The Soret band of H2P was only slightly shifted to longer or shorter wavelengths in reaction with weak and strong acids, respectively. The results show that the presence of aryl or at least alkyl substituents at the meso positions of porphyrin macrocycle is necessary for the observation of significant red shifts of the Soret band. In the case of the Q(0,0) band, large blue shifts of the band were observed for the dications that correlate with the absence of any π electron-donating group at the meso position. In 1H NMR spectra, signals for both the β and meso protons were shifted downfield, which shows the negligible decrease in the porphine ring current caused by the out-of-plane distortion of the macrocycle. While ab initio calculations show a saddle shaped conformation for [H4P]2+, H4P(CF3COO)2 was found to adopt an unusual wave conformation that clearly differs from that of previously characterized dications of meso-tetra(aryl)- and meso-tetra(alkyl)porphyrins. Also, the calculations on monoprotonated species show that [H3P]+ and H3P(CF3COO) adopt a nearly saddle type and dome shaped conformation, respectively. On the other hand, the energies of absorption bands of H4P(CF3COO)2 calculated at the TD-B3LYP/cc-pVDZ level of theory predicted the red shift of the Soret band and the blue shift of the Q(0,0) bands that are in accord with the results of UV-vis studies. The results revealed the role played by the acid molecules on the blue shift of the Q(0,0) band of the diprotonated species. Furthermore, the calculated changes in the bond lengths and bond angles show that the involvement of in-plane nuclear reorganization (IPNR) in the observed red shifts of the Soret and Q(0,0) bands cannot be excluded.


 Please wait while we load your content...
Please wait while we load your content...