Electronic transport properties of silicon carbide molecular junctions: first-principles study
Yi Muab,
Zhao-Yi Zengc,
Yan Chenga and
Xiang-Rong Chen*a
aInstitute of Atomic and Molecular Physics, College of Physical Science and Technology, Sichuan University, Chengdu 610064, China. E-mail: ycheng66@qq.com
bSchool of Physics and Electronic Engineering, Sichuan Normal University, Chengdu 610066, China
cCollege of Physics and Electronic Engineering, Chongqing Normal University, Chongqing 400047, China
First published on 12th September 2016
Abstract
The contact geometry and electronic transport properties of a silicon carbide (SiC) molecule coupled with Au (1 0 0) electrodes are investigated by performing density functional theory plus the non-equilibrium Green's function method. We perform simulations of the Au–SiC–Au junction breaking process by calculating the conductance in four different anchoring geometries and obtain the equilibrium conductance and the projected density of states of junctions in the optimal position. The hollow–hollow configuration is found to be the most stable contact geometry with the largest conductance. From the calculation of restoring force and the spatial electron density differences after the structural break, we conclude that the Si–C bond is more stable than Au–C and Au–Si bonds in the single-molecular molecular junction. Moreover, the behavior of the junction currents is revealed under small bias. All junctions exhibit a linear current–voltage relationship, indicating characteristic metallic behavior at low bias voltage. The asymmetry of the I–V curves reflects the asymmetry of the molecule and the contact geometry. The origin of the transport spectrum of the junctions is discussed with the molecular projected self-consistent Hamiltonian (MPSH) states. The calculated results prove that the coupling morphology of the SiC molecule connected with electrodes, the distance and the external bias voltage have a great effect on the conductance of nanoscale junctions.
1. Introduction
Single-molecule transport junctions have received great attention since they form an excellent platform for investigating transport characteristics in nanoscale electronic devices.1–7 These structures can act as active building blocks, such as diodes, transistors, switches and rectification, with advanced electronic functionality and can work as interconnectors which may help to minimize the size of microelectronic circuits and enhance performance. During past decades great efforts have been devoted to the field of single-molecule transport junctions. Experimentally, visualization and manipulation of individual molecules became possible by versatile techniques such as scanning tunneling microscopy (STM),8,9 scanning tunneling microscope-based break junctions (STM-BJs)10 and mechanically controlled break junctions (MCBJs).11,12 The electronic properties of single molecules attached to metal electrodes, which play an essential role in establishing mechanically stable and reproducible contacts, have been measured successfully by using these powerful techniques. In terms of theoretical studies, the simplicity of single-molecule junctions based on direct bonding of a small molecule between two metallic electrodes provides an ideal system for the investigation of fundamental questions related to molecular electronics. After years of intensive study, the basic physics that governs the behaviours of the single molecules has been discovered and this capability allows us to interpret the existing experiments and design new ones.13–19Silicon carbide (SiC), being mechanically extremely hard and chemically inert,20 is one of the most important IV–IV compound semiconductors. The uniqueness of silicon carbide properties arises from the nature of the Si–C bond, which is among the strongest chemical bonds in matter (bond dissociation energy > 350 kJ mol−1). Consequently, this provides a very good chemical and thermal stability as well as very high melting temperature, high electrical conductance, high mechanical properties and hardness. Its excellent properties make it an excellent candidate for molecular devices, catalyst supports, and so on. It is widely used in a number of important applications, mostly in high-power, high-temperature and high-frequency electronics.21–27 SiC sustains various stable nanostructures28–30 which have been fabricated experimentally.29,30 Such low dimensionality is expected to exhibit properties that their bulk counterparts may not have.31,32
Intensive research has focused on correlated mechanical, optical and electrical properties.33–36 Mohammad et al.37 showed that transport properties in SiC nanowires can be greatly enhanced by quantum confinement and dielectric confinement. Jia et al.38 found that the conductance and the current–voltage curve of SiC nanotubes (SiCNTs) have been influenced by increasing the length of SiCNT and explained this by electron tunneling theory.
Although the SiC nanostructures and their transport properties have been studied,33–38 many of the fundamental electronic transport properties of a single SiC molecule junction have not been fully characterized, including the anchoring geometries, distance and external bias. It is well-known that the properties of materials are determined by their chemical bonds and arrangement. The crystalline structure of SiC can be considered to consist of the close-packed stacking of double layers of Si and C atoms.39 Each C or Si atom is surrounded by four Si or C atoms in strong tetrahedral sp3 bonds.40 Other SiC compounds such as two-dimensional (2D) SiC sheets and nanotubes are compounds with sp2 bonding. It should be noted that the diatomic molecule SiC studied in this work is a linear molecule composed of a carbon atom and a silicon atom covalently combined. Its chemical and physical properties are quite different from those of the bulk and nanostructures. We design a typical model in which the single molecule connects to the electrodes directly to truly harness the potential of a metal-molecule-mental system. The hybridization of molecular states with metallic electrode states results in a different electronic structure for the combined system. We explore the atomic contacts in the geometry of the tip-substrate arrangement, such as those of STM-BJ and MCBJ, simulating the Au–SiC–Au junction breaking processes in four different anchoring geometries, and calculate the current–voltage curve of these junctions at the equilibrium position. Our results clearly show that all the single-molecular junctions exhibit linear I–V curves, indicating characteristic metallic behaviour in the low bias voltages. From the calculation of the restoring force and the spatial electron density differences after the structural break, we conclude that the Si–C bond is more stable than Au–C and Au–Si bonds in the single-molecular junction. The origin of the transport spectrum of the junctions is discussed with the molecular projected self-consistent Hamiltonian (MPSH) states. The MPSH analysis implies that the contact geometry and external bias have a great impact on the energy and spatial distribution of the frontier molecular orbitals near the Fermi level (Ef), leading to different molecular conductance.
This paper is organized as follows. The theoretical model and computational details are given in Section 2. The results and discussion are presented in Section 3, and the summary of the main results is given in Section 4.
2. Simulation model and computational details
In this paper, inspired by the mechanically controlled break junctions (MCBJ), we perform theoretical calculations for the electronic structure based on density-functional theory (DFT)41 implemented in the SIESTA code,42 which uses nonlocal norm-conserving Troullier–Martins pseudopotentials,43 factorized in the Kleinman–Bylander form44 to describe the effect of the core electrons, and linear combination of finite-range numerical atomic orbitals to describe the valence states. The electronic transport properties are investigated by the TranSIESTA method that allows for first-principles quantum chemical modelling of molecules under non-equilibrium conditions.42 This method is based on the non-equilibrium Greens function (NEGF) technique,45 which has been interfaced with the SIESTA electronic structure package by calculating the density matrix of the system self-consistently46 when the system is under an external bias. An important feature of the TranSIESTA method is that it treats the entire system (molecule and electrodes) with chemical accuracy.47 Our theoretical model is composed of a single SiC molecule coupling with two semi-infinite Au (100) metal electrodes with the lattice parameter 4.08 Å. This two-probe system can be divided into three regions, i.e. the left electrode, the right electrode, and the central scattering region, which includes a SiC molecule, and seven and six Au atomic layers, respectively, on each side to screen the perturbation effect.48It is of great importance to study the effect of the contact geometries since the actual contact geometries have not been specified in experiments. In our theoretical studies, for the Au–SiC–Au junction system, several distinct contact structures were studied, as is shown in Fig. 1, including (a) SiC connected to pyramidal-shaped electrodes at the top site with the molecular axis parallel to the transport direction (z-axis), (b) SiC connected to pyramidal-shaped electrodes at the hollow site to the left and at the top site to the right (molecular axis parallel to the z-axis), (c) SiC connected to pyramidal-shaped electrodes at the top site to the left and at the hollow site to the right (molecular axis parallel to the z-axis), and (d) SiC connected to two hollow sites with the molecular axis parallel to the z-axis. The four-atom pyramidal-shaped structure mentioned above represents the tip. The two semi-infinite electrodes are considered to be perfect crystals and the chemical potential is well approximated by that of a perfect bulk electrode. For the scattering region the electronic potential is calculated self-consistently for each applied bias.49–51 The current via a molecule can be obtained from the Landauer–Büttiker formula52
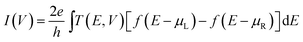 | (1) |
| T(E) = Tr[ΓL(E)GR+M(E)ΓR(E)GRM(E)] | (2) |
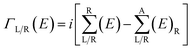 is the anti-Hermitian part of the self-energy. The self-energies
is the anti-Hermitian part of the self-energy. The self-energies 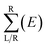 and
and 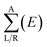 are introduced into the effective Hamiltonian51 in consideration of the semi-infinite effect of the left (right) electrode. GR and GA are the retarded and advanced Green's function of the scattering region containing all the information about the electronic structure of the extended molecule attached to the contacts.
are introduced into the effective Hamiltonian51 in consideration of the semi-infinite effect of the left (right) electrode. GR and GA are the retarded and advanced Green's function of the scattering region containing all the information about the electronic structure of the extended molecule attached to the contacts.
For the system at equilibrium, the conductance G of the two-probe device is calculated by using the Fisher–Lee relation53
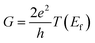 | (3) |
In the DFT calculation, we use the Perdew–Zunger form55 of the local-density approximation (LDA) to the exchange-correlation functional. Nonlocal scalar-relativistic Troullier–Martins pseudopotentials43 are generated from the configurations: Au (5d106s1), Si(3s23p2), and C(2s22p2). In all the calculations, valence electrons are expanded in the single-zeta plus single polarization basis set (SZP) for Au atoms and the double-zeta plus single polarization basis sets (DZP) for Si and C atoms.
The electrodes have an fcc crystalline structure and are oriented along the (1 0 0) direction. The unit cell of the extended molecule comprises a SiC molecule and 13 Au atomic layers each containing 3 × 3 atoms in the surface plane. The periodic boundary condition is applied in the basal plane orthogonal to the transport direction with four irreducible k-points in the two-dimensional Brillouin zone. A k-grid sampling of 2 × 2 × 100 for the Au electrodes is employed. The cut-off energy and the iterated convergence criterion for total energy are set to 300 Ry and 10−4, respectively. In addition, the charge density is integrated over 50 energy points along the semi-circle and 10 energy points along the line in the complex plane, and 20 poles are used for the Fermi distribution.
3. Results and discussion
The simulation started with compression by decreasing the gap between the gold pyramids and the SiC molecule. From this point we simulated the stretching process of the molecular junction by increasing the distances along the z-length of the unit cell in steps of 0.5 Å until the molecular junction was completely broken. At each step, optimization is achieved by allowing the molecule and the apex to relax, while keeping the rest of the gold layers fixed.56 In general, ab initio geometry optimization shows that the SiC molecule remains perpendicular to the electrode with the binding geometry largely unaffected. We refer to these as the optimal configuration through out the paper.In Fig. 2, we show the cohesion energy, ΔE = E(Au electrodes + SiC molecule) − E(SiC molecule) − E(Au electrodes), as a function of atomic distance dz for all the configurations. It is easy to see that for all the four configurations, ΔE(dz) is a parabola with minimum energy located at the equilibrium distance dz,eq. After numerical fitting of the data using a parabolic function, we have evaluated the equilibrium distance for each configuration. After optimization, dz,eq = 13.082 Å in Fig. 2(a), 10.459 Å in Fig. 2(b), 10.37 Å in Fig. 2(c) and 8.229 Å in Fig. 2(d). The distance dz,eq signifies the optimal position whose energy is a minimum, indicating that the system will naturally form if the electrodes are free to relax. Comparing all the configurations, the cohesion energy of each system at the optimal position is different in each case and it increases in turn from configuration (a) to configuration (d). To verify the validity of the employed method and the reliability of the atomic pseudo-potentials used in this work, we calculate the Au–Si, Au–C and Si–C bond lengths when the junctions are in the optimal equilibrium position. For the top–top structure the calculated Au–Si bond length (2.27 Å) as well the Au–C bond length (1.90 Å) agree with the values found in both experiments (dAu–Si = 2.26 Å,57 dAu–C = 1.92 Å58) and other theoretical studies (dAu–Si = 2.28 Å,59 dAu–C = 1.98 Å60). The Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond length, dSi–C, of 1.66 Å is remarkably short compared to a typical Si–C bond (1.88 Å).61 This fits well with the experimental value of 1.61 Å for the length of the carbon–silicon triple bond.62 For configurations (b), (c) and (d), the Si–C single bonds are found to be longer: dSi–C = 1.71 Å, 1.72 Å and 1.84 Å, respectively. By comparison, the Si–C bond length of configuration (d) is in excellent agreement with the Si–C bond length of 1.88 Å observed in SiC.61 The Si–C bond length difference is presumably due to difference in nearest-neighbor coordination number (CN) and atomic-interaction between Au, Si and C atoms. For configuration (d) Si and C atoms have the greatest nearest-neighbor coordination number as well the greatest atomic-interaction between atom and electrode on its side (4 Au atoms); hence the Si–C bond length is the longest. Comparatively, in configuration (a) Si and C atoms have the smallest nearest-neighbor coordination number as well the weakest atomic-interaction between atom and electrode on its side (only 1 Au atom); hence the Si–C bond length is the shortest, different from the others.
C bond length, dSi–C, of 1.66 Å is remarkably short compared to a typical Si–C bond (1.88 Å).61 This fits well with the experimental value of 1.61 Å for the length of the carbon–silicon triple bond.62 For configurations (b), (c) and (d), the Si–C single bonds are found to be longer: dSi–C = 1.71 Å, 1.72 Å and 1.84 Å, respectively. By comparison, the Si–C bond length of configuration (d) is in excellent agreement with the Si–C bond length of 1.88 Å observed in SiC.61 The Si–C bond length difference is presumably due to difference in nearest-neighbor coordination number (CN) and atomic-interaction between Au, Si and C atoms. For configuration (d) Si and C atoms have the greatest nearest-neighbor coordination number as well the greatest atomic-interaction between atom and electrode on its side (4 Au atoms); hence the Si–C bond length is the longest. Comparatively, in configuration (a) Si and C atoms have the smallest nearest-neighbor coordination number as well the weakest atomic-interaction between atom and electrode on its side (only 1 Au atom); hence the Si–C bond length is the shortest, different from the others.
After obtaining the junction geometry at each stage in the stretching process, we then computed the electrical conductance as a function of distance dz in each configuration (also in Fig. 2). The conductance is obtained from the electron transmission function T(E), evaluated at the Fermi energy. In Fig. 2(a), when the junction is stretched from dz ∼ 10.809 Å to dz ∼ 11.809 Å, the conductance slightly increases from 1.16G0 to 1.18G0. Then for dz > 11.809 Å, the conductance starts to decline. When dz = 15.309 Å, the Au–C bond breaks and the conductance (at dz ∼ 15.309 Å) of 0.17G0 jumps abruptly to 0.018G0. A similar trend is observed in Fig. 2(b) and (c) with conductance increasing monotonically at first. As dz increases, the conductance decreases. In Fig. 2(b) the conductance of 0.06G0 at dz ∼ 12.769 Å decreases to 0.006G0 at dz ∼ 13.269 Å after the Au–C bonds breaks. In Fig. 2(c) the conductance of 0.1G0 at dz ∼ 12.269 Å decreases to 0.017G0 at dz ∼ 12.769 Å after the Au–Si bond breaks. Fig. 2(d) behaves differently from the other three configurations. The conductance first decreases from 2.91G0 at dz ∼ 7.229 Å to 1.86G0 at dz ∼ 8.729 Å, and then increases to 1.95G0 at dz ∼ 9.229 Å; next it goes down. After the Au–C bond breaks, the conductance of 0.12G0 at dz ∼ 10.729 Å drops to 0.015G0 at dz ∼ 11.229 Å. We also note that just before the Au–Si bond breaks, the conductance jumps faster to a small value than it does just before the Au–C bond breaks during the same stretch. Fig. 2 also illustrates the tendency for a distinct, monotonic decrease in the conductance with stretching distance. The conductance displays an overall decrease by 1 order of magnitude after the contact breaks for every 0.5 Å stretch, and the value of the conductance rapidly decreased into the 10−2 to 10−4 range. In general, when the contact is pulled apart in different configurations, even small changes in the local atomic distance dz can lead to significant changes in the conductance of the junction, indicating that the conductance is sensitive to the tiny variation in the contact distance and anchoring geometries, namely, to the local atomic rearrangement.63 We also find that the equilibrium conductance of the SiC molecule in each configuration at the optimal position is 0.83G0 in Fig. 2(a), 1.42G0 in Fig. 2(b), 0.88G0 in Fig. 2(c) and 1.81G0 in Fig. 2(d), showing that all the junctions of Au–SiC–Au have good conductivity. In particular, when the device is in hollow–hollow configuration the conductance of the junction at the optimal position reaches a maximum with the expected Si–C bond length.
To get the atomic force information between the atoms as the two contact distance is pulled apart, we computed the restoring force as a function of distance dz. We put together the cohesion energy ΔE and the tensile force Fz in Fig. 3 to show their relationship more clearly. The restoring force is computed as64
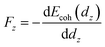 | (4) |
We can understand the broken bond through coordination numbers. In structure (a), the Au atom has a higher coordination number of 5 compared to the Si and C atoms whose coordination numbers are both 2. When the two contact distance is pulled apart continuously the weak (Au–C) bond breaks rather than the Au–Si and Si–C bonds. The case in structure (d) is similar to structure (a): the broken bond is the weak (Au–C) bond. In structure (b), the Si atom and Au atom have the same coordination number of 5, that is, the Si atom and Au atom have the same status, so the Si atom has the higher coordination number compared to the C atom, and the broken bond is the weak (Au–C) bond as well. Actually, the coordination number of C atoms and the type of broken bonds are the same in configurations (a) and (b); thus the calculated maximum forces agree with each other. In structure (c), the C atom, whose coordination number is the same as the Au atom, has the same status as the Au atom. The C atom has a higher coordination number than the Si atom, so the broken bond is the Au–Si bond rather than the Si–C bond. It should be noted that the SiC molecule bonded to the side of the Au atoms moves as a whole perpendicular to the lead surface throughout the elongation process in the four configurations, indicating the presence of strong covalent bonding between Si and C atoms. The Si–C bond is more stable than the Au–C and Au–Si bonds in this single-molecular junction model.
In addition, we concentrate on the spatial electron density difference when the pulling force is beyond the maximum achieved force and the structure breaks, as illustrated in Fig. 4. The electron density difference, ρ′(r) = ρ(r) − ρatoms(r), between the self-consistently calculated electron density of the junctions after the structural break, ρ(r), and that of free atoms placed at the same positions, ρatoms(r), describes the changes in electron density that occur for a given electronic transition. It is possible to “see” bonds with electron density difference by discovering where electrons build up or are depleted and where atoms get together. Fig. 4 exhibits the uneven distribution of valence electrons of the junctions in the broken structure. The electrons are distributed between the Au atom and the Si atom, the Si atom, and the C atom and the C atom and the Au atom, implying that they form strong covalent bonds with the nearest-neighbouring atoms. It is easy to see that the charge is more localized on the Si–C atom rather than the right/left Au atoms, which may be put down to the fact that Si and C atoms form stronger covalent bonds than Au–C and Au–Si bonds, consistent with the above discussion. Furthermore, we find a density increase in the SiC molecular center, and therefore a charge accumulation occurs in the “bond” of SiC. In spite of the fact that both constituents of SiC are Group IV elements with similar valence electron configuration, they behave differently in quantum transport.
To understand the transport properties and the structure of the electronic transport channel of the junctions in the optimal position, we analyze the transmission function T (E, V = 0) and the orbital resolved projected density of states (PDOS) of the Au–SiC–Au junctions at the optimal distance for the four configurations, which are depicted in Fig. 5. By default, the Fermi energy of the Au electrodes defines the zero of energy, Ef = 0. The PDOS is related to the molecular energy level, which is different from the levels of the free molecule once it is bonded to the electrodes. The hybridization with the metal levels broadens the molecular levels and the modified energy levels determine the characteristics of transmission peaks. That is to say, the formation of transmission peaks is related to the molecular orbitals. To find the origin of the transport spectrum of the junctions, the molecular projected self-consistent Hamiltonian (MPSH) is obtained. The self-consistent Hamiltonian is projected onto the Hilbert space spanned by the basis functions of the molecule (including the SiC molecule and anchoring groups) in consideration of their interaction. The eigenstates of MPSH can be considered as molecular orbitals renormalized by the molecule–electrode interaction. The MPSH states energies near the Fermi level are also shown in Fig. 5. It is noted that the different behavior of transmission and PDOS spectra implies different transport mechanisms. In Fig. 5(a) the transmission spectrum exhibits sharp transmission resonance at approximately −0.37 eV, which mainly arises from tunneling via HOMO (degenerate states). The resonance is probably due to the weak coupling on the two ends. However, the narrow peak is away from the Fermi level and the HOMO state contributes little to conductance; hence the equilibrium conductance is only 0.82. In the case of configurations (b)–(d), where SiC binds at least at one side at the hollow site, the electronic coupling is stronger than that for configuration (a), presumably due to the enhanced overlap between the Si, C and Au orbitals. As a consequence, there is no resonance at Ef, but instead, T(E, V) has a broad feature around the Fermi level. In Fig. 5(b) the major transmission peaks, located at −0.63 eV and 0.47 eV, correspond to the HOMO and the LUMO states, respectively. As for Fig. 5(c), its transmission close to Ef blends into a flat and broad transmission feature. The almost negligible bump is related to the LUMO state, which is nearer to Ef. It is easy to see that configuration (d) has the strongest electronic coupling compared to the other configurations by observing the degree of broadening in the transmission spectrum. The equilibrium conductance is twice as large as configuration (a). It appears that the major transmission peak located around −1 eV may arise from tunneling via the HOMO−1, HOMO−2, HOMO−3 and HOMO−4 states, considering its broadness. And the relatively narrow peak at 0.14 eV corresponds to the LUMO states.
In order to prove that the electron transport tunnel is primarily formed by the coupling of the SiC molecule and the Au electrodes, we show the transmission functions of all the configurations with the SiC molecule removed in Fig. 6. It is obvious that the electron transmission is insignificant in Fig. 6(a)–(c) without the SiC molecule; more specifically, the probability of electronic direct tunneling from one electrode to the other is small. But for the case of Fig. 6(d), the electronic direct tunneling makes a non-ignorable contribution to its biggest conductance. The calculated PDOS of the Au atoms (not shown) reveals that the densities of states dx2−y2 + dxy, dxz + dyz, and dz2 are very large around −2.0 eV. So the transport channel without the SiC molecule around −2.0 eV is mainly formed by the Au dx2−y2 + dxy, dxz + dyz, and dz2 orbitals, with a contribution from s as well. Comparing the transmission spectra in Fig. 6(d) and 5(d) the peak of the transmission without the SiC molecule around −2.0 eV is just overlapping the valley of the transmission with the SiC molecule; therefore the transmission values at around −2.0 eV for junction (d) are larger than those with the SiC molecule.
Fig. 7 shows the modified wave functions of the frontier orbitals at zero bias voltage, which play important roles in electronic transportation. In Fig. 7(a) and (b) the HOMO is composed of two degenerate π (px and py) orbitals, leading to two degenerate channels contributing to the transmission. In Fig. 7(c) it has the degenerated HOMO−1. In Fig. 7(d) the MPSH eigenstates are not degenerated, due to the asymmetry of the projected region. If a much larger symmetric projected region is chosen, configuration (d) will exhibit degenerated HOMO−1 (not shown). Compared with the other three configurations, the HOMO−1 and HOMO in Fig. 7(a) are relatively slightly localized in the SiC molecule, which decreases the transmission coefficients near the Ef since the electron transport ability is weakened.66 It is easy to see that the orbitals in Fig. 7(b)–(d) are delocalized, especially in Fig. 7(d), coupling the scattering region and the electrodes, which results in strongest conductance. The electrons can easily flow through the molecule, leading to relatively large currents. The above discussions demonstrate that the contact geometry has a great impact on the energy and spatial distribution of the frontier molecular orbitals near the Ef, leading to different molecular conductances.
As we know, the variation in the transport properties is a result of both the details of the frontier orbitals of SiC molecule and the applied voltage. The external bias changes the Hamiltonian of the junction, and has an effect on the junction conductance. Fig. 8 illustrates the current–voltage relationship of the junction for different contacts under a bias voltage from −1.2 V to 1.2 V. When a positive bias is applied, the right electrode is positive. In general, all the I–V curves are linear-like, exhibiting characteristic metallic behavior at the voltage considered. The current value with a bias voltage ranging from −1.2 V to 1.2 V follows the configuration order (d) > (b) > (c) > (a). Considering the symmetry of the device, symmetric I–V characteristics are expected in the case of symmetric couplings.14,15 In contrast, our I–V curve is asymmetric, with larger current for V < 0 than for V > 0 in Fig. 8(a)–(d), while in Fig. 8(b) it is the opposite. In other words, the I–V curve of the asymmetric molecule is asymmetric with respect to voltage inversion, which has been confirmed in experiments.67 Such asymmetry is probably due to the asymmetric contact geometry or the polar SiC molecule itself, which is composed of two different kinds of atoms, Si and C. An additional case is that for the GaN molecular junction,13 where the I–V curves are nonlinear and asymmetric, indicating that the asymmetric junction has a semiconductor-like characteristic. From the above cases of SiC and GaN molecular junctions, we know that the electronic properties of molecular junctions can be regulated as desired by an appropriate design of the molecule since the I–V properties are related to the properties of the molecular structure.
When a bias is applied, the junction is driven out of equilibrium. The electronic transport properties at different bias voltages depend on the shift of the transmission peaks. To better understand the non-equilibrium properties of this two-probe system, we investigate the transmission spectrum T(E,V) of the junctions when the bias is −1.2 V, −0.6 V, 0 V, 0.6 V, 1.2 V, as shown in Fig. 9. The transmission of the junction is different from that of V = 0 because the two electrodes maintain different chemical potentials due to external bias. In Fig. 9(a), we observe a significant shift of the HOMO resonance to the negative energy direction as the bias voltage increases. That is to say, the electronic states of the SiC molecule, which contribute to the transmission peak, are moving toward lower energy together with the electronic states of the positively biased electrode. The reason may be that the orbital localized in one side of the molecule tends to follow the chemical potential of its adjacent electrode under a bias voltage.68 Such a shift of the HOMO moves it away from the Au Fermi level; therefore the transmission at Ef becomes smaller. However, the bias window is getting larger, i.e. the integral range increases; hence the current increases as well, which can be seen in Fig. 8. In Fig. 9(b) the conductance is increasing with high positive bias and the transmission function at positive bias is larger than that at negative bias. In Fig. 9(b)–(d) the transmission function around the Ef increases with the increasing negative bias, while it decreases with the positive bias. Comparing these four configurations, it is obvious that the order of the transmission spectra in the bias window is T(d) > T(b) > T(c) > T(a), which leads to the current value in the order I(d) > I(b) > I(c) > I(a), in line with Fig. 8. It should be noted that the transmission function in Fig. 9(a)–(d) at negative bias is larger than that at positive bias, while the situation in Fig. 9(b) is the opposite. This leads to larger current at negative bias in Fig. 8(a)–(d) and small current in Fig. 8(b).
To understand the effect of the bias further, the evolution of MPSH eigenvalues at different biases is shown in Fig. 10. The HOMO, LUMO and the HOMO–LUMO gap (HLG) are given as a function of the bias. Fig. 10(a) shows that the electron tunneling is mainly through the HOMO and the LUMO at zero bias. With larger negative bias the LUMO gets much closer to the Fermi level. From Fig. 10(b) it is obvious that the HOMO plays the major role in electronic transmission. Fig. 10(c) and (d) demonstrate that as the negative bias is increased, the electron tunneling is mainly through the LUMO and the HOMO, respectively. When the bias becomes larger, more eigenchannels enter into the bias window, serving as conducting channels. In configuration (d) the hybridization with the Au metal states is so strong that the HLG is the smallest of the four configurations. It's interesting that the SiC molecule stays whole with a Si–C bond length of 1.84 Å, while serving as a bridge between the Au leads. From Fig. 10 we can observe that at larger negative bias the number of available eigenchannels is much greater than that at the positive bias. Therefore, the transmission and its integral in the bias window at larger negative bias should be higher than those at the positive bias, consistent with what is observed in the transmission spectra in Fig. 9 and I–V plots in Fig. 8, respectively. However, in Fig. 10(b), as the positive bias increases, not only the HOMO, but also the HOMO−1 and the HOMO−2 enter into the bias window. With more available eigenchannels at positive bias than that at negative bias, its current at positive bias is greater than that at negative bias. Fig. 10 also indicates that the MPSH eigenvalues and HLG are largely modified by the contact geometry and the bias.
In addition, the differential conductance measured in experiment generally enhanced with an increase in the bias voltage for single-channel models with a transmission function below 0.5.69 In contrast, the inset in Fig. 8 shows that the differential conductance varies with the increase in bias. Actually, in our Au–SiC–Au system more than one channel contributes to the electron transport. The existence of multiple channels may affect the shape of the differential conductance shown in the inset of Fig. 8.70
4. Conclusions
In summary, we present a study on the electronic transport properties of a SiC molecule sandwiched between two semi-infinite Au (100) metal electrodes in four different anchoring configurations by performing a first-principles calculation with the use of DFT together with the NEGF method. We performed simulations of the Au–SiC–Au nanoscale junction breaking process by calculating the corresponding conductance in four different anchoring geometries. We find that conductance varies significantly with dz in the four configurations, indicating that the conductance of the junction is sensitive to the local atomic rearrangement. The obtained conductance of SiC in four configurations at the optimal position is 0.83G0 for configuration (a), 1.42G0 for configuration (b), 0.88G0 for configuration (c) and 1.81G0 for configuration. Compared with the four configurations, the hollow–hollow configuration is the most stable contact geometry with the largest conductance, showing the strongest electronic coupling between the SiC molecule and the electrodes, which manifests itself in the broad T(E; V = 0) around Ef. From the restoring force and the spatial electron density differences after the structural break, we can conclude that the Si–C bond is more stable than the Au–C and Au–Si bonds in the single-molecular junction. In addition, we reveal the current of the junction at the optimal position under small bias for the four configurations. All the I–V curves of the junctions are linear, exhibiting characteristic metallic behavior in the low bias voltage. The asymmetry of the I–V curves reflects the asymmetry of the molecule and the contact geometry. The origin of the transport spectrum of the junctions is discussed with respect to MPSH states. In general, the calculated results prove that the coupling morphology of a SiC molecule connected with electrodes, the distance and external bias voltage have an important effect on the transport properties of the nanoscale junctions. We hope these investigations are meaningful to modeling and simulation in silicon carbide nanoscale electronic devices.Acknowledgements
The authors would like to thank the support by the National Natural Science Foundation of China (Grant No. 11204192, 11174214) and the NSAF Joint Fund Jointly set up by the National Natural Science Foundation of China and the Chinese Academy of Engineering Physics (Grant No. U1430117).References
- I. Díez-Pérez, J. Hihath, Y. Lee, L. Yu, L. Adamska, M. A. Kozhushner, I. I. Oleynik and N. Tao, Nat. Chem., 2009, 1, 635–641 CrossRef PubMed.
- M. L. Perrin, E. Burzurí and H. S. J. van der Zant, Chem. Soc. Rev., 2015, 44, 902–919 RSC.
- S. Kubatkin, A. Danilov, M. Hjort, J. Cornil, N. S. Hansen, P. Hedegård and T. Bjørnholm, Nature, 2003, 425, 698–701 CrossRef CAS PubMed.
- S. Y. Quek, M. Kamenetska, M. L. Steigerwald, H. J. Choi, S. G. Louie, M. S. Hybertsen, J. B. Neaton and L. Venkataraman, Nat. Nanotechnol., 2009, 4, 230–234 CrossRef CAS PubMed.
- A. Batra, P. Darancet, Q. Chen, J. S. Meisner, J. R. Widawsky, J. B. Neaton, C. Nuckolls and L. Venkataraman, Nano Lett., 2013, 13, 6233–6237 CrossRef CAS PubMed.
- S. Fujii, T. Tada, Y. Komoto, T. Osuga, T. Murase, M. Fujita and M. J. Kiguchi, J. Am. Chem. Soc., 2015, 137, 5939–5947 CrossRef CAS PubMed.
- H. Song, Y. Kim, Y. H. Jang, H. Jeong, M. A. Reed and T. Lee, Nature, 2009, 462, 1039–1043 CrossRef CAS PubMed.
- Z. J. Donhauser, B. A. Mantooth, K. F. Kelly, L. A. Bumm, J. D. Monnell, J. J. Stapleton, D. W. Price Jr, A. M. Rawlett, D. L. Allara, J. M. Tour and P. S. Weiss, Science, 2001, 292, 2303–2307 CrossRef CAS PubMed.
- B. Q. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907 CrossRef CAS PubMed.
- M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252–254 CrossRef CAS.
- R. H. M. Smit, Y. Noat, C. Untiedt, N. D. Lang, M. C. van Hemert and J. M. van Ruitenbeek, Nature, 2002, 419, 906–909 CrossRef CAS PubMed.
- T. Zhang, Y. Cheng and X. R. Chen, RSC Adv., 2014, 4, 51838–51844 RSC.
- F. T. Liu, Y. Cheng, F. B. Yang and X. R. Chen, Chin. Phys. Lett., 2013, 30, 107303 CrossRef.
- J. X. Yu, Y. Cheng, S. Sanvito and Y. Cheng, Appl. Phys. Lett., 2012, 100, 103110 CrossRef.
- M. Koentopp, C. Chang, K. Burke and R. Car, J. Phys.: Condens. Matter, 2008, 20, 083203 CrossRef.
- X. Zhong, R. Pandey, A. R. Rocha and S. P. Karna, J. Phys. Chem. Lett., 2010, 1, 1584–1589 CrossRef CAS.
- V. M. García-Suárez, A. R. Rocha, S. W. Bailey, C. J. Lambert, S. Sanvito and J. Ferrer, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045437 CrossRef.
- K. H. Khoo, J. B. Neaton, H. J. Choi and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115326 CrossRef.
- M. E. Levinshtein, S. L. Rumyantsev and M. S. Shur, Properties of Advanced Semiconductor Materials: GaN, AIN, InN, BN, SiC, SiGe, John Wiley & Sons, New York, NY, USA, 2001, pp. 93–96 Search PubMed.
- T. H. Lee, S. Bhunia and M. Mehregany, Science, 2010, 329, 1316–1318 CrossRef CAS PubMed.
- M. A. Capano and R. J. Trew, MRS Bull., 1997, 22, 19–23 CrossRef CAS.
- Y. T. Yang, K. L. Ekinci, X. M. H. Huang, Y. T. Yang, K. L. Ekinci, X. M. H. Huang, L. M. Schiavone, M. L. Roukes, C. A. Zorman and M. Mehregany, Appl. Phys. Lett., 2001, 78, 162–164 CrossRef CAS.
- W. Yang, H. Araki, C. Tang, S. Thaveethavorn, A. Kohyama, H. Suzuki and T. Noda, Adv. Mater., 2005, 17, 1519–1523 CrossRef CAS.
- G. Cheng, T. H. Chang, Q. Qin, H. Huang and Y. Zhu, Nano Lett., 2014, 14, 754–758 CrossRef CAS PubMed.
- R. Wu, K. Zhou, C. Y. Yue, J. Wei and Y. Pan, Prog. Mater. Sci., 2015, 72, 1–60 CrossRef CAS.
- K. Zekentes and K. Rogdakis, J. Phys. D: Appl. Phys., 2011, 44, 133001 CrossRef.
- J. W. Lyver and E. Blaisten-Barojas, J. Comput. Theor. Nanosci., 2011, 8, 529–534 CrossRef CAS.
- C. Pham-Huu, N. Keller, G. Ehret and M. J. Ledoux, J. Catal., 2001, 200, 400–410 CrossRef CAS.
- W. L. X. Zhou and Y. Zhang, Appl. Phys. Lett., 2006, 89, 223124 CrossRef.
- A. I. Yanson, G. R. Bollinger, H. E. Van den Brom, N. Agraït and J. M. van Ruitenbeek, Nature, 1998, 395, 783–785 CrossRef CAS.
- S. Tongay, R. T. Senger, S. Dag and S. Ciraci, Phys. Rev. Lett., 2004, 93, 136404 CrossRef CAS PubMed.
- J. Sołtys, J. Piechota, M. Łopuszyński and S. Krukowski, New J. Phys., 2010, 12, 043024 CrossRef.
- M. Schnabel, M. Canino, S. Kühnhold-Pospischil, J. López-Vidrier, T. Klugermann, C. Weiss, L. López-Conesa, M. Zschintzsch-Dias, C. Summonte, P. Löper, S. Janz and P. R. Wilshaw, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195317 CrossRef.
- N. Singh, K. Singh, A. Pandey and D. Kaur, Mater. Lett., 2016, 164, 28–31 CrossRef CAS.
- A. Gali, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 085416 CrossRef.
- S. N. Mohammad, Nanotechnology, 2012, 23, 285707 CrossRef PubMed.
- J. M. Jia, S. P. Ju, D. Shi and K. F. Lin, J. Appl. Phys., 2012, 111, 013704 CrossRef.
- P. T. B. Shaffer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 477–488 CrossRef CAS.
- R. B. Wu, K. Zhou, C. Y. Yue, J. Wei and Y. Pan, Prog. Mater. Sci., 2015, 72, 1–60 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- M. Brandbyge, J. L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401–165417 CrossRef.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2005 CrossRef CAS.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428 CrossRef CAS.
- A. P. Jauho, N. S. Wingreen and Y. Meir, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 5528–5544 CrossRef CAS.
- P. Ordejón, E. Artacho and J. M. Soler, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, R10441 CrossRef.
- K. Stokbro, J. Taylor and M. Brandbyge, J. Am. Chem. Soc., 2003, 125, 3674–3675 CrossRef CAS PubMed.
- J. Taylor, Ab initio Modelling of Transport in Atomic Scale Devices, Ph. D. thesis, McGill University of Canada, Montreal, 2000, pp. 79–80.
- C. Caroli, R. Combescot, P. Nozieres and D. Saint-James, J. Phys. C: Solid State Phys., 1971, 4, 916–929 CrossRef.
- L. V. Keldysh, J. Exp. Theor. Phys., 1965, 20, 1018–1026 Search PubMed.
- S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, Cambridge, U. K., 1995, pp. 152–153 Search PubMed.
- M. Büttiker, Y. Imry, R. Landauer and S. Pinhas, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6207–6215 CrossRef.
- D. S. Fisher and P. A. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6851–6854 CrossRef CAS.
- J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245407 CrossRef.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- R. B. Pontes, A. R. Rocha, S. Sanvito, A. Fazzio and A. J. R. Silva, ACS Nano, 2011, 5, 795–804 CrossRef CAS PubMed.
- J. J. Scherer, J. B. Paul, C. P. Collier, A. O'Keefe and R. J. Saykally, J. Chem. Phys., 1995, 103, 9187–9192 CrossRef CAS.
- D. S. Eggleston, D. F. Chodosh, R. L. Webb and L. L. Davis, Acta Crystallogr., Sect. A: Found. Crystallogr., 1986, 42, 36–38 CrossRef.
- S. Gautam, N. Goel and K. Dharamvir, RSC Adv., 2014, 4, 13927–13933 RSC.
- C. Boehme and G. Frenking, Organometallics, 1998, 17, 5801–5809 CrossRef CAS.
- J. J. Sumakeris, L. B. Rowland, R. S. Kern, S. Tanaka and R. F. Davis, Thin Solid Films, 1993, 225, 219–224 CrossRef CAS.
- T. C. Smith, H. Li, D. J. Clouthier, C. T. Kingston and A. J. Merer, J. Chem. Phys., 2000, 112, 3662–3670 CrossRef CAS.
- I. S. Kristensen, D. J. Mowbray, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2008, 20, 374101 CrossRef CAS PubMed.
- M. Okamoto and K. Takayanagi, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 7808–7811 CrossRef CAS.
- H. J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152 CrossRef CAS.
- Z. Q. Fan and K. Q. Chen, Appl. Phys. Lett., 2010, 96, 053509 CrossRef.
- H. B. Weber, J. Reichert, R. Ochs, D. Beckmann, M. Mayor and H. v. Löhneysen, Phys. E, 2003, 18, 231–232 CrossRef CAS.
- G. P. Zhang, G. C. Hu, Y. Song, Z. L. Li and C. K. Wang, J. Phys. Chem. C, 2012, 116, 22009–22014 CAS.
- O. Tal, M. Krieger, B. Leerink and J. M. van Ruitenbeek, Phys. Rev. Lett., 2008, 100, 196804 CrossRef CAS PubMed.
- S. Kaneko, Desigen and Control of the Metal-Molecule Interface for Highly Conductive Single Molecular Junctions, Ph. D. thesis, Tokyo Institute of Technology, Tokyo, 2016, p. 63.
| This journal is © The Royal Society of Chemistry 2016 |










