Structural, elastic and thermo-electronic properties of paramagnetic perovskite PbTaO3
Shakeel Ahmad Khandy* and
Dinesh C. Gupta*
Condensed Matter Theory Group, School of Studies in Physics, Jiwaji University, Gwalior – 474 011, MP, India. E-mail: sosfizix@gmail.com
First published on 26th April 2016
Abstract
Self-consistent ab initio calculations with highly precise spin-polarised, density functional theory (DFT) have been performed for the first time, to study the structural stability, mechanical and magneto-electronic properties of cubic perovskite PbTaO3. The DFT as well as the analytically calculated values of tolerance factor, in addition to stable-phase optimization, mechanical and elastic properties show stability of the present material in the cubic phase with a reasonably stiff nature and ductile properties. The symmetric spin-polarised band structure of both the spin (up and down) channels reveals zero spin polarisation at the Fermi level. Moreover, the insignificant total and individual spin magnetic moments of adjacent atoms and magnetic susceptibility calculations via the post-DFT treatment predict the paramagnetic nature of the material. Based on results of the present study, the paramagnetic metal PbTaO3 material is considered a promising candidate in designing new electrode materials.
Introduction
Perovskite oxides and their derivatives have attracted researchers across the world in recent decades due to physical properties such as high-temperature superconductivity, radioactive waste encapsulation, colossal magneto-resistance and multi-ferroic properties, which make these ceramic materials an important tool for various fascinating technological applications including optoelectronics, solid-oxygen fuel cells, transducers, spintronics, gas sensing and shape memory devices.1–4 Exploration of new materials and the modification/tailoring of their desired properties continues to be an area of active research.Cubic oxides of tantallum are interesting members of the titanic perovskite family. Ta-Based perovskites are generally paramagnetic metal oxides that could shape future-generation electrode material design technology. Reliable mechanical strength vis-à-vis applied strain, structural stability and chemical environment make these materials feasible as high-quality functional oxides to furnish electrode materials with efficient electrical conductivity.5 The compounds CaTaO3 and SrTaO3 have been observed experimentally to crystallize in a cubic structure with the space group of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.6,7 Ali et al.8 reported the theoretical paramagnetic and metallic properties of cubic MTaO3 (M = Ca, Sr, Ba) perovskites. Moreover, SnTaO3 oxide has been reported to be a paramagnetic metal9 with cubic structure.10 No theoretical or experimental data on PbTaO3 compound are available in the literature. Thus, we hereby investigate for the first time the structural, mechanical electronic and magnetic properties of this compound theoretically.
m.6,7 Ali et al.8 reported the theoretical paramagnetic and metallic properties of cubic MTaO3 (M = Ca, Sr, Ba) perovskites. Moreover, SnTaO3 oxide has been reported to be a paramagnetic metal9 with cubic structure.10 No theoretical or experimental data on PbTaO3 compound are available in the literature. Thus, we hereby investigate for the first time the structural, mechanical electronic and magnetic properties of this compound theoretically.
Computational details
To calculate electronic properties and total energies, the full-potential linearized augmented plane wave method (FP-LAPW) is employed.11 To solve the Kohn–Sham equations, an iterative method is used. For exchange–correlation energies, three different methods—Perdew–Burke–Ernzerhof generalized gradient approximation (GGA-PBE),12 generalized gradient approximation with Hubbard U(GGA+U),13,14 and spin orbit coupling (GGA+U (SOC))15,16 have been used as they seem to be crucial in handling correlated electron systems, especially the transition metal (TM) oxides, which possess the d- and f-states. Strongly correlated electron systems are not sufficiently described by the LSDA method. The effective Hubbard parameter Ueff(U − J) with J = 0 in a physically meaningful way is applied where U is the on-site Coulomb interaction, and J, the exchange parameter. In the present study, the Ueff value is altered from 3 eV to 7 eV. A plane wave cut-off of RMTKMAX = 7 is used to restrict the plane-wave number, and for Brillouin zone (BZ) integration, the tetrahedral method is employed with a sufficiently dense mesh of 3000 k-points centered at the Γ point following the Monkhorst and Pack convention. Zero charge leakage from the core and total energy convergence are ensured. The charge and energy convergence criteria are set to 10−4 e and 10−4 Ry, respectively, so as to ensure that the self-consistent calculations are accurate and fully converged. Reliability of elastic properties obtained via first principles calculation is highly recognized. To compute the three independent elastic constants, a rigorous strain (energy/second-order derivative) method is used in the present study in which the ground-state lattice is strained by applying a small amount of isotropic as well as rhombohedral and tetragonal strains, so as to keep the volume constant, that is, only shape changes.17Structural properties
PbTaO3 crystallizes in a cubic structure (Fig. 1) with space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, where atoms are sited as Pb (0, 0, 0), Ta (0.5, 0.5, 0.5) and O (0, 0.5, 0.5), (0.5, 0, 0.5), (0.5, 0.5, 0) positions. To achieve the optimization of structure and geometry of the crystal, Birch Murnagan's equation of state is used to fit the total energy per unit cell versus volume. The stable ground state for PbTaO3 is clarified by optimizing the 1 × 2 × 1 supercell for all three magnetic configurations (paramagnetic-PM, ferromagnetic-FM and antiferromagnetic-AFM) considered for this compound. For the AFM phase, the spin of Ta atom is reserved up (↑) in one cell and down (↓) in the second cell. From the self-consistent pressure–volume optimization plot, as shown in Fig. 2, it is clear that the paramagnetic phase has lower ground-state energy, and hence, a thermodynamically stable configuration for PbTaO3 is determined. Subsequently, the various optimised structural parameters including lattice constant, bulks modulus, derivative of bulk modulus and total energy presented in Table 1 are calculated. Moreover, an empirical (ionic radii) method is also employed to calculate the lattice constant using the following relation:18
m, where atoms are sited as Pb (0, 0, 0), Ta (0.5, 0.5, 0.5) and O (0, 0.5, 0.5), (0.5, 0, 0.5), (0.5, 0.5, 0) positions. To achieve the optimization of structure and geometry of the crystal, Birch Murnagan's equation of state is used to fit the total energy per unit cell versus volume. The stable ground state for PbTaO3 is clarified by optimizing the 1 × 2 × 1 supercell for all three magnetic configurations (paramagnetic-PM, ferromagnetic-FM and antiferromagnetic-AFM) considered for this compound. For the AFM phase, the spin of Ta atom is reserved up (↑) in one cell and down (↓) in the second cell. From the self-consistent pressure–volume optimization plot, as shown in Fig. 2, it is clear that the paramagnetic phase has lower ground-state energy, and hence, a thermodynamically stable configuration for PbTaO3 is determined. Subsequently, the various optimised structural parameters including lattice constant, bulks modulus, derivative of bulk modulus and total energy presented in Table 1 are calculated. Moreover, an empirical (ionic radii) method is also employed to calculate the lattice constant using the following relation:18| a0 = α + β(rM + rO) + γ(rTa + rO) | (1) |
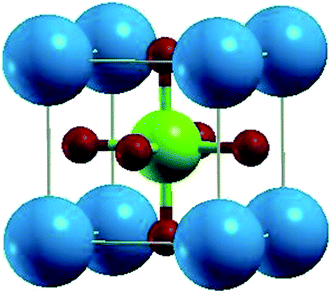 | ||
Fig. 1 The cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) crystal structure of PbTaO3. The blue, green and red spheres denote Pb, Ta and O atoms, respectively. m) crystal structure of PbTaO3. The blue, green and red spheres denote Pb, Ta and O atoms, respectively. | ||
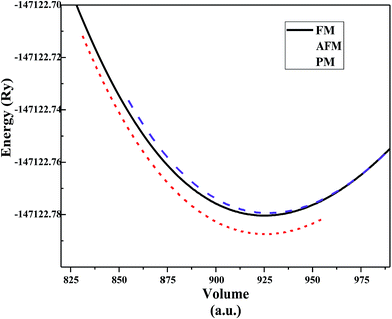 | ||
Fig. 2 Calculated double cell optimization curves of PbTaO3 for paramagnetic, ferromagnetic and anti-ferromagnetic phases in Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m configuration. m configuration. | ||
| Parameter | GGA | Analytical |
|---|---|---|
| Lattice constant (Å) | 4.09 | 4.08 |
| Bulk modulus (GPa) | 190.74 | |
| B′ | 4.65 | |
| Volume (a.u.)3 | 925.48 | |
| Tolerance factor (t) | 0.99 | 0.99 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Bond lengths (Å) | ||
| Pb–O | 2.89 | |
| Pb–Ta | 3.54 | |
| Ta–O | 2.05 | |
| ΔE = EPM − EAFM (Ry) | −0.006 | |
The knowledge of bond lengths enables us to predict the tolerance factor (t) of a perovskite structure and thus reliability of the crystal structure for a particular compound. The calculation of t can be obtained via two possible methods: ionic radii method18 and bond length (Goldschmidt)20 method with the formulae in eqn (2) and (3), respectively.
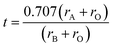 | (2) |
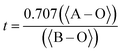 | (3) |
Analytically calculated as well as DFT computed values for the present material's tolerance factor (t = 0.99 as shown in Table 1) determines the distortion of a perovskite from the ideal cubic structure because the t in the range 0.93–1.04 is closer to unity, meaning minimum distortion and thus closer to cubic structure stability.21–23 Hence our results match theoretically calculated tolerance factors of SnTaO3, CaTaO3 and SrTaO3,6–10,24 with almost the same electronic configuration. These materials experimentally crystallize in a simple cubic structure. This theoretically justifies the cubic structure of PbTaO3 perovskite.
Mechanical stability
The structural stability and mechanical properties of cubic PbTaO3 perovskite have been extracted from the understandings of elastic stiffness constants Cij (C11, C12 and C44). In the present material, due to cubic symmetry, there are only three independent elastic constants, C11, C12 and C44, which are determined by using the cubic elastic code embedded in the Wien2k package. The Viogt Reuss Hill method is used for estimating the elastic characteristics using Cij values derived from compliance constants Sij's of the single, cubic crystal. Employing eqn (4), Viogt's shear GV and Reuss's shear GR moduli, which represent upper and lower limits of true polycrystalline constants, are averaged to compute the Hill's shear modulus G. Further, the bulk modulus B = (C11 + C12)/3 and Young's modulus Y = 9GVB/(GV + 3B) are derived from the calculated elastic constants.25–27
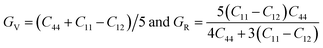 | (4) |
The calculated cubic constants for PbTaO3 given in Table 2 are all positive and satisfy the cubic stability condition: C12 < B < C11 and the generalized Born (mechanical stability) criteria: (C11 − C12) > 0, (C11 + 2C12) > 0 and C44 > 0.28 Thus, we can say the material is elastically stable. The large obtained value of the bulk modulus, which is related to the hardness of a material, suggests the incompressible nature of PbTaO3. Covalently bonded materials are characterized by the higher value of the shear modulus. Similarly, Young's modulus is directly linked with stiffness of a material because maximizing the Y, the harder the material and hard materials have covalent bonds between constituent atoms.29 Henceforth, the calculated values of the bulk modulus and Young's modulus evidently indicate the stiff and covalent nature of the present material, which therefore may be a candidate for fabrication of superhard materials.
| Parameter | C11 | C12 | C44 | C′′ | Y | G | υ | B/G | A |
|---|---|---|---|---|---|---|---|---|---|
| PbTaO3 | 348.03 | 111.92 | 1.57 | 110.35 | 133.2 | 24.29 | 0.384 | 7.85 | 0.013 |
Microcracks in the material are associated with Zener's anisotropic factor A = 2C44/(C11 − C12) of a crystal. The calculated anisotropy factor (A = 0.013) is less than 1, which suggests that PbTaO3 is elastically anisotropic. Materials with A > 1 are said to be isotropic in nature.30 The calculated value of Cauchy's pressure, C′′ = (C12 − C44) presented in Table 2 implies the presence of metallic bonds; a positive Cauchy pressure value for a material represents a metallic bond and a negative value is a characteristic of angular bonds.30 Also, the compound's ductility is defined by a relatively high value of the Pugh ratio (B/G > 1.75), while brittleness is characterized by lower values of B/G. Therefore, the Cauchy pressure and Pugh ratio values indicate that the present compound is a ductile material.
Another property called Poisson's ratio υ can be calculated using υ = (3B − Y)/6B, which is directly related to the extent of bonding in the material. For covalent solids, it is less than 0.1, while for ionic solids this value is 0.25. However, for metallic materials, the range is 0.25–0.5.31 The present value of υ = 0.38 for PbTaO3 specifies that the material is metallic. This can also be accentuated by the positive value of Cauchy's pressure, which indicates the presence of non-central interatomic forces, rather than central forces attributed to the zero value of Cauchy's pressure. Hereafter, the overall DFT computed elastic and mechanical properties of PbTaO3 are considered to be metallic, stiff and ductile.
Electronic properties
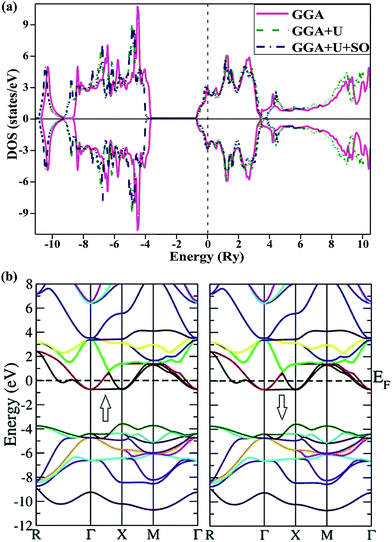
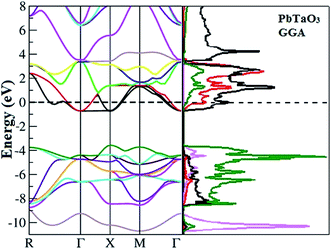
Equilibrium lattice parameters are required for calculating the spin-polarised band structures via the three different methods (GGA, GGA+U and GGA+U+SO). Total densities of states and electronic band structures thus obtained were plotted for both spin phases and as seen in Fig. 3, they are alike, indicating no significant spin polarization. The figure clearly illustrates the metallic nature of the compound in ferromagnetic configuration (both the spin states: spin up and spin down). The calculated band structure and density states for the paramagnetic phase of PbTaO3 by GGA (see Fig. 4) clearly indicate that the material is natural, with no alteration in the results when compared with the ferromagnetic phase. This is elucidated by the crossing of the conduction band minima at the Fermi level, which reaches −0.75 eV in the valence band. From the density states plot, we inferred that the valence band stretches from −10.8 eV to −4.5 eV, and is largely populated by 2p and 4s bands of O and Pb atoms, respectively. The conduction band is fully occupied by Ta-5d, O-2p and Pb-6p states, and extends from −0.8 eV to 10.5 eV. In particular, we plotted the spin-dependent partial density of states (PDOS) for Ta, Pb and O in Fig. 5 to predict the influence of constituent electronic states for individual atoms on total density of states. It is clear that the conduction band (−10.8 eV to −4.5 eV) is occupied by 2s and 6p states. At the Fermi level, the conduction band leaps through the valence band up to −0.75 eV, which occurs due to splitting of d-states of Ta; there is a peak nearby at 3 eV, which is due to partially filled Pb-6p states.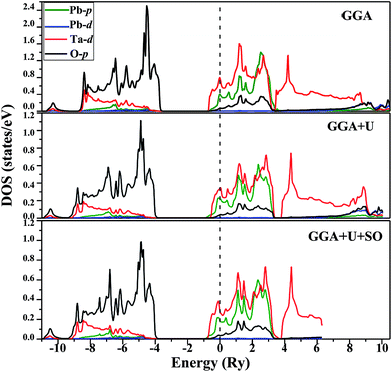 | ||
| Fig. 5 Spin-polarized partial density of states (PDOS) of the PbTaO3 at equilibrium lattice constant by, GGA, GGA+U and GGA+U (SOC). | ||
Likewise, it is clear from the partial PDOS that the metallic nature of the compound is the result of p–d hybridization of t2g-states of Ta and p-states of Pb atom, inclusive of a small contribution from O-2p states. According to an earlier report, the d-band splitting (i.e., t2g and eg) in 5d transition metal (TM) oxides makes them metallic32 and the same occurs in the midst of symmetric densities for 5dt2g and deg in both spin phases. Thus, the metallicity property of PbTaO3 as elucidated by inclusive spin-dependent partial density of states is justified. The on-site parameter for the Ta-d states is applied and variation of Ueff up to 7 eV produces little difference in the band structure and overall DOS. Therefore, similar arguments are also put forward for results given in Fig. 5 obtained via GGA+U and GGA+U (SOC) with very little difference in calculated densities due to localization of d-states in the transition metal atom.
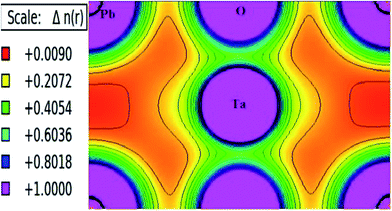
Moreover, first-principle calculations are actively used to evaluate electronic charge density, leading to determining the charge distribution in an atom, which in turn also establish the bond character between compound atoms. Thus, in a given system charge density acts as an indicator for chemical bonding; however, it includes contributions from non-bonding electrons and hence provides an overall charge density. The spin-polarized electronic charge densities of PbTaO3 are shown in Fig. 6. They clearly portray the existence of a covalent bond between Ta and O, while the Pb–Ta and Ta–Ta–O bonds are ionic in nature. Both types of bonds, covalent as well as ionic, are present in this material.
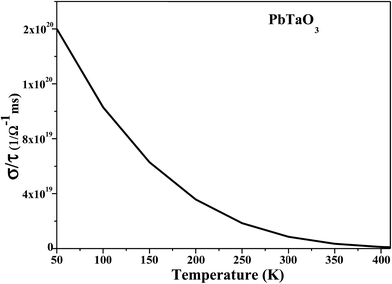
In addition, the BoltzTraP code33 was employed to evaluate electrical conductivity, which is a measure of free charge-carrier flow of the material. For metals, electrical conductivity increases with declining temperature due to maximum density of free electrons in the conduction band. At 50 K, maximum conductivity of 3.96 × 1020 (ohm m)−1 s−1, as seen in the plot between electrical conductivity by time factor (s/t) versus temperature (Fig. 7). An exponential decrease in electrical conductivity is observed with the increase in temperature, and from 200 K onward the linear trend continues. SrTaO3 has been reported to have a sub-layer with high formation energy for oxygen vacancy, and thus oxygen migration toward the electrodes can be blocked by this material.34 Paramagnetic cubic oxides like BaMoO3, SrMoO3 and SrRuO3 show identical results, such as metallicity and reasonable electrical conductivity, and are being used as electrode materials.35–38 PbTaO3, then, is expected to serve as an efficient electrode material.
Magnetic properties
In the present study, we investigated in detail the ground-state magnetic properties of the lead tantalum oxide (PbTaO3) using diverse methods as stated earlier. The employment of different exchange correlation potentials is done only to obtain appropriate information on interaction among the constituent atoms of PbTaO3. Also, the individual and total spin magnetic moments were calculated using three approximations—GGA, GGA+U, and GGA+U (SOC)—respectively, for all atoms at different sites in the cell in order to find possible exhibition of magnetism and to examine the effect of spin on this material. The interstitial magnetic moment by GGA+U is 0.00043 μB, and the magnetic moments at Pb, Ta and O sites are 0.00015 μB, 0.00041 μB and −0.00023 μB, respectively.The negative spin magnetic moment of O shows opposite alignment with respect to other atomic moments. This opposition causes a nearly total decrease in the net spin magnetic moment of the cell. The magnetic response of the material is very feeble as observed from the insignificant total magnetic moment equal to 0.00058 μB. The negligible magnetic moment in such compounds leading to their paramagnetic performance is due to unpaired electrons present in atomic orbitals. Paramagnetic materials attain magnetism only when kept in externally applied magnetic fields; otherwise they have no magnetic moment, which is also confirmed by negligible spin polarization as well as symmetric band structures.39 A similar trend was found for total and individual magnetic moments, that is, negligible amounts when GGA and GGA+U (SOC) are employed. Two of the three constituent atoms Pb and Ta for the crystal structure are paramagnetic, while the third atom, oxygen, is non-magnetic. Therefore, application of interaction parameters yields an insignificant variation in the magnetic character and overall DOS of the material.
For paramagnetic materials, the magnetic susceptibility χ and temperature are inversely proportional, and follow the Curie–Weiss law:40
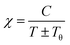 | (5) |
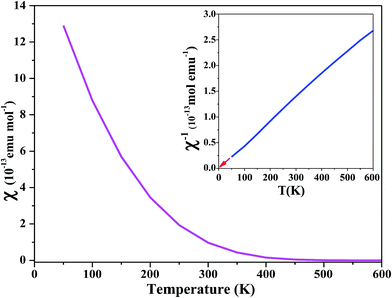 | ||
| Fig. 8 Magnetic susceptibility (χ) and inverse of magnetic susceptibility (χ−1) plots versus temperature of PbTaO3. | ||
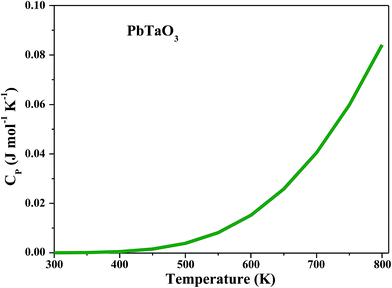
Specific heat capacity for the material is an intensive property independent of system size, which yields a degree of temperature change per unit of the substance by absorbing heat, is also calculated. Excellent cooling agents used in diverse industries generally have a high value of specific heat capacity. The plot between molar-specific heat at constant pressure CP (J mol−1 K−1) and temperature T (K) in Fig. 9 shows that CP remains constant from 0 K to 450 K and then increases exponentially up to 800 K, reaching the limit of phase transition. Thus, it is well established from the overall DOS, ground-state energy, feeble magnetism and magnetic susceptibility that PbTaO3 is a metallic paramagnetic material.
Conclusion
Electronic, structural, mechanical and magnetic properties of cubic PbTaO3 were studied via the FP-LAPW method within spin-polarized density functional theory. The theoretically calculated structural, elastic and electronic parameters of this compound demonstrate the ductility and stability of this material in the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m configuration. Cohesive energies in different phases show stability of the paramagnetic phase and chemical bonding, which is explained by the electronic charge densities in this compound. The bond between Pb–Ta and Ta–Ta–O is nearly ionic with strong covalency between Ta and O. Also, metallicity is confirmed by similar types of spin-polarized band structures. The optimized magnetic phase, calculated total (DOS) with an insignificant total magnetic moment and BoltzTraP calculations, reveal the paramagnetic nature of this compound. These properties suggest that the material is a promising candidate in the design of hard materials and in electrode fabrication.
m configuration. Cohesive energies in different phases show stability of the paramagnetic phase and chemical bonding, which is explained by the electronic charge densities in this compound. The bond between Pb–Ta and Ta–Ta–O is nearly ionic with strong covalency between Ta and O. Also, metallicity is confirmed by similar types of spin-polarized band structures. The optimized magnetic phase, calculated total (DOS) with an insignificant total magnetic moment and BoltzTraP calculations, reveal the paramagnetic nature of this compound. These properties suggest that the material is a promising candidate in the design of hard materials and in electrode fabrication.
Notes and references
- L. L. Hench, D. E. Clark and A. B. Harker, J. Mater. Sci., 1986, 21, 1457 CrossRef CAS.
- Y. Moritomo, A. Asamitsu, H. Kuwahara and Y. Tokura, Nature, 1996, 380, 141 CrossRef CAS.
- N. A. Spaldin and M. Fiebig, Science, 2005, 309, 391 CrossRef CAS PubMed.
- J. M. De Teresa, M. R. Ibarra, P. A. Algarabel, C. Ritter, C. Marquina, J. Blasco, J. Garcia, A. D. Moral and Z. Arnold, Nature, 1997, 386, 256 CrossRef.
- G. Koster, L. Klein, W. Siemons, G. Rijnders, J. S. Dodge, C. B. Eom, D. H. A. Blank and M. R. Beasley, Rev. Mod. Phys., 2012, 84, 253 CrossRef CAS.
- M. Gasperin, Acta Crystallogr., 1958, 11, 739 CrossRef CAS.
- M. A. Rodriguez, T. J. Boyle, B. A. Hemandez, C. D. Buchheit and M. O. Eatough, J. Mater. Res., 1996, 11, 2282 CrossRef CAS.
- Z. Ali, I. Khan, I. Ahmad, M. S. Khan and S. J. Asadabadi, Mater. Chem. Phys., 2015, 162, 308 CrossRef CAS.
- Z. Ali, I. Khan, I. Ahmad and B. Amin, Intermetallics, 2012, 31, 287 CrossRef CAS.
- A. Majid and Y. S. Lee, Advances in Information Sciences and Service Sciences, 2010, 2, 175 Search PubMed.
- P. Blaha, K. Schwarz, P. Sorantin and S. B. Trickey, Comput. Phys. Commun., 1990, 59, 399–415 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- L. J. Bennett and G. Jones, Phys. Chem. Chem. Phys., 2014, 16, 21032 RSC.
- E. V. Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505 CrossRef.
- D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107–31014 CrossRef CAS.
- M. Jamal, Cubic-elastic, http://www.WIEN2k.at/reg_user/unsupported/cubic-elast/, 2012.
- R. Ubic, J. Am. Ceram. Soc., 2007, 90, 3326 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- J. B. Goodenogh, Rep. Prog. Phys., 2004, 67, 1915 CrossRef.
- L. E. Russel, D. L. Harrison and N. H. Brett, J. Nucl. Mater., 1960, 2, 310 CrossRef.
- N. Xu, H. Zhao, X. Zhou, W. Wei, X. Lu, W. Ding and F. Li, Int. J. Hydrogen Energy, 2010, 35, 7295 CrossRef CAS.
- Z. Li, M. Yang, J. S. Park, S. H. Wei, J. J. Berry and K. Zhu, Chem. Mater., 2016, 28, 284–292 CrossRef CAS.
- L. Q. Jiang, J. K. Guob, H. B. Liua, M. Zhua, X. Zhoua and P. Wuc, et al., J. Phys. Chem. Solids, 2006, 67, 1531 CrossRef CAS.
- W. Voigt, Ann. Phys., 1889, 38, 573 CrossRef.
- A. Reuss, Z. Angew. Math. Phys., 1929, 9, 49 CrossRef CAS.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- D. C. Gupta and I. H. Bhat, Mater. Chem. Phys., 2014, 146, 303 CrossRef CAS.
- D. C. Gupta and S. Kulshrestha, J. Phys. Soc. Jpn., 2010, 79, 2 CrossRef.
- M. Chauhan and D. C. Gupta, Diamond Relat. Mater., 2013, 40, 96 CrossRef CAS.
- D. G. Pettifor, Mater. Sci. Technol., 1992, 8, 345 CrossRef CAS.
- C. Santi and T. Jarlborg, J. Phys.: Condens. Matter, 1997, 9, 9563 CrossRef.
- G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67 CrossRef CAS.
- C. L. Hung, Y. L. Chueh, T. B. Wu and L. J. Chou, J. Appl. Phys., 2005, 97, 034105 CrossRef.
- M. S. Park and B. I. Min, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 052405 CrossRef.
- C. de la Calle, J. A. Alonso, M. Garcia-Hernandez and V. Pomjakushin, J. Solid State Chem., 2006, 179, 1636 CrossRef CAS.
- H. H. Wang, G. Z. Yang, D. F. Cui, H. B. Lu, T. Zhao and F. Chen, et al., J. Vac. Sci. Technol., A, 2001, 19, 930 CAS.
- G. Koster, L. Klein, W. Siemons, G. Rijnders, J. S. Dodge, C. B. Eom, D. H. A. Blank and M. R. Beasley, Rev. Mod. Phys., 2012, 84, 253 CrossRef CAS.
- H. Gotoh, Y. Takeda, H. Asano, J. Zhong, A. Rajanikanth and K. Hono, Appl. Phys. Express, 2009, 2, 13001 CrossRef.
- S. Blundell, Magnetism in Condensed Matter, Oxford University Press, New York, USA, 2001 Search PubMed.
| This journal is © The Royal Society of Chemistry 2016 |