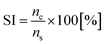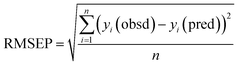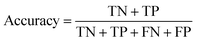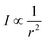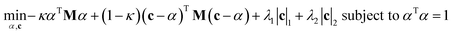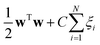On feature selection for supervised learning problems involving high-dimensional analytical information

Abstract

Several computational methods were applied to feature selection for supervised learning problems that can be encountered in the field of analytical chemistry. Namely, Genetic Algorithm (GA), Firefly Algorithm (FA), Particle Swarm Optimization (PSO), Least Absolute Shrinkage and Selection Operator (LASSO), Least Angle Regression Algorithm (LARS), interval Partial Least Squares (iPLS), sparse PLS (sPLS), and Uninformative Variable Elimination-PLS (UVE-PLS). Methods were compared in two case studies which cover both supervised learning cases; (i) regression: multivariate calibration of soil carbonate content using Fourier transform mid-infrared (FT-MIR) spectral information, and (ii) classification: diagnosis of prostate cancer patients using gene expression information. Beside quantitative performance measures: error and accuracy often used in feature selection studies, a qualitative measure, the selection index (SI), was introduced to evaluate the methods in terms of quality of selected features. Robustness was evaluated introducing artificially generated noise variables to both datasets. Results of the first case study have shown that in order of decreasing predictive ability and robustness: GA > FA ≈ PSO > LASSO > LARS (errors of 1.775, 4.504, 4.055 mg g⁻¹, 10.085, and 10.510 mg g⁻¹) are recommended for application in regression involving spectral information. In the second case study, the following trend: GA > PSO > FA ≈ LASSO > LARS (accuracies of 100, 95.12 and 90.24%) has been observed. Strong robustness has been observed in the regression case with no decrease in SI for GA, and SI decreasing from 28.85 to 10.26, and 36.11 to 21.05%, for FA and PSO, respectively. In the classification case, only LARS exhibited a considerable decrease in accuracy upon introduction of noise features. Major sources of errors were identified and mostly originated from the analytical methods themselves, which confirmed strong applicability of the evaluated feature selection methods.

---

Introduction

Tremendous achievements in science have led to an exponential increase in computational power, while complex problems are unavoidable in dealing with real systems. Since the costs of generating a large number of features per sample are steadily decreasing, massive datasets have become quite common. From gene experiments in which one deals with large numbers of pixels, to spectroscopy in which one deals with thousands of generated spectra, and gigabytes of data. With the considerable increase of features, the risk of using irrelevant ones increases. Classical statistics has been challenged by this increasing dimensionality. Hence, feature selection is crucial to obtain knowledge from massive data.

High-dimensional problems, in which the number of features greatly exceeds the number of samples are non-deterministic polynomial-time-hard.¹ In order to tackle this, many classical methods were developed, such as: Akaike's information criterion (AIC),² Bayesian information criterion (BIC),³ forward, backward, and bidirectional stepwise regression.⁴ Although in principle useful, these classical methods are infeasible for high-dimensional data, since they can lead to poor predictions⁵ or overfitting^6,7 if the number of features greatly exceeds the number of samples. Clearly novel methods are required to handle this data.

In this work, performance of five computational methods: Genetic Algorithm (GA),⁸ Firefly Algorithm (FA),⁹ Particle Swarm Optimization (PSO),¹⁰ Least Absolute Shrinkage and Selection Operator (LASSO),¹¹ and Least Angle Regression Algorithm (LARS)¹² was compared in feature selection for supervised learning problems in two case studies. Namely, (i) prediction of soil carbonate content obtained by the Scheibler method¹³ from Fourier transform mid-infrared (FT-MIR) spectral information, and (ii) classification of prostate cancer patients based on tumor cell percentage index from gene expression information.

Feature selection is essential in spectroscopy,¹⁴ since a large number of spectral features can be measured in a few samples. Consequently, numerous works^15–31 are being continuously published in which spectral feature selection methods are developed and/or applied. One of the most notable studies regarding this topic was published by Balabin and Smirnov.¹⁵ They have compared stepwise Multiple Linear Regression (stepwise MLR),⁴ interval Partial Least Squares (iPLS),¹⁶ Moving Window Partial Least Squares (MWPLS),¹⁷ (Modified) Changeable Size Moving Window PLS (CSMWPLS/MCSMWPLSR),^18,19 Searching Combination Moving Window PLS (SCMWPLS),²⁰ Successive Projections Algorithm (SPA),²¹ Uninformative Variable Elimination-Partial Least Squares (UVE-PLS),²² UVE-SPA,²³ Simulated Annealing (SA),³² and GA coupled with PLS (SA-PLS, GA-PLS), and iPLS (GA-iPLS) applied in model development for prediction of several biodiesel characteristics from spectral features. The authors used Root Mean Square Error of Prediction (RMSEP) as a performance measure of studied feature selection methods. Based on RMSEP they observed that feature selection with MLR as a regression of choice results in models with poorer predictive ability than the full spectrum PLS model. On the other hand methods coupled with PLS outperform it. They were grouped into two groups by the authors: low effective methods (iPLS, MWPLS, CSMWPLS, SCMWPLS, MCSMWPLSR, and SPA), and highly effective methods (UVE-PLS, UVE-SPA, SA, GA, and GA-iPLS).

For evaluation of performance in feature selection studies in spectroscopy, predictive ability is often used as a measure of performance. However, performance of feature selection methods is not one-dimensional. In this work, not only predictive ability, but also a qualitative metric which represents the rate of selecting true features was introduced. Using it is advantageous because it shows how many selected features highly influence the response, and are thereby meaningful.

Regarding gene expression, data from DNA micro arrays contain valuable information used in cancer diagnostics.³³ However, thousands of features can be measured in only a few experiments. Using all of them often results in biologically meaningless classification, because most genes are irrelevant for cancer patient diagnosis. This makes feature selection absolutely crucial³⁴ for cancer patients diagnosis using gene expression data. Recently Bolón-Canedo et al.,³⁴ published a work which covered the most widely used feature selection methods in microarray data classification. The authors evaluated Correlation Feature Selection (CFS),³⁵ Fast Correlation-Based Filter (FCBF),³⁶ the INTERACT algorithm,³⁷ Information Gain,³⁸ ReliefF,³⁹ minimum Redundancy Maximum Relevance (mRMR),⁴⁰ and Support Vector Machines based on Recursive Feature Elimination (SVM-RFE)⁴¹ on several datasets. Their findings indicate high dependence on the classifier, the feature selection method, and particularly the dataset. CFS method and the INTERACT algorithm have shown to be superior, and surprisingly SVM-RFE did not yield best results, regardless of the fact that SVM was shown to be the best classifier.

In both case studies evaluated in this work, robustness of the feature selection methods was tested by adding artificial noise features to the datasets. Decrease in SI, increase in error, and decrease in accuracy were monitored.

Experimental

Case study 1

The first case study involved prediction of soil carbonate content from FT-MIR spectral information. Experimental data was obtained from Bruckman and Wriessnig.⁴² Mean soil carbonate content of 5.4 wt%, ranging from 0.5 to 19.6 wt% was obtained using the Scheibler¹³ method. It corresponds to 41 soil samples with carbonate contents of 4.6–196.4 mg g⁻¹. In the first case study, true features represent features corresponding to peaks indicative of calcite and dolomite.^43,44 These spectral bands were determined based on FT-MIR analysis of their pure forms.

Using only the true features considerably reduces the model complexity. Instead of 7466 only 1274 features are used. Since the FT-MIR resolution was high (0.341 cm⁻¹), this lead to a loss of sensitivity, due to increased noise.⁴⁵ Pre-processing (Fig. 1) the full spectra remedied the issue. As part of the pre-processing, all the wavenumbers >3750 cm⁻¹ were removed, whereas the average values of other wavenumbers were calculated pairwise. This resulted in a reduction of resolution to 0.682 cm⁻¹, and the number of features to 3473, and 641 for full and true pre-processed spectral regions, respectively.

Fig. 1 FT-MIR pre-processed spectrogram of 41 soil samples. Pink regions correspond to spectral features indicative of spectra corresponding to pure calcite and dolomite.

Prior to feature selection, Kennard and Stone algorithm⁴⁶ was employed to uniformly divide 41 samples into 29 training, and 12 validation samples. For evaluation of performance, we used the selection index (SI), a ratio between the number of selected true (n_c), and the total number of selected features (n_s):

For evaluation of robustness, 3473 × 41 normally distributed random numbers were added to the spectral data. Decrease in SI and increase in RMSEP were used as robustness metrics. Objective function for GA, FA, and PSO was RMSEP for models built using PLS regression:

where n represents number of validation samples. For LASSO and LARS, PLS was used as means to construct a model out of selected features. All the methods were further compared to the full PLS model, as well as three feature selection methods for spectroscopy: iPLS, sparse PLS (sPLS),⁴⁷ and UVE-PLS.

Case study 2

For the second case study, we used 148 prostate samples obtained from Vaccine Research Institute of San Diego.^48,49 The experiments involved study of prostate cancer gene expression profiles. Total RNA from 148 prostate samples with various amount of different cell types was hybridized to Affymetrix U133A arrays. The percentages of different cell types varied among samples and were determined by a pathologist. In this work, RNA from 148 prostate samples, and 22 283 gene expressions, were considered. They were extracted from gene expression omnibus (GEO) and normalized to transform them into data arrays. Tumor cell percentage (p) was used to distinguish and divide patients. For 71 patients p was zero, 65 patients had p in [0.1, 0.8], while for 12 patients it was not reported. 71 patients were considered healthy (class: 0, no cancer) and 65 were considered non-healthy (class: 1, cancer present). Hence, 136 samples were included in the study. Here, 146 samples were also uniformly divided into a training set with 95, and validation set with 41 samples using the Kennard and Stone algorithm.⁴⁶ Number of selected features was optimized in two intervals: [10:10:100], and [100:100:2000]. Upon finding the optimal number of features, each was varied in ±3 features with an increment of one. For LARS, and LASSO the maximum number of selected features was 2000. The fitness function for GA, FA, and PSO was (1 − accuracy) of the Support Vector Machine (SVM)^50,51 classifier:
where TP stands for true positives, TN for true negatives FP for false positives, and FN for false negatives.

For evaluation of robustness, 22 283 × 136 normally distributed random numbers were added to the gene expression data. Decrease in accuracy, and number of selected noise features were used as robustness metrics.

Theoretical

Genetic algorithms (GA)

GAs represent a family of evolutionary optimization algorithms based on Darwin's theory of evolution developed by Holland in 1975.⁸ Since, the basis of the algorithm(s) is survival of the fittest, a population of chromosomes, i.e., solutions is evolved in the direction of better ones. Those chromosomes represent the elite which survive to the next generation, while the remaining are replaced with children as a result of breeding. As in natural evolution, mutations are possible.

Firefly algorithm (FA)

FA is an optimization algorithm based on the behaviour and flashing light of fireflies developed by Yang.⁹ Primary roles of such flashes are to attract mating partners and prey, as well as to serve as a warning mechanism. Intensity of the light flashes (I) at a distance r from its source is defined by the inverse square law:
and is related to the fitness function. FA is based on three rules: (i) a firefly can be attracted to other fireflies regardless of sex, (ii) attractiveness of a firefly is proportional to its brightness, and (iii) brightness is affected or determined by the fitness function.

Particle swarm optimization (PSO)

PSO is an optimization algorithm developed by Kennedy and Eberhart.¹⁰ In PSO, the population consists of solutions (particles), which beside their position also have a velocity. These are defined by the following equations:

v_i = v_i + c₁rnd₁()(p_i − x_i) + c₂rnd₂()(p_b,i − x_i)

x_i+1 = x_i + v_i

where c₁ and c₂ represent positive constants, rnd₁(), and rnd₂() represent two random number (uniformly distributed in [0,1]) generation functions. Parameter x_i is the i-th particle, p_i is the best previous position of the i-th particle, b is the best particle, whereas v_i represents the velocity of particle i. Hence, each particle flies in the direction of better solutions.

Least absolute shrinkage and selection operator (LASSO)

LASSO is a shrinkage and selection method for MLR developed by Tibshirani.¹¹ For a set of predictors (X) and the response y, the model:

ŷ = b₀ + b₁x₁ + b₂x₂ + … + b_nx_n

is fit by imposing the following constraint:

min(∑(y − ŷ)²) subject to ∑|b_j| ≤ λ

where b_j, is the coefficient of the j-th predictor and λ is a tuning parameter. If λ is too large, the constraint has no effect. Hence, it should be tuned for a particular model.

Least angle regression algorithm (LARS)

LARS algorithm, developed by Efron et al.¹² is a stepwise variant of LASSO. It consists of these steps: (i) all coefficients b_j are equal to zero; (ii) obtain the predictor x_j most correlated with y, include it, and calculate the residuals r = y − ŷ; (iii) increase the coefficient b_j in the direction of the sign of its correlation with y, calculate residuals, and stop when another predictor x_k contains as much correlation with r as x_j; (iv) increase (b_j, b_k) in their combined least squares direction, until another predictor x_m contains as much correlation with the residual r; and (v) continue until all the predictors are in the model.

Partial least squares (PLS)

In this work, PLS⁵² based on the SIMPLS⁵³ algorithm was used for regression. For true features, the model with four latent variables (LVs) yielded the lowest error. Hence, this number was used for all the subsequent models.

Interval partial least squares (iPLS)

iPLS is a sequential search method developed by Nørgaard et al.¹⁶ for selection of a best subset of features. Its basis is developing local equidistant PLS models. The method can be used in two modes: forward, and backward. In forward iPLS intervals are successively included in the process, whereas in backward iPLS, the process starts by including all features, after which intervals are successively removed.

Sparse PLS (sPLS)

sPLS is a method developed by Chun and Keleş.⁴⁷ Its basis is imposing sparsity within the constitution of PLS. In that manner, both dimension reduction and feature selection are performed simultaneously. In sPLS the following constraint is used to obtain a solution for a surrogate vector (c) instead of the original direction vector (α):
where matrix M is:

M = X^TYY^TX

and κ, λ₁, λ₂ are parameters defining amount of sparsity.

Uninformative variable elimination-partial least squares (UVE-PLS)

UVE-PLS is an algorithm developed by Centner et al.²² for feature selection in PLS. It consists of the steps: (i) determine the optimal number of LVs; (ii) create a noise matrix R with the same dimension as X, and add to the end; (iii) compute PLS models for XR with leave-one-out procedure, and obtain a coefficient matrix B; (iv) compute the c criterion, i.e., sample mean over standard deviation ratio for coefficients of each variable j; (v) determine the maximum c of the artificial matrix; (vi) remove all original variables with c ≤ c (maximum of R).

Support vector machines (SVM)

SVM^50,51 is a machine learning method for linear and non-linear problems developed by Vapnik. The SVM classifier is based on the idea of planes which define decision boundaries. Features are mapped into a higher feature space using a kernel function. In this work, C-SVM was used which involves minimization of the function:
subject to the following constraints:

y_i(w^Tϕ(x_i) + b) ≥ 1 − ξ_i and ξ_i ≥ 0, i = 1, 2, …, N

where C is the capacity constant, w is the vector of coefficients, b a constant, whereas ξ_i represents parameters for handling non-separable data, and ϕ is the kernel function, which was the radial basis function in this work.

Feature selection methods' hyper-parameter optimization

Iterative grid search was performed for optimization of hyper-parameters and features. For GA, FA, and PSO, number of features was varied in [6:6:636], while for LARS and LASSO 640 was set as the maximum number of selected features. As for hyper-parameters: for GA, three cross-over (scattered, single-point and two-point) and selection (uniform, tournament and roulette) functions were varied. Subsequently, cross-over fraction and mutation rate were varied in [0.2:0.2:0.8]. For FA, the randomization parameter (α), and the attractiveness variation (γ), in [0.2:0.2:0.8], and in [0.2:0.1:1.0], respectively. For PSO, swarm size was fixed at 200, with 500 iterations, while minimum neighbourhood size was varied in [0.2:0.1:1.0]. Additionally, in the second case study, SVM parameters were tuned. For GA-SVM, FA-SVM, and PSO-SVM, they were a part of units within a population, while for LASSO-SVM and LARS-SVM cross-validation was used to determine their optimal values. For iPLS, interval size was varied in: [6:2:60] and [50:2:60], for forward and backward modes, respectively. Number of intervals was not fixed for forward iPLS. Instead, intervals were iteratively added/removed until there was no more improvement in model error. For backward iPLS the number of intervals was fixed to 60.

Feature selection methods evaluation

In the first case study, three performance criteria were used: predictive ability, rate of selecting true features and robustness. Due to small number of samples, confidence intervals of RMSEP were computed using bootstrapping.⁵⁴ In the second case study, accuracy, and receiver operating characteristic (ROC)⁵⁵ curves were used to evaluate performance.

Results and discussion

Case study 1

In the first case study, performance of feature selection methods was evaluated in modelling soil carbonate content from FT-MIR information. It is summarized in Table 1.

Table 1 Performance of feature selection methods for the first case study

Model	ns	SI^a	RMSEP^a	RE^b	ns^c	SI^d	RMSEP^d
a For models with FT-MIR features.b Average relative error expressed in percentages.c Number of selected noise features.d For models with FT-MIR + noise features. All the abbreviations are explained in the text. SI is expressed in percentages, whereas RMSEP values are expressed in mg g^−1.
GA-PLS	18	22.22	1.775	5.29	11	22.22	1.838
FA-PLS	156	28.85	4.504	17.86	83	10.26	4.700
PSO-PLS	38	36.11	4.007	18.58	9	21.05	8.521
LASSO-PLS	30	23.33	10.085	35.69	6	22.22	55.123
LARS-PLS	28	35.72	10.510	45.88	17	17.86	45.364
iPLS (forw.)	72	56.95	8.267	26.06	0	49.07	20.117
iPLS (back.)	473	39.54	9.427	42.48	46	36.58	37.660
UVE-PLS	358	41.06	9.719	30.07	55	38.13	18.376
sPLS	310	59.68	8.330	34.59	7	52.47	22.461
True PLS	641	n.a.	6.565	21.62	n.a.	n.a.	n.a.
Full PLS	3473	n.a.	11.440	58.69	n.a.	n.a.	n.a.

---

Hyper-parameters of GA, FA, and PSO were optimized. In case of GA, optimal were the roulette selection and single-point cross-over function with a fraction of 0.8, and mutation rate of 0.2. All the models gave ample predictions, as evident from Fig. 2 where the points are evenly dispersed along the ideal y = x line. Despite that, selected subsets included a number of spectral features which were out of the ranges of true regions.

Fig. 2 Predictive ability plots for GA-PLS, FA-PLS, PSO-PLS, LASSO-PLS, LARS-PLS, iPLS, UVE-PLS, and sPLS models. Royal blue filled circles represent the training set, while the empty royal blue circles represent the validation set samples. For iPLS: royal blue circles represent forward, whereas pink circles represent backward iPLS (training samples: 29; validation samples: 12).

GA-PLS, FA-PLS, LASSO-PLS, and LARS-PLS cover nearly all, while sPLS covers all true spectral regions except the features from the 1740 cm⁻¹ region (Fig. 3). Highest number of true features: 59.68, 56.95, 39.54, and 41.06% was selected by sPLS, iPLS (forward and backward), and UVE-PLS methods, respectively.

Fig. 3 Spectral features selected by each feature selection method. Legend: (1) GA-PLS, (2) FA-PLS, (3) PSO-PLS, (4) LASSO-PLS, (5) LARS-PLS, (6) iPLS (forward), (7) iPLS (backward), (8) UVE-PLS, and (9) sPLS. Light grey regions depict true spectral regions corresponding to calcite and dolomite according to ref. 43 and 44.

This was rather expected, since both iPLS, and UVE-PLS are methods designed for spectral data, while sPLS does not ignore correlation between features.⁵⁶

On the other hand, their RMSEP values were the highest, which means that even the true ranges contain noise, and there still could be predictive features outside of them. Lowest RMSEP values were obtained for GA-PLS, FA-PLS, and PSO-PLS (Table 1). It can be observed from Fig. 4 that GA-PLS has the narrowest confidence interval, followed by PSO-PLS, and FA-PLS, while for other models they are far wider. This makes GA-PLS the most accurate model.

Fig. 4 RMSEP confidence intervals computed using 1000 bootstrapping iterations (α = 0.05). Legend: (1): GA-PLS, (2): FA-PLS, (3): PSO-PLS, (4): LASSO-PLS, (5): LARS-PLS, (6): forward iPLS, (7): backward iPLS, (8): sPLS, (9): UVE-PLS, (10): true PLS, and (11): full PLS.

Although GA selected 11 artificial out of 18 total selected features, its SI did not decrease, while its error slightly increased: to 1.838 (−0.476; +0.670) g mg⁻¹. GA exhibited strong robustness, and the low error coincides with a previous study on feature selection in quantitative structure-retention relationships⁵⁷ modelling of peptides.¹⁴ It was followed by PSO-PLS, with adequate predictive ability and robustness. Its SI decreased from 36.11 to 21.05%, while its RMSEP increased to 8.521 (−3.250; +4.973) mg g⁻¹. The results led us to believe that GA, FA, and PSO perform well for feature selection in regression regardless of the type of predictors (e.g., spectral data, molecular descriptors). On the other hand, sPLS had an SI of 59.68%. This high value was attributed to the ability to handle highly correlated features. Despite its seemingly high robustness (7 out of 310 artificial features selected), its error considerably increased: to 22.461 (−6.816; +7.964) mg g⁻¹. This means that the selected noise features had a considerable influence on the modelled response. Similarly, SI values for UVE-PLS, LASSO-PLS, and LARS-PLS decreased from 41.06 to 38.13, 23.33 to 22.22, and 35.72 to 17.86%, while their errors considerably increased to 18.376 (−6.647; +18.346), 55.123 (−15.073; +21.194) and 45.364 (−13.907; +18.392), respectively. Forward iPLS had the second highest SI, and amongst 72 selected, 56.95% belong to regions with true spectral features. Clearly, it has a strong ability to handle highly inter-correlated features by merging them into equidistant intervals. Notwithstanding, it was found that its RMSEP had a wide confidence interval (Fig. 4). This result is not odd, since the features selected by forward iPLS belong to only two out of five true spectral regions (Fig. 3). iPLS was shown to be highly robust, as its SI just slightly decreased: from 56.95 to 49.07%, and 39.54 to 36.58% for forward and backward iPLS, respectively. It can be concluded that iPLS in forward mode is the best method for development of a prediction model from spectral information, from a point of view of feature selection. However, it is evident that there is definitely valuable information outside of the three selected intervals which corresponds to other soil carbonate species. On the other hand, FA, applied for feature selection on four occasions,^14,30,31,58 out of which on three occasions in spectral feature selection,^14,30,31 coupled with PLS, has shown to be a robust method (SI decreased from 28.85 to 10.26% with only a slight increase in RMSEP). It exhibited adequate error: 4.504 (−1.430; +1.891) mg g⁻¹. This result indicates that FA requires improvement in handling highly inter-correlated features, because its error is higher than of GA and PSO, which have more narrow confidence intervals of RMSEP (Fig. 4). Higher errors could be attributed to the metaheuristic algorithms getting trapped in a local minimum, which is odd, since e.g., GAs provide stochastic search ability of achieving the global minimum.⁵⁹ More probable source of errors is from the Scheibler method¹³ itself which has relatively low analytical precision and sensitivity towards the actual type of carbonate present in the samples. In addition, the GA, FA, and PSO-PLS have outperformed the true PLS model. Although it might seem obvious that the PLS model constructed out of only true features should be the most predictive, this does not always have to be so. There are other carbonate species present in the analysed soil samples that correspond to spectral features outside the true regions. Also, manual deletion of features may cause using regions which can seemingly be unimportant, but still contain useful information for the model.¹⁷

Finally, the most predictive of the developed models, the GA-PLS model exhibited an error in prediction of soil carbonate content of 1.775 (−0.761; +1.549) mg g⁻¹ which is well within the limits of error found in literature.^60–63

Case study 2

In the second case study, performance of feature selection methods was evaluated in feature selection for classification of prostate cancer patients based on the tumour cell percentage index from gene expression information. Support Vector Machines (SVM)^50,51 was used as a classifier. Its two parameters: width of the radial basis function, and the cost parameter were optimized simultaneously to feature selection for GA-SVM, FA-SVM, and PSO-SVM models, whereas 7-fold cross-validation was used for LASSO-SVM and LARS-SVM. Optimal SVM parameters are summarized in Table 2. Optimal number of selected features was found to be 10, 37, and 7 for GA, FA, and PSO, respectively.

Table 2 Optimal SVM parameters, and performance of feature selection methods for the second case study

Model	γ	C	Accuracy^a	ns^b	Accuracy^c
a For models with gene expression features.b Number of selected noise features.c For models with gene expression + noise features. All the abbreviations are explained in the text. Accuracies are expressed in percentages.
GA-SVM	1.594	2572	100.00	0	100.00
FA-SVM	3.687	2149	95.12	4	90.24
PSO-SVM	2.056	507	95.12	1	92.68
LASSO-SVM	3.700	4800	95.12	58	90.24
LARS-SVM	1.800	5000	90.24	52	68.29

---

Optimal selection function for GA was uniform, while the optimal cross-over function was scattered. Its optimal parameters were found to be 0.2 mutation rate, and 0.8 cross-over fraction giving 100% accuracy. For FA, optimal values of the randomization parameter (α), and the attractiveness variation (γ) were 0.2, and 0.1, respectively. Maximum accuracy was achieved for the 0.4 neighbourhood size for PSO. Top accuracies were achieved for the GA-SVM classifier, followed by the FA-SVM, PSO-SVM and LASSO-SVM classifiers. For all three the accuracy was 95.12%. These results suggest that metaheuristic algorithms, and the LASSO algorithm are first-rate in handling classification problems, but FA and PSO perform far better for regression problems. On the other hand LARS-SVM exhibited considerably lower accuracy of 90.24%. High accuracies were also confirmed by plotting ROC curves (Fig. 5). True and false positive rates were computed based on Bayesian posterior probabilities. All the methods have high areas under the curve (AUC). It can be observed from Fig. 5 that LASSO-SVM has the largest AUC. It was followed by GA-SVM, PSO-SVM, LARS-SVM, and FA-SVM. LASSO-SVM and PSO-SVM classifiers exhibited ROC values higher than their accuracies.

Fig. 5 ROC curves for GA-PLS, FA-PLS, PSO-PLS, LASSO-PLS, and LARS-PLS classification models.

This suggests that both PSO-SVM and LASSO-SVM classifiers are seemingly the most accurate in terms of true and false positive rates. Since the prediction threshold, i.e., threshold for dichotomizing the values of distances from the class-separating hyperplane, had a value of 0.5, and an ROC curve represents the average of accuracies computed for all threshold values, this is indeed possible.

Therefore, although LASSO-SVM has an accuracy lower than GA-SVM, FA-SVM, and PSO-SVM, it retains a higher AUC which means it separates the classes better regardless of the threshold value. All the feature selection methods exhibited a high degree of data compression: 99.96%, 99.83%, 99.97%, 99.72%, and 99.58%, for GA, FA, PSO, LASSO, and LARS, respectively. GA-SVM has shown to be strongly robust, because with addition of noise its accuracy did not decrease and no noise features were selected. Accuracy of FA-SVM reduced to 90.24% for four included noise features. This led to a conclusion that both GA, and FA are highly resistant to small changes in the predictors. Accuracy of all the other classifiers decreased upon introduction of noise features (Table 2) with the largest decrease for LARS-SVM: to 68.29% for 52 selected noised variables. For PSO-SVM the accuracy slightly reduced (Table 2) for one selected noise feature. The changes in accuracies were confirmed by AUC reduction (Fig. 5), except for FA-SVM and PSO-SVM for which AUC increased.

Conclusions

In conclusion, GA, FA, and PSO demonstrated superiority in the first case study. There, GA-PLS and PSO-PLS yielded the lowest errors: 1.775 (−0.761; +1.549) and 4.007 (−1.065; +1.510) mg g⁻¹ which are within values commonly found in literature. They were followed by FA-PLS which yielded an adequate error of 4.504 (−1.430; +1.891) mg g⁻¹, but in a wider confidence interval. This could indicate that FA-PLS requires improvement in handling highly correlated features. All three methods have exhibited strong robustness after introduction of noise features, which is crucial since even the slightest measurement noise might influence prediction error. It was shown that sPLS is highly resistant to structural changes in the predictive features, but it still exhibited a high error. Hence, despite its strong ability to handle highly inter-correlated features, it still needs improvement to be appropriate for spectral data. UVE-PLS, LASSO-PLS, and LARS-PLS were not highly robust, exhibiting extremely high errors for models with added noise. This was especially evident from the classification case in which LARS-SVM exhibited a drastic decrease in accuracy. On the other hand, GA-SVM yielded final models with perfect accuracy, FA-SVM, PSO-SVM, and LASSO-SVM final models with 95.12% accuracy, whereas the LARS-SVM final model had a 90.24% accuracy. Here, GA, PSO, and LASSO were found to be highly robust, with accuracies nearly unchanged upon introduction of noise features. Other sources of errors were identified and it was found that they mostly originate from the analytical methods themselves.

Therefore, it was confirmed that GA was strongly applicable for feature selection in both regression and classification, FA, PSO and LARS in regression rather than classification, whereas LASSO was applicable in classification problems in these two applications of analytical chemistry.

Conflict of interest

Both authors declare no conflict of interest.

Acknowledgements

This work was supported by a Pukyong National University Research Grant for 2015 and the Brain Busan 21 Project in 2015.

References

1. M. Linial and N. Linial, Science, 1995, 268, 481–482.
2. H. Akaike, in Second International Symposium on Information Theory, ed. B. N. Petrov and F. Csaki, Akademiai Kiado, Budapest, 1973, pp. 267–281.
3. S. Palminteri, M. Khamassi, M. Joffily and G. Coricelli, Nat. Commun., 2015, 6, 8096.
4. M. A. Efroymson, in Mathematical methods for digital computers, WILEY-VCH Verlag, New York, 1960, pp. 191–203.
5. Y. Saeys, I. Inza and P. Larranaga, Bioinformatics, 2007, 23, 2507–2517.
6. P. W. Laud and J. G. Ibrahim, J. R. Stat. Soc. Ser. B, 1995, 57, 247–262.
7. Š. Ukić, M. Novak, P. Žuvela, N. Avdalović, Y. Liu, B. Buszewski and T. Bolanča, Chromatographia, 2014, 77, 985–996.
8. J. H. Holland, Sci. Am., 1992, 267, 66–72.
9. X. S. Yang, Lect. Notes Comput. Sci., 2009, 5792, 169–178.
10. J. Kennedy and R. C. Eberhart, Proc. IEEE Int. Conf. Neural Networks, 1995, 39–43.
11. R. Tibshirani and R. S. Society, J R Stat Soc, Ser B, 1996, 58, 267–288.
12. R. Tibshirani, I. Johnstone, T. Hastie and B. Efron, Ann. Stat., 2004, 32, 407–499.
13. H. Pellit and J. Salleron, Sci. Am., 1880, 10, 4002–4003.
14. P. Žuvela, J. J. Liu, K. Macur and T. Bączek, Anal. Chem., 2015, 87, 9876–9883.
15. R. M. Balabin and S. V. Smirnov, Anal. Chim. Acta, 2011, 692, 63–72.
16. L. Nørgaard, A. Saudland, J. Wagner, J. P. Nielsen, L. Munck and S. B. Engelsen, Appl. Spectrosc., 2000, 54, 413–419.
17. Z. Xiaobo, Z. Jiewen, M. J. W. Povey, M. Holmes and M. Hanpin, Anal. Chim. Acta, 2010, 667, 14–32.
18. Y. P. Du, Y. Z. Liang, J. H. Jiang, R. J. Berry and Y. Ozaki, Anal. Chim. Acta, 2004, 501, 183–191.
19. J.-H. Jiang, R. J. Berry, H. W. Siesler and Y. Ozaki, Anal. Chem., 2002, 74, 3555–3565.
20. S. Kasemsumran, Y. P. Du, K. Murayama, M. Huehne and Y. Ozaki, Anal. Chim. Acta, 2004, 512, 223–230.
21. S. F. C. Soares, A. A. Gomes, M. C. U. Araujo, A. R. G. Filho and R. K. H. Galvão, TrAC Trends Anal. Chem., 2013, 42, 84–98.
22. V. Centner, D. L. Massart, O. E. de Noord, S. de Jong, B. M. Vandeginste and C. Sterna, Anal. Chem., 1996, 68, 3851–3858.
23. S. Ye, D. Wang and S. Min, Chemom. Intell. Lab. Syst., 2008, 91, 194–199.
24. D. Wu, Y. He, P. Nie, F. Cao and Y. Bao, Anal. Chim. Acta, 2010, 659, 229–237.
25. I. P. Soares, T. F. Rezende, R. C. Silva, E. V. R. Castro and I. C. P. Fortes, Energy & Fuels, 2008, 22, 2079–2083.
26. H. C. Goicoechea and A. C. Olivieri, J. Chem. Inf. Comput. Sci., 2002, 42, 1146–1153.
27. F. Allegrini and A. C. Olivieri, Anal. Chim. Acta, 2011, 699, 18–25.
28. M. J. Baker, J. Trevisan, P. Bassan, R. Bhargava, H. J. Butler, K. M. Dorling, P. R. Fielden, S. W. Fogarty, N. J. Fullwood, K. A. Heys, C. Hughes, P. Lasch, P. L. Martin-Hirsch, B. Obinaju, G. D. Sockalingum, J. Sulé-Suso, R. J. Strong, M. J. Walsh, B. R. Wood, P. Gardner and F. L. Martin, Nat. Protoc., 2014, 9, 1771–1791.
29. D. D. S. Fernandes, A. A. Gomes, G. B. da Costa, G. W. B. da Silva and G. Véras, Talanta, 2011, 87, 30–34.
30. L. C. M. de Paula, A. S. Soares, T. W. de Lima, A. C. B. Delbem, C. J. Coelho and A. R. G. Filho, PLoS One, 2014, 9, e114145.
31. M. Goodarzi and L. dos Santos Coelho, Anal. Chim. Acta, 2014, 852, 20–27.
32. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, Science, 1983, 220, 671–680.
33. Y. H. Yang and N. P. Thorne, in Statistics and science: a Festschrift for Terry Speed, ed. D. R. Goldstein, Institute of Mathematical Statistics, Beachwood, OH, 2003, vol. 40, pp. 403–418.
34. V. Bolón-Canedo, N. Sánchez-Maroño, A. Alonso-Betanzos, J. M. Benítez and F. Herrera, Inf. Sci. (Ny)., 2014, 282, 111–135.
35. T. Li, C. Zhang and M. Ogihara, Bioinformatics, 2004, 20, 2429–2437.
36. M. A. Hall and A. Smith Lloyd, in Proceedings of the Twelfth international Florida Artificial intelligence Research Society Conference, ed. A. N. Kumar and I. Russell, AAAI Press, Menlo Park, 1999, pp. 235–239.
37. L. Yu and H. Liu, in Proceedings of the Twentieth International Conference on Machine Learning, ed. T. Fawcett and N. Mishra, AAAI Press, Menlo Park, 2003, pp. 856–864.
38. Z. Zhao and H. Liu, in Proceedings of the 20th International Joint Conference on Artificial Intelligence, ed. M. Veloso, AAAI Press, Menlo Park, 2007, pp. 1156–1161.
39. M. D. Ritchie, E. R. Holzinger, R. Li, S. A. Pendergrass and D. Kim, Nat. Rev. Genet., 2015, 16, 85–97.
40. N. Qin, F. Yang, A. Li, E. Prifti, Y. Chen, L. Shao, J. Guo, E. Le Chatelier, J. Yao, L. Wu, J. Zhou, S. Ni, L. Liu, N. Pons, J. M. Batto, S. P. Kennedy, P. Leonard, C. Yuan, W. Ding, Y. Chen, X. Hu, B. Zheng, G. Qian, W. Xu, S. D. Ehrlich, S. Zheng and L. Li, Nature, 2014, 513, 59–64.
41. I. Guyon, J. Weston, S. Barnhill and V. Vapnik, Mach Learn, 2002, 46, 389–422.
42. V. J. Bruckman and K. Wriessnig, Environ. Chem. Lett., 2013, 11, 65–70.
43. J. Ji, Y. Ge, W. Balsam, J. E. Damuth and J. Chen, Mar. Geol., 2009, 258, 60–68.
44. M. Tatzber, F. Mutsch, A. Mentler, E. Leitgeb, M. Englisch and M. H. Gerzabek, Appl. Spectrosc., 2010, 64, 1167–1175.
45. M. Khanmohammadi, S. Armenta, S. Garrigues and M. de la Guardia, Vib. Spectrosc., 2008, 46, 82–88.
46. R. W. Kennard and L. A. Stone, Technometrics, 1969, 11, 137–148.
47. H. Chun and S. Keleş, J. R. Stat. Soc. Series B Stat. Methodol., 2010, 72, 3–25.
48. Y. Wang, X.-Q. Xia, Z. Jia, A. Sawyers, H. Yao, J. Wang-Rodriquez, D. Mercola and M. McClelland, Cancer Res., 2010, 70, 6448–6455.
49. Z. Y. Jia, Y. P. Wang, A. Sawyers, H. Z. Yao, F. Rahmatpanah, X. Q. Xia, Q. A. Xu, R. Pio, T. Turan, J. A. Koziol, S. Goodison, P. Carpenter, J. Wang-Rodriguez, A. Simoneau, F. Meyskens, M. Sutton, W. Lernhardt, T. Beach, J. Monforte, M. McClelland and D. Mercola, Cancer Res., 2011, 71, 2476–2487.
50. V. N. Vapnik, Statistical Learning Theory, John Wiley & Sons, New York, 1998.
51. V. N. Vapnik, S. E. Golowich and A. J. Smola, in Advances in Neural Information Processing Systems, ed. M. Press, Cambridge, 1997, vol. 9, pp. 281–287.
52. H. Wold, in Encyclopedia of Statistical Sciences, WILEY-VCH Verlag, New York, 1985, vol. 6, pp. 581–591.
53. S. de Jong, Chemom. Intell. Lab. Syst., 1993, 18, 251–263.
54. B. Efron, Biometrika, 1981, 68, 589–599.
55. T. A. Lasko, J. G. Bhagwat, K. H. Zou and L. Ohno-Machado, J Biomed Inf., 2005, 38, 404–415.
56. P. Bastien, F. Bertrand, N. Meyer and M. Maumy-Bertrand, Bioinformatics, 2015, 31, 397–404.
57. R. Kaliszan, Chem. Rev., 2007, 107, 3212–3246.
58. H. Banati and M. Bajaj, Int. J. Comput. Sci. Issues, 2011, 8, 473–480.
59. M. Afshar, A. Gholami and M. Asoodeh, Korean J. Chem. Eng., 2014, 31, 496–502.
60. C. Du, Z. Ma, J. Zhou and K. W. Goyne, Sensors Actuators B Chem., 2013, 188, 1167–1175.
61. L. P. D'Acqui, A. Pucci and L. J. Janik, Eur. J. Soil Sci., 2010, 61, 865–876.
62. B. Stenberg, R. A. Viscarra Rossel, A. M. Mouazen and J. Wetterlind, Adv. Agron., 2010, 107, 163–215.
63. C. M. Müller, B. Pejcic, L. Esteban, C. D. Piane, M. Raven and B. Mizaikoff, Sci. Rep., 2014, 4, 6764.

---