Porous ceramic stabilized phase change materials for thermal energy storage
Songyang Liuabc and
Huaming Yang*abc
aCentre for Mineral Materials, School of Minerals Processing and Bioengineering, Central South University, Changsha 410083, China. E-mail: hmyang@csu.edu.cn; Fax: +86-731-88710804; Tel: +86-731-88830549
bKey Laboratory for Mineral Materials and Application of Hunan Province, Central South University, Changsha 410083, China
cState Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China
First published on 29th April 2016
Abstract
This paper aimed to develop a novel form-stable composite phase change material (PCM) by infiltrating molten Na2SO4 into a mullite-corundum porous ceramic preform (M-PCP). Sufficient coal-series kaolinite (Kc), aluminum hydroxide, aluminum fluoride and graphite were mixed and subsequently heated in air at 1450 °C to produce M-PCP. The microstructure, thermal properties and thermal reliability of the composite PCMs were characterized by thermogravimetric and differential scanning calorimetry, X-ray diffraction and scanning electron microscopy. The results indicate that the M-PCP/Na2SO4 was 54.33 J g−1 at its melting temperature of 882.17 °C. Impregnation experiments and numerical simulation demonstrated high-temperature chemical compatibility and wettability between molten Na2SO4 and M-PCP. The M-PCP/Na2SO4 composite showed good thermal stability after 30 thermal shock cycles, and could potentially be used in the thermal energy storage field.
1. Introduction
With the rapid development of science and technology, the demand for energy is increasing. The mismatch between energy supply and demand has become increasingly prominent. Thermal energy storage not only reduces the mismatch but also improves the performance and reliability of energy systems and plays an important role in conserving energy. In recent years, phase change materials (PCMs) for latent heat thermal energy storage (LHTES) have received great interest in relation to the efficient use of thermal energy.1–4 Using PCMs for LHTES has become the preferred method because of their safety, stability, high energy storage density and constant phase change temperature.5–9 A large number of organic and inorganic substances and eutectics have been studied as PCMs.10–12 However, compared with these indisputable advantages, there are still many deficiencies in the application of PCMs. One the one hand, it is hard to control the materials during the phase transition. On the other hand, the high degree of supercooling results in hysteresis of the thermal response. The problems are expected to be solved by preparing form-stable composite PCMs.13,14 In order to stabilize the PCMs, a large number of porous inorganic materials or silicate minerals have been studied, such as montmorillonite or bentonite,15–18 halloysite,19–22 attapulgite,23–26 expanded perlite,27–30 diatomite,31–33 vermiculite,34–36 and kaolinite.37,38Among the PCMs investigated, Na2SO4 has been found to exhibit many desirable characteristics, such as high latent heat, good thermal reliability after a large number of melt/freeze cycles and commercial availability at reasonable cost.39,40 Despite these desirable properties, the application of Na2SO4, has been hampered in many ways by the complicated energy storage systems and the leakage of the PCMs. Therefore, various methods have been developed to solve these problems.
Recently, a new type of PCM/ceramic composite material, based on a porous ceramic preform with the phase change material distributed in the pores, has aroused much attention for its attractive properties. It not only integrates the advantages of traditional phase change materials and the sensible heat of the ceramics, but is also expected to solve the application problem, particularly because of its encapsulation, low thermal conductivity and the fact that it is not corrosive to the preform. Most previous research was aimed at studying the impregnation of PCMs into the porous ceramic preform prepared by either mixed sintering41,42 or the sol–gel method.43,44 But its lower phase transition temperature, specific heat capacity and its poor thermal shock resistance to a large extent limit its application as a high temperature thermal energy storage material.45–48 Therefore, it is necessary to fabricate novel composites which can improve the thermal energy storage effectively and which are expected to show high performance.
Mullite (3Al2O3·2SiO2) and mullite-based ceramic materials have a close thermal expansion match, low density, and excellent high-temperature strength.49,50 Kc has been studied extensively in the last few decades for serving the conventional ceramics industry and there has been renewed interest in the conversion of Kc to mullite, due to its low cost and relatively low sintering temperature. It is worth mentioning that the mullite made by the conventional method is generally dense on account of the excess SiO2 existing in Kc. Therefore, the addition of a certain amount of Al(OH)3 powder can reduce the amount of glass phase (SiO2), increase the amount of mullite51 and improve the overall properties of the composite.
In the present work, we aimed to prepare an M-PCP/Na2SO4 composite to be used for thermal energy storage. Kc and aluminum hydroxide were the main raw materials. Aluminum fluoride and graphite power were used as the cosolvent and pore former. A corundum-mullite porous ceramic preform (C-PCP) was also prepared by adding different amounts of Kc to investigate the effect of the Kc content on the properties of the M-PCP/Na2SO4 composite. In addition, the structure, thermal stability, and high temperature thermal performance of the composites were investigated systematically.
2. Experimental
2.1 Materials preparation
The typical chemical composition of the Kc obtained from Datong, Shanxi, China is (mass%): SiO2, 45.5; Al2O3, 37.9. It was passed through a 74 μm sieve before use. Aluminum hydroxide and aluminum fluoride were supplied by Xilong Chemical Co., Ltd., and Tianjin Guangfu Institute of Superfine Chemical Industry., China. The graphite powders and Na2SO4 were purchased from Tianjin Kemiou Reagent Co., Ltd., and Aladdin Industrial Corporation., China. The graphite powders were employed as the pore-former to fabricate pores for the composite. Water and Na2SO4 were used as the binder and PCM, respectively. In our experiment, the M-PCP was prepared by the method using the addition of the pore-forming agent. 70 g Kc, 30 g Al(OH)3, 10 g AlF3 and 10 g graphite were added to a ball mill and ball-milled for 2 h at a rotation speed of 200 rpm to obtain homogeneous slurries. The composite was kept at 80 °C for 24 h, and then mixed with 5% of binder (water) in a mortar. The mixed powders were pressed into the specimens under 20 MPa by using a steel die. To burn out graphite, the green compact of M-PCP was heated to 850 °C with a heating rate of 2 °C min−1, and then to 1450 °C with a heating rate of 5 °C min−1. The M-PCP/Na2SO4 composite was subsequently prepared by spontaneous melt infiltration of molten Na2SO4 PCM into the porous ceramic preform. This was done at different impregnation temperatures (900–1100 °C) and different time periods (0.5–2.5 h). Meanwhile, the C-PCP was also prepared by the method using the addition of the pore-forming agent. 30 g Kc, 70 g Al(OH)3, 10 g AlF3 and 10 g graphite were added to a ball mill and ball-milled for 2 h at a rotation speed of 200 rpm to obtain homogeneous slurries. The composite was kept at 80 °C for 24 h, and then mixed with 5% of binder (water) in a mortar. The mixed powders were pressed into the specimens under 20 MPa using a steel die. The compositions of the mixed powders for preparing the M-PCP and C-PCP in this study are listed in Table 1. To burn out graphite, the green compact of C-PCP was also heated to 850 °C with a heating rate of 2 °C min−1 and then to 1450 °C with a heating rate of 5 °C min−1. Then, the C-PCP/Na2SO4 composite was prepared by the spontaneous infiltration method.| Samples | Kc | Al(OH)3 | AlF3/Kc + Al(OH)3 | Graphite/Kc + Al(OH)3 |
|---|---|---|---|---|
| 1 | 70 | 30 | 10 | 10 |
| 2 | 30 | 70 | 10 | 10 |
2.2 Characterization
X-ray diffraction (XRD) patterns were obtained using an X-ray diffraction apparatus (DX-2700) with an acceleration voltage of 40 kV and an emission current of 40 mA at a scanning rate of 9° min−1 from 5° to 80° of 2θ. The pore size distribution of C-PCP and M-PCP was measured by mercury intrusion porosimetry (AutoPore IV 9500). The morphology of the samples was observed using a scanning electron microscope (SEM, FEI Quanta-200). The open porosity was determined by the Archimedes method with distilled water as the liquid medium. Thermogravimetry-differential scanning calorimetry (TG-DSC) was performed in air using a NETZSCH STA449C thermal analyzer at 10 °C min−1. The thermal stability of the Na2SO4, M-PCP/Na2SO4 composite and the phase change properties of the Na2SO4, and M-PCP/Na2SO4 and C-PCP/Na2SO4 composites were determined by TG-DSC analysis. A thermal cycling test was conducted to investigate the thermal shock resistance of the M-PCP/Na2SO4 composite after repeated thermal cycles. The infiltration ratio refers to the weight percentage of the infiltrated Na2SO4 to the total weight of the composite, and it can be evaluated by:
 | (1) |
 | (2) |
2.3 Numerical model
The physical model of the porous ceramic material is a rectangular solid 80 mm × 40 mm × 5 mm. When the temperature exceeds the melting point of Na2SO4, the Na2SO4 starts to melt and impregnate into the preform. Finally, the melt begins to crystallize and forms the phase change material composite after cooling. The following assumptions are made in the present study: (a) the pore structure of the porous ceramic preform is invariable; (b) the PCM is homogeneous and isotropic; (c) the flow in the melt is laminar and the viscous dissipations are negligible; (d) the system is in a local thermal equilibrium condition; (e) the volume variation resulting from the phase change is negligible. The mathematical model, describing the transient phase change process combined with natural convection heat transfer, is formulated with 2D coordinates. For the phase change region inside the PCM, an enthalpy-porosity approach is used. Consequently, based on the aforementioned assumptions, the continuity, momentum, and thermal energy equations can be expressed as follows:Continuity:
| ∂t(ρ) + ∂i(ρui) = 0 | (3) |
Momentum:
| ∂t(ρui) + ∂j(ρuiuj) = μ∂jjui − ∂iP + ρgi + Si | (4) |
Thermal energy:
| ∂t(ρh) + ∂t(ρΔH) + ∂i(ρuih) = ∂i(k∂iT) | (5) |
In these relations, ui is the fluid velocity, ρ is the PCM's density, μ is the dynamic viscosity, P is the pressure, g is the gravitational acceleration, k is the thermal conductivity and h is the sensible enthalpy which is defined as follows:
 | (6) |
The enthalpy, H, is therefore:
| H = h + ΔH | (7) |
 | (8) |
In eqn (2), Si are the Darcy's law damping terms (as source term) that are added to the moment equation due to phase change effect on convection. It is defined as follows:
 | (9) |
The coefficient C is a mushy zone constant which is fixed at a value of 105 kg m−3 s−1 for the present study. The model for the numerical study is created using pre-processor software GAMBIT 2.3.16. Meshing of the numerical model is generated and the boundary is applied at an appropriate surface. In this study, the grid is implemented using the GAMBIT software and then exported to FLUENT for problem solving. The numerical solution is implemented using a commercial CFD program Fluent 6.3.26.
3. Results and discussion
Photographs of the mixed raw powders, green compact, PCP, and PCP/Na2SO4 composites, pore size distributions of the M-PCP and C-PCP, and XRD patterns of the samples are shown in Fig. 1. The linear shrinkage of the M-PCP/Na2SO4 composites has not changed during the process of preparation, which demonstrates good creep resistance at high temperature. As can be seen from Fig. 1e, the pore size distributions of the two porous ceramic preforms are comparatively centralized, and mainly distributed from 2 to 4 μm. There are no significant differences in pore size distribution between them. Fig. 1f shows the XRD patterns of the raw materials, Na2SO4, and M-PCP/Na2SO4 and C-PCP/Na2SO4 composites. The characteristic peaks of Na2SO4 appear at 19.1°, 28.1°, 28.9°, 32.1° and 33.9°. As for the raw materials, the diffraction peaks observed at 2θ = 12.3°, 21.4° are indexed to the characteristics of kaolinite (JCPDS 14-0164), 2θ = 18.3° is indexed to the characteristic of gibbsite (JCPDS 33-0018), 2θ = 24.9° is indexed to the characteristic of aluminum fluoride and 2θ = 26.6° is indexed to the characteristic of graphite (JCPDS 26-1079). The characteristic reflections of Na2SO4, C-PCP and M-PCP can be seen from the XRD patterns of the C-PCP/Na2SO4 and M-PCP/Na2SO4 composites after Na2SO4 was impregnated into the two porous ceramic preforms in Fig. 1f and 2a. This indicates that Na2SO4 was successfully loaded into the C-PCP and M-PCP. In order to investigate how the change in the content of Kc affects the properties of the PCP/Na2SO4 composite, two kinds of PCP were studied systematically. The corundum-mullite porous ceramic preform (C-PCP) was prepared by adding different amounts of Kc. As can be seen from Table 1 and Fig. 2a, when the mass ratio of Kc and Al(OH)3 is 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, the main crystallization of the sample is mullite, and the second phase is corundum; whereas, if the mass ratio of Kc and Al(OH)3 is 3
3, the main crystallization of the sample is mullite, and the second phase is corundum; whereas, if the mass ratio of Kc and Al(OH)3 is 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, the main crystallization of the sample is corundum, and the second phase is mullite. Fig. 2b and c show the typical microstructures of the two porous ceramic preforms C-PCP and M-PCP. On the one hand, we can clearly see that the sheet-like morphology of mullite is formed when a small amount of Kc (30%) is added. On the other hand, when the addition of Kc reached a high level (70%), it displayed a different microstructure evolution, and the morphology of mullite could be converted to needle-like grains. As can be seen from Fig. 2e and f, the majority of the pores of the two porous ceramic preforms C-PCP and M-PCP have been blocked by the melting PCM Na2SO4. There exists good wettability between Na2SO4 PCM and PCP, which leads to the process of infiltration by capillary force. Na2SO4 is held in the network of the PCP by capillary force and forms the PCM composite after the melt crystallization.
7, the main crystallization of the sample is corundum, and the second phase is mullite. Fig. 2b and c show the typical microstructures of the two porous ceramic preforms C-PCP and M-PCP. On the one hand, we can clearly see that the sheet-like morphology of mullite is formed when a small amount of Kc (30%) is added. On the other hand, when the addition of Kc reached a high level (70%), it displayed a different microstructure evolution, and the morphology of mullite could be converted to needle-like grains. As can be seen from Fig. 2e and f, the majority of the pores of the two porous ceramic preforms C-PCP and M-PCP have been blocked by the melting PCM Na2SO4. There exists good wettability between Na2SO4 PCM and PCP, which leads to the process of infiltration by capillary force. Na2SO4 is held in the network of the PCP by capillary force and forms the PCM composite after the melt crystallization.
 | ||
| Fig. 1 Photographs of (a) mixed raw powders, (b) green compact, (c) M-PCP and (d) M-PCP/Na2SO4 composite, (e) pore size distribution of M-PCP and C-PCP, (f) XRD patterns of the samples. | ||
 | ||
| Fig. 2 XRD patterns of (a) M-PCP and C-PCP, SEM images of (b) C-PCP, (c) M-PCP, (e) C-PCP/Na2SO4 composite, (f) M-PCP/Na2SO4 composite and (d) corresponding EDS spectra of C-PCP, M-PCP. | ||
The thermal properties of the composite PCMs mainly consist of thermal storage and release performance, and thermal reliability or stability after a long period of utilization. The phase change temperature and phase change enthalpy of Na2SO4, and C-PCP/Na2SO4 and M-PCP/Na2SO4 composites were investigated by DSC thermal analysis (Fig. 3a). The DSC curve of Na2SO4 is used as a reference to evaluate the variations in thermal properties of the two composites. The phase change temperature (Tm) and latent heat (ΔH) of Na2SO4 are 882.31 °C and 116.7 J g−1. Compared with Na2SO4, the phase change temperatures of the C-PCP/Na2SO4 and M-PCP/Na2SO4 composites are 881.96 °C and 882.17 °C, respectively. The latent heats of the C-PCP/Na2SO4 and M-PCP/Na2SO4 composites are 49.52 J g−1 and 54.33 J g−1, respectively. Table 2 shows that the open porosity of the M-PCP is larger than that of C-PCP, which indicates that M-PCP has more adsorption sites than C-PCP. The infiltration rate of M-PCP is also larger than that of C-PCP, indicating that the M-PCP has the better infiltration effect. The more PCM is filled into the porous ceramics preform, the greater the improvement in latent heat achieved. Therefore, the latent heat of the M-PCP/Na2SO4 composite is larger than that of the C-PCP/Na2SO4 composite. The thermal properties should be stable and exhibit no or minimal change after long periods of use. Therefore, thermal cycling tests were conducted to investigate the thermal reliability of the composite PCMs. There is almost no change in the appearance of the M-PCP/Na2SO4 composite phase change material after 30 thermal cycles (Fig. 3c). By contrast, there are a lot of cracks after 30 thermal cycles for the C-PCP/Na2SO4 composite, which indicates that the PCM Na2SO4 may be leaking from the C-PCP. This result shows that the thermal reliability of the M-PCP/Na2SO4 is superior to that of the C-PCP/Na2SO4 composite. This is mainly because the excess SiO2 in Kc would be consumed in forming the needle-like structure of mullite. Meanwhile, the mullite with its rigid frame structure will improve the thermal shock resistance of the samples.
| Samples | Open porosity (wt%) | Infiltration rate (wt%) |
|---|---|---|
| C-PCP/Na2SO4 | 53.33 | 45.16 |
| M-PCP/Na2SO4 | 56.21 | 49.51 |
The thermal stabilities of Na2SO4 and M-PCP/Na2SO4 were also analyzed by TG (Fig. 3b). The Na2SO4 and M-PCP/Na2SO4 are stable from room temperature to high temperatures up to 1000 °C. Based on this analysis, we may conclude that the M-PCP/Na2SO4 composite has a good thermal stability. It is observed that the phase change temperatures of the sample are very close to the original composite phase change materials after 30 thermal cycles (Fig. 3d), and that the latent heats of the samples are slightly lower than those of the original materials. Meanwhile, no leakage of Na2SO4 was observed after thermal cycling, which can be explained by the fact that the Na2SO4 is held in the network of the M-PCP by capillary force and surface tension force. Fig. 3d shows the SEM image of the M-PCP/Na2SO4 composite after 30 thermal cycles. It is observed that the morphology of M-PCP/Na2SO4 has no obvious variation in comparison with the PCM composite before (Fig. 2f) and after 30 thermal cycles (Fig. 3d). In conclusion, the M-PCP/Na2SO4 composite shows excellent thermal reliability.
We have studied the high temperature stability of Na2SO4 and M-PCP/Na2SO4 experimentally. We also studied the thermodynamic feasibility experimentally. The vapor pressure of Na2SO4 is low at high temperature, which shows that the volatilization of the phase-change material is very weak. In the gas–liquid–solid system, the overall possible chemical reactions in the process of impregnation are expressed by eqn (10)–(13).
 | (10) |
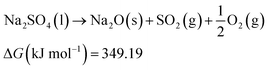 | (11) |
 | (12) |
 | (13) |
To illustrate the theoretical feasibility of the route proposed below, the thermodynamic parameters at 1300 K in the process of impregnation were calculated. From the results of the thermodynamic calculation, the Gibbs free energy changes (ΔG) are 371.90 and 349.19 kJ mol−1 > 0 for eqn (10) and (11), respectively. So, eqn (10) and (11) cannot proceed, which indicates the PCM Na2SO4 has good thermodynamic thermal stability. On this basis we analyzed the stability of the MCPCP/Na2SO4 composite. The Gibbs free energy changes (ΔG) are 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 205.05 and 186.21 kJ mol−1 > 0 for eqn (12) and (13), respectively, so the equation cannot proceed spontaneously in the impregnation process, which means that the mixed system (PCM Na2SO4 and M-PCP preform) is thermodynamically stable.
205.05 and 186.21 kJ mol−1 > 0 for eqn (12) and (13), respectively, so the equation cannot proceed spontaneously in the impregnation process, which means that the mixed system (PCM Na2SO4 and M-PCP preform) is thermodynamically stable.
The infiltration ratio and the relative density are the two main factors used to evaluate the high temperature chemical compatibility of Na2SO4 and the M-PCP/Na2SO4 composite and to investigate the infiltration effects of the molten Na2SO4 into the porous ceramic preform. Fig. 4 shows the infiltration process of the PCM Na2SO4 being impregnated into the M-PCP. The M-PCP/Na2SO4 composite was fabricated by a spontaneous infiltration method. At the beginning, the M-PCP was covered by a certain amount of Na2SO4, and the PCM Na2SO4 would melt gradually and impregnate into the pores of M-PCP through the effects of surface tension and capillarity when the temperature moved beyond its melting point. Parts of the pores in the M-PCP would be blocked by the melting Na2SO4. Finally, the PCM would be gradually solidified as the temperature decreased. Fig. 5 indicates the effects of the infiltration process on the infiltration ratio and the relative density process on the ratio and the relative density of the composite. The high temperature chemical compatibility between Na2SO4 and the M-PCP composite were analyzed. In order to investigate the effects of the infiltration temperature on the infiltration ratio and relative density of the M-PCP/Na2SO4 composite, the infiltration temperature was varied from 900 °C to 1100 °C with the infiltration time fixed at 1 h. Similarly, in order to study the effects of the infiltration time on the infiltration ratio and relative density of the M-PCP/Na2SO4 composite, the infiltration time was varied from 0.5 h to 2.5 h with the infiltration temperature fixed at 1000 °C.
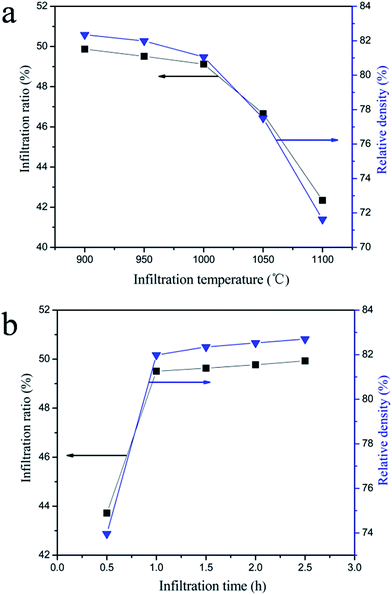 | ||
| Fig. 5 The effects of the infiltration temperature (a) and infiltration time (b) on the ratio and relative density of the M-PCP/Na2SO4 composite. | ||
With the increase in infiltration temperature, the infiltration ratio and relative density decrease slightly from 900 °C to 1000 °C (Fig. 5a), and then decrease obviously when the infiltration temperature is between 1000 °C and 1100 °C. According to previous research,52 along with the increase in the infiltration temperature, the surface tension, viscosity and the wetting angle of the molten salts decrease, whereas there is little change in viscosity and the wetting angle of the molten salts. In consequence, under certain infiltration times, the surface tension of the molten Na2SO4 has become a principal factor for infiltration temperatures between 900 °C and 1100 °C. With the increase in temperature, the surface tension of the molten salts decreases. This results in a decrease in the high temperature chemical compatibility between Na2SO4 and the M-PCP composite. To prevent the blockage of the pores by the solidification of the molten Na2SO4 in the process of infiltration, 900–1000 °C should be chosen as the optimum range according to the infiltration experiments. Further research is needed to ascertain at what temperature the optimal high temperature chemical compatibility between Na2SO4 and the M-PCP/Na2SO4 composite can be obtained. It can be seen (Fig. 5b) that the infiltration ratio and relative density increase rapidly with an increase in the infiltration time. The infiltration ratio and relative density tend to be constant after 1 h. Therefore, 1 h was chosen as the optimal infiltration time.
With the aim of producing thermal control applications of solid liquid phase change materials, the heat transfer numerical simulation between phase change materials and phase change composite materials is indispensable. The study of the heat transfer process between them plays an important part in determining the structure which will optimize the design and the effective utilization of thermal control systems for phase change composite materials. The numerical simulation of heat transfer in the solid–liquid phase change process for porous mediums includes the heat transfer calculation for the phase change materials and porous mediums. Fig. 6 shows the temperature profiles in the M-PCP/Na2SO4 composite during heat storage and heat retrieval. The temperature field changes from the inside to the outside during heat storage (Fig. 6a–d). By comparison and analysis, we find that the changes in the temperature gradients are less marked from 0.75 h to 1.5 h, mainly because the temperature in the furnace is lower than the melting temperature of Na2SO4. Then, the PCM Na2SO4 will melt gradually and impregnate the pores of M-PCP when the temperature in the furnace is above its melting point. The temperature gradients changed significantly from 1.5 h to 3 h. This phenomenon can be attributed to the melting characteristics of Na2SO4. At the beginning of the phase transition, melting of pure Na2SO4 was accelerated during heat storage (melting), due to the intensive natural convection in the melted Na2SO4. The existence of natural convection can provide the PCM composite with a large heat transfer coefficient and small thermal resistance, and this makes the change in temperature gradients obvious. The temperatures in the furnace will reach 950 °C and 1000 °C when the melting times are 2.25 and 3 h, respectively. The heat transfer performance of the M-PCP composite at the heating time of 3 h is higher than that of 2.25 h, and it will obtain a higher impregnation rate of Na2SO4. This means that the high temperature chemical compatibility between Na2SO4 and M-PCP/Na2SO4 will achieve better effects at 1000 °C.
By contrast, Fig. 6e–h show that for the temperature field changes from the outside to the inside during heat retrieval, the temperature gradients of each layer are becoming more stable. In the heat retrieval (cooling) duration, since Na2SO4 is impregnated in the pores of M-PCP, natural convection is consequently hampered. Therefore, freezing of the M-PCP/Na2SO4 composite is typically dominated by thermal conduction. While modelling the melting and freezing of the M-PCP/Na2SO4 composite, the natural convection and thermal conduction were taken into account at different durations. By comparison and analysis, the optimal heat transfer performance of the M-PCP/Na2SO4 composite can be achieved at 1000 °C.
4. Conclusions
The novel form-stable M-PCP/Na2SO4 composite was fabricated by a spontaneous infiltration method. The structure, morphology and thermal properties of the M-PCP/Na2SO4 composite have been fully studied in this paper. The PCM Na2SO4 can be successfully loaded into the M-PCP. The phase constitution and microstructure of the two porous ceramic preforms were systemically studied. The results showed that when the addition of Kc is increased from 30% to a high level (70%), the morphology of mullite in the PCP is converted from sheet-like to needle-like grains, which can better promote the thermal shock resistance of the PCM composite. The DSC results indicate that the phase change temperature of the M-PCP/Na2SO4 composite is 882.17 °C and the latent heat is 54.33 J g−1. The thermal cycling test and thermodynamic feasibility analysis results show that the M-PCP/Na2SO4 composite has better thermal reliability and chemical stability. Infiltration experiments and numerical simulations showed that the optimal infiltration rate, heat transfer performance and high temperature chemical compatibility of the M-PCP/Na2SO4 composite were achieved at 1000 °C. In conclusion, the prepared M-PCP/Na2SO4 composite might potentially be used in a thermal energy storage system.Acknowledgements
This work was supported by the National Science Fund for distinguished Young Scholars (51225403), the National Natural Science Foundation of China (41572036), the State Key Laboratory of Powder Metallurgy, Central South University (2015-19) and the Central South University Graduate Independent Exploration Innovation Program (2015zzts087).Notes and references
- T. Li, Z. Wu and H. Kao, Energy, 2013, 55, 752–761 CrossRef CAS.
- K. Pielichowska and K. Pielichowski, Prog. Mater. Sci., 2014, 65, 67–123 CrossRef CAS.
- M. K. Rathod and J. Banerjee, Renewable Sustainable Energy Rev., 2013, 18, 246–258 CrossRef CAS.
- A. Sarι, C. Alkan and A. Karaipekli, Appl. Energy, 2010, 87, 1529–1534 CrossRef.
- F. Agyenim, N. Hewitt, P. Eames and M. Smyth, Renewable Sustainable Energy Rev., 2010, 14, 615–628 CrossRef CAS.
- M. M. Farid, A. M. Khudhair, S. A. K. Razack and S. Al-Hallaj, Energy Convers. Manage., 2004, 45, 1597–1615 CrossRef CAS.
- Y. Konuklu, M. Unal and H. O. Paksoy, Sol. Energy Mater. Sol. Cells, 2014, 120, 536–542 CrossRef CAS.
- Q. Peng, J. Ding and X. Wei, Appl. Energy, 2010, 87, 2812–2817 CrossRef CAS.
- S. Liu and H. Yang, Energy Technol., 2015, 3, 77–83 CrossRef CAS.
- T. Qian, J. Li, X. Min, W. Guan, Y. Deng and L. Ning, J. Mater. Chem. A, 2015, 3, 8526–8536 CAS.
- Y. Yuan, N. Zhang, W. Tao, X. Cao and Y. He, Renewable Sustainable Energy Rev., 2014, 29, 482–498 CrossRef CAS.
- Z. Chen, M. Qin and J. Yang, Energ. Build., 2015, 106, 175–182 CrossRef.
- S. Liu and H. Yang, Appl. Clay Sci., 2014, 101, 277–281 CrossRef CAS.
- C. Li, J. Ouyang and H. Yang, Phys. Chem. Miner., 2013, 40, 681–689 CrossRef CAS.
- K. Peng, L. Fu, J. Ouyang and H. Yang, Adv. Funct. Mater., 2016, 26, 2666–2675 CrossRef CAS.
- N. Sarier, E. Onder, S. Ozay and Y. Ozkilic, Thermochim. Acta, 2011, 524, 39–46 CrossRef CAS.
- M. Li, Z. Wu, H. Kao and J. Tan, Energy Convers. Manage., 2011, 52, 3275–3281 CrossRef CAS.
- K. Peng, L. Fu, H. Yang and J. Ouyang, Sci. Rep., 2016, 6, 19723 CrossRef CAS PubMed.
- Y. Zhang, A. Tang, H. Yang and J. Ouyang, Appl. Clay Sci., 2016, 119, 8–17 CrossRef CAS.
- D. Mei, B. Zhang, R. Liu, Y. Zhang and J. Liu, Sol. Energy Mater. Sol. Cells, 2011, 95, 2772–2777 CrossRef CAS.
- J. Jin, L. Fu, J. Ouyang and H. Yang, Sci. Rep., 2015, 5, 12429 CrossRef PubMed.
- J. Zhang, X. Zhang, Y. Wan, D. Mei and B. Zhang, Sol. Energy, 2012, 86, 1142–1148 CrossRef CAS.
- X. He and H. Yang, Dalton Trans., 2015, 44, 1673–1679 RSC.
- D. Yang, S. Shi, L. Xiong, H. Guo, H. Zhang, X. Chen, C. Wang and X. Chen, Sol. Energy Mater. Sol. Cells, 2016, 144, 228–234 CrossRef CAS.
- X. He, Q. Yang, L. Fu and H. Yang, Funct. Mater. Lett., 2015, 8, 1550056 CrossRef CAS.
- Y. Zhang, C. Yu, P. Hu, W. Tong, F. Lv, P. K. Chu and H. Wang, Appl. Clay Sci., 2016, 119, 96–102 CrossRef CAS.
- J. Zhang, X. Guan, X. Song, H. Hou, Z. Yang and J. Zhu, Energ. Build., 2015, 92, 155–160 CrossRef.
- A. Karaipekli and A. Sarι, Renewable Energy, 2008, 33, 2599–2605 CrossRef CAS.
- A. Sarι, A. Karaipekli and C. Alkan, Chem. Eng. J., 2009, 155, 899–904 CrossRef.
- K. Peng, J. Zhang, H. Yang and J. Ouyang, RSC. Adv., 2015, 5, 66134–66140 RSC.
- S. Karaman, A. Karaipekli, A. Sarι and A. Biçer, Sol. Energy Mater. Sol. Cells, 2011, 95, 1647–1653 CrossRef CAS.
- S.-G. Jeong, J. Jeon, J.-H. Lee and S. Kim, Int. J. Heat Mass Transfer, 2013, 62, 711–717 CrossRef CAS.
- Y. Konuklu, O. Ersoy and O. Gokce, Appl. Therm. Eng., 2015, 91, 759–766 CrossRef CAS.
- A. Karaipekli and A. Sarι, Solar Energy, 2009, 83, 323–332 CrossRef CAS.
- O. Chung, S.-G. Jeong and S. Kim, Sol. Energy Mater. Sol. Cells, 2015, 137, 107–112 CrossRef CAS.
- C. Li and H. Yang, J. Am. Ceram. Soc., 2013, 96, 2793–2798 CrossRef CAS.
- A. Sarι, Energ. Build., 2015, 96, 193–200 CrossRef.
- C. Li, L. Fu, J. Ouyang, A. Tang and H. Yang, Appl. Clay Sci., 2015, 115, 212–220 CrossRef CAS.
- M. Liu, W. Saman and F. Bruno, Renewable Sustainable Energy Rev., 2012, 16, 2118–2132 CrossRef CAS.
- M. M. Kenisarin, Renewable Sustainable Energy Rev., 2010, 14, 955–970 CrossRef CAS.
- T. Nomura, N. Okinaka and T. Akiyama, Mater. Chem. Phys., 2009, 115, 846–850 CrossRef CAS.
- R. Tamme, U. Taut and C. Streuber, Sol. Energ. Mater., 1991, 24, 386–396 CrossRef CAS.
- L. Zhang, H. Shi, W. Li, X. Han and X. Zhang, Thermochim. Acta, 2013, 570, 1–7 CrossRef CAS.
- X. Zhou, H. Xiao, J. Feng, C. Zhang and Y. Jiang, Compos. Sci. Technol., 2009, 69, 1246–1249 CrossRef CAS.
- R. Liu, F. Zhang, W. Su, H. Zhao and C. Wang, Sol. Energy Mater. Sol. Cells, 2015, 134, 268–274 CrossRef CAS.
- D. Kearney, B. Kelly, U. Herrmann, R. Mahoney, R. Cable and H. Price, J. Sol. Energy Eng., 2003, 125, 170–176 CrossRef CAS.
- U. Herrmann, B. Kelly and H. Price, Energy, 2004, 29, 883–893 CrossRef CAS.
- C. Li, L. Fu, J. Ouyang and H. Yang, Sci. Rep., 2013, 3, 1–8 Search PubMed.
- Y. Jing, X. Deng, J. Li, C. Bai and W. Jiang, Ceram. Int., 2014, 40, 1329–1334 CrossRef CAS.
- M. H. Talou and M. A. Camerucci, J. Eur. Ceram. Soc., 2015, 35, 1021–1030 CrossRef CAS.
- G. Chen, H. Qi, W. Xing and N. Xu, J. Membr. Sci., 2008, 318, 38–44 CrossRef CAS.
- W.-K. Rhim and K. Ohsaka, J. Cryst. Growth, 2000, 208, 313–321 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |



