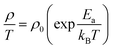Effect of dual-doping on the thermoelectric transport properties of CaMn_1−xNb_x/2Ta_x/2O₃

Abstract

The dual-substituted CaMn_1−xNb_x/2Ta_x/2O₃ is synthesized by solid-state reaction and it's crystal structure-thermoelectric property relationship is established. Rietveld refinement confirms the formation of a single phase orthorhombic structure with a gradual increase of cell parameters and bond lengths with doping level. The electrical resistivity (ρ) shows non-metal like temperature dependence. The ρ-value decreases with increasing doping level indicating an increase in charge-carrier concentration through formation of Mn³⁺ ions with e¹_g electron in the Mn⁴⁺ matrix of CaMn_1−xNb_x/2Ta_x/2O₃. The shallow region observed around 500 K in the resistivity curve is interpreted as the formation of local charge-ordering clusters due to the presence of oxygen vacancies in CaMn_1−xNb_x/2Ta_x/2O₃. The Seebeck coefficient initially decreases with temperature as expected from increasing charge carrier concentration. Above 600 K, the Seebeck coefficient increases with temperature as oxygen vacancies start playing the dominant role. The relatively low thermal conductivity of CaMn_1−xNb_x/2Ta_x/2O₃ results from the damping of local vibration through substitution of heavier ions of Nb and Ta as well as crystallographic distortion. The dual-substituted CaMn_1−xNb_x/2Ta_x/2O₃ shows a maximum power factor of 200 μW m⁻¹ K⁻² and dimensionless figure-of-merit (ZT) of 0.15 at x = 0.04, arising from low electrical resistivity of 15 mΩ cm, a moderate Seebeck coefficient of −176 μV K⁻¹ and low thermal conductivity of 1.2 W m⁻¹ K⁻¹.

---

Introduction

The widespread strategies for the production of electrical energy that rely on fossil fuels are having a negative impact on the environment. The global trend of increasing demand for energy requires alternative and environmentally benign sources of energy that are adequately competitive with conventional technologies.^1–3 Alternative renewable energy sources such as biomass, hydropower, wind, geothermal or solar energy, are becoming an important support to compensate limited fossil fuel resources. Among the above mentioned energy-conversion technologies, there has been a resurgence of interest in thermoelectric as the major part of the world's overall energy resources such as solar radiation, geothermal heat or industrial and automobile exhaust are discharged as waste heat into the environment without practical application. Therefore, technologies for harnessing the dissipating heat from various sources are highly desired. Direct thermoelectric power conversion that excludes any mechanical intermediate stages, is one of the most promising aspects to make potential contributions towards lowering greenhouse gas emissions and providing cleaner form of energy.^4–6

Thermoelectric power generation requires three major pieces of technology: thermoelectric materials, thermoelectric modules and systems that interface with the heat source. Thermoelectric materials generate electricity while in a temperature gradient.⁵ The key parameter that defines the thermoelectric materials is the ‘dimensionless figure of merit’, ZT, which is derived from the combination of three physical properties; thermal conductivity (κ), electrical conductivity (σ) and Seebeck coefficient (S), ZT = (S²σ/κ)T, where T is the temperature.⁵ A thermoelectric module converts heat (Q) into electrical power (P) with efficiency η. The efficiency of a thermoelectric generator depends predominantly on the temperature difference ΔT = T_H − T_C across the device and is typically expressed as:⁷

It is apparent from the above expression that not only the ZT value but also the maximum temperature plays a primary role in determining the efficiency of the thermoelectric devices. In this respect, oxide materials have advantages. Although the oxide based thermoelectric materials have slightly lower ZT compared to that of the conventional metallic alloys, the deficiency is highly compensated because of the capability of the oxides at elevated temperatures. Further, oxide materials are cost effective, chemically and thermally stable at elevated temperature in air, non-toxic and will be free from hazardous Pb and expensive Te in comparison with the conventional Bi–Te or Pb–Te based thermoelectric alloys.^8–11

Thermoelectric transition metal oxides can be categorized in four different classes based on their crystal structure: (i) wide band-gap semiconductor oxides, (ii) perovskite based oxides, (iii) layered cobalt oxides and (iv) layered oxychalcogenides.¹² Among the transition metal oxides, perovskite manganites based on CaMnO₃ is an antiferromagnetic Mott–Hubbard insulator exhibits large electrical resistivity and high thermopower both at room temperature and at higher temperatures. CaMnO₃ is well known for becoming semiconductor to metallic at narrow doping levels as it is at the edge of Meta-Insulator (M-I) transition.^13–15 Nominal electron doping both at A (Ca²⁺) and B-sites (Mn⁴⁺) of CaMnO₃ results drastic decrease of electrical resistivity; keeping relatively high thermopower. The promising thermoelectric performances of CaMnO₃ is reported in literature through substitution on A-site^16–28 by rare-earth ions, Y³⁺ and Bi³⁺ as well as on B-site^29–34 by Nb⁵⁺, Ta⁵⁺, Mo⁶⁺ and W⁵⁺. It is reported that, among the A-site doped samples Yb³⁺ doped CaMnO₃ shows highest ZT;^17,18 whereas regarding B-site doping, Nb-doped samples have the highest figure-of-merit.^30,32 Recently, we have reported improved thermoelectric performances in dual-substituted Ca_1−xLn_xMn_1−xNb_xO₃ (Ln = Gd, Yb and Lu).^35,36 In Ca_1−xLn_xMn_1−xNb_xO₃, the substitution at Ca-site by trivalent rare-earth ions along with Nb⁵⁺ at Mn-site drastically modifies the thermoelectric properties. The enhanced lattice distortion in Ca_1−xLn_xMn_1−xNb_xO₃ arises from the formation of Mn³⁺ ions leading to formation of oxygen vacancies.

It is reported in the literature that, the doping of CaMnO₃ at Mn sites with pentavalent and hexavalent d⁰ elements of Nb^V, Ta^V, W^VI, Mo^VI modifies the electrical resistivity behavior of this phase, by significantly reducing the electrical resistivity both at room temperature and high temperature as the doping element content increases.^{29,30,32–34} The introduction of a cation with a valency higher than (IV) such as Nb^V or Ta^V on the manganese sites of CaMnO₃ induces the formation of Mn³⁺ (t³_2ge¹_g) species in the Mn⁴⁺ (t³_2ge⁰_g) matrix according to the ideal formula of CaMn^IV_1−2xMn^III_x(Nb^V,Ta^V)_xO₃. In this paper, we investigated the effect of dual-substitution at B-site of CaMnO₃ by two pentavalent ions of Nb⁵⁺ and Ta⁵⁺; CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08) to establish a structure-property correlation.

Experimental

The dual-substituted polycrystalline samples of CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08) were synthesized by the conventional high temperature solid–state reactions. The starting materials were high-purity CaCO₃, MnO₂, Nb₂O₅ and Ta₂O₅ powders from Alfa Aesar. Initially, the stoichiometric ratio of these powders were mixed well in ball mill for 2 h, calcined at 1000 °C and annealed at 1200 °C for several hours with intermediate grinding. The annealed powders were reground and pressed into pellets. The pellets were sintered in air at 1325 °C for 10 h and slowly cooled to room temperature. The phase composition and crystal structure of CaMn_1−xNb_x/2Ta_x/2O₃ were determined by powder X-ray diffraction (XRD). A Rigaku Ultima IV X-ray diffractometer was used to record powder XRD patterns. For structure refinement, XRD data were collected in the 2θ range of 5–70° with a step size of 0.01°. Rietveld refinement of powder XRD data were carried out by least-squares refinement method and were refined for lattice parameters, scale factor, background (shifted Chebyshev background function), pseudo-Voigt profile function (U, V, W, and X), atomic coordinates and isothermal temperature factors (U_iso) using GSAS program.³⁷ SEM and EDX analyses were carried out in LEO Electron microscopy from Oxford Instruments. The electrical resistivity (ρ) and Seebeck coefficient (S) measurements were carried out on a bar-shaped sample (2 × 2 × 13 mm³) between 300 and 950 K at ambient pressure using ULVAC RIKO ZEM 3. The thermal conductivity (κ) measurements were carried out on a disk-shaped sample (2 mm thickness × 12 mm diameter) by laser flash technique using FLASHLINE 5000 thermal conductivity system.

Results and discussions

Fig. 1(a–d) shows scanning electron micrographs of as-sintered samples of CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08). The SEM micrograph exhibits the grains of irregular lumps with rounded corners and smooth grain interfaces. It is observed from the micrograph that no substantial morphological changes occurred due to Nb and Ta dual-substitution in CaMnO₃. The grain size distribution is narrow, ranging from 3–5 μm irrespective of the concentration of the substituent. However, on closer look it is observed that the level of porosity decreases with increasing the dopant concentration of CaMn_1−xNb_x/2Ta_x/2O₃, indicating grain growth with clear grain boundaries.

Fig. 1 SEM micrographs showing of as sintered pellets of (a) CaMn_0.98Nb_0.01Ta_0.01O₃, (b) CaMn_0.96Nb_0.02Ta_0.02O₃, (c) CaMn_0.94Nb_0.03Ta_0.03O₃ and (d) CaMn_0.92Nb_0.04Ta_0.04O₃.

Fig. 2(a–e) shows the XRD pattern of CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08) compositions that indicate the formation of single phase orthorhombic perovskite structure with Pnma space group. Rietveld refinement is done considering orthorhombic perovskite structure (a_o ≈ c_o ≈ a_c√2 and b_o ≈ 2a_c where o and c stands for orthorhombic and cubic, respectively) with Pnma space group (Fig. 2(a–e)). The refinement shows that the pattern can be completely indexed as GdFeO₃-type orthorhombic perovskite structure³⁸ (Fig. 2(a–e)). Table 1 summarizes the refined lattice parameters, R-factors, bond lengths and bond angles. The unidentified peak at 2θ = 33° with low intensity (<1%) belongs to the minor phase of orthorhombic CaMn₂O₄ with Pmab space group (JCPDS file no. 76-0516). The variation of the refined lattice parameters; a, b and c and the cell volume V with dopant concentration for CaMn_1−xNb_x/2Ta_x/2O₃ system are displayed in Fig. 2(f) and summarizes in Table 1. On closer look on Fig. 2(f) and Table 1, it is observed that, the lattice parameters and cell volume increase with increasing the Na and Ta concentration in CaMn_1−xNb_x/2Ta_x/2O₃ compositions. This observation can be well understood based on the fact that the resultant ionic radius of the B-site substituent; Nb_VI⁵⁺ (0.640 Å) and Ta_VI⁵⁺ (0.640 Å), are much larger than that of Mn_VI⁴⁺ (0.530 Å).³⁹ The relationship of the lattice parameters of orthorhombic perovskite; a_o, b_o/√2 and c_o can provide a measure of the distortion of the unit cell of CaMn_1−xNb_x/2Ta_x/2O₃. There are two types of orthorhombic perovskite structure; the O-type orthorhombic structure, characterized by the relationship c ≤ b/√2 ≤ a, exists when the degree of lattice deformation is relatively small, while, the O′-type orthorhombic structure, with b/√2 ≤ c ≤ a, exists in the case of enhanced lattice deformation.⁴⁰ In the present paper, the relationship of lattice parameters of CaMn_1−xNb_x/2Ta_x/2O₃ follows c ≤ b/√2 ≤ a indicating O-type orthorhombic structure with relatively less lattice deformation (Table 1). Further, the distortion from ideal perovskite structure can be demonstrated by the evolution of Goldsmith tolerance factor (t). Goldsmith tolerance factor (t) for ABO₃-type perovskite is calculated from the following equation where r represents the ionic radii of respective ions.⁴⁰

Fig. 2 Rietveld refinements from powder XRD data of (a) CaMn_0.99Nb_0.005Ta_0.005O₃, (b) CaMn_0.98Nb_0.01Ta_0.01O₃, (c) CaMn_0.96Nb_0.02Ta_0.02O₃, (d) CaMn_0.94Nb_0.03Ta_0.03O₃, (e) CaMn_0.92Nb_0.04Ta_0.04O₃ and (f) lattice parameters and cell volume of the CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08) as a function of x as derived from PXRD data.

Table 1 Refined lattice parameters, R-factors, bond distances, bond angles and calculated tolerance factors (t) for CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08)

	CaMn1−xNbx/2Tax/2O3
	x = 0.01	x = 0.02	x = 0.04	x = 0.06	x = 0.08
a (Å)	5.2923(2)	5.3006(3)	5.3121(4)	5.3151(4)	5.3260(6)
b (Å)	7.4545(5)	7.4609(4)	7.4742(6)	7.4773(6)	7.4877(8)
c (Å)	5.2700(3)	5.2758(2)	5.2836(4)	5.2876(4)	5.2887(6)
b/√2	5.2719	5.2764	5.2858	5.2880	5.2954
V (Å^3)	207.913(7)	208.648(1)	209.779(3)	210.141(2)	210.91(4)
Rwp	3.60	3.39	3.90	3.97	4.28
Rp	2.35	2.26	2.52	2.45	2.64
RF	11.5	12.40	12.16	11.33	10.57
χ^2	4.55	4.65	4.26	5.21	4.97
〈Mn–O〉	1.899	1.920	1.944	1.959	1.965
Mn–O1–Mn (°)	152.391(2)	150.919(7)	150.586(3)	150.586(3)	150.179(4)
Mn–O2–Mn (°)	162.194(2)	163.645(5)	165.696(6)	164.649(1)	165.105(7)
t	0.9286	0.9280	0.9270	0.9259	0.9252

---

The tolerance factor is a structural parameter that describes the geometrical distortion for ABO₃-type perovskite. An ideal perovskite structure normally describes by t of 1. The shifting of t towards t < 1 indicates enhanced geometric distortion in the perovskite lattice. Table 1 listed the tolerance factor of CaMn_1−xNb_x/2Ta_x/2O₃ system. The tolerance factor less than unity and the decrease in t value with doping level indicates enhancement of geometric distortion in CaMn_1−xNb_x/2Ta_x/2O₃ system. Table 1 also represents the bond lengths and bond angles for (Mn,Nb,Ta)O₆ octahedral. The average bond length increases with increasing the Nb/Ta concentration. The increase in Mn–O bond lengths clearly indicate the increase of Mn³⁺ ions and decrease of Mn⁴⁺ ions in the dual-substituted CaMnO₃ matrix as ionic radii of Mn³⁺ (0.645 Å) is larger than Mn⁴⁺ (0.530 Å). The significant lowering of octahedral bond angle from linearity (180°) induces tilting of (Mn,Nb,Ta)O₆ that results in Mn–O–Mn zig–zag chain in CaMn_1−xNb_x/2Ta_x/2O₃. This structural distortion arises from electron doping in the form of substitution of pentavalent Nb and Ta in the tetravalent Mn-sites of CaMnO₃.

The temperature dependence of electrical resistivity (ρ) of CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08) is shown in Fig. 3(a). It is reported in the literature that undoped CaMnO₃ shows typical semiconductor like behaviour (dρ/dT < 0) with the resistivity as high as 0.2 Ω.cm at 1000 K (Fig. 3(b) inset). The dual-substituted CaMn_1−xNb_x/2Ta_x/2O₃ also shows non-metallic nature of transport behaviour at the entire temperature range of 300 to 1000 K. However the ρ values of Nb and Ta dual-substituted CaMnO₃ are one order of magnitude lower than that of undoped CaMnO₃. The resistivity curves of CaMn_1−xNb_x/2Ta_x/2O₃ represent characteristic of semiconductor samples in which resistivity decreases with temperature showing the values ρ_1000K = 24 mΩ cm for x = 0.01 and ρ_1000K = 12 mΩ cm for x = 0.08. The remarkable reduction of electrical resistivity can be attributed to the formation of Mn³⁺ (t³_2ge¹_g) cation in the Mn⁴⁺ (t³_2ge⁰_g) matrix of CaMnO₃ due to dual-substitution of Nb⁵⁺ and Ta⁵⁺. This observation is further supported from the crystallographic analyses that the increase in Mn–O bond lengths with dual-substitution is directly related to the increase of Mn³⁺ ions as ionic radius of Mn³⁺ is larger than Mn⁴⁺ ions. Based on the valence equilibrium, the formation of an appreciable concentration of Mn³⁺ introduces free electrons in the e_g orbital. The electrons in the e_g levels act as a charge carrier in Mn³⁺–O–Mn⁴⁺ framework and reduce ρ through movement of electron by hopping mechanism. On closer look of the resistivity curve, it is observed that there is a shallow region around 500 K. To understand the origin of the shallow region in the resistivity curve, two singly doped compositions of CaMn_0.96Nb_0.04O₃ and CaMn_0.92Ta_0.08O₃ are prepared with high dopant concentration of Nb and Ta, respectively. The resistivity curves of singly doped CaMnO₃ show similar semiconductor like behaviour with shallow region around 500 K (Fig. 3(b)). Therefore, the appearance of shallow region is independent of the nature of dopant rather appearing due to high level of electron doping in the CaMnO₃ system. Fig. S1 and S2† show the electrical resistivity as a function of temperature for x ≥ 0.06 of CaMn_1−xNb_x/2Ta_x/2O₃ for both heating and cooling cycles. Although the shallow region around 500 K is more dominant in the heating curve the same is also present in the cooling curve indicating the behavior inherent in nature. Further in the case of CaMn_1−xNb_x/2Ta_x/2O₃ system, although there is a decrease of resistivity with increasing the concentration of Nb and Ta, the change of resistance is very marginal above x ≥ 0.04. It is well known that the doping level dependence of resistivity is not linear when the doping level exceeds the optimal concentration as other factors starts playing role apart from charge carrier concentrations.^41–43 It is well known that the electron doping CaMnO₃ system generates oxygen vacancies that acts as a defect centre.^44–46 When the electron concentration reaches a certain magnitude, the defect centre may cause the local charge ordering in the system that may be responsible for the anomaly in the resistivity values. The low dopant concentration introduce electrons to the e_g level of Mn ions giving rise to electronic delocalization and consequent reduction in resistivity, however, at higher dopant concentration the local charge-ordering clusters form, resulting in the localization of electrons and followed by anomaly in resistivity curve. Therefore, for higher concentration of Nb and Ta the increase in resistivity at 500 K is very prominent than the lower Nb and Ta doping. After sudden increase of few milliohms resistivity saturates and results in the shallow region at the resistivity curve.

Fig. 3 Temperature dependence of electrical resistivity of (a) CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08) and (b) singly doped CaMn_0.96Nb_0.04O₃ and CaMn_0.92Nb_0.08O₃. Inset (a) shows the variation of ρ(T) with x for CaMn_1−xNb_x/2Ta_x/2O₃ (0.04 ≤ x ≤ 0.08).

Fig. 4(a) shows the temperature dependence of thermopower (S) of CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08). The negative S value in the whole measured temperature range confirms that the dominant charge carriers are electrons. It was earlier observed for co-substituted Ca_1−xLn_xMn_1−xNb_xO₃ system that Seebeck coefficient increases with increasing the temperature. In the case of Ca_1−xLn_xMn_1−xNb_xO₃, where the incorporation of trivalent Ln at Ca-site and pentavalent Nb at Mn-site cause formation of mixed valency of Mn³⁺ (t³_2ge¹_g) and Mn⁴⁺ (t³_2ge⁰_g), the theoretical thermopower value is expressed by the modified Heikes formula.⁴⁷ The mathematical expression of modified Heikes formula is as follows that indicates the temperature independence of Seebeck coefficient at higher temperature.

where g₃ and g₄ are the electronic degeneracy of Mn³⁺ and Mn⁴⁺ and x is the concentration of Mn³⁺ ions in Mn sites. However, in the case of dual-substituted CaMn_1−xNb_x/2Ta_x/2O₃, it is observed from the Fig. 4 that thermopower is dependent on the temperature and initially decreases with temperature up to 500–600 K and then slowly increases (Table 2). Thereby, the temperature dependence of thermopower of CaMn_1−xNb_x/2Ta_x/2O₃ cannot be explained through modified Heikes formula. Similar phenomena are also observed for the singly doped composition of CaMnO₃ with higher concentration of Nb and Ta (Fig. 4(b)). Fig. S1 and S2† show the Seebeck coefficient as a function of temperature for x ≥ 0.06 of CaMn_1−xNb_x/2Ta_x/2O₃ for both heating and cooling cycles. The reversible behavior of Seebeck coefficient with temperature confirms that the above phenomenon is inherent in nature and depends on the off-stoichiometry. The parent CaMnO₃ exhibits a large thermopower (S) which decreases with temperature. This is attributed to the low charge carrier concentration of undoped CaMnO₃ and thereby interpreted as semiconductor-like behaviour. The dual-substitutions at Mn⁴⁺ by pentavalent Nb⁵⁺ and Ta⁵⁺ induce Mn³⁺ ions with e¹_g configuration as electron carrier. The introduction of electron carrier through substitution indicates the lowering of thermopower values that is seen in the present composition of CaMn_1−xNb_x/2Ta_x/2O₃ up to the temperature limit of 600 K. However, increase of thermopower with temperature above 600 K clearly indicates the presence of more than one independent charge carrier that play and crucial role in explaining the temperature dependence of thermopower at high temperatures.⁴⁸

Fig. 4 Temperature dependence of Seebeck coefficient of (a) CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08) and (b) singly doped CaMn_0.96Nb_0.04O₃ and CaMn_0.925Nb_0.08O₃.

Table 2 The experimental (S_Expt) thermopower values and activation energies for conduction (E_a) of CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08)

Expected electron concentration	SExpt (μV K^−1) at 300 K	SExpt (μV K^−1) at 600 K	SExpt (μV K^−1) at 950 K	Ea (meV)
x = 0.01	−200	−142	−172	113
x = 0.02	−187	−113	−182	94
x = 0.04	−167	−106	−176	55
x = 0.06	−120	−93	−131	51
x = 0.08	−110	−76	−94	51

---

The increase in Seebeck coefficient with temperature is reported for the off-stoichiometric CaMnO_3−δ.^44–46 The partial reduction of CaMnO₃ causes formation of five-coordinated Mn³⁺ centres with oxygen vacancies that arranged in a zig–zag pattern along the ac-direction of the lattice. This results in formation of defect centres in the crystal system and thereby causes change in entropy with temperature. In the case of dual-substituted CaMn_1−xNb_x/2Ta_x/2O₃, oxygen vacancy arises due to the incorporation of pentavalent Nb/Ta causing the reduction of Mn⁴⁺ and formation of Mn³⁺. According to the Kröger–Vink notation, the reduction of metal (Mn) site can be formulated as: .

It is well known that the temperature dependence of S can be quantitatively explained by Mott's small polaron hopping transport model that can be simplified in two terms, the charge carrier concentration and the average change of system entropy.⁴⁹ The presence of oxygen vacancy associated defect centres causes additional contribution on the entropy of the system on and above the electron carrier concentrations above 600 K result in increase in Seebeck coefficient as a function of temperature.

The transport mechanism of dual-substituted CaMn_1−xNb_x/2Ta_x/2O₃ can be well understood according to Mott's adiabatic small polaron conduction model that describes the linear fit of ρ(T) curve. In this framework, ρ(T) shows linear relationship with the inverse of temperature and expressed as:^49,50

where, E_a is the activation energy for electrical conduction, T is the absolute temperature, ρ₀ is the constants. Therefore, Mott's small polaron hopping model predicts a linear fit in ln(ρ/T) vs. 1/T plots at high temperature (T > θ_D/2; where θ_D is the Debye temperature). In the case of the manganese-based perovskite oxides, the experimental value of Debye temperature is reported to around 400 K.^51–53 Fig. 5 shows the linear curve fitting of ln(ρ/T) vs. 1/T plot for CaMn_1−xNb_x/2Ta_x/2O₃ above 400 K. Thus, the transport mechanism of dual-substituted CaMn_1−xNb_x/2Ta_x/2O₃ in the high temperature range (T > 200 K) can be interpreted by the small polaron hopping conduction theory of Mott. The activation energy for conduction (E_a) has been calculated from the slope and summarized in Table 2. The activation energy of conduction is the energy required for an electron to hop. It is observed that the gradual decrease of activation energy (E_a) of conduction with increasing the doping level (x) i.e. with electron concentration. The decrease of E_a indicates that an increase of the Mn³⁺ concentration is favourable for the formation of polaron followed by polaron-hopping conduction.

Fig. 5 The linear curve fitting for ln(ρ/T) versus 1000/T plots for CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08) series.

The power factor (S²/ρ) is calculated from the measured electrical resistivity and Seebeck coefficient of CaMn_1−xNb_x/2Ta_x/2O₃ and plotted as a function of temperature in Fig. 6. The power factor as a function of temperature also shows similar behaviour as of electrical resistivity and thermopower. The power factor initially decreases, reached minimum at 600 K and then increases further. The larger power factor of 200 μW m⁻¹ K⁻² at 950 K is obtained for CaMn_0.96Nb_0.02Ta_0.02O₃ due to the relatively lower resistivity of 15 mΩ cm and moderate Seebeck coefficient of −176 μV K⁻¹.

Fig. 6 The temperature dependence of the power factor (S²/ρ) for CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08) series.

Fig. 7(a) shows the temperature dependence of thermal conductivity (κ) of CaMn_1−xNb_x/2Ta_x/2O₃ (0.02 ≤ x ≤ 0.06). The thermal conductivity was calculated from the following formula of κ = DC_pd, where D = thermal diffusivity, C_p = specific heat capacity and d = density of the materials. It is reported in the literature that undoped CaMnO₃ shows the thermal conductivity as high as 3.5 W m⁻¹ K⁻¹ at 300 K.⁵⁴ Thermal conductivity of dual-substituted CaMn_1−xNb_x/2Ta_x/2O₃ is much lower than that of CaMnO₃. Fig. 7(a) shows that the κ decreases with temperature as well as with increasing co-doping showing lowest κ of 1.14 for CaMn_0.94Nb_0.03Ta_0.03O₃ at 973 K.

Fig. 7 The temperature dependence of the (a) thermal conductivity (κ) and (b) dimension less figure-of-merit (ZT) of CaMn_1−xNb_x/2Ta_x/2O₃ (0.02 ≤ x ≤ 0.06).

The comparison of thermal conductivity is carried out between the dual-substituted CaMn_1−xNb_x/2Ta_x/2O₃ samples with densities around ∼3.90 g cm⁻³ as they were prepared by similar methodology. However, there is a decreasing trend of thermal conductivities that is observed with increasing the doping level and the effects related to that. The comparison has been tabulated at Table 3 where it clearly shows that the decrease in thermal conductivity from κ_{973 K} = 1.34 W m⁻¹ K⁻¹ for x = 0.02 to κ_{973 K} = 1.15 W m⁻¹ K⁻¹ for x = 0.06 of CaMn_1−xNb_x/2Ta_x/2O₃. Therefore the decrease in thermal conductivity solely depends on the enhanced doping level. The thermal conductivity (κ) is the sum of the phonon component (κ_ph) and carrier component (κ_e). It is reported that for the materials with ρ > 1 Ω cm, κ_e is negligible. However, in the case of CaMn_1−xNb_x/2Ta_x/2O₃ the electrical resistivity is much lower in the range of milliohms. The electronic contribution of the κ can be calculated from Widemann–Franz law as κ_e = LTσ (where L = 2.45 × 10⁻⁸ W Ω K⁻² is the Lorentz number). Table 3 shows the electronic and phonon contribution of thermal conductivity. The electronic contribution increases with increasing the doping content of Nb and Ta due to the increased carrier concentrations. The highest κ_e is calculated to 0.19 W m⁻¹ K⁻¹ at 973 K for CaMn_0.92Nb_0.04Ta_0.04O₃, which is the 16% contribution to the total thermal conductivity values at that temperature. The phonon thermal conductivity estimated by subtraction of the electronic thermal conductivity from the total thermal conductivity as summarized in Table 3. This implies, in the case of CaMn_0.92Nb_0.04Ta_0.04O₃, the phonon thermal conductivity is the dominant component in the total thermal conductivity. Further, on closer look it is observed from Table 3 that the κ_ph also decreases with increasing the doping level of Nb and Ta. The decrease of phonon thermal conductivity with doping can be interpreted in two ways: (i) crystallographic distortion arises from the change of ionic radii due to dual-substitution of Nb (r_Nb = 0.640 Å) and Ta (r_Ta = 0.640 Å) at Mn-site (r_Mn = 0.530 Å) and (ii) substitution by heavier elements (high atomic mass of Nb and Ta) to damping the local vibration.⁵⁵ The atomic mass difference at Mn-site (m_Nb = 92.906, m_Ta = 180.947 and m_Mn = 54.938) due to substitution of Nb and Ta significantly affects κ_ph due to shortening of the mean-free-path while crystallographic distortion is having very little influence.

Table 3 The electronic (κ_el) and lattice (κ_ph) thermal conductivity values for CaMn_1−xNb_x/2Ta_x/2O₃ (0.04 ≤ x ≤ 0.08)

x	ρ at 973 K (Ω m)	κel at 973 K (W m^−1 K^−1)	κph at 973 K (W m^−1 K^−1)	κph at 973 K (W m^−1 K^−1)
0.02	0.0001591	0.15	1.19	1.34
0.04	0.0001377	0.17	1.1	1.27
0.06	0.0001277	0.19	0.96	1.15

---

The dimensionless figure-of-merit (ZT) is plotted as a function of temperature in Fig. 7(b). The ZT value increases with increasing the temperature as well as the doping level. The composition CaMn_0.96Nb_0.02Ta_0.02O₃ exhibits the highest ZT value of 0.15 at 973 K arising from its low thermal conductivity (κ ∼ 1.2 W m⁻¹ K⁻¹), low electrical conductivity (ρ ∼ 16 mΩ cm) and moderate Seebeck coefficient (S ∼ −176 μV K⁻¹).

Conclusions

In this paper we have investigated the crystal structure and high temperature thermoelectric properties of dual-doped CaMn_1−xNb_x/2Ta_x/2O₃ (0.01 ≤ x ≤ 0.08). The cell parameters and Mn–O bond angles increases with increasing the doping level indicating formation of Mn³⁺ ions in the Mn⁴⁺ matrix of CaMnO₃ as r_Mn³⁺ > r_Mn⁴⁺.The reduction Mn⁴⁺ to Mn³⁺ with e¹_g electron in turn helps in reduction of electrical conductivity without much altering the Seebeck coefficient value that results in highest power factor of 200 μW m⁻¹ K⁻² at 973 K for CaMn_0.96Nb_0.02Ta_0.02O₃. The thermal conductivity remains relatively low due to damping of local vibration through substitution of heavier ions of Nb and Ta as well as crystallographic distortion leading to highest ZT value of 0.15 at 973 K for CaMn_0.96Nb_0.02Ta_0.02O₃.

Acknowledgements

We thank Dr A Roy Choudhury, IISER Mohali for powder XRD data, Ms Kalavati, NAL for SEM and Dr R Ramadurai, IIT Hyderabad for thermoelectric measurements. Financial support by Council of Scientific and Industrial Research and Science and Engineering Research Board, Department of Science and Technology, Government of India (SERB/F/4679/2013-14) are gratefully acknowledged.

References

1. F. J. DiSalvo, Thermoelectric cooling and power generation, Science, 1999, 238, 703–706.
2. L. E. Bell, Cooling, heating, generating power, and recovering waste heat with thermoelectric systems, Science, 2008, 321, 1457–1461.
3. G. J. Snyder and E. S. Toberer, Complex thermoelectric materials, Nat. Mater., 2008, 7, 105–114.
4. T. M. Tritt, Recent Trends in Thermoelectric Materials Research I & II, in Semiconductors and semimetals, Academy Press, USA, 2001.
5. D. M. Rowe, Thermoelectrics Handbook : Micro to Nano, CRC Press, Taylor & Francis Group, USA, 2006.
6. B. I. Ismail and W. H. Ahmed, Thermoelectric power generation using waste-heat energy as an alternative green technology, Recent Pat. Electr. Eng., 2009, 2, 27–39.
7. G. J. Snyder, Small thermoelectric generators, Electrochem. Soc. Interface, 2008, 54–56.
8. H. Ohta, K. Sugiura and K. Koumoto, Recent progress in oxide thermoelectric materials: p-type Ca₃Co₄O₉ and n-type SrTiO₃, Inorg. Chem., 2008, 47, 8429–8736.
9. J. W. Fergus, Oxide materials for high temperature thermoelectric energy conversion, J. Eur. Ceram. Soc., 2012, 32, 525–540.
10. K. Koumoto, Y. F. Wang, R. Zhang, A. Kosuga and R. Funahashi, Oxide thermoelectric materials: A nanostructuring approach, Annu. Rev. Mater. Res., 2010, 40, 363–394.
11. N. N. Van and N. Pryds, Nanostructured oxide materials and modules for high-temperature power generation from waste heat, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2013, 4, 023002.
12. A. Nag and V. Shubha, Oxide thermoelectric materials: A structure-property relationship, J. Electron. Mater., 2014, 43, 962–977.
13. Z. Zeng, M. Greenblatt and M. Craft, Large magnetoresistance in antiferromagnetic CaMnO_3−δ, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8784–8788.
14. D. B. Marsh and P. E. Parris, High-temperature thermopower of LaMnO₃ and related systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16602.
15. Y. Wang, Y. Sui, J. Cheng, X. Wang, Z. Lu and W. Su, High temperature metal−insulator transition induced by rare-earth doping in perovskite CaMnO₃, J. Phys. Chem. C, 2004, 113, 12509–12516.
16. B. T. Cong, T. Tsuji, P. X. Thao, P. Q. Thanh and Y. Yamamura, High-temperature thermoelectric properties of Ca_1−xPr_xMnO_3−δ (0 ≤ x < 1), Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 352, 18–23.
17. D. Flahaut, T. Mihara, R. Funahashi, N. Nabeshima, K. Lee, H. Ohta and K. Koumoto, Thermoelectrical properties of A-site substituted Ca_1−xRe_xMnO₃ system, J. Appl. Phys., 2006, 100, 084911.
18. Y. Wang, Y. Sui and W. Su, High temperature thermoelectric characteristics of Ca_0.9R_0.1MnO₃ (R = La,Pr,…,Yb), J. Appl. Phys., 2008, 104, 093703.
19. A. Kosuga, Y. Isse, Y. Wang, K. Koumoto and R. Funahashi, High-temperature thermoelectric properties of Ca_0.9−xSr_xYb_0.1MnO_3−δ, J. Appl. Phys., 2009, 105, 093717.
20. Y. Wang, Y. Sui, H. Fan, X. Wang, Y. Su, W. Su and X. Liu, High Temperature Thermoelectric Response of Electron-Doped CaMnO₃, Chem. Mater., 2009, 21, 4653–4660.
21. F. Kawashima, X. Y. Huang, K. Hayashi, Y. Miyazaki and T. Kajitani, Structure and high-temperature thermoelectric properties of the n-type layered oxide Ca_2−xBi_x−δMnO_4−γ, J. Electron. Mater., 2009, 38, 1159–1162.
22. J. Lan, Y. H. Lin, H. Fang, A. Mei, C. W. Nan, Y. Liu, S. Xu and M. Petersz, High-temperature thermoelectric behaviors of fine-grained Gd-doped CaMnO₃ ceramics, J. Am. Ceram. Soc., 2010, 93, 2121–2124.
23. Y. Wang, Y. Sui, X. Wang and W. Su, Enhancement of thermoelectric efficiency in (Ca,Dy)MnO₃–(Ca,Yb)MnO₃ solid solutions, Appl. Phys. Lett., 2010, 97, 052109.
24. H. Taguchi, T. Kugi, M. Kato and K. Hirota, Fabrication of (Ca_1−xLa_x)MnO₃ ceramics with a high relative density and their power factor, J. Am. Ceram. Soc., 2010, 93, 3009–3011.
25. S. M. Choi, C. H. Lim and W. S. Seo, Thermoelectric properties of the Ca_1−xR _xMnO₃ perovskite system (R: Pr, Nd, Sm) for high-temperature applications, J. Electron. Mater., 2011, 40, 551–556.
26. Y. Wang, Y. Sui, X. Wang and W. Su, Effects of substituting La³⁺, Y³⁺ and Ce⁴⁺ for Ca²⁺ on the high temperature transport and thermoelectric properties of CaMnO₃, J. Phys. D: Appl. Phys., 2009, 42, 055010.
27. C.-J. Liu, A. Bhaskar and J. J. Yuan, High-temperature transport properties of Ca_0.98RE_0.02MnO_3−δ (RE = Sm, Gd, and Dy), Appl. Phys. Lett., 2011, 98, 214101.
28. F. P. Zhang, Q. M. Lu, X. Zhang and J. X. Zhang, Preparation and improved electrical performance of the Pr-doped CaMnO_3−δ thermoelectric compound, Phys. Scr., 2013, 88, 035705.
29. A. Maignan, C. Martin, C. Autret, M. Hervieu, B. Raveaua and J. Hejtmanek, Structural–magnetic phase diagram of Mo-substituted CaMnO₃: consequences for thermoelectric power properties, J. Mater. Chem., 2002, 12, 1806–1811.
30. L. Bocher, M. H. Aguirre, D. Logvinovich, A. Shkabko, R. Robert, M. Trottmann and A. Weidenkaff, CaMn_1−xNb_xO₃ (x ≤ 0.08) perovskite-type phases as promising new high-temperature n-type thermoelectric materials, Inorg. Chem., 2008, 47, 8077–8085.
31. T. Okuda and Y. Fujii, Co-substitution effect on the magnetic, transport, and thermoelectric properties of the electron-doped perovskite manganite CaMnO₃, J. Appl. Phys., 2010, 108, 103702.
32. G. Xu, R. Funahashi, Q. Pu, B. Liu, R. Tao and G. Wang, Zejun Ding, High-temperature transport properties of Nb and Ta substituted CaMnO₃ system, Solid State Ionics, 2004, 171, 147–151.
33. M. Miclau, J. Hejtmanek, R. Retoux, K. Knizek, Z. Jirak, R. Frésard, A. Maignan, S. Hébert, M. Hervieu and C. Martin, Structural and magnetic transitions in CaMn_1−xW_xO₃, Chem. Mater., 2007, 19, 4243–4251.
34. S. Populoh, M. Trottmann, M. H. Aguire and A. Weidenkaff, Nanostructured Nb-substituted CaMnO₃ n-type thermoelectric material prepared in a continuous process by ultrasonic spray combustion, J. Mater. Res., 2011, 26, 1947–1952.
35. A. Nag, F. DSa and V. Shubha, Doping induced high temperature transport properties of Ca_1−xGd_xMn_1−xNb_xO₃ (0 ≤ x ≤ 0.1), Mater. Chem. Phys., 2015, 151, 119–125.
36. A. Nag and R. S. C. Bose, High temperature transport properties of co-substituted Ca_1−xLn_xMn_1−xNb_xO₃ (Ln = Yb, Lu; 0.02 ≤ x ≤ 0.08), Mater. Res. Bull., 2016, 74, 41–49.
37. A. C. Larson and R. B. von Dreele, General Structure Analysis System Report LAUR 86-748; Los Alamos National Laboratory, Los Alamos, NM, 1990.
38. W. Paszkowicz, J. Piętosa, S. M. Woodley, P. A. Dłużewski, M. Kozłowski and C. Martin, Lattice parameters and orthorhombic distortion of CaMnO₃, Powder Diffr., 2010, 25, 46–59.
39. R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
40. R. H. Mitchell, Perovskites – Modern and Ancient, Almez Press Inc., Ontario, Canada, 2002.
41. D. Vega, C. Ramos, H. Aliaga, M. T. Causa, B. Alascio, M. Tovar, G. Polla, G. Leyva, P. König and I. Torriani, Charge ordering in the electron doped Ca_1−xY_xMnO₃ manganites, Phys. B, 2002, 320, 37–39.
42. B. Raveau, Y. M. Zhao, C. Martin, M. Hervieu and A. Maignan, Mn-Site Doped CaMnO₃: Creation of the CMR Effect, J. Solid State Chem., 2000, 149, 203–207.
43. M. Miclau, J. Hejtmanek, R. Retoux, K. Knizek, Z. Jirak, R. Frésard, A. Maignan, S. Hébert, M. Hervieu and C. Martin, Structural and Magnetic Transitions in CaMn_1−xW_xO₃, Chem. Mater., 2007, 19, 4243–4251.
44. M. Molinari, D. A. Tomsett, S. C. Parker, F. Azough and R. Freer, Structural, electronic and thermoelectric behaviour of CaMnO₃ and CaMnO_(3−δ), J. Mater. Chem. A, 2014, 2, 14109–14117.
45. J. Briático, B. Alascio, R. Allub, A. Butera, A. Caneiro, M. T. Causa and M. Tovar, Double-exchange interaction in electron-doped CaMnO_3−δ, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 14020–14023.
46. M. Schrade, R. Kabir, S. Li, T. Norby and T. G. Finstad, High temperature transport properties of thermoelectric CaMnO_3−δ – Indication of strongly interacting small polaron, J. Appl. Phys., 2015, 115, 103705.
47. P. M. Chaikin and G. Beni, Thermopower in the correlated hopping regime, Phys. Rev. B: Solid State, 1976, 13, 647.
48. A. Bhaskar, Z.-R. Yang and C.-J. Liu, Electronic transport of co-doped misfit layered cobaltites, J. Mater. Sci.: Mater. Electron., 2015, 26, 9463–9469.
49. N. F. Mott and E. A. Davis, in Electronic Processes in Noncrystalline Materials, Clarendon, Oxford, 1971.
50. G. N. Austin and N. F. Mott, Polarons in crystalline and non-crystalline materials, Adv. Phys., 1969, 18, 41–102.
51. J. J. Hamilton, E. L. Keatley, H. L. Ju, A. K. Raychaudhuri, V. N. Smolyaninova and R. L. Greene, Low-temperature specific heat of La_0.67Ba_0.33MnO₃ and La_0.8Ca_0.2MnO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 14926.
52. M. R. Lees, O. A. Petrenko, G. Balakrishnan and D. McK, Paul, Specific heat of Pr_0.6(Ca_1−xSr_x)_0.4MnO₃ (0 <∼ x <∼ 1), Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1298.
53. S. Mollah, G. Anjum and H. D. Yang, Non-adiabatic polaron hopping conduction in CaMn_1−xCr_xO₃ (0 ≤ x ≤ 0.3), J. Phys. Chem. Solids, 2009, 70, 489–494.
54. X. Y. Huang, Y. Miyazaki and T. Kajitani, High temperature thermoelectric properties of Ca_1−xBi_xMn_1−yV_yO_3−δ (0 ≤ x = y ≤ 0.08), Solid State Commun., 2008, 145, 132–136.
55. D. Flahaut, T. Mihara, R. Funahashi, N. Nabeshima, K. Lee, H. Ohta and K. Koumoto, J. Appl. Phys., 2006, 100, 084911.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra06032c

---