DOI:
10.1039/C6RA05986D
(Paper)
RSC Adv., 2016,
6, 47325-47336
Tunneling effect in vitamin E recycling by green tea†
Received
7th March 2016
, Accepted 6th May 2016
First published on 6th May 2016
Abstract
Recycling reactions of natural vitamin E (α-tocopherol) by catechins contained in green tea were studied with a double-mixing stopped-flow spectrophotometer. The second-order reaction rate constants of the catechins and deuterated analogues were determined by using a simulation, the activation energies were obtained from the temperature dependences, and the deuterium kinetic-isotope effects were examined. From these results, a tunneling effect was found to play an important role in the vitamin E recycling reactions by the catechins, and the structure–activity relationship was clarified. Furthermore, conditions under which the tunneling effect manifests itself in various vitamin E recycling reactions in biological systems and foods were suggested. A new α-tocopherol-recycling capacity assay-method was also proposed, and named an ATREC assay-method after the acronym.
1. Introduction
Tunneling is one of the most significant features of quantum mechanics, whose laws govern the microscopic world.1 Interestingly enough, the tunneling effect also manifests itself in various macroscopic vital functions.1–10 Through reaction-rate measurements of normal and deuterated samples, we have suggested1,11–15 that the tunneling effect really plays an important part in some vital antioxidant-reactions and recycling reactions of lipid-soluble vitamin E within cellular membranes (Fig. 1 and its caption1,16,17). Our experimental results of the recycling reaction of vitamin E by lipid-soluble ubiquinol-10 (ref. 1, 12, 13 and 15) are consistent with the computational results.8,9
 |
| | Fig. 1 Scheme of production of lipid peroxyl radical (LOO˙) in cellular membrane, and system of antioxidant and recycling actions of vitamin E (α-tocopherol, α-TocH).1,16,17 Through hydrogen abstraction caused usually by light, radicals, metal or irradiation, an unstable lipid radical (L˙) is first formed from lipid (LH). The L˙ radical reacts with oxygen to produce relatively stable LOO˙, which attacks another LH to produce L˙ again (chain reaction) and is regarded as one of causes of aging.32 α-TocH is an excellent chain-breaking antioxidant, and an antioxidant reaction between α-TocH and LOO˙ results in production of lipid hydroperoxide (LOOH) and α-tocopheroxyl radical (α-Toc˙). To prevent consumption of α-TocH and to avoid prooxidant reactions producing L˙ (LOO˙) from α-Toc˙ and LH (LOOH),31 α-Toc˙ is recycled to α-TocH by some reactions. The α-TocH-recycling reactions take place between α-Toc˙ and ubiquinol (UQH2) etc. within the membrane and between α-Toc˙ and CatH etc. at the interface of the membrane and the water phase. UQH2 predominantly found in human cells is ubiquinol-10 (UQ10H2, see ref. 15). UQH˙ refers to a dehydroubiquinol radical. | |
It was also predicted computationally that the tunneling effect plays an important role in the antioxidant reactions of (−)-epicatechin (Scheme 1, abbreviated as EC), one of water-soluble tea catechins (CatHs).6,7 However, no experimental answer to the question whether or not the tunneling effect really manifests itself for CatHs has yet been reported to the best of our knowledge. A reason for the absence of the experimental results may be that the reaction rates of tea catechins18–21 are much less than those reported previously for the other antioxidants,1,11–13,15,22 so that some slow side-reactions prevent evaluation of the slow reaction rates of deuterated CatHs (CatDs). However, we have recently found a good solution by using a simulation,23,24 and here attempt to examine whether or not the tunneling effect really plays a major role in radical scavenging reactions of CatHs.
 |
| | Scheme 1 Structures of molecules used in the present study and nomenclature of benzene ring system. | |
CatHs are widely found in high concentration in plants and foods, especially in green tea and to a lesser extent in black tea.25,26 After ingestion of green tea, CatHs content of human plasma (mostly water) increases very much.27–29 In biological systems, water-soluble CatHs are considered to function as scavengers of reactive oxygen species in the water phase and membrane surface.18–21,30 Accordingly, CatHs would play a role in the vitamin E recycling reaction19,20 at interfaces between the cellular membranes and the water phase (Fig. 1 and reaction (1)) rather than in some radical scavenging reactions within the membranes.30
| |
 | (1) |
where α-Toc˙, α-TocH and Cat˙ denote α-tocopheroxyl radical, α-tocopherol (a natural vitamin E,
Scheme 1) and a dehydrocatechin radical, respectively.
kr stands for the second-order reaction rate-constant. Through reaction
(1), radical matter is excreted from the membrane to the water phase (
Fig. 1), prooxidant reactions producing lipid-origin radicals from α-Toc˙ are hindered,
1,31 and thus cellular aging would be delayed.
32 Reaction
(1) is essentially a proton- or hydrogen-transfer reaction, which is a very simple chemical-process readily subject to accurate measurements and quantitative theoretical analyses. It would be especially interesting to study the tunneling effect in the proton or hydrogen transfer.
In the work presented here, we have studied the recycling reactions of natural α-TocH and the deuterated analogue (α-TocD) by natural CatHs and CatDs with a double-mixing stopped-flow spectrophotometer,15,22 which allows us to follow kinetics of reactions of short-lived radicals such as α-Toc˙. We have determined the second-order reaction rate constants (kr) by using the simulation as mentioned above,23,24 obtained the activation energies from the temperature dependences, and examined the deuterium kinetic-isotope effects. From these results, we have found that the tunneling effect plays an important role in reaction (1), and clarified the structure–activity relationship. Furthermore, we have suggested conditions under which the tunneling effect manifests itself in various α-TocH-recycling reactions. We have also proposed a new α-TocH-recycling capacity assay-method, and named it ATREC assay-method after the acronym.
2. Materials and methods
2.1. Sample preparation
The structures of molecules used in this work are shown in Scheme 1. DL-α-TocH and EC were obtained from Calbiochem and Sigma, respectively. (−)-Epicatechin gallate (ECG), (−)-epigallocatechin (EGC) and (−)-epigallocatechin gallate (EGCG) were purchased from Funakoshi. 5-Methoxyresorcinol (MR), 4-methylcatechol (MC), 5-methylpyrogallol (MP) and methylgallate (MG) were obtained from Tokyo Chemical Industry. MR and MG can be regarded as models of A and G rings of CatHs, respectively (Scheme 1). MC and MP are models of catechol and pyrogallol B rings, respectively (Scheme 1). Ethanol (EtOH) and deuterium oxide (D2O) were purchased from Wako. Ethanol-d1 (EtOD) was obtained from Central Chemicals. These samples were used without purification. Water-d0 (H2O) was purified by ion exchange. According to the method reported previously,33 we prepared 2,6-di-t-butyl-4-(4′-methoxyphenyl)phenoxyl radical (ArO˙), which was made to react with α-TocH so as to produce α-Toc˙ (see Subsection 2.2).
To obtain kinetic data of reaction (1) and to examine the deuterium kinetic-isotope effects, EtOH (EtOD) and H2O (D2O) were mixed in a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio to obtain a mixed solvent EtOH/H2O (EtOD/D2O) because α-Toc˙ and ArO˙ are ethanol-soluble and CatHs are water-soluble. EtOH/H2O (EtOD/D2O) solutions of α-TocH (α-TocD) and ArO˙ were respectively produced by first dissolving α-TocH and ArO˙ in EtOH (EtOD) and then adding H2O (D2O). When CatHs and α-TocH were dissolved in solvents containing deuterated alcohol, replacement of the hydrogen atoms of the OH groups (hydroxy H-atoms) by deuterons was easily accomplished, and CatDs and α-TocD were obtained. The deuteration was verified by proton NMR.
1 volume ratio to obtain a mixed solvent EtOH/H2O (EtOD/D2O) because α-Toc˙ and ArO˙ are ethanol-soluble and CatHs are water-soluble. EtOH/H2O (EtOD/D2O) solutions of α-TocH (α-TocD) and ArO˙ were respectively produced by first dissolving α-TocH and ArO˙ in EtOH (EtOD) and then adding H2O (D2O). When CatHs and α-TocH were dissolved in solvents containing deuterated alcohol, replacement of the hydrogen atoms of the OH groups (hydroxy H-atoms) by deuterons was easily accomplished, and CatDs and α-TocD were obtained. The deuteration was verified by proton NMR.
2.2. Measurements
In this work, as explained in detail later, kinetic data of reaction (1) are measured, together with those of a radical scavenging reaction of α-TocH1,16,17 (reaction (2)) and those of a bimolecular reaction of α-Toc˙ (reaction (3)).23| |
 | (2) |
| |
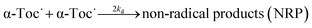 | (3) |
where ArOH denotes 2,6-di-t-butyl-4-(4′-methoxyphenyl)phenol. ks and 2kd stand for the second-order reaction rate constants. Reaction (2) is followed by reactions (1) and (3), which compete with each other.
The kinetic data of reaction (1) were obtained by using a Unisoku RSP-1000-03F double-mixing stopped-flow spectrophotometer under a nitrogen atmosphere at 15–37 °C. The error in the temperature reading was less than 0.5 °C. First α-Toc˙ was prepared by mixing equal volumes of EtOH/H2O (EtOD/D2O) solutions of ArO˙ and α-TocH (α-TocD) (reactions (2-H) and (2-D)) in the first-mixing unit of the stopped-flow spectrophotometer.
| |
 | (2-H) |
| |
 | (2-D) |
where ArOD denotes 2,6-di-
t-butyl-4-(4′-methoxyphenyl)phenol-
d1.
kHs and
kDs stand for the second-order reaction rate-constants. As reported previously,
1,11,13 the tunneling effect plays a part in reaction
(2) that is a proton (hydrogen) transfer reaction.
After a few seconds, equal volumes of the resultant mixture and an EtOH/H2O (EtOD/D2O) solution of a CatH (CatD) were mixed (reactions (1-H) and (1-D)) in the second mixing unit,15,22 and a decay curve of α-Toc˙ was measured.
| |
 | (1-H) |
| |
 | (1-D) |
where
kHr and
kDr denote the second-order reaction rate-constants. Reaction
(1-H) (reaction
(1-D)) was studied under pseudo-first-order conditions ([CatH(CatD)] ≫ [α-Toc˙], where the brackets [ ] indicate the molar concentration (mol L
−1) of the species between the brackets). The prepared [CatH(CatD)] was chosen so that [α-Toc˙] would not greatly decrease from the initial concentration within the time required to completely mix CatH (CatD) with α-Toc˙ and to make the solution homogeneous. The kinetic data of reaction
(1) between α-Toc˙ and each of MR, MC, MP and MG were also obtained in a manner similar to that mentioned above. The tunneling effect may play a role in reaction
(1) that is a proton (hydrogen) transfer reaction.
When reaction (1) is slow, that is, when kr or [CatH (CatD)] is small, decay of α-Toc˙ through reaction (3) is not negligible, and both of reactions (1) and (3) contribute to the decay observed here. Since the present kinetic measurements are made in polar EtOH/H2O and EtOD/D2O, reaction (3) can be regarded as the disproportionation reaction given in Scheme 2, and the dimer formation does not play a major role in the decay of α-Toc˙.23 Since reaction (3) is not a proton (hydrogen) transfer reaction, the tunneling effect plays only a negligible part in reaction (3) in contrast to reactions (1) and (2). To show significant differences in reaction kinetic data between the presence and absence of the tunneling effect, the kinetic data of reaction-(3)s in EtOH/H2O and EtOD/D2O (reactions (3-H) and (3-D)) were also measured.
| |
 | (3-H) |
| |
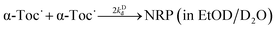 | (3-D) |
where 2
kHd and 2
kDd denote the second-order reaction rate constants.
 |
| | Scheme 2 Disproportionation reaction of α-Toc˙. | |
To accurately evaluate the kinetic data of reaction (1), formation and decay curves of α-Toc˙ during reaction (2-H) (reaction (2-D)) and the subsequent reaction (3-H) (reaction (3-D)) were obtained by using a Unisoku RSP-1000-03F single-mixing stopped-flow spectrophotometer. Then, equal volumes of EtOH/H2O (EtOD/D2O) solutions of ArO˙ and α-TocH (α-TocD) were mixed under a nitrogen atmosphere. The dead time during which the spectrophotometer cannot record any data point after mixing two solutions was 10–20 ms. The measurements were made under pseudo-first-order conditions ([α-TocH(α-TocD)] ≫ [ArO˙]).
3. Results and discussion
3.1. Reaction (2)
The change in absorption spectrum measured during reaction (2-H) was shown in Fig. 3 of ref. 22. Although ArO˙ was stable in the absence of α-TocH, when an EtOH/H2O solution containing excess α-TocH was added to the ArO˙ solution, the ArO˙ absorption peak disappeared immediately, an α-Toc˙ peak appeared, and the isosbestic points were observed.
3.2. Fast reaction-(1)
In this subsection, evaluation of kinetic data of fast reaction-(1) is described. Then, decay of α-Toc˙ through reaction (3) is negligible.
The change in absorption spectrum measured during reaction (1-H) between normal MP (having the natural distribution of hydrogen isotopes) and α-Toc˙ in EtOH/H2O at 25 °C is shown in Fig. 2, where the α-Toc˙ absorption peak disappears over time. MP radical is so short-lived that the peak is not seen in the spectrum. Fig. 3 shows the absorption decay of α-Toc˙ during reaction (1-H) with MP in EtOH/H2O at 25 °C. The absorption decay of α-Toc˙ is well characterized as a single-exponential decay, indicating that reaction (3-H) is negligibly slower than reaction (1-H). The absorption decay is accelerated as the prepared [MP] increases.
 |
| | Fig. 2 Change in absorption spectrum (at 20 ms intervals) during reaction (1-H) between α-Toc˙ and MP in EtOH/H2O at 25 °C. The prepared [MP] is 0.129 mM. The arrow indicates a decrease in absorbance of α-Toc˙. | |
 |
| | Fig. 3 Absorbance decay of α-Toc˙ at 429 nm during reaction (1-H) between α-Toc˙ and MP in EtOH/H2O at 25 °C. The prepared [MP]s for the data shown with red, green, blue and pink open circles are 4.31 × 10−2, 8.62 × 10−2, 0.129 and 0.172 mM, respectively. The solid curves show the best-fitting curves by standard linear least-squares analyses. | |
The pseudo-first-order rate constant kobsd of fast reaction-(1-H) between MP and α-Toc˙ can be evaluated by using a standard linear least-squares analysis for each of the single-exponential absorbance decay-curves of α-Toc˙. The experimental equation is given as
| | |
−d[α-Toc˙]/dt = kobsd[α-Toc˙]
| (5) |
Each fitting curve given in
Fig. 3 agrees well with the experimental one. The rate equation of reaction
(1-H) is expressed as
| | |
−d[α-Toc˙]/dt = (k0 + kHr[MP])[α-Toc˙]
| (6) |
where
k0 stands for the first-order rate constant for the natural decay of α-Toc˙ in EtOH/H
2O, and
kHr is the second-order rate constant of reaction
(1-H) between MP and α-Toc˙.
kobsd in
eqn (5) is given by
where
k0 is much less than
kHr[MP] under our experimental conditions. Since [MP] is nearly constant during reaction
(1-H) under pseudo-first-order conditions ([MP] ≫ [α-Toc˙]),
kHr can be evaluated from the slope of the plot of
kobsd versus the prepared [MP] (
Fig. 4). The
kHr values of reaction
(1-H) with MP in EtOH/H
2O at 25 and 15–37 °C are listed in
Tables 1 and S1,
† respectively. The
kHr value increases as the temperature increases.
 |
| | Fig. 4 Dependence of kobsd on prepared [MP] in reaction (1-H) between α-Toc˙ and MP in EtOH/H2O. The temperatures in the measurements of the data shown with red squares, green circles, blue triangles, pink inverted-triangles and dark-yellow diamonds are 15, 20, 25, 30 and 37 °C, respectively. The solid lines show the best-fitting lines by standard linear least-squares analyses. | |
Fig. 5 shows the Arrhenius plot of the kHr values of MP in EtOH/H2O. A linear relationship with a negative slope between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHr and the reciprocal of the absolute temperature (1/T) can be seen in the plot, from which the activation energy (EH) and the frequency factor (AH) can be evaluated according to eqn (8).
kHr and the reciprocal of the absolute temperature (1/T) can be seen in the plot, from which the activation energy (EH) and the frequency factor (AH) can be evaluated according to eqn (8).
| |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHr = −0.434EH/RT + log kHr = −0.434EH/RT + log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH AH
| (8) |
where
R denotes the gas constant.
EH and log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH
AH are listed in
Table 1.
 |
| | Fig. 5 Arrhenius plots of kHr for reaction (1-H) between α-Toc˙ and MP in EtOH/H2O (red open squares), of 2kHd and 2kDd for reactions (3-H) and (3-D) in EtOH/H2O and EtOD/D2O (green open and filled circles, respectively), and of kHr and kDr for reactions (1-H) and (1-D) between α-Toc˙ and EGC in EtOH/H2O and EtOD/D2O (blue open and filled triangles, respectively). The solid lines show the best-fitting lines by standard linear least-squares analyses. | |
Table 1 kHr, kDr and kHr/kDr at 25 °C, EH, ED, ED–EH, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH, log
AH, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD and ATREC values of CatHs (CatDs) and related molecules
AD and ATREC values of CatHs (CatDs) and related molecules
| Molecule |
kHr or kDr/M−1 s−1 |
kHr/kDr |
EH or ED/kJ mol−1 |
ED–EH/kJ mol−1 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH or log AH or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ADa ADa |
ATREC |
Because log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH (log AH (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD) was obtained by extrapolating the linear log AD) was obtained by extrapolating the linear log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHr (log kHr (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kDr) versus 1/T plot in a limited 1/T range around room temperature to the intercept, this value has a large uncertainty. The kinetic data were obtained in EtOH/H2O. The kinetic data were obtained in EtOD/D2O. Reliable data was not obtained. Ref. 22: Na+AsH− and Na+AsD− denote sodium ascorbate-d0 (vitamin C) and -d3 respectively. Ref. 15: UQ10H2 and UQ10D2 respectively denote ubiquinol-10-d0 and -d2, whose kinetic data were obtained in EtOH and EtOD. kDr) versus 1/T plot in a limited 1/T range around room temperature to the intercept, this value has a large uncertainty. The kinetic data were obtained in EtOH/H2O. The kinetic data were obtained in EtOD/D2O. Reliable data was not obtained. Ref. 22: Na+AsH− and Na+AsD− denote sodium ascorbate-d0 (vitamin C) and -d3 respectively. Ref. 15: UQ10H2 and UQ10D2 respectively denote ubiquinol-10-d0 and -d2, whose kinetic data were obtained in EtOH and EtOD. |
| EC-Hb |
1.20 × 103 |
4.7 |
28 ± 1 |
∼10 |
8.0 |
4.4 × 10−4 |
| EC-Dc |
2.56 × 102 |
|
∼40 |
|
∼9 |
9.4 × 10−5 |
| ECG-Hb |
3.43 × 103 |
— |
26.9 ± 0.5 |
|
8.2 |
1.3 × 10−3 |
| ECG-Dc |
—d |
|
— |
|
— |
— |
| EGC-Hb |
2.41 × 104 |
9.7 |
13.6 ± 0.6 |
10 |
6.8 |
8.8 × 10−3 |
| EGC-Dc |
2.49 × 103 |
|
24 ± 2 |
|
7.5 |
9.1 × 10−4 |
| EGCG-Hb |
2.31 × 104 |
5.1 |
15.0 ± 0.7 |
13 |
7.0 |
8.5 × 10−3 |
| EGCG-Dc |
4.49 × 103 |
|
28 ± 1 |
|
8.5 |
1.6 × 10−3 |
| MRb |
<102 |
|
— |
|
— |
<10−4 |
| MCb |
4.48 × 103 |
|
22.0 ± 0.9 |
|
7.5 |
1.6 × 10−3 |
| MPb |
1.75 × 105 |
|
10 ± 2 |
|
7.1 |
6.4 × 10−2 |
| MGb |
2.11 × 103 |
|
24.6 ± 0.4 |
|
7.6 |
7.7 × 10−4 |
| Na+AsH−b,e |
2.73 × 106 |
5.6 |
4.0 ± 0.4 |
2.4 |
7.1 |
1.0 |
| Na+AsD−c,e |
4.87 × 105 |
|
6.4 ± 0.1 |
|
6.8 |
0.18 |
| UQ10H2f |
2.12 × 105 |
18.3 |
4.5 ± 0.1 |
6.1 |
6.1 |
— |
| UQ10D2f |
1.16 × 104 |
|
10.6 ± 0.7 |
|
5.9 |
— |
3.3. Slow reaction-(1)
As mentioned above, when reaction (1) is slow, decay of α-Toc˙ through reaction (3) is not negligible, and both of reactions (1) and (3) contribute to the decay. In this subsection, evaluation of kinetic data of such a slow reaction-(1) is described.
3.3.1. Evaluation of 2kd. First the 2kHd (2kDd) value of reaction (3-H) (reaction (3-D)) was evaluated to accurately estimate the kinetic data of reaction (1-H) (reaction (1-D)). Then, the kHs (kDs) value of reaction (2-H) (reaction (2-D)) was also obtained as noted below.Since the rate of ArO˙-scavenging in reaction (2-H) equals that of α-Toc˙-formation, the rate equations of reactions (2-H) and (3-H) are expressed as23
| | |
−d[ArO˙]/dt = kHs[α-TocH][ArO˙]
| (9) |
| | |
d[ArOH]/dt = kHs[α-TocH][ArO˙]
| (10) |
| | |
−d[α-TocH]/dt = kHs[α-TocH][ArO˙]
| (11) |
| | |
d[α-Toc˙]/dt = kHs[α-TocH][ArO˙] − 2kHd[α-Toc˙]2
| (12) |
| | |
d[NRP]/dt = 2kHd[α-Toc˙]2
| (13) |
and relations among the molar concentrations are given by
| | |
[ArO˙]t′ + [ArOH]t′ = [ArO˙]0
| (14) |
| | |
[α-TocH]t′ + [α-Toc˙]t′ + 2[NRP]t′ = [α-TocH]0
| (15) |
| | |
−[ArO˙]t′ + [α-TocH]t′ = −[ArO˙]0 + [α-TocH]0
| (16) |
where [ ]
0 and [ ]
t′ indicate the concentrations of the species between the brackets at
t = 0 and
t′, respectively. Similar equations also hold in reactions
(2-D) and
(3-D). These equations can be solved numerically by using the fourth-order Runge–Kutta method as reported previously.
23
Fig. 6 shows a rise-and-decay curve of α-Toc˙ absorbance at 429 nm during reactions (2-H) and (3-H) in EtOH/H2O at 25 °C, together with the curve simulated according to the above-mentioned equations. In the simulation, kHs, 2kHd, [ArO˙]0, [α-TocH]0 and the molecular extinction coefficient ε are set to the values given in the caption of Fig. 6. The simulation curve agrees well with the experimental one. The rise and decay of the curve come from reaction (2-H) and the subsequent reaction (3-H), respectively. The experimental and simulation curves of [α-Toc˙] at 15–37 °C are given in Fig. S1,† in which ε is assumed to be independent of the temperature. The curves of α-Toc˙ absorbance during reaction (2-D) and the subsequent reaction (3-D) in EtOD/D2O at 25 °C can also be obtained (Fig. 6) by assuming that ε in EtOD/D2O is the same as that in EtOH/H2O. The rise of the curve obtained in EtOD/D2O is slower than that in EtOH/H2O, which indicates kDs < kHs. The curves of [α-Toc˙] during reactions (2-D) and (3-D) at 15–37 °C are given in Fig. S2.† The kHs, kDs, 2kHd, 2kDd values and the ratio (kHs/kDs and 2kHd/2kDd) at 25 °C are given in Table 2, and the kHs, kDs, 2kHd and 2kDd values at 15–37 °C are listed in Table S1.†
 |
| | Fig. 6 Rise-and-decay curves of α-Toc˙ absorbance at 429 nm during reactions (2) and (3) in EtOH/H2O and EtOD/D2O at 25 °C (red and green open circles, respectively), and the curves simulated by setting kHs = 8.20 × 103 M−1 s−1, 2kHd = 1.21 × 103 M−1 s−1, [ArO˙]0 = 7.85 × 10−2 mM, [α-TocH]0 = 6.33 mM and ε = 3420 M−1 cm−1 in eqn (9)–(16) (red solid curve) and by setting kDs = 4.00 × 102 M−1 s−1, 2kDd = 0.95 × 103 M−1 s−1, [ArO˙]0 = 0.230 mM, [α-TocD]0 = 2.12 mM and ε = 3420 M−1 cm−1 in those similar to eqn (9)–(16) (green solid curve). Reaction (3) follows reaction (2). Rise-and-decay curves of relative α-Toc˙ absorbance are plotted in this figure, while those of [α-Toc˙] are plotted in Fig. S1 and S2.† | |
Table 2 kHs, kDs, 2kHd, 2kDd, kHs/kDs and 2kHd/2kDd at 25 °C, EH, ED, ED–EH, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH and log
AH and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD for reactions (2) and (3), and ARAC values
AD for reactions (2) and (3), and ARAC values
| Rate constant/M−1 s−1 |
Rate constant ratio |
EH or ED/kJ mol−1 |
ED–EH/kJ mol−1 |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH or log AH or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ADa ADa |
ARAC |
Because log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH and log AH and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD were respectively obtained by extrapolating the linear log AD were respectively obtained by extrapolating the linear log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHs and log kHs and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kDs (log kDs (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2kHd and log 2kHd and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2kDd) versus 1/T plots in a limited 1/T range around room temperature to the intercepts, these values have a large uncertainty. The kinetic data were obtained in EtOH/H2O. The kinetic data were obtained in EtOD/D2O. 2kDd) versus 1/T plots in a limited 1/T range around room temperature to the intercepts, these values have a large uncertainty. The kinetic data were obtained in EtOH/H2O. The kinetic data were obtained in EtOD/D2O. |
| kHs = 8.20 × 103b |
kHs/kDs = 20.5 |
13.1 ± 0.2 |
11 |
6.2 |
1.0 |
| kDs = 0.40 × 103c |
|
24 ± 1 |
|
6.8 |
0.049 |
| 2kHd = 1.21 × 103b |
2kHd/2kDd = 1.3 |
8.6 ± 0.7 |
∼0 |
4.6 |
|
| 2kDd = 0.95 × 103c |
|
9 ± 1 |
|
4.6 |
|
Fig. 5 also shows the Arrhenius plots of the 2kHd and 2kDd values in EtOH/H2O and EtOD/D2O, respectively. Linear relationships with negative slopes between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2kHd (log
2kHd (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2kDd) and 1/T can be seen in the plots. The plots of the 2kHd and 2kDd values are close to each other in slope and intercept. The Arrhenius plots of the kHs and kDs values for reactions (2-H) and (2-D) in EtOH/H2O and EtOD/D2O respectively are given in Fig. S3.† The EH and log
2kDd) and 1/T can be seen in the plots. The plots of the 2kHd and 2kDd values are close to each other in slope and intercept. The Arrhenius plots of the kHs and kDs values for reactions (2-H) and (2-D) in EtOH/H2O and EtOD/D2O respectively are given in Fig. S3.† The EH and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH values in EtOH/H2O for reactions (2-H) and (3-H) and the corresponding values in EtOD/D2O (ED and log
AH values in EtOH/H2O for reactions (2-H) and (3-H) and the corresponding values in EtOD/D2O (ED and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD) for reactions (2-D) and (3-D) can be estimated from the Arrhenius plots as in Subsection 3.2, and those values are given in Table 2 together with the ED–EH values.
AD) for reactions (2-D) and (3-D) can be estimated from the Arrhenius plots as in Subsection 3.2, and those values are given in Table 2 together with the ED–EH values.
Since reaction (3) is not a proton (hydrogen) transfer reaction in contrast to reactions (1) and (2), the tunneling effect plays only a negligible part in reaction (3). For the readers' convenience in understanding the following subsections, we will below describe significant differences in reaction kinetic data between the presence and absence of the tunneling effect by using reactions (2) and (3). In general, when the tunneling effect plays an important role, a substantial deuterium kinetic-isotope effect appears, and great values of the above-mentioned rate-constant ratio (kHs/kDs or 2kHd/2kDd) and ED–EH are obtained.34,35 As shown in Table 2, the kHs/kDs value for reaction (2) (20.5) exceeds the maximum semiclassical ratio (6–8).34,35 The ED–EH value (11 kJ mol−1) also exceeds the maximum semiclassical difference (1.3–4.2 kJ mol−1).34,35 These results clearly show that the tunneling effect plays an important role in reaction (2) as reported previously.1,11,13 In contrast, the 2kHd/2kDd (1.3) and ED–EH (∼0 kJ mol−1) values for reaction (3) do not exceed the maximum semiclassical values.34,35 So a substantial deuterium kinetic-isotope effect is not seen in reaction (3), and we can confirm that the tunneling effect really plays only a negligible part in reaction (3). Like this, from the deuterium kinetic-isotope effect, we can estimate to what extent the tunneling effect contributes to the reaction in question.
In principle, Arrhenius plots of tunneling reactions deviate from linear relationships at low temperature. However, direct experimental observations of curvature in Arrhenius plots due to tunneling are rare in practice.36 In fact, although the tunneling effect plays an important role in reaction (2), linear relationships between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHs and 1/T are seen in Fig. S3.† The reason for this is that the temperature region used in the present experiments is limited.1,13 The temperature region is likely to correspond to region II in Fig. 3 of ref. 36.
kHs and 1/T are seen in Fig. S3.† The reason for this is that the temperature region used in the present experiments is limited.1,13 The temperature region is likely to correspond to region II in Fig. 3 of ref. 36.
3.3.2. Evaluation of kinetic data of reaction (1). Next the kHr (kDr) value of reaction (1-H) (reaction (1-D)) was evaluated. When both of reactions (1) and (3) contribute to the decay of α-Toc˙, the rate equations of reactions (1-H) and (3-H) are expressed as24,37| | |
−d[α-Toc˙]/dt = kHr[CatH][α-Toc˙] + 2kHd[α-Toc˙]2
| (17) |
Integration of eqn (17) leads to24,37| |
 | (18) |
where the 2kHd value is obtained in Subsection 3.3.1.Fig. 7 shows some decay curves of α-Toc˙ absorbance at 429 nm during reaction (3-H) and reaction (1-H) between α-Toc˙ and normal EGC (EGC-H) in EtOH/H2O at 25 °C, together with the curves simulated according to eqn (18). In the simulation, the kHr and [α-Toc˙]0 values are set to those given in the caption. The ε value is obtained in Subsection 3.3.1. The decay is accelerated as the prepared [EGC-H] increases. The simulation curves agree well with the experimental ones. Reactions (1-H) and (3-H) compete with each other. The curves obtained during reaction (3-D) and the competitive reaction (1-D) between α-Toc˙ and deuterated EGC (EGC-D) in EtOD/D2O at 25 °C are given in Fig. S4.† The kHr, kDr values and the ratio (kHr/kDr) at 25 °C are given in Table 1. The kHr and kDr values at 15–37 °C are listed in Table S1.†
 |
| | Fig. 7 Decay curves of α-Toc˙ absorbance at 429 nm during reaction (3-H) and reaction (1-H) between α-Toc˙ and EGC-H in EtOH/H2O at 25 °C (open circles), and the curves simulated by setting kHr = 2.41 × 104 M−1 s−1, 2kHd = 1.21 × 103 M−1 s−1, [α-Toc˙]0 = 2.58 × 10−5 M and ε = 3420 M−1 cm−1 in eqn (18) (solid curves). The prepared [EGC-H]s for the data shown with red, green, blue and pink open circles are 4.15 × 10−2, 8.29 × 10−2, 0.124 and 0.166 mM, respectively. Reactions (1-H) and (3-H) compete with each other. | |
Fig. 5 also shows the Arrhenius plots of the kHr and kDr values of EGC-H and EGC-D in EtOH/H2O and EtOD/D2O, respectively. Linear relationships with negative slopes between log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHr (log
kHr (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kDr) and 1/T can be seen in the plots. In contrast to the plots of the 2kHd and 2kDd values given in Subsection 3.3.1, the plots of the kHr and kDr values are different in slope and intercept from each other. The EH and log
kDr) and 1/T can be seen in the plots. In contrast to the plots of the 2kHd and 2kDd values given in Subsection 3.3.1, the plots of the kHr and kDr values are different in slope and intercept from each other. The EH and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH (ED and log
AH (ED and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD) values for reaction (1-H) (reaction (1-D)) with EGC-H (EGC-D) can be estimated from the plots as in Subsection 3.2, and are given in Table 1 together with the ED–EH values.
AD) values for reaction (1-H) (reaction (1-D)) with EGC-H (EGC-D) can be estimated from the plots as in Subsection 3.2, and are given in Table 1 together with the ED–EH values.
The curves obtained during reaction (3) and the competitive reaction (1) between α-Toc˙ and each of CatHs, CatDs, MR, MC and MG in EtOH/H2O (EtOD/D2O) at 25 °C are given in Fig. S5–S12.† The kHr, kDr and kHr/kDr values at 25 °C are listed in Table 1. The kHr and kDr values at 15–37 °C are listed in Table S1.† Their Arrhenius plots are given in Fig. S13–S18.† The EH and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH (ED and log
AH (ED and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD) values for reaction (1) are also listed in Table 1 together with the ED–EH values.
AD) values for reaction (1) are also listed in Table 1 together with the ED–EH values.
3.4. Tunneling effect
The experimental results given in Table 1 show that the tunneling effect plays an important role in reaction (1) between α-Toc˙ and each of EC, EGC and EGCG. In fact, the ED–EH values (∼10, 10 and 13 kJ mol−1 in EC, EGC and EGCG, respectively) exceed the maximum semiclassical difference (1.3–4.2 kJ mol−1).34,35 The kHr/kDr value for EGC (9.7) also exceeds the maximum semiclassical ratio (6–8).34,35 The tunneling effect would also play a part in reaction (1) with ECG besides in those with EC, EGC and EGCG. It is very interesting that the microscopic quantum-mechanical tunneling effect could manifest itself in a macroscopic vital function such as α-TocH recycling that is made by CatHs at interfaces between cellular membranes and the water phase. With regard to contribution of the tunneling effect to radical-scavenging reactions, previous computational results by Tejero et al.6,7 are consistent with our present experimental ones, although the calculations were made for a reaction between water-soluble EC and a model of lipid-soluble radicals (methylperoxyl radical).
Judging from the criteria for the maximum semiclassical values mentioned above, the tunneling effect contributes not only to the α-TocH recycling made by water-soluble CatHs but also to the recycling by lipid-soluble ubiquinol-10 (UQ10H2),15 whose kinetic data are also in Table 1. However, in the recycling made by water-soluble vitamin C (sodium ascorbate, Na+AsH−), the contribution of the tunneling effect is suppressed as shown in Table 1.22 Thus, whether or not the tunneling effect plays a major role depends on the antioxidant reagent employed in the α-TocH recycling (CatHs, UQ10H2 or Na+AsH−). The reason for this can be explained in the following way.
In a simple physical picture, the tunneling effect does not have a great influence on deuterium (D) transfer compared with protium (1H) transfer.34,35 The D transfer essentially proceeds by jumping semiclassically over the potential barrier, and the activation energy of the D transfer (ED) approximately reflects the real reaction potential-barrier of the semiclassical jump as explained previously.15 When the real potential barrier in the α-TocH recycling is low (Na+AsH−; ED = 6.4 kJ mol−1), the 1H transfer prefers to proceed by jumping semiclassically over the low potential barrier, and the tunneling effect does not play an important role even in the 1H transfer. In contrast, when the barrier is high (EGC, EGCG and UQ10H2; ED = 24, 28 and 10.6 kJ mol−1, respectively), the semiclassical jump over the barrier is not advantageous and 1H tunneling takes place below the transition state of the reaction. The tunneling then allows 1H to cut a corner on the potential energy surface. As a result, a substantial deuterium kinetic-isotope effect appears in the α-TocH recycling made by each of CatHs and UQ10H2,15 but the effect is suppressed in the recycling by Na+AsH−.22
3.5. Structure–activity relationship in tunneling
The kHr value of reaction (1) caused by each of CatHs and the related molecules at 25 °C (Table 1) increases in the order of| | |
MR ≪ EC < MG < ECG < MC ≪ EGCG ∼ EGC ≪ MP
| (19) |
A structure–activity relationship similar to inequality (19) is also seen in their ArO˙-scavenging reactions and reductions of stable artificial 5,7-diisopropyltocopheroxyl radical to 5,7-diisopropyltocopherol.20,21 The EH value given in Table 1 also decreases in the order of| | |
EC ∼ ECG > MG > MC ≫ EGCG > EGC > MP
| (20) |
Inequalities (19) and (20) are similar to each other except for the inverted direction of the inequality sign.
Since reaction (1) is a hydrogen transfer, the kHr value increases with increasing susceptibility to the hydrogen transfers from hydroxy (OH) groups in A, B and G rings contained in CatHs. The susceptibility depends on individual OH groups. The tunneling effect plays an important role in the hydrogen transfer as described in Subsection 3.4.
MR can be regarded as a model of the A ring of CatHs (Scheme 1). Since the reactivity of MR is negligible as shown in Table 1, the A ring will not play a part in the α-TocH recycling (reaction (1)).
MC can be regarded as a model of catechol B ring of EC and ECG (Scheme 1), and the kHr values of MC, EC and ECG (Table 1) are much greater than that of MR, which is a model of the A ring. In the catechol B ring, the H atom of the hydroxy group written in green in Scheme 3a is susceptible to the hydrogen transfer, because the intramolecular hydrogen bonding to the hydroxy O-atom38 weakens the O–H bond written in green. In fact, the intramolecular hydrogen bonding seemingly makes the O-atom pseudo-trivalent (C–O, O–H and the hydrogen bond), although it is inherently divalent. As a result, the O–H bond-order decreases, the bond is weakened, and then the hydroxy H-atom is easily pushed out of the B ring. In other words, the intramolecular hydrogen bonding activates the hydrogen transfer. Furthermore, since the rotational barrier of the B ring is low,38 the B ring can orient itself so as to react α-Toc˙ efficiently. Therefore, an α-Toc˙ target-site of EC and ECG in reaction (1) will be the catechol B-ring as well as a methylperoxyl-radical target-site of EC,6 and the tunneling effect will play an important role in the 1H transfer from the catechol B ring.
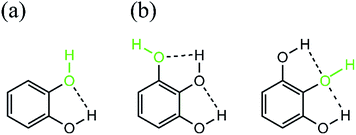 |
| | Scheme 3 (a) Catechol. (b) Pyrogallol. | |
MP can be regarded as a model of pyrogallol B ring of EGC and EGCG (Scheme 1). The kHr values of MP, EGC and EGCG containing a pyrogallol ring are much greater than those of MC, EC and ECG containing a catechol ring instead (Table 1). Furthermore, the EH values of MP, EGC and EGCG are much less than those of MC, EC and ECG, respectively. Accordingly, the α-TocH-recycling activity of the pyrogallol ring in MP, EGC and EGCG will be higher than that of the catechol ring in MC, EC and ECG. In fact, H-atom of each pyrogallol hydroxy-group written in green in Scheme 3b is more susceptible to the hydrogen transfer (1H tunneling) than that of catechol, because two intramolecular hydrogen bonds38,39 activate the hydrogen transfer from the pyrogallol ring.
EC has only the A and B rings, and the OH group at the 3-position is replaced by the G ring in ECG (Scheme 1). MG can be regarded as a model of the G ring. Since the kHr values of ECG and MG are greater than those of EC and MR respectively (Table 1), the G ring would also play a part in the α-TocH recycling through the 1H tunneling. In fact, the difference in kHr value between ECG and EC (2.23 × 103 M−1 s−1) is close to the kHr value of MG (2.11 × 103 M−1 s−1). However, since the kHr value of MG is less than those of MC and MP, the activity of the α-TocH recycling caused by the G ring will be less than that by the B ring. Although two intramolecular hydrogen bonds activate the hydrogen transfer in MG as well as in MP (Scheme 1), the kHr value of MG is much less than that of MP. The reason for this may be that electron transfer plays a role in reaction (1) as well as in α-TocH recycling made by UQ10H215 and the electron-accepting property of –COOCH3 group in MG prevents the electron transfer from MG to α-Toc˙.
EGC has only the A and B rings, and the OH group at the 3-position is replaced by the G ring in EGCG (Scheme 1). The molecular-structural difference between EGC and EGCG is thus the same as that between EC and ECG. However, the kHr values of EGC and EGCG are close to each other (Table 1), whereas the kHr value of ECG is greater than that of EC as mentioned above. Although the G ring seems unlikely to participate in the α-TocH-recycling activity of EGCG, the presence of the G ring plays a role in the α-TocH recycling by ECG. At present we cannot make an unambiguous reason for this, but we suggest a possible explanation in the following. Since the B ring of EGCG is bulkier than that of ECG (Scheme 1), it might hinder α-Toc˙ from approaching the G ring and the steric hindrance might suppress the α-TocH-recycling activity in EGCG. Another possibility to account for the similar kHr value between EGC and EGCG is to consider previously-suggested interaction between the B and G rings in EGCG.39 In any case, a detailed elucidation of the mechanism of reaction (1) with EGCG may still require further work.
Although MP is a model of the pyrogallol B ring of EGC and EGCG, the kHr value of MP is much greater than those of EGC and EGCG (Table 1). The reason for this might also be steric hindrance in EGC and EGCG, because the EH value of MP is less than those of EGC and EGCG. The A ring might also hinder α-Toc˙ from approaching the reactive B ring in EGC and EGCG. Similar steric hindrance may also been seen in EC, because the kHr and EH values of MC are respectively greater and less than those of EC (Table 1).
In summary, when the steric hindrance and inter-ring interaction are absent, the activity of the α-TocH recycling (1H tunneling) caused by each ring contained in CatHs will increase in the order of
| | |
A ring ≪ G ring < catechol B ring ≪ pyrogallol B ring
| (21) |
A structure–activity relationship similar to inequality
(21) is also seen in the ArO˙-scavenging reactions and reductions of stable artificial 5,7-diisopropyltocopheroxyl radical to 5,7-diisopropyltocopherol by CatHs.
20,21
3.6. ATREC values
In previous works, we developed aroxyl-radical- and singlet-oxygen-absorption capacity assay methods, and named them ARAC and SOAC methods respectively after the acronyms.40,41 The ARAC method was an alternative to ORAC method (oxygen-radical absorbing capacity method),42 which was most widely used to assess antioxidant capacities against free radicals but whose validity was regrettably doubted by U.S. Department of Agriculture in 2012.43 In the present work, the free radical absorption capacities are obtained by tracing reactions (2-H) and (2-D) according to the ARAC method (ARAC values) and listed in Table 2. Our SOAC method has been successfully applied to various singlet-oxygen quenching antioxidants and food extracts. The ARAC values and the singlet-oxygen absorption capacities (SOAC values) so far reported are summarized in our database.44
Since radical matter is excreted from cellular membrane to the water phase through α-TocH recycling made by a hydrophilic antioxidant (Fig. 1), total estimation of antioxidant and α-TocH-recycling capacities is necessary for clarification of the whole membrane protection from oxidative damage. However, with respect to the α-TocH recycling, we have not yet started developing a method of assessing the capacity. Accordingly, in the present paper, we propose a new α-TocH-recycling capacity assay method based on the procedures explained in Subsections 3.2 and 3.3, and name it ATREC method after the acronym.
Basically, on the basis of the second-order rate constant (kRHr) of the following reaction, we estimate the α-TocH-recycling capacity (ATREC value) of a molecule containing at least one hydrogen-donating group (RH).
| |
 | (1′) |
Here, R˙ denotes a radical produced from RH. Reaction
(1) can be regarded as a kind of reaction
(1′). We inspect reaction
(1′) as explained in Subsection 3.2 or 3.3 depending on the magnitude of the reaction rate, and evaluate the
kRHr value. The ATREC value of RH is defined in the following equation.
| |
 | (22) |
where

denotes the second-order rate constant of reaction
(1′) between α-Toc˙ and sodium ascorbate (RH = Na
+AsH
−). The

value in EtOH/H
2O was previously reported
22 and given in
Table 1. The ATREC value is a quantity without a unit and directly connected to the second-order rate constants (
kRHr and

) of reaction
(1′). The ATREC values obtained in the present work are listed in
Table 1.
As shown in Table 1, the ATREC values of CatHs are 0.01–1% of that of Na+AsH−. However, when RH is hydrophilic like CatHs and Na+AsH− (vitamin C), the whole activity of the α-TocH recycling (reaction (1′)) in biological systems is proportional to the product of the ATREC value and RH's local concentration near the membrane surface, as understood from Fig. 1. CatHs are found in high concentrations in foods such as green tea. For instance, dried green-tea leaves include >25 wt% of CatHs, and EGCG showing a high ATREC value has the highest concentration (>11 wt%).45 Consumption of green tea is high in Asia (>2 cups per day in Japan).46 After ingestion of green tea, human plasma level of CatHs increases very much.27−29 Furthermore, inherently-hydrophilic CatHs also have some lipophilic properties and could bind low-density lipoproteins (LDL) much more efficiently than vitamin C could bind,47,48 although the normal concentration of CatHs in plasma is about 10% of that of vitamin C.20 Thus, considerable CatHs would be localized near the membrane surface,30 whereas most vitamin C would be delocalized over the water phase. As a result, the local concentration of CatHs near the membrane surface after ingestion of green tea would be much greater than that of vitamin C. Although the ATREC values of CatHs are less than that of vitamin C, a considerable part of CatHs could then participate in the α-TocH recycling at the interface between the membrane and the water phase,30 while only a small part of vitamin C, which happens to be near the membrane surface, could recycle α-TocH. Accordingly, the result of the present kinetic study suggests that CatHs prevent consumption of α-TocH through reaction (1) (α-TocH recycling) after ingestion of green tea and protect the systems from oxidative damage by using the tunneling effect.
4. Conclusions
In the work presented here, we have studied the recycling reactions of natural α-TocH (α-TocD) by CatHs (CatDs) (reaction (1)) with a double-mixing stopped-flow spectrometer, which allows us to follow kinetics of reactions of short-lived radicals such as α-Toc˙. We have determined the kHr (kDr) values by using the simulation explained in Subsection 3.3, obtained the EH (ED) values from the temperature dependences, and examined the deuterium kinetic-isotope effects. From these results, we have found that the tunneling effect plays an important role in reaction (1). It is interesting that the microscopic quantum-mechanical tunneling effect could manifest itself in a macroscopic vital function such as the α-TocH recycling at interfaces between cellular membranes and the water phase. At first glance, this is in conflict with our intuition as in Schrödinger's cat,49 in which a paradox lies in clever coupling of the microscopic quantum domain and the macroscopic vital domain. In reality, however, living cells might know quantum mechanics very well and use it effectively. Furthermore, we have clarified the structure–activity relationship in reaction (1), and suggested conditions under which the tunneling effect plays a major role in reaction (1′). We have also proposed a new α-TocH-recycling capacity assay-method, and named it ATREC assay-method after the acronym.
Acknowledgements
This paper is dedicated to Professor Emeritus Tetsuo Miyazaki of Nagoya University who was the editor of ref. 1 and passed away on March 11, 2015 at the age of 75 years from prostate cancer. We express our sincere thanks to Dr Takuhiro Kakiuchi of Ehime University for his valuable help in an early stage of this work. Our thanks are also due to Dr Aya Kuranaka, formerly Ouchi, of Ehime University (now at Osaka Delica Foods Co., Ltd.) for her skillful technical help during the course of the experiments. This work was partly supported by JSPS KAKENHI Grant Number 15K07431.
References
- Atom Tunneling Phenomena in Physics, Chemistry, and Biology, ed. T. Miyazaki, Springer, Berlin, 2004, and references cited therein Search PubMed.
- H. Sekiya and K. Sakota, Excited-state double-proton transfer in a model DNA base pair: resolution for stepwise and concerted mechanism controversy in the 7-azaindole dimer revealed by frequency- and time-resolved spectroscopy, J. Photochem. Photobiol., C, 2008, 9, 81 CrossRef CAS.
- L. Masgrau and D. G. Truhlar, The importance of ensemble averaging in enzyme kinetics, Acc. Chem. Res., 2015, 48, 431 CrossRef CAS PubMed.
- J. P. Klinman, Dynamically achieved active site precision in enzyme catalysis, Acc. Chem. Res., 2015, 48, 449 CrossRef CAS PubMed.
- A. Kohen, Role of dynamics in enzyme catalysis: substantial versus semantic controversies, Acc. Chem. Res., 2015, 48, 466 CrossRef CAS PubMed.
- I. Tejero, N. González-García, À. González-Lafont and J. M. Lluch, Tunneling in green tea: understanding the antioxidant activity of catechol-containing compounds. A variational transition-state theory study, J. Am. Chem. Soc., 2007, 129, 5846 CrossRef CAS PubMed.
- T. Westgate, Quantum quirk responsible for antioxidant behaviour. Green tea's secret tunnelling revealed, Chem. World, 2007, 30 Search PubMed.
- T. Yamamoto and S. Kato, Ab initio calculation of proton-coupled electron transfer rates using the external-potential representation: a ubiquinol complex in solution, J. Chem. Phys., 2007, 126, 224514 CrossRef PubMed.
- T. Inagaki and T. Yamamoto, Critical role of deep hydrogen tunneling to accelerate the antioxidant reaction of ubiquinol and vitamin E, J. Phys. Chem. B, 2014, 118, 937 CrossRef CAS PubMed.
- C. R. Lamberson, L. Xu, H. Muchalski, J. R. Montenegro-Burke, V. V. Shmanai, A. V. Bekish, J. A. McLean, C. F. Clarke, M. S. Shchepinov and N. D. Porter, Unusual kinetic isotope effects of deuterium reinforced polyunsaturated fatty acids in tocopherol-mediated free radical chain oxidations, J. Am. Chem. Soc., 2014, 136, 838 CrossRef CAS PubMed.
- S. Nagaoka, A. Kuranaka, H. Tsuboi, U. Nagashima and K. Mukai, Mechanism of antioxidant reaction of vitamin E. Charge transfer and tunneling effect in proton-transfer reaction, J. Phys. Chem., 1992, 96, 2754 CrossRef CAS.
- S. Nagaoka, Y. Nishioku and K. Mukai, Tunneling effect in the regeneration reaction of vitamin E by ubiquinol, Chem. Phys. Lett., 1998, 287, 70 CrossRef CAS.
- S. Nagaoka, M. Inoue, C. Nishioka, Y. Nishioku, S. Tsunoda, C. Ohguchi, K. Ohara and K. Mukai, Tunneling effect in antioxidant, prooxidant, and regeneration reactions of vitamin E, J. Phys. Chem. B, 2000, 104, 856 CrossRef CAS.
- T. Kakiuchi, K. Mukai, K. Ohara and S. Nagaoka, Tunneling effect in antioxidant reaction of flavonoid, Bull. Chem. Soc. Jpn., 2009, 82, 216 CrossRef CAS.
- A. Ouchi, S. Nagaoka and K. Mukai, Tunneling effect in regeneration reaction of vitamin E by ubiquinol, J. Phys. Chem. B, 2010, 114, 6601 CrossRef CAS PubMed.
- G. W. Burton and K. U. Ingold, Vitamin E as an in vitro and in vivo antioxidant, Ann. N. Y. Acad. Sci., 1989, 570, 7 CrossRef CAS PubMed.
- M. G. Traber and J. Atkinson, Vitamin E, antioxidant and nothing more, Free Radical Biol. Med., 2007, 43, 4 CrossRef CAS PubMed.
- I. Nakanishi, K. Miyazaki, T. Shimada, K. Ohkubo, S. Urano, N. Ikota, T. Ozawa, S. Fukuzumi and K. Fukuhara, Effects of metal ions distinguishing between one-step hydrogen- and electron-transfer mechanisms for the radical-scavenging reaction of (+)-catechin, J. Phys. Chem. A, 2002, 106, 11123 CrossRef CAS.
- B. Zhou, L.-M. Wu, L. Yang and Z.-L. Liu, Evidence for α-tocopherol regeneration reaction of green tea polyphenols in SDS micelles, Free Radical Biol. Med., 2005, 38, 78 CrossRef CAS PubMed.
- K. Mukai, S. Mitani, K. Ohara and S. Nagaoka, Structure–activity relationship of the tocopherol-regeneration reaction by catechins, Free Radical Biol. Med., 2005, 38, 1243 CrossRef CAS PubMed.
- S. Mitani, A. Ouchi, E. Watanabe, Y. Kanesaki, S. Nagaoka and K. Mukai, Stopped-flow kinetic study of the aroxyl radical-scavenging action of catechins and vitamin C in ethanol and micellar solutions, J. Agric. Food Chem., 2008, 56, 4406 CrossRef CAS PubMed.
- S. Nagaoka, T. Kakiuchi, K. Ohara and K. Mukai, Kinetics of the reaction by which natural vitamin E is regenerated by vitamin C, Chem. Phys. Lipids, 2007, 146, 26 CrossRef CAS PubMed.
- K. Mukai, A. Ouchi, A. Mitarai, K. Ohara and C. Matsuoka, Formation and decay dynamics of vitamin E radical in the antioxidant reaction of vitamin E, Bull. Chem. Soc. Jpn., 2009, 82, 494 CrossRef CAS.
- A. Ouchi, M. Ishikura, K. Konishi, S. Nagaoka and K. Mukai, Kinetic study of the prooxidant effect of α-tocopherol. Hydrogen abstraction from lipids by α-tocopheroxyl radical, Lipids, 2009, 44, 935 CrossRef CAS PubMed.
- C. A. Rice-Evans, N. J. Miller and G. Paganga, Structure-antioxidant activity relationships of flavonoids and phenolic acids, Free Radical Biol. Med., 1996, 20, 933 CrossRef CAS PubMed.
- H. M. Graham, Green tea composition, consumption and polyphenol chemistry, Prev. Med., 1992, 21, 334 CrossRef CAS PubMed.
- M.-J. Lee, Z.-Y. Wang, H. Li, L. Chen, Y. Sun, S. Gobbo, D. A. Balentine and C. S. Yang, Analysis of plasma and urinary tea polyphenols in human subjects, Cancer Epidemiol. Biomarkers Prev., 1995, 4, 393 CAS.
- P. G. Pietta, P. Simonetti, C. Gardana, A. Brusamolino, P. Morazzonic and E. Bombardelli, Catechin metabolites after intake of green tea infusions, BioFactors, 1998, 8, 111 CrossRef CAS PubMed.
- C. S. Yang, L. Chen, M.-J. Lee, D. Balentine, M. C. Kuo and S. P. Schantz, Blood and urine levels of tea catechins after ingestion of different amounts of green tea by human volunteers, Cancer Epidemiol. Biomarkers Prev., 1998, 7, 351 CAS.
- J. Terao, M. Piskula and Q. Yao, Protective effect of epicatechin, epicatechin gallate, and quercetin on lipid peroxidation in phospholipid bilayers, Arch. Biochem. Biophys., 1994, 308, 278 CrossRef CAS PubMed.
- E. Niki and N. Noguchi, Dynamics of antioxidant action of vitamin E, Acc. Chem. Res., 2004, 37, 45 CrossRef CAS PubMed.
- D. Harman, Aging: overview, Ann. N. Y. Acad. Sci., 2001, 928, 1 CrossRef CAS PubMed.
- A. Rieker and K. Scheffler, Die Beteiligung von Phenylresten an der Aroxylmesomerie, Liebigs Ann. Chem., 1965, 689, 78 CrossRef CAS.
- R. P. Bell, The Tunnel Effect in Chemistry, Chapman and Hall, London, 1980, pp.77–105 Search PubMed.
- H. Kwart, Temperature dependence of the primary kinetic hydrogen isotope effect as a mechanistic criterion, Acc. Chem. Res., 1982, 15, 401 CrossRef CAS.
- T. Jonsson, M. H. Glickman, S. Sun and J. P. Klinman, Experimental evidence for extensive tunneling of hydrogen in the lipoxygenase reaction: implications for enzyme catalysis, J. Am. Chem. Soc., 1996, 118, 10319 CrossRef CAS.
- A. Watanabe, N. Noguchi, A. Fujisawa, T. Kodama, K. Tamura, O. Cynshi and E. Niki, Stability and reactivity of aryloxyl radicals derived from a novel antioxidant BO-653 and related compounds. Effects of substituent and side chain in solution and membranes, J. Am. Chem. Soc., 2000, 122, 5438 CrossRef CAS.
- D. Botten, G. Fugallo, F. Fraternali and C. Molteni, Structural properties of green tea catechins, J. Phys. Chem. B, 2015, 119, 12860 CrossRef CAS PubMed.
- Y. Takeuchi, K. Okuno, H. Yoshioka and H. Yoshioka, Characteristics of the OH radical scavenging activity of tea catechins, J. Radioanal. Nucl. Chem., 2007, 272, 455 CrossRef CAS.
- S. Nagaoka, K. Nagai, Y. Fujii, A. Ouchi and K. Mukai, Development of a new free radical absorption capacity assay method for antioxidants: aroxyl
radical absorption capacity (ARAC), J. Agric. Food Chem., 2013, 61, 10054 CrossRef CAS PubMed.
- A. Ouchi, K. Aizawa, Y. Iwasaki, T. Inakuma, J. Terao, S. Nagaoka and K. Mukai, Kinetic study of the quenching reaction of singlet oxygen by carotenoids and food extracts in solution. Development of a singlet oxygen absorption capacity (SOAC) assay method, J. Agric. Food Chem., 2010, 58, 9967 CrossRef CAS PubMed.
- G. Cao, H. M. Alessio and R. G. Cutler, Oxygen-radical absorbance capacity for antioxidants, Free Radical Biol. Med., 1993, 14, 303 CrossRef CAS PubMed.
- U.S. Department of Agriculture, Agricultural Research Service, http://www.ars.usda.gov/services/docs.htm?docid=15866, accessed May 2016.
- S. Nagaoka, AbsorptionCapacity.accdb, http://chem.sci.ehime-u.ac.jp/%7Estruct1/int_naga.pdf, accessed May 2016.
- Z. Y. Wang, M.-T. Huang, Y.-R. Lou, J.-G. Xie, K. R. Reuhl, H. L. Newmark, C.-T. Ho, C. S. Yang and A. H. Conney, Inhibitory effects of black tea, green tea, decaffeinated black tea, and decaffeinated green tea on ultraviolet B light-induced skin carcinogenesis in 7,12-dimethylbenz[a]anthracene-initiated SKH-1 mice, Cancer Res., 1994, 54, 3428 CAS.
- N. Kurahashi, S. Sasazuki, M. Iwasaki, M. Inoue and S. Tsugane, Green tea consumption and prostate cancer risk in Japanese men: a prospective study, Am. J. Epidemiol., 2008, 167, 71 CrossRef PubMed.
- J. A. Vinson, J. Jang, Y. A. Dabbagh, M. M. Serry and S. Cai, Plant polyphenols exhibit lipoprotein-bound antioxidant activity using an in vitro oxidation model for heart disease, J. Agric. Food Chem., 1995, 43, 2798 CrossRef CAS.
- C. Sánchez-Moreno, A. Jiménez-Escrig and F. Saura-Calixto, Study of low-density lipoprotein oxidizability indexes to measure the antioxidant activity of dietary polyphenols, Nutr. Res., 2000, 20, 941 CrossRef.
- E. Schrödinger, The present situation in quantum mechanics: a translation of Schrödinger's “cat paradox” paper, Proc. Am. Philos. Soc., 1980, 124, 323 (Naturwissenschaften, 1935, 23, 807) Search PubMed , 823 and 844.
Footnote |
| † Electronic supplementary information (ESI) available: kHr, kDr, kHs, kDs, 2kHd and 2kDd values for reactions (1)–(3) in EtOH/H2O and EtOD/D2O at 15–37 °C (Table S1). Rise-and-decay curves of [α-Toc˙] during reaction (2) and the subsequent reaction (3) at 15–37 °C, and the simulated curves (Fig. S1 and S2). Arrhenius plots of kHs and kDs values for reaction (2) (Fig. S3). Decay curves of α-Toc˙ absorbance during reaction (3) and the competitive reaction (1) between α-Toc˙ and each of CatHs, CatDs, MR, MC and MG at 25 °C (Fig. S4–S12). Arrhenius plots of kHr and kDr values for reaction (1) between α-Toc˙ and each of CatHs, EGCG-D, MC and MG (Fig. S13–S18). See DOI: 10.1039/c6ra05986d |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  *,
Akiko Nitta,
Ai Suemitsu and
Kazuo Mukai
*,
Akiko Nitta,
Ai Suemitsu and
Kazuo Mukai


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio to obtain a mixed solvent EtOH/H2O (EtOD/D2O) because α-Toc˙ and ArO˙ are ethanol-soluble and CatHs are water-soluble. EtOH/H2O (EtOD/D2O) solutions of α-TocH (α-TocD) and ArO˙ were respectively produced by first dissolving α-TocH and ArO˙ in EtOH (EtOD) and then adding H2O (D2O). When CatHs and α-TocH were dissolved in solvents containing deuterated alcohol, replacement of the hydrogen atoms of the OH groups (hydroxy H-atoms) by deuterons was easily accomplished, and CatDs and α-TocD were obtained. The deuteration was verified by proton NMR.
1 volume ratio to obtain a mixed solvent EtOH/H2O (EtOD/D2O) because α-Toc˙ and ArO˙ are ethanol-soluble and CatHs are water-soluble. EtOH/H2O (EtOD/D2O) solutions of α-TocH (α-TocD) and ArO˙ were respectively produced by first dissolving α-TocH and ArO˙ in EtOH (EtOD) and then adding H2O (D2O). When CatHs and α-TocH were dissolved in solvents containing deuterated alcohol, replacement of the hydrogen atoms of the OH groups (hydroxy H-atoms) by deuterons was easily accomplished, and CatDs and α-TocD were obtained. The deuteration was verified by proton NMR.





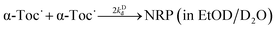



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHr and the reciprocal of the absolute temperature (1/T) can be seen in the plot, from which the activation energy (EH) and the frequency factor (AH) can be evaluated according to eqn (8).
kHr and the reciprocal of the absolute temperature (1/T) can be seen in the plot, from which the activation energy (EH) and the frequency factor (AH) can be evaluated according to eqn (8).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHr = −0.434EH/RT + log
kHr = −0.434EH/RT + log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH
AH
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH are listed in Table 1.
AH are listed in Table 1.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH, log
AH, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD and ATREC values of CatHs (CatDs) and related molecules
AD and ATREC values of CatHs (CatDs) and related molecules
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH or log
AH or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ADa
ADa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH (log
AH (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD) was obtained by extrapolating the linear log
AD) was obtained by extrapolating the linear log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHr (log
kHr (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kDr) versus 1/T plot in a limited 1/T range around room temperature to the intercept, this value has a large uncertainty.b The kinetic data were obtained in EtOH/H2O.c The kinetic data were obtained in EtOD/D2O.d Reliable data was not obtained.e Ref. 22: Na+AsH− and Na+AsD− denote sodium ascorbate-d0 (vitamin C) and -d3 respectively.f Ref. 15: UQ10H2 and UQ10D2 respectively denote ubiquinol-10-d0 and -d2, whose kinetic data were obtained in EtOH and EtOD.
kDr) versus 1/T plot in a limited 1/T range around room temperature to the intercept, this value has a large uncertainty.b The kinetic data were obtained in EtOH/H2O.c The kinetic data were obtained in EtOD/D2O.d Reliable data was not obtained.e Ref. 22: Na+AsH− and Na+AsD− denote sodium ascorbate-d0 (vitamin C) and -d3 respectively.f Ref. 15: UQ10H2 and UQ10D2 respectively denote ubiquinol-10-d0 and -d2, whose kinetic data were obtained in EtOH and EtOD.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH and log
AH and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD for reactions (2) and (3), and ARAC values
AD for reactions (2) and (3), and ARAC values
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH or log
AH or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ADa
ADa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH and log
AH and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD were respectively obtained by extrapolating the linear log
AD were respectively obtained by extrapolating the linear log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHs and log
kHs and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kDs (log
kDs (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2kHd and log
2kHd and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2kDd) versus 1/T plots in a limited 1/T range around room temperature to the intercepts, these values have a large uncertainty.b The kinetic data were obtained in EtOH/H2O.c The kinetic data were obtained in EtOD/D2O.
2kDd) versus 1/T plots in a limited 1/T range around room temperature to the intercepts, these values have a large uncertainty.b The kinetic data were obtained in EtOH/H2O.c The kinetic data were obtained in EtOD/D2O.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2kHd (log
2kHd (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2kDd) and 1/T can be seen in the plots. The plots of the 2kHd and 2kDd values are close to each other in slope and intercept. The Arrhenius plots of the kHs and kDs values for reactions (2-H) and (2-D) in EtOH/H2O and EtOD/D2O respectively are given in Fig. S3.† The EH and log
2kDd) and 1/T can be seen in the plots. The plots of the 2kHd and 2kDd values are close to each other in slope and intercept. The Arrhenius plots of the kHs and kDs values for reactions (2-H) and (2-D) in EtOH/H2O and EtOD/D2O respectively are given in Fig. S3.† The EH and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH values in EtOH/H2O for reactions (2-H) and (3-H) and the corresponding values in EtOD/D2O (ED and log
AH values in EtOH/H2O for reactions (2-H) and (3-H) and the corresponding values in EtOD/D2O (ED and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD) for reactions (2-D) and (3-D) can be estimated from the Arrhenius plots as in Subsection 3.2, and those values are given in Table 2 together with the ED–EH values.
AD) for reactions (2-D) and (3-D) can be estimated from the Arrhenius plots as in Subsection 3.2, and those values are given in Table 2 together with the ED–EH values.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHs and 1/T are seen in Fig. S3.† The reason for this is that the temperature region used in the present experiments is limited.1,13 The temperature region is likely to correspond to region II in Fig. 3 of ref. 36.
kHs and 1/T are seen in Fig. S3.† The reason for this is that the temperature region used in the present experiments is limited.1,13 The temperature region is likely to correspond to region II in Fig. 3 of ref. 36.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kHr (log
kHr (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kDr) and 1/T can be seen in the plots. In contrast to the plots of the 2kHd and 2kDd values given in Subsection 3.3.1, the plots of the kHr and kDr values are different in slope and intercept from each other. The EH and log
kDr) and 1/T can be seen in the plots. In contrast to the plots of the 2kHd and 2kDd values given in Subsection 3.3.1, the plots of the kHr and kDr values are different in slope and intercept from each other. The EH and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH (ED and log
AH (ED and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD) values for reaction (1-H) (reaction (1-D)) with EGC-H (EGC-D) can be estimated from the plots as in Subsection 3.2, and are given in Table 1 together with the ED–EH values.
AD) values for reaction (1-H) (reaction (1-D)) with EGC-H (EGC-D) can be estimated from the plots as in Subsection 3.2, and are given in Table 1 together with the ED–EH values.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AH (ED and log
AH (ED and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AD) values for reaction (1) are also listed in Table 1 together with the ED–EH values.
AD) values for reaction (1) are also listed in Table 1 together with the ED–EH values.

 denotes the second-order rate constant of reaction (1′) between α-Toc˙ and sodium ascorbate (RH = Na+AsH−). The
denotes the second-order rate constant of reaction (1′) between α-Toc˙ and sodium ascorbate (RH = Na+AsH−). The  value in EtOH/H2O was previously reported22 and given in Table 1. The ATREC value is a quantity without a unit and directly connected to the second-order rate constants (kRHr and
value in EtOH/H2O was previously reported22 and given in Table 1. The ATREC value is a quantity without a unit and directly connected to the second-order rate constants (kRHr and  ) of reaction (1′). The ATREC values obtained in the present work are listed in Table 1.
) of reaction (1′). The ATREC values obtained in the present work are listed in Table 1.



