DOI:
10.1039/C6RA05724A
(Paper)
RSC Adv., 2016,
6, 41506-41515
Effect of a triple contact line on the thermokinetics of dropwise condensation on an immiscible liquid surface
Received
3rd March 2016
, Accepted 18th April 2016
First published on 20th April 2016
Abstract
Within the framework of classical nucleation theory, a thermokinetic model is developed for the line-tension-associated condensation on an immiscible liquid substrate considering both interfacial and peripheral molecular transport. Along with the free energy minimization principle, a modified classical theory, based on detailed balance analysis, has been employed to determine relevant thermokinetic parameters for heterogeneous nucleation of water droplets as a function of the pseudo-contact angle, submergence angle, and equivalent Young's contact angle. A triple contact line is found to have a considerable effect on both thermodynamics with the associated line tension and kinetics with the related peripheral molecular transport. The growth rate of the formed droplet increases for lower values of the pseudo-contact angle and submergence angle. Besides, positive line tension increases for higher values of the pseudo-contact angle and submergence angle and lower values of the equivalent Young's contact angle, while negative line tension exhibits a reverse trend. With decreasing pseudo-contact angle and submergence angle and increasing equivalent Young's contact angle, the free energy barrier decreases appreciably. Subsequently, the rate of nucleation increases which, in turn, suggests the possibility of condensation enhancement under such conditions. Using the heterogeneous nucleation experimental data, the present thermokinetic formulation is capable of estimating the values of microscopic contact angles and line tension of a given lenticular three-phase system.
1. Introduction
In recent years, there has been a considerable interest in the scientific community in the formation and self-assembly of ordered patterns of microporous structures, i.e. ‘breath figures’.1–3 The key mechanism that determines the formation and the subsequent growth of the condensing droplets in the breath figures is dropwise condensation.4 Dropwise condensation or droplet nucleation5 on rigid or soft elastic6 substrates is not only an abundant natural phenomenon7 but also has several natural processes7 and industrial applications.8 Although associated with various simplified assumptions, Classical Nucleation Theory (CNT) is adopted most widely to describe the phenomena of heterogeneous nucleation.9 Thermokinetic models have also been developed for heterogeneous nucleation on diverse geometrical substrates namely planar,10,11 spherical,12–16 conical17–19 etc. In this context, it needs to be mentioned that mostly rigid substrates are considered for all the aforesaid geometries.20
When a droplet forms in between an ambient supersaturated vapour and an extrinsic substrate, a triple contact line where all the three distinct phases intersect each other always exists.21 The three-phase contact line tension, which can be considered as the one-dimensional equivalent to the interfacial tension, plays a pivotal role when the droplet becomes small.22 The effect of contact line tension cannot be neglected in the phenomenon of nucleation of nano-sized droplets on rigid planar,23–28 spherical,29–32 or conical33 substrates. Moreover, along with the interfacial molecular transport11,13,17 through the vicinity of the droplet–vapour interface, the peripheral molecular transport33–35 in the neighbourhood of the triple line from the thin adsorbed layer should be considered during the initial stage of nucleation. So, the presence of triple line is found to have a considerable effect on the thermokinetics of heterogeneous nucleation on rigid substrates. However, less attention was paid towards the thermokinetic mechanism of heterogeneous nucleation on an immiscible liquid substrate considering the effect of triple line.36–40
In this paper, we have developed a modified CNT-based thermokinetic model for condensation on an immiscible liquid surface, considering the combined effect of the line tension and the peripheral molecular flux. Under steady-state condition, we have studied some thermokinetic traits of heterogeneous nucleation of a lenticular droplet in terms of various associated physico-chemical properties, kinetic characteristics, ambient conditions, and geometric parameters. Based on a rigorous analytical treatment, a quantitative assessment of growth rate and nucleation rate has been made considering dropwise condensation of lens-shaped water droplets from supersaturated water vapours on immiscible liquid surfaces. Further, using the experimental data on nucleation, the microscopic wettability and line tension for a water lens on n-dodecane substrate have been evaluated to get a better perception of wetting and nucleation in this unique configuration.
2. Thermokinetic model
2.1 Model for intra-cluster growth
Dropwise condensation or droplet nucleation of a supersaturated vapor is a specific example of the activated process called first-order phase transition.5 The objective of the nucleation theory is to measure the net flux at which the clusters grow to a critical size, beyond which the spontaneous formation of new stable phase, i.e. growth, is observed. The thermokinetics of nucleation according to CNT is based on the capillarity approximation.9 Initially, clusters are formed due to the effect of thermal fluctuations. The clusters of the liquid phase, i.e. the droplets in the present case, are continuously being formed and destroyed due to these fluctuations. In the present work, it is assumed that the concentration of droplets is small and the molecular association is absent in the supersaturated vapor. So, the droplets can only grow or shrink through the single-molecular events considering the above-mentioned assumptions. Accordingly, the growth or shrinkage of a cluster can be formulated by a series of reversible bimolecular reactions| |
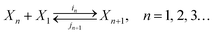 | (1) |
where Xn is the cluster containing n molecules.10
The rate equations for cluster growth or shrinkage can be given by
| |
 | (2) |
where the unsteady-state nucleation rate can be written as
| | |
Jn = inρn − jn+1ρn+1,
| (3) |
ρ is the equilibrium cluster concentration and
i and
j are the time rates of inward and outward molecular flux respectively.
9,10
The equilibrium cluster concentration, which can be defined as the energetic probability of the appearance of a cluster, is one of the major parameters in the formulation of the present thermokinetic model. We have adopted Dillmann–Meier expression for the equilibrium cluster concentration which can be formulated as41
| |
 | (4) |
where the number density
nv, of the supersaturated vapour can be expressed by assuming the metastable phase as an ideal gas:
| | |
nv = pv/kBT = Spsatv/kBT,
| (5) |
kB is the Boltzmann constant,
T is the temperature,
S (≥1) is the degree of supersaturation,
pv and
psatv are the pressure of the ambient vapour under the supersaturated and the saturated conditions.
The Gibbs free energy change related to the formation of a cluster can be given by9,10
where Δ
FH and Δ
FV is the variation in the Helmholtz and volumetric free energy respectively.
In this context, a geometric model is needed for determining the energy barrier. Consider the formation of a lenticular cluster of lateral radius r from its supersaturated vapor on a liquid surface as depicted in Fig. 1. The cluster or the droplet (β) is formed at the interface between the metastable phase (α) and the liquid substrate (γ). θ and ϕ are the pseudo-contact angle and the submergence angle respectively as illustrated in Fig. 1. Rαβ (=r/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and Rβγ (=r/sin
θ) and Rβγ (=r/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) are the associated radii of curvature needed to describe the lenticular droplet.
ϕ) are the associated radii of curvature needed to describe the lenticular droplet.
 |
| | Fig. 1 Schematic of the geometric model for heterogeneous nucleation on an immiscible liquid substrate. | |
So, the Helmholtz free energy change (ΔFH) is related to the variation in the free energy due to the line tension and other associated interfacial tensions. ΔFH can then be expressed as31
| | |
ΔFH = σαβAαβ + σβγAβγ − σαγAp + τLαβγ,
| (7) |
where
σij is the corresponding interfacial tension between
i and
j phases,
τ is the line tension acting at the triple line. The various relevant geometrical parameters can be expressed as
| |
Aαβ = 2πRαβ2 × (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), θ),
| (8) |
| |
 | (9) |
| |
Ap = πRαβ2 × sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ,
| (10) |
and
| |
Lαβγ = 2πRαβ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. θ.
| (11) |
Moreover, the volumetric free energy change (ΔFV) is associated with the variation in the free energy related to the difference in pressure (Δp) between the formed droplet and the supersaturated vapour. ΔFV can be expressed as32
where
| |
Δp = nlkBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S, S,
| (13) |
and
| |
 | (14) |
where
n is the number of molecules within the cluster,
nl is the number density of the condensed phase, and
| |
 | (15) |
The dimensionless cluster volume (0 ≤ f ≤ 1) is a well-known parameter in the study of heterogeneous nucleation and widely known as potency factor or shape factor. The factor can also be given by eqn (14) irrespective of the geometric model of heterogeneous nucleation on the rigid planar, conical, or spherical substrates.9–19 However, the radius of curvature, Rαβ is replaced by the radius of the formed cluster or droplet when rigid substrate is considered. Besides, this dimensionless parameter becomes the parameter corresponding to the planar-substrate-mediated nucleation for ϕ = 0°. Then, the liquid substrate acts like a solid substrate for which f = 0.25 × (2 − 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + cos3
θ + cos3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). When line tension is not included in the thermodynamic formulation of heterogeneous nucleation, then f can also be considered as the ratio of the free energy barrier based on any geometric model19 of heterogeneous nucleation to the free energy barrier corresponding to homogeneous nucleation.
θ). When line tension is not included in the thermodynamic formulation of heterogeneous nucleation, then f can also be considered as the ratio of the free energy barrier based on any geometric model19 of heterogeneous nucleation to the free energy barrier corresponding to homogeneous nucleation.
The associated limiting conditions of the present physical model are shown in Fig. 2 using a θ − ϕ plane. For the stability of a three-phase system, the criterion θ + ϕ ≤ 180° must be satisfied. This restricts the occurrence of dropwise condensation on an immiscible liquid surface within the triangular zone XYZ. It is interesting to note that all the vertices as well as the sides of this triangle represent very unique cases of condensation on liquid substrates. For example, Case A (f = 0) occurring at vertex X (θ = 0°, ϕ = 0°) represents a thin film of condensate on the substrate, which further suggests the occurrence of the completely wetting transition. On the other hand, Case B (f = 1) occurring at vertex Y (θ = 180°, ϕ = 0°) suggests the occurrence of the drying transition. At vertex Z (θ = 0°, ϕ = 180°), Case C represents a hypothetical situation when the interfacial area between the droplet and the supersaturated vapour phase reduces to zero. This is unphysical as far as condensation is concerned and is also supported by the fact that f = −1 in this case. The side ZX ((θ = 0°, 0° < ϕ < 180°) represents Case D (f = 0) with planar interface between the droplet and he supersaturated vapour. A reverse configuration of the interface is represented by the Case E which occurs for the condition given by side XY (ϕ = 0°, 0° ≤ θ ≤ 180°). In this case, the liquid substrate behaves like a rigid substrate with f = 0.25 × (2 − 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + cos3
θ + cos3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) as discussed above.9,10 Finally, the side YZ (0° < θ < 180° and ϕ = 180∘ − θ) represents a typical Case F where the droplet is spherical with f = 1. Within XYZ one can expect lenticular droplet formation on a liquid substrate, which is the case of present investigation.
θ) as discussed above.9,10 Finally, the side YZ (0° < θ < 180° and ϕ = 180∘ − θ) represents a typical Case F where the droplet is spherical with f = 1. Within XYZ one can expect lenticular droplet formation on a liquid substrate, which is the case of present investigation.
 |
| | Fig. 2 Depiction of the various limiting conditions of the present geometric model based on the pseudo-contact angle (θ) and the submergence angle (ϕ). | |
From the kinetics of heterogeneous nucleation, as mentioned earlier, the molecular transport (schematically depicted in Fig. 3) can occur by two means: (i) the interfacial molecular transport through the vicinity of the droplet–vapour interface and (ii) the peripheral molecular transport in the neighbourhood of the triple line from the thin adsorbed layer on the substrate. So, the inward molecular flux per unit time or the forward rate can be given as33
 |
| | Fig. 3 Illustration of the mechanism of interfacial (subscript ‘surf’) and peripheral (subscript ‘line’) molecular transport to (i) or from (j) the cluster. | |
The contribution of the forward rate based on the interfacial molecular transport can be expressed as
where
α is the sticking coefficient and
υ is the molecular impingement rate.
9
The contribution of the forward rate based on the peripheral molecular transport is found to be
| |
 | (18) |
where
δ is the average jumping distance,
Eads is the adsorption energy, and
Edif is the diffusion energy.
33
The molecular impingement rate or the molecular flux per unit interfacial area and per unit time can be expressed as
| |
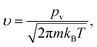 | (19) |
where
m is the molecular mass of the phase forming the cluster.
10
Moreover, the inward molecular flux to the droplet per unit time can be rewritten as
where the forward rate at saturated ambient condition can be evaluated as
| |
 | (21) |
and
| |
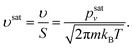 | (22) |
As mentioned earlier, the formed droplet can grow or shrink due to the thermal fluctuations. So, both the inward and the outward molecular flux per unit time is required for determining the net growth rate of the droplet.42 In the present paper, the Kinetic Nucleation Theory (KNT),43 initially developed by Katz, has been used to determine the outward molecular flux from the droplet per unit time.
From eqn (3), under saturated conditions (Jn = 0), one can easily obtain
where the kinetic factor can be expressed as
| |
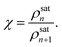 | (24) |
Besides, saturated (S = 1) cluster concentration becomes
| |
 | (25) |
So, the kinetic factor, χ can be approximated as
| |
 | (26) |
Therefore, differentiating ΔFH, as expressed in eqn (7), with respect to Rαβ, one gets
| |
 | (27) |
In this context, the condition for mechanical equilibrium is found to be44
| |
 | (28) |
and
| |
τ = Rαβ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(σαγ − σαβ θ(σαγ − σαβ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − σβγ θ − σβγ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ). ϕ).
| (29) |
After some elaborate algebraic manipulations using eqn (27)–(29), ∂ΔFH/∂Rαβ can be expressed as
| |
 | (30) |
From eqn (4), one can get
| |
 | (31) |
Using eqn (30) and (31), it can be shown that
| |
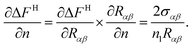 | (32) |
Using eqn (26), the kinetic factor is evaluated as
where Kelvin number (Ke) is given by
| |
 | (34) |
So, the outward molecular flux from the droplet per unit time or the backward rate can be expressed as
| |
j = isat![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ke). exp(Ke).
| (35) |
In the present thermokinetic formulation, the mean free path is found to be much larger than the molecular size of the droplet. Accordingly, the growth of the formed droplet can be safely assumed to be kinetically limited. Moreover, the growth rate can be approximated to be proportional to the difference between the forward and the backward rates of molecular transport and can be expressed as34
| |
 | (36) |
Finally, the growth rate (in terms of one of the curvature of the lenticular droplet, Rαβ) can be expressed as
| |
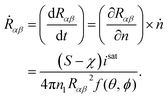 | (37) |
2.2 Model for inter-cluster nucleation
Apart from the growth rate, the steady-state nucleation rate is another major thermokinetic parameter for heterogeneous condensation. Theoretically, the rate of nucleation (J) is the number of clusters that appears per unit time, per unit area of the substrate. Now, using eqn (20) and (23), one can obtain| |
 | (38) |
Dividing both sides of eqn (3) by inρsatnSn, we get
| |
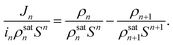 | (39) |
From eqn (39), one gets
| |
 | (40) |
where
N =
n + 1. Now, when
N → ∞,
| |
 | (41) |
Therefore, the rate of nucleation based on KNT under steady-state condition can be given by
| |
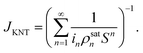 | (42) |
It can be shown that the rate of nucleation obtained from KNT (JKNT) is (1/S) times that obtained from CNT (JCNT). The factor (1/S) is known as Courtney factor.45 In the present analyses, JCNT is first formulated and JKNT is then determined using
| |
 | (43) |
Within the framework of CNT, the steady-state heterogeneous nucleation rate can be expressed as9
| |
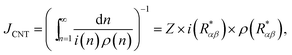 | (44) |
where
Z, the Zeldovich factor, is given by
10| |
 | (45) |
After differentiation from eqn (12), one can obtain
| |
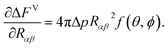 | (46) |
Using eqn (31) and (46), one gets
| |
 | (47) |
From eqn (32) and (47), we get
| |
 | (48) |
To obtain the critical parameters of heterogeneous condensation, the change in the Gibbs free energy with respect to the size (Rαβ or n) of the cluster needs to be maximized:
| |
 | (49) |
So, from eqn (48) and (49), one can obtain
| |
 | (50) |
and
Using eqn (31) and (48), one can have
| |
 | (52) |
which in turn satisfies the maximality condition.
Substituting the value of ∂2ΔG/∂n2 from eqn (52) in (45), the Zeldovich factor can be given by
| |
 | (53) |
where the corresponding Zeldovich factor for homogeneous nucleation can be evaluated as
| |
 | (54) |
So, the free energy barrier is found to be
| |
 | (55) |
where the corresponding energy barrier for homogeneous nucleation can be expressed as
9,10| |
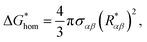 | (56) |
the associated line tension contribution to the energy barrier can be given by
| |
 | (57) |
τ* is the line tension under critical conditions, i.e. critical line tension, and it can be evaluated with the help of eqn (28) and (29). It may also be noted that for a zero value of line tension g becomes unambiguously zero as the two bracketed terms in the right hand side of the equation become equal.
Further, the non-dimensional parameter related to the three interfacial tension values ((σαγ − σβγ)/σαβ) is a constant and can be replaced by a cosine function,
| |
 | (58) |
It may appear that θY is a hypothetical angle, defined artificially. However, one may identify the striking similarity of the expression in eqn (58) with the corresponding expression for nucleation on a planar solid substrate in the absence of line tension. θY in that case is the Young's contact angle. In the present situation of dropwise condensation on an immiscible liquid surface, θY may be taken as the “equivalent Young's contact angle” which bears the same functional relationship with the three interfacial tensions. Our conjecture is further supported by the fact that for Case E (Fig. 2), without line tension the contact angle of the condensed phase simply reduces to θ = cos−1((σαγ − σβγ)/σαβ).
Considering geometric and peripheral contributions to the energy barrier according to eqn (55), the modified rate of nucleation can be expressed as
where the rate of nucleation, which sans the effect of line tension, can be given by
| |
J′ = J0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(ΔG*hom/kBT) × f(θ, ϕ)), exp(−(ΔG*hom/kBT) × f(θ, ϕ)),
| (60) |
the pre-exponential kinetic factor can be expressed as
| | |
J0 = nv2/3i(R*αβ)Z/S,
| (61) |
and the associated line tension contribution to the rate of nucleation,
i.e. peripheral factor, can be shown as
| | |
β = exp(−(ΔG*hom/kBT) × g(θY, θ, ϕ)).
| (62) |
So, the various thermokinetic parameters, e.g. the energy barrier, the growth rate, the nucleation rate etc. can be readily evaluated using the present formulation under steady state condition.
3. Results and discussion
3.1 Comparison of peripheral and interfacial molecular transport
Within the framework of the present analytical model, several thermokinetic parameters are readily evaluated considering heterogeneous condensation of lens-shaped droplets of a liquid from its supersaturated vapour on immiscible liquid surfaces. The theory developed in the preceding sections is generic in nature. However, to get a feel of the magnitude of the physical parameters, some important results are derived for condensation of water.
A quantitative comparison between the two routes of molecular transport, one through the vapour–liquid interface and other through the contact line, during dropwise condensation can be given by
| |
 | (63) |
where

(=
Rαβ/
R*αβ) is the non-dimensional droplet size. From
eqn (50) one can estimate,
R*αβ = 1.5 nm for the formation of water droplet from its supersaturated vapour. It can be found from
eqn (63) that
ψ is inversely proportional to the size of the cluster, which further suggests that the peripheral molecular transport will be large when the cluster is small. The contour plot in
Fig. 4 depicts the variation of
ψ with respect to
Rαβ and
θ. From
Fig. 4,
ψ is of the order of 10
2 for lower substrate wettability and when the radius of the droplet is more than the critical radius. For an over-critical-sized clusters, the increase in
Rαβ with a decrease in
θ lowers the influence of the peripheral molecular transport. Moreover, the peripheral molecular flux has a much higher value than the interfacial molecular flux for an under-critical-sized cluster and for the lower wettable substrates. Besides,
ψ is independent of the submergence angle and the equivalent Young's contact angle.
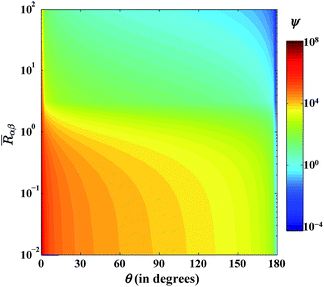 |
| | Fig. 4 Quantitative comparison of interfacial and peripheral molecular transport (ψ) with respect to the pseudo-contact angle (θ) and the dimensionless size of the cluster  T = 300 K, S = 2, nl = 3.342 × 1028 molecule per m3, σαβ = 7.174 × 10−2 J m−2, α = 1, δ = 3.2 × 10−10 m, Eads = 2.9 × 10−20 J per molecule, Edif = 2.9 × 10−21 J per molecule. T = 300 K, S = 2, nl = 3.342 × 1028 molecule per m3, σαβ = 7.174 × 10−2 J m−2, α = 1, δ = 3.2 × 10−10 m, Eads = 2.9 × 10−20 J per molecule, Edif = 2.9 × 10−21 J per molecule. | |
3.2 Growth rate
The cluster growth rate is the difference between the rates of the change of the molecular transport to and from the cluster respectively. The variation of the growth rate as a function of pseudo-contact angle and submergence angle is shown in the contour plot in Fig. 5 considering θ + ϕ ≤ 180°. From eqn (37), the rate of droplet growth can be considered to be proportional to the length of the triple contact line, because the peripheral component of the molecular transport is much greater than the interfacial component as mentioned earlier. The growth rate of the formed droplet increases with the decrease of the pseudo-contact angle and the submergence angle as can be seen from Fig. 5.
 |
| | Fig. 5 Variation of cluster growth rate as a function of the pseudo-contact angle (θ) and the submergence angle (ϕ). Rαβ = 2R*αβ, T = 300 K, S = 2, nl = 3.342 × 1028 molecule per m3, m = 2.982 × 10−26 kg per molecule, psatv = 3570 N m−2, σαβ = 7.174 × 10−2 J m−2, α = 1, δ = 3.2 × 10−10 m, Eads = 2.9 × 10−20 J per molecule, Edif = 2.9 × 10−21 J per molecule. | |
In the three-phase system with very low values of θ and ϕ (limiting Case A in Fig. 2), the growth rate of the cluster enhances drastically as the tendency of adsorption increases. On the other hand, an appreciable reduction in the growth rate can be observed for the higher values of θ and ϕ (limiting Cases B and F in Fig. 2). At this point, it may be mentioned that for most of the three-phase systems, 30° ≤ θ, ϕ ≤ 150°. Therefore, 30° ≤ θ, ϕ ≤ 150° is considered in all the subsequent contour plots.
3.3 Critical line tension
A quantitative estimation of the critical line tension can be made using the present thermokinetic formulation and it can be expressed as| |
 | (64) |
Very few literatures have reported the magnitude of the line tension for the three-phase lenticular system, it is found that the numerical value of the line tension is in the range of 10−11 to 10−9 N for rigid46–50 as well as liquid37 substrates and it can be both positive and negative as can be observed from eqn (64). From the present model, the value of line tension under critical condition is found to be of the order of 10−10 N as can be seen from Fig. 6 considering θ + ϕ ≤ 180°. So, the estimated value of the critical line tension is in conformity its range reported literature. From Fig. 6, it can also be observed that the negative value of line tension increases with the decrease of pseudo-contact angle and submergence angle, while its variation with equivalent Young's contact angle has reverse trend. Moreover, the negative line tension has the maximum value near the complete wetting transition (Case A in Fig. 2), while near the drying transition (Case B in Fig. 2), one may expect the minimum of positive line tension.
 |
| | Fig. 6 Variation of critical line tension (τ*) as a function of the pseudo-contact angle (θ), the submergence angle (ϕ), and the equivalent Young's contact angle (θY). T = 300 K, S = 2, nl = 3.342 × 1028 molecule per m3, m = 2.982 × 10−26 kg per molecule, psatv = 3570 N m−2, σαβ = 7.174 × 10−2 J m−2, α = 1, δ = 3.2 × 10−10 m, Eads = 2.9 × 10−20 J per molecule, Edif = 2.9 × 10−21 J per molecule. | |
3.4 Nucleation rate
In the present case, the nucleation rate can be defined as the number of the droplets formed per unit time and per unit area of the immiscible liquid substrate. From our thermokinetic model, triple contact line is found to have an appreciable effect on the rate of nucleation. In other words, the triple-line-associated peripheral molecular flux and line tension have a considerable influence on the kinetic pre-factor (J0) and the peripheral factor (β).
Now, before going to the generalized conditions, let us first consider various associated limiting cases of heterogeneous condensation on an immiscible liquid surface as shown in Fig. 2.
Liquid substrate can behave like a flat rigid substrate when ϕ = 0 (Cases A, B, and E). So, planar-substrate-induced condensation can be considered under these circumstances. Moreover, barrierless condensation (f = 0) is likely to occur for the Cases A and D while the Cases B and F are related to homogeneous condensation (f = 1) theoretically. The Case C is an unfeasible situation in case of dropwise condensation on an immiscible liquid surface as mentioned earlier.
Fig. 7 depicts the variation of the nucleation rate (J) as a function of pseudo-contact angle (θ), submergence angle (ϕ), and equivalent Young's contact angle (θY) considering θ + ϕ ≤ 180°. The nucleation rate is found to increase considerably for lower values of θ and ϕ and higher values of θY, suggesting an enhancement of condensation is possible under such conditions. Similarly, condensation hindrance is encountered for higher values of θ and ϕ and lower values of θY as illustrated in Fig. 7. Besides, the line tension has a significant influence on the steady-state nucleation rate as mentioned earlier and it can be easily conceivable from Fig. 6 and 7. As negative line tension reduces the energy barrier substantially, the steady-state nucleation rate enhances and promotes dropwise condensation with the decrease of θ and ϕ and the increase of θY. Similarly, for higher values of θ and ϕ and lower values of θY, suppression of dropwise condensation is likely for a positive line tension.
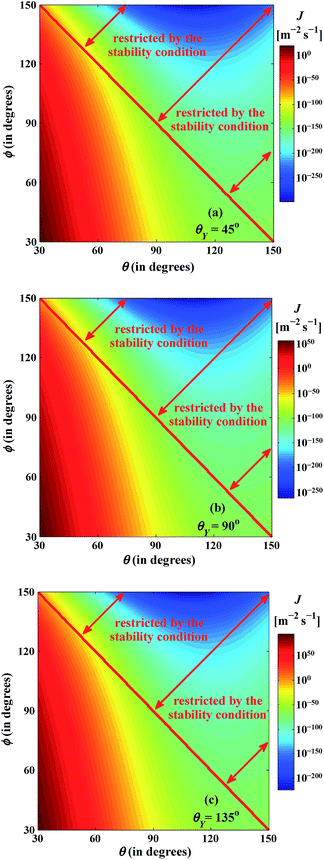 |
| | Fig. 7 Variation of nucleation rate (J) as a function of the pseudo-contact angle (θ), the submergence angle (ϕ), and the equivalent Young's contact angle (θY). T = 300 K, S = 2, nl = 3.342 × 1028 molecule per m3, m = 2.982 × 10−26 kg per molecule, psatv = 3570 N m−2, σαβ = 7.174 × 10−2 J m−2, α = 1, δ = 3.2 × 10−10 m, Eads = 2.9 × 10−20 J per molecule, Edif = 2.9 × 10−21 J per molecule. | |
3.5 Prediction of microscopic wetting behaviour of a three-fluid system
Along with the experimental data for the rate of nucleation, the present thermokinetic model, further, can be used to predict the microscopic wetting behavior of the three-phase lenticular system. Once the nucleation rate is known, one can determine the exact values of line tension and microscopic wetting angle from the CNT-based principles.31 However, this methodology is applied only to the spherical-seed-mediated nucleation. The present KNT-based thermokinetic model for droplet nucleation on an immiscible liquid surface can be extended to estimate nano-scale wetting behavior.
In principle, the rate of nucleation (J) can be obtained from the experimental study of nucleation. If the kinetic mechanism of heterogeneous nucleation is known quantitatively, then the value of the free energy barrier can be easily determined. However, it is found from most of the studies that the theoretical value of the free energy barrier based on CNT is of much higher order of magnitude than the experimental value for a given three-phase system. Interestingly, these theoretical analyses based on CNT neglect line tension; though it should not be ignored in the primitive period of the heterogeneous nucleation. Moreover, the exact value of line tension is not known a priori especially for a given three-phase lenticular system. Despite the debate pertaining to the absolute value of line tension, from most of the experiments as well as theory, its range has been obtained within 10−11 to 10−9 N (Section 3.3). This suggests an implicit method to estimate the magnitude and the sign of line tension by equating the expressions of the free energy barrier based on theory and experiment.
For the extension of the present formulation, the results of the experiment reporting dropwise condensation of supersaturated water vapors on n-dodecane51 substrate with S = 1.35 and T = 298 K is considered. Along with the various thermo-physical properties of water (both liquid and vapor phases),52 the presumed values of several kinetic parameters is used to evaluate the contact angle and the microscopic wetting angle. For the earlier mentioned supersaturated water vapor–water–dodecane three-phase system, the microscopic contact angles (θ and ϕ) can be obtained numerically by solving the following two-unknown equations, i.e.  and h = f(a, b) + g(a, b), where a = cos
and h = f(a, b) + g(a, b), where a = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, b = cos
θ, b = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,
ϕ,  and
and  It can further be mentioned that the dimensionless free energy barrier, h, is also a function of a and b, as it can be expressed as h = ln(J0/J)/(ΔG*hom/kBT). It can be shown that h is weakly dependent on a and b and can be considered as a constant with a value 0.0397 by substituting various macroscopic properties, i.e. a = 0.8454 and b = −0.6807 for the present case. Besides, the other input parameters for the present system are J = 4.91 × 109 m−2 s−1, σαβ = 0.072 J m−2, σβγ = 0.05246 J m−2, and σγα = 0.02513 J m−2.51 After solving the above-mentioned equations, the microscopic wetting angles are found to be θ = 46.72° and ϕ = 92.18°, while the macroscopic wetting angles are 32.28° and 132.9° respectively. It can be easily perceived how the triple line effects the phenomena of wetting as well as nucleation. Further, the line tension can be evaluated using eqn (29) as −5.67 × 10−9 N. The magnitude of line tension lies within the appreciable range estimated from the experimental evidence. Therefore, this heuristic technique of estimation of line tension by comparing theoretical formulation and experimental results justifies the present theoretical formulation and further supports the current conclusions obtained from the present thermokinetic analyses.
It can further be mentioned that the dimensionless free energy barrier, h, is also a function of a and b, as it can be expressed as h = ln(J0/J)/(ΔG*hom/kBT). It can be shown that h is weakly dependent on a and b and can be considered as a constant with a value 0.0397 by substituting various macroscopic properties, i.e. a = 0.8454 and b = −0.6807 for the present case. Besides, the other input parameters for the present system are J = 4.91 × 109 m−2 s−1, σαβ = 0.072 J m−2, σβγ = 0.05246 J m−2, and σγα = 0.02513 J m−2.51 After solving the above-mentioned equations, the microscopic wetting angles are found to be θ = 46.72° and ϕ = 92.18°, while the macroscopic wetting angles are 32.28° and 132.9° respectively. It can be easily perceived how the triple line effects the phenomena of wetting as well as nucleation. Further, the line tension can be evaluated using eqn (29) as −5.67 × 10−9 N. The magnitude of line tension lies within the appreciable range estimated from the experimental evidence. Therefore, this heuristic technique of estimation of line tension by comparing theoretical formulation and experimental results justifies the present theoretical formulation and further supports the current conclusions obtained from the present thermokinetic analyses.
4. Conclusions
By adopting a rigorous analytical treatment, a modified CNT-based thermokinetic model has been developed for the line-tension-associated condensation on immiscible liquid substrates considering both peripheral and interfacial molecular flux. Along with the free energy minimization principle, kinetic nucleation theory (KNT) has been espoused to evaluate various thermokinetic parameters for heterogeneous droplet nucleation of supersaturated water vapours in terms of pseudo-contact angle, submergence angle, and equivalent Young's contact angle. The wettability based on the equivalent Young's contact angle, defined in the present formulation, is basically associated with the planar-substrate-induced condensation in the absence of line tension. In the present study, this angle bears the same functional relationship with the three interfacial tensions, i.e. classical Young's equation.
Triple contact line has an extensive effect on both thermodynamics (line tension) and kinetics (peripheral molecular transport), because both the peripheral contribution to the free energy barrier and the peripheral molecular flux are proportional to the length of the triple contact line. As in the case of rigid-substrate-mediated nucleation, in the present case also, the thin adsorbed layer on liquid surface plays a vital role in the kinetic mechanism of nucleation. The peripheral molecular flux through the neighbourhood of the triple line from the thin adsorbed layer is about two orders of magnitude higher than the interfacial molecular flux at the droplet–vapour interface. The growth rate of the formed droplet increases when both the pseudo-contact angle and the submergence angle decreases. For lower values of the pseudo-contact angle and the submergence angle and higher values of the equivalent Young's contact angle, the line tension becomes negative and it diminishes the energy barrier subsequently. Under these conditions, the nucleation rate increases and further, enhances dropwise condensation. Similarly, the line tension becomes positive for higher values of the pseudo-contact angle and the submergence angle and lower values of the Young's contact angle and the enhancement in the energy barrier is possible under such conditions. Moreover, the rate of nucleation decreases and dropwise condensation inhibition can be feasible under such conditions. As a demonstration, the complete geometrical description of a condensing lenticular droplet of water on n-dodecane surface along with the line tension has been estimated from the derived theory using a heuristic technique of estimation by comparing theoretical formulation and experimental results of the rate of nucleation. So, the present extended thermokinetic model is supposed to illustrate a physical insight in the context of the study of the breath figures for the enhancement or the hindrance of heterogeneous condensation on immiscible liquid substrates.
In this regard, it can be mentioned that a thermokinetic model has been developed for droplet nucleation or first-order vapor-to-liquid phase transition in the present work. The principal driving factor for droplet nucleation is the supersaturation in the ambient. Similar thermokinetic model can also be developed for liquid-to-vapor phase transition. Only modification will be the different principal driving factor for different mechanisms of liquid-to-vapor phase transition, e.g. superheat in case of nucleate boiling and undersaturation in case of cavitation or evaporation. Therefore, the present thermokinetic model can serve as a guide in the development of generic physical model associated with bubble nucleation (nucleate boiling or cavitation) or droplet evaporation53–56 on a liquid surface.
Notes and references
- H. Ma, L. Kong, X. Guoa and J. Hao, RSC Adv., 2011, 1, 1187–1189 RSC.
- J. Blaschke, T. Lapp, B. Hof and J. Vollmer, Phys. Rev. Lett., 2012, 109, 068701 CrossRef PubMed.
- A. Zhang, H. Bai and L. Li, Chem. Rev., 2015, 115, 9801–9868 CrossRef CAS PubMed.
- R. N. Leach, F. Stevens, S. C. Langford and J. T. Dickinson, Langmuir, 2006, 22, 8864–8872 CrossRef CAS PubMed.
- P. G. Debenedetti, Nature, 2006, 441, 168–169 CrossRef CAS PubMed.
- M. Sokuler, G. K. Auernhammer, M. Roth, C. Liu, E. Bonacurrso and H. Butt, Langmuir, 2010, 26, 1544–1547 CrossRef CAS PubMed.
- D. Beysens, Atmos. Res., 1995, 39, 215–237 CrossRef CAS.
- F. Family and P. Meakin, Phys. Rev. Lett., 1988, 61, 428–432 CrossRef CAS PubMed.
- K. F. Kelton and A. L. Greer, Nucleation in condensed matter – applications in materials and biology, Elsevier, Amsterdam, 2010 Search PubMed.
- V. I. Kalikmanov, Nucleation Theory, Springer, Heidelberg, 2012 Search PubMed.
- W. Xu, Z. Lan, B. Peng, R. Wen and X. Ma, RSC Adv., 2014, 4, 31692–31699 RSC.
- N. Fletcher, J. Chem. Phys., 1958, 29, 572–576 CrossRef CAS.
- X. Y. Liu, J. Chem. Phys., 1999, 111, 1628–1635 CrossRef CAS.
- D. Xu and W. L. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 052101 CrossRef.
- M. Qian and J. Ma, J. Chem. Phys., 2009, 130, 214709 CrossRef PubMed.
- M. Qian and J. Ma, J. Cryst. Growth, 2012, 355, 73–77 CrossRef CAS.
- W. Xu, Z. Lan, B. Peng, R. Wen and X. Ma, RSC Adv., 2015, 5, 812–818 RSC.
- J. M. Campbell, F. C. Meldrum and H. K. Christenson, J. Phys. Chem. C, 2015, 119, 1164–1169 CAS.
- M. Yarom and A. Marmur, Langmuir, 2015, 31, 8852–8855 CrossRef CAS PubMed.
- M. Yarom and A. Marmur, Adv. Colloid Interface Sci., 2015, 22, 743–754 CrossRef PubMed.
- J. W. Gibbs, The Scientific Papers, Dover, New York, 1961, vol. 1 Search PubMed.
- L. Schimmele, M. Napiórkowski and S. Dietrich, J. Chem. Phys., 2007, 127, 164715 CrossRef CAS PubMed.
- D. Kashchiev, Nucleation, Butterworth-Heinemann, Oxford, 2000 Search PubMed.
- R. D. Gretz, J. Chem. Phys., 1966, 45, 3160–3161 CrossRef CAS.
- R. D. Gretz, Surf. Sci., 1966, 5, 239–251 CrossRef CAS.
- G. Navascues and P. Tarazona, J. Chem. Phys., 1981, 75, 2441–2446 CrossRef CAS.
- A. L. Greer, Scr. Mater., 2010, 62, 899–903 CrossRef CAS.
- S. K. Singha, P. K. Das and B. Maiti, J. Chem. Phys., 2015, 142, 104706 CrossRef PubMed.
- A. D. Scheludko, J. Colloid Interface Sci., 1985, 104, 471–476 CrossRef.
- M. Lazaridis, J. Colloid Interface Sci., 1993, 155, 386–391 CrossRef CAS.
- A. I. Hienola, P. M. Winkler, P. E. Wagner, H. Vehkamäki, A. Lauri, A. Napari and M. Kulmala, J. Chem. Phys., 2007, 126, 094705 CrossRef CAS PubMed.
- M. Iwamatsu, Langmuir, 2015, 31, 3861–3868 CrossRef CAS PubMed.
- S. K. Singha, P. K. Das and B. Maiti, J. Chem. Phys., 2015, 143, 204703 CrossRef PubMed.
- X. Luo, Y. Fan, F. Qin, H. Gui and J. Liu, J. Chem. Phys., 2014, 140, 024708 CrossRef PubMed.
- Y. Fan, F. Qin, X. Luo, J. Zhang, J. Wang, H. Gui and J. Liu, J. Aerosol Sci., 2015, 87, 17–27 CrossRef CAS.
- A. Steyer, P. Guenoun, D. Beysens and C. M. Knobler, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 1086–1090 CrossRef.
- A. Aleksandrov, B. Toshev and A. Sheludko, Langmuir, 1991, 7, 3211–3215 CrossRef CAS.
- A. A. Nepomnyashchy, A. A. Golovin, A. E. Tikhomirova and V. A. Volpert, Phys. Rev. E, 2006, 74, 021605 CrossRef CAS PubMed.
- F. Eslami and J. A. W. Elliott, J. Phys. Chem. B, 2011, 115, 10646–10653 CrossRef CAS PubMed.
- L. Yang, X. Quan, P. Cheng and Z. Cheng, Int. J. Heat Mass Transfer, 2014, 78, 460–467 CrossRef.
- A. Dillmann and G. E. A. Meier, J. Chem. Phys., 1991, 94, 3872 CrossRef CAS.
- D. Turnbull and B. Vonnegut, Ind. Eng. Chem., 1952, 44, 1292–1298 CrossRef CAS.
- J. L. Katz and H. Wiedersich, J. Colloid Interface Sci., 1977, 61, 351–355 CrossRef CAS.
- J. S. Rowlinson and B. Widom, Molecular Theory of Capillarity, Dover, New York, 1989 Search PubMed.
- W. G. Courtney, J. Chem. Phys., 1962, 36, 2009–2017 CrossRef CAS.
- T. Getta and S. Dietrich, Phys. Rev. E, 1998, 57, 655–671 CrossRef CAS.
- T. Pompe and S. Herminghaus, Phys. Rev. Lett., 2000, 85, 1930–1933 CrossRef CAS PubMed.
- J. Y. Wang, S. Betelu and B. M. Law, Phys. Rev. E, 2001, 63, 031601 CrossRef CAS PubMed.
- A. Checco, P. Guenoun and J. Daillant, Phys. Rev. Lett., 2003, 91, 186101 CrossRef PubMed.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739–805 CrossRef CAS.
- A. D. Alexandrov and M. Z. Avramov, Colloid Polym. Sci., 1993, 271, 162–172 CAS.
- http://www.webbook.nist.gov/chemistry/fluid/ for Thermophysical Properties of Fluid Systems.
- M. E. R. Shanahan and K. Sefiane, Kinetics of triple line motion during evaporation, in Contact Angle, Wettability and Adhesion, ed. K. L. Mittal, CRC Press, 2009, vol. 6, pp. 19–32 Search PubMed.
- A. Cazabat and G. Guénab, Soft Matter, 2010, 6, 2591–2612 RSC.
- H. Y. Erbil, Adv. Colloid Interface Sci., 2012, 170, 67–86 CrossRef CAS PubMed.
- N. M. Kovalchuka, A. Trybalaa and V. M. Starov, Curr. Opin. Colloid Interface Sci., 2014, 19, 336–342 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  ,
Prasanta Kumar Das* and
Biswajit Maiti
,
Prasanta Kumar Das* and
Biswajit Maiti
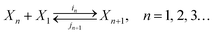


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and Rβγ (=r/sin
θ) and Rβγ (=r/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) are the associated radii of curvature needed to describe the lenticular droplet.
ϕ) are the associated radii of curvature needed to describe the lenticular droplet.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ),
θ),

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,
θ,
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ.
θ.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S,
S,


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + cos3
θ + cos3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). When line tension is not included in the thermodynamic formulation of heterogeneous nucleation, then f can also be considered as the ratio of the free energy barrier based on any geometric model19 of heterogeneous nucleation to the free energy barrier corresponding to homogeneous nucleation.
θ). When line tension is not included in the thermodynamic formulation of heterogeneous nucleation, then f can also be considered as the ratio of the free energy barrier based on any geometric model19 of heterogeneous nucleation to the free energy barrier corresponding to homogeneous nucleation.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + cos3
θ + cos3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) as discussed above.9,10 Finally, the side YZ (0° < θ < 180° and ϕ = 180∘ − θ) represents a typical Case F where the droplet is spherical with f = 1. Within XYZ one can expect lenticular droplet formation on a liquid substrate, which is the case of present investigation.
θ) as discussed above.9,10 Finally, the side YZ (0° < θ < 180° and ϕ = 180∘ − θ) represents a typical Case F where the droplet is spherical with f = 1. Within XYZ one can expect lenticular droplet formation on a liquid substrate, which is the case of present investigation.


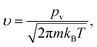

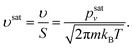
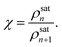




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(σαγ − σαβ
θ(σαγ − σαβ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − σβγ
θ − σβγ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ).
ϕ).


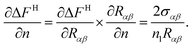

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ke).
exp(Ke).

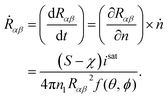

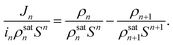


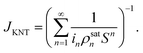

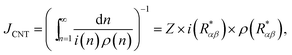

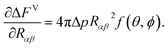








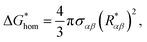


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−(ΔG*hom/kBT) × f(θ, ϕ)),
exp(−(ΔG*hom/kBT) × f(θ, ϕ)),

 (=Rαβ/R*αβ) is the non-dimensional droplet size. From eqn (50) one can estimate, R*αβ = 1.5 nm for the formation of water droplet from its supersaturated vapour. It can be found from eqn (63) that ψ is inversely proportional to the size of the cluster, which further suggests that the peripheral molecular transport will be large when the cluster is small. The contour plot in Fig. 4 depicts the variation of ψ with respect to Rαβ and θ. From Fig. 4, ψ is of the order of 102 for lower substrate wettability and when the radius of the droplet is more than the critical radius. For an over-critical-sized clusters, the increase in Rαβ with a decrease in θ lowers the influence of the peripheral molecular transport. Moreover, the peripheral molecular flux has a much higher value than the interfacial molecular flux for an under-critical-sized cluster and for the lower wettable substrates. Besides, ψ is independent of the submergence angle and the equivalent Young's contact angle.
(=Rαβ/R*αβ) is the non-dimensional droplet size. From eqn (50) one can estimate, R*αβ = 1.5 nm for the formation of water droplet from its supersaturated vapour. It can be found from eqn (63) that ψ is inversely proportional to the size of the cluster, which further suggests that the peripheral molecular transport will be large when the cluster is small. The contour plot in Fig. 4 depicts the variation of ψ with respect to Rαβ and θ. From Fig. 4, ψ is of the order of 102 for lower substrate wettability and when the radius of the droplet is more than the critical radius. For an over-critical-sized clusters, the increase in Rαβ with a decrease in θ lowers the influence of the peripheral molecular transport. Moreover, the peripheral molecular flux has a much higher value than the interfacial molecular flux for an under-critical-sized cluster and for the lower wettable substrates. Besides, ψ is independent of the submergence angle and the equivalent Young's contact angle.

 and h = f(a, b) + g(a, b), where a = cos
and h = f(a, b) + g(a, b), where a = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, b = cos
θ, b = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,
ϕ,  and
and  It can further be mentioned that the dimensionless free energy barrier, h, is also a function of a and b, as it can be expressed as h = ln(J0/J)/(ΔG*hom/kBT). It can be shown that h is weakly dependent on a and b and can be considered as a constant with a value 0.0397 by substituting various macroscopic properties, i.e. a = 0.8454 and b = −0.6807 for the present case. Besides, the other input parameters for the present system are J = 4.91 × 109 m−2 s−1, σαβ = 0.072 J m−2, σβγ = 0.05246 J m−2, and σγα = 0.02513 J m−2.51 After solving the above-mentioned equations, the microscopic wetting angles are found to be θ = 46.72° and ϕ = 92.18°, while the macroscopic wetting angles are 32.28° and 132.9° respectively. It can be easily perceived how the triple line effects the phenomena of wetting as well as nucleation. Further, the line tension can be evaluated using eqn (29) as −5.67 × 10−9 N. The magnitude of line tension lies within the appreciable range estimated from the experimental evidence. Therefore, this heuristic technique of estimation of line tension by comparing theoretical formulation and experimental results justifies the present theoretical formulation and further supports the current conclusions obtained from the present thermokinetic analyses.
It can further be mentioned that the dimensionless free energy barrier, h, is also a function of a and b, as it can be expressed as h = ln(J0/J)/(ΔG*hom/kBT). It can be shown that h is weakly dependent on a and b and can be considered as a constant with a value 0.0397 by substituting various macroscopic properties, i.e. a = 0.8454 and b = −0.6807 for the present case. Besides, the other input parameters for the present system are J = 4.91 × 109 m−2 s−1, σαβ = 0.072 J m−2, σβγ = 0.05246 J m−2, and σγα = 0.02513 J m−2.51 After solving the above-mentioned equations, the microscopic wetting angles are found to be θ = 46.72° and ϕ = 92.18°, while the macroscopic wetting angles are 32.28° and 132.9° respectively. It can be easily perceived how the triple line effects the phenomena of wetting as well as nucleation. Further, the line tension can be evaluated using eqn (29) as −5.67 × 10−9 N. The magnitude of line tension lies within the appreciable range estimated from the experimental evidence. Therefore, this heuristic technique of estimation of line tension by comparing theoretical formulation and experimental results justifies the present theoretical formulation and further supports the current conclusions obtained from the present thermokinetic analyses.




