Characterization of tungsten monomeric oxide species supported on hydroxylated silica; a DFT study
Hazar Guesmia,
Robert Grybos*b,
Jarosław Handzlikc and
Frederik Tielens*d
aCNRS-UM2-ENSCM-UM1, UMR 5253, Institut Charles Gerhardt Montpellier, Ecole Nationale Supérieure de Chimie de Montpellier, 8 rue de l'Ecole Normale, 34296 Montpellier, France
bJerzy Haber Institute of Catalysis and Surface Chemistry, Niezapominajek 8, Kraków, Poland
cFaculty of Chemical Engineering and Technology, Cracow University of Technology, ul. Warszawska 24, 31-155 Kraków, Poland
dSorbonne Université, UPMC Univ Paris 06, UMR 7574, Laboratoire Chimie de la Matière Condensée, Collège de France, 11 place Marcelin Berthelot, 75231 Paris Cedex 05, France. E-mail: frederik.tielens@upmc.fr
First published on 13th April 2016
Abstract
A DFT based characterization of tungsten oxide supported on amorphous hydroxylated silica is presented. The different molecular organizations are investigated on the surface topology and tungsten oxygen coordination. The presence of mono- and di-grafted species is discussed and rationalized, using an atomistic thermodynamic approach. The presence of W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups are preferred over W–OH groups and the grafting coordination is dominated by the degree of hydration of the silica surface. At room temperature di-oxo digrafted and mono-oxo-tetragrafted species are in competition regulated by the ambient degree of hydration which also affects the silanol density of the silica support. A comparison between tungsten and the other group VI elements confirms a greater chemical difference with Cr than with Mo.
O groups are preferred over W–OH groups and the grafting coordination is dominated by the degree of hydration of the silica surface. At room temperature di-oxo digrafted and mono-oxo-tetragrafted species are in competition regulated by the ambient degree of hydration which also affects the silanol density of the silica support. A comparison between tungsten and the other group VI elements confirms a greater chemical difference with Cr than with Mo.
1. Introduction
Supported transition metal oxides are among the most important catalytic systems used today.1 The most common supports are silicate based materials (in particular silica and zeolites), alumina and titania, not only because of their specific physico-chemical properties but also due to their abundance and relatively low price. In particular, a wide range of catalytically active transition metal oxides is supported on amorphous silica.2,3Tungsten oxide supported on silica is mainly used as an industrial catalyst for olefin metathesis.4,5 Originally, it was used to transform propene into ethene and butene in the triolefin Phillips process.6 At present, since the world demand for propene is rapidly increasing,7 tungsten oxide catalyzes a reverse reaction. Other uses include selective oxidation of, among others, methane,8–10 styrene,11 propylene12 and methanol.13 It is also used for photocatalytic water splitting.14
The structure and character of WOx/silica catalyst has been studied by a wide range of experimental techniques.3,15,16 Also, models of isolated oxo-tungsten species were synthesized and characterized.17 A combined DFT-NMR study found that the terminal W–OH groups are weakly acidic and very stable.18 On high surface area catalysts, a well-dispersed and reduction-resistant layer of tungsten oxide covers the active sites of silica surface.8
The catalytic activity is generally attributed to the well-dispersed surface forms of tungsten oxide rather than the crystalline WO3 phase.11,13,14,19–25 At low coverage, the surface sites are usually found to be isolated tungsten monomers, either mono-oxo3,26 or di-oxo,3,26 or dimers27 and oligomers,28 at least under dehydrated conditions. Discrimination between different types of monomers is not trivial, however. Vibrational spectrum obtained by in situ Raman spectroscopy shows dominant band in the range 975–991 cm−1 associated with W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration.3,15,26,28–30
O stretching vibration.3,15,26,28–30
It was at first ascribed to the mono-oxo form due to lack of the asymmetric component, characteristic for the di-oxo form.15,29 However, when a weak signal at 968 cm−1 was discovered, it was identified as originating from the asymmetric stretching vibration of the di-oxo monomer and the dominant band was re-interpreted as a proof that the tungsten oxide monomers on the silica surface are mainly di-oxo.3,26 Existence of the mono-oxo form was tied to another band at 1014–1015 cm−1.3,26,28
In one case the same band was interpreted as originating from polymeric WO5/WO6 forms.30 Co-existence of mono-oxo and di-oxo forms on the surface was confirmed by 18O–16O isotope exchange experiments.3 Comparison of Raman peak intensities show that the mono-oxo/di-oxo ratio depends on temperature and at higher temperatures the di-oxo form dominates.26
To the best of our knowledge, no theoretical ab initio studies on realistic tungsten oxide forms on amorphous silica support are available. To fill this gap, we have performed an extensive density functional theory (DFT) study to find the most stable structures of isolated monomeric tungsten oxide species and to characterize them by vibrational analysis.
2. Methodology
Models and methods used in this study are consistent with our previous reports on vanadium,31 niobium,32 chromium33,34 and molybdenum,35 allowing for direct comparison of the results.2.1. Computational details
All calculations are performed using ab initio plane-wave pseudopotential approach as implemented in VASP.36,37 The Perdew–Burke–Ernzerhof (PBE) functional38,39 has been chosen to perform the periodic DFT calculations. The valence electrons are treated explicitly and their interactions with the ionic cores are described by the Projector Augmented-Wave method (PAW),37,40 which allows to use a low energy cut off equal to 400 eV for the plane-wave basis. The Gamma point is used in the Brillouin-zone integration. The positions of all the atoms in the super cell are relaxed until the total energy differences decrease below 10−4 eV (forces acting on atoms fall below 0.01 eV Å−1).Vibrational spectra have been calculated for selected surface species within the harmonic approximation. Only the tungsten center and its first and second neighbors (O–Si and OH groups) are considered in the Hessian matrix. This matrix is computed by the finite difference method followed by a diagonalization procedure. The eigenvalues of the resulting matrix lead to the frequency values. The assignment of the vibrational modes is done by inspection of the corresponding eigenvectors. A scaling factor of 0.9659 was used according to Halls et al.41
2.2. Surface model description
A model of hydrated SiO2 slab was used, as described in the original paper42 and in our vanadium oxide/SiO2,31 niobium oxide/SiO2,32 chromium oxide/SiO2,34 molybdenum oxide/SiO2 (ref. 35) and gold/SiO2 (ref. 43 and 44) studies, and also in the studies of hydrated SiO2 surfaces.45,46 The silica model reproduces experimentally established ring size distribution, Si–O–Si and O–Si–O angles, overall density of silanol groups and their partition into several types (isolated, associated, geminate) (see Fig. 1). | ||
| Fig. 1 Side view of the unit cell of the amorphous silica surface model on which di-oxo, W(VI) oxide cluster is grafted (W atom in blue). | ||
The supercell dimensions are 12.77 Å × 17.64 Å × 25.17 Å and it contains 27 silicon atoms. Without water, the formula can be written as pure silicon oxide – (SiO2)27. In the presence of water, the surface of silicon oxide becomes hydroxylated. Silanol OH groups are formed through hydrolysis of the siloxane Si–O–Si bridges according to the reaction:
| –(Si–O–Si)– + H2O → –Si–OH, HO–Si– | (1) |
Therefore the hydroxylated surface of amorphous silica can by represented by a formula (SiO2)x(H2O)y, where two surface silanol groups are formed for each H2O molecule. Specifically, the supercell of our model has an overall formula Si27O67H26 which can be written as (SiO2)27(H2O)13.
2.3. Monomer grafting
Synthesis of a grafted W(VI)–SiO2 catalyst is presented in the literature as a series of steps:3,47–49 impregnation with the precursor (in aqueous or non-aqueous solution) at room temperature, low-temperature drying, overnight at 800 K, and high-temperature calcination, several hours at 800 K.Thus, it is empirically shown that a high temperature and dehydration conditions are necessary to obtain the multi-grafted tungsten oxide species.
The catalyst precursor is modeled by a WO2(OH)2 molecule. One such species is added to the silica unit cell resulting in a coverage of 0.44 monomers per nm2, a typical coverage found in working catalysts.50
Grafting of WO2(OH)2 molecule can result in several different structures with different number of: (i) tungstenyl W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O oxygen atoms, (ii) –OH hydroxyl groups and (iii) W–O–Si bridges to the surface. Theoretically up to four silanols may be involved in the reaction yielding different modes of grafting: mono, di, tri and tetra. Structures involving different silanol types: isolated (Si–OH), vicinal (HO–Si–O–Si–OH), geminate (HO–Si–OH) and non-vicinal (two Si–OH groups not directly connected) on the surface were considered. In every case, however, the oxidation state of tungsten remains +VI. Creation of the W–O–Si link can be represented by a following simplified reaction:
O oxygen atoms, (ii) –OH hydroxyl groups and (iii) W–O–Si bridges to the surface. Theoretically up to four silanols may be involved in the reaction yielding different modes of grafting: mono, di, tri and tetra. Structures involving different silanol types: isolated (Si–OH), vicinal (HO–Si–O–Si–OH), geminate (HO–Si–OH) and non-vicinal (two Si–OH groups not directly connected) on the surface were considered. In every case, however, the oxidation state of tungsten remains +VI. Creation of the W–O–Si link can be represented by a following simplified reaction:
| –Si–OH, HO–Si– + W → –Si–OH, W–O–Si– + H | (2) |
Thermodynamic analysis, described below, is used to explore the stability of various monomer surface forms under varying conditions. However, in order to probe and compare the grafting sites present on the amorphous silica surface, a complete and systematic series of tungsten monomer models are investigated (see Fig. 2), in analogy to chromium and molybdenum.33–35
 | ||
| Fig. 2 Different geometries as a function of its hydration state for the supported W oxide grafted on amorphous silica. | ||
2.4. Thermodynamic analysis
The surface of a heterogeneous catalyst is in direct contact with the gas phase. Therefore its surface structure can change dynamically with varying conditions – temperature and partial pressures of constituents of the gas phase. In our study we considered an isolated tungsten(VI) monomer with varying number of tungstenyl oxygen (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and hydroxyl (–OH) groups. Tungsten is at its highest oxidation state due to calcination procedure. It is convenient to describe monomers with varying number of
O) and hydroxyl (–OH) groups. Tungsten is at its highest oxidation state due to calcination procedure. It is convenient to describe monomers with varying number of ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and –OH groups in terms of the number of anchoring (grafting) linkages it creates with the surface in order to retain its formal oxidation state.
O and –OH groups in terms of the number of anchoring (grafting) linkages it creates with the surface in order to retain its formal oxidation state.
In order to establish the stable tungsten surface monomer under different conditions an atomistic thermodynamic analysis has to be performed. Possible forms of mono- (A, B, C), di- (D, E, F), tri- (G, H) and tetra-grafted (I) W(VI) monomer on the surface are presented in Fig. 2. To take into account deviations in surface composition and the presence of gas phase, one introduces appropriate chemical potentials to calculate an approximation of the Gibbs free-surface energy. Assuming that the surface is in thermodynamic equilibrium with the gas phases, the chemical potentials are related to a given temperature T and pressure p. This procedure enables to extend the 0 K and zero pressure DFT results to experimentally relevant environments, thereby bridging the gap between ultra-high vacuum like conditions, and temperatures and gas phase pressures that are applied in realistic catalytic conditions. The grafting process can be described as a reaction between the surface and the precursor, with consumption or liberation of water. Appropriate equations for each model is given below (eqn (3)):
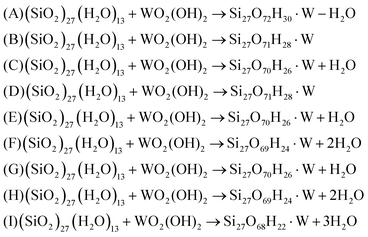 | (3) |
The W(VI)/silica system is considered to be in contact with a gaseous water reservoir. Starting from a calculated electronic energy, the free energy of water/W(VI)/silica interface under known thermodynamic conditions may be estimated following the approximations used by Digne et al.,52 as originating from Kaxiras et al.53 and Qian et al.54 Main assumptions are that there is no variation of the chemical potential of the surface upon adsorption and that the gas phase as a perfect gas. In the proposed scheme, the free energy of water (including the ZPE correction) in the gas phase is:
ΔG(H2O) = E(H2O) + ((ΔHG − TΔSG(T)) + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(p/p°)) ln(p/p°))
| (4) |
Using the above mentioned formalism, the approximated free energy of the grafting reactions for the formation of the mono-, di-, tri and tetra-grafted W(VI) monomers at equilibrium conditions, can be expressed as (eqn (5)):
 | (5) |
Only the ΔG of water depends on T and p, therefore energies of models B and D will not depend on the temperature. In principle, increasing temperature will tend to remove water from the monomer and at high temperatures model I should be most stable. Note, however, that it requires four links to the surface, i.e. four hydroxyl groups in a specific arrangement. Such sites are much less common on the surface than the ones for mono- or bi-grafted monomers. Therefore, in the real system, the amount of tetra-grafted monomers will be less than predicted from thermodynamic analysis.
In this approach, we consider that the energies of the different types of grafting transitions are independent of the degree of hydration of the silica surface. It is known experimentally that silanols are stable at silica surfaces until 673 K. Above this temperature, silanols begin to condensate into siloxane bridges.56 Thus, our model with 5.8 OH nm−2 corresponding to conditions of a hydroxylated surface, remains valid until the temperature of 673 K.
3. Results
3.1. Monomers at surface sites
Similarly to Mo,35 the W center is surrounded by four oxygen atoms in a slightly distorted tetrahedral symmetry, unless nearby surface OH groups are close enough to create a W–O bridge. If the structure is flexible enough, the monomer can attain a penta coordinated trigonal bi-pyramidal symmetry. Such structures will be discussed after the more common tetrahedron case.In Table 1 we present grafting energies for all possible grafting possibilities (germinal (g), vicinal (v), and non-vicinal (n) on the silica slab considered for structure F) – negative values indicate thermodynamically stable structures. The different grafting sites are shown in Fig. 3 in ref. 35. Even for thermodynamically unstable structures, the monomer stays at the surface, due to a kinetic barrier. When two water molecules are available, monomers can detach from the surface as WO2(OH)2 and leave two silanol groups behind. When only one H2O is present, the monomer leaves as WO3. If we allow for the possibility of creating Si–O–Si siloxane bridges, then two more situations can be envisioned: (i) with one water present the monomer leaves as WO2(OH)2, (ii) with no water, the monomer leaves as WO3.
| WO2(OH)2 | WO3 | |
|---|---|---|
| Geminal | ||
| g1 | 1.79 | −1.65 |
| g2 | 1.72 | −1.72 |
| g3 | 1.50 | −1.93 |
| g4 | 1.79 | −1.63 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Vicinal | ||
| v1 | 0.64 | −2.81 |
| v2 | 0.41 | −3.04 |
| v3 | 0.71 | −2.73 |
| v4 | −0.03 | −3.50 |
| v5 | 0.38 | −3.07 |
| v6 | 0.49 | −2.97 |
| v7 | 0.22 | −3.23 |
| v8 | 0.85 | −2.61 |
| v9 | 0.31 | −3.18 |
| v10 | 0.38 | −3.07 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Non-vicinal | ||
| n1 | −0.25 | −3.72 |
| n2 | −0.11 | −3.58 |
| n3 | −0.12 | −3.58 |
| n4 | −0.05 | −3.51 |
| n5 | 0.05 | −3.41 |
| n6 | 0.26 | −3.20 |
| n7 | −0.02 | −3.48 |
| n8 | 0.32 | −3.13 |
| n9 | 0.00 | −3.45 |
| n10 | −0.14 | −3.60 |
| n11 | 0.03 | −3.44 |
| n12 | 0.09 | −3.38 |
| n13 | −0.20 | −3.66 |
For anchoring, geminate sites are energetically disfavored due to their high rigidity. In abundance of water, the monomers are barely stable at the surface. The adsorption energy is between 1.50 and 1.79 eV indicating an unstable structure. Vicinal sites are more flexible and can accommodate a W monomer with adsorption energies between −0.03 and 0.85 eV. Monomers are more stable on the flexible non-vicinal sites – all adsorption energies are below 0.32 eV. Few structures show stable adsorption, although only barely stable as the best adsorption energy is only −0.25 eV. It seems that structures with more hydrogen bonds are more stable, but no clear correlation could be found.
As noted above, without large excess of water vapor available, anchored monomers can only detach from the grafting sites as WO3 species. This reaction still requires one water molecule to recreate two surface hydroxyl groups. The monomer stability with respect to gaseous WO3 in the presence of traces of water is very high – energies required to remove a monomer from the surface range from 1.63 to over 3.72 eV. Without water, WO3 can still be removed if the anchoring Si centers are close enough to create a siloxane bridge. However, this reaction pathway is expected to require even more energy.
The geometry of the monomer does not vary much between different grafting sites (see Table 2). The tungstenyl W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds have lengths between 1.71 and 1.74 Å, depending on the number of hydrogen bonds between surface and the monomer. If no such hydrogen bonds are present, both W
O bonds have lengths between 1.71 and 1.74 Å, depending on the number of hydrogen bonds between surface and the monomer. If no such hydrogen bonds are present, both W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds are 1.74 Å. The formation of hydrogen bonds with one tungstenyl oxygen atom has a weaker effect on the bond length than the coordination of the W atom, which is in line with the idea that the W
O bonds are 1.74 Å. The formation of hydrogen bonds with one tungstenyl oxygen atom has a weaker effect on the bond length than the coordination of the W atom, which is in line with the idea that the W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dipole moment is smaller than for the two other group VI elements. This decrease in iconicity was already observed for the group V elements.55,57 The angle between W
O dipole moment is smaller than for the two other group VI elements. This decrease in iconicity was already observed for the group V elements.55,57 The angle between W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds is usually 108–109° with some deviations induced by hydrogen bonds.
O bonds is usually 108–109° with some deviations induced by hydrogen bonds.
| Model | d(W–OH) | d(W–OSi) | d(W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
A(OWO) |
|---|---|---|---|---|
| A | 1.914 | 1.921 | ||
| 1.928 | ||||
| 1.928 | ||||
| 1.937 | ||||
| 1.99 | ||||
| B | 1.899 | 1.961 | 1.751 | |
| 1.908 | ||||
| 1.917 | ||||
| C | 1.907 | 1.882 | 1.734 | 108.23 |
| 1.739 | ||||
| D | 1.889 | 1.934 | ||
| 1.903 | 1.942 | |||
| 1.961 | ||||
| 1.965 | ||||
| E | 1.943 | 1.933 | 1.722 | |
| 1.912 | 1.912 | |||
| F | 1.890 | 1.737 | ||
| 1.893 | 1.738 | 108.19 | ||
| G | 1.849 | 1.938 | ||
| 1.934 | 1.938 | |||
| 1.946 | 2.030 | |||
| H | 1.915 | 1.890 | 1.733 | |
| 1.904 | ||||
| 2.052 | ||||
| I | 1.916 | 1.715 | ||
| 1.929 | ||||
| 1.954 | ||||
| 1.973 |
The lengths of W–OSi bonds anchoring the monomer to the surface range from 1.84 to 2.05 Å, but for the di-oxo digrafted situation a W–OSi bond distance of 1.89 Å is calculated. The angle between those bonds vary between 128° and 137° (up to 155° in the B-structure). The W coordination is 4 in structures C and F (see OWO angles in Table 2), 5 in structures B, D, E, H and I, and 6 in structures A and G.
3.2. Thermodynamic stability
Fig. 2 shows mono- (structure: A, B, C), di- (structure: D, E, F), tri- (structure: G, H) and tetra-grafted (structure: I) W-oxide species on silica support. Note that the tri- and tetra-grafted species need the presence of three and four neighboring silanol sites, respectively, in a specific arrangement which is not as common as mono- and di-grafting sites, and thus depends on the silanol density at the silica surface. Additionally, monomers are stabilized by creation of hydrogen bonds with surface silanols.Grafting of tungsten oxide species on amorphous silica surface has a relatively small effect on the silica framework, and is comparable with what has been found in our previous study on the grafting of oxides on silica.31–35
The hydrogen bond network, on the other hand is heavily affected by grafting. Depending on their local density, silanols on a clean surface interact with their neighbors forming an H-bond network. The grafting process perturbs the local H-bond network in two ways: (i) surface hydroxyl groups are removed upon grafting; (ii) the W oxide units might also form hydrogen bonds with the silica support. In the models studied, the W–OH groups bind to surface silanols stabilizing the structure while the W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups do not form hydrogen bonds.
O groups do not form hydrogen bonds.
Considering the reaction energy ΔEreact of Table 3 calculated according to the eqn (5) for the best grafting modes as a function of hydration rate. For W oxide values of −2.71, −2.46, −2.35, −1.49 and −1.56 eV for +1, 0, −1, −2, and −3 water molecules are obtained, corresponding to the models A, D, C, F, and I, respectively. All reaction energies are exothermic for grafting WO2(OH)2, indicating that the adsorption of the MO2(OH)2 with M = Cr, Mo, or W, is favored for W compared with Mo and Cr, with respect to the initial situation (hydroxylated silica and H2MO4 in the gas phase). Interesting to note is that following this reaction scheme the MO2(OH)2 transition metal precursor reacts more favorably when going down the column of the group VI elements (Cr to W) in the periodic Table.
| Modela | ΔEreact | ΔEreact35 | ΔEreact34 |
|---|---|---|---|
| Group VI metal | W | Mo | Cr |
| a See Fig. 2. | |||
| A: surface + MO4H2 + 1H2O | −2.71 | −0.49 | −0.26 |
| B: surface + MO4H2 | −2.18 | −0.26 | −0.89 |
| C: surface + MO4H2–1H2O | −2.35 | −0.76 | −2.09 |
| D: surface + MO4H2 | −2.46 | −0.18 | 0.13 |
| E: surface + MO4H2–1H2O | −2.34 | −0.39 | −0.80 |
| F: surface + MO4H2–2H2O | −1.49 | 0.02 | −1.33 |
| G: surface + MO4H2–1H2O | −1.26 | 1.04 | 1.72 |
| H: surface + MO4H2–2H2O | −0.85 | 1.06 | 0.34 |
| I: surface + MO4H2–3H2O | −1.56 | 0.38 | 0.42 |
Another point which is revealed by this reaction energy analysis, is that the most favorable models associated to the different degrees of hydration are different between Cr and Mo on one hand, and W on the other. For Cr and Mo model B is favored against model D for W, the other structures' relative reaction energy differences do not change the overall stability trend between the models. This might be interpreted by the higher coordination chemistry for W compared with Mo and Cr (see Fig. 2).
Nevertheless, it should be noted that the results in Table 3 report electronic energies only, which are identical to the free energy at 0 K. Under given temperature T and pressure p, the contributions of entropy and chemical potentials have to be taken into account in the free energies.
Fig. 3 shows the surface free energy Γ, defined as the free energy per surface area (the reaction free energy of grafting that was approximated divided by the surface of our slab, or multiplied by surface coverage of W), of the mono-, di-, tri- and tetra-grafted W(VI)-complexes on the silica surface as a function of temperature (T) for a water partial pressure (p) equivalent to the ambient air water partial pressure (pw = 1500 Pa).58 At these conditions, the mono-grafted model A is the most stable until T = 100 K, followed by the mono-grafted models C in the temperature range of 100–220 K and finally at T > 215 K the tetra-grafted complex (model I) is found as the most stable configuration. It should be noted that the tetra grafted species (mono-oxo species), although observed experimentally between 473–1073 K is statistically disfavored due to the low probability to have four silanols in one nest. Taking this constraint into account it is the F structure (di-grafted di-oxo species) that appears to dominate at T > 400 K. These results are fully consistent with the experimental procedure used in the synthesis of W(VI)-supported catalysts by grafting methods,3 where samples are heated and annealed at high temperatures to obtain W di-oxo surface structures. Note that such species correspond to completely dehydrated conditions. In hydrated conditions (high water pressure or low temperature) mono-grafted model with W–OH group could be stabilized. Hydroxylated di-oxo species are predicted to be stable in the range of 100–400 K depending on the silanol density at the surface. However, at ambient conditions on low silanol density silica surfaces the di-oxo W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species are expected to dominate completely the W oxide supported geometries.
O species are expected to dominate completely the W oxide supported geometries.
 | ||
| Fig. 3 Phase diagram (surface energy vs. temperature) showing the stability ranges for the different grafted W oxide geometries. | ||
In summary, the three grafted W(VI) species may exist on a silica surface depending on the experimental conditions. They are supposed to reversibly interconvert in the presence of water, and they might coexist on the surface.
3.3. Vibrational frequency analysis
Lee and Wachs3,26 concluded that under dehydrated conditions the W(VI) oxide forms on silica are predominantly present as isolated dioxo and isolated monooxo W(VI) species. Their relative concentration varies with temperature with the dioxo W(VI) oxide species dominant at elevated temperatures. Nevertheless, tungsten species might be also present as oligomeric oxide species,28 crystalline WO3 (ref. 16, 26 and 28) and bulk-like amorphous WO3.28 Experimentally, this point seems to be still under debate,3,26,28,30 since monomers3,26 or oligomers31 are concluded to be dominant surface species both from Raman and UV-vis, while on the crystalline phase it rather depends on the preparation method and the W loading.Comparing the theoretical frequencies with the experimental ones,3,26 we can conclude that the model containing the most similarities with the experiment are models F and I (di- and mono- oxo tungsten species, respectively). Interesting to note is that Chauvin et al.28 propose oligomers, which might correspond to model H monomers.
This was concluded with the use of a scaling factor for the frequencies, independently from the type of bond and normalized on the well-known silanol vibration. This approach has been used with success in former studies31,32,34,35 According to Lee et al.3,26 the surface tungsten oxide species on the supported WO3/SiO2 catalyst are present as both dioxo (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )2W(–O–Si)2 and monoxo O
)2W(–O–Si)2 and monoxo O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) W(–O–Si)4 surface species, giving rise to Raman bands for νsym (W(
W(–O–Si)4 surface species, giving rise to Raman bands for νsym (W(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)2) at 985 cm−1 and νsym (W
O)2) at 985 cm−1 and νsym (W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) at 1014 cm−1. The corresponding asymmetric νasym (W(
O) at 1014 cm−1. The corresponding asymmetric νasym (W(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)2) vibration appears as a shoulder at 968 cm−1 and the bending δ(O–W–O) mode at 346 cm−1.3,26,59,60
O)2) vibration appears as a shoulder at 968 cm−1 and the bending δ(O–W–O) mode at 346 cm−1.3,26,59,60
The calculated vibrational frequencies are tabulated in Table 4. Vibrational analysis shows that the W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond vibrations are not as cleanly decoupled from others as was in the case for chromium.34 Only the frequency of asymmetric W
O bond vibrations are not as cleanly decoupled from others as was in the case for chromium.34 Only the frequency of asymmetric W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration can be easily given. The calculated values (not show in the table) range from 973 to 1001 cm−1 due to various hydrogen bonds arrangements, which in turn depend on the hydration level. In effect, a wide band cantered around 991 cm−1 should appear in the spectrum. From these results combined with the thermodynamic calculations, one can conclude that the vibrational frequencies calculated for model structures F and I confirm the experimental results presented in ref. 3 and 26, which supposes a competition between mono-oxo and di-oxo species, originating from the availability of the silanol groups on the silica surface. The grafting of these oxide species does not only depend on the concentration or coverage of silanol groups on the surface but also their distribution. In other words, in order to have mono-oxo-species one needs have 4 silanols grouped close together, whereas for the di-oxo species only two silanols close to each other is sufficient. The proportion of the mono/di-oxo species is thus not only dependent on the degree on hydration or the silanol coverage.
O vibration can be easily given. The calculated values (not show in the table) range from 973 to 1001 cm−1 due to various hydrogen bonds arrangements, which in turn depend on the hydration level. In effect, a wide band cantered around 991 cm−1 should appear in the spectrum. From these results combined with the thermodynamic calculations, one can conclude that the vibrational frequencies calculated for model structures F and I confirm the experimental results presented in ref. 3 and 26, which supposes a competition between mono-oxo and di-oxo species, originating from the availability of the silanol groups on the silica surface. The grafting of these oxide species does not only depend on the concentration or coverage of silanol groups on the surface but also their distribution. In other words, in order to have mono-oxo-species one needs have 4 silanols grouped close together, whereas for the di-oxo species only two silanols close to each other is sufficient. The proportion of the mono/di-oxo species is thus not only dependent on the degree on hydration or the silanol coverage.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group in mono- or di-oxo-configuration in the different models studied (frequencies in cm−1)
O group in mono- or di-oxo-configuration in the different models studied (frequencies in cm−1)
W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (scaled 0.96) O (scaled 0.96) |
Exp.3,26 | |
|---|---|---|---|
| B | 1008 | 968 | |
| C(sym) | 1037 | 995 | |
| C(asym) | 987 | 947 | |
| E | 1039 | 997 | |
| F(sym) | 1024 | 983 | 985 |
| F(asym) | 981 | 942 | 968 |
| H | 1033 | 991 | |
| I | 1055 | 1013 | 1014 |
4. Conclusion
W(VI)-oxide species supported on hydroxylated amorphous silica were modeled using periodic DFT. A systematic series of tungsten oxide monomer species were investigated as a function of their degree of hydration. The local geometry and energetics are discussed. From an atomistic thermodynamic approach the competition of the tungsten mono and di-oxo species is revealed, depending on the silanol density at the silica surface and thus the preparation method. Vibrational frequencies compared with experimental Raman data could confirm the presence of mono- and di-oxo species, with W![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrations at 985, 968 and 1014 cm−1. It was shown that W–OH groups are only present at high degrees of hydration and low temperatures (below 220 K), which can be excluded at catalyst working temperatures. The di-grafted di-oxo species (model F) is expected to dominate over the more stable tetra grafted mono-oxo species due to the low silanol density at the catalyst silica surface.
O vibrations at 985, 968 and 1014 cm−1. It was shown that W–OH groups are only present at high degrees of hydration and low temperatures (below 220 K), which can be excluded at catalyst working temperatures. The di-grafted di-oxo species (model F) is expected to dominate over the more stable tetra grafted mono-oxo species due to the low silanol density at the catalyst silica surface.
As a general conclusion compiling the results from our former studies we have calculated that in comparison with the other two group VI elements (Mo and Cr), supported W oxide species shows similar geometrical properties with supported Mo oxide species, with both elements having di-oxo species being the dominant one above 100 K at ambient vapor pressure, whereas for Cr the di-oxo species become dominant only above 400 K. M–OH groups are predicted to be more common for W follow by Cr. Mo has the least affinity to have a M−OH groups.
Acknowledgements
This work was performed using HPC resources from GENCI-[CCRT/CINES/IDRIS] (Grant 2015-[x2015082022]) and the CCRE of Université Pierre et Marie Curie. Dr B. Diawara from LCPS ENS Paris is kindly acknowledged for providing us with ModelView used in the visualization of the structures. RG acknowledges support from Polish National Science Centre under grant no. 2011/03/B/ST4/.References
- Z. Ma and F. Zaera, Heterogeneous Catalysis by Metals. In Encyclopedia of Inorganic Chemistry, John Wiley & Sons, Ltd, 2006 Search PubMed
.
- S. Chempath, Y. H. Zhang and A. T. Bell, DFT Studies of the Structure and Vibrational Spectra of Isolated Molybdena Species Supported on Silica, J. Phys. Chem. C, 2007, 111, 1291–1298 CAS
.
- E. L. Lee and I. E. Wachs, In Situ Raman Spectroscopy of SiO2-Supported Transition Metal Oxide Catalysts: An Isotopic O-18–O-16 Exchange Study, J. Phys. Chem. C, 2008, 112, 6487–6498 CAS
.
- T. Ono, M. Anpo and Y. Kubokawa, Catalytic Activity and Structure of MoO3 Highly Dispersed on SiO2, J. Phys. Chem., 1986, 90, 4780–4784 CrossRef CAS
.
- E. Le Roux, M. Taoufik, C. Coperet, A. de Mallmann, J. Thivolle-Cazat, J. M. Basset, B. M. Maunders and G. J. Sunley, Development of Tungsten-Based Heterogeneous Alkane Metathesis Catalysts through a Structure–Activity Relationship, Angew. Chem., Int. Ed., 2005, 44, 6755–6758 CrossRef CAS PubMed
.
- L. F. Heckelsberg, R. L. Banks and G. C. Bailey, A Tungsten Oxide on Silica Catalyst for Phillips Triolefin Process, Ind. Eng. Chem. Prod. Res. Dev., 1968, 7, 29–31 CrossRef CAS
.
- Global Propylene Market, http://www.researchandmarkets.com/research/8t49zx/the_global.
- A. de Lucas, J. L. Valverde, P. Canizares and L. Rodriguez, Partial Oxidation of Methane to Formaldehyde over W/SiO2 Catalysts, Appl. Catal., A, 1999, 184, 143–152 CrossRef CAS
.
- N. D. Spencer, C. J. Pereira and R. K. Grasselli, The Effect of Sodium on the MoO3-SiO2-Catalyzed Partial Oxidation of Methane, J. Catal., 1990, 126, 546–554 CrossRef CAS
.
- M. A. Banares, J. L. G. Fierro and J. B. Moffat, The Partial Oxidation of Methane on MoO3/SiO2 Catalysts – Influence of the Molybdenum Content and Type of Oxidant, J. Catal., 1993, 142, 406–417 CrossRef CAS
.
- F. Adam and A. Iqbal, The Liquid Phase Oxidation of Styrene with Tungsten Modified Silica as a Catalyst, Chem. Eng. J., 2011, 171, 1379–1386 CrossRef CAS
.
- N. Giordano, M. Meazza, A. Castellan, J. C. J. Bart and V. Ragaini, Structure and Catalytic Activity of MoO3. SiO2 Systems. 3. Mechanism of Oxidation of Propylene, J. Catal., 1977, 50, 342–352 CrossRef CAS
.
- J. M. Jehng, H. C. Hu, X. T. Gao and I. E. Wachs, The Dynamic States of Silica-Supported Metal Oxide Catalysts During Methanol Oxidation, Catal. Today, 1996, 28, 335–350 CrossRef CAS
.
- G. Liu, X. Wang, X. Wang, H. Han and C. Li, Photocatalytic H-2 and O-2 Evolution over Tungsten Oxide Dispersed on Silica, J. Catal., 2012, 293, 61–66 CrossRef CAS
.
- D. S. Kim, M. Ostromecki and I. E. Wachs, Surface Structures of Supported Tungsten Oxide Catalysts under Dehydrated Conditions, J. Mol. Catal. A: Chem., 1996, 106, 93–102 CrossRef CAS
.
- J. E. Herrera, J. H. Kwak, J. Z. Hu, Y. Wang and C. H. F. Peden, Synthesis of Nanodispersed Oxides of Vanadium, Titanium, Molybdenum, and Tungsten on Mesoporous Silica Using Atomic Layer Deposition, Top. Catal., 2006, 39, 245–255 CrossRef CAS
.
- J. Jarupatrakorn, M. P. Coles and T. D. Tilley, Synthesis and Characterization of Mo Osi((Obu)-Bu-T)(3) (4) and Mo2 ((Osiobu)-Bu-T)(3) (2) (M = Mo, W): Models for Isolated Oxo-Molybdenum and -Tungsten Sites on Silica and Precursors to Molybdena- and Tungsta-Silica Materials, Chem. Mater., 2005, 17, 1818–1828 CrossRef CAS
.
- J. Z. Hu, J. H. Kwak, Y. Wang, M. Y. Hu, R. V. Turcu and C. H. F. Peden, Characterizing Surface Acidic Sites in Mesoporous-Silica-Supported Tungsten Oxide Catalysts Using Solid-State NMR and Quantum Chemistry Calculations, J. Phys. Chem. C, 2011, 115, 23354–23362 CAS
.
- T. I. Bhuiyan, P. Arudra, M. N. Akhtar, A. M. Aitani, R. H. Abudawoud, M. A. Al-Yami and S. S. Al-Khattaf, Metathesis of 2-Butene to Propylene over W-Mesoporous
Molecular Sieves: A Comparative Study between Tungsten Containing Mcm-41 and Sba-15, Appl. Catal., A, 2013, 467, 224–234 CrossRef CAS
.
- F. Verpoort, G. Dedoncker, A. R. Bossuyt, L. Fiermans and L. Verdonck, Angle-Resolved and Depth Profiling Xps Investigation of a Monolayer Niobium Oxide Catalyst, J. Electron Spectrosc. Relat. Phenom., 1995, 73, 271–281 CrossRef CAS
.
- Y. D. Wang, Q. L. Chen, W. M. Yang, Z. K. Xie, X. Xu and D. Huang, Effect of Support Nature Onwo(3)/SiO2 Structure and Butene-1 Metathesis, Appl. Catal., A, 2003, 250, 25–37 CrossRef CAS
.
- A. Spamer, T. I. Dube, D. J. Moodley, C. van Schalkwyk and J. M. Botha, The Reduction of Isomerisation Activity on a Wo3/SiO2 Metathesis Catalyst, Appl. Catal., A, 2003, 255, 153–167 CrossRef CAS
.
- J.-C. Hu, Y.-D. Wang, L.-F. Chen, R. Richards, W.-M. Yang, Z.-C. Liu and W. Xu, Synthesis and Characterization of Tungsten-Substituted Sba-15: An Enhanced Catalyst for 1-Butene Metathesis, Microporous Mesoporous Mater., 2006, 93, 158–163 CrossRef CAS
.
- S. Lwin and I. E. Wachs, Olefin Metathesis by Supported Metal Oxide Catalysts, ACS Catal., 2014, 4, 2505–2520 CrossRef CAS
.
- L.-F. Chen, J.-C. Hu, Y.-D. Wang, K. Zhu, R. Richards, W.-M. Yang, Z.-C. Liu and W. Xu, Highly Efficient Tungsten-Substituted Mesoporous Sba-15 Catalysts for 1-Butene Metathesis, Mater. Lett., 2006, 60, 3059–3062 CrossRef CAS
.
- E. L. Lee and I. E. Wachs, In Situ Spectroscopic Investigation of the Molecular and Electronic Structures of SiO2 Supported Surface Metal Oxides, J. Phys. Chem. C, 2007, 111, 14410–14425 CAS
.
- Y. Iwasawa, Chemical Design Surfaces for Active Solid Catalysts, Adv. Catal., 1987, 35, 187–264 CAS
.
- J. Chauvin, K. Thomas, G. Clet and M. Houalla, Comparative Influence of Surface Tungstate Species and Bulk Amorphous WO3 Particles on the Acidity and Catalytic Activity of Tungsten Oxide Supported on Silica, J. Phys. Chem. C, 2015, 119, 12345–12355 CAS
.
- D. S. Kim, M. Ostromecki and I. E. Wachs, Preparation and Characterization of WO3/SiO2 Catalysts, Catal. Lett., 1995, 33, 209–215 CrossRef CAS
.
- E. I. Ross-Medgaarden and I. E. Wachs, Structural Determination of Bulk and Surface Tungsten Oxides with UV-Vis Diffuse Reflectance Spectroscopy and Raman Spectroscopy, J. Phys. Chem. C, 2007, 111, 15089–15099 CAS
.
- M. M. Islam, D. Costa, M. Calatayud and F. Tielens, Characterization of Supported Vanadium Oxide Species on Silica: A Periodic DFT Investigation, J. Phys. Chem. C, 2009, 113, 10740–10746 CAS
.
- D. C. Tranca, A. Wojtaszek-Gurdak, M. Ziolek and F. Tielens, Supported and Inserted Monomeric Niobium Oxide Species on/in Silica: A Molecular Picture, Phys. Chem. Chem. Phys., 2015, 17, 22402–22411 RSC
.
- J. Handzlik, R. Grybos and F. Tielens, Structure of Monomeric Chromium(VI) Oxide Species Supported on Silica: Periodic and Cluster DFT Studies, J. Phys. Chem. C, 2013, 117, 8138–8149 CAS
.
- H. Guesmi and F. Tielens, Chromium Oxide Species Supported on Silica: A Representative Periodic DFT Model, J. Phys. Chem. C, 2012, 116, 994–1001 CAS
.
- H. Guesmi, R. Gryboś, J. Handzlik and F. Tielens, Characterization of Molybdenum Monomeric Oxide Species Supported on Hydroxylated Silica; a DFT Study, Phys. Chem. Chem. Phys., 2014, 16, 18253–18260 RSC
.
- G. Kresse and J. Furthmuller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS
.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple (Vol. 77, Pg 3865, 1996), Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS
.
- P. E. Blochl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef
.
- M. D. Halls, J. Velkovski and H. B. Schlegel, Harmonic Frequency Scaling Factors for Hartree-Fock, S-Vwn, B-Lyp, B3-Lyp, B3-Pw91 and Mp2 with the Sadlej Pvtz Electric Property Basis Set, Theor. Chem. Acc., 2001, 105, 413–421 CrossRef CAS
.
- F. Tielens, C. Gervais, J. F. Lambert, F. Mauri and D. Costa, Ab Initio Study of the Hydroxylated Surface of Amorphous Silica: A Representative Model, Chem. Mater., 2008, 20, 3336–3344 CrossRef CAS
.
- A. Wojtaszek, I. Sobczak, M. Ziolek and F. Tielens, Gold Grafted to Mesoporous Silica Surfaces, a Molecular Picture, J. Phys. Chem. C, 2009, 113, 13855–13859 CAS
.
- A. Wojtaszek, I. Sobczak, M. Ziolek and F. Tielens, The Formation of Gold Clusters Supported on Mesoporous Silica Material Surfaces: A Molecular Picture, J. Phys. Chem. C, 2010, 114, 9002–9007 CAS
.
- A. Cimasa, F. Tielens, M. Sulpizic, M.-P. Gaigeota and D. Costa, The Amorphous Silica-Liquid Water Interface Studied by Ab Initio Molecular Dynamics (Aimd): Local Organization in a Global Disorder, J. Phys.: Condens. Matter, 2014, 26, 244106, DOI:10.1088/0953-8984/26/24/244106
.
- M. Pfeiffer-Laplaud, D. Costa, F. Tielens, M.-P. Gaigeot and M. Sulpizi, Bimodal Acidity at the Amorphous Silica/Water Interface, J. Phys. Chem. C, 2015, 119, 27354–27362 CAS
.
- T. J. Dines and S. Inglis, Raman Spectroscopic Study of Supported Chromium(Vi) Oxide Catalysts, Phys. Chem. Chem. Phys., 2003, 5, 1320–1328 RSC
.
- W. K. Jozwiak, W. Ignaczak, D. Dominiak and T. P. Maniecki, Thermal Stability of Bulk and Silica Supported Chromium Trioxide, Appl. Catal., A, 2004, 258, 33–45 CrossRef CAS
.
- E. Groppo, C. Lamberti, S. Bordiga, G. Spoto and A. Zecchina, The Structure of Active Centers and the Ethylene Polymerization Mechanism on the Cr/Sio2 Catalyst: A Frontier for the Characterization Methods, Chem. Rev., 2005, 105, 115–183 CrossRef CAS PubMed
.
- E. M. E. van Kimmenade, A. E. T. Kuiper, K. Tamminga, P. C. Thune and J. W. Niemantsverdriet, Surface Science Model for the Phillips Ethylene Polymerization Catalyst: Thermal Activation and Polymerization Activity, J. Catal., 2004, 223, 134–141 CrossRef CAS
.
- F. Tielens, F. De Proft and P. Geerlings, Density Functional Theory Study of the Conformation and Energetics of Silanol and Disiloxane, J. Mol. Struct.: THEOCHEM, 2001, 542, 227–237 CrossRef CAS
.
- M. Digne, P. Sautet, P. Raybaud, P. Euzen and H. Toulhoat, Hydroxyl Groups on Gamma-Alumina Surfaces: A DFT Study, J. Catal., 2002, 211, 1–5 CrossRef CAS
.
- E. Kaxiras, Y. Baryam, J. D. Joannopoulos and K. C. Pandey, Abinitio Theory of Polar Semiconductor Surfaces .1. Methodology and the (2 × 2) Reconstructions of Gaas(111), Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 9625–9635 CrossRef CAS
.
- G. X. Qian, R. M. Martin and D. J. Chadi, 1st-Principles Study of the Atomic Reconstructions and Energies of Ga-Stabilized and as-Stabilized Gaas(100) Surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 7649–7663 CrossRef CAS
.
- F. Tielens, Exploring the Reactivity of Intraframework Vanadium, Niobium and Tantalum Sites in Zeolitic Materials Using the Molecular Electrostatic Potential, J. Mol. Struct.: THEOCHEM, 2009, 903, 23–27 CrossRef CAS
.
- V. Bolis, B. Fubini, L. Marchese, G. Martra and D. Costa, Hydrophilic and Hydrophobic Sites on Dehydrated Crystalline and Amorphous Silicas, J. Chem. Soc., Faraday Trans., 1991, 87, 497–505 RSC
.
- F. Tielens, Exploring the Reactivity of Framework
Vanadium, Niobium, and Tantalum Sites in Zeolitic Materials Using Dft Reactivity Descriptors, J. Comput. Chem., 2009, 30, 1946–1951 CrossRef CAS PubMed
.
- A. Guyot, G. E. Curtis and W. Libbey, Smithsonian Meteorological Tables: Based on Guyot's Meteorological and Physical Tables, 1896 Search PubMed
.
- G. Mestl and T. K. K. Srinivasan, Raman Spectroscopy of Monolayer-Type Catalysts: Supported Molybdenum Oxides, Catal. Rev.: Sci. Eng., 1998, 40, 451–570 CAS
.
- F. Arena and A. Parmaliana, Scientific Basis for Process and Catalyst Design in the Selective Oxidation of Methane to Formaldehyde, Acc. Chem. Res., 2003, 36, 867–875 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2016 |
