Adsorption properties of CH4 and CO2 in quartz nanopores studied by molecular simulation†
Haoyang Suna,
Wenchao Sunb,
Hui Zhaoa,
Yange Suna,
Dianrui Zhanga,
Xiaoqing Qia and
Ying Li*a
aKey Laboratory of Colloid and Interface Chemistry of State Education Ministry, Shandong University, Jinan, Shandong 250100, P. R. China. E-mail: yingli@sdu.edu.cn; Fax: +86 0531 88364464; Tel: +86 0531 88362078
bSchool of Petroleum Engineering, China University of Petroleum (East China), Qingdao, Shandong 266580, P. R. China
First published on 21st March 2016
Abstract
In this work, grand canonical Monte Carlo (GCMC) and molecular dynamics (MD) simulation methods were used to study the adsorption properties of CH4 and CO2 as single components and binary mixtures in modeled quartz nanopores (d ∼ 2 nm), of which the surface was hydroxylated to different degrees. The variation of the adsorption and molecular diffusion characteristics of CH4 and CO2 as a function of temperature and pressure were determined, and the competitive adsorption of CH4 and CO2 was investigated. As single components, both the adsorption of CH4 and CO2 in the nanopore is described well by the Langmuir model, and the diffusion capacities of the gas molecules in a non-supercritical state are much larger than that in a supercritical state. It was found that there is a tight adsorption layer of CH4 with a thickness of 3–5 Å in the nanopore, while CO2 molecules adsorb tightly as a whole phase, especially in the supercritical fluid state. In the binary mixed system, CO2 preferentially adsorbs to the nanopore surface compared to CH4 due to the strong interactions between the CO2 molecule and the hydrophilic groups on the pore surface. An obvious competitive adsorption of CO2 and CH4 occurs at certain temperature ranges (313–353 K) with increasing pressure. And the degree of surface hydroxylation has significant contributions to the adsorption selectivity of CO2 over CH4. This work provides microscopic information about adsorption properties of CH4 and CO2 in nanopores at the molecular level for the purpose of guidance towards the application of shale gas extraction by flowing CO2.
1. Introduction
CH4 is a kind of typical clean fossil fuel with the advantages of high energy efficiency and large reserves, which is the main component of emerging unconventional resources for shale gas.1–4 Much research has confirmed that CO2 is adsorbed preferentially over CH4 onto the organic/mineral surface in gas shale and could displace methane. Enhanced gas recovery (EGR) using CO2 (CO2-EGR) is recognized as one remarkable technique for a combined carbon sequestration and shale gas production strategy.5–9According to the references in the literature, nano-scale pores constitute up to 80% of the total effective porosity in gas shale, they are classified into three types by the pore diameter, micropore (d < 2 nm), mesopore (d = 2–50 nm) and macropore (d > 50 nm).2,10,11 The adsorption properties of CH4 in nanopores have significant contributions to shale gas extraction. The competitive adsorption of CH4 and CO2 in nanopores is a key factor in elucidating CO2-EGR processes that play a considerable role in not only the displacement of CH4 with CO2 injection, but also storage of CO2 trapped inside the gas shale pore, which would both be undoubtedly influenced by wettability and capillary effects. Many conventional experimental methods, including mercury injection, low-pressure gas adsorption, and nuclear magnetic resonance have been used to yield information about shale pores and the adsorption capacity of gases in shale.12–14 It has to be stated that the complicated composition and pore structures of real shale makes finding the specific micro adsorption characteristics of the gases in shale difficult, let alone definitively revealing the microscopic mechanism. Investigations of the properties of gas molecules in the nanopores at the molecular level, particularly the effect of pore size and composition on the adsorption and desorption behavior of gases, is significant while still unclear.
Preferable adsorption of the injected gas onto the organic matter is considered to be the primary mechanism for the displacement of methane and CO2 trapping. Actually, the organic carbon content in gas shale ranges from less than 1% to as high as 25% (in some organic-rich beds).15–18 While the inorganic mineral portion of the shale, such as quartz, calcite, clay minerals, and muscovite mica account for a large proportion,2,4,19 according to literature reports, the content of quartz could be as high as 87% in shale from the Qaidam Basin in China;2 hence, studies about the adsorption of CO2 and CH4 in a quartz nanopore is meaningful.
In the last decade, studies about the adsorption and diffusion capacities of CH4 and CO2 in nanoporous materials like zeolites and metal organic frameworks (MOFs) have been extensively reported.20–22 Molecular simulation approach were shown to be capable of describing the adsorption capacities of various gases in different nanoporous materials and had provided guidance on the design and application of nanoporous materials for zeolites and MOFs.23–29
In this study, models of quartz nanopores that imitate the layer condition with different hydroxylation surfaces were constructed. The adsorption and motion behavior of pure, and binary mixed, CH4 and CO2 were investigated by the grand canonical Monte Carlo (GCMC) and molecular dynamics (MD) simulation methods (GCMC/MD). Adsorption capacities of pure CH4 and CO2 along with the competitive adsorption of binary mixed CH4/CO2 were studied. How the adsorption capacity can be affected by the hydrophilic/hydrophobic properties of the nanopore surface was also discussed.
2. Models and methodology
2.1 Modeling of quartz nanopores and surfaces
The model of a quartz nanopore with a diameter of ∼2 nm and a depth of 2.16 nm was constructed in a similar manner to previous publications,30–32 digging a cylindrical hole in an α-quartz block (51.1 × 49.1 × 21.6 Å), all the atoms lying along the z axis with the diameter of ∼2 nm were removed (Fig. 1a). Nanopores with different active surfaces were obtained by adjusting the amount of hydroxyl and methyl groups added to unsaturated Si bond on the pore surface (Fig. 1b). The nanopore surface, which was fully hydroxylated with silanol groups with a coverage fraction of 8–9 hydroxyls per nm2, and the surface hydrophobicity were adjusted by replacing the hydroxyl groups with methyl groups. The whole sorbent, including the quartz block and the pore surface groups, were regarded as rigid during the entire simulation. The charges of atoms were calculated by the electrostatic potential (ESP) fitting method.25 For the SiOH group, the charges of Si, O and H atoms were qSi–SiOH = 0.8025e, qO–SiOH = −0.4725e and qH–SiOH = 0.25e, respectively. For SiCH3 group, the charge of the Si atom is the same as qSi–SiOH. Charges of C and H atoms were qC–SiCH3 = −0.294e and qH–SiCH3 = 0.053e, respectively. For the sorbate, CO2 (ref. 33) was present as a three-site rigid molecule with the charges of C and O atoms at qC = 0.576e and qO = −0.288e, respectively, the bond length of C–O was 1.18 Å and the bond angle ∠OCO was 180°. The CH4 (ref. 34) molecule was present as a five-site rigid model with the charges of C and H atoms at qC = −0.66e and qH = 0.165e, respectively, and the C–H bond length was 1.09 Å.2.2 Computer simulation details
According to literature, Dreiding35 and UFF36 force fields, as well as the COMPASS force field,38–42 are often used in simulation studies related to gas adsorption in nanoporous zeolites and MOFs to produce mechanism verification of adsorption.23,25–27,37 No unique method or force field is assigned to definitely determine the parameters used in computer simulations. In consideration of the actual complex layer condition, which is different from gas adsorption in specific crystal structures, the whole simulation was presented by the general COMPASS force field to produce the CH4 and CO2 adsorption properties and the Materials Studio (MS) software package was used. The Lennard-Jones 9-6 potential was introduced to describe the van der Waals (vdW) term, the coulombic function was used to demonstrate the electrostatic interactions.The adsorption processes of CH4 and CO2 in nanopores were performed by the grand canonical Monte Carlo (GCMC) method using the sorption module of MS. The vdW interactions were performed by the atom based summation method, while the electrostatic interactions based on coulombic function were summed by the Ewald method with an accuracy of 10−4 kcal mol−1. Performances of adsorption simulations were obtained after an equilibration process of 5 × 106 steps and a calculation process of 5 × 106 steps at a certain pressure ranging from 10 kPa to 20 MPa at different temperatures.
The motion and diffusion properties of the adsorbed gases in nanopores were carried out by molecular dynamics (MD) simulations. The NPT (isothermal and isobaric) ensemble was used to perform the MD simulation with a time step of 1 fs in a run time of 5.0 ns. The Nose and Berendsen algorithm was selected for the temperature thermostat and pressure barostat, respectively. The mean square displacement (MSD) method was introduced to describe the motion properties of gas molecules in the nanopores.
3. Results and discussion
3.1 Adsorption and diffusion properties of pure CH4 in a quartz nanopore
The adsorption capacity of pure CH4 in a nanopore over diverse temperatures is shown in Fig. 2, which is in good agreement with the Langmuir isotherm model of single components and is described by the follow equation:
 | (1) |
 | ||
| Fig. 2 Adsorption isotherms (solid line) and the fitted Langmuir isotherm model (open symbol) of pure CH4 in a quartz nanopore with 100% surface hydroxylation at various temperatures. | ||
The adsorption density distributions of pure CH4 in a quartz nanopore under different pressures are shown in Fig. 3. We can clearly see that the CH4 molecules adsorb to the surface of the nanopore preferentially. The thickness of the adsorption layer of CH4 with increasing pressure at 323 K is shown in Fig. 4, the tightly adsorbed layer of CH4 on the nanopore surface is approximately one molecule-layer thick (3–5 Å), and about 70–80% of the adsorbed CH4 molecules are located in the tightly adsorbed layer, while the others located outside the layer were non-tightly adsorbed, which might be due to the limit of the nanopore size and the steric hindrance effect of the tightly adsorbed CH4 molecules.
 | ||
| Fig. 3 Density distribution of pure CH4 in a quartz nanopore with 100% surface hydroxylation at pressures of 4 MPa (a), 8 MPa (b), 15 MPa (c) and 20 MPa (d), T = 323 K. | ||
The diffusion capacities of CH4 molecules in the nanopore were calculated by MSD and diffusion coefficient (D) with the follow equations:
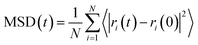 | (2) |
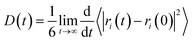 | (3) |
 | ||
| Fig. 5 Variation of MSDs of CH4 molecules adsorbed in various locations inside the nanopore versus simulation time at pressures of 4 MPa (a) and 10 MPa (b), T = 323 K. | ||
3.2 Adsorption and diffusion properties of pure CO2 in a quartz nanopore
The adsorption capacity of pure CO2 in a nanopore at various temperatures is shown in Fig. 6, which matches well with the Langmuir model described by eqn (1). The Langmuir constants of pure CO2 in a quartz nanopore are shown in Table S2† with all correlation coefficients (R2) larger than 0.99. This is consistent with the results of a recent experimental study about the adsorption properties of CO2 in shale from Longmaxi Fm, China.49 From Fig. 6, we can observe that the adsorbance of CO2 inside the quartz nanopore rapidly attains saturation as the pressure increases to 7.4 MPa (approximately the critical pressure of CO2) and then slightly increases with further pressure increase (7.4–20 MPa), indicating that the adsorption loading of CO2 hardly increases as the pressure increases to a supercritical state. | ||
| Fig. 6 Adsorption isotherms (solid line) and the fitted Langmuir model isotherms (open symbol) of pure CO2 in a quartz nanopore with 100% surface hydroxylation at various temperatures. | ||
The density distribution of pure CO2 inside the nanopore (Fig. 7) shows that CO2 molecules also preferentially adsorb on the surface of the nanopore. In contrast to CH4 molecules, which form a tightly adsorbed layer close to the pore surface, layered adsorbance of CO2 in the quartz nanopore only occurs at pressures lower than 7 MPa, beyond that the CO2 molecules fill in the quartz nanopore as a whole phase under supercritical conditions. This not only attributes to the strong interactions between the CO2 molecules and the hydroxyl groups on the surface of the nanopore but also the interactions between CO2 molecules (Fig. 8).
 | ||
| Fig. 7 Density distribution of pure CO2 in a quartz nanopore with 100% surface hydroxylation at pressures of 3 MPa (a), 6 MPa (b), 14 MPa (c) and 20 MPa (d), T = 323 K. | ||
 | ||
| Fig. 8 Images of the equilibration state of CO2 molecules adsorbed in a quartz nanopore with 100% surface hydroxylation at pressures of 3 MPa (a), 6 MPa (b) and 10 MPa (c), T = 323 K. | ||
The MSDs of the CO2 molecules located in different positions inside the nanopore are calculated and shown in Fig. 9. It can be seen that the diffusion capacity of CO2 in a quartz nanopore at non-supercritical state (Fig. 9a) is much larger than that at a supercritical state (Fig. 9b), and the adsorption of CO2 as a supercritical fluid in the nanopore is very tight. Comparing with CH4, the MSDs of CO2 are lower, whether in a non-supercritical or supercritical state, which corresponds to the strong interactions between the CO2 molecules and the hydroxyl groups on the nanopore surface. At pressures higher than the critical pressure, the MSDs of CO2 molecules located at different positions in the nanopore are similar and small. This indicates that the CO2 molecules at a supercritical state fill into the nanopore as a whole phase.
 | ||
| Fig. 9 Variation of MSDs of CO2 molecules in various adsorbed locations inside the nanopore versus simulation time at pressures of 6 MPa (a) and 10 MPa (b), T = 323 K. | ||
3.3 Adsorption properties of binary mixed CH4 and CO2 in a quartz nanopore
The adsorption isotherms of CH4 and CO2 in a mixture in a nanopore are shown in Fig. 10. In contrast to the adsorption isotherm of pure CH4, two adsorption stages emerge for CH4 in a mixture at temperature T < 353 K (Fig. 10a). At the beginning, the adsorption loading of CH4 rapidly reaches a nearly saturated state at low pressures (10 kPa to 4.6 MPa), after that, the adsorption loading has a slight increase followed by decreases with further increases in pressure. Simultaneously, the adsorption loading of CO2 (Fig. 10b) increases continuously, indicating that competitive adsorption is obviously occurring in the binary mixed CH4/CO2. | ||
| Fig. 10 Adsorption isotherms of binary mixed CH4 (a) and CO2 (b) in a quartz nanopore with 100% surface hydroxylation at various temperatures. | ||
The selectivity parameter S is used to describe the competitive adsorption capacity of CH4 and CO2 in the mixture, which is defined by the following equation:
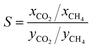 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kPa), the SCO2/CH4 is always larger than 4 and increases as the temperature decreases, which is mainly attributed to strong interactions between CO2 molecules and hydroxyl groups on the surface of the pore when compared with CH4. The diversity of the interactions between CO2, CH4 molecules and the sorbent atoms might recede at high temperatures.
000 kPa), the SCO2/CH4 is always larger than 4 and increases as the temperature decreases, which is mainly attributed to strong interactions between CO2 molecules and hydroxyl groups on the surface of the pore when compared with CH4. The diversity of the interactions between CO2, CH4 molecules and the sorbent atoms might recede at high temperatures.
 | ||
| Fig. 11 Selectivity of CO2 over CH4 in the nanopore with 100% surface hydroxylation at various temperatures. | ||
3.4 Effect of the degree of quartz nanopore surface hydroxylation on the adsorption properties of CH4 and CO2
The adsorption isotherms of pure CH4, CO2 and the binary mixtures of CH4 and CO2 in nanopores with different degrees of surface hydroxylation at 323 K are shown in Fig. 12. It was found that the adsorption amount of CH4 increases with increasing surface hydrophobicity while the adsorption amount of CO2 is opposite. This indicates that the methyl groups on the surface significantly enhance the adsorption of CH4 while adversely affecting CO2 molecules. Because the hydroxyl groups have polar interactions with CO2 molecules, the increase of the hydrophilicity of the sorbent surface promotes the preferable adsorption of CO2 molecules compared with CH4. So the selectivity of CO2 over CH4 decreases with increasing surface hydrophobicity and the competitive adsorption of CO2/CH4 is weakened with increasing nanopore surface hydrophobicity at 323 K, as shown in Table 1. | ||
| Fig. 12 Adsorption isotherms of pure CH4 (a), CO2 (b) and the binary mixtures of CH4 (c) and CO2 (d) in nanopores with different degrees of surface hydroxylation at 323 K. | ||
| Pressure (kPa) | Selectivity of CO2 over CH4 | ||
|---|---|---|---|
| 60% hydroxylation | 30% hydroxylation | 100% methylation | |
| 500 | 4.86 | 2.64 | 1.45 |
| 1200 | 4.37 | 2.46 | 1.59 |
| 3000 | 4.22 | 2.99 | 2.09 |
| 5000 | 4.58 | 3.15 | 2.37 |
| 8000 | 5.49 | 4.04 | 2.54 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
6.37 | 5.94 | 4.03 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
11.18 | 5.65 | 4.55 |
The adsorption density distribution of binary mixed CH4 and CO2 in quartz nanopores with diverse hydroxylation surfaces are shown in Fig. 13. In order to show the adsorption position clearly for CH4 and CO2 separately, the orders of magnitudes of the CH4 and CO2 are different. It could be found that in Fig. 13a–c, CH4 molecules preferentially adsorb onto the methyl sites while CO2 molecules adsorb onto the hydroxyl sites preferentially, which is mainly attributed to the interaction strength between CO2 and CH4 molecules and the surface functional groups mentioned above. This demonstrates that the hydrophilicity of the nanopore surface has significant contributions to the adsorption of CO2 while the increase of hydrophobicity benefits the adsorption of CH4.
4. Conclusion
In this study, the adsorption properties of pure and binary mixed CH4 and CO2 in mimetic models of quartz shale nanopores with different hydrophilic/hydrophobic surface were investigated. For pure components, both the adsorption of CH4 and CO2 could be described using Langmuir isotherms and the diffusion capacities of the pure component at non-supercritical states is much larger than at supercritical states. A tightly adsorbed layer of CH4 molecules with an approximate thickness of 3–5 Å is observed while CO2 molecules are trapped inside the nanopore as a whole phase more tightly compared with CH4 at supercritical states. This is attributed to the strong interactions between CO2 molecules and also CO2 molecules with nanopore surface hydroxyl groups.For the binary mixed CH4/CO2 system, an obvious competitive adsorption occurs in the researched temperature range T < 373 K, and the SCO2/CH4 increases when the pressure is larger than the critical pressure of CH4 because the coulombic and hydrogen bonding interactions between CO2 molecules and the hydroxyl groups on the pore surface are stronger than CH4.
It was also found that the hydrophilic/hydrophobic properties of the nanopore surface has a significant effect on the adsorption of gases. The CO2 molecules prefer to adsorb near hydroxyl groups due to polar interactions while CH4 molecules adsorb near methyl sites preferentially. Hydrophilicity of the nanopore surface has significant contributions to the adsorption of CO2 molecules and increases in hydrophobicity benefits the adsorption of CH4.
According to the investigation results of the paper, the adsorption properties of CH4 and CO2 into a quartz nanopore in a certain temperature and pressure range are revealed. The competitive adsorption of CH4/CO2 was discovered by simulations at the molecular level. This can be very helpful for better understanding the microscopic adsorption states of gas component molecules in shale, and might provide guidance in shale gas extraction.
Conflict of interest
The authors declare no competing financial interests.Acknowledgements
The funding of National Science Fund of China (No. 21473103 and 61575109) are gratefully acknowledged.References
- D. Lozano-Castello, J. Alcaniz-Monge, M. A. De la Casa-Lillo, D. Cazorla-Amorós and A. Linares-Solano, Fuel, 2002, 81, 1777 CrossRef CAS.
- Y. J. Li, X. Y. Li, Y. L. Wang and Q. C. Yu, Mar. Pet. Geol., 2015, 62, 44 CrossRef CAS.
- M. Gasparik, A. Ghanizadeh, P. Bertier, Y. Gensterblum, S. Bouw and B. M. Krooss, Energy Fuels, 2012, 26, 4995 CrossRef CAS.
- J. Tan, B. Horsfield, R. Fink, B. Krooss, H. M. Schulz and E. Rybacki, et al., Energy Fuels, 2014, 28, 2322 CrossRef CAS.
- R. S. Middleton, J. W. Carey, R. P. Currier, J. D. Hyman, Q. Kang and S. Karra, et al., Appl. Energy, 2015, 147, 500 CrossRef CAS.
- J. Q. Shi, S. Mazumder, K. H. Wolf and S. Durucan, Transp. Porous Media, 2008, 75, 35 CrossRef CAS.
- A. Busch, Y. Gensterblum, B. M. Krooss and N. Siemons, Int. J. Coal Geol., 2006, 66, 53 CrossRef CAS.
- G. Ceglarska-Stefańska and K. Zarębska, Fuel Process. Technol., 2002, 77, 423 CrossRef.
- P. Kowalczyk, P. A. Gauden, A. P. Terzyk, S. Furmaniak and P. J. Harris, J. Phys. Chem. C, 2012, 116, 13640 CAS.
- Y. G. Hou, S. He, J. Z. Yi, B. Q. Zhang, X. H. Chen and Y. Wang, Adv. Pet. Explor. Dev., 2014, 41, 272 CrossRef.
- T. Cao, Z. Song, S. Wang, X. Cao, Y. Li and J. Xia, Mar. Pet. Geol., 2015, 61, 140 CrossRef CAS.
- M. C. Wright, R. W. Court, F. C. A. Kafantaris, F. Spathopoulos and M. A. Sephton, Fuel, 2015, 153, 231 CrossRef CAS.
- C. Nichols and N. Victor, Energy Strategy Reviews, 2014, 7, 39 CrossRef.
- B. Bai, M. Elgmati, H. Zhang and M. Wei, Fuel, 2013, 105, 645 CrossRef CAS.
- Y. Altowairqi, R. Rezaee, B. Evans and M. Urosevic, J. Pet. Sci. Eng., 2015, 133, 392 CrossRef CAS.
- M. Mokhtari and A. N. Tutuncu, J. Pet. Sci. Eng., 2015, 133, 496 CrossRef CAS.
- H. Tian, L. Pan, T. Zhang, X. Xiao, Z. Meng and B. Huang, Mar. Pet. Geol., 2015, 62, 28 CrossRef CAS.
- L. Chen, Q. Kang, R. Pawar, Y. L. He and W. Q. Tao, Fuel, 2015, 158, 650 CrossRef CAS.
- L. Ji, T. Zhang, K. L. Milliken, J. Qu and X. Zhang, Appl. Geogr., 2012, 27, 2533 CAS.
- J. Jiang, R. Babarao and Z. Hu, Chem. Soc. Rev., 2011, 40, 3599 RSC.
- T. Düren, Y. S. Bae and R. Q. Snurr, Chem. Soc. Rev., 2009, 38, 1237 RSC.
- R. B. Getman, Y. S. Bae, C. E. Wilmer and R. Q. Snurr, Chem. Rev., 2011, 112, 703 CrossRef PubMed.
- T. Düren, L. Sarkisov, O. M. Yaghi and R. Q. Snurr, Langmuir, 2004, 20, 2683 CrossRef.
- K. V. Kumar and F. Rodríguez-Reinoso, RSC Adv., 2012, 2, 9671 RSC.
- S. Zhuo, Y. Huang, J. Hu, H. Liu, Y. Hu and J. Jiang, J. Phys. Chem. C, 2008, 112, 11295 CAS.
- R. Babarao, J. Jiang and S. I. Sandler, Langmuir, 2008, 25, 5239 CrossRef PubMed.
- Y. Chen, Z. Hu, K. M. Gupta and J. Jiang, J. Phys. Chem. C, 2011, 115, 21736 CAS.
- P. López-Aranguren, S. Builes, J. Fraile, A. López-Periago, L. F. Vega and C. Domingo, RSC Adv., 2015, 5, 104943 RSC.
- F. Cao, Y. Sun, L. Wang and H. Sun, RSC Adv., 2014, 4, 27571 RSC.
- K. Shirono and H. Daiguji, J. Phys. Chem. C, 2007, 111, 7938 CAS.
- K. Shirono, N. Tatsumi and H. Daiguji, J. Phys. Chem. B, 2009, 113, 1041 CrossRef CAS PubMed.
- M. D. Elola, J. Rodriguez and D. Laria, J. Phys. Chem. B, 2011, 115, 12859 CrossRef CAS PubMed.
- J. Zhou, X. Zhu, J. Hu, H. Liu, Y. Hu and J. Jiang, Phys. Chem. Chem. Phys., 2014, 16, 6075 RSC.
- S. Rives, H. Jobic, A. Beale and G. Maurin, J. Phys. Chem. C, 2013, 117, 13530 CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897 CrossRef CAS.
- A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024 CrossRef.
- R. Babarao, S. Dai and D. Jiang, J. Phys. Chem. C, 2011, 115, 8126 CAS.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338 CrossRef CAS.
- A. Mace, N. Hedin and A. Laaksonen, J. Phys. Chem. C, 2013, 117, 24259 CAS.
- A. Comotti, A. Fraccarollo, S. Bracco, M. Beretta, G. Distefano and M. Cossi, et al., CrystEngComm, 2013, 15, 1503 RSC.
- L. Erra, C. Tedesco, V. R. Cipolletti, L. Annunziata, C. Gaeta and M. Brunelli, et al., Phys. Chem. Chem. Phys., 2012, 14, 311 RSC.
- Y. Yue, J. A. Rabone, H. Liu, S. M. Mahurin, M. R. Li and H. Wang, et al., J. Phys. Chem. C, 2015, 119, 9442 CAS.
- J. A. Ritter and R. T. Yang, Ind. Eng. Chem. Res., 1987, 26, 1679 CrossRef CAS.
- T. F. Rexer, M. J. Benham, A. C. Aplin and K. M. Thomas, Energy Fuels, 2013, 27, 3099 CrossRef CAS.
- E. Garcia-Perez, J. B. Parra, C. O. Ania, A. Garcia-Sanchez, J. M. Van Baten and R. Krishna, et al., Adsorption, 2007, 13, 469 CrossRef CAS.
- R. Babarao, Z. Hu, J. Jiang, S. Chempath and S. I. Sandler, Langmuir, 2007, 23, 659 CrossRef CAS PubMed.
- K. Morishige, J. Phys. Chem. C, 2011, 115, 9713 CAS.
- T. Le, A. Striolo and D. R. Cole, J. Phys. Chem. C, 2015, 119, 15274 CAS.
- B. Sun, Y. Zhang, Q. Du and H. Shen, J. Univ. Pet., China, Ed. Nat. Sci., 2013, 37, 95 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra05083b |
| This journal is © The Royal Society of Chemistry 2016 |



