Mono- and di-nuclear nickel(ii) complexes derived from NNO donor ligands: syntheses, crystal structures and magnetic studies of dinuclear analogues†
Abstract
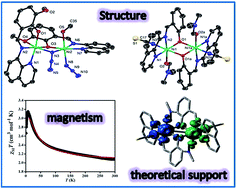
The present report deals with the synthesis and structural characterisation of a mononuclear (1), a di(phenoxido)-bridged dinuclear (2) and a phenoxido/azide bridged dinuclear (3) nickel(II) complexes derived from NNO donor Schiff base ligands. Structural studies reveal that, in all complexes, the nickel(II) ions are hexa-coordinated in a distorted octahedral environment in which tridentate NNO ligand binds the metal centre in the meridional configuration. The variable-temperature (2–300 K) magnetic susceptibility measurements of dinuclear analogues (2 and 3) show that the interaction between the metal centres is moderately ferromagnetic (J = 15.6 cm−1 for 2 and J = 15.3 cm−1 for 3). Broken symmetry density functional calculations of exchange interaction have been performed on complexes 2 and 3 and provide a good numerical estimate of J values (J = 10.31 cm−1 for 2 and J = 17.63 cm−1 for 3) to support the experimental results. Most importantly, compound 2 is only the second example where ferromagnetic coupling is operative in the class of di(phenoxido)-bridged dinickel(II) complexes. The bridging Ni–O–Ni angle being close to the crossover region would provide significant information to get better insight into the magneto-structural correlation in these systems. On the other hand, compound 3 is an important addition to a family of very few hetero-bridged (phenoxido/azide) discrete compounds of nickel(II).

 Please wait while we load your content...
Please wait while we load your content...