Density functional theory study of Li binding to graphene

Abstract

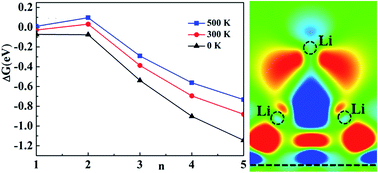
Using first-principle calculations, we studied the interaction between Li and graphene by considering two kinds of models, which are related to the configurations of Li adsorption and the concentration of Li on graphene. In a low concentration, the 2s state of Li is fully unoccupied due to charge transfer. With the increase of Li concentration, the 2s state is broadened and occupied partly by electrons. With a high concentration, such as Li : C = 1 : 6, Li cluster adsorption seems to become popular by the free formation energy of clusters with thermal effects.

---

1. Introduction

Great attention has been paid to graphene, due to its unique physical and chemical properties, since its discovery in 2004.^1–4 As a stable single sheet of carbon atoms with a honeycomb lattice, graphene has become attractive for potential applications in electrochemical storage devices, such as anodes for rechargeable Li batteries and electrodes for supercapacitors.^5–9 Since both sides of it can hold adsorbents and its edges can interact with other molecules, a graphene sheet is expected to have extra storage sites and therefore has a possibly higher capacity than graphite.^10,11

Since the 1990s, graphite has been used as an anode material for lithium-ion batteries (LIBs). However, the theoretical capacity limit of 3D graphite is only 372 mA h g⁻¹, leading to its limited performance. Recent experimental studies demonstrated that lowering the dimensionality of conventional anode materials via nanotechnology can achieve higher capacities, such as fullerene,¹² carbon nanotubes,¹³ silicon nano-wires,¹⁴ and graphene.¹⁵ Among them, with its single atomic-layer thickness and excellent performance, graphene has attracted more attention.^16,17 Some experimental results have shown that graphene nanosheets and oxidized graphene nanoribbons can absorb higher amounts of Li than graphite.^8,18 Much theoretical and experimental work has focused on the capacity, generally via modifications of cathode or anode materials. However, certain shortcomings of LIBs, such as instability lead to battery failure under overcharging or overvoltage conditions. The limit on capacity results in a short time of discharge. Thus, more attention should also be paid on the stabilities of electrode materials, such as Li cluster nucleation on graphene leading to dendrite formation and failure of the Li-ion battery.

Theoretical investigations can help to deeply understand the different experimental phenomena and the nature of the interaction between Li and low-dimension carbon.^19–21 The stability and nucleation of Li on graphene has barely been studied.^21,22 The calculations of Khantha et al. show that Li can be adsorbed on graphene planes with a binding energy of 0.934–1.598 eV,²³ and Chan et al. demonstrated that different adsorption positions have different adsorption energies.²⁴ For the hollow, bridge and top sites of graphene, the adsorption energies of Li atoms are 1.096, 0.773 and 0.754 eV, respectively.²⁴ The interaction between Li and layered carbon structures is found to have a classic ionic characteristic.^25,26 The vacancy defects, such as single-vacancy and double-vacancy, can help to enhance the storage capacity of Li on graphene.^27,28 In porous graphene networks, the plating of lithium metal is possible.²⁹ B-doping can promote the adsorption of Li on graphene.³⁰ Fan et al. found that small Li clusters can be formed on graphene with increased Li content.^21,22 Liu et al. further estimated the concentration-dependent nucleation barrier for Li on graphene using first principle calculations.³¹

In this work, we investigate the stability of Li adsorption on graphene by considering both the effects of Li concentration and Li cluster configurations with first-principle methods. We analyze the change of electronic structure due to Li atoms and Li clusters with the effect of Li concentration. By introducing a chemical potential, we also analyze the stability of Li clusters adsorbed on graphene with a thermal effect.

2. Computational methods

The calculations^32,33 are performed based on density functional theory with projector augmented wave (PAW) potentials as implemented in the Vienna Ab-intio Simulation Package (VASP).³⁴ The generalized gradient approximation (GGA) with the parametrization of Perdew–Burke–Ernzerhof (PBE)³⁵ is used to deal with the exchange-correlation of interacting electrons. The k-space integral and the plane-wave basis are chosen to ensure that the total energy is converged at a 1 meV per atom level. A kinetic energy cutoff of 500 eV is used for the plane wave expansion and the Monkhorst–Pack method is used to sample the k points in the Brillouin zone. Spin-polarized calculations are performed to account for possible magnetism of graphene with the adsorption of Li atoms and clusters. The lattice constant of graphene is chosen to be 2.464 Å, which is from the calculation of graphite and is slightly larger than the experimental value of 2.46 Å. Based on the primitive cell, different supercells including the hexagonal structures, 2 × 3, 3 × 3, 4 × 3, 5 × 3 and , as the ideal models, are used to simulate the effect of Li_n cluster adsorption on the electronic structure. To avoid the spurious coupling effect between graphene layers along the z-axis, when a Li atom or cluster is adsorbed on graphene, the vacuum separation in the models is set to 18 Å. The Brillouin zones of the supercell, , 2 × 3, 3 × 3, 4 × 3 and 5 × 3 are sampled with the Γ-centered k-point grid of 22 × 22, 20 × 12, 12 × 12, 10 × 12, 12 × 8 and 14 × 12, respectively.

3. Results and discussion

3.1 Electronic properties of Li adsorption on graphene

In order to evaluate the Li-doping effect on the anode performance of lithium-ion batteries, six types of Li cluster adsorbed on graphene can be found in Fig. 1(a)–(f). The initial structures are relaxed to obtain the most stable configurations, and the resulting C–C bond length of the pristine graphene is 1.403 Å, which is in agreement with previous results.^36,37 Table 2 shows the distance between Li atoms and graphene, and that between Li atoms, which are obtained after the structures in Fig. 1 are fully relaxed. It was found that the distance between the nearest-neighbor Li atoms is similar to or less than the distance between Li atoms in bulk Li. This means the formation of Li-clusters. The distance between an Li atom and graphene is short, compared to that of Li–Li. This implies the strong adsorption of Li on graphene.

Fig. 1 Schematic representation of (a) LiC₆, (b) Li₂C₁₂, (c) Li₃C₁₈, (d) *Li₃C₁₈ for two-layer Li adsorbed on graphene, (e) Li₄C₂₄ for two-layer Li adsorbed on graphene, and (f) Li₅C₃₀ for two-layer Li adsorbed on graphene.

Table 1 Electron numbers of Li atoms in the top and bottom layer of Li clusters adsorbed on graphene

	nLi-bottom (e)	nLi-top (e)
Li2C12	0.19
*Li3C18	0.23	0.22
Li3C18	0.17
Li4C24	0.22	0.14

---

Table 2 The distance (Å) between Li–graphene and Li–Li atoms for the Li-adsorbed graphene corresponding to the structure models in Fig. 1. Note that No. and d represent the Li atom marked in Fig. 1 and the distance between Li and graphene or that between Li atoms, respectively

	Li–gra						Li–Li
	No.	d	No.	d	No.	d	No.	d	No.	d	No.	d
LiC6		1.86
Li2C12	1	1.87	2	1.91				2.97
Li3C18	1	1.99	2	1.99	3	1.99	(1–2)	2.93	(2–3)	2.93	(1–3)	2.92
Li3C18*	1	1.91	2	4.48	3	1.91	(1–2)	2.87	(2–3)	2.87	(1–3)	2.50
Li4C24	1	1.86	2	1.87			(1–2)	2.85	(2–3)	2.89	(1–3)	2.85
	3	1.87	4	4.42			(1–4)	3.05	(2–4)	3.04	(3–4)	3.04
Li5C30	1	2.19	2	1.94			(1–2)	3.05	(2–3)	3.49	(3–4)	3.35
	3	2.08	4	1.95			(1–4)	3.13	(1–5)	3.21	(2–5)	2.94
	5	4.26					(3–5)	3.66	(4–5)	2.92

---

The electronic structure of graphene has been modified substantially due to the presence of Li impurities. Fig. 2 shows the density of states (DOS) of Li-adsorbed graphene Li₂C₁₂, *Li₃C₁₈ and Li₄C₂₄, corresponding to Fig. 1(b), (d) and (e), respectively. For pristine graphene, the band structure has a zero-gap, and the valence and conduction bands touch each other with conical band dispersion near the Dirac point, where the Fermi level is located. It is found that their DOS closely matches that of pristine graphene, except for the contribution from Li. In addition, the Fermi level shifts up into the conduction band due to electron injection into the π* band.

Fig. 2 The DOS of Li-adsorbed graphene Li₂C₁₂, *Li₃C₁₈ and Li₄C₂₄, corresponding to Fig. 1(b), (d) and (e), respectively. Note that the total DOS is the sum of spin-up and spin-down bands.

Compared with pristine graphene, the Fermi level of Li adsorbed on graphene is shifted up about 1.55 eV. In order to further analyze the nature of the Li–graphene interaction and electron transfer, we compute the partial density of states (PDOS) and charge-density difference of Li clusters on graphene as shown in Fig. 3. Fig. 3A–C shows the DOS for Li₂C₁₂, Li₃C₁₈, *Li₃C₁₈ and Li₄C₂₄, of which Fig. 3B(a) and (b) are the DOS of Li₃C₁₈ and *Li₃C₁₈, respectively. Their Fermi levels shift up into the conduction band, due to charge transferred from Li to graphene. Their PDOS of adsorbed Li (left-vertical) and isolated Li ions (right-vertical) are in Fig. 3D(a–d). From the comparison of the PDOS of isolated Li, the 2s peak of adsorbed Li of Li₂C₁₂, Li₃C₁₈, *Li₃C₁₈ and Li₄C₂₄, become flat due to the interaction between Li and C. The flat width is mainly influenced by graphene. In order to analyze the charge transfer quantitatively, the shift of the Fermi level (ΔE_F) is calculated for the Li-adsorbed graphene. The charge transfer (ΔQ_DOS) can be obtained by the integral of the DOS of free graphene from the energy of the Dirac point (E_D) to the energy of E_D + ΔE_F,²⁴ and the details are shown in Table 1. We find that electrons around Li are very rare, due to the difference of electronegativity between Li and C. The characteristics of an ionic bond are obvious for the interaction of Li and graphene.³⁸

Fig. 3 The DOS and PDOS of (A) pristine graphene and Li-adsorbed graphene Li₂C₁₂, (B) Li₃C₁₈ and *Li₃C₁₈, (C) Li₄C₂₄, (D) the PDOS of adsorbed Li of the structures corresponding to Fig. 1(b–e), and (E) calculated charge density difference in the xz plane for the region through the Li cluster for *Li₃C₁₈. Note that the DOS of (B(b)) and PDOS of (D(c)) are that of *Li₃C₁₈, and (B(a) and D(b)) are that of Li₃C₁₈. The red and blue colors in (E) represent charge accumulation and depletion, respectively.

In Fig. 3E, we analyzed the charge redistribution resulting from Li₃ cluster adsorption on graphene on the basis of the charge density difference in real space by the formula,

ΔCH(r) = CH_Li–g(r) − CH_Li(r) − CH_g(r), (1)

where CH_Li–g(r), CH_Li(r) and CH_g(r) are the real-space electronic charge distributions of the Li-adsorbed graphene, isolated Li cluster, and free graphene, respectively. The spatial redistribution of charge within the cluster, as well as in the immediate vicinity of the support-cluster interface in *Li₃C₁₈, can be observed clearly in the plot. The red and blue regions in the plot indicate the areas of charge accumulation and depletion, respectively. The charge transferred from the Li cluster to graphene is, however, quite sensitive to the nature of support. For the first-layer Li adsorbed on graphene, the charge is transferred from Li to the more electronegative C atoms, as evidenced by the blue region representing charge depletion. The transferred charge remains in the region between Li and the nearest neighbor C atoms, shown by the red regions representing charge accumulation and the formation of ionic bond. But for second-layer Li and first-layer Li, a covalent bond is formed, and the charge is kept in the local region between two Li atoms because of the Coulomb interaction.

Fig. 4 shows the DOS and the PDOS of Li atoms adsorbed on graphene with different concentrations of Li (LiC₁₂, LiC₂₄ and LiC₃₂). A single Li adatom binds to graphene by donating its electron to the delocalized π* states of graphene, and becomes fully ionized. The PDOS of Li ions show that almost all of the charge of Li is transferred to the π* states of graphene, and this results in an unoccupied 2s state of Li under a low concentration of Li. Following the increase of Li concentration, 2s states from Li are broadened due to hybridization among 2s states and some charges still occupy the widened 2s states. This can result in the decrease of interaction between Li ions and graphene.

Fig. 4 The DOS and PDOS of LiC₁₂, LiC₂₄ and LiC₃₂. Note that the total DOS and PDOS are the sum of spin-up and spin-down bands.

3.2 Thermal stability of Li cluster adsorption on graphene

In order to investigate the stability of Li adsorbed on graphene, we analyzed the adsorption energy as a function of Li concentration on graphene. The adsorption energy in studies of surface adsorption is usually defined to describe the stability of the adsorbate on surface via the formula, ΔE_ad = (E_gra+Lix − E_gra − xE_Li)/x, where E_gra+Lix is the total energy of the compound in which Li atoms/clusters are adsorbed on graphene, E_gra is that of the isolated graphene, E_Li is that of an isolated Li atom, and x is the number of Li atoms in the cluster adsorbed on graphene. As shown in Fig. 5, the black line represents the stability of the same structure with different Li concentrations, and the other (red line) is the same Li concentration with different structures. It is found that for the same configuration of Li ions adsorbed on graphene, the adsorption energy increases as the Li concentration decreases. As we all know, this is because of the Coulomb repulsion between Li ions on graphene. For the other case, in which Li nanostructures with different configurations are adsorbed on graphene, we found that Li clusters with certain sizes constitute the most stable state. Among the different configurations with the same Li concentration of 16.7%, the Li₄ cluster in Li₄C₂₄ is the most stable adsorption state. From the above comparison, it can be seen that two layer Li atoms adsorbed on graphene for *Li₃C₁₈ is more stable than single layer Li atoms adsorbed on graphene for Li₃C₁₈. Thus, the stability is due to both Li concentration and Li cluster configuration.

Fig. 5 Adsorption energy as a function of Li concentration for Li adsorption on graphene, and the same Li concentration with different configurations for an Li concentration of 16.7%. Note that the structures with different concentrations of Li are calculated with the unit cell 4 × 4, 3 × 4 and 2 × 3, respectively.

In order to consider the thermal effect, we consider the free formation energy of Li clusters adsorbed on graphene by introducing chemical potential μ with the formula,

ΔG(n) = E(Li_n@graphene) − E(graphene) − nμ(Li@Li_xC) (2)

For chemical potential μ under a certain concentration, x (x is the ratio of Li to C, x = Li : C), of Li, we can consider a reference state that is a low concentration of Li adsorbed on graphene with a random distribution on the hexagonal center of the graphene surface. Thus, the chemical potential with an entropy S induced by the random distribution of Li atoms can be expressed by the formula,

μ(Li@Li_xC) = [E(Li_xC) − E(C)]/x − TS(x), (3)

with S(x) = −k_B[ln 2x + (1 − 2x)ln(1 − 2x)/2x], where k_B is the Boltzmann constant. Here, the Li concentration of 16.7% is considered for the formation of clusters with different sizes on graphene, as shown in Fig. 6a. As the size, n, of the cluster is larger than 2, the cluster adsorbed on the graphene begins to be more stable than the adsorption of a single Li atom. We consider the variation of free formation energy with increasing temperature. The two typical temperatures, 300 K and 500 K, are used to compare with the results under 0 K. The formation energies for the cluster size n > 2 are negative, meaning that Li clusters can be formed even under the thermal effect. The formation energy is decreased with the temperature increasing. This can be attributed to the change of chemical potential with temperature. As shown in the change trend chart of μ–T in Fig. 6b, the chemical potential decreases with increasing temperature.

Fig. 6 (a) Free formation energies of Li clusters on graphene as a function of cluster size n under different temperatures, (b) the change trend chart of chemical potential μ and temperature at a concentration of x = 1/6.

4. Conclusion

We have investigated the stability of Li adsorption on graphene using first-principles methods and analyzed the effects of both Li concentration and Li cluster configuration on the stability of anode materials. The interaction between Li and pristine graphene has been studied in detail, with the analysis of electronic properties and charge distribution. Ionic bonding between Li and C is considered to describe effectively the interaction between Li and carbon in the sp² carbon system, and the charge transfer controls the interaction of the Li–carbon nanostructure. We also analyzed the free formation energy of Li clusters on graphene with thermal effects by introducing a chemical potential with fixed Li concentrations. The free formation energy is found to decrease with the increase of temperature, while Li clusters (size n > 2) can still be adsorbed stably on graphene. It is expected that the results from this atomistic simulation will shed some light on the deep understanding of Li-storage on graphene and the cycling stability and dendrite formation in Li-ion batteries with graphene-based materials as the anode.

Acknowledgements

The authors would like to acknowledge the Natural Science Foundation of Changchun Normal University, the Natural Science Foundation of Jilin Province (No. 2014-0101061JC) and the National Natural Science Foundation of China (No. 11504123) for providing financial support for this research.

References

1. M. J. Allen, V. C. Tung and R. B. Kaner, Chem. Rev., 2010, 110, 132–145.
2. A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870–873.
3. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200.
4. X. S. Li, W. W. Cai, J. H. An, S. Kim, J. Nah, D. X. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312–1314.
5. E. Yoo, J. Kim, E. Hosono, H. Zhou, T. Kudo and I. Honma, Nano Lett., 2008, 8, 2277–2282.
6. H. Jiang, P. S. Lee and C. Li, Energy Environ. Sci., 2013, 6, 41–53.
7. P. C. Lian, X. F. Zhu, S. Z. Liang, Z. Li, W. S. Yang and H. H. Wang, Electrochim. Acta, 2010, 55, 3909–3914.
8. G. X. Wang, X. P. Shen, J. Yao and J. Park, Carbon, 2009, 47, 2049–2053.
9. L. Jaber-Ansari, K. P. Puntambekar, H. Tavassol, H. Yildirim, A. Kinaci, R. Kumar, S. J. Saldana, A. A. Gewirth, J. P. Greeley, M. K. Chan and M. C. Hersam, ACS Appl. Mater. Interfaces, 2014, 6, 17626–17636.
10. H. Yildirim, A. Kinaci, Z. J. Zhao, M. K. Chan and J. P. Greeley, ACS Appl. Mater. Interfaces, 2014, 6, 21141–21150.
11. J. Song, B. Ouyang and N. V. Medhekar, ACS Appl. Mater. Interfaces, 2013, 5, 12968–12974.
12. E. Buiel and J. Dahn, Electrochim. Acta, 1999, 45, 121–130.
13. G. T. Wu, C. S. Wang, X. B. Zhang, H. S. Yang, Z. F. Qi, P. M. He and W. Z. Li, J. Electrochem. Soc., 1999, 146, 1696–1701.
14. C. K. Chan, H. Peng, G. Liu, K. McIlwrath, X. F. Zhang, R. A. Huggins and Y. Cui, Nat. Nanotechnol., 2008, 3, 31–35.
15. X. Zhao, C. M. Hayner, M. C. Kung and H. H. Kung, ACS Nano, 2011, 5, 8739–8749.
16. B. Z. Jang, C. G. Liu, D. Neff, Z. N. Yu, M. C. Wang, W. Xiong and A. Zhamu, Nano Lett., 2011, 11, 3785–3791.
17. D. Wang, D. Choi, J. Li, Z. Yang, Z. Nie, R. Kou, D. Hu, C. Wang, L. V. Saraf, J. Zhang, I. A. Aksay and J. Liu, ACS Nano, 2009, 3, 907–914.
18. T. Bhardwaj, A. Antic, B. Pavan, V. Barone and B. D. Fahlman, J. Am. Chem. Soc., 2010, 132, 12556–12558.
19. A. Ferre-Vilaplana, J. Phys. Chem. C, 2008, 112, 3998–4004.
20. G. E. Froudakis, Nano Lett., 2001, 1, 531–533.
21. A. M. Garay-Tapia, A. H. Romero and V. Barone, J. Chem. Theory Comput., 2012, 8, 1064–1071.
22. X. Fan, W. T. Zheng, J. L. Kuo and D. J. Singh, ACS Appl. Mater. Interfaces, 2013, 5, 7793–7797.
23. M. Khantha, N. A. Cordero, L. M. Molina, J. A. Alonso and L. A. Girifalco, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 125422.
24. K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430.
25. P. V. C. Medeiros, F. D. Mota, A. J. S. Mascarenhas and C. M. C. de Castilho, Nanotechnology, 2010, 21, 115701.
26. M. Klintenberg, S. Lebegue, M. I. Katsnelson and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085433.
27. D. Datta, J. W. Li, N. Koratker and V. B. Shenoy, Carbon, 2014, 80, 305–310.
28. Y. H. A. Kinaci, Z.-J. Zhao, M. K. Y. Chan and J. P. Greeley, ACS Appl. Mater. Interfaces, 2014, 6, 21141–21150.
29. R. Mukherjee, A. V. Thomas, D. Datta, E. Singh, J. W. Li, O. Eksik, V. B. Shenoy and N. Koratkar, Nat. Commun., 2014, 5, 3710.
30. R. P. Hardikar, D. Das, S. S. Han, K. R. Lee and A. K. Singh, Phys. Chem. Chem. Phys., 2014, 16, 16502–16508.
31. M. Liu, A. Kutana, Y. Liu and B. I. Yakobson, J. Phys. Chem. Lett., 2014, 5, 1225–1229.
32. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
33. P. K. W. Hohenberg, Phys. Rev. B: Condens. Matter Mater. Phys., 1964, 136, B864–B871.
34. G. Kresse and J. Furthmüller, J. Comput. Mater. Sci., 1996, 6, 15–50.
35. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
36. G. M. Yang, H. Z. Zhang, X. F. Fan and W. T. Zheng, J. Phys. Chem. C, 2015, 119, 6464–6470.
37. X. F. Fan, W. T. Zheng and J. L. Kuo, ACS Appl. Mater. Interfaces, 2012, 4, 2432–2438.
38. X. F. Fan, L. Liu, J. L. Kuo and Z. X. Shen, J. Phys. Chem. C, 2010, 114, 14939–14945.

---

Footnote

† Electronic supplementary information (ESI) available: Including the electronic properties of individual lithium clusters (Li₂ Li₃ Li₄) with the distribution of charge density and density of states, and the structures of the models with atomic coordinates used in the text. See DOI: 10.1039/c6ra00101g

---