Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effect of hydrogen on the evolution of intergranular cracking: a cross-scale study using first-principles and cohesive finite element methods
Xin
Wei
a,
Chaofang
Dong
*a,
Zhanghua
Chen
b,
Kui
Xiao
a and
Xiaogang
Li
a
aCorrosion and Protection Centre, Key Laboratory for Corrosion and Protection (MOE), University of Science and Technology Beijing, Beijing 100083, China. E-mail: cfdong@ustb.edu.cn; Fax: +86-10-62334005; Tel: +86-10-62333931-518
bSchool of Mathematics and Physics, University of Science and Technology Beijing, Beijing, 100083, China
First published on 3rd March 2016
Abstract
A combination of first-principles and cohesive finite element (CFE) cross-scale calculations is performed to examine the effect of hydrogen on the intergranular cracking of aluminum. First-principles calculations based on density functional theory are investigated to assess the adsorption and diffusion of H along the Al (111) surface and the cohesive energies of the grain boundaries (GBs) with different H concentrations. CFE calculations are used to simulate the evolution of intergranular cracking induced by hydrogen segregation in GBs. To combine first-principles calculations and CFE modelling, the GB cohesive energies are used as inputs for the fracture energies in the CFE calculations. The results show that H atoms diffuse into the interstitial sites in the bulk material and segregated to the GBs by overcoming the energy barriers. The cohesive energies of the GBs decrease linearly with increasing of H concentration. The application of these cross-scale approaches is very efficient for investigating the evolution of hydrogen induced intergranular cracking.
1. Introduction
Intergranular cracking is the primary failure mode for stress corrosion cracking (SCC) of high-strength Al alloys under atmospheric conditions. It has been widely suggested that hydrogen embrittlement (HE) induced by the diffusion of hydrogen increases a material's susceptibility to SCC.1,2 Sample preparation, processing, and the service environment can result in residual hydrogen in materials. F. Y. Guo et al.3 studied the dissociation adsorption of a H2O molecule on an Al (111) surface using first-principle calculations based on density functional theory (DFT). The method of transition states search (TSS) was adopted to investigate the energy barriers of H2O dissociation on Al (111) surfaces. The results show that the hydrogen atom dissociating from H2O needs to overcome a 248.32 kJ mol−1 of energy barrier on clean Al (111) surface, while the dissociating energy barrier decreases to 128.53 kJ mol−1 on the O pre-adsorbed Al (111) surface with the aid of O atom. H and OH dissociated from H2O can be adsorbed on surface by the form of chemical bond separately.The mechanisms for SCC in metals can be classified as either (i) anodic or (ii) cathodic, e.g. hydrogen evolution, adsorption, diffusion, or embrittlement. Stress-assisted localized dissolution was initially considered the mechanism for intergranular stress corrosion cracking, and this perspective persisted until the effect of hydrogen on the fracture process was identified.4 When hydrogen is adsorbed from the external environment onto the material, it preferentially diffuses along grain boundaries (GBs), eventually causing embrittlement. H atoms can diffuse to depths of several millimetres toward regions of high stress, become trapped at gain boundaries, and induce intergranular fractures without any contribution from the corrosion process.5
The behaviour of HE leads to a degradation of mechanical properties6–8 such as fracture resistance, elongation to failure, and transition from ductility to brittleness, all of which are induced by interactions with hydrogen. The three fundamental mechanisms for HE, namely, hydride-induced embrittlement,11 hydrogen-enhanced decohesion,12 and hydrogen-enhanced localized plasticity12,13 have been well documented.9–13 Experimental and theoretical efforts14–17 using conventional mechanical and in situ tests have been conducted to understand the mechanism for HE. One approach involves measuring the differences in mechanical properties between a hydrogen-charged sample and an uncharged hydrogen sample.18,19 However, providing a control to guarantee the reproducibility of the results is difficult for such tests. In situ testing techniques such as environmental transmission electron microscopy (TEM) can address the dislocation nucleation, multiplication, and movement, all of which can significantly influence the mechanical properties of the metals. Most metals such as Fe, Al, Ni, and their alloys have been subjected to in situ TEM tests to investigate the effect of hydrogen gas introduction to the TEM chamber on the mobility of dislocations observed in the experiments.13 However, in situ tests20,21 have stringent requirements for experimental environments and conditions that limit their range of applications.
Because of the difficulties of experimental testing for HE, calculation and simulation methods have been proposed. Finite element (FE) method and damage mechanics model have been applied to SCC.22,23 It is also necessary to investigate the role of GBs damage in intergranular cracking behavior. The cohesive element approach can be used to explicitly account for the damage to GBs and has been reported in a number of cases in the literatures.24–28 Igor Simonovski and Leon Cizelj28 used a cohesive element approach to model intergranular cracking at the grain level in which cohesive elements with zero physical thickness were directly inserted between the adjacent grains. The fracture energy is one of the most parameters for cohesive finite elements (CFE) calculations, which usually estimated by some approximate algorithms.27,28 The process for the calculation of fracture energy is complex with an obvious fluctuation, while the GB fracture energies can be defined as the cohesive energies which can be deduced by surface energies and GB energies. Many experimental and theoretical29–33 efforts have been made to determine the surface and GB energies. Vasily V. Bulatov et al.29 presented and justified a concise hypothesis on the topography of the functional space of interface energies and constructed a closed-form function that quantitatively describes energy variations in the 5-space of macroscopic parameters defining grain boundary geometry. This function is universal for the crystallography class of face-centered cubic metals. L. Vitos et al.30 have used DFT to establish a database of surface energies for low index surfaces of 60 metals in the periodic table. The results show that the surface energy of Al (111), Al (100) and Al (110) is 1.199, 1.347 and 1.271 J m−2. The work of W. R. Tyson et al.33 shows that the surface energy of Al (111) is 1.143 J m−2.
This paper presents a novel method that combines first-principles and cohesive finite element (CFE) calculations to avoid the inaccuracy of conventional mechanical tests and the complexity of in situ tests. This method can be used in conjunction with experimental tests. The primary objective of this work is to understand the effect of hydrogen on the evolution on intergranular crack initiation and propagation in a cross-scale process from an atomic to a macroscopic scale. We initially report a first-principle study on the adsorption and diffusion of H atoms fracture energy is obtained by first-principle calculation through grain boundary energy and surface energy. Finally, a 3D finite element model of a polycrystalline material containing GBs with cohesive elements is then presented to investigate the effect of H on the intergranular cracking of a high-strength aluminium alloy.
2. Computational models
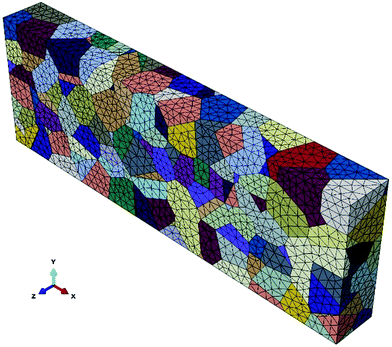
Fig. 1 shows a schematic of the entire cross-scale process. H atoms are adsorbed onto the surface from the outer environment, diffuse into the bulk and segregate to the GBs to decrease the cohesive energy, which can be obtained by first-principles calculations. The weakened GBs easily crack when stressed. The evolution of intergranular cracking is studied using CFE calculations.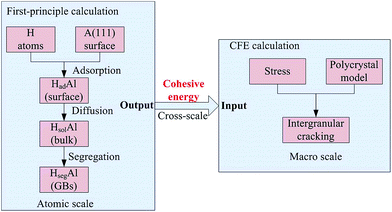 | ||
| Fig. 1 The schematic of the entire cross-scale process for the effect of H on intergranular cracking. | ||
2.1 The first-principles calculation
All calculations of atomic models presented in this section are performed using the MedeA-VASP 5.3 program,34,35 a fast and highly reliable electronic structure method based on density functional theory (DFT).36 The calculations are conducted with a plane-wave basis via the projector-augmented wave method.37 The GGA-PBE exchange–correlation function38 is used to describe the interaction. The convergence for the electronic iterations is 10−5 eV and is attained by using a normal (blocked Davidson) algorithm. Periodical boundary conditions are used, creating an infinite, periodically repeating system. A spin-polarized magnetic calculation is performed to account for the scalar spin-up and spin-down magnetic moments for each atom. The post-processing of the results involved structural and charge density constructs using VESTA.39| EGBcoh = γ1surf + γ2surf − γGB | (1) |
The surface energy can be obtained from:
| γsurf = (Esurf − nEbulkAl atom)/2A | (2) |
The GB energy can be calculated as follows:
| γGB = (EGB − n1EbulkAl atom − n2EbulkAl atom)/2A | (3) |
We assume that H atoms bond with each other to form H2 molecules that escape from GBs through cracks when the intergranular cracks are produced and have no effect on the fresh surfaces. The equation for the hydrogen induced decohesion for GBs is
 | (4) |
| γHGB = γGB + (EHGB − EGB)/A | (5) |
Substituting eqn (2)–(5) into eqn (1), the cohesive energy of the GB with H atoms is:
| EHcoh = E1surf + E2surf + mEH2 + EGB − 2EHGB/2A | (6) |
Each term can be calculated directly using VASP software.
More than 10 types of atomic models of GBs are simulated to calculate the cohesive energies based on their surface and GBs energies. Different concentrations of H atoms are introduced into GBs with different twist angles and misorientations to quantify the decrease in GB cohesive energy according to eqn (6).
2.2 The CFE calculation
| E1 = 92.1 GPa, E2 = E3 = 86.7 GPa, μ12 = 0.34, μ13 = 0.32, μ23 = 0.33, |
The remaining Poisson's ratios can be calculated using:
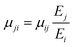 | (7) |
For an anisotropic elasticity material, the relationship between stress and strain is
 | (8) |
| Constant | C 11 | C 22 | C 33 | C 12 | C 13 | C 23 | C 44 | C 55 | C 66 |
| Value (Gpa) | 91.9 | 86.52 | 86.52 | 43.89 | 43.90 | 41.63 | 41.63 | 43.9 | 43.89 |
A cohesive zone approach45–47 with damage initiation and evolution as implemented in ABAQUS is used as a constitutive law for the GBs. The 3D cohesive elements are embedded into the grain boundaries to represent all possible fracture paths. The constitutive response of the cohesive elements is based on the traction–separation law that assumes initial linear elastic behaviour followed by the initiation and evolution of damage (see Fig. 3).
The bilinear traction–separation laws represent the relationship between traction T and crack opening displacement δ, where the indices n, s, and t denote the normal and two orthogonal shear directions of the cohesive elements, respectively. T0n (T0s, T0t) refers to the maximum traction that the cohesive element can bear before failure, δ0 is the critical separation at which the effective traction T reaches the maximum traction T0, δf is the separation at failure (assumed to be 20δ0) and the area under the curve Gc is the fracture energy. The tractions of a cohesive element Tn, Ts, and Tt are given by the following equation:
 | (9) |
3. Results and discussion
3.1 The adsorption and dissolution of H atoms on Al (111) surface
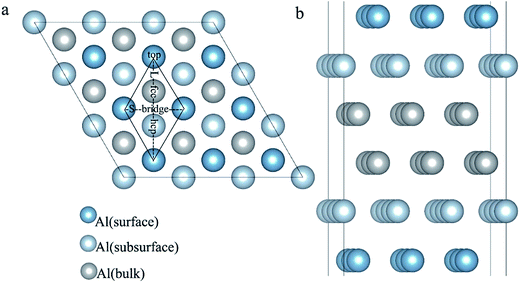
The surface energy and work function of a clean 6-layer-Al (111) surface are 1.06 J m−2 and 4.12 eV, respectively, which agree well with the corresponding experimental values of 1.14 J m−2 (ref. 33) and 4.24 eV.48Fig. 4 shows the four highly symmetric adsorption sites (top, bridge, fcc, and hcp) that are considered. The adsorption and solution energies are calculated according to the following expression:| Eads/sol = EAl (111) + nEH − EAl (111)–nH | (10) |
The adsorption structures for the four symmetric adsorption sites are calculated for the adsorption of a single H atom onto the Al (111) surface with a H atom coverage of 1/9 ML. A single H atom can only be adsorbed onto the fcc site and top sites, and if the initial site of the H atom is an hcp or bridge, it will spontaneously migrate to fcc site. The geometric parameters, adsorption energies and charge transfer are shown in Table 2. For the fcc-site adsorption, the average distance between the Al and H atoms is 1.92 Å, which is larger than the distance for top-site adsorption, 1.62 Å. A shorter distance between Al atom and H atom implies a stronger interaction, however, it is not reasonable to determine the adsorption strength only based on the distance because the H atom can bond with one Al atom on the surface and three Al atoms at fcc site. The fcc-site adsorption energy is 2.03 eV is larger than the top-site adsorption energy of 1.85 eV indicating that fcc sites are more stable adsorption site than top site on Al (111) surface at the coverage of 1/9 ML.
| Stable structures | Average distance (Å) Al–H | Solution energy (eV) | Charge transfer Al → H |
|---|---|---|---|
| H(fcc) | 1.92 | 2.03 | 0.91 |
| H(top) | 1.62 | 1.85 | 0.61 |
| H(TIS1-1) | 1.87 | 1.52 | 1.20 |
| H(TIS1-2) | 1.91 | 1.62 | 1.06 |
| H(OIS1) | 2.07 | 1.54 | 1.29 |
| H(TIS2) | 1.87 | 1.62 | 1.12 |
| H(OIS2) | 2.05 | 1.54 | 1.32 |
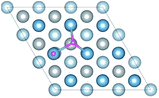
H atoms can diffuse into interstitial sites in the bulk through the surface. There are five types of subsurface and bulk interstitial sites, including tetrahedral interstice sites (TIS) and octahedral interstice sites (OIS), as shown in Fig. 5. The geometric parameters, solution energies, and charge transfer are listed in Table 2. Compared with the adsorption of a single H atom on the surface, the dissolutions in bulk occur with a lower energy and higher charge transfer, as illustrated in Fig. 6. The adsorption energy increases with the charge transfer when H atom is on the surface, while the solution energy exhibits an inverse relationship with the charge transfer when H atom is in the interstitial sites. It can be inferred that the relationships are primarily due to the change in number of neighbouring Al atoms around the H atom.
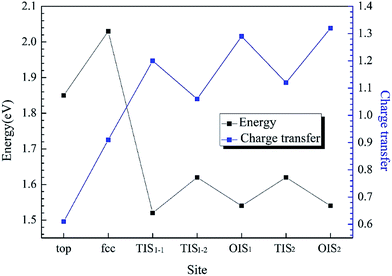 | ||
| Fig. 6 The adsorption energy and solution energy of single H atom along Al (111) surface and corresponding charge transfer with different sites at an H coverage of 1/9 ML. | ||
With the coverage of H atoms increases to 2/9 ML, five stable adsorption structures are achieved, as shown in Table 3. Two H atoms are adsorbed on a six-layer (3 × 3) Al (111) surface. H atoms can still only be adsorbed onto fcc site and top sites. Due to the differences in adsorption energy, the site stability ranking is as follow:
| H(fcc) − H(fcc) > H(fcc) − H(top) − S > H(fcc) − H(top) − L > H(top) − H(top) − L > H(top) − H(top) − S. |
The ranking further illustrates that the fcc site is a more stable site than the top site. The geometric parameters, adsorption energies and charge transfer are shown in Table 4. The adsorption energies are consistent with the sum of the adsorption of single H atom and the charge transfer remains almost the same as for single fcc site or top site adsorption compared with the previous calculation listed in Table 2. To investigate the effect of H coverage on adsorption behaviour, a smaller surface (2 × 3) supercell is constructed with an H coverage of 1/3 ML. The stable adsorption structures are shown in Table 5. Compared with the geometric parameters, adsorption energies and charge transfer for an H coverage of 2/9 ML, the adsorption structures for an H coverage of 1/3 ML are similar (Table 4), except for the formation of H2. Comparing the H coverage of 2/9 ML with that of 1/3 ML, the adsorption energies of two H atoms on Al (111) surface basically remain the same for the same adsorption behaviour, which is equal to the sum of single H atom adsorption on the same site. The reason is that the distance between H–H (see Table 4) is much larger than the sum of radius of H atom (∼1.6 Å) so that there is no interaction between H atoms. We infer that the coverage of H has no obvious effect on the adsorption behaviour, when H adsorb on Al (111) surface by the form of atom. H2 produces when the H–H distance is small enough for H2 to form at the initial structure H(fcc)–H(bridge) or H(hcp)–H(bridge) at the H coverage of 1/3 ML. The phenomenon is not observed at an H coverage of 2/9 ML indicating that the formation of H2 is related with to the coverage of H atoms. We infer that the formation of H2 will become easier as the H coverage increases. The generation of H2 can cause hydrogen blistering theory,49 which is an important factor for HE.
| Coverage (ML) | Stable structures | Average distance (Å) | Adsorption energy (eV) | Charge transfer | |||
|---|---|---|---|---|---|---|---|
| Al–H(fcc) | Al–H(top) | H–H | H(fcc) | H(top) | |||
| 2/9 | H(fcc)–H(fcc) | 1.92 | — | 2.71 | 4.07 | 0.90 | — |
| H(fcc)–H(top)–S | 1.90 | 1.62 | 2.38 | 3.90 | 0.90 | 0.62 | |
| H(fcc)–H(top)–L | 1.93 | 1.62 | 3.45 | 3.89 | 0.90 | 0.60 | |
| H(top)–H(top)–S | — | 1.62 | 2.85 | 3.70 | 0.58 | 0.58 | |
| H(top)–H(top)–L | — | 1.62 | 4.94 | 3.77 | 0.60 | 0.60 | |
| 1/3 | H(fcc)–H(fcc) | 1.93 | — | 2.68 | 4.20 | 0.90 | — |
| H(fcc)–H(top)–S | 1.90 | 1.62 | 2.34 | 3.93 | 0.90 | 0.61 | |
| H(fcc)–H(top)–L | 1.93 | 1.63 | 3.35 | 3.92 | 0.88 | 0.62 | |
| H(top)–H(top)–S | — | 1.62 | 2.85 | 3.70 | — | 0.57 | |
| H(top)–H(top)–L | — | 1.62 | 4.91 | 3.77 | — | 0.59 | |
| H2 formation | — | — | 0.75 | 4.52 | — | — | |
3.2 Diffusion pathways for hydrogen from surface to bulk
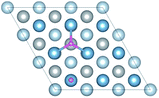
The diffusion properties of H atoms provides a good reference for H atoms segregation at GBs. The diffusion pathways of H atom are investigated using a TSS method at an H coverage of 1/9 ML to gain an insight into the transition from surface to bulk diffusion. There are multiple possible pathways for diffusion from fcc, the stable adsorption site, to bulk OIS2, the stable solution site. As shown in Fig. 7a, the H atom jumps from the top site to the fcc site on the surface with a diffusion energy barrier of 7.02 kJ mol−1, which is higher than that of H diffusion along the top–bridge–fcc pathway (3.66 kJ mol−1) or the top–hcp–bridge pathway (3.71 kJ mol−1). In contrast, the energy barriers of the fcc–top, fcc–bridge and fcc–hcp pathways, which are 17.79, 8.24 and 13.73 kJ mol−1 respectively, are higher. This indicates that the H atom at the top site prefers to jump through the bridge or hcp site to the fcc site. However, diffusion from fcc site to other sites on the surface is difficult.For the diffusion from surface to subsurface, we considered the diffusion path from the bridge, fcc and hcp sites on the surface to the TIS1-1, TIS1-2 and OIS1 sites on the subsurface. The diffusion energy barriers for the H atom jumping bridge to TIS1-1, bridge to OIS1, fcc to TIS1-1, fcc to OIS1, hcp to TIS1-1 and hcp to OIS1 are 47.98, 43.28, 49.88 and 54.15, 40.15 and 50.22 kJ mol−1, respectively. Thus, it is much more difficult for the H atom to jump from surface to subsurface than to different sites on the surface. We infer that this higher energy barrier is due to the change of the number of neighboring Al atoms around H atom. The migrations of the H atom within the subsurface are also investigated. The energy barriers between the TISs, TIS1-1 and TIS1-2, are 14.58 kJ mol−1 and 24.28 kJ mol−1, which indicates that the two TISs are not equally site influenced by the surface. The energy barriers of TIS1-1–OIS1 and TIS1-2–OIS1 are 7.54 kJ mol−1 and 13.06 kJ mol−1, respectively.
For the diffusion of the H atom from subsurface to bulk, four pathways, namely, TIS1-1–TIS2, TIS1-2–OIS2, OIS1–TIS2 and OIS1–OIS2, were considered. The energy barriers for the four pathways are 15.73, 24.41, 17.44 and 16.58 kJ mol−1, respectively. For the migration of H the atom within the bulk material, TIS2–OIS2, the energy barrier is 16.75 kJ mol−1.
In conclusion, the optimal diffusion pathway of H from the surface to the bulk is fcc–hcp–TIS1-1–TIS2, as shown in Fig. 7b. The H atom at the fcc site jumps to the subsurface TIS1-1 site through the hcp site and finally reaches the TIS2 bulk site. The transition state (TS) of the fcc–hcp path occurs at the hcp site and the energy barrier is 13.73 kJ mol−1. The TS for the hcp–TIS1-1 pathway occurs at the position close to the TIS1-1 site with a much higher energy battier of 40.15 kJ mol−1. The diffusion energy barrier for the TIS1-1–TIS2 path decreases to 15.73 kJ mol−1 and the TS occurs at the 3/4 site between the TIS1-1 and the TIS2 sites.
3.3 The effect of hydrogen on intergranular cracking of Al alloys
H atoms prefer to diffuse from an outer environment to the bulk along GBs50 where the energy barrier for diffusion is much lower than that at a complete surface. The ability to resist intergranular cracking is related to the strength of the GBs, which can be quantified using the cohesive energy. The cohesive energy is determined by the surface energy and GB energy. The surface energies of the (111), (100) and (110) planes are 1.06 J m−2, 1.25 J m−2 and 1.28 J m−2, respectively, and are consistent with previous calculation and experimental results.51 The energies of the more than 10 types of GBs generated by [110], [100] and [111] twist angles with different misorientations are shown in Table 6 and are consistent with previous work.52,53 The energies of the GB with a [110] twist angle indicate that there is no obvious fluctuation with the increasing of misorientation but that there is a greater energy gap between different twist angles. The cohesive energy of the GBs have been calculated using eqn (1)–(3) with the first-principle method. The cohesive energy varies little for the GBs with the same twist angle because the same surface energy and similar GBs energies. The cohesive energies of GB [001]/22.6°, [011]/38.9°, and [111]/60° with different H concentrations have been calculated using eqn (4)–(6). The cohesive energy decreases linearly with the increasing H atoms concentrations (see Fig. 8), which indicates a hydrogen induced decohesion of HE mechanism. Comparing the slope of the lines, the effect of H on the decohesion for the three GBs is different. The cohesive energies of GBs with the same H concentrations are determined by their initial values and its descending rate.| Twist axis | Misorientation ° | γ GB J m−2 | γ surf J m−2 | E coh J m−2 |
|---|---|---|---|---|
| [110] | 9.45 | 0.69 | 1.28 | 1.87 |
| [110] | 10.02 | 0.65 | 1.91 | |
| [110] | 13.7 | 0.66 | 1.90 | |
| [110] | 14.42 | 0.59 | 1.97 | |
| [110] | 19.47 | 0.66 | 1.90 | |
| [110] | 22 | 0.67 | 1.89 | |
| [110] | 29.5 | 0.69 | 1.87 | |
| [110] | 31.59 | 0.60 | 1.96 | |
| [110] | 35.26 | 0.63 | 1.93 | |
| [110] | 44.71 | 0.63 | 1.93 | |
| [111] | 21.79 | 0.25 | 1.06 | 1.87 |
| [111] | 30 | 0.18 | 1.94 | |
| [100] | 22.6 | 0.35 | 1.25 | 2.15 |
| [100] | 28.07 | 0.41 | 2.09 | |
| [100] | 36.87 | 0.25 | 2.25 |
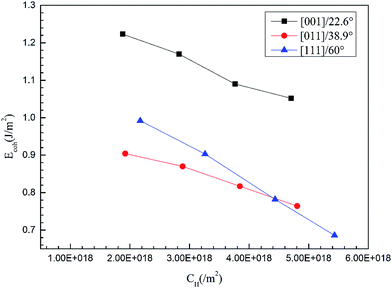 | ||
| Fig. 8 The cohesive energies of GBs [001]/22.6°, [011]/38.9°, and [111]/60° as a function of H concentrations. | ||
3.4 The CFE simulation of intergranular cracking
To further investigate the hydrogen induced decohesion for GBs, the evolution of intergranular cracks is explored using a CFE method. It begins to appear slight stress concentration in GBs instead of cracks, when the cohesive energy decreases to about 1.5 J m−2. So we set eight linearly decreasing values of the cohesive energies less than 1.5 are adopted to simulate the intergranular cracking behaviour of the 2024 Al alloy described in Section 2.2. The cohesive energies and other input parameters according to the traction–separation law for the CFE calculation in Table 7.| G c = Ecoh (mJ mm−2) | T 0n (MPa) | K nn (MPa) | K ss = Ktt (MPa) |
|---|---|---|---|
| 1.406 × 10−3 | 140.6 | 140.66 × 106 | 52.86 × 106 |
| 1.336 × 10−3 | 133.6 | 133.6 × 106 | 50.23 × 106 |
| 1.265 × 10−3 | 126.5 | 126.5 × 106 | 47.56 × 106 |
| 1.195 × 10−3 | 119.5 | 119.5 × 106 | 44.92 × 106 |
| 1.125 × 10−3 | 112.5 | 112.5 × 106 | 42.29 × 106 |
| 1.055 × 10−3 | 105.5 | 105.5 × 106 | 39.66 × 106 |
| 0.984 × 10−3 | 98.4 | 98.4 × 106 | 36.99 × 106 |
| 0.914 × 10−3 | 91.4 | 91.4 × 106 | 34.36 × 106 |
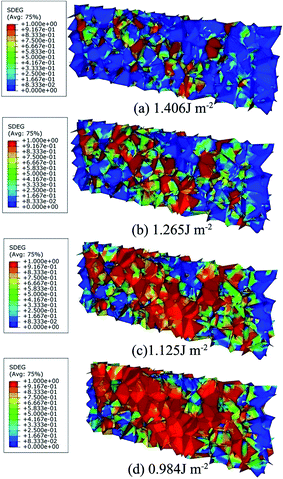
Fig. 9 shows the Mises stress nephogram of 3D polycrystal model with different fracture energies. The stress is inhomogeneously distributed in the model because the grains are randomly orientated. The microcracks usually initiates at a triple line (marked by white arrows) where several grains come together on the surfaces or in the interior of the material. Although there is a stress concentration (marked by red box) at the GBs, no obvious cracks are found on the surface for a fracture energy of 1.406 J mol−1. When the fracture energy decreases to 1.265 J mol−1, the stress concentrations expend from the GBs to the interior of the grains, producing microcracks. The stress concentrations are relaxed because of the crack propagation when the fracture energy is 1.125 J mol−1 and multiple cracks are observed on the surface. The cracks propagate along GBs, which may lead to the fracture of the polycrystal as the fracture energy decreases further.
Fig. 10 shows the GB damage evolution defined as scalar stiffness degradation (SDEG) according to different fracture energies. The red cohesive elements (SDEG = 1) have failed, suggesting that cracks initiated. To quantify the degree of the damage, the number of failed cohesive elements is determined.
Fig. 11 shows that the percentage of failed elements increases with decreasing fracture energy and that the descending rate firstly increases and then decreases. The polycrystal fractures completely when the descending rate of damage approaches zero. Fig. 12 shows the relationship between the percentage of failed elements and the deformation displacement of polycrystal with different fracture energies. The percentage of failed elements increases with the increasing of deformation displacement. For equivalent deformation displacement, the polycrystal with a lower fracture energy fractures more easily.
 | ||
| Fig. 11 The percentage of failed cohesive elements (Ddam) as a function of cohesive energies (Ecoh) under uniaxial tension. | ||
 | ||
| Fig. 12 The relationship between the percentage of failed cohesive elements and deformation displacement of the polycrystalline models under the uniaxial tension with different cohesive energies. | ||
The results of the CFE calculations reveal that the initiation and propagation of cracks is closely associated with the fracture energy, which is sensitive to the H concentrations segregated in the GBs. The simulation is a good representation for the hydrogen-induced decohesion of GBs HE mechanism.
4. Conclusions
The approach presented here combines first-principles and CFE calculations to investigate the effect of H atoms on intergranular cracking from an atomic scale to a grain level. The effects of H atoms on intergranular embrittlement from the adsorption and diffusion of H atoms to intergranular cracking induced by H segregation was studied. The simulations and calculations investigated the intergranular embrittlement mechanism from an energy standpoint. The new approach realizes the cross-scale calculation via the calculation of cohesive energy. H atoms can be adsorbed on fcc site and top site. Fcc site is the most stable H-adsorbed site on Al (111) surface at the coverages of 1/9, 2/9 and 1/3 ML, and top site takes second place. H2 can be generated when the coverage of H atoms increases to 1/3 ML. The optimal diffusion pathway from the most stable surface fcc site to the TIS site which is more stable than OIS in bulk, is fcc–hcp–TIS1-1–TIS2. The migration of H atom is easier on surface than that in the interior and H atom must overcome a higher energy barrier to move from surface to subsurface. Subsequently, the energy barrier for bulk migration of the H is lower. The segregation of H atoms at GBs weakens the strength of GBs. The cohesive energies of GBs decrease linearly with increasing of H concentrations. Thus CFE calculations effectively simulate the evolution of intergranular cracking, which is a good representation for HE of hydrogen induced decohesion for GBs.Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 51222106), the Fundamental Research Funds for the Central Universities (No. 230201306500002) and National Basic Research Program of China (973 Program) (No. 2014CB643300).References
- P. V. Petroyiannis, A. T. Kermanidis, P. Papanikos and Sp. G. Pantelakis, Theor. Appl. Fract. Mech., 2004, 41, 173–183 CrossRef CAS.
- R. G. Song, W. Dietzel, B. J. Zhang, W. J. Liu, M. K. Tseng and A. Atrens, Acta Mater., 2004, 52, 4727–4743 CrossRef CAS.
- F. Y. Guo, C. G. Long, J. Zhang, Z. Zhang, C. H. Liu and K. Yu, Appl. Surf. Sci., 2015, 324, 584–589 CrossRef CAS.
- R. J. Gest and A. R. Troiano, Corrosion, 1974, 30, 274–279 CrossRef CAS.
- E. Pouillier, A.-F. Gourgues, D. Tanguy and E. P. Busso, Int. J. Plast., 2012, 34, 139–153 CrossRef CAS.
- H. Matsui, H. Kimura and S. Moriya, J. Mater. Sci. Eng., 1979, 40, 207–216 CrossRef CAS.
- G. Bertolino, G. Meyer and J. Perez Ipiña, J. Alloys Compd., 2002, 330–332, 408–413 CrossRef CAS.
- H. Ji, I. I.-J. Park, S.-M. Lee and Y.-K. Lee, J. Alloys Compd., 2014, 598, 205–212 CrossRef CAS.
- A. Troiano, Trans. ASM, 1960, 52, 54–80 Search PubMed.
- J. Hirth, Metall. Trans. A, 1980, 11, 861–890 CrossRef.
- D. F. Teter, I. M. Robertson and H. K. Birnbaum, Acta Mater., 2001, 49, 4313–4323 CrossRef CAS.
- M. Koyama, C. C. Tasan, E. Akiyama, K. Tsuzaki and D. Raabe, Acta Mater., 2014, 70, 174–187 CrossRef CAS.
- P. J. Ferreira, I. M. Robertson and H. K. Birnbaum, Acta Mater., 1998, 46, 1749–1757 CrossRef CAS.
- M. Niwa, T. Shikama and A. Yonezu, J. Mater. Sci. Eng. A, 2015, 624, 52–61 CrossRef CAS.
- J. Song and W. A. Curtin, Acta Mater., 2011, 59, 1557–1569 CrossRef CAS.
- Z. Guo, M. Zhao, C. Li, S. Chen and L. Rong, J. Mater. Sci. Eng. A, 2012, 555, 77–84 CrossRef CAS.
- O. M. Alyousif and R. Nishimura, Corros. Sci., 2012, 52, 7–13 CrossRef.
- Y. Wang, X. Wang, J. Gong, L. Shen and W. Dong, Int. J. Hydrogen Energy, 2014, 39, 13909–13918 CrossRef CAS.
- L. Zhang, Z. Li, J. Zheng, Y. Zhao, P. Xu, C. Zhou and X. Li, Int. J. Hydrogen Energy, 2013, 38, 8208–8214 CrossRef CAS.
- A. Barnoush and H. Vehoff, Acta Mater., 2010, 58, 5274–5285 CrossRef CAS.
- A. Barnoush and H. Vehoff, Corros. Sci., 2008, 50, 259–267 CrossRef CAS.
- S. G. Xu and Y. L. Zhao, Eng. Failure Anal., 2013, 34, 24–34 CrossRef CAS.
- M. Kikuchi, Y. Wada, Y. Shimizu and Y. L. Li, Int. J. Pressure Vessels Piping, 2012, 90–91, 2–8 CrossRef CAS.
- T. Luther and C. Konke, Eng. Fract. Mech., 2009, 76, 2332–2343 CrossRef.
- P. Zhang, M. Karimpounr, D. Balint, J. Lin and D. Farrugia, Comput. Mater. Sci., 2012, 64, 84–89 CrossRef.
- I. Simonovski and L. Cizelj, Comput. Mater. Sci., 2011, 50, 1606–1618 CrossRef.
- J. Zhang, Z. H. Chen and C. F. Dong, J. Mater. Eng. Perform., 2015, 24, 4908–4918 CrossRef CAS.
- I. Simonovski and L. Cizelj, Eng. Fract. Mech., 2013, 110, 364–377 CrossRef.
- V. V. Bulatov, B. W. Reed and M. Kumar, Surf. Sci., 2014, 65, 161–175 CAS.
- L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollár, Surf. Sci., 1998, 411, 186–202 CrossRef CAS.
- P. J. Feibelman, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 13740–13746 CrossRef CAS.
- M. Yamamoto, C. T. Chan and K. M. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 7932–7939 CrossRef CAS.
- W. R. Tyson and W. A. Miller, Surf. Sci., 1977, 62, 267–276 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, J. Phys. Chem. B, 1996, 54, 11169–11186 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev. A, 1965, 140, 1133–1138 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew and K. Burke, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- R. F. W. Bader, Atoms in Molecules-A Quantum Theory, Oxford University Press, New York, 1990 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- R. Quey, P. R. Dawson and F. Barbee, Comput. Meth. Appl. Mech. Eng., 2011, 200, 1729–1745 CrossRef.
- M. N. Krivosheina, S. V. Kobenko and M. A. Kozlova, J. Phys.: Conf. Ser., 2009, 181, 012083 CrossRef.
- T. Luther and C. Konle, Eng. Fract. Mech., 2009, 76, 2332–2343 CrossRef.
- P. Zhang, M. Karimpounr, D. Balint, J. Lin and D. Farrugia, Comput. Mater. Sci., 2012, 64, 84–89 CrossRef.
- I. Simonovski and L. Cizelj, Comput. Mater. Sci., 2011, 50, 1606–1618 CrossRef.
- H. B. Michaelson, J. Appl. Phys., 1977, 48, 4729–4733 CrossRef CAS.
- J. B. Condon and T. Schober, J. Nucl. Mater., 1993, 207, 1–24 CrossRef CAS.
- A. Oudriss, J. Creus, J. Bouhattate, C. Savall, B. Peraudeau and X. Feaugas, Scr. Mater., 2012, 66, 37–40 CrossRef CAS.
- L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollár, Surf. Sci., 1998, 411, 186–202 CrossRef CAS.
- V. V. Bulatov, B. W. Reed and M. Kumar, Acta Mater., 2014, 65, 151–175 CrossRef.
- D. L. Olmsted, S. M. Foiles and E. A. Holm, Acta Mater., 2009, 57, 3694–3703 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |