 Open Access Article
Open Access ArticleField-induced slow relaxation of magnetization in dinuclear and trinuclear CoIII⋯MnIII complexes†
Ivan Nemec ,
Radovan Herchel
,
Radovan Herchel ,
Zdeněk Trávníček* and
Tomáš Šilha
,
Zdeněk Trávníček* and
Tomáš Šilha
Regional Centre of Advanced Technologies and Materials & Department of Inorganic Chemistry, Faculty of Science, Palacký University, 17. listopadu 12, 771 46 Olomouc, Czech Republic. E-mail: zdenek.travnicek@upol.cz; Fax: +420 585 634 954
First published on 22nd December 2015
Abstract
Two new dinuclear, [Co(3EtO-L5)(μ-CN)Mn(L4a)Cl] (1) and [Co(3EtO-L5)(μ-CN)Mn(L4a)Br] (2), and two trinuclear [{Co(3EtO-L5)(μ-CN)}2Mn(L4a)]I (3) and [{Co(3EtO-L5)(μ-CN)}2Mn(L4a)](NO3) (4) complexes were prepared and thoroughly characterized (H23EtO-L5 = N,N′-bis(3-ethoxy-2-hydroxybenzylidene)-1,6-diamino-3-azahexane, L4a2− = N,N′-ethane-bis(salicylideneiminate)dianion). The crystal structures were determined for all four compounds, while the static and dynamic magnetic properties were studied only for compounds 1–3. It has been revealed by simultaneous fitting of temperature and field dependent magnetic data and by using the spin Hamiltonian formalism involving the axial anisotropy term that the manganese(III) atoms possess relatively large and negative axial magnetic anisotropy in 1–3, with D = −3.9(2) cm−1 in 1, −4.9(2) cm−1 in 2, and −4.1(1) cm−1 in 3. These results were supported by ab initio CASSCF calculations which were in good agreement with the experimental ones, however, a small rhombicity was calculated contrary to the experimental evaluations: Dcalc(Ecalc/Dcalc) = −3.2 cm−1 (0.04) in 1, −3.0 cm−1 (0.03) in 2, and −3.6 cm−1 (0.04) in 3. The measurements of dynamic magnetic data confirmed that compounds 1–3 represent a new type of Mn(III) field-induced single-ion magnet. The peak maxima of the frequency dependent out-phase susceptibility were below the lowest accessible temperature in all the three cases (i.e. below 1.9 K) and this prevented us from the construction of the Argand diagram. Nevertheless, the approximate procedure for extracting the spin-reversal barrier (Ueff) and relaxation time (τ0) was used, and the values of Ueff ranging from 11 to 20 K and t0 from 0.1 to 19 × 10−7 s were obtained.
Introduction
Compounds exhibiting slow relaxation of magnetization (SRM), so called single-molecule magnets (SMMs), attract great attention in the field of molecule-based magnetic materials research. Their potential utilization in molecular spintronics and information storage devices has been intensively studied.1 SMMs can behave as molecular nanomagnets possessing distinct magnetic states separated by an energy barrier for spin reversal, while the height of this barrier is controlled by magnetic anisotropy of paramagnetic centre/centres of a molecule. Therefore, the rational design of such materials consists mostly of tuning of uniaxial magnetic anisotropy to large negative values (described by the zero-field splitting parameter D); however, there are several examples of mononuclear compounds exhibiting SRM and having positive D values.2The MnIII atom in a hexacoordinate environment is due to its electronic structure in the high-spin state (HS, S = 2, t32g e1g, 5E ground spectroscopic term) subject of Jahn–Teller distortion.3 As a result, a significant prolongation of two opposite chromophore bond lengths and thus formation of an axially elongated tetragonal bipyramidal coordination polyhedron is observed. This geometry is favourable for the occurrence of relatively large and negative uniaxial magnetic anisotropy, as it was observed on numerous examples previously.4 Therefore, paramagnetic compounds involving the MnIII atoms are the promising objects for the preparation and study of compounds exhibiting SRM. Especially, the MnIII compounds involving tetradentate salen-like Schiff base ligands [L42− stands for a general abbreviation of a tetradentate salen-like ligand, salen2− = N,N′-ethane-bis(salicylideneiminate) dianion, further abbreviated as L4a2−,] are the auspicious candidates for the preparation of magnetically interesting compounds. This is due to the ability of L42− compounds to act as ligands forming the equatorial plane in complexes with axially elongated coordination geometries with expectable negative magnetic anisotropy. Previous reports on the observation of SRM in [MnIII(L4)]-type compounds dealt with three basic structural types, i.e. polynuclear compounds (a) involving the [MnIII(L4)]+ subunit coordinated by bridging ligands or complexes,5 (b) involving the phenoxo bridged dimeric subunits [{MnIII(L4)}2]2+ which are further coordinated in apical positions by ligands/complexes,6 and (c) involving the [MnIII(L4)(Solv)]+ subunits (Solv = water or alcohol molecule) coordinated by cyanidometallates.7 In the latter group, the very first example of the MnIII SMM with only one paramagnetic centre (so called Single-Ion Magnet, SIM) has been reported recently. The heterobimetallic CoIII–CN–MnIII compound shows relatively small negative D = −3.3 cm−1 and SRM occurs below 3 K.8
Previously, we reported on heterobimetallic [CoIII(3EtO-L5)(μ-CN)FeIII(L4a)Cl] compound (further abbreviated as CoFeCl, where H23EtO-L5 = N,N′-bis(3-ethoxy-2-hydroxybenzylidene)-1,6-diamino-3-azahexane), having relatively large magnetic anisotropy (D = +1.47 cm−1) on a usually very isotropic FeIII atom. This was most probably caused by a rather long NCN–Fe–Cl axial formed by bond lengths Fe–NCN = 2.236(2) and Fe–Cl = 2.4075(7) Å (NCN = the cyanido nitrogen atom).9 Inspired by these findings we attempted to prepare the MnIII analogues of the aforementioned compounds, which should possess large uniaxial magnetic anisotropy accentuated by the expected axially elongated tetragonal bipyramidal coordination polyhedron of the MnIII atom. Furthermore, in order to analyse the influence of the halido ligand exchange on magnetic properties, we tried to prepare a series of CoMnX compounds (with X = F−, Cl−, Br−, I−). However, we were able to prepare only two isostructural compounds with the formulas [Co(3EtO-L5)(μ-CN)Mn(L4a)Cl] (1) and [Co(3EtO-L5)(μ-CN)Mn(L4a)Br] (2). The other syntheses involving iodide and fluoride anions resulted in [{Co(3EtO-L5)(μ-CN)}2{Mn(L4a)]I (3) and [{Co(3EtO-L5)(μ-CN)}2Mn(L4a)](NO3) (4). Herein, we report on the syntheses, crystal structures (1–4) and thorough investigations of magnetic properties of the compounds 1–3. While our main intention was to study influence of the different axial ligand fields (and different axial lengths) on magnetic anisotropy of the Mn(III) atom, the magnetic properties of 4 were not studied due to the structural similarity with compound 3.
Results
Synthesis
Compounds 1, 2 and 3 were prepared in a similar way. The [Co(3EtO-L5)(CN)] precursor complex9 was mixed with the corresponding [Mn(L4a)X] or [Mn(L4a)(H2O)]I compounds (X = Cl− in 1, Br− in 2) in methanol and they were stirred under heating for 15 minutes. The solution was filtered to a beaker and left to cool down. Then, the beaker was sealed with aluminium foil and placed in a big flask with diethyl ether. Single crystals of high quality were obtained by slow diffusion of diethyl ether to the mother liquor. The products of the first two reactions were identified as [Co(3EtO-L5)(μ-CN)Mn(L4a)Cl] (1) and [Co(3EtO-L5)(μ-CN)Mn(L4a)Br] (2), while the described reaction resulted in an unexpected trinuclear product [{Co(3EtO-L5)(μ-CN)}2{Mn(L4a)]I (3, Scheme 1) in the case of the iodido precursor complex. The attempts to synthesise the fluoride analogous of 1 and 2 were performed in two distinct ways. Firstly, the previously reported polymeric [Mn(L4a)(μ-F)]n compound10 was reacted with [Co(3EtO-L5)(CN)] in methanol. The length of heating and stirring varied from 15 minutes to 24 hours. However, the slow diffusion of diethyl ether led only to crystallization of the precursor complexes in every case. Secondly, in order to avoid the formation of the [Mn(L4a)(μ-F)]n polymer we used the [Mn(L4a)Cl] precursor, which was subsequently reacted with AgNO3 (AgCl was filtered off) in methanol. Then, the solution was mixed with the solid of [Co(3EtO-L5)(CN)] and NaF was added after 10 min of stirring. After 30 minutes of heating and stirring, the reaction mixture was filtered, cooled down and left to undergo slow-diffusion of diethyl ether as in the previous cases. The resulting crystalline product did not contain fluoride anions and again as in the case of 3, it was a trinuclear complex with the formula of [{Co(3EtO-L5)(μ-CN)}2Mn(L4a)](NO3) (4).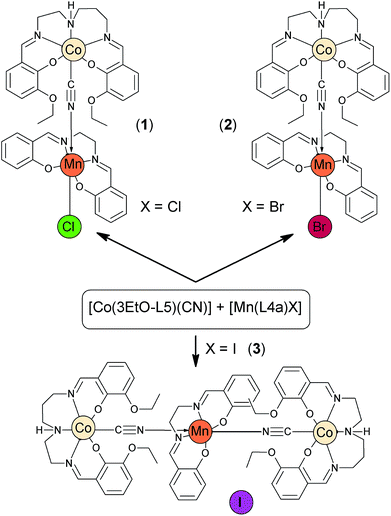 | ||
| Scheme 1 Schematic representations of complexes 1–3 and their preparations. Note: the preparation of complex 4 is described in the text below. | ||
Crystal structure of 1 and 2
The crystal structures of 1 and 2 are isostructural, crystallizing in monoclinic space group P21 (Table 1) and they are also isostructural with the previously reported compound [Co(3EtO-L5)(μ-CN)Fe(L4a)Cl].9| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| a R1 = ∑(|Fo| − |Fc|)/∑|Fo|.b wR2 = {∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]}1/2. | ||||
| Formula | C40H43N6O6Cl1Co1Mn1 | C40H43N6O6Br1Co1Mn1 | C64H72N10O10I1Co2Mn1 | C64H72N10O10Co2Mn1 |
| Mr | 853.12 | 897.58 | 1441.01 | 1314.14 |
| Crystal system | Monoclinic, P21 | Monoclinic, P21 | Monoclinic, P21c | Monoclinic, C2c |
| a/Å | 8.5566(3) | 8.5862(3) | 12.0234(5) | 35.108(2) |
| b/Å | 19.8560(7) | 19.6159(8) | 18.2991(9) | 9.1128(4) |
| c/Å | 11.1842(3) | 11.3835(4) | 27.7995(9) | 23.8187(18) |
| β/° | 100.397(3) | 100.884(4) | 93.97(3) | 126.0410(10) |
| V/Å3 | 1868.99(11) | 1882.79(12) | 6101.7(5) | 6161.7(6) |
| Z | 2 | 2 | 4 | 4 |
| Dc/g cm−3 | 1.516 | 1.583 | 1.569 | 1.417 |
| μ/mm−1 | 0.910 | 1.894 | 1.316 | 0.801 |
| F(000) | 884 | 920 | 2952 | 2739 |
| Reflections collected/unique | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300/6236 300/6236 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736/6070 736/6070 |
44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514/10 514/10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 625 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 119/5246 119/5246 |
| Data/restraints/parameters | 6236/1/481 | 6070/1/499 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625/2/804 625/2/804 |
5246/2/378 |
| Goodness-of-fit (GOF) on F2 | 0.978 | 0.933 | 0.866 | 0.922 |
| R1, wR2 (I > 2σ(I))a,b | 0.0272/0.0596 | 0.0297/0.0560 | 0.0441/0.0872 | 0.0338/0.0785 |
| R1, wR2 (all data)a,b | 0.0317/0.0606 | 0.0376/0.0574 | 0.0939/0.0809 | 0.0519/0.0816 |
| CCDC number | 1434760 | 1434761 | 1434762 | 1434763 |
The crystal structures of 1 and 2 consist of dinuclear [Co(3EtO-L5)(μ-CN)Mn(L4a)X] (X = Cl, and Br, respectively) molecules in which the metal atoms are bridged by the cyanido ligand (Co–CN–Mn linkage, Fig. 1). The arrangement of the metal atoms and the bridging ligand is slightly bent with the Co–C–Mn angles equal to 163.6° in 1 and 163.7° in 2. The CoIII centre is coordinated by three nitrogen and two oxygen atoms from the 3EtO-L52− ligand. The sixth coordination site is occupied by the carbon atom from the bridging cyanido ligand. The chromophore bond lengths are typical for the low-spin (LS) state with the lengths ranging from 1.89 to 1.91 Å for Co–C, from 1.91 to 1.96 Å for Co–N, and from 1.90 to 1.91 Å for Co–O bonds (Table 2). The coordination polyhedrons of the CoIII atoms can be described as slightly distorted octahedrons in both compounds. The MnIII central atoms are also hexacoordinate with four equatorial donor atoms (N2O2) coming from the L4a2− ligand. The axial ligands are represented by one cynido nitrogen (NCN) and one halogen atom, thus forming the {MnN3O2Cl} (1) and {MnN3O2Br} (2) chromophores. The bond lengths within the equatorial plane are significantly shorter than those in axial due to the Jahn–Teller effect on the MnIII atoms. This can be documented by the comparison of the Mn–N bond lengths: the equatorial manganese–imino nitrogen (Mn–Nim) bond lengths are much shorter (1.91–1.95 Å) than the axial Mn–NCN bond lengths (2.380(3) in 1 and 2.325(4) Å in 2). The Jahn–Teller prolongation of the bond lengths along the axis of the dz orbitals is further accentuated by long Mn–X lengths (2.5498(10) in 1 and 2.7394(8) Å in 2). When comparing these values with the bond lengths in the previously reported CoFeCl compound, the Jahn–Teller effect in the MnIII compounds is even more apparent: d(Fe–NCN) = 2.236(2) Å and d(Fe–Cl) = 2.4075(7) Å.9
In the crystal structures of 1 and 2, the dinuclear molecules are connected through the N–H⋯X hydrogen bonds, which arranges the individual molecules into one dimensional polymeric supramolecular chains, (Fig. 2) with d(N⋯Cl) = 3.189(3) in 1 and d(N⋯Br) = 3.306(4) Å in 2. The prolongation of the donor⋯acceptor distances upon substitution of the halido ligand reflects the decrease in the halide electronegativity along with growing atomic radius and polarizability.
Crystal structures of 3 and 4
The crystal structures of 3 and 4 are similar and they are composed of trinuclear [{Co(3EtO-L5)(μ-CN)}2Mn(L4a)]+ cations which are charge balanced by iodide (in 3) or nitrate (in 4) anions. The geometry of the trinuclear Co–CN–Mn–NC–Co fragment is bent with the Co–Mn–Co angle equal to 157.9° in 3 and 159.2° in 4 (Fig. 1). In 3, the whole trinuclear complex molecule is in the asymmetric unit, while in 4, a two-fold rotational axis goes through the manganese atom, and therefore only a half of the complex molecule is symmetrically independent. Similarly to 1 and 2, the CoIII coordination polyhedrons in 3 and 4 can be described as slightly distorted octahedrons with the {CoN3O2C} chromophores. The chromophore bond lengths correspond to the LS nature of the CoIII centre with the lengths ranging from 1.89 to 1.90 Å for Co–C, from 1.91 to 1.97 Å for Co–N, and from 1.90 to 1.91 Å for Co–O bonds (Table 2). The MnIII atom is hexacoordinate with the {MnN4O2} chromophores in both compounds. The bond lengths within the equatorial planes are very similar to those found in 1 and 2 (d(Mn–Nim) = 1.97–1.98 Å, d(Mn–O) = 1.88–1.89 Å, Table 2). The axial is formed by two NCN atoms from two coordinated [Co(3EtO-L5)(CN)] fragments. Again, due to the Jahn–Teller effect long axial bonds are observed as follows: d(Mn–NCN) = 2.283(3), 2.347(3) Å in 3 and 2.316(2) in 4 (two Mn–NCN bonds are equivalent due to symmetry). It can be concluded that compounds 3 and 4 have a slightly shorter axial than compounds 1 and 2 (Table 2).In the crystal structure of 3 the trinuclear complex molecules are assembled in 1D supramolecular chains through N–H⋯O hydrogen bonding between the nitrogen atoms from the amine groups and oxygen atoms from the ethoxy groups; both located on the [Co(3EtO-L5)(CN)]− moieties of neighbouring trinuclear complex molecules. Each complex molecule is held by its in-chain neighbour by two N–H⋯O hydrogen bonds thus forming a synthon with the R22(14) ring topology (Fig. 2).11 The distances of these non-covalent contacts are rather long: d(N⋯O) = 3.307(4) and 3.168(4) Å.
The crystal structure of 4 consists of [{Co(3EtO-L5)(μ-CN)}2Mn(L4a)]+ molecules held together by N–H⋯O hydrogen bonding between the nitrogen atom from the amine group and ethoxy group with the distance d(N⋯O) = 3.173(4) Å. Packing of the [{Co(3EtO-L5)(μ-CN)}2Mn(L4a)]+ molecules in the crystal structure of 4 is rather different from packing observed for 3; the complex molecules form a 2D layer structure in which each trinuclear complex interacts with four other complex molecules via four N–H⋯O hydrogen bonds (Fig. 3). Due to the two fold rotational axis on the manganese(III) atom together with inversion centres located in between the molecules only one of these four hydrogen bonds is symmetrically independent. Its length is rather long again: d(N⋯O) = 3.173(4) Å.
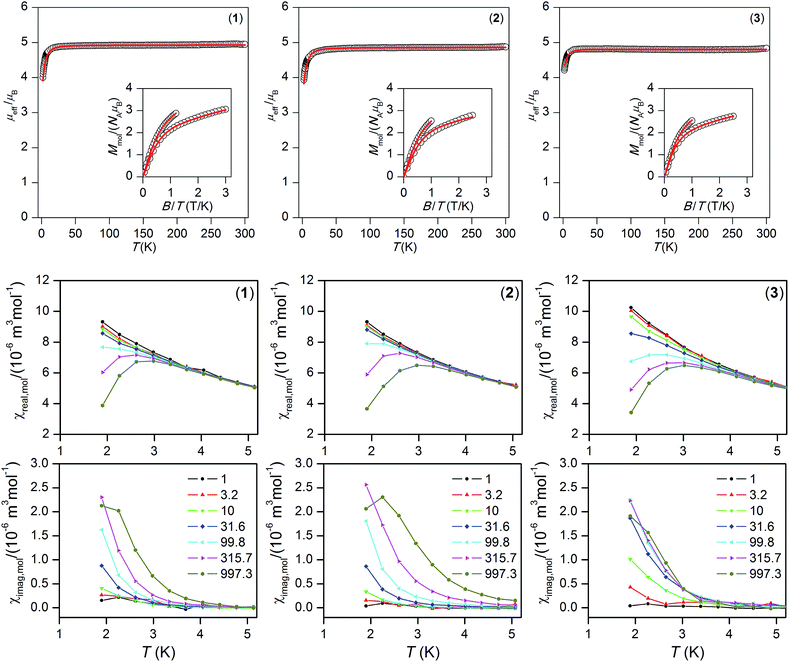 | ||
| Fig. 3 Top: the temperature dependence of the effective magnetic moment derived from molar magnetization measured at B = 0.1 T and reduced isothermal magnetizations measured at T = 2 and 5 K. Empty circles: experimental data. Red full lines: calculated data using eqn (1), with parameters listed in Table 1. Bottom: AC susceptibility data measured at non-zero static magnetic field, BDC = 0.4 T. Lines serve as guides for the eyes. | ||
Static magnetic properties
The temperature and field dependent magnetic properties of compounds 1–3 were measured on a SQUID magnetometer and are depicted in Fig. 3. The room temperature value of the effective magnetic moment μeff is found in the range of 4.8–4.9 μB, which is close to the spin-only value for S = 2 equal to 4.90 (g = 2.0). The μeff is almost constant down to 30 K, and then decreases to the value ≈ 4 μB which may indicate zero-field splitting on the MnIII atoms and also the possibly of weak intermolecular interactions. Moreover, the isothermal magnetizations do not saturate to Mmol/NAμB = 4.0 at maximum applied field for any of 1–3, which can be also explained by significant zero-field splitting. For that reason, the subsequent spin Hamiltonian, involving the single ion axial (D) and rhombic (E) ZFS parameters, Zeeman term and molecular field correction zj, were postulated12| Ĥ = D(Ŝz2 − Ŝ2/3) + E(Ŝx2 − Ŝy2) + μBBagŜa − zj〈Ŝa〉Ŝa | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, sin
φ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, cos
φ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). The molar magnetization in the a-direction of the magnetic field, Ma, was numerically calculated as
θ). The molar magnetization in the a-direction of the magnetic field, Ma, was numerically calculated as
 | (2) |
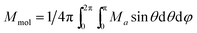 | (3) |
Both, temperature and field dependent magnetic data were fitted simultaneously in order to obtain a consistent set of parameters; however, we found that the fitting procedure was not sensitive enough to the rhombicity of the systems (E/D ratio), and so we fixed E/D = 0. This is also supported by multi-configurational complete active space self-consistent field (CASSCF) calculations, where E/D was found to be less than 0.04 (Table 3). Consequently, the single-ion axial ZFS parameter D was found in the range from −3.9 to −4.4 cm−1 (Fig. 3).13 These values are close to other MnIII complexes listed in Table 3.
| Compound {chromophore} | giso | D/cm−1 (E/cm−1) | zj/cm−1 | Ueff/K | t0/10−7 s | BDC/T |
|---|---|---|---|---|---|---|
| a Ligand abbreviations: 5-TMAM-(R)-salmen = (R)-N,N′-(1-methylethylene)bis(5-trimethylammoniomethylsalicylideneiminate); H4opbaCl2 = N,N′-3,4-dichloro-o-phenylenebis(oxamic acid), py = pyridine, Ph4P+ = tetraphenylphosphonium(1+); dbm = dibenzoylmethanido(1−); TBA = tetra-n-butylammonium(1+); DMSO = dimethyl sulfoxide. | ||||||
| 1 {MnO2N2N′Cl} | 2.013(3) | −3.9(2) | −0.10(1) | 12.9–20.2 | 0.13–2.9 | 0.20 |
| 12.2–13.9 | 1.3–6.1 | 0.40 | ||||
| 2 {MnO2N2N’Br} | 1.986(3) | −4.4(2) | −0.14(1) | 11.7–15.6 | 0.7–3.8 | 0.20 |
| 11.0–14.2 | 2.9–12.0 | 0.40 | ||||
| 3 {MnO2N2N′2} | 1.961(3) | −4.1(1) | +0.062(8) | 11.6–18.3 | 0.2–8.0 | 0.20 |
| 11.1–19.3 | 0.2–19.2 | 0.40 | ||||
| [Mn(5-TMAM(R)-salmen)(H2O)Co(CN)6]·7H2O·MeCN (ref. 8) {MnO2O′N2N′} | 2.0 | −3.3 | −0.07 | 13.4 | 0.8 | 0.0 |
| 16.5 | 2.9 | 0.45 | ||||
| Ph4P[Mn(opbaCl2)(py)2] (ref. 15) {MnO4N2} | 1.998(1) | −3.271(1) (−0.105(1)) | 18.1 | 1.24 | 0.10 | |
| [Mn{(OPPh2)2N}3] (ref. 16) {MnO6} | 2.0 | −3.4 | 10.1–11.9 | 0.5–1.4 | 0.225–0.40 | |
| [Mn(dbm)3] (ref. 17) {MnO6} | 2.12 | −4.52 (0.71) | 16.5 | 2.3 | 0.20 | |
| [Mn(dbm)2(DMSO)2](ClO4) (ref. 17) {MnO4O′2} | 2.05 | −3.42 (0.74) | 24.2 | 0.094 | 0.15 | |
| [Mn(dbm)2(py)2](ClO4) (ref. 17) {MnO4N2} | 2.00 | −4.46 (0.93) | 26.6 | 0.92 | 0.15 | |
| TBA7H10[Mn(SiW9O34)2]·3H2O (ref. 18) {MnO6} | 2.08 | −5.28 (−0.00119) | — | — | 0.10 | |
Dynamic magnetic properties
The AC susceptibility data measured in zero static magnetic field showed no out-of-phase susceptibility signal (Fig. S1, ESI†), but the field dependent measurement at the lowest temperature (1.9 K) confirmed field-induced slow relaxation of magnetization in 1–3 (Fig. S2†). Therefore, the AC susceptibility data were measured at non-zero static magnetic field, BDC = 0.2 and 0.4 T, for various frequencies of small AC field as depicted in Fig. 3, and S3 in ESI,† respectively. Clearly, the out-of-phase signal is frequency dependent, but lower temperature would be needed to see maxima on out-of-phase susceptibilities.This prevented us from constructing the Argand (Cole–Cole) diagram and analysing the data to obtain information about the spin reversal barrier by a one-component Debye model. Nevertheless, at least the approximate relationship14
| ln(χ′′/χ′) = ln(2πfτ0) + U/kT | (4) |
Theorethical calculations of spin Hamiltonian parameters
With the aim to support the outcomes of the analysis of magnetic data, multi-reference ab initio calculations based on state-averaged complete-active-space self-consistent field (SA-CASSCF) wave functions complemented by N-electron valence second-order perturbation theory (NEVPT2) were done using ORCA software. The active space was set to the metal-based d-orbitals, CAS(4,5). Firstly, the calculations were performed on the molecular geometries of the whole complex units for [Co(3EtO-L5)(μ-CN)Mn(L4a)Cl] of 1 and [Co(3EtO-L5)(μ-CN)Mn(L4a)Br] of 2. Due to the fact that such calculations are time-consuming, especially for compound 3, which has a larger number of atoms than compounds 1 and 2, we decided to test the possibility to truncate the molecular geometry of complex compounds 1–3 into geometrical fragments without the diamagnetic CoIII subunits as [(CN)Mn(L4a)Cl]− (1′), [(CN)Mn(L4a)Br]− (2′) and [(CN)2Mn(L4a)]− (3′). The achieved parameters of g-tensors and D-tensors are summarized in Table 4. It is evident that the geometry truncation led only to minor changes in D-values, i.e. less than 0.15 cm−1 for 1 and 2, and this is usually within the experimental error. The calculated values are in good agreement with the experimentally derived ones, we observed slightly lower calculated D-values, which may be attributed to the neglecting of spin–spin contribution to the D-tensor. Next, the rhombicity of the studied compounds was found very low, E/D < 0.05 justifying the neglecting of the E-term in fitting the magnetic data. Furthermore, the main axes of the D-tensor are visualized in Fig. 4 for the molecular fragment 1′ showing that the easy axis of magnetization can be identified with the Jahn–Teller axis, hence with the CN–Mn–Cl bonds.| D/cm−1 | E/D | g1, g2, g3 | giso | |
|---|---|---|---|---|
| a Molecular fragments: [Co(3EtO-L5)(μ-CN)Mn(L4a)Cl] (1), [Co(3EtO-L5)(μ-CN)Mn(L4a)Br] (2), [(CN)Mn(L4a)Cl]− (1′) [(CN)Mn(L4a)Br]− (2′) and [(CN)2Mn(L4a)]− (3′). | ||||
| 1 | −3.24 | 0.036 | 1.977, 1.994, 1.995 | 1.989 |
| 1′ | −3.38 | 0.035 | 1.976, 1.994, 1.995 | 1.988 |
| 2 | −3.03 | 0.025 | 1.978, 1.994, 1.995 | 1.989 |
| 2′ | −3.18 | 0.025 | 1.979, 1.994, 1.994 | 1.988 |
| 3′ | −3.58 | 0.044 | 1.977, 1.994, 1.995 | 1.988 |
 | ||
| Fig. 4 Molecular structure of [(CN)Mn(L4a)Cl]− (1′) overlaid with D-tensor axes derived from ab initio calculations. Hydrogen atoms were omitted for clarity. | ||
Conclusions
In this article we reported on the synthesis and properties of new heterobimetalic CoIII⋯MnIII compounds. Two novel dinuclear, [Co(3EtO-L5)(μ-CN)Mn(L4a)Cl] (1) and [Co(3EtO-L5)(μ-CN)Mn(L4a)Br] (2), and two new trinuclear [{Co(3EtO-L5)(μ-CN)}2{Mn(L4a)]I (3) and [{Co(3EtO-L5)(μ-CN)}2Mn(L4a)](NO3) (4) compounds were prepared. The crystal structures were determined for all four herein presented compounds but magnetic properties were studied only for compounds 1–3 in greater details due to the structural similarity of compounds 3 and 4. The magnetic data analysis, involving the spin Hamiltonian with the axial zero-field splitting term, revealed a relatively large and negative value of the axial magnetic anisotropy parameter D (in cm−1): −3.9(2) in 1, −4.9(2) in 2, and −4.1(1) in 3. The experimental study was supported by ab initio calculations at the CASSCF level of theory and the values of Dcalc, which are in good agreement with the experimentally derived parameters, were obtained. Furthermore, small rhombicity (Ecalc) for compounds 1–3 was proposed: Dcalc (Ecalc/Dcalc) = −3.2 cm−1 (0.04) in 1, −3.0 cm−1 (0.03) in 2 and −3.6 cm−1 (0.04) in 3. In summary, it has been found that the value of the D parameter does not depend neither on the axial length or lowering of the ligand-field strength by the ligand exchange significantly. This can be documented by two contrasting examples. The longest axial length is observed for 2 (N–Mn–Br type, d(N⋯Br) = 5.058(4) Å, angle (N–Mn–Br) = 174.5(1)°) and this compound possesses also the largest negative D value (−4.9 cm−1). The shortest axial length is found in 3 (N–Mn–N type, d(N⋯N) = 4.617(5) Å, angle (N–Mn–N) = 171.3(1)°) but the value of the D parameter (−4.1 cm−1) does not adopt a value much different from that observed for 2.The measurements of dynamic magnetic data confirmed that compounds 1–3 behave as field-induced single-ion magnets. The peak maxima of frequency dependent out-phase susceptibility (in static magnetic field of 0.4 T) were in all three cases below the lowest accessible temperature (1.9 K) and thus, we were not able to construct the Argand (Cole–Cole) diagram. Therefore, we used an approximate relationship for the extraction of the relaxation time (τ0) and spin reversal barrier (U) and this was applied to low temperature data and higher applied frequencies and as a result the values of Ueff ranging from 11 to 20 K and t0 from 0.1 to 19 × 10−7 s were obtained.
Experimental
Materials
All the starting chemicals were of analytical reagent grade and were used as received. CoCl2·4H2O, MnCl2·4H2O, MnBr2, MnI2, NaCN, AgNO3, solvents and the organic compounds 2-hydroxy-benzaldehyde, 3-ethoxy-2-hydroxybenzaldehyde, ethane-1,2-diamine, N-(2-aminoethyl)-1,3-propanediamine, and triethylamine (Et3N) were obtained from commercial sources (Sigma-Aldrich Co., Acros Organics Co., Lachema Co. and Fluka Co.).Synthesis of precursor complexes
The manganese(III) complexes were prepared according to the literature procedures.19 From the conductivity measurements it is apparent that iodide anion in [Mn(L4a)]I is not coordinated to MnIII atom.Synthesis of complexes 1, 2, 3 and 4
Dark crystals of complexes 1–3 were obtained from a methanol solution (10 mL) of the corresponding precursor complexes (0.1 mmol) combined with a methanol/acetonitrile (10/10 mL) solution of [Co(3-EtO-L5)(CN)] (1) (0.1 mmol). The solutions were mixed and the resulting mixture was stirred at room temperature for 1 h. Slow diffusion of diethyl ether into the resulting solution in a closed bottle afforded black single crystals. Black crystals were filtered off, washed twice with cold methanol, diethyl ether and dried in vacuum.The single crystals of 4 were prepared by the method involving NaF and AgNO3 as described in the Synthesis chapter. In order to prepare a pure phase system the crystals of complex 4 were obtained by a different procedure. A methanol solution (10 mL) of complex 1 was mixed with a water solution (5 mL) of AgNO3 (stoichiometric amount). A white powder (AgCl) was filtered off. Black crystals of 4 were obtained by slow diffusion of diethyl ether into the mother liquor in a closed bottle after a week.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1633 s ν(C
N); 1633 s ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar; 1600 s ν(C
N)ar; 1600 s ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar; 1538m ν(C
N)ar; 1538m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1467m ν(C
C)ar; 1467m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1437m ν(C
C)ar; 1437m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1385w; 1337w; 1324w; 1300m; 1240w; 1224w; 1216w; 1172w; 1153w; 1133w; 1089w; 1078w; 1057w; 1036w; 1009w; 900w; 854w; 798w; 764m; 753m; 627w.
C)ar; 1385w; 1337w; 1324w; 1300m; 1240w; 1224w; 1216w; 1172w; 1153w; 1133w; 1089w; 1078w; 1057w; 1036w; 1009w; 900w; 854w; 798w; 764m; 753m; 627w.![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1647w ν(C
N); 1647w ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar; 1622vs ν(C
N)ar; 1622vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar; 1598m ν(C
N)ar; 1598m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1539m ν(C
C)ar; 1539m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1466m ν(C
C)ar; 1466m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1433s ν(C
C)ar; 1433s ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1385m; 1321w; 1296m; 1241w; 1213m; 1150w; 1130w; 1108w; 1079w; 1039w; 970w; 899w; 877w; 853w; 797w; 749m; 625w.
C)ar; 1385m; 1321w; 1296m; 1241w; 1213m; 1150w; 1130w; 1108w; 1079w; 1039w; 970w; 899w; 877w; 853w; 797w; 749m; 625w.![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 2131s ν(C
N); 2131s ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1622s ν(C
N); 1622s ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar; 1574m ν(C
N)ar; 1574m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1552m ν(C
C)ar; 1552m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1496m ν(C
C)ar; 1496m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1432w; 1415w; 1396w; 1354m; 1332w; 1251m; 1200w; 1174w; 1163w; 1128w; 1085w; 1008w; 970m; 885w; 742w; 738m; 724w; 663w.
C)ar; 1432w; 1415w; 1396w; 1354m; 1332w; 1251m; 1200w; 1174w; 1163w; 1128w; 1085w; 1008w; 970m; 885w; 742w; 738m; 724w; 663w.![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1621s ν(C
N); 1621s ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar; 1606s ν(C
N)ar; 1606s ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar; 1572m ν(C
N)ar; 1572m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1493m ν(C
C)ar; 1493m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1467m ν(C
C)ar; 1467m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1442m ν(C
C)ar; 1442m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1372w; 1331w; 1316w; 1313m; 1253w; 1238w; 1165w; 1149w; 1137w; 1096w; 1082w; 1063w; 1047w; 1014w; 954w; 872w; 799w; 751m; 744m.
C)ar; 1372w; 1331w; 1316w; 1313m; 1253w; 1238w; 1165w; 1149w; 1137w; 1096w; 1082w; 1063w; 1047w; 1014w; 954w; 872w; 799w; 751m; 744m.General methods
Elemental analysis (CHN) was performed on a FLASH 2000 CHN Analyser (ThermoFisher Scientific). Infrared spectra of the complexes were recorded on a ThermoNicolet NEXUS 670 FT-IR spectrometer using the ATR technique on a diamond plate in the range 600–4000 cm−1. The reported FT-IR intensities were defined as w = weak, m = medium, s = strong, and vs = very strong. The magnetic data were measured on powdered samples pressed into pellets using a MPMS XL-7 Quantum Design SQUID magnetometer. The experimental data were corrected for the diamagnetism of the constituent atoms by using Pascal's constants.Single-crystal X-ray analysis details
X-ray measurements on the selected crystals of 1, 2, 3 and 4 were performed on an Oxford Diffraction Xcalibur™2 equipped with a Sapphire2 CCD detector using Mo-Kα radiation at 100 K. The CrysAlis program package (version 1.171.33.52, Oxford Diffraction) was used for data collection and reduction.20 The molecular structures were solved by direct methods SHELX-2014 and all non-hydrogen atoms were refined anisotropically on F2 using full-matrix least-squares procedure SHELXS-2014.21 All the hydrogen atoms were found in differential Fourier maps and their parameters were refined using a riding model with Uiso(H) = 1.2 (CH, CH2, OH) or 1.5 (CH3) Ueq. Non-routine aspects of the structure refinement are as follows: in 3, two ethoxy groups are disordered over two positions; in 4, the electron density from heavily disordered nitrate anion was removed by SQUEEZE procedure.22Theoretical methods
All theoretical calculations were performed with an ORCA 3.0 computational package.23 All calculations employed the chain-of-spheres (RIJCOSX) approximation to exact exchange.24 The polarized triple-ζ-quality basis set def2-TZVP(-f) were used for all atoms except for carbon and hydrogen, for which the def2-SVP basis set was chosen.25 The ZFS and g tensors were calculated by using self-consistent field (SA-CASSCF) wave functions26 complemented by N-electron valence second order perturbation theory (NEVPT2).27 The active space of the CASSCF calculation was set to five d-orbitals of MnIII (CAS(4,5)). The state-averaged approach was used, in which all 5 quintet, 45 triplet and 50 singlet states were equally weighted. The ZFS parameters, based on dominant spin–orbit coupling contributions from excited states, were calculated through quasi-degenerate perturbation theory (QDPT),28 in which approximations to the Breit–Pauli form of the spin–orbit coupling operator (SOMF approximation)29 and the effective Hamiltonian theory30 were utilized. The energies of calculated excited states and their contributions to the D-tensors are listed in Tables S1 and S2 (ESI†).Acknowledgements
We acknowledge the financial support from the National Programme of Sustainability I (LO1305) of the Ministry of Education, Youth and Sports of the Czech Republic.Notes and references
- (a) D. Gatteschi, R. Sessoli, and J. Villain, Molecular Nanomagnets, Oxford University Press, New York, 2006 Search PubMed; (b) M. Ganzhorn and W. Wernsdorfer, in Molecular Magnets, ed. J. Bartolomé, F. Luis and J. F. Fernández, Springer Berlin Heidelberg, 2014, pp. 319–364 Search PubMed.
- R. Herchel, L. Váhovská, I. Potočňák and Z. Trávníček, Inorg. Chem., 2014, 53, 5896–5898 CrossRef CAS PubMed.
- H. Miyasaka, A. Saitoh and S. Abe, Coord. Chem. Rev., 2007, 251, 2622–2664 CrossRef CAS.
- R. Boča, Coord. Chem. Rev., 2004, 248, 757–815 CrossRef.
- (a) J. Dreiser, A. Schnegg, K. Holldack, K. S. Pedersen, M. Schau-Magnussen, J. Nehrkorn, P. Tregenna-Piggott, H. Mutka, H. Weihe, J. Bendix and O. Waldmann, Chem.–Eur. J., 2011, 17, 7492–7498 CrossRef CAS PubMed; (b) K. S. Pederson, J. Dreiser, J. Nehrkorn, M. Gysler, M. Schau-Magnussen, A. Schnegg, K. Holldack, R. Bittl, S. Piligkos, H. Weihe, P. Tregenna-Piggott, O. Waldmann and J. Bendix, Chem. Commun., 2011, 47, 6918–6920 RSC.
- (a) R. Ababei, Y. Li, O. Roubeau, M. Kalisz, N. Bréfuel, C. Coulon, E. Harté, X. Liu, C. Mathoniére and R. Clérac, New J. Chem., 2009, 33, 1237–1248 RSC; (b) J. H. Yoon, J. H. Lim, H. C. Kim and C. S. Hong, Inorg. Chem., 2006, 45, 9613–9615 CrossRef CAS PubMed; (c) T. M. Ross, S. M. Neville, D. S. Innes, D. R. Turner, B. Moubaraki and K. S. Murray, Dalton Trans., 2010, 39, 149–159 RSC; (d) T. Šilha, I. Nemec, R. Herchel and Z. Trávníček, CrystEngComm, 2015, 15, 5351–5358 RSC.
- (a) J. Dreiser, K. S. Pedersen, A. Schnegg, K. Holldack, J. Nehrkorn, M. Sigrist, P. Tregenna-Piggott, H. Mutka, H. Weihe, V. S. Mironov, J. Bendix and O. Waldmann, Chem.–Eur. J., 2013, 19, 3693–3701 CrossRef CAS PubMed; (b) K. S. Pedersen, M. Schau-Magnussen, J. Bendix, H. Weihe, A. V. Palii, S. I. Klokishner, S. Ostrovsky, O. S. Reu, H. Mutka and P. L. W. Tregenna-Piggott, Chem.–Eur. J., 2010, 16, 13458–13464 CrossRef CAS PubMed.
- R. Ishikawa, R. Miyamoto, H. Nojiri, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2013, 52, 8300–8302 CrossRef CAS.
- I. Nemec, P. Zoufalý, R. Herchel and Z. Trávníček, Inorg. Chem. Commun., 2013, 35, 50–53 CrossRef CAS.
- T. Birk, K. S. Pedersen, S. Piligkos, C. A. Thuesen, H. Weihe and J. Bendix, Inorg. Chem., 2011, 50, 5312–5314 CrossRef CAS PubMed.
- J. Bernstein, R. E. Davis, L. Shimoni and N. L. Chang, Angew. Chem., Int. Ed. Engl., 1995, 34, 1555–1573 CrossRef CAS.
- R. Boča, A Handbook of Magnetochemical Formulae, Elsevier, Amsterdam, 2012 Search PubMed.
- The standard deviations were calculated as σi = (Pii−1·S/(N − k))−1/2, where Pii = ∑(δμn/δai·δμn/δaj) and S = ∑(μn − μexpn)2 with n = 1 to N; ai and aj are fitted parameters, N is number of experimental points (sum of temperature and field dependent data), μn and μexpn are the calculated and experimental effective magnetic moments for given temperature and magnetic field. The σi was then multiplied by Student's t95% to provide confidence limits with 95% probabilities listed in text.
- J. Bartolomé, G. Filoti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 014430 CrossRef.
- J. Vallejo, A. Pascual-Álvarez, J. Cano, I. Castro, M. Julve, F. Lloret, J. Krzystek, G. De Munno, D. Armentano, W. Wernsdorfer, R. Ruiz-García and E. Pardo, Angew. Chem., Int. Ed., 2013, 52, 14075–14079 CrossRef CAS PubMed.
- A. Grigoropoulos, M. Pissas, P. Papatolis, V. Psycharis, P. Kyritsis and Y. Sanakis, Inorg. Chem., 2013, 52, 12869–12871 CrossRef CAS PubMed.
- L. Chen, J. Wang, Y.-Z. Liu, Y. Song, X.-T. Chen, Y.-Q. Zhang and Z.-L. Xue, Eur. J. Inorg. Chem., 2015, 271–278 CrossRef CAS.
- R. Sato, K. Suzuki, T. Minato, M. Shinoe, K. Yamaguchi and N. Mizuno, Chem. Commun., 2015, 51, 4081–4084 RSC.
- (a) D. J. Gravert and J. H. Griffin, Inorg. Chem., 1996, 35, 4837–4847 CrossRef CAS PubMed; (b) Y. Ciringh, S. W. Gordon-Wylie, R. E. Norman, G. R. Clark, S. T. Weintraub and C. P. Horwitz, Inorg. Chem., 1997, 36, 4968–4982 CrossRef CAS.
- CrysAlis CCD and CrysAlis RED, Version 1.171.33.52, Oxford Diffraction Ltd, England, 2009 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71(1), 3–8 CrossRef PubMed.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- (a) A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef CAS; (b) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC; (c) A. Schaefer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef CAS.
- P. A. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- (a) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS; (b) C. Angeli, R. Cimiraglia and J. P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS; (c) C. Angeli, R. Cimiraglia and J. P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS; (d) C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, J. Chem. Phys., 2004, 121, 4043–4049 CrossRef CAS PubMed; (e) C. Angeli, B. Bories, A. Cavallini and R. Cimiraglia, J. Chem. Phys., 2006, 124, 054108 CrossRef PubMed.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef PubMed.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1434760–1434763. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5ra23922b |
| This journal is © The Royal Society of Chemistry 2016 |


