Exploiting the interplay of quantum interference and backbone rigidity on electronic transport in peptides: a step towards bio-inspired quantum interferometers

Abstract

Electron transfer in peptides provides an opportunity to mimic nature for applications in bio-inspired molecular electronics. However, quantum interference effects, which become significant at the molecular level, have yet to be addressed in this context. Electrochemical and theoretical studies are reported on a series of cyclic and linear peptides of both β-strand and helical conformation, to address this shortfall and further realize the potential of peptides in molecular electronics. The introduction of a side-bridge into the peptides provides both additional rigidity to the backbone, and an alternative pathway for electron transport. Electronic transport studies reveal an interplay between quantum interference and vibrational fluctuations. We utilize these findings to demonstrate two distinctive peptide-based quantum interferometers, one exploiting the tunable effects of quantum interference (β-strand) and the other regulating the interplay between the two phenomena (3₁₀-helix).

---

Design, System, Application

The design of bio-inspired single-molecule devices requires a fundamental understanding of electron transport in peptides. We recently demonstrated that linking the side-chains of amino acids within a peptide with a covalent constraint impedes intramolecular charge transfer, by restricting the precise backbone torsional motion required by a hopping mechanism to facilitate such transfer through the peptide. However, quantum interference effects, which become significant at the molecular level, must be taken into account in order to investigate the possibility of an interplay between quantum interference and vibrational fluctuations (backbone flexibility) in single-peptide circuits. Here, the effects of destructive quantum interference were found to occur in the cyclic β-strand peptide through the backbone and the additional tunneling pathway provided by the side-bridge constraint. On the other hand, the linear β-strand was found to exhibit a strong Fano-type resonance, thus providing an attractive candidate for a wide range of sensing applications, such as temperature, pH and magnetic field. Furthermore, an interplay between quantum interference and backbone rigidity on electronic transport was established in both cyclic and linear helical peptides, which constitutes a unique design of peptide-based quantum interferometer, with applications in areas such as biosensing, information processing, thermoelectrics, and high resolution spectroscopy.

Introduction

Molecular electronics provides an opportunity to go beyond the physical limitations of conventional silicon-based electronics, with the ultimate goal being to develop functional single molecule-based devices.^1,2 Electronic transport in peptides offers real advantages in this context as a peptide backbone can be specifically functionalized to allow precision-branching and hence the design of well-defined three-dimensional molecular circuitry. Peptides can also be specifically constrained into well-defined secondary structures such as helices and β-strands that are known to play a role in electron transfer.³ With this in mind, we recently demonstrated that linking the side-chains of amino acids within a peptide with a covalent constraint, introduced by either Huisgen cycloaddition⁴ or ring closing metathesis,⁵ impedes charge transfer. A peptide can be constrained in this way into a well-defined helical or β-strand conformation with the appropriate choice of linker. In both cases, the associated increase in backbone rigidity restricts the vibrational fluctuations (torsional motion) necessary for facile electron transfer through the peptide.⁶ However the side-chain tether also provides an alternative electron transfer pathway, and hence opportunity to develop a parallel circuit (Fig. 1a, left). Here the electron wave traversing the backbone from sections M0 to M2 reaches the first juncture and splits into two individual waves, propagating along the backbone (M1) and side-bridge (M3) respectively. They re-emerge at the second juncture and superimpose to form a resultant wave, eventually passing through the backbone (section M2). This wave will have either greater or lower amplitude than the original (i.e. the effects of quantum interference⁷) if the two individual waves differ in amplitude and phase arising from the different structural and chemical compositions of sections M1 and M3. Hence, electronic transport through a single molecule multi-pathway circuit of this type cannot simply be explained in terms of classical physics, in particular Kirchhoff's superposition laws.^8–10 As such, quantum interference must be taken into account in a single-molecule circuit. This critical dynamic phenomenon is governed by the physical, chemical and electronic properties of the molecule, and thus can be manipulated through conformational control, polarization or electrochemical gating.¹¹ For reasons discussed above peptides are ideal for such studies, however the effects of quantum interference on electronic transport in these structures are unknown. Thus, such studies would greatly advance fundamental knowledge in this emerging area of research. An ability to control these effects in peptides through direct manipulation of electron wavefunctions would also provide access to practical peptide-based sensor technologies, and novel logic gates and memory devices.

Fig. 1 (a) Schematic representation of single-peptide circuits containing cyclic/parallel (left) and simple/linear (right) pathways. Here M0, M1 and M2 represent consecutive sections of the peptide backbone while M3 denotes the amide-containing side-bridge (left) or side-chain (right). Yellow regions represent gold electrodes. (b) Synthetic peptides 1 and 2 (β-strand) and, 3 and 4 (3₁₀-helix).

Previous studies involving single-molecule circuits containing small non-peptide compounds, report a correlation between quantum interference and thermally activated transport (vibrational fluctuations)¹² with the latter stimulated by either variation of temperature¹³ or excitation of specific vibrational modes.^14,15 In contrast, vibrational fluctuations in peptides are typically stronger owing to their larger overall dimensions and mass, with femtosecond time scale rotations unique to peptides.¹⁶ Thus a full investigation of the effects of both dynamic phenomena is required to progress the field of peptide-based molecular circuitry. Considering this, we now present electrochemical studies on a series of new peptides to determine whether a side-bridge constraint can influence electron transport by providing an alternative pathway, hence revealing the effects of quantum interference; or simply increase the backbone rigidity of the peptide to impede such transport, hence revealing the effects of vibrational fluctuations. Peptides 1 and 3 were constrained into well-defined secondary structures (β-strand and 3₁₀-helical respectively) with an amide-containing side-bridge, while peptides 2 and 4 are direct linear analogues (Fig. 1b). The experimental study is complemented by high-level density functional theory (DFT) studies coupled with the non-equilibrium Green's function to simulate electronic transport in each peptide, to further identify the effects from both vibrational fluctuations and quantum interference.

Results and discussion

Design and conformational analysis of peptides

Peptides 1, 2 and 3 were synthesized using solution phase chemistry, while the linear hexapeptide 4 was synthesized using solid phase peptide synthesis as detailed in the ESI.† The geometries of peptides 1–4 were defined by 2D NMR spectroscopy. Specifically, CαH(i) to NH(i + 1), CβH₂(i) to NH(i + 1) and sequential NH(i) to NH(i + 1) ROESY correlations were observed for peptides 1 and 2 (Fig. S1 and S2†), indicative of a β-strand conformation.¹⁷ Furthermore, ¹H NMR J_NHCαH coupling constants consistent with a β-strand structure¹⁸ were observed for these peptides. The conformations of 3 and 4 were confirmed as 3₁₀-helical, based on observed CαH(i) to NH(i + 1) and medium range CαH(i) to NH(i + 2) ROESY correlations⁵ (Fig. S3 and S4†). Ostensibly, the only structural difference between each of these cyclic (1 and 3) and linear peptides (2 and 4) is the presence (or absence) of the side-bridge constraint.

¹H NMR and 2D NMR spectroscopy were also used to confirm the geometry of peptides 5–8 (the N-Boc protected analogues of 1–4, see Fig. 2a). Peptides 5 and 6 were confirmed as β-strand, with CαH(i) to NH(i + 1), CβH₂(i) to NH(i + 1) and sequential NH(i) to NH(i + 1) ROESY correlations evident¹⁷ (Fig. S5 and S6†). In particular, CαH(i) to NH(i + 1) and medium range CαH(i) to NH(i + 2) ROESY correlations were observed for 7 and 8 (Fig. S7† and 2b), indicative of a 3₁₀-helical structure. IR spectroscopy further confirmed the conformation of each of the N-Boc protected lactam macrocycles (5 and 7). A strong peak at 1636 cm⁻¹ with a small shoulder at 1687 cm⁻¹ was found for 5 (Fig. 2c), representative of the Amide I band. Another strong peak was observed at 1525 cm⁻¹ (Amide II) and a broad peak at 3289 cm⁻¹ (Amide A). Each of these peaks is characteristic of a β-strand conformation.^19,20 A strong peak at 1654 cm⁻¹ representative of the Amide I band was observed for 7 (Fig. S8†), indicative of a 3₁₀-helical structure.²¹

Fig. 2 (a) Structures of N-Boc protected peptides 5 and 6 (β-strand) and, 7 and 8 (3₁₀-helix). (b) ROESY spectrum of peptide 8, showing CαH(i) to NH(i + 1) and medium range CαH(i) to NH(i + 2) correlations. (c) IR spectrum representative of N-Boc protected β-strand peptide 5. (d) The lowest energy conformer for peptide 7 optimized by the hybrid B3LYP method with Lanl2dz basis set for Fe atom and 6-31G** basis set for other atoms.

Molecular modeling was used to further define the backbone geometries of peptides 5–8 (Fig. 2d and S9†). The Boc protection group was used for the respective N-termini as free amines are known to give rise to unrealistic electrostatic interactions, resulting in unstable lowest energy conformers.²² The models for the two N-Boc protected β-strand peptides show that the macrocyclic 5 is 0.42 Å shorter than its linear analogue 6 (from first to last carbonyl carbons, see Table S1†). All other dimensions crucial to the characterization of a β-strand conformation, such as NH(i) to NH(i + 1), CαH(i) to NH(i + 1) and CβH₂(i) to NH(i + 1) distances, are comparable to literature values²³ (Tables S2 and S3†). The models indicate that the backbone lengths of peptides 7 and 8 (from first to last carbonyl carbons, see Tables S4 and S5†) are strikingly similar, differing by no more than 0.17 Å. The mean intramolecular hydrogen bond length for the macrocyclic 7 is only 0.05 Å shorter than its linear analogue 8 (Tables S4–S6†). The models also demonstrate that each of these peptides adopts a 3₁₀-helical conformation, with the average dihedral angles in peptide 7 deviating from an ideal 3₁₀-helix by no more than 3.7° and 4.8° for Φ and ψ respectively, and 2.2° (Φ) and 3.2° (ψ) in peptide 8 (Table S7†). Thus, the ¹H NMR and IR spectra, together with the molecular modeling data, confirm that peptides 5 and 6 share a common β-strand geometry, while peptides 7 and 8 share a similar 3₁₀-helical geometry.

Electron transfer in peptides

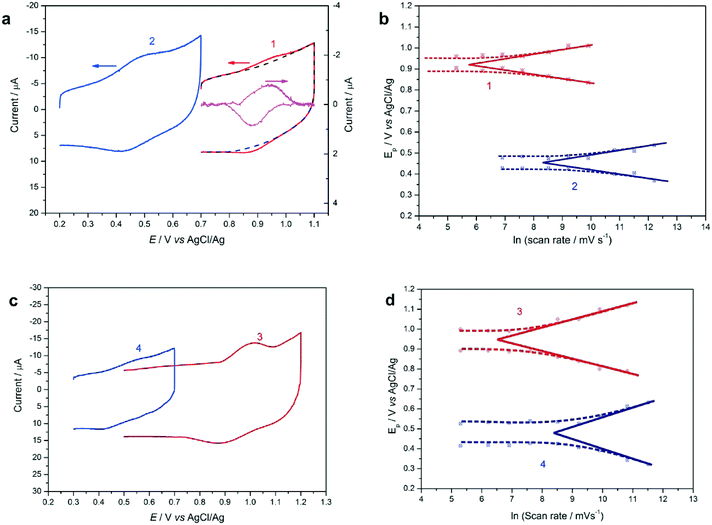
Each of the peptides 1–4 was separately attached to vertically aligned single-walled carbon nanotube array/gold (SWCNTs/Au) electrodes²⁴ in order to study their electron transfer kinetics. This proven method was chosen to provide a high surface concentration of attached redox probes and hence high sensitivity and reproducibility of electrochemical measurement.^4,25,26 Analysis of the electrochemical results for the β-strand peptides 1 and 2, and the 3₁₀-helical peptides 3 and 4, reveals a pair of redox peaks in each cyclic voltammogram, characteristic of a one-electron oxidation/reduction reaction (Fc+/Fc) (Fig. 3a, c and S10†). The surface concentrations of the peptides were determined by integrating background subtracted peak areas, and ranged between 2.03 × 10⁻¹⁰ and 4.37 × 10⁻¹⁰ mol cm⁻² (Table 1). These values are comparable to other carbon nanotube electrode studies.^5,6,24 The formal potentials (E_o) and apparent electron transfer rate constants (k_et) were estimated using Laviron's formalism (Fig. 3b and d, Table 1). While peptides 1 and 2 share a common β-strand backbone conformation, 1 is further constrained into this geometry by the side-bridge to provide increased backbone rigidity, and an alternative electron tunneling pathway. The observed electron transfer rate constant for the cyclic peptide 1 was 5.92 s⁻¹, while that of the direct linear analogue 2 was almost 15-fold greater (86.67 s⁻¹). A dramatic shift to the positive in the formal potential of the cyclic peptide 1 was also observed (471 mV) compared with that of the linear 2 (Fig. 3, Table 1). Peptides 3 and 4 also share a common geometry, in this case 3₁₀-helical. Again a significant difference of approximately one order of magnitude was observed in the electron transfer rate constants of the two peptides, with values of 9.34 s⁻¹ and 83.65 s⁻¹ for 3 and 4 respectively. A considerable formal potential increase of 482 mV was observed for 3, which is comparable to the results from the β-strand peptides 1 and 2 (471 mV).

Fig. 3 (a) Cyclic voltammograms for β-strand peptides 1 and 2 immobilized on SWCNTs/Au electrodes at 5 V s⁻¹. Pink inset derived from the original curve (red), by subtracting the background current (dashed lines). (b) Peak potential versus ln(scan rate) for peptides 1 and 2 after background current subtraction. (c) Cyclic voltammograms for 3₁₀-helical peptides 3 and 4 immobilized on SWCNTs/Au electrodes at 5 V s⁻¹. (d) Peak potential versus ln(scan rate) for peptides 3 and 4 after background current subtraction.

Table 1 Electron transfer rate constants (k_et), surface concentrations and formal potentials (E_o) for the β-strand peptides (1 and 2) and 3₁₀-helical peptides (3 and 4)

Peptide	Surface concentration (×10^−10 mole cm^−2)	E o (V vs. AgCl/Ag)	k et (s^−1)
β-Strand
1	2.46 ± 0.25	0.927	5.92 ± 0.47
2	3.68 ± 0.41	0.456	86.67 ± 7.95
310-Helical
3	4.37 ± 0.38	0.924	9.34 ± 1.58
4	2.03 ± 0.19	0.442	83.65 ± 7.64

---

This large disparity between the electrochemical properties of both cyclic and linear peptides, was observed despite their distinctive secondary structures, either β-strand or helix. Our earlier studies^4,5 suggest that this may be the result of the additional backbone rigidity imparted by the side-bridge constraint, which restricts the precise backbone torsional motion required by a hopping mechanism to facilitate intramolecular electron transfer through the peptide.^16,27 However, it is also possible that the side-chain tether can provide an additional electron transport pathway. The effects of quantum interference should also appear in this type of single molecule multi-pathway system.^28,29 Thus these effects must be taken into account in order to investigate the possibility of an interplay between quantum interference and vibrational fluctuations (backbone rigidity) in single-peptide circuits.

Quantum interference effects

To achieve this, theoretical approaches to charge transport based on density functional theory (DFT), coupled with the non-equilibrium Green's function (NEGF),³⁰ were used to investigate quantum interference effects in molecular junctions containing peptides 9–12 (Fig. 4a and 5a). Each of these peptides share an identical amino acid sequence with their respective synthetic analogues 1–4, however the redox active ferrocene moieties have been replaced by thiol anchoring groups to enable the formation of molecular junctions. This design was formulated as electrochemical measurements for peptides bearing a ferrocene moiety, and STM conductance of peptides terminated with two thiol groups both reveal crucial insights into electronic transport properties.^27,31,32 The transmission spectra of molecular junctions containing individual peptides were computed at different bias voltages, ranging from −2 V to 2 V, in order to calculate the current, and ultimately conductance, through the respective molecular junctions.

Fig. 4 (a) Schematic of molecular junctions comprising parallel (cyclic peptide 9, analogue of 1) and simple (linear peptide 10, analogue of 2) circuits for use in charge transport simulations (yellow spheres represent the gold electrodes). (b) Transmission spectra for the parallel (cyclic peptide 9, red) and simple (linear peptide 10, blue) circuits at a bias voltage of 0 V. The anti-resonance and Fano-type peaks are highlighted by black and green dashed ovals respectively. Inset: The line shape of a typical Fano-type transmission resonance. (c) Left and right-side eigenchannels for the parallel (cyclic peptide 9, top) and simple (linear peptide 10, bottom) circuits at E − E_F = 0 eV (blue spheres denote nitrogen, red = oxygen, grey = carbon, and white = hydrogen). Purple and light blue areas correspond to the positive and negative signs of the almost real-valued wavefunction, clearly showing a discontinuous (top) and continuous (bottom) distribution of the wavefunction density for molecular junctions comprising peptides 9 and 10, respectively. (d) Computed I–V curves for the parallel (cyclic peptide 9, red) and simple (linear peptide 10, blue) circuits at bias voltages between −2.0 V and 2.0 V.

Fig. 5 (a) Schematic of molecular junctions comprising parallel (cyclic peptide 11, analogue of 3) and simple (linear peptide 12, analogue of 4) circuits for use in charge transport simulations (yellow spheres represent the gold electrodes). (b) Transmission spectra for the parallel (cyclic peptide 11, red) and simple (linear peptide 12, blue) circuits at a bias voltage of 0 V. (c) Both left and right-side eigenchannels for the parallel (cyclic peptide 11, top) and simple (linear peptide 12, bottom) circuits at E − E_F = 0 eV (blue spheres denote nitrogen, red = oxygen, grey = carbon, and white = hydrogen). Purple and light blue areas correspond to the positive and negative signs of the almost real-valued wavefunction, clearly showing a discontinuous distribution of the wavefunction density for molecular junctions comprising peptides 11 and 12, respectively. (d) Computed I–V curves for the parallel (cyclic peptide 11, red) and simple (linear peptide 12, blue) circuits at bias voltages between −2.0 V and 2.0 V.

β-strand peptides. Peptides 9 and 10 (Fig. 4a) were separately bound between two gold electrodes via thiol groups that contribute efficient electronic coupling at the peptide/electrode interface,^27,33 to form a molecular junction with an S–S distance of 18 Å (Table S8†). The transmission function for the molecular junction containing peptide 9 was found to be significantly lower than that of peptide 10 at a bias voltage of 0 V (Fig. 4b). The electronic transport within the molecular junction containing peptide 9 is predominantly defined by the highest occupied molecular orbital (HOMO), while the electronic transport through peptide 10 is determined by the lowest unoccupied molecular orbital (LUMO). A relatively narrow HOMO–LUMO energy gap (0.3 eV) was found for the constrained peptide 9, whereas a slightly smaller energy gap (0.15 eV) exists for the linear 10, which is evident in Fig. S12.† Notably, the cyclic peptide 9 exhibits one strong negative dip in transmission close to the Fermi energy, with the transmission coefficient exceeding 1 × 10⁻¹³ near 0.85 eV (see black highlighted area in Fig. 4b). This broad feature containing almost symmetric peaks is considered the opposite of a transmission resonance, namely an anti-resonance,^34,35 which is known to be a direct result of destructive quantum interference.^11,36 The appearance of anti-resonance in the transmission spectrum of 9 is a definitive consequence of the divergent charge transport pathways in the cyclic peptide, that differ both spatially and energetically.³⁷ This is evidenced in both the left and right-side eigenchannels of peptide 9 (Fig. 4c), which are especially useful for interpreting the contributions from particular molecular orbitals (energies) for electron transport through the molecular junction.³⁸ The eigenchannels of cyclic peptide 9 exhibit a discontinuous distribution of the wavefunction density along both the backbone and side-bridge (Fig. 4c, top). In contrast, the computed eigenchannels span the entire pathway between the two gold electrodes in the molecular junction containing the linear peptide 10, exhibiting a continuous electron waveform along the backbone represented by the consecutive purple and light blue regions (Fig. 4c, bottom). Furthermore, sharp asymmetric peaks were observed in the transmission spectra of both peptides (see green highlighted areas in Fig. 4b), characteristic of distinct Fano-type resonances.³⁹ These resonances are unique to T-shaped or branched molecules, such as those depicted in Fig. 1a. They are attributed to the interference between a specific side-group and the main conduction channel (i.e. peptide backbone), as evidenced in the eigenchannels of both peptides by the orbital overlap at the intersection of the amide-containing side-group and the backbone. Additionally, the delocalized molecular orbitals along the side-chain of leucine in the linear peptide 10 were found to contribute to the main conduction channel through a strong orbital overlap between the side-chain and the backbone. However, the molecular orbitals of the leucine side-chain in the cyclic peptide 9 show no contribution to the conduction channel over the backbone (Fig. 4c). Fano-type resonances possess an inherent sensitivity to changes in geometry and local environment, with small perturbations able to induce dramatic resonance or line shape shifts.⁴⁰ Hence the linear β-strand peptide 10 presents as a particularly attractive candidate for a wide range of sensing applications by monitoring the changes in the transmission spectrum as a function of local environment, such as temperature, pH and magnetic field.

Additionally, the current–voltage (I–V) characteristics of peptides 9 and 10 were calculated (see Fig. 4d). For bias voltages between −1.5 V and 1.5 V, the current for both peptides is relatively symmetric, but greater in the linear 10 relative to the constrained 9. Interestingly, the current for 9 was found to increase rapidly as the voltage increased from −1.5 V to −2.0 V, reaching 49 pA at −2.0 V. In contrast, the current for 9 was 7 pA at 2.0 V. This phenomenon suggests the occurrence of rectification in the cyclic peptide 9. However electrochemical measurements were unable to shed further light, as electrochemistry was conducted in the range required for oxidation/reduction of the redox active ferrocene moiety, i.e. between 0.1 V and 1.1 V vs. Ag/AgCl.²⁷ The conductance values for the cyclic and linear peptides, 9 and 10, were calculated to be 1.1 × 10⁻¹¹ S and 2.3 × 10⁻¹⁰ S respectively, within the bias range of −1.5 V to 1.5 V (Fig. 4d). These results correspond remarkably well to those from the electrochemical study, where the electron transfer rate constant for the constrained peptide 1 (5.92 s⁻¹) was also found to be more than one order of magnitude lower than that of the linear peptide 2 (86.67 s⁻¹). A similar correlation was previously found for β-strand linear/cyclic peptides attached to electrode(s) comprising a triazole linker.²⁷ Destructive quantum interference is always accompanied by a reduction in the rate of electron transfer,^41,42 which was observed with the cyclic peptide 9. Despite peptides 9 and 10 sharing a common β-strand conformation, the effects of destructive quantum interference were found to occur essentially in the cyclic peptide, through the heterogenous backbone and the additional tunneling pathway provided by the side-bridge constraint. Thus we have shown that a peptide-based quantum interferometer can be achieved through the introduction of a side-chain bridge, with further modification enabling direct tuning of the transmission phase shift, and hence a level of control over quantum interference effects.

3₁₀-Helical peptides. Peptides 11 and 12 were separately bound between two gold electrodes via thiol groups, separated by an S–S distance of 17 Å (Fig. 5a, Table S8†). The transmission spectra for molecular junctions containing the helical peptides 11 and 12 were found to be similar at a bias voltage of 0 V (Fig. 5b). Contrary to the results obtained for the β-strand peptides, both transmission functions exhibit four strong dips close to the Fermi energy, with the transmission coefficient exceeding 1 × 10⁻¹⁶ at 0.85 eV. The presence of multiple anti-resonance peaks⁴³ in both molecular junctions indicates multi-tunneling electron transport pathways in peptides 11 and 12. These peptides adopt a 3₁₀-helical conformation, which is defined by three residues per turn of the helix. Unlike the β-strand peptides, both helical peptides contain five intramolecular hydrogen bonds, linking the carbonyl groups of the amino acids in the i positions to the amide hydrogens in the i + 3 positions. These bonds would likely provide shortcuts for electron transport,^16,44 and thus contribute to the multi-tunneling pathways. The computed eigenchannels for both helical peptides exhibit a discontinuous waveform along their backbones, and the side-bridge of 11 (Fig. 5c). These discontinuous waveforms found in both helical peptides indicate the occurrence of destructive quantum interference, similar to the molecular junction comprising the cyclic β-strand peptide 9. Notably, the computed conductance values for the cyclic and linear helical peptides, 11 and 12, were found to be remarkably similar, 3.1 × 10⁻¹⁴ S and 3.2 × 10⁻¹⁴ S respectively, using the relatively symmetric I–V curves within the bias range of −1.5 V to 1.5 V (Fig. 5d). However, the electron transfer rate constant observed for the cyclic helical peptide 3 (9.34 s⁻¹) was approximately one order of magnitude lower than that of the linear peptide 4 (83.65 s⁻¹). No such correlation was found between the computed conductance values and the observed electron transfer rate constants in the helical peptides (3 and 4; 11 and 12), which contrasts data for the β-strand peptides (1 and 2; 9 and 10). This suggests that a different charge transfer mechanism must be operating in the helical peptides, giving rise to the destructive quantum interference effects found in both 11 and 12.

Linear helical peptides are known to undergo electron transfer via a thermally activated hopping mechanism.^32,44–46 Although the elastic transport simulations for the molecular junction comprising the linear helical peptide 12 (analogue of 4) demonstrate the existence of destructive quantum interference effects, the vibrational fluctuations along the flexible backbone lead to a quenching of these effects at room temperature, which is reflected in the higher electron transfer rate constant (83.65 s⁻¹). As apparent in Fig. 5b and c, these quantum interference effects are present in the linear helical peptide, but they are masked by the more dominant vibrational fluctuations. High level calculations based on the Marcus theory of electron transfer,⁴⁷ in conjunction with the latest constrained density functional theory (cDFT),⁴⁸ have shown that with the introduction of a side-bridge into the cyclic peptide 3, the reorganization energy for each sequential electron transfer step⁴⁹ increases between 3.14–6.97 kcal mol⁻¹,^4–6 in relation to that in the linear peptide 4. This additional reorganization energy barrier restricts the necessary vibrational fluctuations (torsional motions) that lead to facile intramolecular electron transfer along the peptide backbone. The effect from the additional reorganization energy barrier is reflected in the lower electron transfer rate constant (9.34 s⁻¹) observed in peptide 3. Hence quantum interference effects come to the fore, as demonstrated by the anti-resonance peaks (Fig. 5b). These findings provide direct evidence of interplay between destructive quantum interference effects and vibrational fluctuations. Both phenomena were found to contribute to charge transfer to varying degrees, depending on the extent of backbone rigidity. This represents a unique form of peptide-based quantum interferometer, where the effects of destructive quantum interference are enhanced by increasing backbone rigidity through the introduction of a side-bridge constraint, whilst reducing vibrational fluctuations required by a hopping mechanism. Destructive quantum interference is likely to be a critical factor in the design of future molecular devices. Hence, these exciting findings offer a new approach to control charge transfer in peptides through the modulation of electron wavefunctions and backbone rigidity, which paves the way for the design of interference-controlled components, with applications in areas such as biosensing, cybersecurity, quantum information processing, thermoelectrics, and high resolution spectroscopy.

Conclusions

In summary, electrochemical and theoretical studies are reported on a series of novel peptides in order to investigate the interplay of quantum interference and backbone rigidity on electronic transport. Peptides 1 and 3 were synthesized and further constrained into well-defined secondary structures (β-strand and 3₁₀-helical respectively) by an amide-containing side-bridge, while peptides 2 and 4 are direct linear analogues. Experimental studies revealed a large disparity between the electrochemical properties of both cyclic and linear peptides, despite their distinctive secondary structures. The observed electron transfer rate constants for the cyclic peptides 1 and 3 were approximately one order of magnitude lower than their linear counterparts 2 and 4. A considerable formal potential increase of more than 470 mV was also observed for both cyclic peptides 1 and 3, compared with their linear counterparts. Complementary high level electronic transport simulations were used to investigate quantum interference effects in molecular junctions containing peptides 9–12 (analogues of 1–4). Despite peptides (cyclic 9 and linear 10) sharing a common β-strand conformation, the effects of destructive quantum interference were found to occur essentially in the cyclic 9 through the backbone and the additional tunneling pathway provided by the side-bridge constraint, while the linear 10 was found to exhibit a strong Fano-type resonance. The effects of destructive quantum interference were found to occur in both helical peptides (cyclic 11 and linear 12). However, these effects are masked by the more dominant vibrational fluctuations in the linear helical peptide 12 at room temperature. With the introduction of a side-bridge into the cyclic peptide 11, the effects of quantum interference come to the fore as the vibrational fluctuations are suppressed by the additional backbone rigidity imparted by the constraint. These findings provide direct evidence of an interplay between destructive quantum interference effects and vibrational fluctuations in the helical peptides, with both phenomena found to contribute to charge transfer to varying degrees, depending on the extent of backbone rigidity. We have thus demonstrated the principles of two distinctive peptide-based quantum interferometers through the manipulation of molecular orbitals by judicial chemical and structural design. One exploits the tunable effects of destructive quantum interference (β-strand), while the other regulates the interplay between quantum interference and vibrational fluctuations of the backbone (3₁₀-helical). These important fundamental advances to our knowledge of quantum interference effects on electronic transport in peptides bring us a step closer to realizing our ultimate goal to design, assemble and control functional devices from the bottom up.

Experimental

Peptide synthesis

Peptides 1–4 were synthesized as detailed in the ESI.† Each peptide was purified using reverse phase HPLC prior to the attachment to SWCNTs/Au electrodes for electrochemical analysis.

Peptide 1. ¹H NMR (600 MHz, DMSO-d₆): δ 8.54 (d, 1H, NH, J = 7.9 Hz), 8.36 (d, 1H, NH, J = 7.6 Hz), 8.07 (br s, 3H, NH), 7.79 (br s, 1H, NH), 7.55 (m, 1H, NH), 4.41–4.34 (m, 2H, 2 × CαH), 4.19–3.93 (m, 9H, Cp), 4.07 (br s, 2H, CH₂Fc), 3.88 (br s, 1H, CαH), 3.28 (m, 1H, CHHNH), 2.79 (m, 1H, CHHNH), 2.32–1.05 (m, 13H, 6 × CH₂, CH), 0.90–0.87 (dd, 6H, (CH₃)₂ Leu, J = 9.3, 6.6 Hz). ¹³C NMR (150 MHz, DMSO-d₆): δ 171.63, 171.29, 170.68, 168.36, 157.88, 70.92, 69.38, 68.92, 68.37, 67.33, 67.14, 51.81, 51.77, 51.58, 45.45, 41.49, 40.04, 37.45, 36.69, 30.19, 28.76, 25.20, 24.26, 23.98, 22.99, 22.63, 21.86, 19.50. HRMS (m/z): [M + H]⁺_calcd = 568.2586, [M + H]⁺_found = 568.2582.

Peptide 2. ¹H NMR (600 MHz, DMSO-d₆): δ 8.48 (d, 1H, NH, J = 8.1 Hz), 8.16 (d, 1H, NH, J = 7.3 Hz), 8.07 (d, 3H, NH, J = 4.0 Hz), 8.01 (br s, 1H, NH), 7.77 (t, 1H, NH, J = 5.4 Hz), 4.39 (dd, 1H, CαH, J = 14.1, 8.8 Hz), 4.31 (m, 1H, CαH), 4.20–3.94 (m, 11H, Cp, CH₂Fc), 3.76 (dd, 1H, CαH, J = 11.2, 5.7 Hz), 2.99 (dd, 2H, CH₂NH, J = 13.1, 6.8 Hz), 1.78 (s, 3H, CH₃), 1.71–1.61 (m, 3H, CH₂, CH), 1.49–1.45 (m, 2H, CH₂), 1.39–1.35 (dd, 2H, CH₂, J = 14.3, 7.1 Hz), 1.32–1.26 (dt, 2H, CH₂, J = 14.9, 7.2 Hz), 1.22 (d, 3H, CH₃, J = 6.3 Hz), 0.90–0.86 (dd, 6H, (CH₃)₂ Leu, J = 15.2, 6.6 Hz). ¹³C NMR (150 MHz, DMSO-d₆): δ 171.8, 171.5, 169.3, 168.8, 158.3, 71.3, 69.8, 69.3, 68.8, 67.8, 67.5, 52.4, 51.5, 48.5, 41.2, 38.6, 37.8, 31.3, 24.4, 23.5, 23.0, 21.9, 18.8. HRMS (m/z): [M + H]⁺_calcd = 570.2737; [M + H]⁺_found = 570.2743.

Peptide 3. ¹H NMR (600 MHz, DMSO-d₆): δ 8.30 (s, 1H, NH), 8.08 (s, 1H, NH), 7.75 (d, 1H, NH), 7.72 (m, 1H, NH), 7.54 (s, 1H, NH), 7.49 (m, 1H, NH), 7.33 (s, 1H, NH), 7.18 (t, 1H, NH), 4.25–3.90 (m, 12H, Cp, CH₂Fc, CαH), 3.85 (m, 1H, CαH), 3.04–2.90 (m, 2H, CH₂NH), 2.30–1.80 (m, 4H, 4 × CHH), 1.80–1.10 (m, 28H, 8 × CH₃, 2 × CH₂). ¹³C NMR (150 MHz, DMSO-d₆): δ 173.66, 172.51, 172.26, 171.96, 169.20, 166.27, 149.91, 144.91, 105.60, 100.89, 85.08, 84.44, 78.30, 77.34, 68.80, 67.45, 68.34, 66.99, 66.97, 66.92, 56.38, 56.02, 55.70, 53.68, 44.99, 43.47, 38.72, 31.50, 29.46, 28.95, 28.53, 24.89. HRMS (m/z): [M]⁺_calcd = 794.3778, [M]⁺_found = 794.3778.

Peptide 4. ¹H NMR (600 MHz, DMSO-d₆): δ 8.51 (s, 1H, NH), 8.13 (s, 1H, NH), 8.10 (s, 3H, NH₃), 7.84 (t, 1H, NHCH₂), 7.68 (s, 1H, NH), 7.63 (s, 1H, NH), 7.43 (m, 1H, NH), 7.34 (br s, 1H, NH), 4.55–3.50 (m, 12H, Cp, CαH, CH₂), 3.02 (m, 2H, NHCH₂), 1.76 (s, 3H, COCH₃), 1.68 (m, 2H, CH₂), 1.45–1.20 (m, 34H, 2 × CH₂, 10 × CH₃). ¹³C NMR (150 MHz, DMSO-d₆): δ 174.81, 174.35, 173.74, 173.47, 172.21, 171.81, 169.00, 128.89, 127.25, 121.35, 119.99, 109.72, 68.41, 66.90, 56.31, 56.10, 56.01, 55.93, 55.79, 53.26, 40.03, 38.30, 37.69, 30.45, 29.14, 28.87, 26.00, 25.38, 25.10, 24.97, 24.50, 24.20, 23.50, 23.37, 23.24, 22.60. HRMS (m/z): [M + H]⁺_calcd = 811.4164, [M + H]⁺_found = 811.4162.

Preparation of vertically aligned single-walled carbon nanotube array/gold (SWCNTs/Au) electrodes

P2-SWCNTs (Carbon Solutions, USA) were functionalized using previously reported methods.⁵⁰ CNTs were then suspended in a solution of DMSO containing 0.2 mg mL⁻¹ CNTs, 0.25 mg mL⁻¹ DCC and 0.14 mg mL⁻¹ DMAP. Polished flat gold disk electrodes (2 mm diameter) were cleaned in 25% v/v H₂O₂/KOH (50 mM) for 20 min and then electrochemically cleaned by cycling between 0 and 1.5 V vs. Ag/AgCl in 50 mM KOH. This cleaning process yielded clean gold surfaces with peak separations of 59 mV in 1 mM [Ru(NH₃)₆]Cl₃ solution. The clean surfaces were then incubated in cysteamine for 24 h resulting in exposed amine groups. These substrates were then exposed to the functionalized SWCNTs/DMSO suspensions for 24 h, after which they were rinsed with propan-2-ol and dried under nitrogen flow. The surfaces were then exposed to 0.01 M ferrocene-derivatized peptide in DMF solution containing 0.5 M HATU and 0.5 M DIPEA for 48 h before being further rinsed and dried.

Electrochemical measurements

All electrochemical measurements were taken with a CHI 650D electrochemical analyzer (CH Instruments Inc) with ohmic-drop correction at room temperature. A peptide modified gold surface formed the working electrode, with a platinum mesh and AgCl/Ag wire used as the counter and reference electrodes, respectively. The AgCl/Ag reference electrode was calibrated after each experiment against the ferrocene/ferrocenium couple. Ferrocene-derivatized peptide electrodes were electrochemically characterized in 0.1 mol L⁻¹ tetra-n-butylammonium hexafluorophosphate (TBAPF₆)/CH₃CN solutions. The digitized, background-subtracted curves were analyzed using a Data Master 2003 program.

Optimization for lowest energy conformers

The lowest energy conformers for all N-protected peptides were determined in the gas phase using the Gaussian 09 package,⁵¹ with tight convergence criteria using a hybrid B3LYP method with 6-31G** basis set for all C, H, N, O atoms, and Lanl2dz basis set for Fe atom in order to define the backbone conformations of all peptides. Results were further analyzed using the GaussView 5.0 package.

Electronic transport calculations

The molecular junctions were designed using the three system model (extended molecule), including the left electrode lead, central device region, and right electrode lead. The electrode leads were modeled in a 4 × 4 × 6 Au(111) unit cell, as detailed in the ESI† (as shown in Fig. S11†). Each of peptides 9–12 was wired between the gold electrodes via thiol anchoring groups. The structural relaxation of each molecular junction was carried out until the force on each atom was smaller than 0.05 eV Å⁻¹. Subsequent transmission calculations were conducted with the non-equilibrium Green's function approach combined with density functional theory (NEGF-DFT) in a supercell 2 × 2 × 1. This technique yields the transmission spectrum, detailing the probability of an electron with a given energy passing through the junction. Current–voltage characteristic curves were obtained using the TranSIESTA computational package,³⁰ which employs periodic boundary conditions in the xy directions and defines the z axis to be the transport direction. A linear combination of atomic orbitals (LCAO) is expanded to be the Kohn–Sham orbitals. Eigenchannels were computed using the Inelastica package.³⁸ The valence electronic orbitals of the systems were described using double-ζ polarized basis sets, and a cut-off energy of 250 Ry was used. The Brillouin zone was sampled as a Monkhorst–Pack grid using 4 × 4 × 10 k-points.

Acknowledgements

This work was financially supported by the Australian Research Council (ARC) Centre of Excellence for Nanoscale BioPhotonics (CNBP). We acknowledge the Australian National Fabrication Facility for providing the analytical facilities. Computational aspects of this work were supported by an award under the National Computational Merit Allocation Scheme for J. Y. on the National Computing Infrastructure (NCI) National Facility at the Australian National University.

Notes and references

1. M. Ratner, Nat. Nanotechnol., 2013, 8, 378–381.
2. A. Xiang, H. Li, S. Chen, S.-X. Liu, S. Decurtins, M. Bai, S. Hou and J. Liao, Nanoscale, 2015, 7, 7665–7673.
3. S. Kracht, M. Messerer, M. Lang, S. Eckhardt, M. Lauz, B. Grobety, K. M. Fromm and B. Giese, Angew. Chem., Int. Ed., 2015, 54, 2912–2916.
4. J. Yu, J. R. Horsley, K. E. Moore, J. G. Shapter and A. D. Abell, Chem. Commun., 2014, 50, 1652.
5. J. R. Horsley, J. Yu, K. E. Moore, J. G. Shapter and A. D. Abell, J. Am. Chem. Soc., 2014, 136, 12479–12488.
6. J. X. Yu, J. R. Horsley and A. D. Abell, Electrochim. Acta, 2016, 209, 65–74.
7. S. Sangtarash, H. Sadeghi and C. J. Lambert, Nanoscale, 2016, 8, 13199–13205.
8. C. Joachim, Nat. Nanotechnol., 2012, 7, 620–621.
9. H. Vazquez, R. Skouta, S. Schneebeli, M. Kamenetska, R. Breslow, L. Venkataraman and M. S. Hybertsen, Nat. Nanotechnol., 2012, 7, 663–667.
10. S. V. Aradhya, J. S. Meisner, M. Krikorian, S. Ahn, R. Parameswaran, M. L. Steigerwald, C. Nuckolls and L. Venkataraman, Nano Lett., 2012, 12, 1643–1647.
11. C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888.
12. M. Berritta, D. Z. Manrique and C. J. Lambert, Nanoscale, 2015, 7, 1096–1101.
13. T. Hines, I. Diez-Perez, J. Hihath, H. Liu, Z.-S. Wang, J. Zhao, G. Zhou, K. Muellen and N. Tao, J. Am. Chem. Soc., 2010, 132, 11658–11664.
14. D. Xiao, S. S. Skourtis, I. V. Rubtsov and D. N. Beratan, Nano Lett., 2009, 9, 1818–1823.
15. Y. Hu, L. Zeng, A. J. Minnich, M. S. Dresselhaus and G. Chen, Nat. Nanotechnol., 2015, 10, 701–706.
16. E. W. Schlag, S. Y. Sheu, D. Y. Yang, H. L. Selzle and S. H. Lin, Angew. Chem., Int. Ed., 2007, 46, 3196–3210.
17. A. D. Pehere and A. D. Abell, Org. Lett., 2012, 14, 1330–1333.
18. S. R. L. Fernando, G. V. Kozlov and M. Y. Ogawa, Inorg. Chem., 1998, 37, 1900–1905.
19. A. D. Pehere, C. J. Sumby and A. D. Abell, Org. Biomol. Chem., 2013, 11, 425–429.
20. W. Zhuang, T. Hayashi and S. Mukamel, Angew. Chem., Int. Ed., 2009, 48, 3750–3781.
21. A. Lakhani, A. Roy, M. De Poli, M. Nakaema, F. Formaggio, C. Toniolo and T. A. Keiderling, J. Phys. Chem. B, 2011, 115, 6252–6264.
22. N. A. Burton, M. J. Harrison, J. C. Hart, I. H. Hillier and D. W. Sheppard, Faraday Discuss., 1998, 110, 463–475.
23. P. Gillespie, J. Cicariello and G. L. Olson, Pept. Sci., 1997, 43, 191.
24. J. J. Gooding, R. Wibowo, J. Q. Liu, W. R. Yang, D. Losic, S. Orbons, F. J. Mearns, J. G. Shapter and D. B. Hibbert, J. Am. Chem. Soc., 2003, 125, 9006–9007.
25. P. Diao and Z. F. Liu, Adv. Mater., 2010, 22, 1430.
26. K. E. Moore, B. S. Flavel, J. Yu, A. D. Abell and J. G. Shapter, Electrochim. Acta, 2013, 89, 206–211.
27. J. R. Horsley, J. Yu and A. D. Abell, Chem. – Eur. J., 2015, 21, 5926–5933.
28. M. Kiguchi, Y. Takahashi, S. Fujii, M. Takase, T. Narita, M. Iyoda, M. Horikawa, Y. Naitoh and H. Nakamura, J. Phys. Chem. C, 2014, 118, 5275–5283.
29. M. Magoga and C. Joachim, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 16011–16021.
30. M. Brandbyge, J. L. Mozos, P. Ordejon, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401.
31. L. Scullion, T. Doneux, L. Bouffier, D. G. Fernig, S. J. Higgins, D. Bethell and R. J. Nichols, J. Phys. Chem. C, 2011, 115, 8361–8368.
32. Y. Arikuma, H. Nakayama, T. Morita and S. Kimura, Angew. Chem., Int. Ed., 2010, 49, 1800.
33. H. Liu, J. Zhao, F. Boey and H. Zhang, Phys. Chem. Chem. Phys., 2009, 11, 10323–10330.
34. C. M. Guedon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. J. van der Molen, Nat. Nanotechnol., 2012, 7, 304–308.
35. P. Gehring, H. Sadeghi, S. Sangtarash, C. S. Lau, J. Liu, A. Ardavan, J. H. Warner, C. J. Lambert, G. Andrew, D. Briggs and J. A. Mol, Nano Lett., 2016, 16, 4210–4216.
36. D. Z. Manrique, C. Huang, M. Baghernejad, X. Zhao, O. A. Al-Owaedi, H. Sadeghi, V. Kaliginedi, W. Hong, M. Gulcur, T. Wandlowski, M. R. Bryce and C. J. Lambert, Nat. Commun., 2015, 6, 6389.
37. G. C. Solomon, D. Q. Andrews, R. H. Goldsmith, T. Hansen, M. R. Wasielewski, R. P. Van Duyne and M. A. Ratner, J. Am. Chem. Soc., 2008, 130, 17301–17308.
38. M. Paulsson and M. Brandbyge, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115117.
39. D. Nozaki, H. Sevincli, S. M. Avdoshenko, R. Gutierrez and G. Cuniberti, Phys. Chem. Chem. Phys., 2013, 15, 13951–13958.
40. B. Luk'yanchuk, N. I. Zheludev, S. A. Maier, N. J. Halas, P. Nordlander, H. Giessen and C. T. Chong, Nat. Mater., 2010, 9, 707–715.
41. N. Darwish, I. Diez-Perez, P. Da Silva, N. Tao, J. J. Gooding and M. N. Paddon-Row, Angew. Chem., Int. Ed., 2012, 51, 3203–3206.
42. A. Saraiva-Souza, M. Smeu, L. Zhang, A. G. Souza Filho, H. Guo and M. A. Ratner, J. Am. Chem. Soc., 2014, 136, 15065–15071.
43. D. Q. Andrews, G. C. Solomon, R. H. Goldsmith, T. Hansen, M. R. Wasielewski, R. P. Van Duyne and M. A. Ratner, J. Phys. Chem. C, 2008, 112, 16991–16998.
44. J. Yu, O. Zvarec, D. M. Huang, M. A. Bissett, D. B. Scanlon, J. G. Shapter and A. D. Abell, Chem. Commun., 2012, 48, 1132–1134.
45. B. Giese, M. Wang, J. Gao, M. Stoltz, P. Müller and M. Graber, J. Org. Chem., 2009, 74, 3621–3625.
46. D. E. Lopez-Perez, G. Revilla-Lopez, D. Jacquemin, D. Zanuy, B. Palys, S. Sek and C. Aleman, Phys. Chem. Chem. Phys., 2012, 14, 10332–10344.
47. R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196.
48. B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2012, 112, 321–370.
49. J. Yu, D. M. Huang, J. G. Shapter and A. D. Abell, J. Phys. Chem. C, 2012, 116, 26608–26617.
50. K. E. Moore, B. S. Flavel, A. V. Ellis and J. G. Shapter, Carbon, 2011, 49, 2639–2647.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pommel, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010.

---

Footnote

† Electronic supplementary information (ESI) available: Full synthesis and extended computational details, conformational analysis, and ¹H NMR spectra. See DOI: 10.1039/c6me00077k

---