The construction and application of Markov state models for colloidal self-assembly process control
Xun
Tang
 a,
Michael A.
Bevan
b and
Martha A.
Grover
a,
Michael A.
Bevan
b and
Martha A.
Grover
 *a
*a
aSchool of Chemical & Biomolecular Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA. E-mail: martha.grover@chbe.gatech.edu
bDepartment of Chemical and Biomolecular Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
First published on 21st December 2016
Abstract
Markov state models have been widely applied to study time sequential events in a variety of disciplines. Due to their versatility for representing system stochasticity, Markov state models hold the promise to simplify simulation and design control policies for colloidal self-assembly systems. In this manuscript, we investigate the effects of state discretization, transition time, sampling approach, and the number of samples on the accuracy of a Markov state model for a colloidal self-assembly process. The model accuracy is evaluated based on the performance of the optimal control policy, calculated with a Markov decision process-based optimization framework, for controlling a Brownian dynamics simulation to produce perfect crystals. The results suggest using a dynamic sampling, a transition time similar to the system characteristic time, a clustering-based state discretization, and an average of at least five samples per state, to efficiently build an accurate Markov state model.
Design, System, ApplicationColloidal self-assembly has been widely studied to produce ordered structures for new materials with novel photonic properties. However, the defect-free structures that are required for applications are difficult to fabricate using self-assembly. One promising strategy is to use model-based feedback control to correct defects formed during the process. Here we use the Markov decision process formulation of dynamic programming. To fully utilize this approach, the model needs to be both accurate and fast in predicting the system dynamics. Markov state models are able to capture the system stochasticity and predict the dynamics fast enough for control policy calculation. However, building an accurate Markov state model is nontrivial. Our work provides insights on how to efficiently build an accurate Markov state for a high-dimensional stochastic system, using sampled data. The results from this study appear to be general principles that could provide guidelines for model-based control of other microscale and nanoscale assembly processes. |
1 Introduction
Colloidal self-assembly is a process where particles suspended in solution converge to an ordered structure without external interference.1 An ordered assembly of colloidal particles at nano- and micro-meter scales has the ability to interact with light for unique photonic properties. Materials made of these highly ordered structures can be applied as reconfigurable circuit elements,2 invisibility cloaks,3 semiconductors,4 and light harvesting materials.5–7 Understanding colloidal self-assembly dynamics could help design control policies to rapidly produce high quality crystalline structures, and this can be achieved via predictive models.The colloidal self-assembly process can be simulated with Monte Carlo simulation,8 molecular dynamics,9,10 and Brownian dynamics.11,12 These simulations can provide accurate approximations of the system dynamics, but it is time-consuming to conduct simulations in a high-dimensional system, especially when the timescale of assembly spans from milliseconds to hours.13 Moreover, to account for the statistical effects in a stochastic process, it is even more challenging to conduct enough repetitions of these simulations. Alternatively, time-series models like the Markov state model can be built with a reduced-order state to shorten the amount of simulation time. These models are still constructed using output from the high-dimensional simulations, but once constructed, they can be evaluated quickly.
Markov state models have been widely studied in many fields including biology,14,15 and economics,16 as well as colloidal self-assembly processes.13,17,18 A Markov state model can be formulated as either a continuous- or a discrete-time model. A discrete-time Markov state model is characterized by a set of discrete time points T, a set of system states S, and a probability transition matrix P(a), which stores the transition probabilities between different states under an input a.19 Since a continuous state Markov model is challenging, the system state is typically discretized.20,21
A Markov state model describes a process as a memoryless time series, where the state at the next time step depends only on the current state and the action used.19 It captures the system stochasticity with a transition matrix, which is usually estimated based on a large number of system samples. Therefore, a Markov state model could provide a broader view of the system dynamics distribution, compared to a single stochastic trajectory.22,23 A recent study reported that by using order parameters to reduce the system dimension and describe the system state, a reduced-order Markov state model can not only provide reliable approximations of the high-dimensional system dynamics, it can also enable the design of an optimal control policy for rapid assembly of defect-free two-dimensional colloidal crystals.13
Building a reduced-order Markov state model for a high-dimensional system is nontrivial, as it requires an appropriate selection of the set of the reduced-order coordinates, to capture the features of interest and to reliably represent the system dynamics. The accuracy of a Markov state model also requires an accurate transition matrix P(a), which is mainly affected by the following three factors:19,22,24,25 (1) training samples, for calculation of the transition probabilities; (2) transition time Δt, after which the transitions are counted; (3) state discretization, where a continuous state space is discretized into discrete states. Although numerous studies have been reported on the construction of Markov state models,19 efficiently building an accurate Markov state model for a high-dimensional system is still challenging.13,17
In this study, focusing on a SiO2 colloidal self-assembly process, we investigate the effects of the aforementioned three factors on the Markov state model accuracy in approximating this high-dimensional stochastic system. The model accuracy is evaluated based on the performance of the Markov state model-based optimal control policies, since the ultimate application of the model is to design the control strategies to rapidly produce two-dimensional defect-free crystals.
The paper is organized as follows: Section 2 describes the colloidal system; Section 3 describes order parameters, transition time, sampling approach, and state discretizations; Section 4 describes the calculation of the control policy; Section 5 presents the results; Sections 6 and 7 provide discussions and conclusions.
2 Self-assembly process
The colloidal self-assembly process considered in this study is the same as in previous studies.11,13,26,27 The particles are suspended in deionized water in a batch system, and four electrodes are attached around the container to generate an electric field. The system is monitored in real-time with an optical microscope, and Fig. 1 shows a top-view of the particles in the system under the microscope. When the electric field is turned on, induced dipolar interactions compress particles into the electric field minimum at the quadrupole center, which initiates quasi-2D crystallization. Different amplitudes of the voltage generate different levels of compression, and therefore different configurations of the particles (Fig. 2). In this study, two voltage levels are considered: λ = 0.2 and λ = 19.7. The input λ is the dimensionless representation of voltage, which indicates how strongly the relative energy of the electric field mediated compression is compared to the thermal energy kT.13 The low input λ = 0.2 can be used to relax the system to a fluid-like state (Fig. 2a), if defective states (Fig. 2b and c) form after a strong compression from λ = 19.7. The value of the high input (λ = 19.7) is chosen to: (1) provide a strong compressing force for rapid assembly and maintenance of the assembled structure; (2) confine particles to form a two-dimensional planer structure without three-dimensional stacking. The problem of interest here is how to efficiently build accurate Markov state models to represent the system dynamics in a compact manner and to compute a model-based optimal control policy for rapid assembly of a defect-free crystal (see Fig. 2d). | ||
| Fig. 1 Top-view of the SiO2 colloidal particles with a radius of ∼1.5 μm with an optical microscope and digital camera to enable monitoring of particle trajectories in real-time. Adapted with permission from Tang et al.13 Copyright (2016) American Chemical Society. | ||
3 Markov state model
3.1 Order parameters
The system is simulated with an experimentally validated Brownian dynamics simulation, using the x, y coordinates of each individual particle.11 Such a detailed force balance model is able to accurately represent the system dynamics using a high dimensional representation (i.e. 2N, with N being the number of particles). However, tracking particle coordinates to monitor the system state is usually computationally demanding. In addition, for systems where overall system level properties, such as ordering, are of more interest than individual particle locations, a set of aggregate variables, i.e. order parameters, is often used to characterize the assembly. These aggregate variables can be identified by conducting dimensionality reduction on the high-dimensional system.Dimensionality reduction can be implemented with either numerical methods or physical interpretations, or a combination of both. Numerical approaches include both linear techniques like principal component analysis28,29 and factor analysis;30 and nonlinear techniques like diffusion maps31,32 and isomap.30,33 Numerical algorithms are generally straightforward to implement using widely distributed software. However, the resulting variables from numerical dimensionality reduction usually bear no physical meaning, and this makes it challenging to uncover a physical phenomenon.
Alternatively, constructing aggregate variables with domain knowledge can potentially provide physically meaningful parameters to better illustrate the complex system dynamics.34 In a colloidal self-assembly process, if the feature of interest is the compactness of the particles, then radius of gyration, Rg, can be used to quantify the root-mean square distance between particles within an ensemble; if the local order of a structure is of interest, then the averaged number of nearest neighbors can be used, such as C6 for a 2-D hexagonal structure; if the global order is needed, then global orientation parameters which describe the particle-particle bond orientation, like ψ6, can be used. Other examples include pair-correlation or distribution functions,35 volume fraction,36 and dihedral angles.37
The use of physically meaningful parameters solves the problem of relating the numerical values to a physical phenomenon, however this approach not only requires domain knowledge, it also requires extensive validation. Therefore, a combination of the numerical approach and physical interpretation has been advocated.34 In Bevan et al.,38 a diffusion map is used to verify the use of Rg and C6 in quantifying defect formation in a depletion-force-mediated colloidal self-assembly process. A combination of physical interpretation and numerical techniques could not only provide physically meaningful order parameters, it could also provide mathematical justification to the selection.11,39
The choice of the reduced-order state plays an important role in determining the accuracy of any reduced-order model, including the Markov state model.40–43 Three candidate order parameters were considered: Rg, C6, and ψ6, and order parameters ψ6 and C6 are selected because: first, C6 and Rg capture the similar dynamics, but C6 is more sensitive to small changes compared to Rg (illustrated in Fig. 2); second, the formation of grain boundaries can be quantified reliably with ψ6 and C6, and a 98% yield was achieved with an optimal control policy using these two order parameters.13
Specifically, ψ6 is defined as:
 | (1) |
 | (2) |
The number of neighbors within the first peak of a coordination radius of particle j is NC,j, and θjk is the angle between particle j and k with an arbitrary reference direction. C6 is defined as:
 | (3) |
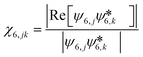 | (4) |
 is the complex conjugate of ψ6,k. The connectivity χ6,jk is used to compute the local order parameter for six-fold connectivity C6,j,
is the complex conjugate of ψ6,k. The connectivity χ6,jk is used to compute the local order parameter for six-fold connectivity C6,j, | (5) |
3.2 Transition time Δt
The transition time is one important factor that affects the accuracy of a Markov state model. The validity of Markov state models builds on the Markovian assumption of a memory-free state. If the transition time is too short, it is possible that previous history also has an effect on the future dynamics.44 This phenomenon violates the Markovian assumption that future dynamics only depends on the current state instead of previous history. The memory effects can be lessened with a longer transition time.23,44 In addition, a transition time that is too short could also result in the system being artificially trapped in meta-stable states or kinetic bottlenecks, such that the system would not be able to evolve to other states. These states become absorbing states in the transition matrix, and are problematic in the calculation of a control policy. On the other hand, if the transition time is too long, it will result in a loss of intermediate information. In addition to limiting the time resolution of the model, the performance of the model-based control policy will also suffer since fewer switches in the input will be possible.One way to identify the appropriate transition time is through trial-and-error. In this approach, modeling errors from models built with different transition times are compared, the one that gives an acceptably low modeling error is identified and the associated transition time is selected. Modeling error evaluation can be achieved with system kinetics analysis-based approaches, such as mean first passage time analysis,14 or spectral theory-based lag time test, such as implied timescale test and Chapman–Kolmogorov test.19,23
Alternatively, if the characteristic time of a physical system is obtainable with either domain knowledge, or experimental observations, then it can provide a guideline for an appropriate transition time. In practice, the trial-and-error approach can be combined with physical interpretation to identify the best transition time. Previous findings suggest that the system in this study has a characteristic time of approximately 100 s.13 Given the fact that assembly takes only 1000 s, longer transition times are not considered here, as they would not resolve the dynamics or enable much control action. Consequently, models with Δt = 10 s, 50 s and 100 s are studied in this manuscript.
3.3 Sampling
The Markov state model is data driven, and the accuracy of any data-driven model depends on the training samples. For a deterministic process, the challenge in building a globally accurate model comes from generating samples to cover all feasible system states, particularly for states that are rarely visited. The situation is more challenging in a stochastic process, like the colloidal self-assembly system. Due to system stochasticity, multiple samples are required for each state to ensure a reliable estimation of the transition probabilities.17To generate samples, a time-constant or time-varying (i.e. dynamic) input trajectory can be used. Sampling with time-constant input is straightforward to implement. However it is often challenging to sample all the important states (associated with all input levels), using a single input level. In addition, states that can only be reached by a dynamic input trajectory will not be sampled with a constant input. These states can be important from the perspective of control, where switches between different inputs are specified. One challenge associated with a dynamic sampling is the design of the switching frequency. The switching time should be longer than the transition time in order to obtain a sample that can be used for the construction of the transition matrix. For this reason, a realization of simulated data with a fixed switching frequency can only be used for transition times shorter than the switching time. When the transition time is not yet determined, the switching frequency in a dynamic sampling scheme constrains the maximum transition time that can be used in the Markov state model.
Samples can be collected from either long-time simulations or short-time simulations. Long-time simulation trajectories include the long-term behavior of the system—thus it can provide information on the characteristic time of the system. However, for systems with meta-stable states, long-time simulation trajectories can be inefficient if the simulation becomes trapped.22,37 As a result, long-time molecular or detailed dynamics simulations may require a large amount of storage space. To save storage space, intermediate information is often discarded. With short-time simulations, one can use constant inputs to run simulations from a predefined set of states.
The main sampling pool in this study is constructed with BD simulations using time-varying input trajectories that randomly switch between the two input levels every 100 s. Specifically, a total of 500 realizations with initial states from fluid, defective and highly crystalline regions are conducted, with each realization simulated for 2000 s. The rationale behind this sampling approach is to increase the number of states visited, by exciting the system using random switches.
3.4 State discretization
State discretization is important and nontrivial. A discretization that is too coarse could group together configurations that have different dynamics, and discretization that is too fine could result in a prohibitively large number of states to sample in transition matrix estimation.19,23,24,45 Moreover, if the system state is too big, it could cause difficulties in control policy calculation,20 which is known as “curse of dimensionality” in dynamic programming. Therefore a tradeoff between coarse and fine discretization is needed.States can be discretized according to their kinetic similarities, where states with similar transition speeds are grouped together.17,25,45 They can also be discretized geometrically, or using a distance metric-based discretization algorithm. Kinetic-based discretization is usually challenging, since it requires a reliable understanding of the system kinetics. When the system kinetics is not fully understood, discretization geometrically or using a distance metric-based algorithm is simpler to implement.46 We focus on the latter two approaches in this manuscript.
The simplest approach of geometric discretization is to divide the state space into evenly spaced intervals. Gridding is particularly useful if the region of state space is clearly defined and the resolution of the discretization needed to distinguish dynamically different states is known. On the other hand, distance metric-based discretization approaches, such as clustering, group together states that meet a predefined criterion. A common algorithm is the k-means clustering.47 Other methods include hierarchical clustering, fuzzy clustering, and nearest neighbor clustering.19,48–50
Gridding requires no initial samples, and it could help the design of the initial states by providing an exhaustive enumeration of the state space. If one can obtain samples for each individual grid cell, gridding also holds the promise for a globally accurate model. However, discretization with gridding can introduce infeasible states, and this will lead to difficulties in sampling. On the other hand, discretization with clustering algorithms is achieved using whatever samples are available, and this guarantees that all the defined states are reachable. However, the number and the coverage of the samples affects the clustering results significantly. In this study, an evenly-spaced grid and a k-means clustering approach are investigated.
4 Control policy calculation
All the transition matrices in this study were built with the moving window approach specified in Prinz et al.23 An infinite-horizon Markov decision process (MDP) based optimization problem is then formed and solved for a closed-loop optimal control policy. A MDP is characterized by T, S, A, P(a), where S, P(a) are defined previously. The set of discrete control actions A is composed here by the two λ input levels, and T is the set of the discrete time point k.20 With T being infinite, the process is called an infinite-horizon MDP, and the resulting control policy is a static control policy. Considering the simplicity of a static control policy and its previously demonstrated success,13 we focused on the infinite-horizon MDP policies for this study.The optimization of the infinite-horizon MDP is achieved over an infinite number of time steps, and the policy is designed to maximize the objective function at each state:
 | (6) |
The one-stage reward function, R(x, a): S × A → R, is obtained when the system is in state x and control action a is taken. The design of the objective function is aimed to obtain the highest possible crystallinity at each time step, with the one-stage reward function defined as R(x, a) = ψ62. Order parameter C6 was not explicitly included in the objective for the reasons that: first, a high ψ6 state automatically ensures a high C6 value, due to their physical meanings; second, the addition of C6 to the reward function does not significantly affect the control policy according to our findings.
The optimal value function J* and the optimal policy π* for finite-horizon MDP control policy are defined as:
 | (7) |
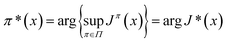 | (8) |
The optimal control policy was solved with dynamic programming via the policy iteration algorithm in the MATLAB MDP Toolbox.52 Solving the optimal control policy takes several seconds on a 3.40 GHz Intel(R) Xeon(R) CPU with 16.0 GB memory. To use the control policy, during operation, the current centers of mass of each particle are analyzed to calculate the two order parameter values. From the order parameters, the input λ for the next control interval, specified by the transition time Δt, is identified in the control policy lookup table. Experimentally, the image processing can be conducted every 100 ms.
5 Results
5.1 Effect of Δt
The goal of this first study is to understand the effects of different transition times using the same initial conditions in the sample set. Three transition times are considered: Δt = 10 s, 50 s and 100 s. In principle, a Markov state model built with a shorter Δt value could resolve more intermediate transition dynamics, compared to a model with a longer Δt. Ideally, the control policy generated with the shorter transition time would lead to the best closed-loop performance, since more switches are possible. However, in practice the model with the shorter transition time is often less accurate, and if the model is inaccurate, then the control policy will also be suboptimal.To build Markov state models for each of the three Δt values, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples (i.e. transition pairs) are used, taken from BD simulations generated under time-varying input trajectories. The MATLAB k-means clustering function is used to discretize the state space into 100 non-overlapping states.
000 samples (i.e. transition pairs) are used, taken from BD simulations generated under time-varying input trajectories. The MATLAB k-means clustering function is used to discretize the state space into 100 non-overlapping states.
As shown in Fig. 3, all three control policies share the same pattern that λ = 0.2 is used in the upper left defective region and λ = 19.7 is used in the fluid and the highly crystalline states. As the transition time increases, more white space, corresponding to unsampled states, appears in the upper left region of the control policy. This is because the system travels a longer distance in the state space over the longer transition time, and therefore the intermediate dynamics are not captured.
The control performance of the three policies is then evaluated with 200 BD simulations, and the results are summarized in Fig. 3d. A perfect crystal is obtained when order parameter ψ6 reaches 0.95 (either during the process or at the end of the process), and the yield is the percentage of simulations that produce a perfect crystal. This definition of yield is referred to here as “endpoint detection,” since it is assumed that the process can be stopped once assembly is detected. All the simulations are initiated from the same initial fluid-like states with the same set of seeds in the random number generator, for each of the three policies.
The averaged input trajectories in Fig. 3d indicate that all three policies achieve the same trend; after an initial use of λ = 19.7, λ = 0.2 is used to relax the system for defect correction, and with increased crystallinity, λ = 19.7 is used to maintain the structure. The yield trajectories indicate that policies with Δt = 50 s and 100 s gave a similar performance with a final yield of 97.5% and 96.5% respectively. However, contrary to the expectation that the shortest transition time model would give the highest model accuracy, the policy with Δt = 10 s gave the lowest yield of 87.5%. This is significantly different from that of the other two, according to a two-tailed t-test with a 95% confidence interval. This phenomenon indicates that the model built with Δt = 10 s is less accurate than the other two.
A mean first passage analysis in Fig. 4 confirms the above interpretation by showing that the Δt = 10 s Markov state model was not able to accurately quantify the relaxation from highly crystalline states, as compared to the other two models. The averaged C6 and ψ6 trajectories from the Markov chain Monte Carlo simulation with both the Δt = 50 s and 100 s models are similar to that of the BD simulations, but the trajectories predicted with the Δt = 10 s model differ significantly from the other three. This is because 10 seconds is significantly shorter than the characteristic relaxation time (∼100 s) as discussed in Tang et al.,13 such that certain samples could not transition out of their original grid cells. Therefore the model could not capture the rapid relaxation compared to that of Δt = 50 s and 100 s.
Further investigations into the Δt = 50 s and 100 s models indicate that the accuracy of models built with a longer Δt value might be more robust to the number of samples, and a long Δt could potentially compensate for inadequacy in sampling. According to Table 1, when sampling is not a limiting factor (more than 1000 samples), both Δt = 50 s and Δt = 100 s policies give similarly satisfying performance. Additional sampling does not show improvements in the yield, but a faster assembly to reach 50% and 80% yield is observed. When sampling is a limiting factor with 100 or 500 samples, additional samples dramatically improve the performance of the policy with 1000 and greater samples for the Δt = 50 s cases. However, less degradation in performance was observed in the Δt = 100 s models, as the number of samples was reduced.
| Sample# | ≥50% time (s) | ≥80% time (s) | Yield (%) | |||
|---|---|---|---|---|---|---|
| 50 s | 100 s | 50 s | 100 s | 50 s | 100 s | |
| 100 | 450 | 300 | N/A | 600 | 72.5 | 89.0 |
| 500 | 300 | 300 | N/A | 650 | 78.0 | 90.0 |
| 1000 | 250 | 250 | 450 | 550 | 97.0 | 95.0 |
| 5000 | 200 | 150 | 400 | 450 | 97.5 | 98.5 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
200 | 150 | 400 | 400 | 97.5 | 96.5 |
Comparison of the control policies for the Δt = 50 s and 100 s models, as shown in Fig. 5, reveals that additional sampling reduces the amount of noise in the control policy, which results from under-sampling. The control policy is calculated based on the reward of using a particular action in each state. If a state is under-sampled and the reward of using either λ level in this state is similar, noise can be introduced in the control policy. For policies computed with 100 samples (Fig. 5a and b), the limited number of samples resulted in states only being sampled under one input, and this input is selected as the optimal action in the policy, since the reward associated with this input is higher than the other input (the state in the Markov state model for the other input is deemed as an absorbing state). Because of this, the use of λ = 0.2 is observed in the highly crystalline states in Fig. 5a and b, and this could result in destroying a perfect crystal at the end of the process. Indeed, if the yield is calculated based on the crystallinity at the end of the 900 s process, only 50% and 60% of the 200 BD simulations were able to produce a perfect crystal, for policies in Fig. 5a and b respectively. However, the yield here is calculated based on the endpoint detection strategy defined in Section 5.1. This further indicates that using random switches along with feedback to terminate the process can lead to surprisingly good performance.
Another observation in Fig. 5 is that when the transition time is shorter than the system characteristic time, the system does not move very far within the short transition time, as indicated by the white space in the upper left region of Fig. 5a. All the samples are collected from BD simulations that started from the lower left region in the state space. With a limited number of samples and a shorter than system characteristic transition time, the upper left defective states are not visited. Therefore, a transition time that is similar to the system characteristic time is suggested, and the following study focuses on Δt = 100 s Markov state models.
5.2 Effect of discretization
To understand the difference between the clustering and the gridding approaches, Markov state models with a transition time of 100 s are built with different numbers of samples. In the clustering approach, the state space is grouped into exactly 100 states; with the gridding approach, the system is discretized to give approximately 100 effective states. Note that an effective state is defined as a state that receives at least one sample under any input.The clustering-based discretization is achieved by grouping states with similar order parameter values, via a k-means algorithm, and the resulting discrete states are all defined and reachable in the system. Therefore, the control policy from the clustering-based Markov state model assigns a control action for every state in the system. When a new state is encountered, this state is assigned to the control action of its nearest cluster. Thus, all states have a control action defined in the control policy.
On the contrary, states discretized with gridding include reachable but not sampled states, as well as unfeasible states. If a reachable state is not sampled under either input, it is necessary to modify the control policy to define an action for these states. In this section, three modifications are considered: 1. applying λ = 0.2 as the default action (i.e. GL); 2. applying λ = 19.7 as the default action (i.e. GH); 3. using extrapolation and interpolation based on the neighboring states' actions to design the control action (i.e. GE).
Fig. 6 shows the gridding-based control policies computed with the same Markov state model, built with the same 1000 samples used for the policy in Fig. 5d. While the control actions in the sampled states remain unchanged, actions for the unsampled states (e.g. region of C6 between 4 and 5) are subjected to the modification approaches. When the policy is modified with extrapolation and interpolation, the structure of the final control policy resembles that of the clustering-based control policy in Fig. 5d, where the majority of the upper left region uses the low input level, and the rest is dominated by λ = 19.7.
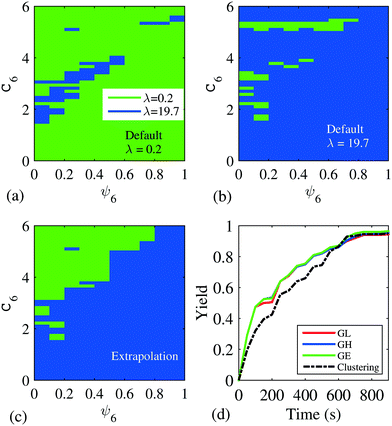 | ||
| Fig. 6 Control policies computed with gridding-based Markov state models, with policy modified to have: (a) default action as λ = 0.2, i.e. GL; (b) default action as λ = 19.7, i.e. GH; (c) modified with extrapolation and interpolation, i.e. GE. (d) Averaged yield (defined as in section 5.1) of 200 controlled BD simulations, using control policies in Fig. 5d and the three gridding-based policies. | ||
Although the difference among the three gridding-based control policies is evident visually, the 200 controlled BD simulation realizations indicate no significant difference in terms of yield, as shown in Fig. 6d. According to the yield trajectories, all three gridding-based policies gave a similar yield. The clustering-based control policy gave a lower yield at the beginning, but reached the similar final yield at the end of the 900 s process.
A more detailed investigation with different numbers of samples confirms the similarity between the different discretization approaches. The results in Table 2 indicate that with additional sampling, both the yield and time required to reach a high yield can be improved. However, with the same number of samples, the four cases do not result in a statistically significant difference. One explanation for this phenomenon is that the majority of the important states are sampled, such that the actions used in the less important and unreachable states do not affect the performance of the control very much.
| Sample# | ≥50% time (s) | ≥80% time (s) | Yield | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GL | GH | GE | GL | GH | GE | GL | GH | GE | |
| 100 | 300 | 250 | 250 | 650 | 800 | 550 | 90.0% | 82.0% | 92.5% |
| 500 | 250 | 150 | 250 | 550 | 600 | 550 | 95.0% | 91.0% | 95.0% |
| 1000 | 150 | 150 | 150 | 450 | 450 | 450 | 94.5% | 95.5% | 96.5% |
| 5000 | 150 | 150 | 150 | 450 | 450 | 450 | 97.0% | 97.0% | 97.0% |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
150 | 150 | 150 | 450 | 450 | 450 | 97.5% | 97.5% | 97.5% |
However, when the system is significantly under-sampled (with 100 samples), the yield of the gridding-based policy indicates a difference between the default use of λ = 19.7 and the other modifications. One explanation is that the use of λ = 19.7 results in a lower chance of relaxation, due to the strong compressing force. As a result, when a defective but unsampled state is encountered, it has a lower chance of being eliminated. This indicates the importance of using physical understanding in designing the default action.
5.3 Effect of numbers of states
To understand the effects of different number of states, Markov state models with 100 s transition time are studied. Since there is no significant difference between the three policy modifications using more than 1000 samples, for simplicity, the gridding-based policies in this section are modified with a default input of λ = 19.7.The state space is discretized into 10, 100, and 1000 clusters in the clustering-based policies, and is discretized to have about 10, 100, and 1000 effective states in the gridding-based policies. Markov state models are built with a set of 1000 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 BD simulation samples respectively, to include the sampling effects as well. Therefore, a total of 12 Markov state models are constructed and compared.
000 BD simulation samples respectively, to include the sampling effects as well. Therefore, a total of 12 Markov state models are constructed and compared.
The 12 optimal control policies, corresponding to the 12 Markov state models, are computed and evaluated with 200 realizations of 900 s BD simulations. The percentage yield of the controlled BD simulations are summarized in Table 3. In general, policies with the clustering-based models are more robust to the number of states, compared to that of the gridding-based models, indicated by the variations among the yields.
| # states | 1000 samples | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 samples 000 samples |
||
|---|---|---|---|---|
| Cluster | Gridding | Cluster | Gridding | |
| 10 | 97.0% | 79.5% | 93.5% | 90.0% |
| 100 | 95.0% | 95.5% | 96.5% | 97.5% |
| 1000 | 82.5% | 81.5% | 92.5% | 86.5% |
One important observation is that, with 1000 states and 1000 samples, policies from the clustering and the gridding-based models gave a decent yield of 82.5% and 81.5% respectively. On average, only half (500) of the states are sampled under each λ, given that the total amount of the transition pairs is 1000. The high yield achieved here is again due to the use of the endpoint detection strategy, and the fact that random toggling leads to good assembly at some point during this process.
Surprisingly, with a coarse discretization of 10 states and 1000 samples, policies from the clustering and the gridding-based models gave a yield of 97.0% and 79.5% respectively. This indicates that if the state space is discretized appropriately (clustering rather than gridding), very few states are actually needed.
Moreover, the results in Table 3 indicate that, in order to reach a yield of over 90%, i.e. a highly accurate model, at least an average of five samples per state are needed to provide a reasonable representation of the system stochasticity. With five samples, a resolution of 0.2 (i.e. 1/5) in the transition probability can be obtained, and this improves the accuracy of the transition matrix compared to that of a lower resolution with fewer samples. Note that the averaged samples per state are calculated as the total number of samples divided by the number of states divided by the total number of λ's (two).
5.4 Effect of sample sources
Results in the previous section indicate that a higher than 95% yield can be achieved with 1000 samples using the clustering approach and Δt = 100 s. However, the characteristics of the samples also matter in the model accuracy. Therefore, in this section, we study the accuracy of the 100-state models built with 1000 samples from the following four sampling approaches: first, 500 samples from each of the constant inputs of λ = 19.7 and λ = 0.2 (i.e. constant); second, 1000 samples from a toggling scheme which uniformly switches between the two input levels every 100 s (i.e. toggling); third, 1000 samples from the controlled results using previously developed control policies (i.e. optimal); fourth, 1000 samples generated with randomly switched input trajectories (i.e. random). All the simulations for samples are initiated in the same fluid states.Samples generated with the constant use of λ = 0.2 are confined in the fluid states due to the small compressing force, while the majority of samples generated with λ = 19.7 are from the assembled states, i.e. states with high C6 value, due to the strong compression. Therefore, two distinct sets of states are sampled under each λ. The unsampled fluid states in λ = 19.7 and the unsampled high C6 states in λ = 0.2 are set as absorbing states, where no transition to other states is observed from these states, in their corresponding Markov state models. The existence of the absorbing states due to under-sampling results in the use of λ = 0.2 in the fluid states and λ = 19.7 in the compact states in the control policy (Fig. 7a), and this eventually leads to the lowest yield of 17.0%.
 | ||
| Fig. 7 Control policies for 100-state models with 1000 samples from BD simulations under: (a) constant input; (b) toggling input; (c) optimal control policy; (d) randomly switched input. | ||
The toggling scheme starts the simulation with 100 s application of λ = 19.7, and switches with λ = 0.2 every 100 s, with the last 100 s using λ = 19.7. This design enables sampling in the assembled states under λ = 0.2 and sampling in the fluid and the final highly crystalline states under λ = 19.7. As a result, the policy in Fig. 7b uses λ = 0.2 in the assembled states with λ = 19.7 used in both the fluid-like and the highly crystalline state.
The control policy built with samples from the optimally controlled BD simulations in Fig. 7c shows that both λ = 19.7 and λ = 0.2 are used in the assembled as well as the fluid states. This is also observed in the policy with samples from BD simulations using randomly switched input trajectories, as shown in Fig. 7d, except that more states have used λ = 0.2 in Fig. 7d. The use of both actions in both regions is usually desired, for reasons that some fluid states need a further relaxation to prevent a potential formation of defect; while some defective states can evolve into ordered states under λ = 19.7, without an immediate relaxation. However, the use of a specific λ in these states is particularly important; and this is why the difference in the two policies results in a different final yield of 72.5% for the policy in Fig. 7c, and 95.0% for the policy in Fig. 7d respectively.
Another important observation in Table 4 is that policy calculated with samples from optimal controlled simulations required the shortest amount of assembly time to reach a 50% yield, but ended up with a low yield of 72.5%. This is because the samples are generated under the optimal control policy. However, as the crystallinity increases in the controlled simulations, where the samples are collected, λ = 19.7 is used for the remainder of the 900 s process. Therefore, the majority of samples from the later process are generated under a constant use of λ = 19.7. This further leads to states only being sampled under λ = 19.7, and they are deemed as absorbing states under λ = 0.2. As a consequence, the policy in Fig. 7c shows a rapid assembly at the beginning but was not able to reach a similar final yield compared to that of the policy in Fig. 7d.
| ≥50% time (s) | ≥80% time (s) | Yield | |
|---|---|---|---|
| Constant | N/A | N/A | 17.0% |
| Toggling | 250 | 650 | 90.0% |
| Optimal | 150 | N/A | 72.5% |
| Random | 250 | 550 | 95.0% |
The results in Table 4 also indicate a similar performance between the policies built with samples from the toggling scheme and the randomly switched input trajectories, in terms of both assembly time and the final yield. The high yield with the policy using toggling samples confirms our previous understanding that the defect correction mechanism is essentially partial relaxation followed by reassembly. However, samples generated with randomly switched input trajectories include richer dynamics than that of the toggling scheme, therefore the policy with randomly switched samples gave the best performance among all the cases.
6 Discussion
A globally accurate model is valuable, but for systems with a large number of rarely visited, or dynamically unimportant states, it would make more sense to focus on the more relevant states. For these systems, sampling schemes that focus more on the states of interest could potentially accelerate the estimation process, as well as providing a useful model. One such approach is adaptive sampling,53 where initial sampling is generated using available states as starting points. Based on the weighting of the clustered states on the model uncertainty, a weighted sampling starting with the updated states are conducted for additional samples. This process is repeated until a satisfying model is achieved. The biased sampling algorithm could be particularly beneficial when conducting a global sampling is costly.To design a control policy, it is important for each input to cover a common state space, in order to enable informed choice of switch between different inputs. However this can be challenging, especially when system dynamics are dramatically different under different inputs. Instead of modifying the calculated policies, one can use estimation techniques, such as interpolation or extrapolation, to estimate the transition probabilities in the unsampled states, before use in policy calculation. The underlying assumption is that dynamics for the neighboring states do not differ significantly. With such a modified transition matrix, one can avoid defining a default action in the control policies for unsampled states with the gridding-based discretization.
Another observation from this study is that, to achieve the same number of effective states, gridding defined a large total number of states. The total number of states is 20, 500, and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for the 10-, 100-, and 1000-effective state models built with gridding in section 5.2 respectively. These extra states make it more challenging to build an accurate model, considering the amount of additional sampling needed. It is also challenging to modify the control policy to deal with unsampled states. One alternative is to discretize the states unevenly to group together the infeasible and less important states. However, finding an appropriate uneven discretization can also be nontrivial. Clustering may be a better and simpler approach, compared to gridding.
000 for the 10-, 100-, and 1000-effective state models built with gridding in section 5.2 respectively. These extra states make it more challenging to build an accurate model, considering the amount of additional sampling needed. It is also challenging to modify the control policy to deal with unsampled states. One alternative is to discretize the states unevenly to group together the infeasible and less important states. However, finding an appropriate uneven discretization can also be nontrivial. Clustering may be a better and simpler approach, compared to gridding.
7 Conclusion
The results demonstrate the effect of state discretization, transition time Δt, sampling approach, and the number of samples on the accuracy of a Markov state model. Optimal control policies are computed with dynamic programming based on the reduced-order Markov state model. The model accuracy is evaluated based on the performance of the control policy in a Brownian dynamics simulation to produce perfect crystals.According to the results, in order to efficiently build an accurate Markov state model, the following settings are suggested: (1) a transition time that is similar to the system characteristic time, (2) a dynamic sampling approach, such as the random switch input trajectory, (3) a clustering algorithm for state space discretization, and (4) a discretization that ensures on average, at least five samples per state. These settings appear to be general principles that could at least provide a starting point for other systems that can be approximated by Markov state models.
The conclusion can also be made that, with the Markov state model based optimal control policy, rapid assembly of a highly crystalline two-dimensional colloidal crystal can be achieved. With the dynamic sampling approach and the clustering discretization, a 97% yield of the perfect crystal is achieved, even though the state space is coarsely discretized into only ten states.
Acknowledgements
The authors thank financial support by the National Science Foundation through the NSF Cyber Enabled Discovery and Innovation Type II grants CMMI-1124678 and 1124648.References
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- J. J. Yang, J. Borghetti, D. Murphy, D. R. Stewart and S. R. Williams, Adv. Mater., 2009, 21, 3754–3758 CrossRef CAS.
- X. Ni, Z. J. Wang, M. Mrejen, Y. Wang and X. Zhang, Science, 2015, 349, 1310–1314 CrossRef CAS PubMed.
- O. D. Velev and A. M. Lenhoff, Curr. Opin. Colloid Interface Sci., 2000, 5, 56–63 CrossRef CAS.
- K. R. Catchpole and A. Polman, Opt. Express, 2008, 16, 21793–21800 CrossRef CAS PubMed.
- M. L. Brongersma, Y. Cui and S. Fan, Nat. Mater., 2014, 13, 451–460 CrossRef CAS PubMed.
- M. J. Mendes, S. Morawiec, F. Simone, F. Priolo and I. Crupi, Nanoscale, 2014, 6, 4796–4805 RSC.
- H. R. Vutukuri, F. Smallenburg, S. Badaire, A. Imhof, M. Dijkstra and A. V. Blaaderen, Soft Matter, 2014, 10, 9110–9119 RSC.
- A. Goyal, C. K. Hall and O. D. Velev, J. Chem. Phys., 2010, 133, 064511 CrossRef PubMed.
- B. L. Victor, D. Lousa, J. M. Antunes and C. M. Soares, J. Chem. Inf. Model., 2015, 55, 795–805 CrossRef CAS PubMed.
- T. D. Edwards, Y. Yang, D. J. Beltran-Villegas and M. A. Bevan, Sci. Rep., 2014, 4, 6132 CrossRef CAS PubMed.
- J. C. Chen and A. S. Kim, Adv. Colloid Interface Sci., 2004, 112, 159–173 CrossRef CAS PubMed.
- X. Tang, B. Rupp, Y. Yang, T. D. Edward, M. A. Grover and M. A. Bevan, ACS Nano, 2016, 10, 6791–6798 CrossRef CAS PubMed.
- R. D. Malmstrom, C. T. Lee, A. T. V. Wart and R. E. Amaro, J. Chem. Theory Comput., 2014, 10, 2648–2657 CrossRef CAS PubMed.
- D. Shukla, C. X. Hernández, J. K. Weber and V. S. Pande, Acc. Chem. Res., 2015, 48, 414–422 CrossRef CAS PubMed.
- A. Briggs and M. Sculpher, PharmacoEconomics, 1998, 13, 397–409 CrossRef CAS PubMed.
- M. R. Perkett and M. F. Hagan, J. Chem. Phys., 2014, 140, 214101 CrossRef PubMed.
- Y. Xue, D. J. Beltran-Villegas, X. Tang, M. A. Beven and M. A. Grover, IEEE Trans. Control Syst. Technol., 2014, 22, 1956–1963 CrossRef.
- An introduction to Markov state models and their application to long timescale molecular simulation, ed. G. R. Bowman, V. S. Pande and N. Frank, Springer, New York, 1st edn, 2014 Search PubMed.
- M. L. Puterman, Markov Decision Processes: Discrete Stochastic Dynamic Programming, Wiley, New York, 1st edn, 2005 Search PubMed.
- J. N. Tsitsiklis, HERMIS-Internat. J. Comput. Math. Appl., 2007, 9, 45–54 Search PubMed.
- V. S. Pande, K. A. Beauchamp and G. R. Bowman, Methods, 2010, 52, 99–105 CrossRef CAS PubMed.
- J.-H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schütte and F. Noé, J. Chem. Phys., 2011, 134, 174105 CrossRef PubMed.
- G. R. Bowman, K. A. Beauchamp, G. Boxer and V. S. Pande, J. Chem. Phys., 2009, 131, 124101 CrossRef PubMed.
- C. Schütte, F. Noé, J. Lu, M. Sarich and E. Vanden-Eijnden, J. Chem. Phys., 2011, 134, 204105 CrossRef PubMed.
- J. J. Juárez and M. A. Bevan, J. Chem. Phys., 2009, 131, 134704 CrossRef PubMed.
- T. D. Edwards, D. J. Beltran-Villegas and M. A. Bevan, Soft Matter, 2013, 9, 9208–9218 RSC.
- L. Rocchi, L. Chiari and A. Cappello, Med. Biol. Eng. Comput., 2004, 42, 71–79 CAS.
- F. Yao, J. Coquery and K.-A. L. Cao, BMC Bioinf., 2012, 13, 1 CrossRef PubMed.
- L. J. P. van der Maaten, E. O. Postma and H. J. van den Herik, Dimensionality reduction: a comparative review, 2008, http://citeseerx.ist.psu.edu/viewdoc/summary? doi=10.1.1.112.5472 Search PubMed.
- R. R. Coifman, I. G. Kevrekidis, M. Maggioni and B. Nadler, Multiscale Model. Simul., 2008, 7, 842–864 Search PubMed.
- R. R. Coifman and S. Lafon, Appl. Comput. Harmon. Anal., 2006, 21, 5–30 CrossRef.
- I. K. Fodor, A survey of dimension reduction techniques, 2002, https://computation.llnl.gov/casc/sapphire/pubs/148494.pdf Search PubMed.
- G. Hummer and I. G. Kevrekidis, J. Chem. Phys., 2003, 118, 10762 CrossRef CAS.
- E. E. Santiso and B. L. Trout, J. Chem. Phys., 2011, 134, 064109 CrossRef PubMed.
- Z. M. Sherman and J. W. Swan, ACS Nano, 2016, 10, 5260–5271 CrossRef CAS PubMed.
- M. A. Rohrdanz, W. Zheng, M. Maggioni and C. Clementi, J. Chem. Phys., 2011, 134, 124116 CrossRef PubMed.
- M. A. Bevan, D. M. Ford, M. A. Grover, B. Shapiro, D. Maroudas, Y. Yang, R. Thyagarajan, X. Tang and R. M. Sehgal, J. Process Control, 2015, 27, 64–75 CrossRef CAS.
- Y. Yang, R. Thyagarajan, D. M. Ford and M. A. Bevan, J. Chem. Phys., 2016, 144, 204904 CrossRef PubMed.
- R. Du, V. S. Pande, A. Y. Grosberg, T. Tanaka and E. S. Shakhnovich, J. Chem. Phys., 1998, 108, 334–350 CrossRef CAS.
- P. L. Geissler, C. Dellago and D. Chandler, J. Phys. Chem., 1999, 103, 3706–3710 CrossRef CAS.
- P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318 CrossRef CAS PubMed.
- A. C. Pan and B. Roux, J. Chem. Phys., 2009, 129, 064107 CrossRef PubMed.
- X. Huang, Y. Yao, G. R. Bowman, J. Sun, L. J. Guibas, G. Carlsson and V. Pande, Pac. Symp. Biocomput., 2010, 134, 228–239 Search PubMed.
- J. D. Chodera, N. Singhal, V. S. Pande, K. A. Dill and W. C. Swope, J. Chem. Phys., 2007, 126, 155101 CrossRef PubMed.
- B. Keller, X. Daura and W. F. van Gunsteren, J. Chem. Phys., 2010, 132, 074110 CrossRef PubMed.
- E. Ikonen, I. Selek and K. Najim, Comput. Chem. Eng., 2016, 93, 293–308 CrossRef CAS.
- A. K. Jain, M. N. Murty and P. J. Flynn, ACM Comput. Surv., 1999, 31, 264–323 CrossRef.
- L. V. Nedialkova, M. A. Amat, I. G. Kevrekidis and G. Hummer, J. Chem. Phys., 2014, 141, 114102 CrossRef PubMed.
- P.-N. Tan, M. Steinbach and V. Kumar, Introduction to Data Mining, Addison-Wesley Longman, Boston, 1st edn, 2005 Search PubMed.
- D. P. Bertsekas, Dynamic Programming and Optimal Control, Athena Scientific, Nashua, 3rd edn, 2005 Search PubMed.
- I. Chades, G. Chapron, M. J. Cros, F. Garcia and R. Sabbadin, Ecography, 2014, 37, 916–920 CrossRef.
- N. Singhal and V. S. Pande, J. Chem. Phys., 2005, 123, 204909 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |




