Elucidating the general principles of cell adhesion with a coarse-grained simulation model

Abstract

Cell adhesion plays an indispensable role in coordinating physiological functions in multicellular organisms. During this process, specific types of cell adhesion molecules interact with each other from the opposite sides of neighboring cells. Following this trans-interaction, many cell adhesion molecules further aggregate into clusters through cis interactions. Beyond the molecule level, adhesion can be affected by multiple cellular factors due to the complexity of membrane microenvironments, including its interplay with cell signaling. However, despite tremendous advances in experimental developments, little is understood about the general principles of cell adhesion and its functional impacts. Here a mesoscopic simulation method is developed to tackle this problem. We illustrated that specific spatial patterns of membrane protein clustering are originated from different geometrical arrangements of their binding interfaces, while the size of clusters is closely regulated by molecular flexibility. Different scenarios of cooperation between trans and cis interactions of cell adhesion molecules were further tested. Additionally, impacts of membrane environments on cell adhesion were evaluated, such as the presence of a cytoskeletal meshwork, the membrane tension and the size effect of different membrane proteins on cell surfaces. Finally, by simultaneously simulating adhesion and oligomerization of signaling receptors, we found that the interplay between these two systems can be either positive or negative, closely depending on the spatial and temporal patterns of their molecular interactions. Therefore, our computational model pave the way for understanding the molecular mechanisms of cell adhesion and its biological functions in regulating cell signaling pathways.

---

I. Introduction

The diverse processes of cell adhesion are crucial in many biological activities, such as tissue morphogenesis in embryonic development,¹ invasion of tumor cells during cancer metastasis,^2,3 distinction of foreign antigens in immune responses,⁴ and regulation of plasticity between neurons.⁵ During adhesion, specific types of membrane proteins, called cell adhesion molecules (CAMs), interact with each other from opposite sides of neighboring cells.^5–8 These interactions either regulate the organization of cytoskeleton or drive various downstream signaling pathways through a series of poorly understood events, finally lead to the changes in cell phenotypes.^9,10 After CAMs from different cells hold together, known as trans-interactions, they aggregate into oligomers with different sizes.^11,12 The lateral clustering of CAMs results in specific spatial patterns at cellular interfaces.¹³ For instance, at the interface between T cells and antigen-presenting cells (APCs), the spatiotemporal patterning of different CAMs induces the formation of immunological synapse (IS).^4,14–16 This process is highly correlated to the activation of T cell signaling. Clustering of CAMs is driven by multiple elements. In many cases, CAMs from a same cell are assembled together directly through their lateral cis interactions. The cis binding interfaces are either located at the extracellular region,¹⁷ or at the cytoplasmic domain of these molecules.¹⁸ Clustering can be further affected by many other cellular factors, such as the diffusive properties of membrane proteins on cell surfaces. More importantly, CAMs can also mediate other adhesion-independent signaling pathways by directly interacting with their cell surface receptors.¹⁹ Understanding the crosstalk between these two processes can help us unravel the molecular mechanisms of both cell adhesion and cell signaling.

The study of cell adhesion has gained tremendous momentum nowadays due to the prominent contributions made on the experimental side. The rapid development of novel imaging techniques has facilitated detailed analysis of the molecular composition peripheral to cell surfaces and dynamics of their components involved,^{4,14–16,18,20–27} although the resolution of current optical microscopy is still infeasible to trace the molecular details of adhesion. Fortunately, structural information of many CAMs has become available from crystallographic analysis, providing first insights into the mechanism of their adhesive interactions.^17,28–33 Despite experimental developments, many fundamental problems are not fully understood, including detailed mechanisms of CAM clustering and functional impacts of interplay between adhesion and signaling. This leaves the opportunity for computational analysis. Because cell adhesions are complicated biological events involving not only interactions between individual molecules, but also the dynamic interplay of their surrounded environments, computational models have been constructed at different scales. A molecule-based simulation technique has been used to study the dynamic properties of specific CAMs,^34–41 such as integrin and T cell receptor. However, these studies depended on the structural information of individual proteins and are not able to reach the system that contains a large amount of molecules. In the meanwhile, cell adhesion has also been extensively studied by a variety of lower-resolution models,^42–51 such as partial differentiation equations (PDE) and lattice-based simulations. These models aimed to describe how collective behaviors of membrane receptors lead to spatial patterning at cellular interfaces. Due to the computational limitation, molecular details are rarely included. Therefore, only a qualitative picture of cell adhesion can be provided by these models.

In this article, a mesoscopic simulation method is developed to study the mechanism of cell adhesion. The cellular interface is represented by a pair of two-dimensional continuous surfaces that are overlapped on top of each other. A large number of CAMs are distributed on each surface. Different from previous low-resolution model, the minimalistic molecular information is incorporated. Each membrane protein is coarse grained into a rigid body with specified size, so that the molecular diffusion along both translational and rotational degrees of freedom can be realistically captured. Moreover, both trans and cis binding sites are explicitly labeled on its surface. A kinetic Monte-Carlo algorithm was implemented to simulate the spatial-temporal evolution of this system. By properly selecting the simulation parameters, such as diffusion constants and binding rates, within biologically relevant ranges, we were able to test the kinetic and thermodynamic properties of CAM clustering, meanwhile decompose the complexity of cell adhesion that is caused by specific membrane environments. In detail, we illustrated that specific clustering patterns of CAMs are originated from different geometrical arrangements of their binding interfaces, while the size of clusters is closely regulated by the flexibility of CAMs. Different scenarios of cooperation between trans and cis interactions were further designed. We found insightful correlations between clustering pathways and cooperative mechanisms. Additional environmental factors were also integrated into our model, including activities of a cytoskeletal meshwork and elasticity of plasma membranes. We demonstrated that they have profound impacts on cell adhesion. Finally, roles of cell adhesion in regulating ligand binding of cell signaling receptors were proposed. As such, our computational model sheds light on both general principles of cell adhesion and its functional implication in signal transduction.

II. Model and methods

II.1 The framework of rigid-body kinetic Monte-Carlo simulations for cell adhesion

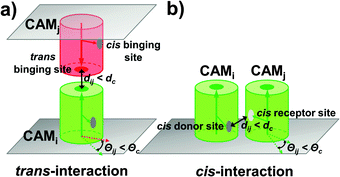
A rigid-body (RB) based model has recently been developed to simulate molecular binding in cellular environments.⁵² The model was extended here to study adhesion of CAMs at cellular interfaces. The cellular interface is represented by two flat surfaces overlapping on top of each other. The distance between two membrane surfaces equals 20 nm, which is a typical value for the experimental observation of the inter-cellular distance. As the initial configuration, CAMs are randomly distributed on both surfaces. Each CAM is simplified as a rigid body of cylinder. The radius of these cylinders is 2.5 nm and the height is 10 nm, as the typical size of a membrane protein.⁵³ Because in the original version of the RB model each molecule had only one binding partner, we placed only one functional site on the surface of each rigid body to delineate the binding interface between two interaction proteins. In clustering of CAMs, however, each protein has multiple binding partners. Therefore, we extended the model representation so that each protein contains more than one binding site. Specifically, there is one functional site at the top of each CAM, called the trans binding site. Two CAMs from the opposite sides of a cellular interface can form a trans-dimer through this site (Fig. 1a). Differently, sites on the side of each CAM are the cis binding sites. The cis binding sites are classified into a cis-donor site and a cis-receptor site. Two CAMs from the same side of a cell surface can form a cis-dimer through an interaction between a cis-donor site on one CAM and a cis-receptor site on the other (Fig. 1b). As we will show in the Results section, different numbers and geometric arrangements of cis binding sites on a CAM will lead to very different spatial patterns of CAM clusters.

Fig. 1 The rigid-body based model was developed to study adhesion of CAMs at cellular interfaces. The cellular interface is represented by two flat surfaces overlapping on top of each other. Each CAM is simplified as a rigid body of cylinder. Two CAMs from the opposite sides of a cellular interface can form a trans-dimer through their trans binding sites (a), while two CAMs from the same side of a cell surface can form a cis-dimer through an interaction between a cis-donor site on one CAM and a cis-receptor site on the other (b). Association between two CAMs is triggered by two criteria: (1) the distance between functional sites of two molecules is below the given distance cutoff d_c; and (2) the relative orientation of two molecules need to fall within specific ranges Θ_c.

Following the initial configuration, the dynamics of the system is simulated by a kinetic Monte-Carlo algorithm. A detailed algorithm was described in our previous study.⁵² Briefly, each time step in this algorithm consists of two scenarios. In the first scenario, all molecules are chosen randomly to make stochastic diffusions with periodic boundary conditions. Different from soluble proteins that can randomly diffuse with three translational and three rotational degrees of freedom, diffusions of membrane proteins tethered on cell surfaces are confined. The confinement of diffusions leads to the restricted rotations along membrane normal and two-dimensional translational movements in the plane of the cell surface. The second scenario simulates the reaction kinetics of the system. Association between two CAMs, either through the trans binding sites or the cis binding sites, is triggered by two criteria: (1) the distance between functional sites of two molecules is below the given distance cutoff d_c; and (2) the relative orientation of two molecules also need to fall within specific ranges, Θ_c, relative to an original dimer (Fig. 1). If both criteria are fulfilled, an association rate k_on is further given to determine the probability of dimerization. In contrast, the probability of dissociation between a trans-dimer or a cis-dimer is determined by the dissociation rate k_off. Different mechanisms of cooperation between trans and cis binding will be studied in the Results section. Finally, the above diffusion-reaction process is iterated until the system reaches equilibrium in both Cartesian and constitutional spaces.

II.2 Model additional cellular and molecular factors in cell adhesion

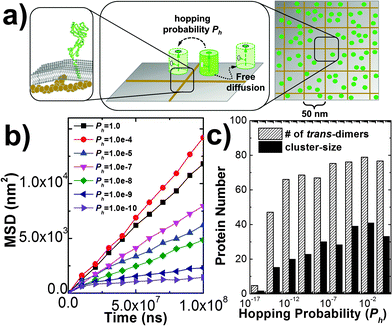
Several new features have been added into the kinetic Monte-Carlo simulation framework to take account for additional cellular and molecular factors in cell adhesion. First, cytoskeletal proteins such as actin filaments and their crosslinking molecules such as Arp2/3 form a meshwork underneath the cell plasma membrane.⁵⁴ Recent experimental evidence showed that the presence of the cytoskeletal meshwork can affect motions of membrane proteins on cell surfaces,⁵⁵ so that the overall behavior of sub-diffusions is obtained. In order to model the effect of cytoskeleton on membrane protein diffusions, we divided cell surfaces into small squares by a two-dimensional array of lattices (Fig. 6a). This follows the idea that plasma membranes in living cells are partitioned into subdomains by the cytoskeletal meshwork. We further assume that movements of membrane proteins from one subdomain of plasma membrane to another are constrained by potential interactions between the trans-membrane domain of the membrane protein and cytoskeleton. Following the assumption, membrane proteins undergo free diffusions within the area of each small square in our simulations. A hopping probability P_h will be assigned to any protein that moves cross the boundary between two neighboring square areas. Given the probability P_h, a protein can hop from one subdomain of the plasma membrane to one of its nearest neighbor. The effect of this hopping diffusion on cell adhesion will be investigated in section Results III.3.

Second, plasma membranes contain different sizes of proteins on their surface. This leads to the variation of inter-membrane distance and deformations of cell surfaces. On the other hand, tension exists in plasma membranes when they undergo structural deformation, due to the interactions between lipid molecules.^56,57 The tension of the cell membrane results in the free energy barrier between receptors with different sizes. Consequently, receptors with similar sizes can be kinetically driven into the same domain in order to minimize bending free energy of the membrane (Fig. 7a), which is known as “kinetic segregation”.⁵⁸ Although cell membranes are simplified by flat surfaces in our model and the inter-cellular distance is a fixed constant, the effects of membrane elasticity and the molecular size are implicitly considered as follows. We assume that under certain circumstances CAMs are surrounded by longer molecules such as glycol-proteins. As a result, diffusions of any two trans-dimers of CAMs are co-localized together so that their distance has to be within certain distance cutoff d_c, due to the free energy barrier originated from membrane elasticity. In detail, for a pair of CAM trans-dimers whose distance d is larger than d₀, a free energy constraint will be added into the Monte-Carlo simulation as −E₀ exp(−(d − d₀)²/δ²). Consequently, any diffusional movement that leads to their distance larger than the cutoff will be rejected with high probability, following the metropolis criterion. The values of d₀, δ and E₀ are related to the size and the strength of the free energy barrier, which is further determined by the membrane microenvironments. The effect of membrane elasticity on cell adhesion will be investigated in section Results III.3.

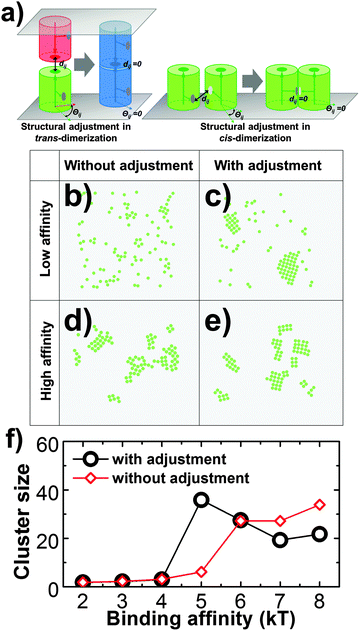
Third, the distant and orientation cutoffs d_c and Θ_c in the RB model define the criteria of forming an encounter complex. These cutoffs allow the structural variations within an ensemble of encounter complexes. In order to complete the association, a conformational transition is needed for an encounter complex so that the final structure of a dimer can be reached. In many cases of protein binding, especially for proteins that contain internal flexibility, this transition requires a large scale conformational change.^59,60 It was widely accepted that many membrane proteins, including most CAMs, consist of multiple structural domains at their extracellular regions.¹⁷ The flexible linkers between domains result in the conformational fluctuations of these proteins.⁶¹ As a result, we assume that for membrane proteins that possess of high molecular flexibility, there is a large-scale conformational rearrangement after they form encounter complexes. However, the RB representation of our model fixes the intermolecular degrees of freedom. In order to capture the role of molecular flexibility in binding and the clustering process of CAMs, an additional step of structural rearrangement was implemented after the association of two proteins. Specifically, after two monomers associate, they will be structurally aligned to the final configuration of a dimer, so that the structural variations in original encounter complexes are vanished (Fig. 3a). This strategy of structural adjustment is applied to both trans-dimerization and cis-dimerization. After association, two CAMs in a trans-dimer diffuse as an entity with a lower diffusion constant at the cellular interface. In contrast, previous experimental evidence indicated that diffusions of CAM's cis-dimers are even much slower than trans-dimers. Therefore, we assume that CAMs stop diffusing when they are involved in cis-interactions. Finally, the function of this structural rearrangement after association can be disabled, which suggests the loss of flexibility. The impacts of structural rearrangement on clustering of CAMs will be studied in section Results III.1.

II.3 Simulate the interplay between cell adhesion and cell signaling

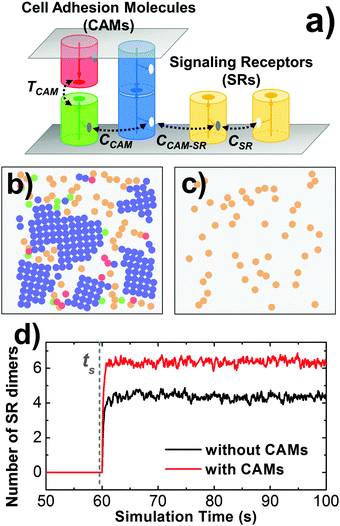
In order to understand the mechanism of interplay between cell adhesion and signaling, we further included signaling receptors into our simulation system. Specifically, in addition to CAMs that are distributed on both sides of the cellular interface, signaling receptors are placed on the lower side (Fig. 8a). Each signaling receptor is also represented by a cylinder with the same size of radius and height. A functional site is located at the side of each protein so that it can dimerize with another signaling receptor or bind to CAMs. Diffusions of these proteins consist of 2D translational movements within cell surfaces and the rotations along the membrane surface normal. To trigger the intercellular signaling, ligand stimulation is introduced into the system at certain time steps of simulations, t_s. Only after t_s, signaling receptors can be stimulated by a given activation probability. If two activated receptors are close to each other and satisfy both distance and orientational binding criteria, they can be dimerized with an association rate. Following the basic framework of cross-membrane signal transduction, dimerized receptors undergo conformational changes at their cytoplasmic domains, which further initiate the intracellular signaling pathways.⁶² Therefore, we simply assume that the number of dimers is directly related to the level of cell signaling.

The impacts of cell adhesion on signaling are reflected by the interactions between CAMs and signaling receptors. In detail, CAMs in our simulations can directly bind to signaling receptors based on current experimental observations. Two specific scenarios were designed to describe the interface between CAMs and signaling receptors. In the first scenario, the binding between a CAM and a signaling receptor shares the same interface (SI) with the signaling receptor dimerization. In this case, each signaling receptor still has one functional site. If it binds to a CAM, it cannot form a dimer with another signaling receptor. In the second scenario, dimerization of signaling receptors and their binding with CAMs are through distinctive interfaces (DIs). In this case, a second functional site is placed on the side of each receptor in addition to the original dimerization site, through which the receptor binds to CAMs. Furthermore, two strategies were implemented to model the temporal regulation of the interplay between adhesion and signaling: (1) CAMs and signaling receptors interact with each other throughout the simulations; and (2) the interactions are turned on only after the stimulation time for activated receptors. For the second strategy, we assume that conformational changes of signaling receptors after ligand stimulation trigger their interactions with CAMs. Taken together, the outcomes of different scenarios and strategies will be specified in section Results III.4.

III. Results

III.1 Characterize the impacts of structural features on membrane protein clustering

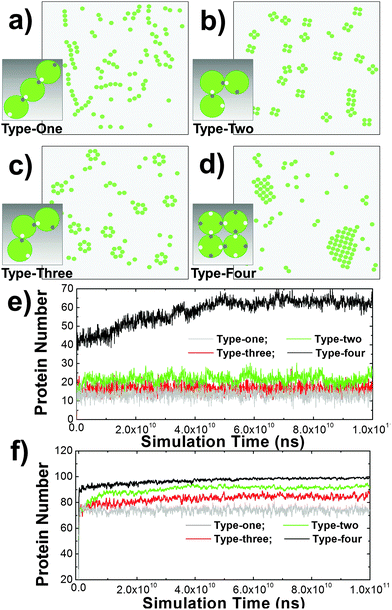
Some membrane proteins can aggregate into small oligomers⁶³ or large clusters without interacting with proteins on the surface of other cells.⁶⁴ Evidence from X-ray crystallography indicates that cis-interactions between these proteins are the major driving force of these spatial organizations.⁶⁵ Furthermore, comparing with the pairwise trans-interaction between proteins from different cells, the multiple binding sites of cis-interactions can lead to a many-body effect. This dynamic property is more important in regulating cell adhesion. Therefore, we start our research from the clustering mechanism of membrane proteins by only considering the cis-interactions of membrane proteins on the surface of a single cell. In detail, 100 proteins were distributed on a 400 nm × 400 nm surface. Different numbers and spatial geometry of cis binding sites were assigned on the side of each protein. Four types of cis-interactions were specifically designed to test the clustering dynamics (from Fig. 2a–d). In the first type, one cis-donor site and one cis-receptor site were assigned to each molecule and their packing angle against the center of mass is 180 degree. In the second type, each protein also contained one cis-donor site and one cis-receptor site and their packing angle is 120 degree. In the third type, each protein also contained one cis-donor site and one cis-receptor site with a packing angle of 90 degree. In the last type, two cis-donor sites and two cis-receptor sites were assigned to each molecule and their packing angle against the center of mass is 90 degree. Binding occurred between a cis-donor site and a cis-receptor site of different proteins with the given association rate and binding affinity.

Fig. 2 Four specific types of cis-interactions were designed to test oligomerization of membrane proteins. When the packing angle between the cis-donor site and the cis-receptor site of type-one molecules against their centers of mass is 180 degree, they were aligned into one-dimensional arrays (a). Differently, when the packing angles between the cis-donor site and the cis-receptor site of type-two and type-three molecules against their centers of mass is 90 and 120 degree (b) and (c), they were oligomerized into small sizes of tetramers and hexamers, respectively. Finally, large-size clusters were formed for type-four proteins, in which there are two cis-donor sites and two cis-receptor sites (d). The numbers of proteins involved in cis-interaction-mediated lateral aggregation are further plotted along simulation time under binding affinities of 5kT (e) and 8kT (f).

Consequently, different spatial patterns were derived by the kinetic Monte-Carlo simulation. As shown in the figure, type-one proteins were aligned into one-dimensional arrays (Fig. 2a), while type-four proteins were condensed into two-dimensional islands (Fig. 2d). Type-two and type-three proteins, on the other hand, were clustered into small sizes of tetramers (Fig. 2b) and hexamers (Fig. 2c), respectively. The numbers of proteins involved in cis-interaction-mediated lateral aggregation are further plotted along simulation time under different values of binding affinity (Fig. 2e and f). The figure suggests that under the same simulation conditions and energetic parameters, type-one proteins formed the least number of cis-interactions, indicating that one-dimensional arrays are the least stable structures. Comparatively, type-two and type-three proteins can be stabilized by forming close ring-like oligomers, leading to higher numbers of cis-interactions. Relative to tetramers, more subunits are involved in hexamers. They were only stabilized under stronger affinity. Finally, each protein in a 2D cluster has four structural neighbors that are interlocked through their cis-interactions. This pattern of proteins is the easiest to form, but the most difficult to dissociate. Therefore, more proteins were involved in cis-interactions than the other three types. Taken together, these results suggest that spatial organizations of membrane proteins and the dynamic processes of their formation on the subcellular scale are determined by the geometric patterns of binding interfaces at the molecular level.

In addition to the spatial arrangement of cis-binding sites, we also tested the effect of molecular flexibility which could play an important role in regulating membrane protein clustering, considering that many membrane proteins consist of multiple domains. In detail, molecular flexibility is modeled by an additional step of structural adjustment after association, as described in the Methods section. The strategy of structural adjustment has been implemented to simulate the 2D clustering of type-four proteins in the system that was introduced above. In a control system, in contrast, this strategy was turned off while values of all other parameters such as the size of the surface area and concentration of proteins remain unchanged. Both systems were simulated under different values of cis binding affinity. The differences in simulation results between these two systems are plotted in Fig. 3f. The figure shows the sizes of maximal clusters found in each system when simulations reached equilibrium. The cluster sizes were counted along a wide range of simulation time and averaged over multiple trajectories. Fig. 3f indicates that the structural adjustment resulted in much larger sizes of clusters under relatively weak binding affinity. In this case, the structural rearrangement between proteins after their association facilitates the initial seeding of clustering. Under stronger affinity, however, the slower kinetics of binding prevented further growth of clusters. In contrast, the slower and linear increase of cluster size along the cis binding affinity is found in the system without structural adjustment. Especially under strong affinity, they can form clusters larger than the system with structural adjustment. As shown in the snapshot (Fig. 3d), we found interconnected clusters with ambiguous boundaries formed under these conditions. Relatively, the shapes of clusters in the system with structural deformation are more regular (Fig. 3c and e). Our simulations therefore highlight the important roles of structural flexibility in regulating the size and shape of protein clusters. Proteins with higher flexibility tend to be clustered together under weaker binding affinity. Under stronger affinity, on the other hand, they tend to form smaller clusters with well-defined shapes than proteins with lower flexibility. As such, we provide new insights into the molecular mechanism that is used to adjust the size of membrane protein clusters. The mechanism we proposed can be experimentally testified by introducing specific mutations at domain linker regions to rigidify the extracellular domains of membrane proteins. Finally, in order to focus on other aspects of cell adhesion, the function of structural adjustment remains enabled in all the following studies.

Fig. 3 In the strategy of structural adjustment (a), two monomers that associate into a trans-dimer or a cis-dimer will be structurally aligned to a final configuration in which the structural variations d_ij and Θ_ij in original encounter complexes are vanished. We found that under relatively low binding affinity (5kT), the systems without structural adjustment (b) cannot form clusters as large as in the system with structural adjustment (c). Under high affinity (8kT), on the other hand, interconnected clusters with ambiguous boundaries were obtained (d). Relatively, the shapes of smaller clusters in the system with structural deformation are more regular (e). For both systems (with and without structural adjustments), the maximal sizes of clusters over a wide range of simulation time and multiple trajectories are plotted under different values of binding affinity (f).

III.2 Elucidate the cooperation between trans and cis interactions in cell adhesion

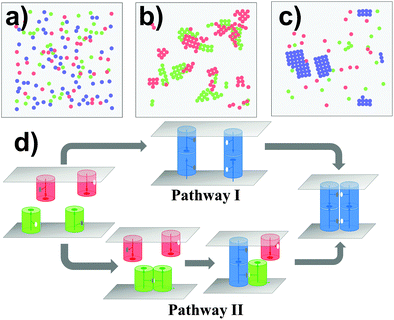
In cell adhesion, trans-interactions are formed between CAMs from opposite surfaces of two neighboring cells. Following the trans-dimerization, new developments in optical and biophysical methods revealed that many CAMs further form higher-order spatial patterns during different processes of adhesion. In parallel, as more and more structural data of CAMs accumulated, it has been found that the extracellular fragments in most of these systems simultaneously contain more than one interacting neighbor. The lateral binding through these structural neighbors, called the cis-interaction, was proposed to drive the assembly of CAMs into high-order spatial clusters at cellular interfaces. Based on the experimental evidence, a general model of CAM incorporating both trans and cis interactions was designed under the RB representation to simulate the clustering kinetics. As described in section Model and Methods II.1, the simulation system contains two overlapping surfaces of 400 nm in length. There are 100 CAMs distributed on each surface. Except the trans binding site that was placed on top of each CAM, two cis-donor sites and two cis-receptor sites with packing angles of 90 degree were further assigned to the side of the molecule. Consequently, the maximal number of lateral structural neighbors for a CAM is four, as the type-four protein discussed in the last section. Given different affinities to the interactions between these trans and cis binding sites, distinctive configurations can be generated by the kinetic Monte-Carlo simulation, as shown from Fig. 4a–c. In these figures, the red and green particles indicate monomers of CAMs on the upper and lower sides of the cell surfaces, and the blue particles indicate the trans-dimers. In Fig. 4a, trans binding affinity is much stronger than the cis affinity. Consequently, a number of trans-dimers are separately distributed at the cellular interface. Differently, when trans binding affinity is much weaker than the cis affinity, some lateral clusters were obtained in different locations of each surface with the formation of few trans-dimers (Fig. 4b). Finally, if both trans and cis interactions are strong enough (Fig. 4c), trans-dimers are condensed into clusters. In addition to the affinities, the process of clustering is further regulated by the binding kinetics of trans and cis interactions. For instance, the minimal cluster of CAMs that contains a cis-interaction between two trans-dimers can be formed through two kinetic pathways (Fig. 4d). In one of the pathway (Pathway I), clustering is initiated by the trans-dimerization, while cis-interactions between CAMs are formed first in the other (Pathway II).

Fig. 4 A generic model of CAMs incorporating both trans and cis interactions was designed under the RB representation to simulate the kinetics of cell adhesion. Different snapshots were generated for different values of trans and cis interactions: (a) trans binding affinity is much stronger than the cis affinity; (b) cis binding affinity is much stronger than the trans affinity; and (c) both trans and cis interactions are strong enough. In addition to the affinities, CAMs can be clustered through different kinetic pathways (d) during adhesion. In one of the pathway (Pathway I), clustering is initiated by the trans-dimerization, while cis-interactions between CAMs are formed first in the other pathway (Pathway II).

In order to simplify the problem of systematically evaluating all potential determinants of clustering, three kinetic scenarios were designed to limit the searching space. Binding affinities were further changed within a wide range under each kinetic scenario. Specifically, in the first scenario, clusters can only be formed through Pathway I. We assume that the association of a cis-dimer between monomers of CAMs is much slower than the trans-dimerization under this scheme. As we proposed in the case of cadherin-based clustering, the trans-dimerization further facilitates the association of cis-interactions by reducing the molecular flexibility.^66–69 However, cadherin-based clustering is not the only mechanism that generally exists in other CAM systems. Therefore, we proposed the second scenario in which clusters can only be formed through Pathway II. Under this scheme, we assume that the association of a trans-dimer can only be accelerated by cis-dimerization. There were similar mechanisms proposed for real biological systems. For instance, the trans-interaction between MHC-1 and receptor Ly49 can only be formed after its cis-dimerization.⁷⁰ Finally, CAMs are allowed to cluster together through both Pathways in the third scenario.

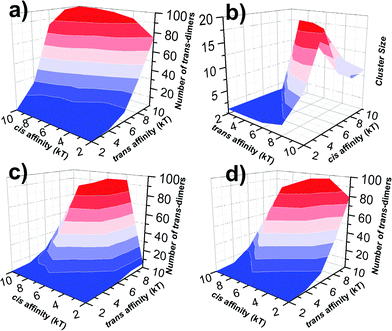
In all three kinetic scenarios, both trans and cis binding affinities were further changed between −2 and −10kT. For each combination, multiple trajectories were carried out. Based on the statistics of these trajectories, we derived the average numbers of trans-dimers and maximal sizes of their clusters to account for the strength and spatial pattern of cell adhesion under different conditions. Their distributions are plotted in Fig. 5 as 3D contours. Fig. 5a presents the profile of adhesion strength for the first kinetic scenario. The x and y axes of the figure represent the values of trans and cis affinity, and the z axis represents the average number of trans-dimers formed with the corresponding affinities. As shown in the figure, the number of trans-dimers increases under strong trans-affinity. More interestingly, under strong cis-affinity, the number of trans-dimers increases further, indicating the positive cooperativity between trans and cis interactions under this kinetic diagram. Relative to the adhesion strength, the profile of trans-dimer cluster sizes was plotted in Fig. 5b under the same index of binding affinities and kinetic scenario. Instead of gradual growth in adhesion strength, a sharp increase of cluster size is observed from the figure, indicating that the clustering process is more like a phase transition. Furthermore, we found that CAMs tend to form smaller clusters under stronger affinities, due to the reason that these locally formed clusters are difficult to dissociate. Comparing with the first scenario, the numbers of trans-dimers formed in the second scenario show a very different distribution (Fig. 5c). The figure implies that there is a negative coupling effect between trans and cis binding affinities. We speculate that under this kinetic scenario, strong lateral binding between monomers of CAMs traps their diffusions, and therefore prevents the trans-dimerization. Finally, Fig. 5d shows a more complicated diagram of adhesion strength in the third scenario, in which a competition between trans and cis interactions was observed. In detail, when cis binding affinity is weak, trans-dimers are formed through Pathway I. On the other hand, when cis binding affinity is stronger, Pathway II becomes dominant, leading to the decreasing number of trans-dimers. The distributions of cluster size for the second and third scenarios are listed in the ESI,† Tables S1 and S2. Taken together, our studies revealed that cell adhesion is under both energetic and kinetic regulation. These factors are interdependent with each other through either positive or negative coupling.

Fig. 5 The strength (number of trans-dimers) and spatial pattern (cluster size) of cell adhesion for all combinations of binding affinities were plotted as 3D contours under different kinetic scenarios. We found that in the first kinetic scenario, the number of trans-dimers increases under strong trans-affinity. Moreover, under strong cis-affinity, the number of trans-dimers increases further, indicating the positive cooperativity between trans and cis interactions (a). We also found a sharp increase in cluster size along with affinities, suggesting that the clustering process is more like a phase transition (b). Relative to the first scenario, the numbers of trans-dimers formed in the second and third kinetic scenarios are plotted in (c) and (d), showing very different distributions. These results indicate that cell adhesion is under close kinetic regulation, which leads to either positive or negative coupling between trans and cis interactions.

III.3 Evaluate the functional roles of membrane environments in cell adhesion

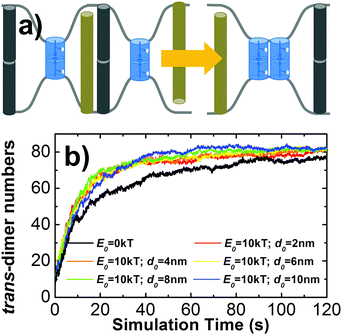
In addition to the kinetic and thermodynamic properties of CAM interactions, cell adhesion can also be affected by many cellular factors due to the special membrane environments. For instance, diffusions of membrane proteins on cell surfaces are impeded by the interactions between transmembrane domains of these proteins and the cytoskeleton which forms a meshwork underneath plasma membranes. As described in sections Model and Methods II.2, the cytoskeletal meshwork is represented by a two-dimensional lattice array which divides cell surfaces into subdomains (Fig. 6a). Specifically, 100 CAMs were distributed on both sides of a two-layer interface of 400 nm in length. Each side of the interface was split into small areas of square of 50 nm in length. The size of the cytoskeletal meshwork was adopted from the experimental observations from red blood cells (RBC),⁷¹ but can be adjusted to any other values. The formation of trans and cis interactions were independent on each other, and their binding affinities were fixed at −6kT and −4kT, respectively. Different from before, each CAM can only undergo free diffusions within each square. The movement of a specific CAM from one square to one of its nearest neighboring square is determined by the hopping probability P_h. By changing the value of this hopping probability, we first quantify the impacts of the cytoskeletal meshwork on diffusive properties of CAMs. The mean square displacements (MSD) of all CAMs along with the average simulation time were calculated. Fig. 6b gives the plots of MSD under different values of P_h. This figure shows that overall CAMs diffuse more slowly under lower P_h. However, it seems that the decrease of diffusion is not monotonous. We speculate that it is due to the uncertainty and stochasticity in the diffusion of membrane receptors on cell surfaces. Furthermore, the nonlinear MSD curve under low hopping probability suggests the feature of sub-diffusion, indicating that CAMs are locally confined in a small region for a long time period. The sub-diffusions of membrane proteins were recently observed in living cells by high-resolution imaging experiments.⁷² We further investigated how the changes in diffusion properties impact the spatial pattern of cell adhesion. Based on the simulation results that are plotted in Fig. 6c, we found that the local confinement of CAMs by the cytoskeletal meshwork not only leads to lower numbers of trans-dimers, but also results in smaller size of clusters. Therefore, our simulation results demonstrated that the existence of the cytoskeleton causes unneglectable impacts on strength and spatial organization of cell adhesion. It is also worth mentioning that diffusions of CAMs can also be artificially modulated. For instance, electron beam lithography was used to locally confine diffusions of membrane receptors on supporting lipid bilayers. When these artificially designed lipid bilayers were exposed to the surfaces of living cells, very different spatial patterns from in vivo adhesion were observed.⁷³ Our simulations are consistent with these experiments about the relation between diffusion and clustering of CAMs during the process of cell adhesion.

Fig. 6 In order to model the cytoskeletal meshwork and its effect on membrane protein diffusions, cell surfaces were divided into small squares by a two-dimensional array of 50 nm in length (a). A protein can hop from one subdomain of the plasma membrane to one of its nearest neighbor with a defined probability P_h. The mean square displacements (MSD) were calculated under different values of P_h (b), in which the nonlinear MSD curve under low hopping probability indicates the feature of sub-diffusion. The histograms plotted in (c) further suggest that the local confinement of CAMs by the cytoskeletal meshwork leads to lower numbers of trans-dimers and smaller size of clusters.

Another factor beyond the molecular level is the deformation of membrane curvature driven by the size difference of cell surface proteins. This effect can lead to the spatial co-localization of membrane proteins with similar size. For instance, it has been proposed that the TCR micro-cluster formation during adhesion between T cells and antigen presenting cells (APC) is initiated by the presence of nearby larger molecules such as integrin and CD15.⁷⁴ In order to model the effect of this confinement, a Gaussian free energy constraint was introduced between two trans-dimers of CAMs whose distance is larger than d₀, as described in section Model and Methods II.2. The concentration and binding parameters remained the same as the system we simulated hop diffusion in the last paragraph. Additionally, different values were used to test the size and strength of the free energy barrier. In specific, the strength of constraint, E₀, was described by either 1kT or 10kT, while the distance cutoff, d₀, was changed from 2 nm to 10 nm, with an interval of 2 nm. For all situations, multiple trajectories were generated and the average number of trans-dimers and the average size of clusters were recorded (listed in the ESI,† Table S3). Comparing with the simulation in which there is no free energy constraint, little difference was observed when E₀ is small (1kT). Under a large value of E₀ (10kT), slightly higher numbers of trans-dimers and larger cluster sizes were found than the system without the free energy constraint. Moreover, we plotted the number of trans-dimers along time throughout the simulation trajectories in order to evaluate the kinetics of the systems (Fig. 7b). As a result, remarkably faster kinetics was observed when free energy constraint was turned on. This suggests a kinetic trapping mechanism that facilitates the formation of an encounter complex between two trans-dimers of CAMs, which in turn accelerates their clustering. Therefore, we illustrated that under certain circumstances such as strong membrane tension, the kinetics of cell adhesion can be regulated by the size-dependent segregation of CAMs. Finally, it is worth mentioning that the kinetics of cell adhesion play an important role in temporally regulating the intracellular signaling pathways, such as the TCR-initiated T cell activation.

Fig. 7 Different sizes of membrane proteins cause the deformations of cell surfaces. The brown and black bars represent the glycol-proteins or long molecules that are repulsive to each other in the extracellular region (a). The tension existing in these curvatures leads to the result that proteins with similar sizes can be kinetically driven into the same domain in order to minimize bending free energy of membrane. By introducing a Gaussian free energy constraint between two trans-dimers of CAMs to model this effect, a remarkably faster kinetics of cell adhesion was obtained when the free energy constraint is strong enough (b). This result provides insights that cell adhesion can be accelerated by the size-dependent segregation of CAMs, which might play functional roles in regulating adhesion-related signaling pathways, such as T cell activation.

III.4 Investigate the dynamic interplay between cell adhesion and cell signaling

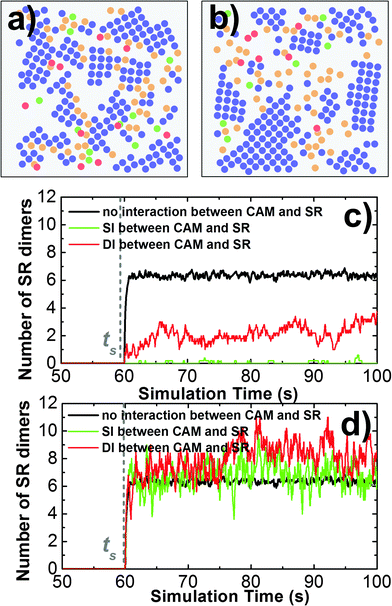
Cell adhesion not only plays an important role in maintaining tissue integrity, it also modulates cell signaling in response to external stimulations. The interplay between adhesion and signaling can be obtained by the interaction between CAMs and intracellular adaptor proteins that are involved in signal transduction in the cytoplasm.⁷⁵ It can also be achieved by a more straightforward way through direct interactions between CAMs and signaling receptors (SRs),⁷⁶ which functional impacts will be studied in this section. As described in section Model and Methods II.3, CAMs and SRs were both simulated in the system. In detail, 200 CAMs were distributed on both sides of a two-layer interface of 300 nm in length. On the lower-bound surface of the interface, 50 SRs were randomly mixed with CAMs as an initial configuration. As shown in Fig. 8a, four different types of interactions are included: (1) the trans-interaction between CAMs (T_CAM); (2) the cis-interaction between CAMs (C_CAM); (3) the cis-interaction between SRs (C_SR) after ligand stimulation; and (4) the cis-interaction between a CAM and a SR (C_CAM–SR). In order to narrow down the variations of the simulation system, the affinities of T_CAM and C_SR were fixed at −10kT and −8kT, while the affinities of the more relevant interactions C_CAM and C_CAM–SR were changed to different values. We first investigated the system in which there is no interaction between CAMs and SRs (affinity of C_CAM–SR equals 0kT). Consequently, we observed that on average about 6 SR dimers were formed when simulations reached equilibrium (Fig. 8d). Changing the affinity of C_CAM did not affect the result, as shown in the ESI,† Table S4. In contrast, CAMs were not included in a control system (Fig. 8c), while all other simulation parameters were fixed. As a result, only 4 SR dimers were observed when simulations reached equilibrium. The presence of CAM increases the effective concentration of SR, therefore increases the probability of SR dimerization. Our results suggest that even without direct interplay, cell adhesion can affect the binding of signaling receptors through creating a crowded environment.

Fig. 8 In order to understand the mechanism of interplay between cell adhesion and signaling, signaling receptors are placed on the lower side in addition to the CAMs that are distributed on both sides of the cellular interface (a). In detail, 200 CAMs were distributed on both sides of a two-layer interface of 300 nm in length. On the lower-bound surface of the interface, 50 SRs were mixed with CAMs (b). In contrast, CAMs were not included in a control system (c). We observed that on average about 6 SR dimers were formed when simulations reached equilibrium after stimulation time t_s, while only 4 SR dimers were formed in the control system (d).

We further assume a direct interplay between adhesion and signaling by turning on the interaction between CAMs and SRs. We first evaluate the situation in which this interaction is not temporally regulated. In other words, CAMs can always bind to SRs. The interaction scenarios of SI and DI were tested, as specified in section Model and Methods II.3. In both scenarios, affinities of C_CAM and C_CAM–SR were changed from 0 to −10kT. Multiple trajectories were carried out for all combinations. In order to understand how cell signaling is affected by adhesion, the numbers of SR dimers were counted through these simulations after they reached equilibrium. Detailed data are listed in the ESI,† Tables S5 and S6. Overall, we found that strong C_CAM–SR interaction decreases the number of SR dimers (Fig. 9c). This effect is more obvious when CAMs and SRs share the same binding interfaces. On the other hand, to understand how cell adhesion is affected by signaling, the sizes of CAM clusters were calculated for all combinations. Detailed data can be found in the ESI,† Tables S7 and S8. We noticed that large sizes of clusters were formed when the affinity of C_CAM equals −2kT if there is no interaction of C_CAM–SR. However, the presence of strong C_CAM–SR interactions reduced the sizes of these clusters, under both SI and DI scenarios. A snapshot from the simulation trajectory (Fig. 9a) indicates that the binding between CAMs and SRs interrupts the cis interactions of CAMs, thus prevents the CAM clusters from continually growing to larger sizes. Therefore, our simulation results suggest that without temporal regulation of the interplay, cell adhesion negatively affects cell signaling. Similarly, the signaling receptor interferes with the clustering in cell adhesion. This negative interplay resulted from the competition of binding between these two processes.

Fig. 9 We turned on the interaction between CAMs and SRs. We first evaluate the situation in which CAMs can always bind to SRs. A snapshot under this situation (a) indicates that the binding between CAMs and SRs interrupts the cis interactions of CAMs. Consequently, we found that the strong interaction between CAMs and SRs decrease the number of SR dimers (c). We further considered the situation in which the interaction between CAMs and SRs can only be turned on after the ligand stimulation time. A snapshot under this situation (b) indicates that the SR dimers are formed at the edges of the original clusters and are stabilized through forming additional interactions with these CAM clusters. Consequently, we found that the strong interaction between CAMs and SRs increases the number of SR dimers (d).

In order to take the temporal regulation of interplay into account, we assume that the interaction between CAMs and SRs can only be turned on after the ligand stimulation time t_s. Before t_s, SRs separately diffuse on the lower bound of cellular interface as monomers, while CAMs form clusters through both T_CAM and C_CAM. Both scenarios of SI and DI were tested, in which affinities of C_CAM and C_CAM–SR were changed from 0 to −10kT. Detailed data of the SR dimer number and the CAM cluster size are listed in the ESI,† Tables S9–S12. We found that when CAMs and SRs interact with each other only after ligand stimulation, the strong C_CAM–SR interaction increases the number of SR dimers if CAMs and SRs do not share the same binding interface (Fig. 9d). Moreover, within the range of C_CAM affinity in which CAMs can form larger clusters, the interactions between CAMs and SRs after ligand stimulation further increase the original size of CAM clusters. A snapshot from the simulation trajectory (Fig. 9b) indicates that CAM clusters can be expanded through the SR dimers that are formed at the edges of the original clusters, while the SR dimers are stabilized through forming additional interactions with these CAM clusters. Without the interaction between CAMs and SRs before ligand stimulation, CAMs can form clusters independent to the cell signaling. This temporal regulation eliminates the effect of competitive binding between CAMs and SRs, leading into a positive coupling. In summary, our simulation results demonstrated that the spatial interplay between cell adhesion and cell signaling is under temporally regulated, which might generate significantly different patterns. Our computational model therefore brings new insights into the molecular mechanisms of both systems.

IV. Concluding discussion

Cells in multicellular organisms coordinate with each other by forming dynamic adhesion. These intercellular contacts are initiated by interactions of CAMs expressed on cell surfaces. The binding of CAMs further triggers their clustering and lead to specific patterns organized at cellular interfaces. Although our knowledge on structural and dynamic details of cell adhesion has been facilitated by recent progresses in microscopic and crystallographic studies, a comprehensive understanding of its molecular mechanism is still missing. The challenge resulted from the fact that cell adhesion is a spatial-temporal process with coupled complexities ranging from the molecular to the cellular scales. In an attempt to tackle the challenge, we introduced a new computational model to study the dynamics of CAM clustering in the specific environment of cellular interface. The rigid-body representation used to describe protein structures ensures that basic molecular details such as global size, the translational and rotational diffusions, and orientational constraint during binding have been properly considered during the simulations of CAM clustering. Various spatial patterns of clusters were obtained by designing different geometries of binding interfaces and mechanisms of cooperation between trans and cis interactions. Additionally, the impacts of subcellular environments were implemented by considering both cytoskeletal activities and membrane fluctuations, resulting in remarkable differences in not only molecular diffusion, but also the kinetic and thermodynamic properties of clustering. By simultaneously simulating clustering of CAMs and oligomerization of signaling receptors in one system, we further tested the interplay between cell adhesion and cell signaling. Interestingly, we found that adhesion and signaling mutually affect each other. The interplay can be either positive or negative, closely dependent on the spatial and temporal patterns of molecular interactions between CAMs and signaling receptors. Our simulations therefore bring new insights into the regulatory mechanisms of cell signaling pathways. Taken together, our studies pave the way for understanding the basic principles of cell adhesion and its biological functions, especially in regulating cell signaling pathways.

There are some issues that cannot be fully addressed due to the simplification of our model. For instance, the cell surface is modeled as a 2D flat surface without fluctuations. In reality, cells can extend membranous protrusions such as filopodia,⁷⁷ in which the cell surfaces are highly curved. However, processes including filopodia occur at the beginning of adhesion when cells have not formed stable contacts with their neighbors. After these processes, it was found that the intercellular distance is a relative constant with small deviation. Moreover, estimates based on membrane elasticity suggest that, within the distance range determined by the average density of CAMs on cell surfaces, the length of membrane fluctuations is typically only a fraction of a few nanometers.⁶¹ Therefore, by focusing our study on the dynamics of CAM clustering, we assume that our simulations are carried out in a system where cells have already formed stable contacts. Second, the plasma membrane is modeled as a homogeneous medium. The composition of lipid molecules in the plasma membrane was not explicitly considered. The changes in lipid composition, such as increased amount of cholesterol, were found to influence membrane fluidity and cause the formation of membrane micro-domain. Consequently, receptors can be compartmentalized by these immobilized membrane micro-domains, termed lipid rafts,^78,79 although the existence of lipid rafts in living cells and their functional roles in cell signaling are still controversial. Nevertheless, the effect of lipid composition on diffusion of membrane receptors can be described in the future by discretizing cell surfaces into small vertexes. Diffusion reaction partial differential equations (DRPDEs)⁸⁰ will be applied to simulate the time evolution of relative concentrations for different lipid molecules around each vertex. The calculated lipid compositions corresponding to a specific vertex will further determine the diffusion coefficient of any receptor passing through the vertex. Finally, the impacts of membrane environments on cell adhesion and receptor clustering were only implicitly incorporated as two independent factors. On the one hand, cytoskeleton was not physically presented in our model. Diffusions of receptors were spatially confined and modulated by assuming the existence of a cytoskeleton meshwork beneath the plasma membrane. On the other hand, although the motions of the plasma membrane were not implemented, the membrane elasticity and its effect on trapping the diffusions of membrane proteins with similar sizes were taken into account by co-localizing the trans-dimerized CAMs within a small region. In summary, full consideration of the above-mentioned issues will raise the realisticity of our simulations, but it goes beyond the scope of the current study. Nevertheless, the simplified treatment given here provided a good starting point for modeling these complex systems.

On real cell surfaces, there are different types of cell adhesion molecules and signaling receptors. The extracellular domains of these molecules all have different sizes. In our rigid-body model, the size of each membrane protein is characterized by the radius and height of the cylinder. Therefore, the size effect of membrane proteins can be reflected by changing the radius and height to represent different types of proteins in the rigid body model. However, the cell membrane is a highly heterogeneous environment. A more realistic simulation of this system requires consideration of further complexities. Some of these complexities can be easily achieved by the future extension of the current model. For instance, surfaces of the plasma membrane are occupied by a large number of membrane receptors and channels. This high concentration of biomolecules has large effects on their diffusions and interactions. Unlike well-documented computational simulations of crowded cytoplasm,^81–83 there are very few studies on membrane systems. Similar to our previous study, the crowding of 2D membrane surfaces can be approached by the RB-based simulation. Furthermore, the total numbers of all receptors in current model are fixed throughout the time of simulations. In fact, the concentrations of proteins on cell surfaces are dynamically controlled by membrane trafficking,⁸⁴ including secretion of proteins to the plasma membrane (exocytosis) and uptake of proteins from the membrane for recycling (endocytosis). While we assume that membrane trafficking is beyond the time scale of receptor clustering, the processes of exocytosis and endocytosis are straightforward to be integrated into current model. These can be done by introducing additional operations to locally generate or eliminate receptors at specific locations of the plasma membrane. Finally, the extracellular regions of some receptors are organized into multiple domains. The linkers between these domains result in molecular flexibility, which effect was not included by representing each receptor as a rigid body. To model molecular flexibility, the current RB model can be upgraded by a new representation in which a multi-domain protein is simulated by a chain of multiple rigid bodies. Each rigid body corresponds to one structural domain in the protein.

Except above-mentioned future improvements, the computational efficiency and generality of the model ensure its wide application to many biological systems that are related to cell adhesion. For instance, detailed kinetic profiles of cadherin-mediated cell adhering can be quantitatively measured by micropipette manipulation. Interestingly, the micropipettes experiment of cadherin's intercellular binding exhibits biphasic kinetics.^85,86 The kinetics of cadherin-mediated cell adhesion can be studied by our computational model, in which the geometry of binding between cadherins can be adopted from the recent crystallographic experiments.⁶⁷ The binding rates of E-cadherin have been measured by NMR spectroscopy and surface plasmon resonance.⁸⁷ These values will be adopted as simulation parameters. To name a few more, the crystal structures of adhesive receptors such as Axonin,^31,88 neural cell adhesion molecules (NCAM)^89,90 and Ephrin receptors⁹¹ reveal the multiple trans and cis binding interfaces in these systems. The rigid-body representation of our model enables us to design the global shape and geometry of binding site location for individual molecules, so that the minimal structural details can be properly reflected during the simulation of their clustering. Information about the binding rates of ligand-receptor interactions can be reached from in vitro experimental measurements, or derived by higher-resolution computational models such as molecular dynamic simulation or Brownian dynamic simulation. On the other hand, we have demonstrated that cell adhesion molecules also actively affect signal transduction through direct interaction with signaling receptors. Previous experiments show that E-cadherin binding modulates epidermal growth factor receptor (EGFR) activation.⁹² And also, the fibroblast growth factor receptor (FGFR) can be activated through direct interaction with NCAM.⁸⁹ These real examples can be tested by our model. Additionally, it was proposed that through interactions with signaling receptors, adhesion molecules can also regulate the local concentration of their cytosolic adapter proteins, thus controlling the intracellular signaling pathways. A multi-scale framework that combines our spatial simulation with mathematical modeling of signaling network will push the envelope of study along this direction.

Acknowledgements

This work was supported by a start-up grant from Albert Einstein College of Medicine. Computational support was provided by Albert Einstein College of Medicine High Performance Computing Center.

References

1. B. M. Gumbiner, Cell adhesion: the molecular basis of tissue architecture and morphogenesis, Cell, 1996, 84(3), 345–357.
2. C. A. Klein, Cancer – The metastasis cascade, Science, 2008, 321(5897), 1785–1787.
3. J. J. Lee and M. T. Lotze, Molecular Basis of Metastasis, N. Engl. J. Med., 2009, 360(16), 1679.
4. M. L. Dustin, The Cellular Context of T Cell Signaling, Immunity, 2009, 30(4), 482–492.
5. L. Shapiro, J. Love and D. R. Colman, Adhesion molecules in the nervous system: Structural insights into function and diversity, Annu. Rev. Neurosci., 2007, 30, 451–474.
6. A. E. Aplin, A. K. Howe and R. L. Juliano, Cell adhesion molecules, signal transduction and cell growth, Curr. Opin. Cell Biol., 1999, 11(6), 737–744.
7. T. Okegawa, et al., The role of cell adhesion molecule in cancer progression and its application in cancer therapy, Acta Biochim. Pol., 2004, 51(2), 445–457.
8. M. A. Schwartz and D. W. DeSimone, Cell adhesion receptors in mechanotransduction, Curr. Opin. Cell Biol., 2008, 20(5), 551–556.
9. J. Heuberger and W. Birchmeier, Interplay of Cadherin-Mediated Cell Adhesion and Canonical Wnt Signaling, Cold Spring Harbor Perspect. Biol., 2010, 2, a002915.
10. D. M. Li and Y. M. Feng, Signaling mechanism of cell adhesion molecules in breast cancer metastasis: potential therapeutic targets, Breast Cancer Res. Treat., 2011, 128(1), 7–21.
11. J. T. Groves and J. Kuriyan, Molecular mechanisms in signal transduction at the membrane, Nat. Struct. Mol. Biol., 2010, 17(6), 659–665.
12. N. C. Hartman and J. T. Groves, Signaling clusters in the cell membrane, Curr. Opin. Cell Biol., 2011, 23(4), 370–376.
13. I. Bethani, et al., Spatial organization of transmembrane receptor signalling, EMBO J., 2010, 29(16), 2677–2688.
14. C. R. F. Monks, et al., Three-dimensional segregation of supramolecular activation clusters in T cells, Nature, 1998, 395(6697), 2–86.
15. A. Grakoui, et al., The immunological synapse: A molecular machine controlling T cell activation, Science, 1999, 285(5425), 21–227.
16. J. B. Huppa and M. M. Davis, T-cell-antigen recognition and the immunological synapse, Nat. Rev. Immunol., 2003, 3(12), 973–983.
17. A. R. Aricescu and E. Y. Jones, Immunoglobulin superfamily cell adhesion molecules: zippers and signals, Curr. Opin. Cell Biol., 2007, 19(5), 543–550.
18. P. Kanchanawong, et al., Nanoscale architecture of integrin-based cell adhesions, Nature, 2010, 468(7323), 580–584.
19. U. Cavallaro and E. Dejana, Adhesion molecule signalling: not always a sticky business, Nat. Rev. Mol. Cell Biol., 2011, 12(3), 189–197.
20. C. Dean, et al., Neurexin mediates the assembly of presynaptic terminals, Nat. Neurosci., 2003, 6(7), 708–716.
21. G. Campi, R. Varma and M. L. Dustin, Actin and agonist MHC-peptide complex-dependent T cell receptor microclusters as scaffolds for signaling, J. Exp. Med., 2005, 202(8), 1031–1036.
22. T. Yokosuka, et al., Newly generated T cell receptor microclusters initiate and sustain T cell activation by recruitment of Zap70 and SLP-76, Nat. Immunol., 2005, 6(12), 1253–1262.
23. T. Yokosuka and T. Saito, The Immunological Synapse, TCR Microclusters, and T Cell Activation, in Immunological Synapse, Springer-Verlag Berlin, Berlin, 2010, p. 81–107.
24. T. Saito and T. Yokosuka, Immunological synapse and microclusters: the site for recognition and activation of T cells, Curr. Opin. Immunol., 2006, 18(3), 305–313.
25. S. Hong, R. B. Troyanovsky and S. M. Troyanovsky, Spontaneous assembly and active disassembly balance adherens junction homeostasis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(8), 3528–3533.
26. S. J. Hong, R. B. Troyanovsky and S. M. Troyanovsky, Cadherin exits the junction by switching its adhesive bond, J. Cell Biol., 2011, 192(6), 1073–1083.
27. K. Salaita, et al., Restriction of Receptor Movement Alters Cellular Response: Physical Force Sensing by EphA, 2, Science, 2010, 27(5971), 1380–1385.
28. G. B. E. Stewart-Jones, et al., A structural basis for immunodominant human T cell receptor recognition, Nat. Immunol., 2003, 4(7), 657–663.
29. B. H. Luo, C. V. Carman and T. A. Springer, Structural basis of integrin regulation and signaling, Annu. Rev. Immunol., 2007, 25, 619–647.
30. T. A. Springer, Adhesion receptors of the immune-system, Nature, 1990, 346(6283), 425–434.
31. J. Freigang, et al., The crystal structure of the ligand binding module of axonin-1/TAG-1 suggests a zipper mechanism for neural cell adhesion, Cell, 2000, 101(4), 425–433.
32. Y. N. He, G. J. Jensen and P. J. Bjorkman, Cryo-Electron Tomography of Homophilic Adhesion Mediated by the Neural Cell Adhesion Molecule L1, Structure, 2009, 17(3), 460–471.
33. D. Kostrewa, et al., X-ray structure of junctional adhesion molecule: structural basis for homophilic adhesion via a novel dimerization motif, EMBO J., 2001, 20(16), 4391–4398.
34. S. Wan, D. R. Flower and P. V. Coveney, Toward an atomistic understanding of the immune synapse: Large-scale molecular dynamics simulation of a membrane-embedded TCR-pMHC-CD4 complex, Mol. Immunol., 2008, 45(5), 1221–1230.
35. V. Maruthamuthu, K. Schulten and D. Leckband, Elasticity and Rupture of a Multi-Domain Neural Cell Adhesion Molecule Complex, Biophys. J., 2009, 96(8), 3005–3014.
36. K. E. Gottschalk and H. Kessler, A computational model of transmembrane integrin clustering, Structure, 2004, 12(6), 1109–1116.
37. D. Craig, et al., Structural insights into how the MIDAS ion stabilizes integrin binding to an RGD peptide under force, Structure, 2004, 12(11), 2049–2058.
38. E. Puklin-Faucher, et al., How the headpiece hinge angle is opened: new insights into the dynamics of integrin activation, J. Cell Biol., 2006, 175(2), 349–360.
39. F. Cailliez and R. Lavery, Cadherin mechanics and complexation: the importance of calcium binding, Biophys. J., 2005, 89(6), 3895–3903.
40. F. Cailliez and R. Lavery, Dynamics and stability of E-cadherin dimers, Biophys. J., 2006, 91(11), 3964–3971.
41. M. Sotomayor and K. Schulten, The allosteric role of the Ca²⁺ switch in adhesion and elasticity of C-cadherin, Biophys. J., 2008, 94(12), 4621–4633.
42. B. M. Slepchenko, et al., Computational cell biology: spatiotemporal simulation of cellular events, Annu. Rev. Biophys. Biomol. Struct., 2002, 31, 423–441.
43. B. M. Slepchenko, et al., Quantitative cell biology with the Virtual Cell, Trends Cell Biol., 2003, 13(11), 570–576.
44. C. Francke, et al., Why the phosphotransferase system of Escherichia coli escapes diffusion limitation, Biophys. J., 2003, 85(1), 612–622.
45. J. Hattne, D. Fange and J. Elf, Stochastic reaction-diffusion simulation with MesoRD, Bioinformatics, 2005, 21(12), 2923–2924.
46. M. Ander, et al., SmartCell, a framework to simulate cellular processes that combines stochastic approximation with diffusion and localisation: analysis of simple networks, Syst. Biol., 2004, 1(1), 129–138.
47. J. V. Rodriguez, et al., Spatial stochastic modelling of the phosphoenolpyruvate-dependent phosphotransferase (PTS) pathway in Escherichia coli, Bioinformatics, 2006, 22(15), 1895–1901.
48. J. R. Stiles and T. M. Bartol, Monte Carlo methods for simulating realistic synaptic microphysiology using MCell, Comput. Neurosci., 2001, 87–127.
49. S. S. Andrews and D. Bray, Stochastic simulation of chemical reactions with spatial resolution and single molecule detail, Phys. Biol., 2004, 1(3–4), 137–151.
50. D. Ridgway, et al., Coarse-grained molecular simulation of diffusion and reaction kinetics in a crowded virtual cytoplasm, Biophys. J., 2008, 94(10), 3748–3759.
51. Z. Frazier and F. Alber, A Computational Approach to Increase Time Scales in Brownian Dynamics-Based Reaction-Diffusion Modeling, J. Comput. Biol., 2012, 19(6), 606–618.
52. Z.-R. Xie, J. Chen and Y. Wu, A coarse-grained model for the simulations of biomolecular interactions in cellular environments, J. Chem. Phys., 2014, 140, 054112.
53. P. Cuatrecasas, Membrane receptors, Annu. Rev. Biochem., 1974, 43(0), 169–214.
54. P. W. Gunning, et al., The evolution of compositionally and functionally distinct actin filaments, J. Cell Sci., 2015, 128(11), 2009–2019.
55. D. M. Leitner, F. L. Brown and K. R. Wilson, Regulation of protein mobility in cell membranes: a dynamic corral model, Biophys. J., 2000, 78(1), 125–135.
56. M. D. Ward, M. Dembo and D. A. Hammer, Kinetics of cell detachment: peeling of discrete receptor clusters, Biophys. J., 1994, 67(6), 2522–2534.
57. M. D. Ward and D. A. Hammer, A theoretical analysis for the effect of focal contact formation on cell-substrate attachment strength, Biophys. J., 1993, 64(3), 936–959.
58. S. J. Davis and P. A. van der Merwe, The kinetic-segregation model: TCR triggering and beyond, Nat. Immunol., 2006, 7(8), 803–809.
59. R. Alsallaq and H. X. Zhou, Prediction of protein-protein association rates from a transition-state theory, Structure, 2007, 15(2), 215–224.
60. H. X. Zhou and P. A. Bates, Modeling protein association mechanisms and kinetics, Curr. Opin. Struct. Biol., 2013, 23(6), 887–893.
61. Y. H. Wu, et al., Transforming binding affinities from three dimensions to two with application to cadherin clustering, Nature, 2011, 475(7357), 510–513.
62. A. Ullrich and J. Schlessinger, Signal transduction by receptors with tyrosine kinase activity, Cell, 1990, 61(2), 203–212.
63. K. Palczewski, Oligomeric forms of G protein-coupled receptors (GPCRs), Trends Biochem. Sci., 2010, 35(11), 595–600.
64. D. Bray, M. D. Levin and C. J. Morton-Firth, Receptor clustering as a cellular mechanism to control sensitivity, Nature, 1998, 393(6680), 85–88.
65. J. M. Duarte, et al., An analysis of oligomerization interfaces in transmembrane proteins, BMC Struct. Biol., 2013, 13, 21.
66. J. Brasch, et al., Thinking outside the cell: how cadherins drive adhesion, Trends Cell Biol., 2012, 22(6), 299–310.
67. O. J. Harrison, et al., The Extracellular Architecture of Adherens Junctions Revealed by Crystal Structures of Type I Cadherins, Structure, 2011, 19(2), 244–256.
68. Y. Wu, et al., Cooperativity between trans and cis interactions in cadherin-mediated junction formation, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(41), 17592–17597.
69. Y. H. Wu, B. Honig and A. Ben-Shaul, Theory and Simulations of Adhesion Receptor Dimerization on Membrane Surfaces, Biophys. J., 2013, 104(6), 1221–1229.
70. W. Held and R. A. Mariuzza, Cis–trans interactions of cell surface receptors: biological roles and structural basis, Cell. Mol. Life Sci., 2011, 68(21), 3469–3478.
71. N. S. Gov and S. A. Safran, Red blood cell membrane fluctuations and shape controlled by ATP-induced cytoskeletal defects, Biophys. J., 2005, 88(3), 1859–1874.
72. H. Jiang, et al., Tracking surface glycans on live cancer cells with single-molecule sensitivity, Angew. Chem., Int. Ed. Engl., 2015, 54(6), 1765–1769.
73. A. C. Greene, et al., Spatial organization of EphA2 at the cell-cell interface modulates trans-endocytosis of ephrinA1, Biophys. J., 2014, 106(10), 2196–2205.
74. J. R. James and R. D. Vale, Biophysical mechanism of T-cell receptor triggering in a reconstituted system, Nature, 2012, 487(7405), 64–69.
75. J. Chen, Z. R. Xie and Y. Wu, Computational Modeling of the Interplay between Cadherin-Mediated Cell Adhesion and Wnt Signaling Pathway, PLoS One, 2014, 9(6), e100702.
76. M. A. Utton, et al., Soluble N-cadherin stimulates fibroblast growth factor receptor dependent neurite outgrowth and N-cadherin and the fibroblast growth factor receptor co-cluster in cells, J. Neurochem., 2001, 76(5), 1421–1430.
77. A. Mogilner and B. Rubinstein, The physics of filopodial protrusion, Biophys. J., 2005, 89(2), 782–795.
78. W. H. Binder, V. Barragan and F. M. Menger, Domains and rafts in lipid membranes, Angew. Chem., Int. Ed. Engl., 2003, 42(47), 5802–5827.
79. D. Lingwood and K. Simons, Lipid Rafts As a Membrane-Organizing Principle, Science, 2010, 327(5961), 46–50.
80. P. M. Kekenes-Huskey, et al., Molecular and subcellular-scale modeling of nucleotide diffusion in the cardiac myofilament lattice, Biophys. J., 2013, 105(9), 2130–2140.
81. T. Ando and J. Skolnick, Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(43), 18457–18462.
82. R. J. Ellis, Macromolecular crowding: obvious but underappreciated, Trends Biochem. Sci., 2001, 26(10), 597–604.
83. S. R. McGuffee and A. H. Elcock, Diffusion, Crowding & Protein Stability in a Dynamic Molecular Model of the Bacterial Cytoplasm, PLoS Comput. Biol., 2010, 6(3), e1000694.
84. R. B. Troyanovsky, E. P. Sokolov and S. M. Troyanovsky, Endocytosis of cadherin from intracellular junctions is the driving force for cadherin adhesive dimer disassembly, Mol. Biol. Cell, 2006, 17(8), 3484–3493.
85. Y. H. Chien, et al., Two stage cadherin kinetics require multiple extracellular domains but not the cytoplasmic region, J. Biol. Chem., 2008, 283(4), 1848–1856.
86. M. D. Langer, et al., N-glycosylation alters cadherin-mediated intercellular binding kinetics, J. Cell Sci., 2012, 125(10), 2478–2485.
87. Y. Li, et al., Mechanism of E-cadherin dimerization probed by NMR relaxation dispersion, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(41), 16462–16467.
88. B. Kunz, et al., Axonin-1/TAG-1 mediates cell-cell adhesion by a cis-assisted trans-interaction, J. Biol. Chem., 2002, 277(6), 4551–4557.
89. V. V. Kiselyov, et al., Structural biology of NCAM homophilic binding and activation of FGFR, J. Neurochem., 2005, 94(5), 1169–1179.
90. V. Soroka, C. Kasper and F. M. Poulsen, Structural Biology of NCAM, in Structure and Function of the Neural Cell Adhesion Molecule Ncam, Springer-Verlag Berlin, Berlin, 2010, p. 3–22.
91. E. Seiradake, et al., An extracellular steric seeding mechanism for Eph-ephrin signaling platform assembly, Nat. Struct. Mol. Biol., 2010, 17(4), 398–402.
92. M. Fedor-Chaiken, et al., E-cadherin binding modulates EGF receptor activation, Cell Commun. Adhes., 2003, 10(2), 105–118.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5mb00612k

---