Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Screening-level models to estimate partition ratios of organic chemicals between polymeric materials, air and water†
Efstathios
Reppas-Chrysovitsinos
,
Anna
Sobek
and
Matthew
MacLeod
*
Department of Environmental Science and Analytical Chemistry (ACES), Stockholm University, SE-10691 Stockholm, Sweden. E-mail: matthew.macleod@aces.su.se
First published on 26th April 2016
Abstract
Polymeric materials flowing through the technosphere are repositories of organic chemicals throughout their life cycle. Equilibrium partition ratios of organic chemicals between these materials and air (KMA) or water (KMW) are required for models of fate and transport, high-throughput exposure assessment and passive sampling. KMA and KMW have been measured for a growing number of chemical/material combinations, but significant data gaps still exist. We assembled a database of 363 KMA and 910 KMW measurements for 446 individual compounds and nearly 40 individual polymers and biopolymers, collected from 29 studies. We used the EPI Suite and ABSOLV software packages to estimate physicochemical properties of the compounds and we employed an empirical correlation based on Trouton's rule to adjust the measured KMA and KMW values to a standard reference temperature of 298 K. Then, we used a thermodynamic triangle with Henry's law constant to calculate a complete set of 1273 KMA and KMW values. Using simple linear regression, we developed a suite of single parameter linear free energy relationship (spLFER) models to estimate KMA from the EPI Suite-estimated octanol–air partition ratio (KOA) and KMW from the EPI Suite-estimated octanol–water (KOW) partition ratio. Similarly, using multiple linear regression, we developed a set of polyparameter linear free energy relationship (ppLFER) models to estimate KMA and KMW from ABSOLV-estimated Abraham solvation parameters. We explored the two LFER approaches to investigate (1) their performance in estimating partition ratios, and (2) uncertainties associated with treating all different polymers as a single “bulk” polymeric material compartment. The models we have developed are suitable for screening assessments of the tendency for organic chemicals to be emitted from materials, and for use in multimedia models of the fate of organic chemicals in the indoor environment. In screening applications we recommend that KMA and KMW be modeled as 0.06 × KOA and 0.06 × KOW respectively, with an uncertainty range of a factor of 15.
Environmental impactAssessments of exposure and human health risk associated with organic chemicals in the indoor environment depend on accurate knowledge of equilibrium partition ratios of the chemicals between polymeric materials found in the indoor environment and air and/or water. We compiled a database of 1273 measurements of partition ratios of 446 different chemicals between nearly 40 different polymeric materials and air or water. We developed empirical models to estimate partition ratios for other chemicals from octanol/water and octanol/air partition ratios, and from Abraham solvation parameters estimated from structure. Our screening-level models can be applied in prospective exposure and risk assessments for chemicals, and to guide the collection of additional data. |
Introduction
The intensity at which chemicals are produced is growing on a global scale. World chemical sales in 2013 increased by about €70 billion compared with 2012, and investment in the synthesis of new chemicals has notably increased over the past five years.1 In the United States, the total production volume of chemicals in 2015 is expected to be 8.3% higher than in 2010.2 Organic chemicals constitute the largest volume of seaborne trade, accounting for nearly half of the total market volume shipped over the past 30 years.3 Construction and housing, light vehicles, consumer products and agriculture are the key end-use markets for chemicals.1,2 Materials produced in these sectors flow through the technosphere, and throughout their life cycle they act as a repository of organic chemicals that can enter the indoor and outdoor environment and eventually cause exposure risks for humans and ecosystems.4,5There is growing interest in developing models to describe and quantify the flow of organic chemicals out of consumer products and materials and into the indoor6 and outdoor7 environment. A notable example is the ExpoCast program, in which the United States Environmental Protection Agency is currently developing rapid, high-throughput exposure models to provide human exposure estimates for thousands of chemicals.8 Exposure modeling for organic chemicals depends on accurate estimation of partition ratios of the chemicals.
Partition ratios describe the distribution of organic chemicals between two phases at equilibrium, and are often used to indicate the direction of diffusion and, generally, to quantitatively describe mass transport phenomena. Partition ratios between polymeric materials and air (KMA) or water (KMW) are required for models of fate and transport of organic chemicals in the indoor environment, e.g. houses, workplaces and vehicles, that have been developed to describe exposure pathways to humans and explain variability of indoor concentrations.6 In recent years there has been increasing interest in measuring partition ratios of organic chemicals for polymers such as polyurethane and polydimethylsiloxane that are present in the indoor environment and also are used as passive samplers of air and water by environmental analytical chemists. Thus, KMA and KMW have been measured for a growing number of substances and materials, but significant data gaps still exist to reliably quantify these partition ratios for the myriad of organic chemicals and polymers that humans might encounter in a typical day.
Single parameter and polyparameter linear free energy relationships (spLFERs and ppLFERs) are semi-empirical modeling approaches that can be applied to estimate partition ratios where measurements are not available. Models based on spLFERs are correlations between the logarithms of two partition ratios that have one phase in common. Octanol has often been used as a surrogate for organic phases in spLFERs, for example in widely used models that estimate partition ratios between organic carbon and water (KOC) from the octanol–water partition ratio (KOW),9 and that estimate partition ratios between aerosols and air from the octanol–air partition ratio (KOA).10
The spLFER approach relies on the embedded assumption that the free energies of transfer of chemicals between phases in the two partition ratios in the correlation are linearly related.11 The ppLFER approach is based on the less stringent assumption that the free energy of transfer between different phases can be quantified as the linear sum of energetic contributions from different types of molecular interactions of the chemical with the phases.11 A common form of ppLFER is based on five empirical chemical descriptors that represent a chemical's ability to participate in molecular interactions through hydrogen bonding acidity (A) and basicity (B), van der Waals dispersive interactions described by the logarithm of the hexadecane–air partition ratio (L) and polarity/polarizability (S), and McGowan characteristic volume (V), which accounts for energy costs to form cavities in solvents to accommodate the chemical.12 Well-calibrated models based on ppLFERs are in general expected to perform better than equally well-calibrated spLFERs, as they account for a diversity of types of molecular interactions, and they have more degrees of freedom than single parameter models.13 There are some cases, however, where the performance of ppLFERs and spLFERs is similar and the two methods can be used interchangeably.14 In any application, the information about molecular interactions and the potential for higher accuracy offered by ppLFERs must be weighed against the additional requirements for data compared to spLFERs.
Our goal in this paper is to develop a suite of alternative semi-empirical LFER models for estimating KMA and KMW, and to evaluate the performance of these models and make recommendations about their utility in different applications such as indoor models of fate and transport, selection of materials for passive sampling, and high-throughput exposure estimation. We assembled a database of 363 KMA and 910 KMW measurements for 446 individual compounds, along with their estimated physicochemical properties. The database includes measurements for nearly 40 individual polymeric materials, collected from 29 studies. Our hypothesis was that spLFER models would be more suitable for screening-level applications where (i) the polymer is treated as a bulk substance or (ii) the chemical and/or polymer are poorly characterized. Accordingly, we hypothesized that ppLFER models developed for better characterized cases of substances and materials would perform better than spLFERs in estimating KMA and KMW.
Materials and methods
Literature search and database
We used Google Scholar to identify studies of potential interest by searching for combinations of keywords such as “partition coefficient”, “material” and “polymer”. Our search yielded an initial set of 45 peer-reviewed journal articles. We screened these papers to exclude measured partition ratios that did not pass certain criteria. Specifically, we excluded studies that reported partition ratios that were obtained via extrapolations from kinetics rather than from direct measurements at equilibrium and/or for which the authors of later literature reviews expressed concerns about whether the partition ratios were measured at equilibrium. We further excluded studies in which partition ratios were measured for sea water since assumptions about the effect of salinity on KMW would contribute to uncertainty in our models. Finally, compounds for which the ABSOLV-estimated logarithm of the acid disassociation constant (pKa) was lower than five (pKa < 5) were excluded to avoid measurements that were likely to have been strongly influenced by partially dissociated acids. Such measurements would probably be outliers and they would contribute to increase the error in our models. We retained six compounds that contain basic functional groups (codeine, L-α-acetylmethadol, L-methadone, meperidine, naltrexone and trimetazidine) in our database.After screening the initial set of 45 peer-reviewed journal articles according to the criteria above, data from 29 articles (ref. 15–43) were included in our database.
Temperature correction and data curation
For each of the compounds in the database, we employed EPI Suite44 to calculate molecular weight, octanol–air partition ratio (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA), octanol–water partition ratio (log
KOA), octanol–water partition ratio (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW), dimensionless Henry's law constant (log
KOW), dimensionless Henry's law constant (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW), vapor pressure and subcooled liquid vapor pressure. We used the ABSOLV software45 to estimate Abraham solvation parameters for the development of ppLFERs. We employed an empirical correlation based on Trouton's rule46 to calculate the internal energy of phase change between air and polymeric materials, and assumed that enthalpy of phase change between water and polymeric materials was 20 kJ mol−1. Then, we used the Van't Hoff equation to adjust the measured KMA and KMW values to a standard reference temperature of 298 K. We used a thermodynamic triangle (air–polymeric material–water) with the EPI Suite values of the Henry's law constant, together with measured values of either KMA or KMW to calculate a complete set of 1273 KMA and KMW values at 298 K. A detailed mathematical description of these steps is included in the ESI.†
KAW), vapor pressure and subcooled liquid vapor pressure. We used the ABSOLV software45 to estimate Abraham solvation parameters for the development of ppLFERs. We employed an empirical correlation based on Trouton's rule46 to calculate the internal energy of phase change between air and polymeric materials, and assumed that enthalpy of phase change between water and polymeric materials was 20 kJ mol−1. Then, we used the Van't Hoff equation to adjust the measured KMA and KMW values to a standard reference temperature of 298 K. We used a thermodynamic triangle (air–polymeric material–water) with the EPI Suite values of the Henry's law constant, together with measured values of either KMA or KMW to calculate a complete set of 1273 KMA and KMW values at 298 K. A detailed mathematical description of these steps is included in the ESI.†
Finally, we achieved a uniform set of “dimensionless” partition ratios by employing material densities to convert the units of partition ratios that were expressed on a volume/mass basis (e.g. mL g−1) to a volume/volume basis. In cases where information on the densities of the polymers was not reported in the studies, we used an average material density value from manufacturers' websites. Densities used in these calculations are included in the spreadsheet that is part of the ESI.†
Model development
We developed a family of models to estimate KMA and KMW from the octanol–air (KOA) and octanol–water (KOW) partition ratios (spLFERs; eqn (1a) and (1b)) and Abraham solvation parameters (ppLFERs; eqn (2a) and (2b)) using simple and multiple linear regression, respectively, i.e.,log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMA = g1 × log KMA = g1 × log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA + h1 KOA + h1 | (1a) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW = g2 × log KMW = g2 × log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW + h2 KOW + h2 | (1b) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMA = aMA × A + bMA × B + lMA × L + sMA × S + vMA × V + c1 KMA = aMA × A + bMA × B + lMA × L + sMA × S + vMA × V + c1 | (2a) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW = aMW × A + bMW × B + lMW × L + sMW × S + vMW × V + c2. KMW = aMW × A + bMW × B + lMW × L + sMW × S + vMW × V + c2. | (2b) |
The phase descriptors aPQ, bPQ, lPQ, sPQ and vPQ describe the differences between any two phases (P, Q) with regard to the same intermolecular interactions, and ci is the constant of the multiple linear regression (eqn (2a) and (2b)). The molecular descriptors (A, B, L, S and V) of the chemicals are listed in ESI.†
We present models for partition ratios to six categories of polymeric materials that are defined based on the 2D chemical structures of their corresponding monomers: polyethylene, polyurethane, polydimethylsiloxane, carbohydrates, polyoxymethylene and nylons. 3D structural differences among the materials associated with properties such as degree of crystallinity, density, porosity and permeability were not taken into account in classifying the polymers into different models. However, the form of our models implicitly assumes that absorption, rather than adsorption, is the dominant partitioning process. Absorptive processes occur between a volume of polymer and a volume of air or water. Therefore we expect differences in the 3D structure among polymers to be reflected in the regression parameters determined when we fit our models. As shown in other studies,47–49 the constants in both LFER approaches are partially determined by the fraction of the matrix that is available/accessible for sorption.
We also developed KMA and KMW models for a generic “bulk material”, which is based on combining all the KMA or KMW measurements in the dataset, regardless of the type of material to which the chemicals partition. The generic bulk material models include more measurements than the sum of the measurements used to develop the six categories of polymeric materials since there are polymers in the database such as polystyrene, acrylate polymer, vinyl, polyethylene terephthalate and polyhydroxyethylmethacrylate32 that are not included in any of the six categories listed above, and for which there were only a few measurements, and materials such as kitchen towel23 for which the 2D chemical structure of the polymeric material was not known. In total, the generic bulk material models contain 93 measurements that are not used to develop models in any of the six material-specific cases.
We calculated the correlation coefficient (R2) and the root mean squared error (RMSE) for each model to quantify uncertainties, assess the relative performance and make recommendations about possible applications for estimating KMA and KMW. For model development and outlier detection we employed the Python Statsmodels package. The outlier detection method we used is based on the adjusted Bonferroni p-values for the studentized residuals.
spLFER models
Initial screening of the database indicated that the slopes gi in spLFER models were frequently not significantly different from 1 at the 95% confidence interval. We therefore chose to force the slope to 1 in all spLFERs to derive simple generic models suitable for screening purposes and/or screening estimations of partition ratios when information on material composition is missing. By forcing the slope gi to 1, we implicitly assume octanol is a good surrogate for the polymeric material or the bulk material described by the model. The intercept (hi) can then be viewed conceptually as a measure of the polymer's equivalent content of octanol or as a measure of the free energy of transfer for a compound between the polymer and octanol, in the form of a material–octanol partition ratio (KMO). If one assumes that the polymers have identical sorption properties as octanol, then the intercept represents a measure of the fraction of the polymeric material available for sorption.When gi = 1, eqn (1a) and (1b) can be written as
| KMA = 10h1[×/÷10RMSE] × KOA | (3a) |
| KMW = 10h2[×/÷10RMSE] × KOW | (3b) |
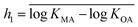 for each modeled set, and h2 is similarly calculated as the arithmetic mean of
for each modeled set, and h2 is similarly calculated as the arithmetic mean of 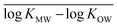 .
.
We expect the spLFER models of KMA and KMW of the same material (i.e.eqn (1a) and (1b)) to have the same intercept when we force the slope to 1, i.e. we expect h1 = h2. This expectation is a result of our data curation process since the value of either of the two partition ratios, KMA or KMW, is dependent on the other, measured value (i.e. KMW or KMA) through a thermodynamic triangle. A deviation between the intercepts of the material–air and a material–water spLFER models for a given material would indicate problems with the application of Trouton's rule or with the calculation of consistent partition coefficients in the thermodynamic triangle made up of KMW, KMA and the dimensionless Henry's law constant, KAW.
The error introduced in the spLFER models by forcing the slope to 1 is accounted for by the RMSE value of the model, which reflects the total uncertainty of each model.
Results
The database
Our database contains measurements for 446 individual organic compounds that are all small molecules with molecular weight lower than 500 g mol−1. Most of these compounds (80%) contain rings, of which 73% are aromatic. Almost half (213/446) of the compounds contain halogen atoms; mainly chlorine (205/446), but there are also a few compounds that contain bromine (3/446), iodine (3/446) or fluorine (2/446). Oxygen atoms are present in 35% of the compounds (157/446), and fewer chemicals contain nitrogen (70/446), sulfur (22/446) and phosphorus (15/446). Alcohols make up 7.5% of the chemicals in the database (34/446).
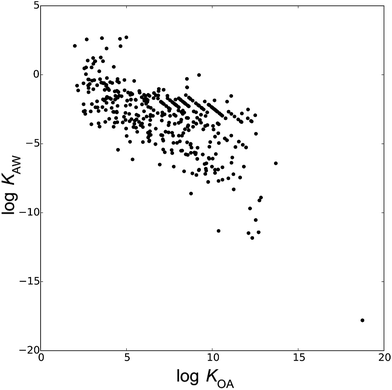
Fig. 1 depicts the 446 compounds of the database in a chemical partitioning space defined by log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA and log
KOA and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW. The database contains chemicals spanning about 20 orders of magnitude of KAW and KOA and about 10 orders of magnitude of KOW, including hydrophobic (log
KAW. The database contains chemicals spanning about 20 orders of magnitude of KAW and KOA and about 10 orders of magnitude of KOW, including hydrophobic (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW > 6), volatile (log
KOW > 6), volatile (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW > 2), and highly water soluble (log
KAW > 2), and highly water soluble (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW < −8) chemicals. The range of chemical space represented in the training sets of semi-empirical models largely determines the applicability domain of the models. A broader domain of applicability renders the prospective power of the models stronger by expanding their range of applicability. Based on the 1273 measurements of the database, we derived a total of 28 different models to estimate KMA or KMW, as described below.
KAW < −8) chemicals. The range of chemical space represented in the training sets of semi-empirical models largely determines the applicability domain of the models. A broader domain of applicability renders the prospective power of the models stronger by expanding their range of applicability. Based on the 1273 measurements of the database, we derived a total of 28 different models to estimate KMA or KMW, as described below.
K MA and KMW models
In Fig. 2–4 we present all 28 models for KMA and KMW with the R2 and RMSE values of each model. Models developed for the same phases (material–air, material–water) are plotted so that they share the same vertical y-axis (experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMA or experimental log
KMA or experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMW) to facilitate comparison between the spLFER and ppLFER approaches. For spLFER models, the horizontal axis is either log
KMW) to facilitate comparison between the spLFER and ppLFER approaches. For spLFER models, the horizontal axis is either log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA (panel a) or log
KOA (panel a) or log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW (panel b), and for ppLFER models, the horizontal axis is the modeled partition ratio derived from the multiple linear regression. For all ppLFER models, simple regressions of the measured and estimated data yielded an intercept of zero and a slope of one, which is confirmation that the multiple linear regression was carried out without error.
KOW (panel b), and for ppLFER models, the horizontal axis is the modeled partition ratio derived from the multiple linear regression. For all ppLFER models, simple regressions of the measured and estimated data yielded an intercept of zero and a slope of one, which is confirmation that the multiple linear regression was carried out without error.
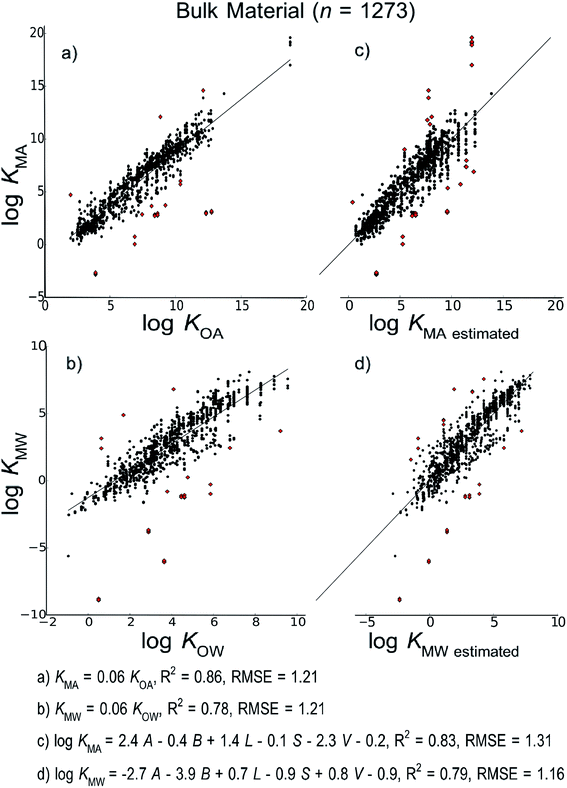 | ||
| Fig. 2 Linear free energy relationship models to estimate material–air (KMA) and material–water (KMW) partition ratios developed using all measurements in the database regardless of material type. | ||
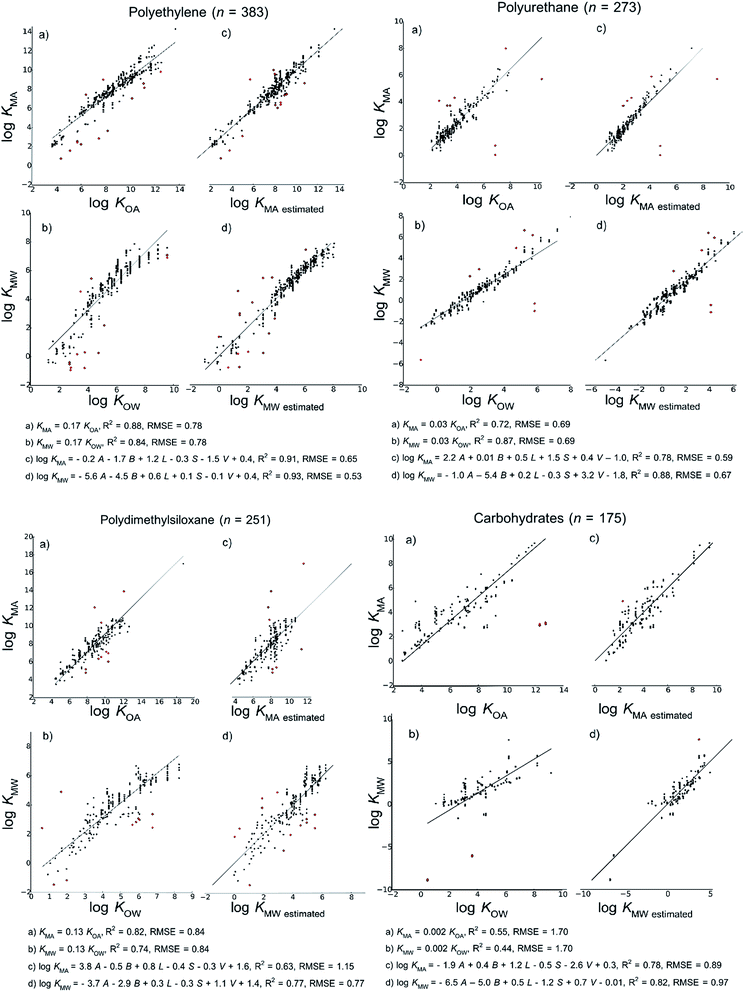
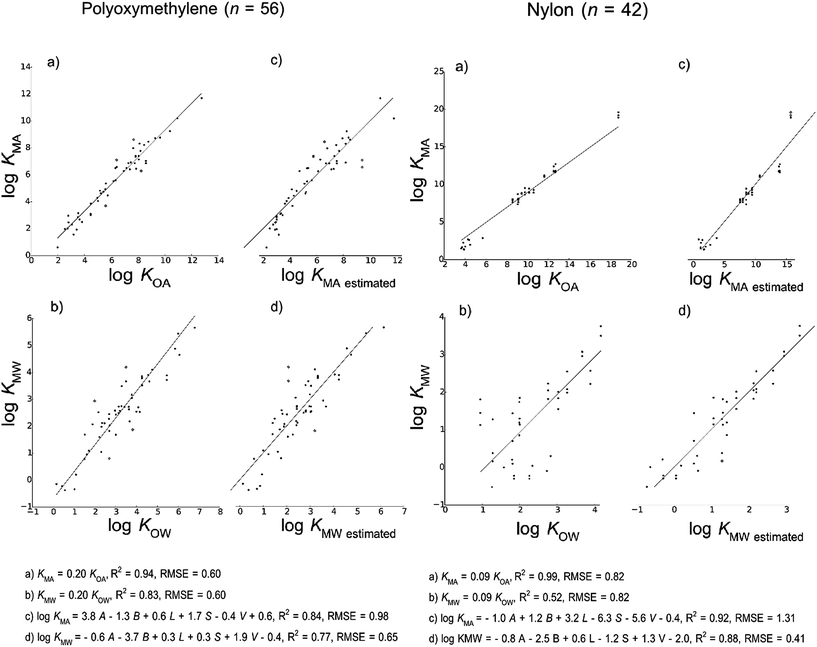
Fig. 2 shows the models developed for the bulk material case, Fig. 3 shows models for the material-specific cases of polyethylene, polyurethane, polydimethylsiloxane and carbohydrates, where the number of observation (n) is over 100, and Fig. 4 shows models for polyoxymethylene and nylon where n is less than 100. This selective presentation of plots is based on a rule of thumb50 according to which multiple linear regression works in the most meaningful way for 10–20 observations per model parameter, including the regression constant. In the case of ppLFER models there are six parameters: the five Abraham solvation parameters and the regression constant. Thus models with n ≥ 100 meet the minimum data requirements for ppLFERs more strictly than models with n < 100. Measurements identified as outliers in each model are indicated in red, and a list of the compounds identified as outliers in each of the 28 models can be found in ESI.†
Discussion
Our initial hypothesis was that spLFERs would prove to be more suitable for screening-level applications where the polymer is treated as a bulk substance or the chemical and/or polymeric material are poorly characterized. Our hypothesis was based on a recognition that although ppLFERs have more degrees of freedom to account for specific and non-specific molecular interactions, this conceptual and mathematical advantage is not utilized in modeling the inconsistent partitioning behavior of poorly characterized material. The generic bulk material models illustrated in Fig. 2 provide a basis to test the hypothesis. The intercept in the spLFER models of the generic bulk material (Fig. 2a and b) is −1.24 and thus KMA = 0.06 × KOA and KMW = 0.06 × KOW. The RMSE of both spLFER bulk models is 1.21, implying that within an uncertainty range of a factor of 15, a wide range of polymers can be modeled as consisting of 6% octanol or as consisting purely of octanol from which 6% is available for sorptive processes. We view this conceptually simple spLFER model as suitable for screening-level applications. The performance metrics of the ppLFERs for the generic bulk material are similar to those of the spLFERs (Fig. 2c and d, RMSE = 1.31 and 1.16). Although the KMW ppLFER model for the bulk material case has slightly lower RMSE than the corresponding spLFER model, considering both RMSE and R2 indicates that spLFER and ppLFER models could be used interchangeably to model the partition ratios of a chemical to a polymeric material. As spLFERs have fewer degrees of freedom and lower data requirements than ppLFERs, our initial hypothesis that spLFER models would be most appropriate for screening-level applications that are based on estimated property data is supported. However in some applications ppLFERs might still be preferred because the equations provide insight into the nature of the intermolecular interactions that determine the partition ratios.Our secondary hypothesis was that the ppLFERs we developed would outperform spLFERs in the material-specific models where the polymers were well characterized. In many of the material-specific models illustrated in Fig. 3 and 4 the model performance metrics for the ppLFERs are indeed better than for the spLFERs. However, the differences in most cases are small. Moreover, there are a few cases (KMA for polydimethylsiloxane, polyoxymethylene and nylon) where spLFERs have lower RMSE and higher R2 values than the corresponding ppLFER models. Therefore, our second hypothesis is weakly supported, but ppLFERs are not markedly superior to spLFERs.
It is clear from theoretical considerations that ppLFER models should outperform spLFER models for specific materials and chemicals with accurate Abraham solvation parameters.13 In studies where partition ratios are measured using a consistent methodology and ppLFERs are developed based on accurately measured Abraham parameters, correlation coefficients can be 0.99 or higher.51–53 The lower correlation coefficients and comparable performance of ppLFERs and spLFERs that we observed in this study reflects limitations of our data quality and comparability that arise from our use of estimated property data and from combining studies primarily based on having a common monomer in the polymeric material.
It is notable that ppLFER models for KMW perform better than the corresponding spLFER models according to both R2 and RMSE in nearly all cases. A possible explanation for the better performance of ppLFERs compared to spLFERs for KMW is the specific H-donor and acceptor interactions between some chemicals and water. Another possible explanation is that calculating KMA through the application of the thermodynamic triangle introduced some random errors that mitigated the advantages of the ppLFER models over the spLFER models. There were initially more experimental KMW values than KMA values, so random errors introduced by the thermodynamic triangle would affect KMA more significantly.
Variability in the polymeric material itself among the various studies that form the basis of each material-specific dataset is another possible source of variability in our material-specific models that might not be well-described by the ppLFER models. A cross-sectional examination of the material-specific models implies a positive correlation between RMSE and the number of studies used to form each polymeric material group. In two material groups that consist of comparable number of observations (polyurethane, n = 273 and polydimethylsiloxane, n = 251), the ppLFER model developed for the partition ratio that was experimentally determined (KMA or KMW – without the application of the thermodynamic triangle) in the largest number of studies (polydimethylsiloxane, 11 studies, water) has higher RMSE values (0.77) than the partition ratio measured in fewer studies (polyurethane, 2 studies, air, RMSE = 0.59).
Another aspect of material variability among the different studies is the age of the material used in the experiments and the overall handling of the material prior to the experimental procedure. In aged polymers some of the covalent bonds in the polymer structure might be degraded,54 leading to a difference in the sorption capacities of an aged and a fresh polymer.
Database and data curation
Our database includes partition ratios for materials and chemicals with a wide range of structural diversity. Semi-empirical LFER models should only be extrapolated to estimate partition ratios for chemicals that are within their domain of applicability, which means to chemicals that are similar to those in the training set. In principle the ppLFERs should have a wider domain of applicability since they represent a diverse set of intermolecular interactions. However, even the ppLFERs should be applied with caution to substances that are not represented in the training set, such as siloxanes, which are not well described by ppLFER models that do not include siloxanes in their training set.55,56 Similarly, compounds with molecular weight greater than 500 g mol−1 and those that combine many different functional groups are not represented in our database and are likely outside the range of applicability of our models.Our database was assembled using EPI Suite's estimated values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW to create a thermodynamic triangle, Trouton's rule to estimate enthalpies of phase change between material and air, and the Van't Hoff equation for temperature adjustment to 298 K. Each of these three calculations contributes to the introduction of uncertainty in the models. We expect spLFER models to be more susceptible to the introduction of random errors than ppLFERs because they have fewer degrees of freedom. EPI Suite's estimations have been found to be generally consistent with estimates of other software,57 but errors introduced by the use of EPI Suite's estimated log
KAW to create a thermodynamic triangle, Trouton's rule to estimate enthalpies of phase change between material and air, and the Van't Hoff equation for temperature adjustment to 298 K. Each of these three calculations contributes to the introduction of uncertainty in the models. We expect spLFER models to be more susceptible to the introduction of random errors than ppLFERs because they have fewer degrees of freedom. EPI Suite's estimations have been found to be generally consistent with estimates of other software,57 but errors introduced by the use of EPI Suite's estimated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KAW would be difficult to detect since they are incorporated consistently through the data curation and model development. Trouton's rule is in theory limited to nonpolar chemicals and compounds that are capable of forming strong hydrogen bonds are typically exceptions to this rule. The Van't Hoff equation is based on the assumption that enthalpy change remains constant over the temperature range under consideration. Our database contains polar compounds that form hydrogen bonds. Also, the temperature range over which the partition ratios were measured in the 29 studies we used to assemble the database spans from 277 K to 373 K. However, uncertainty for most of the models developed in this study is typically a factor of 10, while the range of partition ratios spans several orders of magnitude. This result implies that both Trouton's rule and Van't Hoff equation assumptions are not sufficiently violated to introduce large errors. In all spLFER models the intercept of the KMA and KMW relationships was identical and the RMSEs were similar for models developed for the same group of materials. The internal consistency of the KMA and KMW spLFER models indicates that there were no errors introduced in the calculation of partition ratios using the thermodynamic triangle.
KAW would be difficult to detect since they are incorporated consistently through the data curation and model development. Trouton's rule is in theory limited to nonpolar chemicals and compounds that are capable of forming strong hydrogen bonds are typically exceptions to this rule. The Van't Hoff equation is based on the assumption that enthalpy change remains constant over the temperature range under consideration. Our database contains polar compounds that form hydrogen bonds. Also, the temperature range over which the partition ratios were measured in the 29 studies we used to assemble the database spans from 277 K to 373 K. However, uncertainty for most of the models developed in this study is typically a factor of 10, while the range of partition ratios spans several orders of magnitude. This result implies that both Trouton's rule and Van't Hoff equation assumptions are not sufficiently violated to introduce large errors. In all spLFER models the intercept of the KMA and KMW relationships was identical and the RMSEs were similar for models developed for the same group of materials. The internal consistency of the KMA and KMW spLFER models indicates that there were no errors introduced in the calculation of partition ratios using the thermodynamic triangle.
Model development and performance
A critical point in the development of spLFER models in this study is our decision to force the slope to 1 at the expense of higher RMSE values. We forced the slope to 1 in all spLFER models, even in the 10 cases where this value did not fall within the 95% confidence interval. Forcing the slope to 1 allowed us to deliver simple empirical relationships of the form of eqn (3), and provides a common ground to compare our material-specific spLFER models with each other and with the bulk material spLFER model, through the conceptual lens of the apparent “octanol equivalents” each material exhibits.Our ppLFER models are based on A, B, L, S and V, which is consistent with recommended practice for environmental applications.58 The estimation of these Abraham solvation parameters by ABSOLV is a source of uncertainty for ppLFER models. In the estimation of KMA, there are cases of material-specific spLFERs such as the ones developed for polydimethylsiloxane, polyoxymethylene and nylon that have a lower RMSE than the corresponding ppLFER models. This result contradicts our initial theoretical considerations. In theory, ppLFERs are more accurate than spLFERs – especially when the chemicals and the phases to which they partition are well defined and characterized. A possible explanation for this unexpected result lies in the accuracy (or lack thereof) of ABSOLV's estimations.
Among our spLFER models, those developed for carbohydrates have the highest RMSE, and also much higher RMSE than the corresponding ppLFER models (see Fig. 3). The relatively poor performance of the spLFER models for carbohydrates led us to re-examine this group of materials and we identified a subset of partition ratios that consistently appeared in the outliers. These partition ratios were obtained from the same study and they also clearly defined a different sub-segment of polymeric materials that we initially considered as carbohydrates. This is the sub-segment of paper; it consists of imitation parchment paper, Kraft paper and cardboard. We suspect that paper has different partitioning properties than the rest of the materials that form the carbohydrates aggregation because it has typically undergone various treatments to reach its final state. It is possible that due to crystallinity,49 the cellulose in the paper is not as available for sorptive processes as in the rest of the materials in the carbohydrates group. The models for carbohydrates without the paper sub-segment, as well as the models for the paper sub-segment are included in the ESI.† When the paper sub-segment is removed from the carbohydrates group, the R2 for the spLFER for KMA rises from 0.55 to 0.77 and the RMSE falls from 1.7 to 0.96.
Outliers
We examined the outliers identified in each model to further investigate model performance and behavior. With few exceptions, the outliers identified in the KMA and KMW spLFER models developed for the same group of materials are the same. Moreover, the number of KMA measurements identified as outliers is nearly always equal to the number of KMW measurements, and those partition ratios were all measured at 298 (±5) K. This result largely eliminates the temperature correction as a source of outliers.As discussed above, partition ratios measured in a single study of partitioning between paper and water that were included in our models for ‘carbohydrates’ were frequently identified as outliers, especially in the spLFER models. In general, we believe that studies focused on specific polymers that are not representative of the larger group in which they are collected for modeling purposes would be a source of outliers. The performance metrics for models of the carbohydrates group are markedly better when paper is excluded, which indicates paper has different characteristics than other polymeric materials in the ‘carbohydrates’ group.
Endosulfan I (alpha) is the only compound that is an outlier for two different ppLFER models for specific polymers (polydimethylsiloxane and polyethylene) measured in two different studies, and is also an outlier in both bulk material ppLFER models. In contrast, endosulfan I (alpha) is not an outlier in any spLFER model. Thus the Abraham solvation parameters estimated by ABSOLV for endosulfan I (alpha) may be suspect.
Notable outliers are bisphenol A and 4-deoxypyridoxine in the paper sub-segment, hexane in polyurethane and styrene in crystalline polystyrene. Four out of six of the compounds that contain basic groups were detected as outliers (codeine, L-methadone, naltrexone, trimetazidine), mainly in ppLFER models. This result indicates that the partition ratios of these compounds might have been measured in their disassociated form. Our inspection of the other 44 individual compounds that were identified as outliers in various models did not lead to the identification of other specific chemicals or classes of compounds that were consistently identified as outliers.
Acknowledgements
Financial support for this study was provided by the European Union's Seventh Framework Programme for research, technological development and demonstration under grant agreement no. 316665 (A-TEAM project).References
- CEFIC, European Chemical Industry Facts and Figures 2014, http://www.fr.zone-secure.net/13451/106811/, accessed August 2015.
- ACC, Year-End 2014 Chemical Industry Situation and Outlook American Chemistry Builds Momentum 2014, http://www.files.clickdimensions.com/americanchemistrycom-avo5d/files/year-end2014situationandoutlookf6c2.pdf, accessed August 2015.
- N. Wijnolst and T. Wergeland, in Shipping Innovation, IOS Press BV under the imprint Delft University Press Nieuwe, Amsterdam, 2009, ch. 9, Chemical Tankers, pp. 265–277 Search PubMed.
- C. J. Weschler and W. W. Nazaroff, Atmos. Environ., 2008, 42, 9018–9040 CrossRef CAS.
- R. Weber, A. Watson, M. Forter and F. Oliaei, Waste Manage. Res., 2011, 29, 107–121 CrossRef CAS PubMed.
- I. Liagkouridis, I. T. Cousins and A. P. Cousins, Sci. Total Environ., 2014, 491–492, 87–99 CrossRef CAS PubMed.
- T. E. McKone and M. MacLeod, Annu. Rev. Environ. Resour., 2003, 28, 463–492 CrossRef.
- J. F. Wambaugh, A. Wang, K. L. Dionisio, A. Frame, P. Egeghy, R. Judson and R. W. Setzer, Environ. Sci. Technol., 2014, 48, 12760–12767 CrossRef CAS PubMed.
- R. Seth, D. Mackay and J. Muncke, Environ. Sci. Technol., 1999, 33, 2390–2394 CrossRef CAS.
- T. Harner and T. F. Bidleman, Environ. Sci. Technol., 1998, 32, 1494–1502 CrossRef CAS.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Environmental Organic Chemistry, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2nd edn, 2002 Search PubMed.
- R. W. Taft, J.-L. M. Abboud, M. J. Kamlet and M. H. Abraham, J. Solution Chem., 1985, 14, 153–186 CrossRef CAS.
- K.-U. Goss and R. P. Schwarzenbach, Environ. Sci. Technol., 2001, 35, 1–9 CrossRef CAS PubMed.
- T. N. Brown and F. Wania, Environ. Sci. Technol., 2009, 43, 6676–6683 CrossRef CAS PubMed.
- A. Bodalal, J. S. Zhang and E. G. Plett, Build. Environ., 2000, 35, 101–110 CrossRef.
- P. Mayer, W. H. Vaes and J. L. Hermens, Anal. Chem., 2000, 72, 459–464 CrossRef CAS PubMed.
- R. S. Brown, P. Akhtar, J. Akerman, L. Hampel, I. S. Kozin, L. a. Villerius and H. J. Klamer, Environ. Sci. Technol., 2001, 35, 4097–4102 CrossRef CAS PubMed.
- S. S. Cox, D. Zhao and J. C. Little, Atmos. Environ., 2001, 35, 3823–3830 CrossRef CAS.
- J. F. Müller, K. Manomanii, M. R. Mortimer and M. S. McLachlan, Fresenius' J. Anal. Chem., 2001, 371, 816–822 CrossRef.
- I. Valor, M. Pérez, C. Cortada, D. Apraiz, J. C. Moltó and G. Font, J. Sep. Sci., 2001, 24, 39–48 CrossRef CAS.
- H. A. Leslie, T. L. Ter Laak, F. J. M. Busser, M. H. S. Kraak and J. L. M. Hermens, Environ. Sci. Technol., 2002, 36, 5399–5404 CrossRef CAS PubMed.
- Y. Xu and Y. Zhang, Atmos. Environ., 2003, 37, 2497–2505 CrossRef CAS.
- C. Nerín and E. Asensio, Anal. Chim. Acta, 2004, 508, 185–191 CrossRef.
- T. L. Ter Laak, M. Durjava, J. Struijs and J. L. M. Hermens, Environ. Sci. Technol., 2005, 39, 3736–3742 CrossRef CAS PubMed.
- R. G. Adams, R. Lohmann, L. A. Fernandez, J. K. MacFarlane and P. M. Gschwend, Environ. Sci. Technol., 2007, 41, 1317–1323 CrossRef CAS PubMed.
- I. Kamprad and K.-U. Goss, Anal. Chem., 2007, 79, 4222–4227 CrossRef CAS PubMed.
- J. Kwon, T. Wuethrich, P. Mayer and B. I. Escher, Anal. Chem., 2007, 79, 6816–6822 CrossRef CAS PubMed.
- G. Ouyang, J. Cai, X. Zhang, H. Li and J. Pawliszyn, J. Sep. Sci., 2008, 31, 1167–1172 CrossRef CAS PubMed.
- V. I. Triantafyllou, K. Akrida-Demertzi and P. G. Demertzis, Food Chem., 2007, 101, 1759–1768 CrossRef CAS.
- M. T. O. Jonker, Chemosphere, 2008, 70, 778–782 CrossRef CAS PubMed.
- K. A. Maruya, E. Y. Zeng, D. Tsukada and S. M. Bay, Environ. Toxicol. Chem., 2009, 28, 733–740 CrossRef CAS PubMed.
- A. Baner and O. Piringer, Plastic Packaging, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2008, vol. 91 Search PubMed.
- G. Witt, G. A Liehr, D. Borck and P. Mayer, Chemosphere, 2009, 74, 522–529 CrossRef CAS PubMed.
- L. A. Fernandez, J. K. MacFarlane, A. P. Tcaciuc and P. M. Gschwend, Environ. Sci. Technol., 2009, 43, 1430–1436 CrossRef CAS PubMed.
- S. E. Hale, J. E. Tomaszewski, R. G. Luthy and D. Werner, Water Res., 2009, 43, 4336–4346 CrossRef CAS PubMed.
- F. Smedes, R. W. Geertsma, T. van der Zande and K. Booij, Environ. Sci. Technol., 2009, 43, 7047–7054 CrossRef CAS PubMed.
- M. Zhang and L. Zhu, Environ. Sci. Technol., 2009, 43, 2740–2745 CrossRef CAS PubMed.
- S. E. Hale, T. J. Martin, K.-U. Goss, H. P. H. Arp and D. Werner, Environ. Pollut., 2010, 158, 2511–2517 CrossRef CAS PubMed.
- H.-W. Hung, T.-F. Lin and C. T. Chiou, Environ. Sci. Technol., 2010, 44, 5430–5436 CrossRef CAS PubMed.
- L.-J. Bao, S.-P. Xu, Y. Liang and E. Y. Zeng, Environ. Toxicol. Chem., 2012, 31, 1012–1018 CrossRef CAS PubMed.
- S. Endo, S. E. Hale, K.-U. Goss and H. P. H. Arp, Environ. Sci. Technol., 2011, 45, 10124–10132 CrossRef CAS PubMed.
- C. Huang, D. Duan, M. Yan and S. Wang, Packag. Technol. Sci., 2013, 26, 59–69 CrossRef CAS.
- Y. Choi, Y.-M. Cho and R. G. Luthy, Environ. Sci. Technol., 2013, 47, 6943–6950 CrossRef CAS PubMed.
- US EPA, Estimation Programs Interface Suite™ for Microsoft® Windows v 4.11, United States Environmental Protection Agency, Washington, DC, USA, 2012 Search PubMed.
- ACD/ABSOLV, Version 15.01, Advanced Chemistry Development, Inc., Toronto, ON, Canada, http://www.acdlabs.com, 2015 Search PubMed.
- M. MacLeod, M. Scheringer and K. Hungerbühler, Environ. Sci. Technol., 2007, 41, 2827–2832 CrossRef CAS PubMed.
- P. C. M. Van Noort, Chemosphere, 2012, 87, 125–131 CrossRef CAS PubMed.
- K.-U. Goss, Anal. Chem., 2011, 83, 5304–5308 CrossRef CAS PubMed.
- S. E. Hale, G. Cornelissen and H. P. H. Arp, Environ. Sci. Technol., 2011, 45, 103754 Search PubMed.
- F. E. Harrell, Regression Modeling Strategies, Springer, New York, 2001 Search PubMed.
- S. Endo, S. T. J. Droge and K.-U. Goss, Anal. Chem., 2011, 83, 1394–1400 CrossRef CAS PubMed.
- M. Schneider and K.-U. Goss, Anal. Chem., 2009, 81, 3017–3021 CrossRef CAS PubMed.
- L. Sprunger, A. Proctor, W. E. Acree and M. H. Abraham, J. Chromatogr. A, 2007, 1175, 162–173 CrossRef CAS PubMed.
- B. Gewert, M. M. Plassmann and M. MacLeod, Environ. Sci.: Processes Impacts, 2015, 17, 1513–1521 CAS.
- S. Endo and K.-U. Goss, Environ. Sci. Technol., 2014, 48, 2776–2784 CrossRef CAS PubMed.
- D. Panagopoulos, A. Jahnke, A. Kierkegaard and M. MacLeod, Environ. Sci. Technol., 2015, 49, 12161–12168 CrossRef CAS PubMed.
- X. Zhang, T. N. Brown, F. Wania, E. S. Heimstad and K.-U. Goss, Environ. Int., 2010, 36, 514–520 CrossRef CAS PubMed.
- S. Endo and K.-U. Goss, Environ. Sci. Technol., 2014, 48, 12477–12491 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5em00664c |
| This journal is © The Royal Society of Chemistry 2016 |