Structural and optical properties of methylammonium lead iodide across the tetragonal to cubic phase transition: implications for perovskite solar cells

Abstract

We report temperature resolved UV-vis absorption and spectral photocurrent response measurements of MAPbI₃ thin films and solar cells, together with ab initio simulations, to investigate the changes in material properties occurring across the tetragonal to cubic phase transition. We find that the MAPbI₃ band-gap does not abruptly change when exceeding the tetragonal to cubic transition temperature, but it rather monotonically blue-shifts following the same temperature evolution observed within the tetragonal phase. Car–Parrinello molecular dynamics simulations demonstrate that the high temperature phase corresponds on average to the expected symmetric cubic structure assigned from XRD measurements, but that the system strongly deviates from such a structure in the sub-picosecond time scale. Thus, on the time scale of electronic transitions, the material seldom experiences a cubic environment, rather an increasingly distorted tetragonal one. This result explains the absence of dramatic changes in the optical of MAPbI₃ across the explored temperature range of 270–420 K, which could have important consequences for the practical uptake of perovskite solar cells.

---

Broader context

The rapid efficiency surge of solar cells based on organohalide lead perovskites has been only in part paralleled by a fundamental understanding of the basic materials properties. The prototypical methylammonium lead iodide perovskite, MAPbI₃, shows the presence of various phase transitions occurring in the temperature range of technologically relevant applications. Above 327 K, a change from a tetragonal to a cubic structure is known to occur. The presence of such a tetragonal–cubic transition well within the operative temperature range of a solar cell is a delicate point for the widespread uptake of perovskite solar cells, as it could inherently hinder the real world applications of these devices. Here we demonstrate that the photovoltaic properties of hybrid lead-halide perovskites are not inherently limited by the presence of a phase transition within the solar cell operating regime. In particular, we show the absence of dramatic changes in the optical properties of MAPbI₃ perovskites across the tetragonal to cubic transition, due to structural fluctuations on a sub-picosecond timescale, which make the instantaneous electronic energy levels and band-gap of the formally cubic, high temperature structure to differ only slightly from those of the room temperature stable tetragonal phase.

1. Introduction

Hybrid metal halide perovskites of the type AMX_3−xY_x, with A = cesium (Cs), methylammonium (MA) or formamidinium (FA), M = Sn or Pb, and X, Y = Cl, Br and I, represent one of the most important recent breakthroughs in the field of photovoltaics and optoelectronics in general. Initially investigated in dye-sensitized solar cells,¹ showing an impressive efficiency improvement in just a few years,^2–8 with recently reported record efficiency of ∼20%,⁹ hybrid lead halide perovskites have been successfully implemented also in a variety of optoelectronic applications, such as light emitting devices,¹⁰ lasing¹¹ and water-splitting devices.^12,13 Their success is mainly due to their unique set of electronic properties, such as ambipolar transport properties,^14,15 μm to mm charge carrier diffusion length,^16,17 low intrinsic recombination rate,¹⁸ tunable band gap across the visible region (down to 1.2 eV for the MASnI₃ perovskite),¹⁹ and large absorption coefficient.² Notably, these impressive electronic properties are coupled to the possibility of resorting to low cost solution-based techniques for their synthesis and deposition, or alternatively to vapor deposition methods,⁵ which has further increased the scope for device applications.

In spite of the large body of work, however, there are still many open questions on the basic electro-optical properties of this class of materials and on their possible practical limitations. An important peculiarity that hybrid perovskites share with their fully inorganic counterparts is the presence of various phase transitions, also occurring in the temperature range of technologically relevant applications. An example is provided by the prototypical methylammonium lead iodide perovskite, here-on MAPbI₃. X-ray diffraction (XRD) investigations^19,20 and calorimetric measurements^21,22 highlighted the presence of two phase transitions at 162 K and at 327 K. Poglitsch and Weber assigned the low temperature transition to a change from an orthorhombic-to-tetragonal crystalline structure, and the high temperature one to a change from a tetragonal-to-cubic structure.²⁰ The presence of a tetragonal-to-cubic transition at 327 K, well within the operative temperature range of a solar cell, is a delicate point as it could inherently hinder the real world applications of these devices, because of possible variations across the phase transition of the inherent optoelectronic properties of this class of materials and consequently of its photovoltaic working mechanism.

This point has been partly addressed in a recent paper by Zhang et al.,²³ who investigated the photovoltaic performances of MAPbI₃ in the 80 K to 360 K temperature range, thus across both the orthorhombic–tetragonal and the tetragonal–cubic phase transitions. These authors demonstrated that the photovoltaic parameters of MAPbI₃-based solar cells, especially short circuit current and fill factor, did not change dramatically across the tetragonal–cubic phase transition at 327 K, while they observed a strong efficiency decrease when approaching the orthorhombic phase. These results seem to suggest that there could be no marked distinction between the tetragonal and cubic phases, while the orthorhombic phase shows effectively different photovoltaic properties. An important point to be further explored is whether the fundamental material properties affecting the photovoltaic operational mechanism in perovskite solar cells, i.e. the perovskite band-gap and energy levels, are changing across the tetragonal–cubic phase transition and to what extent. This information is fundamental to the device design, since a significant change in the perovskite electronic structure typically associated with a phase transition is difficult to accommodate in a device whilst maintaining efficient charge extraction with carrier-selective contacts as they must be well matched to the light-absorber over all conditions.

In this paper, we present a coupled experimental and theoretical investigation aimed at clarifying, at an atomistic level, the variation in the structural and optical properties of MAPbI₃ across the tetragonal–cubic phase transition. We perform UV-vis absorption and spectral photocurrent response measurements as a function of temperature both on MAPbI₃ and on MAPbI_3−xCl_x perovskites in the 300–410 K range, comparing with previous results at lower temperatures.²⁴ We observe a gradual blue-shift of the band-gap from room temperature to 410 K, which is not paralleled by the predictions of GW calculations for an abrupt change from the tetragonal to the cubic structure. Car–Parrinello molecular dynamics simulations reveal that the high temperature phase is indeed cubic when considering the time-averaged structure. However, we observe large fluctuations in the PbI₆ octahedra tilting on a sub-picosecond timescale, which make the instantaneous and time-averaged band-gap distinctively wider than the band-gap predicted for the time-averaged structure, consistent with our experimental evidence. This result explains the absence of dramatic changes in the light absorption onset of MAPbI₃ perovskites across the explored temperature range. Most notably, we demonstrate that, as opposed to the ferroelectric properties of inorganic oxide perovskites, the photovoltaic properties of hybrid lead-halide perovskites are not inherently limited by the presence of a phase transition within the solar cell operating regime.

2. Results and discussion

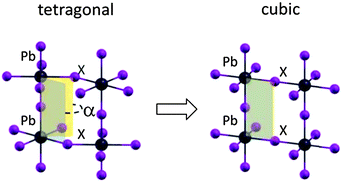
The transition from the room temperature tetragonal phase to the high temperature cubic phase of hybrid lead-halide perovskites has been widely studied in the past. Calorimetric studies by Knop et al.²² and by Onoda-Yamamuro et al.²¹ reported large latent heat during this transition, demonstrating that it is a first-order thermodynamic transition. On the structural side, the tetragonal–cubic transition in MAPbBr₃ and MAPbI₃ has been classified by Mashiyama et al. as displacive.²⁵ The typical “out-of-phase” rotation of the PbI₆ octahedra along the c-axis of the tetragonal phase, the a⁰a⁰c⁻ structure in the Glazer notation,²⁶ gradually reduces upon increasing the temperature, until the octahedra are no longer rotated, on average, thus resulting in a cubic structure classified as a⁰a⁰a⁰, see Fig. 1. The rotation of the octahedra can be quantified by the I–Pb–Pb–I dihedral angle, α in Fig. 1. The gradual reduction of the octahedra tilting in MAPbI₃ is supported by recent structural analyses.^27,28

Fig. 1 Octahedra tilting pattern for the tetragonal (left) to the cubic (right) structure of a MAPbX₃ perovskite (X = halide); the order parameter of the transition, the X–Pb–Pb–X dihedral angle α, is also reported.

In Fig. 2a, we report the UV-vis absorption spectrum of MAPbI₃ from 310 K to 400 K. Data recorded in the full 4.2–400 K temperature range can be found in the ESI.† Within the temperature stability range of the tetragonal phase, we observe a gradual blue-shift of the absorption maximum with increasing temperature from ∼1.61 to ∼1.69 eV (Fig. 2a). For many semiconductors (Si, Ge, GaAs, InP, InAs…) the band gap red-shifts to lower energies with increasing temperature. Some Pb-based compounds instead show the opposite results. In PbS films, for example, lattice dilation increases the band gap.³⁰ A similar result has been theoretically reported for MAPbI₃.^29,31 We fitted this shift with a linear approximation of the empirical Varshni relationship³² in the high temperature limit, according to eqn (1) (note that the absence of an excitonic transition in such temperature range allows for a clean analysis of the band-gap)

E_g(T) = E_g(0) + dE_g/dT × T (1)

where E_g(0) represents the material energy gap at T = 0, while dE_g/dT is a constant parameter characteristic of a given material which has contributions from lattice thermal expansion and electron–phonon interactions.³² The fitting provides an estimate of the temperature dependence of the band gap of dE_g/dT = 257 ± 13 μeV K⁻¹ for MAPbI₃ (Fig. 2b). A recent work confirms this continuous blue-shift of the band gap across the tetragonal–cubic transition for MAPbI₃, and it demonstrates that this is mainly due to the down-shift of the valence band.³³ For MAPbI_3−xCl_x our measured absorption spectra show a similar behavior as for MAPbI₃ but suggest a ∼20 K lower orthorhombic to tetragonal transition temperature for this material, ESI† Fig. S1, in line with the effect of a small percentage of chlorine doping.⁴⁰

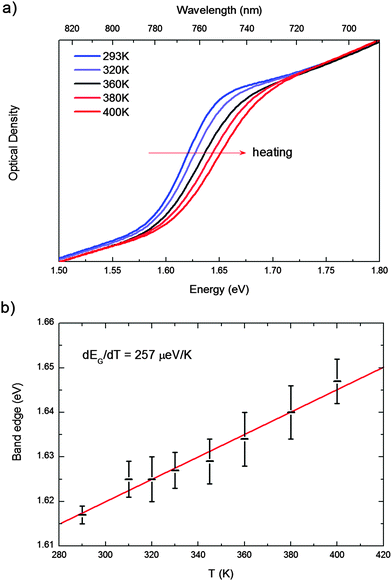Fig. 2 (a) UV-vis absorption spectrum of MAPbI₃ from 310 K to 400 K; (b) evolution of the band gap. The experimental data are fitted according to the equation (eqn (1)) to extrapolate dE_g/dT = 257 ± 13 μeV K⁻¹.

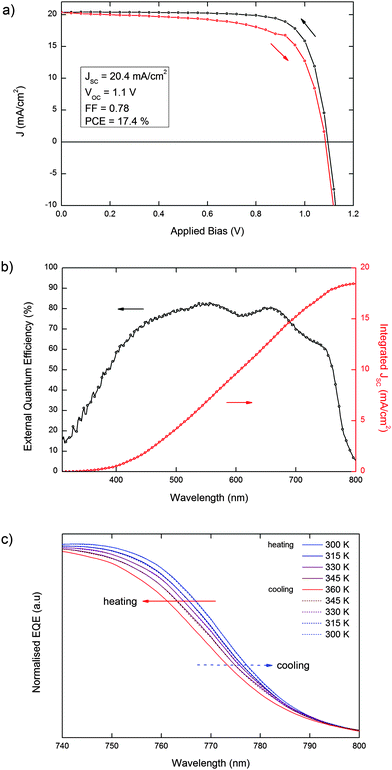
Most notably, our observations are directly translated into the photovoltaic properties of devices based on MAPbI₃, fabricated according to a recently published procedure.³⁴ In Fig. 3a and b, we report the J–V curve and the absolute external quantum efficiency (EQE) of a 17.4% efficient solar cell (see Experimental methods, ESI,† for further details). In Fig. 3c we report the normalized EQE for the same cell scanned across the 300–360 temperature range. The cell was first heated from 300 K to 360 K, above the tetragonal–cubic transition, then cooled down back to 300 K to verify the reversibility of the spectral shift and the absence of permanent changes in the light-harvesting spectrum induced by thermal cycling in MAPbI₃-based solar cells. Upon heating from 300 K to 360 K, we observe a gradual blue-shift of the EQE curve onset, which is related to the increase of the band gap as shown in Fig. 2a, consistent with the changes in the absorption spectrum of bare MAPbI₃ films. Interestingly, we do not observe abrupt variations of the spectral dependence of the photocurrent generation across the tetragonal–cubic phase transition, consistent with the similar short circuit current and efficiencies found by Zhang et al.²³ Cooling down from 360 K to 300 K, we observe a complete recovery of the original spectral shape of the EQE, thus demonstrating that the variation in the band-gap across the tetragonal–cubic phase transition is completely reversible in an efficient functioning device. We repeated the measurements for several MAPbI₃-based devices with power conversion efficiencies >15% (Fig. S2 and S3, ESI†) to ensure the reproducibility of the phenomena. A similar trend was also observed in a MAPbI_3−xCl_x-based device (Fig. S4, ESI†).

Fig. 3 (a) J–V curve and (b) absolute EQE for a MAPbI₃-based solar cell at room temperature. (c) Normalized EQE for the same photovoltaic device across the temperature range of the tetragonal–cubic phase transition.

To provide a rationale for the picture derived from experimental measurements, we performed periodic quantum-mechanical calculations, using the Quantum-Espresso suite of programs.³⁵ First, we calculated the electronic band gap of the orthorhombic, tetragonal and cubic crystals at their optimized geometry. To provide reliable band-gap estimates, we resorted to state-of-art GW calculations with the inclusion of spin–orbit coupling (SOC), currently representing the method of choice for accurate predictions, within 0.1 eV, of the electronic properties of hybrid lead halide perovskites.^36,37 In light of the very small chlorine concentration in MAPbI_3−xCl_x, around a few % at most,^38–41 we limited our simulations to the pristine MAPbI₃ perovskite. For the orthorhombic phase, we used the P_nma structure determined from the XRD measurements at 100 K by Baikie et al.,²⁷ made by four MAPbI₃ units. For the tetragonal phase we used a previously optimized structure,^42,43 again made by four MAPbI₃ units, which is consistent with the XRD structures proposed by Kawamura et al.⁴⁴ and Stoumpos et al.,¹⁹ showing the typical a⁰a⁰c⁻ rotation of the PbI₆ octahedral, Fig. 1a. For the cubic structure, our model is made by eight MAPbI₃ units obtained by replication of two different optimized cubic systems made by one MAPbI₃ unit. The two structures are originated by fixing the inorganic atoms in the crystallographic cubic positions and by relaxing the organic MA cation, hereafter (a), or by allowing the organic and inorganic components to relax (b). In all cases, we used the experimental cell parameters (see the ESI,† for further details).²⁰

The SOC-GW band-gap calculated for the three phases of MAPbI₃ at their optimized structures are reported in Table 1, compared with the experimental data from Fig. 2 and Fig. S1 (ESI†). We predict a red-shift associated with the orthorhombic-to-tetragonal change in the crystal structure, from 1.81 eV to 1.67 eV, in good agreement with the red-shift from 1.65 eV to 1.61 eV observed from the UV-vis measurements, Fig. S1 (ESI†). Note that while for the orthorhombic phase an excitonic feature is clearly visible in the optical spectra, no such feature is distinguishable for the tetragonal phase. Thus for the orthorhombic phase the optical absorption maximum represents a lower-bound for the electronic band-gap, which is the SOC-GW calculated quantity, while the two values may coincide (within few meV) for the tetragonal phase. Our SOC-GW calculated band-gap for the orthorhombic phase agrees with previous data obtained for this system by hybrid functionals including SOC.³² For the high temperature transition instead, SOC-GW calculations predict a large red-shift of the band-gap, amounting to 0.4–0.5 eV, which is clearly inconsistent with the experimental data in Fig. 2.

Table 1 Comparison between the experimental band-gap (eV) of the various phases of MAPbI₃, and the calculated SOC-GW band gap. (a and b) Refer to the two considered cubic structures, see text for definitions. In parenthesis, we report the temperature at which the experimental band gap is evaluated

	Orthorhombic	Tetragonal	Cubic
Exp.	1.65 (4.2 K)	1.61 (160 K)	1.69 (330 K)
SOC-GW	1.81	1.67	1.16^a/1.28^b

---

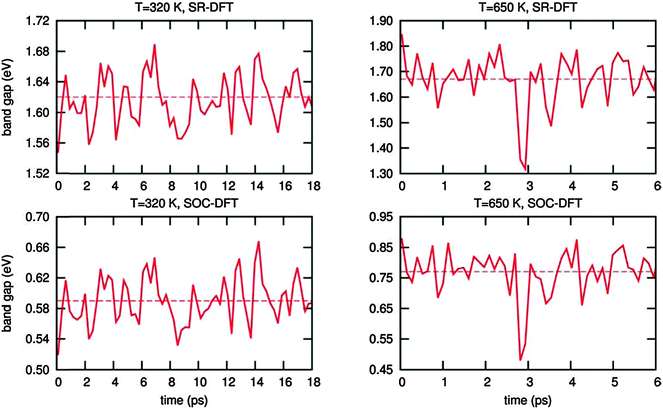
These results demonstrate that, in spite of the expected reliability of SOC-GW calculations, a static picture based on the optimized structures is not able to explain the experimental data for the tetragonal–cubic phase transition. In this sense, several results reported in the literature have questioned the presence of a highly symmetric cubic crystal structure in the high temperature phase of methylammonium lead halide perovskites. XRD studies by Mashiyama et al. pointed out that the Cl anions do not occupy exactly the cubic symmetry positions of MAPbCl₃ at high temperature;⁴⁵ Worhatch et al. observed large rotations of the PbBr₆ octahedra, for the high temperature cubic phase of MAPbBr₃, with the local material structure that can differ from the nominal a⁰a⁰a⁰ structure of Fig. 1;⁴⁶ Abid et al. observed a signal at 66 cm⁻¹ in the Raman spectrum of the high temperature phase of MAPbCl₃, that, due to symmetry reasons, should be silent.⁴⁷ Hybrid lead halide perovskites are well known to show important structural dynamics phenomena at room temperature, in particular, in relation to the rotational motion of the MA cations within the perovskite cubo-octahedral cavity.^20,21,48 To account for these effects on the material structure and consequently on the electronic properties, we performed Car–Parrinello molecular dynamics (CPMD)⁴⁹ simulations on models representative of the room temperature tetragonal phase and of the high temperature cubic phase. For both the tetragonal and cubic phases, we employed a 2 × 2 × 2 replica of the tetragonal crystallographic cell containing 4 MAPbI₃ units (thus a 32 MAPbI₃ system is simulated), using the experimental cell parameters reported by Poglitsch and Weber.²⁰ The employed 2 × 2 × 2 model cell, containing 384 atoms, provides reliable results for the structural properties of the MAPbI₃ perovskite,^43,50 as inferred by comparing the radial distribution function obtained from the theory to the experimental data⁵¹ (Fig. S5, ESI†). The tetragonal phase is simulated at an average temperature of 320 K, using the real atomic masses for all the atoms, except hydrogen which is replaced by deuterium, for a total time simulation of 18 ps, after a few ps of equilibration. The cubic phase is simulated starting from the same structure at an average temperature of 650 K and the total simulation time for the cubic structure is limited to 6 ps, after few ps of equilibration (for further details see the ESI†). First, we analyzed the averaged crystalline structure within the duration of the simulation. The time-averaged structures observed during the CPMD simulation are shown in Fig. 4a and b, respectively, for the 320 K and the 650 K simulations. For the simulation at 320 K, we observe the “out-of-phase” rotation of the PbI₆ octahedra rotation along the c-axis (see Fig. 4a), typical of the tetragonal structure of MAPbI₃.^19,44 For the simulation at 650 K instead, the time-averaged structure is essentially cubic, with only a small residual octahedra tilting, reasonably due to the constraint on the cell parameters, which were fixed to the experimental parameters of the tetragonal phase and are thus shorter with respect to the equilibrium cell parameters of the cubic phase. Thus, the 320 K structure and the 650 K on the ps time scale actually correspond to the nominal a⁰a⁰c⁻ and a⁰a⁰a⁰ structures experimentally evidenced from XRD measurements. The statistical analysis of the dihedral I–Pb–Pb–I angles confirms this result (see Fig. 4c and d). The 320 K structure shows a nearly symmetric distribution typical of the a⁰a⁰c⁻ tetragonal phase, with α maximum values at ±28°. The 650 K structure instead presents a nearly symmetric distribution centered around an α value of 0°. Most notably, the “cubic” structure can strongly deviate from the nominal a⁰a⁰a⁰ structure on a sub-ps time scale, with octahedra tilting values comparable to those observed for the tetragonal 320 K structure. Noteworthily, the probability for a dihedral I–Pb–Pb–I angle in the high temperature phase of being larger or smaller than ±10° is as much as 50%. Thus, locally and on a sub-ps time-scale, the structure is on average significantly distorted with respect to the nominally cubic a⁰a⁰a⁰ symmetry.

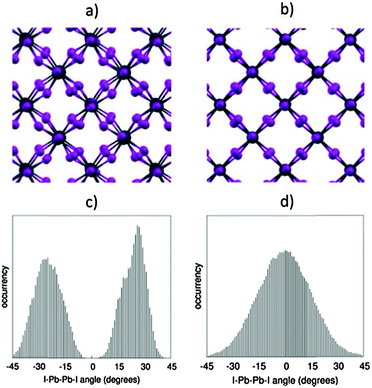Fig. 4 (a and b) Structure at 320 K and 650 K, averaged over the whole CPMD simulation time. (c and d) Distribution of the values assumed by all the I–Pb–Pb–I dihedral angles within the periodic cells, during the CPMD simulation, respectively, for the 320 K simulation (c) and for the 650 K (d). For a definition of the I–Pb–Pb–I dihedral angles, see Fig. 1.

Now, we investigate the effect of these sub-ps dynamical fluctuations on the electronic properties of MAPbI₃. First, we calculate the scalar-relativistic (SR) DFT and the SOC-DFT band-gap of the time-averaged structures. This is accomplished by averaging the atomic positions during the CPMD dynamics at each temperature, leading to the two structures (one for the high T and one for the low T) which are reported in Fig. 4a and b. As previously discussed, SR-DFT fortuitously reproduces the experimental band gap value found by more elaborate SOC-GW calculations,^36,42 while SOC-DFT considerably underestimates the band gap⁵² but it still provides qualitatively similar results to SOC-GW calculations.⁵³ The results are reported in Table 2. The small SOC-DFT band gap obtained for the time-averaged high temperature structure compares well with the data from ref. 37 (0.2 eV) and ref. 53 (0.16 eV). Similarly, for the low temperature time-averaged structure the calculated band-gap is consistent with previous data. We then computed the instantaneous band-gap fluctuations at 320 K and 650 K by explicitly calculating the band-gap of each structure encountered during the structural dynamics, thus considering the effects of the structural deformations on the electronic properties of MAPbI₃ inherently, see Fig. 5 and ESI.† For the dynamics at 320 K, the band-gap oscillates around an average value of 1.62/0.59 eV (SR-DFT/SOC-DFT), thus only slightly increasing with respect to the 1.50/0.40 eV (SR-DFT/SOC-DFT) band-gap computed on the time-averaged structure. At 650 K, the band gap oscillates at around 1.67/0.77 eV (SR-DFT/SOC-DFT), which is significantly larger than the band gap calculated on the time-averaged structure, 1.24/0.04 eV by SR-DFT/SOC-DFT. Most notably, a blue-shift of the band-gap across the tetragonal–cubic structure is observed, from 1.62 eV to 1.67 eV at the SR-DFT level (from 0.59 eV to 0.77 eV at the SOC-DFT level), which agrees quite well with the experimentally observed blue-shift, Table 2. As mentioned above, the present CPMD simulations do not consider the inherent variation of the crystalline cell parameters with temperature,³³ but still they partly recover than observed band-gap variation, pointing at the dynamics of the PbI₆ octahedra rotation across the phase transition as a source of the band-gap increase with increasing temperature.

Table 2 Theoretical band gap calculated on (i) the time-average structure from CPMD simulations and (ii) as the average of the band gap during the CPMD simulations. Band-gaps are evaluated both at the scalar-relativistic (SR-DFT) and at the spin-orbit-coupling (SOC-DFT) level of theory

T (K)	SR-DFT	SOC-DFT
	Band-gap of the time-averaged structure
320	1.50	0.40
650	1.24	0.04
	Average of the instantaneous band-gap
320	1.62	0.59
650	1.67	0.77

---

Fig. 5 Evolution of the band gap during the CPMD simulations for the system at 320 K and at 650 K, evaluated at the SR-DFT and SOC-DFT level of theory. The dashed line represents the band-gap average.

Our data clearly highlight the presence of large fluctuations in the PbI₆ octahedra tilting on a sub-picosecond timescale, which make the instantaneous band-gap and its average value to be distinctively wider than the band-gap predicted for the time-averaged structure, consistent with the experimental evidence. The time evolution of the valence and conduction band edges, whose difference determines the band-gap, seems to be relatively uncorrelated, see Fig. S5, ESI.† Notably, the valence band edge shows larger fluctuations around its average value, in line with the results of ref. 33 pointing at a variation of the valence band as an additional source of band-gap increase.

3. Conclusions

In summary, we have reported a combined experimental and theoretical investigation aimed at unraveling the possible electronic structure changes occurring for pristine MAPbI₃ and chlorine doped MAPbI_3−xCl_x perovskites across the tetragonal–cubic phase transition. Via temperature-resolved UV-vis absorption of bare films and spectral photocurrent response measurements of efficient solar cells, we have demonstrated that the band-gap does not show sharp variations across the tetragonal–cubic phase transition. We have also shown by ab initio molecular dynamics simulations that, within ∼10 ps time-scale, the material structure agrees very well with the tetragonal and cubic symmetry assigned from X-ray diffraction measurements,^19,20,44 while on a sub-picosecond time-scale, typical of the electronic processes probed by UV-vis spectroscopy, we observe that the high temperature phase is strongly distorted with respect to the cubic symmetry. When these instantaneous deviations from the nominal cubic crystalline structure are considered, the blue-shift of the band-gap observed experimentally is correctly reproduced by simulations. This large structural flexibility in the high temperature phase, not only related to the motions of the organic cations but also to fluctuations of the inorganic framework, may explain some literature results that criticized the presence of a rigorously cubic structure in the high temperature phase, as the presence of residual octahedral rotations in the high temperature phase of MAPbBr₃,⁴⁶ the disordered position of the Cl anions⁴⁵ and the presence of a Raman signal at 66 cm⁻¹ in the high temperature phase of MAPbCl₃.⁴⁷ From a technological perspective, these results help to explain the lack of an observable abrupt change in photovoltaic device performance above room temperature²³ as would be expected to be observable if the light-harvester undergoes a phase transition. This is also further evidence indicating that ferroelectricity contributions to the optoelectronic properties, as in traditional inorganic materials,^54–57 are negligible, since the ferroelectric polarizability is expected to change dramatically across the transition between two different crystalline structures. In contrast, this view supports other proposed mechanisms, as the spatial charge localization^50,58 and/or stable band bending effects at the interfaces and grain boundaries,⁵⁹ as the basis of the impressive inherent performance of hybrid lead halide perovskites.

Acknowledgements

The research leading to these results has received funds from the European Union Seventh Framework Programme [FP7/2007%2013] under Grant Agreement No. 604032 of the MESO project.

References

1. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131, 6050–6051.
2. J.-H. Im, C.-R. Lee, J.-W. Lee, S.-W. Park and N.-G. Park, 6.5% Efficient Perovskite Quantum-Dot-Sensitized Solar Cell, Nanoscale, 2011, 3, 4088–4093.
3. M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Efficient Hybrid Solar Cells Based on Meso-Superstructured Organometal Halide Perovskites, Science, 2012, 338, 463–467.
4. J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Graetzel, Sequential Deposition as a Route to High-Performance Perovskite-Sensitized Solar Cells, Nature, 2013, 499, 316–319.
5. M. Liu, M. B. Johnston and H. J. Snaith, Efficient Planar Heterojunction Perovskite Solar Cells by Vapour Deposition, Nature, 2013, 501, 395–398.
6. E. Edri, S. Kirmayer, D. Cahen and G. Hodes, High Open-Circuit Voltage Solar Cells Based on Organic–Inorganic Lead Bromide Perovskite, J. Phys. Chem. Lett., 2013, 4, 897–902.
7. J. M. Ball, M. M. Lee, A. Hey and H. J. Snaith, Low-temperature processed meso-superstructured to thin-film perovskite solar cells, Energy Environ. Sci., 2013, 6, 1739–1743.
8. O. Malinkiewicz, A. Yella, Y. H. Lee, G. M. Espallargas, M. Graetzel, M. K. Nazeeruddin and H. J. Bolink, Perovskite solar cells employing organic charge-transport layers, Nat. Photonics, 2014, 8, 128–132.
9. H. Zhou, Q. Chen, G. Li, S. Luo, T.-B. Song, H.-S. Duan, Z. Hong, J. You, Y. Liu and Y. Yang, Interface engineering of highly efficient perovskite solar cells, Science, 2014, 345, 542–546.
10. S. D. Stranks and H. J. Snaith, Metal-halkide perovskites for photovoltaic and light-emitting devices, Nat. Nanotechnol., 2015, 10, 391–402.
11. H. Zhu, Y. Fu, F. Meng, X. Wu, G. Zizhou, Q. Ding, M. V. Gustafsson, M. T. Trinh, S. Jin and X.-Y. Zhu, Lead halide perovskite nanowire lasers with low lasing threshold and high quality factors, Nat. Mater., 2015, 14, 636–643.
12. J. Luo, J.-H. Im, M. T. Mayer, M. Schreier, M. K. Nazeeruddin, N.-G. Park, S. David Tilley, H. J. Fan and M. Gratzel, Water photolysis at 12.3% efficiency via perovskite photovoltaics and earth-abundant catalysts, Science, 2014, 345, 1593–1596.
13. Y.-S. Chen, J. S. Manser and P. V. Kamat, All solution-processed lead halide perovskite-BiVO₄ tandem assembly for photolytic solar fuels production, J. Am. Chem. Soc., 2015, 137, 974–981.
14. E. Edri, S. Kirmayer, S. Mukhopadhyay, K. Gartsman, G. Hodes and D. Cahen, Elucidating the charge charrier separation and working mechanism of CH₃NH₃PbI_3−xCl_x perovskite solar cells, Nat. Commun., 2014, 5, 3461.
15. E. Edri, S. Kirmayer, A. Henning, S. Mukhopadhyay, K. Gartsman, Y. Rosenwaks, G. Hodes and D. Cahen, Why lead methylammonium tri-iodide perovskite-based colar cells require a mesoporous electron transporting scaffold (but not necessarily a hole conductor), Nano Lett., 2014, 14, 1000–1004.
16. S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber, Science, 2013, 234, 341–344.
17. G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Graetzel, S. Mhaisalkar and T. C. Sum, Long-Range Balanced Electronand Hole-Transport Lengths in Organic-Inorganic CH₃NH₃PbI₃, Science, 2013, 342, 344–347.
18. C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, High Charge Carrier Mobilities and Lifetimes in Organolead Trihalide Perovskites, Adv. Mater., 2014, 26, 1584–1589.
19. C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities and Near-Infrared Photoluminescent Properties, Inorg. Chem., 2013, 52, 9019–9038.
20. A. Poglitsch and D. Weber, Dynamic Disorder in Methylammoniumtrihalogenoplumbates (II) Observed by Millimeterwave Spectroscopy, J. Chem. Phys., 1987, 87, 6373–6378.
21. N. Onoda-Yamamuro, T. Matsuo and H. Suga, Calorimetric and IR spectroscopic studies of phase transitions in methylammonium trihalogenplumbates (II), J. Phys. Chem. Solids, 1990, 51, 1383–1395.
22. O. Knop, R. E. Wasylishen, M. A. White, T. S. Cameron and M. J. M. Van Voort, Alkylammonium lead halides. Part 2. CH₃NH₃PbX₃ (X = C1, Br, I) perovskites: cuboctahedral halide cages with isotropic cation reorientation1, Can. J. Chem., 1990, 68, 412–422.
23. H. Zhang, X. Qiao, Y. Shen, T. Moehl, S. M. Zakeeruddin, M. Gratzel and M. Wang, Photovoltaic behaviour of lead methylammonium triiodide perovskite solar cells down to 80 K, J. Mater. Chem. A, 2015, 3, 11762–11767.
24. V. D'Innocenzo, G. Grancini, M. J. P. Alcocer, A. R. S. Kandada, S. D. Stranks, M. M. Lee, G. Lanzani, H. J. Snaith and A. Petrozza, Excitons Versus Free Charges in Organo-Lead tri-Halide Perovskites, Nat. Commun., 2014, 5, 3586.
25. H. Mashiyama, Y. Kawamura, E. Magome and Y. Kubota, Displacive character of the cubic-tetragonal transition in CH₃NH₃PbIX₃, J. Korean Phys. Soc., 2003, 42, S1026–S1029.
26. A. M. Glazer, The classification of tilted octahedral in perovskites, Acta Crystallogr., 1972, B28, 3384–3392.
27. T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. Whitec, Synthesis and Crystal Chemistry of the Hybrid Perovskite (CH₃NH₃)PbI₃ for Solid-State Sensitised Solar Sell Applications, J. Mater. Chem. A, 2013, 1, 5628–5641.
28. M. T. Weller, O. J. Weber, P. F. Henry, A. Di Pumpo and T. C. Hansen, Complete structure and cation orientation in the perovskite photovoltaic methylammonium lead iodide between 100 and 352 K, Chem. Commun., 2015, 51, 4180–4183.
29. H.-H. Fang, R. Raissa, M. Abdu-Aguye, S. Adjokatse, G. R. Blake, J. Even and M. A. Loi, Photophysics of organic–inorganic hybrid lead iodide perovskite single crystals, Adv. Funct. Mater., 2015, 25, 2378–2385.
30. N. W. Ashcroft and N. D. Mermin, in Solid State Physics, ed. H. R. Winston, Holt Rinehart & Winston, 1976.
31. J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. v. Schilfgaarde and A. Walsh, Atomistic Origins of High-Performance in Hybrid Halide Perovskite Solar Cells, Nano Lett., 2014, 14, 2584–2590.
32. Y. P. Varshni, Temperature dependence of the energy gap in semiconductors, Physica, 1967, 34, 149–154.
33. B. J. Foley, D. L. Marlowe, K. Sun, W. A. Saidi, L. Scudiero, M. C. Gupta and J. J. Choi, Temperature dependent energy levels of methylammonium lead iodide perovskite, Appl. Phys. Lett., 2015, 106, 243904.
34. C. Tao, S. Neutzner, L. Colella, S. Marras, A. R. S. Kandada, M. Gandini, M. De Bastiani, G. Pace, L. Manna, M. Caironi, C. Bertarelli and A. Petrozza, 17.6% stabilized efficiency in low-temperature processed planar perovskite solar cells, Energy Environ. Sci., 2015, 8, 2365–2370.
35. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Coccioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a Modular and Open-Source Software Project for Quantum Simulations of Materials, J. Phys.: Condens. Matter, 2009, 21, 395502.
36. P. Umari, E. Mosconi and F. De Angelis, Relativistic GW Calculations on CH₃NH₃PbI₃ and CH₃NH₃SnI₃ Perovskites for Solar Cell Applications, Sci. Rep., 2014, 4, 4467.
37. F. Brivio, K. T. Butler, A. Walsh and M. van Schilfgaarde, Relativistic Quasiparticle Self-Consistent Electronic Structure of Hybrid Halide Perovskite Photovoltaic Absorbers, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155204.
38. G. Grancini, S. Marras, M. Prato, C. Giannini, C. Quarti, F. De Angelis, M. De Bastiani, G. E. Eperon, H. J. Snaith, L. Manna and A. Petrozza, The impact of the crystallization processes on the structural and optical properties of hybrid perovskite films for photovoltaics, J. Phys. Chem. Lett., 2014, 5, 3836–3842.
39. H. Yu, F. Wang, F. Xie, W. Li, J. Chen and N. Zhao, The role of chlorine in the formation process of “CH3NH3PbI_3−xCl_x perovskite, Adv. Funct. Mater., 2014, 24, 7102–7108.
40. S. Colella, E. Mosconi, P. Fedeli, A. Listorti, F. Gazza, F. Orlandi, P. Ferro, T. Besagni, A. Rizzo, G. Calestani, G. Gigli, F. De Angelis and R. Mosca, MAPbI_3−xCl_x Mixed Halide Perovskite for Hybrid Solar Cells: The Role of Chloride as Dopant on the Transport and Structural Properties, Chem. Mater., 2013, 25, 4613–4618.
41. S. Colella, E. Mosconi, G. Pellegrino, A. Alberti, V. L. P. Guerra, S. Masi, A. Listorti, A. Rizzo, G. G. Condorelli, F. De Angelis and G. Gigli, Elusive presence of chlorine in mixed halide perovskite solar cells, J. Phys. Chem. Lett., 2014, 5, 3532–3538.
42. E. Mosconi, A. Amat, M. K. Nazeeruddin, M. Graetzel and F. De Angelis, First-Principles Modeling of Mixed Halide Organometal Perovskites for Photovoltaic Applications, J. Phys. Chem. C, 2013, 117, 13902–13913.
43. C. Quarti, E. Mosconi and F. De Angelis, Interplay of Orientational Order and Electronic Structure in Methylammonium Lead Iodide: Implications for Solar Cells Operation, Chem. Mater., 2014, 26, 6557–6569.
44. Y. Kawamura, H. Mashiyama and K. Hasebe, Structural study on cubic-tetragonal transition of CH₃NH₃PbI₃, J. Phys. Soc. Jpn., 2002, 71, 1694–1697.
45. H. Mashiyama, Y. Kurihara and T. Azetsu, Disordered cubic perovskite structure of CH₃NH₃PbX₃ (X = Cl, Br, I), J. Korean Phys. Soc., 1998, 32, S156–S158.
46. R. J. Worhatch, H. J. Kim, I. P. Swainson, A. L. Yonkeu and S. J. L. Billinge, Study of local structure in selected organic–inorganic perovskite in the Pm3m phase, Chem. Mater., 2008, 20, 1272–1277.
47. A. Maalej, Y. Abid, A. Kallel, A. Daoud, A. Lautié and F. Romain, Phase transitions and crystal dynamics in the cubic perovskite CH₃NH₃PbCl₃, Solid State Commun., 1997, 103, 279–284.
48. R. E. Wasylishen, O. Knop and J. B. Macdonald, Cation rotation in methylammonium lead halides, Solid State Commun., 1985, 56, 581–582.
49. R. Car and M. Parrinello, Unified Approach for Molecular Dynamics and Density-Functional Theory, Phys. Rev. Lett., 1985, 55, 2471–2474.
50. C. Quarti, E. Mosconi and F. De Angelis, Structural and electronic properties of organo-halide hybrid perovskites from ab initio molecular dynamics, Phys. Chem. Chem. Phys., 2015, 17, 9394–9409.
51. J. J. Choi, X. Yang, Z. M. Norman, S. J. L. Billinge and J. S. Owen, Structure of Methylammonium Lead Iodide Within Mesoporous Titanium Dioxide: Active Material in High-Performance Perovskite Solar Cells, Nano Lett., 2013, 14, 127–133.
52. J. Even, L. Pedesseau, J.-M. Jancu and C. Katan, Importance of Spin–Orbit Coupling in Hybrid Organic/Inorganic Perovskites for Photovoltaic Applications, J. Phys. Chem. Lett., 2013, 4, 2999–3005.
53. A. Amat, E. Mosconi, E. Ronca, C. Quarti, P. Umari, M. K. Nazeeruddin, M. Grätzel and F. De Angelis, Cation-Induced Band-Gap Tuning in Organohalide Perovskites: Interplay of Spin–Orbit Coupling and Octahedra Tilting, Nano Lett., 2014, 14, 3608–3616.
54. Y. Yuan, X. Zhengguo, B. Yang and J. Huang, Arising applications of ferroelectric materials in photovoltaic devices, J. Mater. Chem. A, 2013, 2, 6027–6041.
55. S. Liu, F. Zheng, N. Z. Koocher, H. Takenaka, F. Wang and A. M. Rappe, Ferroelectric domain wall induced band gap reduction and charge separation in organometal halide perovskites, J. Phys. Chem. Lett., 2014, 6, 693–699.
56. A. Stroppa, C. Quarti, F. De Angelis and S. Picozzi, Ferroelectric polarization of CH3NH3PbI3: a detailed study based on density functional theory and symmetry mode analysis, J. Phys. Chem. Lett., 2015, 6, 2223–2231.
57. J. Beilstein-Edmands, G. E. Eperon, M. B. Johnston, H. J. Snaith and P. G. Radaelli, Non-ferroelectric nature of the conductance hysteresis in CH₃NH₃PbI₃ perovskite-based photovoltaic devices, Appl. Phys. Lett., 2015, 106, 173502.
58. J. Ma and L. W. Wang, Nanoscale charge localization induced by random orientations of organic molecules in hybrid perovskite CH₃NH₃PbI₃, Nano Lett., 2015, 15, 248–253.
59. A. Dymshits, A. Henning, G. Segev, Y. Rosenwaks and L. Etgar, The electronic structure of metal oxide/organo metal halide perovskite junctions in perovskite based solar cells, Sci. Rep., 2015, 5, 8704.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental methods; theoretical methods and models; EQE measurements on different MAPbI3 devices; corresponding JV measurements of the devices; EQE of a cell with MAPbI_3−xCl_x; comparison between theoretical and experimental radial distribution function of the MAPbI₃ perovskite; theoretical fluctuation of the band edges. See DOI: 10.1039/c5ee02925b

---