Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Relationships between elastic anisotropy and thermal expansion in A2Mo3O12 materials†
Carl P.
Romao
a,
S. P.
Donegan
bc,
J. W.
Zwanziger
ade and
Mary Anne
White
*ade
aDepartment of Chemistry, Dalhousie University, Halifax, Nova Scotia B3H 4R2, Canada. E-mail: mary.anne.white@dal.ca; Tel: +1-902-494-3894
bDepartment of Materials Science and Engineering, Carnegie Mellon University, Pittsburgh, PA 15213-3890, USA
cBlueQuartz Software, 400 S Pioneer Blvd, Springboro, OH 45066, USA
dInstitute for Research in Materials, Dalhousie University, Halifax, Nova Scotia B3H 4R2, Canada
eDepartment of Physics and Atmospheric Science, Dalhousie University, Halifax, Nova Scotia B3H 4R2, Canada
First published on 24th October 2016
Abstract
We report calculated elastic tensors, axial Grüneisen parameters, and thermal stress distributions in Al2Mo3O12, ZrMgMo3O12, Sc2Mo3O12, and Y2Mo3O12, a series of isomorphic materials for which the coefficients of thermal expansion range from low-positive to negative. Thermal stress in polycrystalline materials arises from interactions between thermal expansion and mechanical properties, and both can be highly anisotropic. Thermal expansion anisotropy was found to be correlated with elastic anisotropy: axes with negative thermal expansion were less compliant. Calculations of axial Grüneisen parameters revealed that the thermal expansion anisotropy in these materials is in part due to the Poisson effect. Models of thermal stress due to thermal expansion anisotropy in polycrystals following cooling showed thermal stresses of sufficient magnitude to cause microcracking in all cases. The thermal expansion anisotropy was found to couple to elastic anisotropy, decreasing the bulk coefficient of thermal expansion and leading to lognormal extremes of the thermal stress distributions.
Introduction
Materials with the general formula A2M3O12, where A is a trivalent cation and M is W or Mo, have the unusual property of linear coefficients of thermal expansion spanning the range from low positive (2.4 × 10−6 K−1) to negative (−9 × 10−6 K−1), including zero.1–5 Their structures have considerable chemical flexibility, as solid solutions can be made incorporating cations with large differences in size (e.g., Al3+ and Y3+).3 Aliovalent substitutions of Zr4+ or Hf4+ with Mg2+ for A3+ can be performed, offering additional possibilities for the tailoring of physical properties within this family.5–8 The structures of these materials are composed of vertex-linked networks of AO6 octahedra and MO4 tetrahedra;9–11 negative contributions to thermal expansion arise from transverse motions of bridging oxygen atoms accompanied by distortion of the AO6 octahedra.9,12 Negative thermal expansion (NTE) has been correlated with the compliance of the A–O ionic bond, and the subsequent distortability of the AO6 octahedra.5,9,12 The open-framework structure allows for unusual thermal expansion and chemical flexibility,4,12,13 and it typically leads to low stiffness in comparison to other oxide ceramics.5,14–17The thermal expansion of materials from the A2M3O12 family is known to be highly anisotropic.15,18 Such anisotropy can cause large thermal stresses and subsequent microcracks in polycrystalline materials with randomly oriented grains.19,20 However, the elastic anisotropy of these materials is generally unknown; furthermore, it is more difficult to determine experimentally than the anisotropy of the coefficient of thermal expansion (CTE). Critically, the mechanical properties determine the ability of thermomiotic (negative thermal expansion)15 materials to counteract positive thermal expansion15,21 and affect the stress distributions in polycrystalline A2M3O12 materials.15 Therefore, the elastic tensors of Al2Mo3O12, Sc2Mo3O12, and ZrMgMo3O12 have been calculated and reported herein. Together with that of Y2Mo3O12 (reported previously),16 we now have elastic constants of an isomorphic family of materials ranging from low positive to large negative thermal expansion.
The study of the anisotropy of the elastic properties of these materials generally has previously been limited to determination of bulk moduli by variable-pressure XRD; the exception is Y2Mo3O12.16 The variable-pressure XRD experiment can yield information about directional compressibilities; for example in Sc2W3O1217 and Sc2Mo3O1214 the compressibility along an axis was shown to be positively correlated with the thermal expansion along that axis. However, this technique has limitations; for example the compressibilities in orthorhombic Al2W3O12 could not be accurately determined due to a pressure-induced phase transition,14 and no information about shear elasticity was obtained. The use of ultrasonic measurement to obtain shear moduli of bulk polycrystalline samples5,16,21 contributes some additional information, but experimental determination of the full elastic tensor would require single crystals for Brillouin spectroscopy or resonant ultrasound spectroscopy.
Therefore, for practical reasons, computational methods are the best choice to study the full elastic anisotropy of A2M3O12 materials, and this is the approach taken herein. There is an associated drawback: the DFT calculations are performed for T = 0 K. Since A2Mo3O12 materials (except Y2Mo3O12) transition to a monoclinic phase upon cooling, the calculations were performed on a phase which is not stable at absolute zero. Therefore the phononic structures contain vibrational modes with negative energy that destabilize the orthorhombic structure.22–24 However, since the orthorhombic–monoclinic phase transition involves rotation of the coordination polyhedra,2 the unstable mode is located away from the Γ point of the Brillouin zone25,26 and the instability is not caused by negative terms in the elastic stiffness tensor.27 Additionally, because many thermomiotic materials have highly temperature-dependent bulk moduli,18,28–30 DFT results will not necessarily match room-temperature elastic constants, but our approach is validated by comparison with experimental behaviour at room temperature.
The energies of the optic phonons at the Γ point were also calculated using DFT. Calculation of the full dispersion relationship would be computationally expensive, however with the large unit cell of the orthorhombic A2M3O12 materials (68 atoms)1,5 there is little dispersion.16,18 Low-energy optic phonon modes in A2M3O12 materials corresponding to polyhedral distortions can have large negative Grüneisen parameters,31,32 and therefore their energies play an important role in the thermal expansion behaviour. Determination of optic phonon frequencies also allows further validation of the calculations by comparison to experimental Raman spectra.
Methods
DFT calculations were carried out using the ABINIT33 code in order to determine the elastic tensors and Γ-point phonon energy of A2M3O12 and AMgM3O12 materials. Computation of elastic tensors and Γ-point phonon energies were performed using the ACENET34 and WestGrid35 clusters, taking advantage of the massive parallelization functionality of ABINIT.36 ABINIT composes wavefunctions as linear combinations of a plane wave basis set and performs calculations in reciprocal space.37,38 Calculations of elastic tensors and phonon frequencies were performed using the response-function capability of ABINIT.39–41 Phonon frequencies were corrected for errors due to finite sampling on the effective charges by imposition of the acoustic sum rule (i.e., requiring that the frequencies of the acoustic branches are zero at Γ).39The CIF2Cell program42,43 was used to create input files from published crystal structure data.5,44,45 PBE GGA exchange–correlation functionals were used in all cases.46 In the cases of Al2Mo3O12 and Sc2Mo3O12, norm-conserving47 pseudopotentials generated using the OPIUM code47–50 from the Bennet and Rappe pseudopotential library51 were used. For ZrMgMo3O12, two-projector optimized norm-conserving Vanderbilt pseudopotentials52 were used. These pseudopotentials were tested by comparison of calculated bulk moduli to experimental values for MgO (−7.2% deviation),53 ZrO2 (−1.6% deviation),54 and Mo (−3.4% deviation),‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 yielding reasonable results.56 The plane wave cut-off energy and k-point grid spacing were determined by convergence studies (Table 1); the criterion used was convergence of the internal pressure to within 1%. A k-point grid spacing smaller than 0.04 Å−1 was used in all cases. The structures were relaxed until the remaining pressure was less than 1 MPa. Changes in the unit cell axis lengths following relaxation are shown in Table 1.
55 yielding reasonable results.56 The plane wave cut-off energy and k-point grid spacing were determined by convergence studies (Table 1); the criterion used was convergence of the internal pressure to within 1%. A k-point grid spacing smaller than 0.04 Å−1 was used in all cases. The structures were relaxed until the remaining pressure was less than 1 MPa. Changes in the unit cell axis lengths following relaxation are shown in Table 1.
| Material | Plane wave cut-off energy/Hartree | k-Point grid dimensions | Change in a relative to experiment/% | Change in b relative to experiment/% | Change in c relative to experiment/% |
|---|---|---|---|---|---|
| Al2Mo3O12 | 30 | 2 × 2 × 2 | 2.2 | 1.7 | 2.0 |
| ZrMgMo3O12 | 35 | 2 × 3 × 3 | 3.0 | 2.1 | 2.0 |
| Sc2Mo3O12 | 35 | 2 × 3 × 3 | 3.0 | 2.1 | 2.1 |
The elastic and CTE tensors of Al2Mo3O12, ZrMgMo3O12, and Sc2Mo3O12 (reported herein) and Y2Mo3O12 (from published studies)16 were used to create models of thermal stress in polycrystals of random texture, following a drop in temperature of 700 K, using the teFFT algorithm described in ref. 57. The teFFT algorithm simulates the elastic response to a change in temperature using a fast Fourier transform (FFT) approach to iteratively solve the constituent equations of thermoelasticity.57,58 Since this method is only computationally limited by the speed of the FFT, simulations should scale with order n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n, where n is the number of nodes used in the model. Additionally, the spectral approach to solving the constituent equations of thermoelasticity only requires a structured rectilinear grid or image as an input, called the Fourier grid, forgoing the need for meshing.57 These aspects resulted in considerable computational time savings by comparison to finite-element methods, allowing much larger models to be studied. The microstructure models used were generated in DREAM.3D59 and consisted of 1190 randomly oriented, equiaxial grains on a 2563 Fourier grid. A section of a modeled microstructure is shown in Fig. 1. Since the spectral approach requires periodic boundary conditions for the model, in the thermoelastic models polycrystalline structures were embedded in a compliant buffer layer. The buffer layer represents a region of infinite elastic compliance, which is created by setting the stress values to zero, and is meant to approximate material surfaces.55 The usage of buffer layers ensures that the effect of elastic anisotropy on the volume thermal expansion could be determined.
n, where n is the number of nodes used in the model. Additionally, the spectral approach to solving the constituent equations of thermoelasticity only requires a structured rectilinear grid or image as an input, called the Fourier grid, forgoing the need for meshing.57 These aspects resulted in considerable computational time savings by comparison to finite-element methods, allowing much larger models to be studied. The microstructure models used were generated in DREAM.3D59 and consisted of 1190 randomly oriented, equiaxial grains on a 2563 Fourier grid. A section of a modeled microstructure is shown in Fig. 1. Since the spectral approach requires periodic boundary conditions for the model, in the thermoelastic models polycrystalline structures were embedded in a compliant buffer layer. The buffer layer represents a region of infinite elastic compliance, which is created by setting the stress values to zero, and is meant to approximate material surfaces.55 The usage of buffer layers ensures that the effect of elastic anisotropy on the volume thermal expansion could be determined.
Relationships between the software packages and computational methods used in this work are shown graphically as a flowchart in the ESI.†
Results and discussion
Elasticity
The calculated elastic stiffness tensor (c) of orthorhombic Al2Mo3O12 (Pbcn setting) is given by: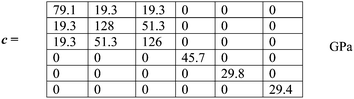 | (1) |
 | (2) |
| Young's modulus/GPa | Shear modulus/GPa | Compressibility/GPa−1 | Poisson ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Y aa | 74.8 | G bc | 45.7 | β aa | 1.05 × 10−2 | μ bc | 0.38 | μ cb | 0.38 |
| Y bb | 105 | G ac | 29.8 | β bb | 4.43 × 10−3 | μ ac | 0.11 | μ ca | 0.15 |
| Y cc | 104 | G ab | 29.4 | β cc | 4.52 × 10−3 | μ ab | 0.11 | μ ba | 0.15 |
Al2Mo3O12 showed elastic anisotropy similar to that of its thermal expansion, with only a small difference between the b- and c-axes. The overall elastic anisotropy of Al2Mo3O12, expressed as the universal anisotropy parameter,61AU, is equal to 1.9. By comparison. Y2Mo3O12 has AU = 3.9.16 Unlike in the case of Y2Mo3O12,16 the axial Young's moduli and directional compressibilities followed the expected trends and were inversely proportional to each other. The Voight–Reuss–Hill (VRH) values62 for the bulk elastic constants of Al2Mo3O12 were determined to be K = 35.3 GPa and G = 36.2 GPa. These stiffnesses are ca. double those determined experimentally for monoclinic Al2Mo3O12 (K = 13.5 ± 1.3 GPa, G = 18.2 ± 0.7 GPa).63 A similar discrepancy was seen in the case of Y2Mo3O12,16 obscuring whether the difference is due to temperature dependence of the elastic constants or the difference between the monoclinic and orthorhombic phases.
The calculated elastic stiffness tensor of orthorhombic ZrMgMo3O12 (P21nb setting) is given by:
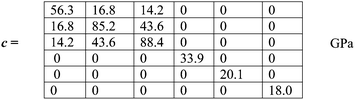 | (3) |
 | (4) |
| Young's modulus/GPa | Shear modulus/GPa | Compressibility/GPa−1 | Poisson ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Y aa | 52.5 | G bc | 33.9 | β aa | 1.45 × 10−2 | μ bc | 0.46 | μ cb | 0.49 |
| Y bb | 61.9 | G ac | 20.1 | β bb | 5.72 × 10−3 | μ ac | 0.11 | μ ca | 0.08 |
| Y cc | 65.6 | G ab | 18.0 | β cc | 6.16 × 10−3 | μ ab | 0.18 | μ ba | 0.15 |
As for Al2Mo3O12, ZrMgMo3O12 shows increased stiffness along its thermomiotic axes both in terms of Young's modulus and compressibility. The stiffnesses of the b- and c-axes were similar even though their CTEs are quite different in magnitude. The overall elastic anisotropy of ZrMgMo3O12 was very similar to that of Al2Mo3O12; both have AU = 1.9. The VRH bulk and shear moduli were 26.5 GPa and 23.8 GPa, respectively. These values are close to those obtained experimentally (K = 31 ± 3 GPa, G = 22 ± 1 GPa).5
The calculated elastic stiffness tensor of orthorhombic Sc2Mo3O12 (Pbcn setting) is given by:
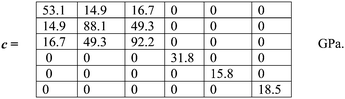 | (5) |
 | (6) |
| Young's modulus/GPa | Shear modulus/GPa | Compressibility/GPa−1 | Poisson ratio | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Y aa | 49.5 | G bc | 31.8 | β aa | 1.57 × 10−2 | μ bc | 0.51 | μ cb | 0.53 |
| Y bb | 60.9 | G ac | 15.8 | β bb | 6.00 × 10−3 | μ ac | 0.13 | μ ca | 0.16 |
| Y cc | 63.1 | G ab | 18.5 | β cc | 4.80 × 10−3 | μ ab | 0.10 | μ ba | 0.12 |
The elastic anisotropy of Sc2Mo3O12 (AU = 2.9) was larger than that of Al2Mo3O12 and ZrMgMo3O12, which could be expected given its larger CTE anisotropy. The VRH values for the bulk and shear moduli were K = 24.0 GPa and G = 22.3 GPa; unlike in the cases of Al2Mo3O12 and Y2Mo3O1216 the calculated bulk modulus of Sc2Mo3O12 is significantly less than the experimental value (K = 32 ± 2 GPa from variable-pressure XRD).14
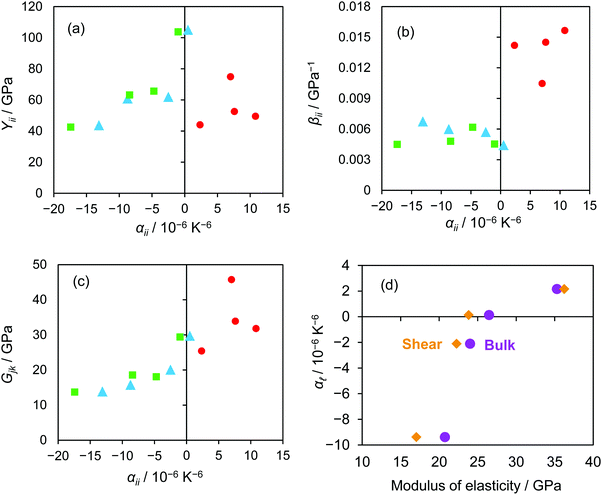
Correlations of axial elastic properties with axial thermal expansion, axial Young's moduli (Yii), axial compressibilities (βii), and directional shear moduli (Gjk) are visualized in Fig. 2 as functions of the axial CTEs (αii)2,5,60 for the three materials described above and Y2Mo3O12.3,16 The elastic behaviours of the thermomiotic b- and c-axes are correlated with their axial CTEs, while such a correlation is not seen for the a-axis. The b- and c-axes are stiffer than the a-axis except in the case of Y2Mo3O12, where the a-axis has a higher Young's modulus but also higher compressibility. Stiffer thermomiotic axes could decrease the bulk CTE of a polycrystal, as the increased stiffness would yield a larger contribution to the bulk expansion. As described below, this effect can be predicted in some cases. The trends in the VRH-averaged isotropic moduli (Fig. 2(d)) are more pronounced than those in the axial stiffnesses. A decrease in overall stiffness with increasingly negative thermal expansion can be seen clearly. When a thermomiotic material is used to counteract positive thermal expansion, its stiffness can be as important as its CTE in determining the amount of CTE reduction achieved,15,20,21,63 and therefore the negative correlation between stiffness and CTE might act to discourage the use of materials such as Y2Mo3O12 in applications. The trend relating the elastic moduli to the CTE is very similar to the previously reported correlation between the A site ionic force and the CTE,5 suggesting that polyhedral distortability is a common factor between thermal expansion and elastic properties in this group of materials.
The materials studied show significantly different behaviour when subjected to different stress conditions. The b- and c-axes show a decrease in uniaxial stiffness (Fig. 2(a)) with increasingly negative thermal expansion. However, when subjected to isotropic pressure (Fig. 2(b)), less variation in the stiffness is seen. These differences illustrate the importance of computational studies of the full elastic tensor, as only βii can be obtained from experimental variable-pressure XRD measurements on polycrystalline samples. The directional shear moduli generally show increased stiffness for G23 by comparison with G13 and G12, which is consistent with the increased stiffness of the b- and c-axes compared to the a-axis. This trend leads to the shear modulus in a plane (Gjk) increasing with the thermal expansion of the axis perpendicular to the plane (αii).
The anisotropic Young's moduli of Al2Mo3O12, ZrMgMo3O12, Sc2Mo3O12, and Y2Mo3O1216 are compared in all directions in Fig. 3. The overall trend of decreased overall stiffness with decreased CTE can be seen clearly, as can variations in the elastic anisotropy. In the case of Al2Mo3O12, the predominant feature is the increased stiffness of the thermomiotic bc-plane relative to the a-axis. However, as the thermal expansion of the material becomes more negative, the stiffness of the bc-plane decreases more dramatically than that along the a-axis. Additionally, the stiffness within the bc-plane becomes more anisotropic, with the [011] and [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1] directions becoming considerably stiffer than [010] and [001]. This results in the relatively large values of G23 and discrepancies between Yii and βii seen in Fig. 2 and the indentations along [010] and [001] seen in Fig. 3.
1] directions becoming considerably stiffer than [010] and [001]. This results in the relatively large values of G23 and discrepancies between Yii and βii seen in Fig. 2 and the indentations along [010] and [001] seen in Fig. 3.
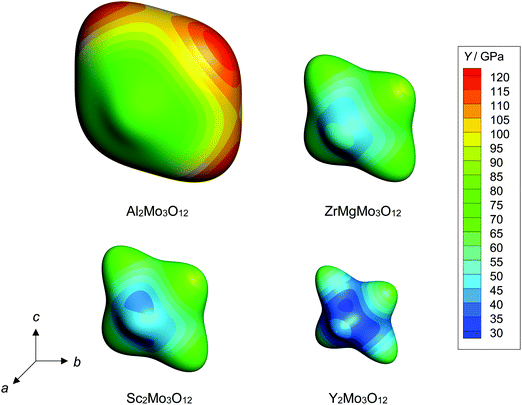 | ||
| Fig. 3 Directional Young's moduli of orthorhombic Al2Mo3O12, ZrMgMo3O12, Sc2Mo3O12, and Y2Mo3O1216 in the Pbcn or P21nb setting, shown as contour plots generated using the nanoHUB Anisotropy Calculator – 3D Visualization Toolkit.64 | ||
Phonon frequencies
The Γ-point optic phonon frequencies calculated in ABINIT are presented in tabular form in the ESI,† and visually in Fig. 4 (along with the previously reported16 phonon spectrum of Y2Mo3O12). Fig. 4 shows the common features of the phonon spectra of the four materials studied: a band of low-energy librational, translational, and bending modes separated from stretching modes with higher energy, with asymmetric stretches at lower energies than symmetric stretches.65,66 As discussed in ref. 5, ZrMgMo3O12 has a larger spread of stretching mode energies due to the splitting of the A site into a Zr site and Mg site, but otherwise its Γ-point phonon spectrum is similar to that of the A2Mo3O12 materials. The energies of the low-energy phonons can be compared more easily in Fig. 4, which shows the cumulative distribution function of the modes below 500 cm−1. The phonons below ca. 200 cm−1 are expected to have negative mode Grüneisen parameters and contribute to NTE, while those of higher energies are expected to have positive or near-zero Grüneisen parameters.31,32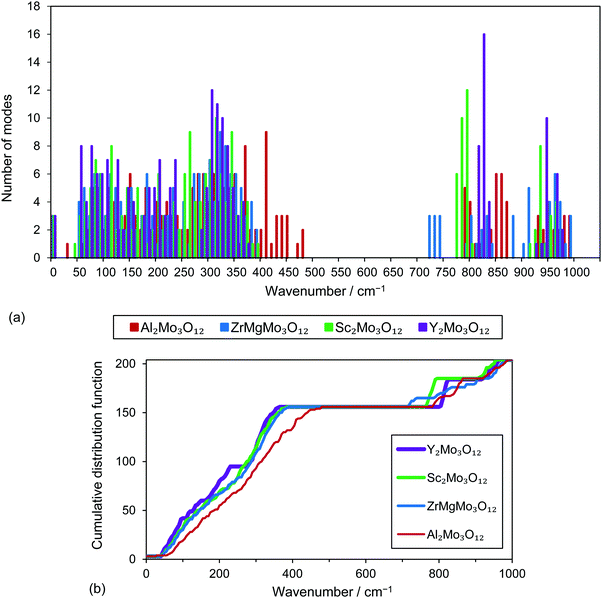 | ||
| Fig. 4 (a) Calculated Γ-point phonon frequencies of A2Mo3O12 materials (including Y2Mo3O12)16 and ZrMgMo3O12, shown as a histogram with 10 cm−1 bin size. (b) Phonon frequencies shown as the cumulative number of modes with an energy less than or equal to a given wavenumber. | ||
Fig. 4 shows that Y2Mo3O12 has significantly more modes with energies below 200 cm−1 and has generally lower phonon energies in this region, which is consistent with its observed NTE over a wide temperature range.4,9 Conversely, Al2Mo3O12 has considerably fewer modes below 200 cm−1, with a much broader distribution of its phonon frequencies in the region below 500 cm−1. Of particular interest is a mode at 26 cm−1 in Al2Mo3O12 which is anomalously low in energy by comparison to the other translational and librational modes in this material. At some point in the Brillouin zone, this mode could be the soft mode with negative frequency that causes the orthorhombic–monoclinic phase transition. The mode distributions for Sc2Mo3O12 and ZrMgMo3O12 are very similar, especially in the region below 200 cm−1. Sc2Mo3O12 has a negative CTE while ZrMgMo3O12 displays ca. zero thermal expansion, implying that the mode Grüneisen parameters of Sc2Mo3O12 are more negative.
The calculated Γ-point phonon frequencies of Al2Mo3O12 and ZrMgMo3O12 are compared to experimental Raman spectra (measured at room temperature) in the ESI.† Overall, the results of this comparison, in addition to the comparison of experimental elastic moduli to calculated values presented above, show that the calculated elastic and phononic properties of these materials, while not quantitatively accurate, show reasonable agreement with the experimental data.
Axial Grüneisen parameters
The axial coefficients of thermal expansion are determined by the anharmonicity of the interatomic potentials, as expressed through Grüneisen parameters, and by the stiffness tensor, which represents the resistance of the lattice to thermal deformation. The present computational analysis does not allow the axial Grüneisen parameters (γii) to be determined directly, but using the calculated anisotropic elastic constants and phonon energies and the experimental CTE tensor the following expression can be invoked:67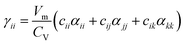 | (7) |
| Material | γ aa | γ bb | γ cc |
|---|---|---|---|
| Al2Mo3O12 | 0.24 | 0.07 | 0.02 |
| ZrMgMo3O12 | 0.18 | −0.16 | −0.23 |
| Sc2Mo3O12 | 0.17 | −0.58 | −0.58 |
| Y2Mo3O12 | −0.35 | −1.11 | −1.20 |
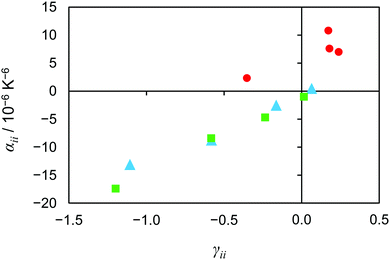
Thermal expansion along the b- and c-axes strongly correlates with the Grüneisen parameter along that axis, suggesting that vibrational modes with negative Grüneisen parameters along those axes are responsible for NTE. Essentially, this high degree of correlation is because the cijαjj and cikαkk terms in eqn (7) have opposite signs and nearly cancel. These terms are due to the Poisson effect, where a strain (in this case, thermally induced) along one axis causes a corresponding strain along the axes perpendicular to it.69 As shown in Tables 2–4, some of the axial Poisson ratios in these materials are quite large, close to the theoretical limit of 0.5 for stable isotropic materials.70 However, NTE along the b- and c-axes increases the CTE along the a-axis due to the Poisson effect. The positive thermal expansion along the a-axis in Y2Mo3O12 is caused entirely by this effect, as γaa is negative. Similarly, the increase in thermal expansion along the a-axis in Sc2Mo3O12 relative to ZrMgMo3O12 and Al2Mo3O12 is due to its larger NTE along the b- and c-axes, as all three materials have similar values of γaa. Therefore, the Poisson effect is responsible for some of the thermal expansion anisotropy which causes microcracking in sintered bodies of A2M3O12 materials.19,20
Thermal stress
Models of thermal stress due to thermal expansion anisotropy showed significant thermal stress in all four modeled materials. Thermal stress extrema reached hundreds of MPa, sufficient to cause significant microcracking, as seen experimentally in Al2Mo3O12 and Al2W3O12.19,20 The thermomiotic b- and c-axes are, on average, placed in tension while the a-axis is in compression due to thermal expansion mismatch. The net stress on the material is zero, as the boundaries are unconstrained. An example cross section of the thermal stress distribution in Y2Mo3O12 can be seen in Fig. 6. The stress extrema are found at grain boundaries where several misaligned grains meet, and can be expected to cause intergranular microcracking.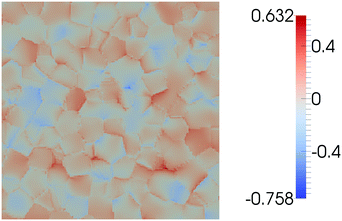 | ||
| Fig. 6 Thermal stress (GPa) in the out-of-plane direction in a modelled Y2Mo3O12 polycrystal following cooling by 700 K. | ||
The effect of elastic anisotropy on the thermal stress distributions can be quantified by comparison to Kreher's model for elastically isotropic polycrystals.71,72 Anisotropic models have lower mean strain energy densities, 〈W〉, as shown in Table 6, indicating that elastic anisotropy acts to decrease thermal stress. In the elastically isotropic case, the average strain in the material is required to be equal to the thermal strain by the (unconstrained) boundary conditions and the conditions of static equilibrium.71,72 When the coupling of elastic anisotropy and thermal expansion anisotropy is included, the thermal expansion of the stiffer axes is slightly more expressed than that of the more compliant axes, which allows some relaxation of the thermal stress. This effect is seen in consolidated polycrystals as deviations from the intrinsic linear CTE (Δα![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ), shown in Table 6. While Δα
), shown in Table 6. While Δα![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is small in comparison to the bulk CTEs of Al2Mo3O12 and Y2Mo3O12, for ZrMgMo3O12 and Sc2Mo3O12 the deviation is of similar magnitude to the intrinsic CTE. Therefore, elastic anisotropy could explain the relatively large differences observed in dilatometric results compared with the intrinsic CTE (e.g. from XRD) for these materials.2,5
is small in comparison to the bulk CTEs of Al2Mo3O12 and Y2Mo3O12, for ZrMgMo3O12 and Sc2Mo3O12 the deviation is of similar magnitude to the intrinsic CTE. Therefore, elastic anisotropy could explain the relatively large differences observed in dilatometric results compared with the intrinsic CTE (e.g. from XRD) for these materials.2,5
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 0) by Kreher's method,71,72 and the present models
= 0) by Kreher's method,71,72 and the present models
| Material | Elastic isotropy | Present models | ||
|---|---|---|---|---|
| 〈W〉/kJ m−3 | 〈W〉/kJ m−3 | Δα![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /10−7 K−1 /10−7 K−1 |
|Δα![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /α /α![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) |/% |/% |
|
| Al2Mo3O12 | 311 | 222 | −2.5 | 10 |
| ZrMgMo3O12 | 493 | 386 | −3.5 | 219 |
| Sc2Mo3O12 | 1338 | 1073 | −11 | 52 |
| Y2Mo3O12 | 837 | 659 | −1.3 | 1 |
The stress distributions within the polycrystals were fit to statistical distributions as described in the ESI.† The distributions in the different materials are generally similar, and using two lognormal distributions for the stress along each axis provides excellent fits to the data (see Fig. S4–S11, ESI†). As the size of the A site cation increases from Al3+ to Y3+, increasing thermal expansion anisotropy is accompanied by decreasing stiffness (vide supra). These two factors have opposite effects on the magnitude of the thermal stresses, resulting in similar stress distributions and extrema. This similarity indicates that it will prove difficult to use chemical control of the A site cation to reduce thermal stress due to thermal expansion anisotropy. When the thermal stresses are sufficiently large to cause microcracking, a further deviation from the intrinsic CTE can be found at elevated temperatures due to crack growth and healing causing expansion and shrinkage, respectively, of the polycrystalline body.19,20
In all cases, the two lognormal distributions in each fit had opposite signs for their prefactors, leading to positive and negative stress extrema each being fit by a single unbounded lognormal tail. The utility of the lognormal distribution in fitting the extreme stresses is likely connected to some underlying physical phenomenon. The lognormal distribution is known to arise as a result of multiplication of a series of random variables, whereas the normal distribution arises from summation of a series of random variables.73 Therefore, the lognormal fit to the stress distribution implies some multiplicative character to their origin. In anisotropic polycrystalline materials, thermal expansion mismatches cause strains in the material, and consequently reaction forces and stresses. In elastically isotropic materials, the interactions of reaction forces throughout the material are isotropic. This isotropy results in the stresses at any point being related to the strains caused by thermal expansion anisotropy throughout the remainder of material additively, and the normal thermal stress distribution is a logical result. However, in a material where the elastic constants are anisotropic, the transfer of stresses through the material is not so simple. The elastic anisotropy leads to the grains reacting differently to the applied strains based on their orientations, with increased stress in stiffer directions and vice versa. Therefore, elastic anisotropy introduces a multiplicative factor into the thermal stress distributions, since the relationship between the stress at a point and the strain at another point is modified by the variations in the stiffness tensor.
Conclusions
Materials in the A2Mo3O12 and AMgMo3O12 families were shown to have significant elastic anisotropy, a finding consistent with their characteristically large CTE anisotropy. The thermomiotic axes of these materials were shown to be stiffer than the PTE axes, which could act to decrease their bulk CTEs. However, the stiffness along the thermomiotic axes decreases with increasingly negative thermal expansion. The stiffness along the PTE axes did not strongly correlate with their CTEs. However, Al2Mo3O12, ZrMgMo3O12, and Sc2Mo3O12 were shown to have similar axial Grüneisen parameters along their PTE axes, with differences in thermal expansion being driven by elastic factors. Calculated Γ-point optic phonon frequencies showed differences between the materials in the low-energy region which correlate with their thermal expansion behaviour, and the optic phonon data compared to experimental Raman spectra validated the results.The thermal stress distributions calculated herein show that thermal expansion anisotropy can cause large thermal stresses in A2M3O12 materials, enough to cause significant microcracking upon heating and cooling. The distributions of the thermal stresses are affected by the properties of the CTE and elastic tensors. The results indicate that the stress distributions in the four members of the A2Mo3O12 family studied are quite similar. In both cases, maximum tensile and compressive thermal stresses on the order of 0.5 GPa can be expected, with positive and negative extrema being well-described by lognormal distributions. The elastic tensors were found to couple with the thermal expansion tensors to produce small deviations in the bulk CTE, which were large by comparison to the intrinsic CTE in the cases of ZrMgMo3O12 and Sc2Mo3O12.
Acknowledgements
We are grateful to NSERC Canada, the U.S. Army Research Office, and the Walter C. Sumner Foundation for support of this work. Portions of this work were supported by Grant No. DE-FE0003840 from the Department of Energy as part of the University Coal Research Program. Computational facilities were provided by ACENET, the regional high-performance computing consortium for universities in Atlantic Canada. ACENET is funded by the Canada Foundation for Innovation (CFI), the Atlantic Canada Opportunities Agency (ACOA), and the provinces of Newfoundland and Labrador, Nova Scotia, and New Brunswick. This research was enabled in part by support provided by WestGrid (http://www.westgrid.ca) and Compute Canada Calcul Canada (http://www.computecanada.ca). The authors are grateful to Dr Ben Anglin and Ricardo Lebensohn for extensive discussions and development of the FFT simulation code, and also thank Prof. Anthony Rollett for his insights and guidance.References
- J. S. O. Evans, T. A. Mary and A. W. Sleight, J. Solid State Chem., 1998, 137, 148–160 CrossRef CAS.
- J. S. O. Evans and T. A. Mary, Int. J. Inorg. Mater., 2000, 2, 143–151 CrossRef CAS.
- T. A. Mary and A. W. Sleight, J. Mater. Res., 1999, 14, 912–915 CrossRef CAS.
- B. A. Marinkovic, P. M. Jardim, R. R. de Avillez and F. Rizzo, Solid State Sci., 2005, 7, 1377–1383 CrossRef CAS.
- C. P. Romao, F. A. Perras, U. Werner-Zwanziger, J. A. Lussier, K. J. Miller, C. M. Calahoo, J. W. Zwanziger, M. Bieringer, B. A. Marinkovic, D. L. Bryce and M. A. White, Chem. Mater., 2015, 27, 2633–26476 CrossRef CAS.
- B. A. Marinkovic, P. M. Jardim, M. Ari, R. R. de Avillez, F. Rizzo and F. F. Ferreira, Phys. Status Solidi B, 2008, 245, 2514–2519 CrossRef CAS.
- T. Suzuki and A. Omote, J. Am. Ceram. Soc., 2004, 87, 1365–1367 CrossRef CAS.
- K. J. Miller, C. P. Romao, M. Bieringer, B. A. Marinkovic, L. Prisco and M. A. White, J. Am. Ceram. Soc., 2013, 96, 561–566 CAS.
- B. A. Marinkovic, M. Ari, R. R. de Avillez, F. Rizzo, F. F. Ferreira, K. J. Miller, M. B. Johnson and M. A. White, Chem. Mater., 2009, 21, 2886–2894 CrossRef CAS.
- W. T. A. Harrison, Mater. Res. Bull., 1995, 30, 1325–1331 CrossRef CAS.
- S. Balamurugan, U. C. Rodewald, T. Harmening, L. van Wuellen, D. Mohr, H. Eckert and R. Poettgen, Z. Naturforsch., B: J. Chem. Sci., 2010, 65, 13–17 CAS.
- L. H. N. Rimmer and M. T. Dove, J. Phys.: Condens. Matter, 2015, 27, 185401 CrossRef PubMed.
- A. L. Goodwin, S. A. Wells and M. T. Dove, Chem. Geol., 2006, 225, 213 CrossRef CAS.
- T. Varga, A. P. Wilkinson, C. Lind, W. A. Bassett and C.-S. Zha, J. Phys.: Condens. Matter, 2005, 17, 4271–4283 CrossRef CAS.
- C. P. Romao, K. J. Miller, C. A. Whitman, M. A. White and B. A. Marinkovic, in Comprehensive Inorganic Chemistry II, ed. J. Reedijk and K. Poeppelmeier, Elsevier, Oxford, UK, 2013, vol. 4, pp. 128–151 Search PubMed.
- C. P. Romao, K. J. Miller, M. B. Johnson, J. W. Zwanziger, B. A. Marinkovic and M. A. White, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 024305 CrossRef.
- T. Varga, A. P. Wilkinson, C. Lind, W. A. Bassett and C.-S. Zha, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 214106 CrossRef.
- M. T. Dove and H. Fang, Rep. Prog. Phys., 2016, 79, 066503 CrossRef PubMed.
- L. P. Prisco, C. P. Romao, M. A. White and B. A. Marinkovic, J. Mater. Sci., 2013, 48, 2986–2996 CrossRef CAS.
- L. P. Prisco, P. I. Pontón, M. V. Guamán, R. R. Avillez, C. P. Romao, M. B. Johnson, M. A. White and B. A. Marinkovic, J. Am. Ceram. Soc., 2016, 99, 1742–1748 CrossRef CAS.
- C. P. Romao, B. A. Marinkovic, U. Werner-Zwanziger and M. A. White, J. Am. Ceram. Soc., 2015, 98, 2858 CrossRef CAS.
- W. Miller, C. W. Smith, D. S. Mackenzie and K. E. Evans, J. Mater. Sci., 2009, 44, 5441–5451 CrossRef CAS.
- A. L. Goodwin, S. A. Wells and M. T. Dove, Chem. Geol., 2006, 225, 213–221 CrossRef CAS.
- T. Schneider, G. Srinivasan and C. P. Enz, Phys. Rev. A: At., Mol., Opt. Phys., 1972, 5, 1528–1536 CrossRef.
- P. B. Allen, Y. R. Chen, S. Chaudhuri and C. P. Grey, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 172102 CrossRef.
- M. T. Dove, M. Gambhir and V. Heine, Phys. Chem. Miner., 1999, 26, 344–353 CrossRef CAS.
- R. A. Cowley, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 4877–4885 CrossRef CAS.
- F. R. Drymiotis, H. Ledbetter, J. B. Betts, T. Kimura, J. C. Lashley, A. Migliori, A. P. Ramirez, G. R. Kowach and J. Van Duijn, Phys. Rev. Lett., 2004, 93, 025502 CrossRef CAS PubMed.
- H. Fang, M. T. Dove and A. E. Phillips, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 214103 CrossRef.
- L. C. Gallington, K. W. Chapman, C. R. Morelock, P. J. Chupas and A. P. Wilkinson, J. Appl. Phys., 2014, 115, 053512 CrossRef.
- L. Wang, F. Wang, P.-F. Yuan, Q. Sun, E.-J. Liang, Y. Jia and Z.-X. Guo, Mater. Res. Bull., 2013, 48, 2724–2729 CrossRef CAS.
- L. H. N. Rimmer and M. T. Dove, J. Phys.: Condens. Matter, 2015, 27, 185401 CrossRef PubMed.
- ABINIT, http://www.abinit.org, accessed 02/05/16.
- ACENET – Advanced Computing Research in Atlantic Canada, http://www.ace-net.ca, accessed 02/05/16.
- WestGrid – Western Canada Research Grid, http://https://www.westgrid.ca, accessed 02/05/16.
- F. Bottin, S. Leroux, A. Knyazev and G. Zerah, Comput. Mater. Sci., 2008, 42, 329–336 CrossRef CAS.
- X. Gonze, B. Amadon and P.-M. Anglade, et al. , Comput. Phys. Commun., 2009, 180, 2582–2615 CrossRef CAS.
- X. Gonze, J.-M. Beuken and R. Caracas, et al. , Comput. Mater. Sci., 2002, 25, 478–492 CrossRef.
- X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10337–10354 CrossRef CAS.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355–10368 CrossRef CAS.
- D. R. Hamann, X. Wu, K. M. Rabe and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035117 CrossRef.
- CIF2Cell, http://sourceforge.net/projects/cif2cell/, accessed 02/05/16.
- T. Björkman, Comput. Phys. Commun., 2011, 182, 1183–1186 CrossRef.
- S. Balamurugan, U. C. Rodewald, T. Harmening, L. van Wuellen, D. Mohr, H. Eckert and R. Poettgen, Z. Naturforsch., B: Chem. Sci., 2010, 65, 13–17 CAS.
- W. T. A. Harrison, Mater. Res. Bull., 1995, 30, 1325–1331 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. R. Hamann, M. Schlüter and C. Chiang, Phys. Rev. Lett., 1979, 43, 1494 CrossRef CAS.
- I. Grinberg, N. J. Ramer and A. M. Rappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 2311 CrossRef CAS.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227(R) CrossRef.
- Opium – pseudopotential generation project, http://opium.sourceforge.net, accessed 02/05/16.
- Rappe Group, http://www.sas.upenn.edu/rappegroup/htdocs/Research/psp_gga.html, accessed 02/05/16.
- D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- Y. Sumino, O. L. Anderson and I. Suzuki, Phys. Chem. Miner., 1983, 9, 38–47 CrossRef CAS.
- C. F. Smith and W. B. Crandall, J. Am. Ceram. Soc., 1964, 47, 624–627 CrossRef CAS.
- J. M. Dickinson and P. E. Armstrong, J. Appl. Phys., 1967, 38, 602–606 CrossRef CAS.
- P. Haas, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085104 CrossRef.
- B. S. Anglin, R. A. Lebensohn and A. D. Rollett, Comput. Mater. Sci., 2014, 87, 209–217 CrossRef.
- S. P. Donegan and A. D. Rollett, Acta Mater., 2015, 96, 212–228 CrossRef CAS.
- DREAM.3D, http://dream3d.bluequartz.net/, accessed 19/07/16.
- M. Ari, P. M. Jardim, B. A. Marinkovic, F. Rizzo and F. F. Ferreira, J. Solid State Chem., 2008, 181, 1472–1479 CrossRef CAS.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 05504 CrossRef PubMed.
- H. M. Ledbetter, J. Appl. Phys., 1973, 44, 1451–1454 CrossRef CAS.
- A. R. Soares, P. I. Ponton, L. Mancic, J. R. M. d'Almeida, C. P. Romao, M. A. White and B. A. Marinkovic, J. Mater. Sci., 2014, 49, 7870–7882 CrossRef CAS.
- nanoHUB.org – Resources: Anisotropy Calculator – 3D Visualization Toolkit, http://https://nanohub.org/tools/matrix2surface, accessed 19/07/16.
- A. C. Torres Dias, C. Luz Lima, W. Paraguassu, K. Pereira da Silva, P. T. C. Freire, J. Mendes Filho, B. A. Marinkovic, K. J. Miller, M. A. White and A. G. Souza Filho, Vib. Spectrosc., 2013, 68, 251–256 CrossRef CAS.
- M. Maczka, W. Paraguassu, A. G. Souza Filho, P. T. C. Freire, J. Mendes Filho, F. E. A. Melo and J. Hanuza, J. Solid State Chem., 2004, 177, 2002–2006 CrossRef CAS.
- S. W. Key, J. Appl. Phys., 1967, 38, 2923–2928 CrossRef CAS.
- C. P. Romao, C. R. Morelock, M. B. Johnson, J. W. Zwanziger, A. P. Wilkinson and M. A. White, J. Mater. Sci., 2015, 50, 3409–3415 CrossRef CAS.
- G. D. Barrera, J. A. O. Bruno, T. H. K. Barron and N. L. Allan, J. Phys.: Condens. Matter, 2005, 17, R217–R252 CrossRef CAS.
- G. N. Greaves, Notes Rec. R. Soc., 2012, 67, 37–58 CrossRef PubMed.
- W. S. Kreher, Comput. Mater. Sci., 1996, 7, 147–153 CrossRef CAS.
- W. Kreher, J. Mech. Phys. Solids, 1990, 38, 115–128 CrossRef.
- H. Mouri, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 042124 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp06356j |
| ‡ Mo was chosen rather than an oxide as the test material because MoO3 has a layered structure and therefore is an unsuitable point of comparison,56 and the bulk modulus of MoO2 has not been reported in the literature. |
| This journal is © the Owner Societies 2016 |