Reactive–convective dissolution in a porous medium: the storage of carbon dioxide in saline aquifers
Received
31st August 2016
, Accepted 22nd November 2016
First published on 25th November 2016
Abstract
We quantify the destabilising effect of a first-order chemical reaction on the fingering instability of a diffusive boundary layer in a porous medium. Using scaling, we show that the dynamics of such a reactive boundary layer is fully determined by two dimensionless groups: Da/Ra2, which measures the timescale for convection compared to those for reaction and diffusion; and βC/βA, which reflects the density change induced by the product relative to that of the diffusing solute. Linear stability and numerical results for βC/βA in the range 0–10 and Da/Ra2 in the range 0–0.01 are presented. It is shown that the chemical reaction increases the growth rate of a transverse perturbation and favours large wavenumbers compared to the inert system. Higher βC/βA and Da/Ra2 not only accelerate the onset of convection, but crucially also double the transport of the solute compared to the inert system. Application of our findings to the storage of carbon dioxide in carbonate saline aquifers reveals that chemical equilibrium curtails this increase of CO2 flux to 50%.
1 Introduction
Dissolution driven convection in porous media has received recent interest in context of the long-term geological storage of carbon dioxide in underground, natural, brine filled caverns, often referred to as saline aquifers.1–4 Following injection into the saline aquifer, dissolution of supercritical carbon dioxide in the host brine causes a local density increase leading to gravitational instability of the diffusive boundary layer and formation of convective fingers. Convection enhances further carbon-dioxide dissolution in the brine.5–7 Such dissolution-driven Rayleigh–Darcy convection has been extensively studied in inert systems, both theoretically3,5,7–16 and experimentally.6,17–20
Chemical reaction of the dissolved carbon dioxide with the underground host rock can lead to long-term sequestration. However, the geochemistry can severely complicate the situation by interacting with the fluid motion, altering the hydrodynamic instability and the spatio-temporal convection patterns.21,22 Previous works on reactive systems have demonstrated stabilizing effects of chemical reaction in the case of the removal of solute from the system.21–26 It has been shown that formation of a solid product can stabilize the diffusive boundary layer, resulting in a delay in the time for onset of convection and a severe reduction of the convective motion. As a result, the lower part of the reservoir may remain unutilised.22,27–33
The effect of chemical reaction on Rayleigh–Darcy convection when the reaction product contributes to the density field has been only partially explored. Previous works34–36 have identified configurations with destabilizing effects of second-order chemical reactions, using linear stability analysis and laboratory experiments. The nonlinear behaviour has only very recently been touched upon experimentally.37,38 The effects of variation in density contrast between the diffusing solute and the reaction product on the complex nonlinear dynamic behaviour of the boundary layer, viz., spatio-temporal concentration profile of the solute and the product and the convective–reactive solute dissolution flux remain unexplored. Moreover, there is substantial scope for theoretical characterization of the nonlinear dynamics of the reactive boundary layer and the dynamic evolution and interaction of the finger patterns along with their sensitivity to the reaction kinetics and the density change induced by the reaction. Additionally, the effects of a first-order chemical reaction on the stability of a boundary layer, when the product contributes to the density field, remain largely unexplored. In this paper, we address all the above gaps in knowledge on reactive boundary layers in porous media. We present a linear stability analysis coupled with numerical simulations, to investigate the stability and the nonlinear dynamics of a diffusive boundary layer undergoing a first-order chemical reaction where the product remains in the liquid phase and induces a density change of the fluid mixture. The effects of reaction on the time for onset of convection and on the intensity of the convective motion are presented. The growth and complex non-linear behaviour of the boundary layer is quantitatively characterized by the spatio-temporal concentration profiles of the reactant and product, along with their sensitivity to the governing parameters. We quantify the accelerated dissolution flux driven by the reaction. The effects of chemical reaction on the formation and interaction of convective fingers are also quantified.
Our findings are of relevance in the geo-storage of carbon dioxide. An example of application is the qualitative and quantitative prediction of convection phenomena in carbonate saline reservoirs, which we discuss in Section 4.
2 Model
2.1 Governing equations
We consider the transport of a solute A as it dissolves at the top of a fluid-saturated porous medium [Fig. 1]. The porous medium is two dimensional, homogeneous, and isotropic. The solute A irreversibly undergoes a first-order chemical reaction with chemical species B present in the host porous rock, resulting in product C that remains in solution: A(aq) + B(s) → C(aq). Both the solute A and the product C contribute to the density of the solution. The solute and the product are advected by the fluid as it moves in the pore space. We assume incompressible, Darcy flow under Boussinesq conditions, so that| |  | (2) |
Here, v = (u,v) is the Darcy velocity vector, p = P − ρrgz is the reduced pressure field, obtained by eliminating hydrostatic pressure from the local pressure P, g is the acceleration due to gravity and j is a vertical unit vector co-directional with the positive z-axis. The isotropic permeability of the porous medium kp and the viscosity of the fluid μ are assumed to be constant. The density of the fluid is assumed to be linearly dependent on the local concentrations of the solute, CA, and the product, CC: ρ = ρr(1 + βACA + βCCC); the reference density ρr is that of the pure fluid and the coefficients of density increase with the concentration of the solute and the product are defined as βA = (1/ρr)∂ρ/∂CA and βC = (1/ρr)∂ρ/∂CC, respectively.
 |
| | Fig. 1 Solute A dissolves in underlying fluid forming a diffusive boundary layer. Dissolution enhances the local density difference between the solute-saturated fluid at the interface and the underlying pure fluid, driving finger formation and convection. Dissolved solute A reacts with reactant species B in the host rock, forming product C, which remains dissolved in the fluid. Chemical reaction alters the spatial distribution of the solute and the product, and changes the density field. | |
The transport of the solute A and product C is described by the advection–diffusion–reaction equations
| |  | (3) |
| |  | (4) |
Here,
t is time and
kra is the reaction rate per unit volume of fluid, where the solid based kinetic rate constant is
kr and the reactive surface area per mole of the solid is
a. The effective diffusivity of a dissolved species in the porous medium is taken as the product of the molecular diffusion coefficient
Di and porosity
φ of the aquifer. We consider
DA =
DC. The effect of dispersion is neglected. Depletion of the species B is neglected. This assumption is valid when the host porous rock is rich in reactive species.
2.2 Nondimensionalization
The governing equations are non-dimensionalised using the scales LC = μDAφ/kpρ0g, ts = LC2/DA, vs = DAφ/LC, ps = μDAφ/kp, and the solubility of solute A in the fluid Cs, giving| |  | (6) |
| |  | (7) |
| |  | (8) |
Here, Da = kraLz2/DAφ is the Damköhler number and Ra = kpρ0gLz/μDAφ is the solutal Rayleigh number. The maximum density contrast between the pure and solute-saturated brine is Δρ0 = ρrβCs. The dynamics of such a reactive boundary layer is therefore fully determined by two dimensionless groups: Da/Ra2, which measures the timescale for convection compared to those for reaction and diffusion, and βC/βA, which reflects the density change induced by the product relative to that of the diffusing solute. We use the above model to study the effects of reaction kinetics on the instability and nonlinear behaviour of the boundary layer, away from chemical equilibrium, as discussed in Section 3. In Section 4 we discuss how the chemical equilibrium can alter the behaviour of the system.
3 Results and discussion
3.1 Time for onset of convection
The time for onset of convection has been obtained from both linear stability analysis and numerical simulations, as detailed in the Appendix. Four different cases are presented in Fig. 2, covering a range of product densities: (a) βC/βA = 0, for which the product does not contribute to the density of the fluid; (b) βC/βA = 1, when the product has the same density coefficient as the reactant, (c) βC/βA = 1.5, for a heavy dissolved product; and (d) βC/βA = 10, for a very heavy dissolved product.
 |
| | Fig. 2 Time for onset of convection (dimensionless) as a function of reaction strength Da/Ra2, for βC/βA in the range 0–10. Results from linear stability analysis, with either quasi-steady assumptions (QSSA) or dominant-mode of the self-similar diffusion operator (DM), are presented. The dotted lines show results from nonlinear numerical simulations (NS). | |
When the product does not contribute to the density of the fluid, the time for onset of convection is seen to increase as reaction strength increases [Fig. 2]. This can be explained by noting that as the solute is consumed by chemical reaction, the density of the layer is reduced, and the onset of convection is delayed. In a system with a product and reactant of equal density coefficients, the onset of convection is accelerated as the reaction strength increases. This behaviour results from the accumulation of product in the boundary layer and a reduction of the concentration of reactant, the latter enhancing diffusive transport and hence reducing the time for onset of convection. For a large product density coefficient (βC/βA = 1.5), the convection onset is accelerated as reaction strength increases. Here, the heavy product contributes to increase the density of the fluid and destabilises the boundary layer earlier. An even larger density contribution from the product (βC/βA = 10), reduces significantly the onset time of convection.
3.2 Convective motion
Numerical simulation was used to study the effects of the formation of a soluble product on the intensity and pattern of convective mixing. The local instantaneous speed has been computed as 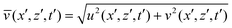 , while the average speed over the whole computation domain at each time instant has been obtained by evaluating
, while the average speed over the whole computation domain at each time instant has been obtained by evaluating  .
.
The evolution of the instantaneous speed field is shown in Fig. 3. Density-coefficient ratios in the range 0 to 1.5 are investigated for Da/Ra2 = 1 × 10−3 [Fig. 3(a–c)]. It is evident that the product density has a significant effect on both the spatial extent and the intensity of convective motion. For βC/βA = 1.5, the convective fingers penetrate deep into the domain at large time, for βC/βA = 1 only half of that depth has appreciable convection, while for βC/βA = 0 the motion is confined to the close proximity of the interface. The intensity of convection is much higher for the heavy product as evident from the colour codes. For low (Da/Ra2 = 0.15 × 10−3), intermediate (Da/Ra2 = 1 × 10−3) and high (Da/Ra2 = 2.49 × 10−3) reaction strengths, the average speed in the whole domain, respectively, doubles, increases by tenfold, and by thousand-fold, as the density ratio increases from zero to 1.5.
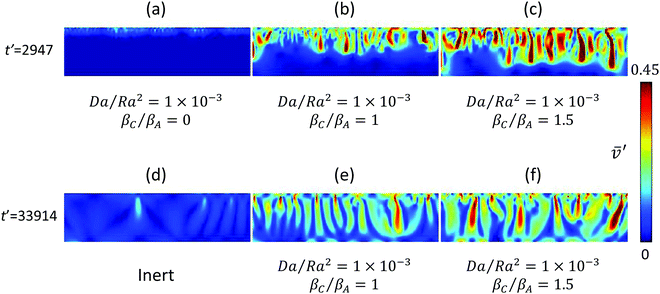 |
| | Fig. 3 Snapshots of the speed field showing the effects of chemical reaction on the convective motion. (a–c) Show enhancement of convection with an increase in density ratio. (d) Shows feeble inert convection after fingers reach the bottom of the domain. (e and f) Show that, in contrast to inert convection, chemical reaction accompanied by soluble products can maintain long-term convection, even after the fingers reach the bottom boundary. | |
It is important to note that for medium (Da/Ra2 = 1 × 10−3) and large (Da/Ra2 = 2.49 × 10−3) reaction strength, with βC/βA = 1 and 1.5, convective motion is maintained long-term, even long after the fingers reach the bottom of the reservoir; this behaviour is in significant contrast to that of an inert system,7,13 where a substantial drop in convection intensity is observed. This behaviour is illustrated in Fig. 3(d–f) for intermediate reaction strength, Da/Ra2 = 1 × 10−3, at a dimensionless time of t′ = 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914. The inert system in Fig. 3(d) exhibits very weak motion, with severely curtailed finger formation and a sparse finger presence. However, for βC/βA = 1 and 1.5 [Fig. 3(e) and (f)], a large number of prominent sinking fingers are distributed throughout the domain, with new fingers forming at the interface. In these cases, the numbers of fingers are almost double of that in the inert case. For intermediate reaction strength, Da/Ra2 = 1 × 10−3, with beta ratio 1 and 1.5 at a dimensionless time of t′ = 34
914. The inert system in Fig. 3(d) exhibits very weak motion, with severely curtailed finger formation and a sparse finger presence. However, for βC/βA = 1 and 1.5 [Fig. 3(e) and (f)], a large number of prominent sinking fingers are distributed throughout the domain, with new fingers forming at the interface. In these cases, the numbers of fingers are almost double of that in the inert case. For intermediate reaction strength, Da/Ra2 = 1 × 10−3, with beta ratio 1 and 1.5 at a dimensionless time of t′ = 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252, the average speed of the whole domain is maintained at ∼70% of the peak speed obtained before the fingers reach the bottom of the domain. For high reaction strength, Da/Ra2 = 2.49 × 10−3, this ratio is maintained at ∼75%. However, for the inert system at the same dimensionless time, the average speed is reduced to 30% of the maximum speed before fingers hit the bottom boundary. Thus, a reaction accompanied by heavier or equal density product formation as the solute can significantly enhance convective mixing and maintain it long term.
252, the average speed of the whole domain is maintained at ∼70% of the peak speed obtained before the fingers reach the bottom of the domain. For high reaction strength, Da/Ra2 = 2.49 × 10−3, this ratio is maintained at ∼75%. However, for the inert system at the same dimensionless time, the average speed is reduced to 30% of the maximum speed before fingers hit the bottom boundary. Thus, a reaction accompanied by heavier or equal density product formation as the solute can significantly enhance convective mixing and maintain it long term.
3.3 Solute and product concentrations
Snapshots of solute and product concentration fields are shown in Fig. 4. We consider two heavy-product scenarios (βC/βA = 1.5, 10) and compare those with the situation of a product with negligible density contribution (βC/βA = 0). At small reaction strength for βC/βA = 0 [Fig. 4(A-i)], at t′ = 2427, tiny solute fingers are observed, which grow downwards individually. As the beta ratio increases, the fingers propagate further down within the same time frame. For βC/βA = 1.5 [Fig. 4(B-i)], fingers have a small tilt from the vertical direction indicating noticeable but minor finger interactions. Within the same time frame, for βC/βA = 10 [Fig. 4(C-i)], the solute fingers penetrate deeply into the domain and exhibit splitting at the roots. The product field exhibits a similar behaviour, albeit with the product concentration being less than that of the reactant.
 |
| | Fig. 4 Snapshots showing the effect of Da/Ra2 and βC/βA on (i) solute concentration and (ii) product concentration. Da/Ra2 increases from top to bottom and βC/βA increases from left to right. Snapshots are shown at dimensionless times t′ = 2427 for A, B, C, E and H; t′ = 3467 for D and G; t′ = 1126 for F and I. | |
For βC/βA = 0, at intermediate reaction strength, finger formation is inhibited and the fingers are confined close to the interface [Fig. 4(D)]. At large reaction strength, convection is completely halted and a diffusive–reactive boundary layer is observed with high product concentration close to the interface [Fig. 4(G)]. In contrast, for βC/βA = 1.5 and intermediate reaction strength [Fig. 4E(i and ii)], both solute and product fingers migrate further compared to case B, with solute fingers being slender and product fingers looking bulky. As reaction strength increases further [Fig. 4(H)], a drastic difference between the finger patterns for the solute and product is observed. Bulky product fingers are conveyed deep into the domain while solute fingers are very thin and remain confined to the interface. For βC/βA = 10, the reactant fingers penetrate deeper into the domain even under strong reaction. In contrast to the case with density ratio 1.5, product fingers are slender and have lower concentration. This is a consequence of the presence of heavy product, which elongates the fingers and enhances lateral diffusion.
There are striking similarities and differences in the finger patterns between situations with (a) low reaction strength and large beta ratio [Fig. 4(C)] and (b) large reaction strength with small beta ratio [Fig. 4(H)]. It is noteworthy that in both the cases plumes penetrate deep in the reservoir with comparable speed. However, for case C the reactant concentration is more prominent than product concentration, while for case H, reactant fingers are small and slim, and product-rich fingers are conveyed down, suggesting the flow is primarily driven by the product.
It is important to consider the depth of the chemically active zone in the reservoir. Chemical reaction introduces a complex, nonlinear competition between reactant depletion and its transport by convection, promoted by the density of a fluid with spatially varying proportions of reactant and products. Our reactive transport simulation suggests that rapid chemical reactions are confined to a shallow region close to the top of the reservoir where the reactant remains localised [Fig. 4(H)]. The deeper part of the reservoir remains chemically inactive; here inert, product-rich fingers prevail and mass transfer occurs through convection and diffusion. For slow chemical reactions and large density ratio, long-lived reactant fingers descend deeper into the domain and a greater part of the reservoir is chemically active. For Da/Ra2 = 2.49 × 10−3 with βC/βA = 1.5, the solute is restricted within half of the total depth of the simulation domain, while for Da/Ra2 = 1 × 10−3 with the same density ratio and for Da/Ra2 = 2.49 × 10−3 with βC/βA = 10, the solute is distributed throughout the whole domain.
The above results suggest that it is worth resolving the finger patterns into solute and product concentration components for a comprehensive understanding of the reactive–convective mixing patterns. The vertical spreading of the solute and the product is further quantified in the horizontally averaged concentration profiles, presented in Fig. 5 and 6, respectively. Horizontally averaged concentration profiles for the solute and the product are defined as  , and
, and  . These plots reveal valuable information about the early-time growth of the boundary layer and long-term dynamic behaviour of the fingering region. Situations with four different combinations of Da/Ra2 and βC/βA are discussed. Each curve represents one time instant, and the same time range is covered in all the plots. The boundary layer grows from the top interface (left) to the bottom of the domain (right) in the figures. At small reaction strength, Da/Ra2 = 0.15 × 10−3 and βC/βA = 1.5 [Fig. 5(a)], upon onset of convection, swelled regions start appearing in concentration profiles. This structure is maintained for some time, after which the concentration gradient is sharpened close to the interface as more solute is conveyed down from the interface. This behaviour is similar to that for inert situations reported by Andres and Cardoso.27 As the product density increases (βC/βA = 10, [Fig. 5(b)]), convection is established more rapidly. More prominent sharpening of the concentration gradient is observed demonstrating pronounced convective removal of solute from the interface and its effective transport towards the bottom of the domain.
. These plots reveal valuable information about the early-time growth of the boundary layer and long-term dynamic behaviour of the fingering region. Situations with four different combinations of Da/Ra2 and βC/βA are discussed. Each curve represents one time instant, and the same time range is covered in all the plots. The boundary layer grows from the top interface (left) to the bottom of the domain (right) in the figures. At small reaction strength, Da/Ra2 = 0.15 × 10−3 and βC/βA = 1.5 [Fig. 5(a)], upon onset of convection, swelled regions start appearing in concentration profiles. This structure is maintained for some time, after which the concentration gradient is sharpened close to the interface as more solute is conveyed down from the interface. This behaviour is similar to that for inert situations reported by Andres and Cardoso.27 As the product density increases (βC/βA = 10, [Fig. 5(b)]), convection is established more rapidly. More prominent sharpening of the concentration gradient is observed demonstrating pronounced convective removal of solute from the interface and its effective transport towards the bottom of the domain.
 |
| | Fig. 5 Horizontally-averaged solute concentration versus depth for times between t′ = 87 and t′ = 3727 with time interval Δt′ = 260 (dimensionless). The boundary layer grows from left (top of the domain) to right (bottom of the domain). | |
 |
| | Fig. 6 Horizontally-averaged product concentration versus depth for times between t′ = 87 and t′ = 3727 with time interval Δt′ = 260 (dimensionless). The boundary layer grows from left (top of the domain) to right (bottom of the domain). | |
As reaction strength increases, for density ratio zero, the swelling and sharpening dynamics is halted, and a diffusive–reactive solute profile prevails close to the interface [Fig. 5(c)]. Contrariwise, for beta ratio 1, swelling starts earlier owing to an earlier onset of convection and the concentration plots fold to substantial extents due to intense motion [Fig. 5(d)]. Despite the pronounced convection, solute does not seem to accumulate near the bottom boundary owing to its rapid consumption by chemical reaction. Solute concentration is restricted to a region up to dimensionless length 300.
At small time, the product concentration remains restricted to a small region close to the upper boundary. The diffusive–reactive boundary layer evolves, with a maximum product concentration at the interface and a monotonic decrease with distance from it. As time progresses, both the thickness of the product region and the product concentration at the interface increase. At small reaction strength, Da/Ra2 = 0.15 × 10−3 and βC/βA = 1.5 [Fig. 6(a)], upon onset of convection, the product concentration at the interface increases more slowly, while products accumulate slightly away from the interface. A bulge in the product concentration profile develops which grows and moves downward with time. For large density ratio [Fig. 6(b)], upon onset of convection, the interface concentration first decreases and then remains virtually constant as the product is quickly transported down. The interface concentration is limited to a smaller value and the profile is relatively uniform. At large time, the product accumulates at the impermeable base.
Fig. 6(c) shows the diffusive–reactive product concentration profile for large reaction strength (Da/Ra2 = 2.49 × 10−3) with density ratio zero. A monotonic product concentration profile continues increasing with time. The interface concentration increases much faster than for the low reaction strength under diffusive transport ([Fig. 6(a)] at small time). At the same large reaction strength, even with the equal density contribution from the product as the solute [Fig. 6(d)], a remarkably different concentration profile is observed, owing to the development of convection. In contrast to the solute concentration profile [Fig. 5(d)], the product is transported deep into the domain.
3.4 Rate of solute dissolution at the top interface
The presence of a heavy reaction product can have considerable impact on the rate of dissolution of solute at the top interface, as demonstrated in Fig. 7. The solute mass flux dissolving at the top boundary is obtained from 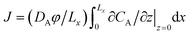 , or in dimensionless form, J′ = JLc/DAφCs. Reaction strengths ranging from Da/Ra2 = 0–2.49 × 10−3 are investigated for βC/βA = 0, 1 and 1.5.
, or in dimensionless form, J′ = JLc/DAφCs. Reaction strengths ranging from Da/Ra2 = 0–2.49 × 10−3 are investigated for βC/βA = 0, 1 and 1.5.
 |
| | Fig. 7 Mass flux of solute dissolving at the top boundary for different combinations of Da/Ra2 and βC/βA: (a) small-time behaviour; (b) small- and large-time behaviours. The inert flux is shown as the black solid line. Reactive cases for Da/Ra2 = 0.15 × 10−3, 1 × 10−3 and 2.49 × 10−3 are represented by solid, dotted and compound lines, respectively; βC/βA = 0, 1 and 1.5 are represented by green, purple and orange lines, respectively. The application to the geo-storage of carbon dioxide in carbonate rich aquifers is shown as the red solid line. | |
At early time, in the diffusion–reaction regime, all flux curves decay towards a minimum value, as the solute concentration gradient decreases owing to vertical diffusion, [Fig. 7(a)]. The flux is mainly determined by the reaction strength and is independent of the density ratio. As reaction strength increases, the flux curves shift up and decay at much slower rate as the concentration gradient is sharpened owing to more pronounced consumption of solute.
Following onset of convection, the dissolution flux recovers. This is illustrated for each Da/Ra2 by the separation of the curves, first for the highest beta ratio, followed by the other lower ratios [Fig. 7(a)]. The flux steadily increases owing to convective transport and reaches a local maximum. For the inert system, this is termed the ‘flux growth’ regime.13
For the reactive system with beta ratio zero, the flux increases with reaction strength, but the curves become flatter owing to suppression of finger formation. In contrast, for βC/βA = 1, 1.5, the flux subsequently drops as fingers interact to a statistically constant value with some fluctuations. The flux is larger for βC/βA = 1.5, than that for βC/βA = 1 owing to the presence of more fingers (see Section 3.5) that quickly propagate downward. The constant flux is reached at an earlier time as the density ratio increases. For higher reaction strength, the flux is maintained at a higher level owing to a more pronounced removal of the solute from the interface by chemical reaction and by advection of a larger number of reactive fingers. At this statistically constant flux regime, fingers reach the bottom of the domain. It has been verified by doubling the depth of the simulation domain that the dissolution flux remains unaffected by the presence of the bottom boundary for intermediate (Da/Ra2 = 1 × 10−3) and large (Da/Ra2 = 2.49 × 10−3) reaction strengths. For low reaction strength (Da/Ra2 = 0.15 × 10−3), following this regime, at large time, the flux gradually decreases (not shown).
The total amount of trapped solute is obtained by integrating the flux J over time curve. For intermediate (Da/Ra2 = 1 × 10−3) and high (Da/Ra2 = 2.49 × 10−3) reaction strengths, with βC/βA = 1.5, the total amount of solute uptake increases by 100% and 169%, respectively, compared to the inert case.
3.5 Formation and dynamic evolution of finger structures
The formation and dynamic evolution of finger patterns are quantified by the power-averaged, instantaneous finger number (see Appendix D), n(t), in the whole simulation domain [Fig. 8(a)]. The effects of chemical reaction on the linear and non-linear finger behaviour are further characterized by measuring the deviation between the average finger number in the reactive and inert simulations at a given time, n(t) − ninert(t), [Fig. 8(b)].
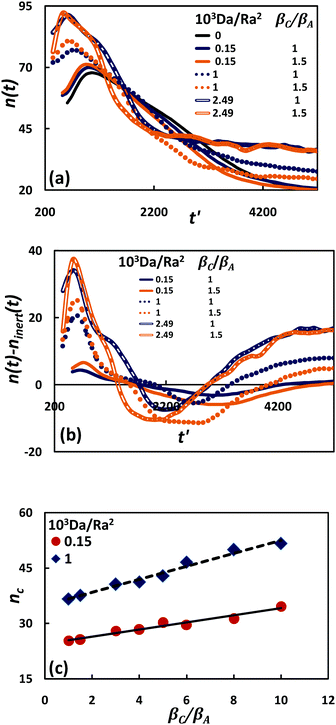 |
| | Fig. 8 Effect of Da/Ra2 and βC/βA on formation and evolution of finger patterns: (a) instantaneous finger number n(t), (b) deviation between finger number in reactive and inert systems, and (c) effect of beta ratio on characteristic finger number, for two different Da/Ra2. Linear trend lines are drawn through the data points. | |
At early times, the finger number increases and reaches a peak value. This maximum number corresponds to the local minimum in the flux curve. This is the finger formation period. As reaction strength increases, the finger number increases and convection develops earlier. The finger number at the time of onset of convection has been found to increase to a small extent as the density ratio increases from 1 to 1.5 [Fig. 8(b)]. Our simulations with larger density contribution from product, βC/βA = 5, 10 (not shown), indicate more substantial increase in finger number. From the above diagram, it is also seen that the reaction strength (Da/Ra2) has a more prominent effect on finger number at the onset than the density ratio.
Beyond the formation period, the fingers grow individually for some time, after which merger occurs, promoted by the interaction of the velocity fields of adjacent fingers.19 As reaction strength increases, the finger number is seen to reduce sharply owing to effective finger coalescence, as clearly visible in Fig. 8(b). In this merging regime, the finger interaction becomes stronger as the beta ratio rises, leading to a larger solute dissolution flux at the interface. At larger time, the finger number decreases further, subsequently remaining constant and maintaining the flux at a steady level. In this regime, a stronger reaction favours a higher finger number and a larger reactive–advective solute dissolution flux at the interface.
The effect of the density ratio on the fingering pattern is further quantified by measuring the finger number corresponding to the time at which fingers reach 50% of the depth of the reservoir. The characteristic finger number, nc, is plotted against βC/βA, for two different Da/Ra2 in Fig. 8(c). The characteristic finger number increases linearly as the density ratio increases, in accord with the large number of slender fingers visible in the concentration contours [Fig. 4(F)].
The formation of more fingers when the density ratio is increased may be explained as follows. In the nonlinear regime, fingers merge with their adjacent neighbours reducing the wave number. In the troughs of the wave solute diffuses from the top into the lower layers and undergoes reaction. When this local boundary layer becomes sufficiently heavy, instability develops, new fingers form transporting dense material to larger depth. As the density coefficient ratio increases, conversion of the solute to large density product enhances the development of the instability. For inert convection, the most unstable wave number at the onset of instability has been reported to vary linearly with Rayleigh number, and therefore linearly with the density contrast.5,8 At the onset of convection, our simulations for the reactive system also suggest a linear increase in finger number with increase in ratio of the density-coefficient of the product to the solute (not shown). We conjecture then that the continuous process of development of incipient instability following finger merger, described above, is responsible for the linear increase of the wave number with the density ratio observed in the nonlinear regime.
4 Application
Finally, we discuss the application of our findings to the storage of carbon dioxide in a carbonate-rich saline aquifer. Marini40 describes the dissolution reaction of limestone in the presence of aqueous carbon dioxide to produce soluble calcium bicarbonate in such a reservoir. Dissolved carbon dioxide in brine forms carbonic acid, which dissociates into hydrogen, bicarbonate and carbonate ions. In the presence of the hydrogen ion, calcite dissolves forming calcium and bicarbonate ions.40| | | CO2(aq) + H2O → H2CO3(aq) | (9a) |
| | | H2CO3(aq) ↔ H+(aq) + HCO3−(aq) | (9b) |
| | | HCO3−(aq) ↔ H+(aq) + CO32−(aq) | (9c) |
| | | CaCO3(s) + H+(aq) ↔ Ca2+(aq) + HCO3−(aq) | (10) |
The ratio of the concentrations of carbonate and bicarbonate ions at pH = 8 is less than 0.01 and even smaller under acidic conditions.40,41 Therefore, by neglecting eqn (9c), the above reactions can be combined as| | | CaCO3(s) + CO2(aq) + H2O ⇌ Ca(HCO3)2(aq). | (11) |
The species CO2(aq), CaCO3(s) and Ca(HCO3)2(aq) are represented by A, B and C, respectively, in our model. Reaction (11) can lead to an order of magnitude increase in the density of the fluid compared to that associated with the dissolution of carbon dioxide in brine (βC/βA ∼ 40).5,42,43 Our analysis can therefore be applied to such situation.
For reaction (9a), the reaction rate constant has been reported as ∼10−2 s−1 and for (9b), even faster.44 Following kinetic data of Marini,40 we estimate the reaction rate constant for reaction (10) as ∼10−4 s−1. Therefore, the dissolution reaction (10) has the slowest rate among the reactions (9) and (10) and is therefore the rate-determining step. Using kinetic data of Marini,40 the overall reaction kinetics can be approximated as first-order with respect to aqueous carbon dioxide. With reservoir permeability kp = 5 × 10−12 m2 and porosity φ = 0.3, we estimate Da/Ra2 = 0.1. Numerical simulations for Da/Ra2 = 0.1 and βC/βA = 10, suggest almost instantaneous onset of convection, within less than one hour after injection of carbon dioxide into the aquifer. The convective fingers are expected to advance downwards in the reservoir at a rate of ∼2 cm h−1.
The above model is suitable for the situations where the chemical reaction does not reach equilibrium since only the forward reaction is considered. This is a valid assumption for slow geochemical reactions. In general, geochemical reactions between aqueous carbon dioxide and porous rocks have slow reaction rates.42 However, for situations where the rate of the chemical reaction is moderately high, as in the example above, the geochemical reaction may reach chemical equilibrium, which will restrict further dissolution of the rock matrix. Our numerical results do indeed show that the local concentrations of calcium bicarbonate and dissolved carbon dioxide can reach equilibrium. Therefore, a modification of the above model is required to incorporate the backward reaction.
A backward reaction has been added to the governing balances as follows:
| |  | (13) |
| |  | (14) |
| |  | (15) |
Here,
krAa and
krC are the rate constants for the forward and backward reactions, respectively. The magnitude of the backward reaction rate constant
krC is calculated from the equilibrium between the local concentrations of calcium bicarbonate and carbon-dioxide(aq):
| | 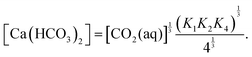 | (16) |
Here,
K1,
K2,
K4 are equilibrium constants for
reactions (9a), (9b) and (10), respectively.
45
Numerical simulations with the modified model for βC/βA = 40, predicts the time for onset of convection to be 3.3 days. The convective fingers are expected to advance downwards in the reservoir at a rate of ∼5 cm per day. Before the fingers reach the bottom of the domain, the solute dissolution flux (dimensionless) at the interface [Fig. 7(b)] is ∼1.5 times that for the inert system. Under reservoir conditions, the carbon-dioxide dissolution flux at the CO2–brine interface is predicted to be 100 ton km−2 day−1 before the fingers reach the bottom of the reservoir; this is almost 1.2 times the flux predicted by Szulczewski et al.46 for similar reservoir properties without geochemical reactions. At large time, the flux gradually decreases, suggesting a shutdown of convection in the long term.
5 Conclusions
A theoretical and numerical study of the development of convection in a diffusive boundary layer, undergoing a first-order chemical reaction, was performed. Scaling of the governing volume, momentum and chemical balances showed that the boundary-layer behaviour is fully determined by two dimensionless groups: the ratio of the Damköhler number and the square of the solutal Rayleigh number, Da/Ra2, and the coefficient of density change of the reaction product species compared to that of the diffusing solute, βC/βA. It was shown that the state of mixing in the convective layer depends strongly on the magnitudes of Da/Ra2, and βC/βA. While βC/βA controls more strongly the time for onset of convection, Da/Ra2 has more effect on the dissolution flux.
Our results show that the presence of the soluble product, even of equal density to the solute, can substantially destabilize and alter the nonlinear, dynamic behaviour of the boundary layer, compared to that for inert convection. Importantly, the situations with larger βC/βA, are characterized by faster moving fingers, accompanied by larger wave numbers. Additionally, higher Da/Ra2 increases the number of fingers at instability and enhances dynamic finger interactions as well. Under slow reaction conditions, solute rich fingers develop slowly and remain almost homogeneous in composition. For a rapid chemical reaction, with moderate βC/βA, heavy product-rich fingers travel deep into the domain, but remain rich in solute close to the interface. As βC/βA increases, the large density contribution from the product elongates both the solute and product fingers, resulting in deeper, chemically active domain. These complex hydrodynamic and chemical interactions lead to accelerated mass transport in the reactive system compared to that in the inert. An increase in Da/Ra2 from zero to 2.49 × 10−3 doubles the dissolution flux.
Our findings were applied to the geo-storage of carbon dioxide in a carbonate saline aquifer. It was shown that the solubility restrictions of calcium carbonate curtail the increase of CO2 flux to 50% of that in the inert system.
Appendix
A. Linear stability analysis
The porous medium is considered to be infinite in the horizontal direction (x′) and semi-infinite in vertical direction (z′, taken as positive downward). This assumption is valid while the finger penetration depth is smaller than the domain depth, i.e., for small time. At time t′ = 0, the entire domain is quiescent, and solute and product free, i.e.v′(x′,z′,0) = 0, CA′(x′,z′,0) = 0, and CC′(x′,z′,0) = 0.
The linear stability analysis has been carried out using two methods: (a) the quasi-steady state approximation and (b) considering the dominant mode of the self-similar diffusion operator. Both these methods have previously been applied for inert systems.8,11 The dominant mode solution does not require the quasi-steady state approximation and has been shown to predict accurately the critical time for the onset of convection for inert systems.8 However, for an inert system the dominant-mode solution has been found to be less accurate at large time and solutions based on the quasi-steady state approximation have been suggested.8 These two methods are therefore mutually complementary since the quasi-steady condition is applicable when time is large. We apply both methods to obtain solutions for the reactive system where the product of the chemical reaction alters the density field. We obtain the time for onset of convection from each solution.
Quasi-steady state approximation (QSSA).
Under the quasi-steady state approximation (QSSA), for a given t we express the concentration perturbations as| | [CA0(η,t),CC0(η,t)] = [CA0*(η),CC0*(η)]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(σt). exp(σt). | (28) |
Then, the linear stability eqn (25)–(27) are degenerated as
| |  | (29) |
| | 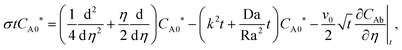 | (30) |
| |  | (31) |
with the boundary conditions,
v0 =
CA0* =
CC0* = 0 at
η = 0 and
v0 → 0, d
CA0*/d
η → 0 and d
CC0*/d
η → 0 as
η → ∞. Here, ∂
CAb/∂
η∣
t and ∂
CCb/∂
η∣
t represent the base concentration gradients at a given time
t. This eigenvalue problem was solved numerically by employing the outward shooting method explained in Kim and Choi's work.
11,28
Dominant mode analysis.
Summation of eqn (26) and (27) yields| | 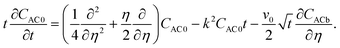 | (32) |
Here, CAC0 = CA0 + CC0 and CACb = CAb + CCb. The non-convective base state profiles CAb and CCb satisfy the boundary conditions CAb = 1, ∂CCb/∂η = 0 at η = 0 and CAb → 0, CCb → 0 as η → ∞. We consider the perturbation boundary conditions CA0 = 0, CC0 = 0, i.e., CAC0 = 0 at η = 0 and CA0 → 0, CC0 → 0, i.e., CAC0 → 0 as η → ∞.
The streamwise operator of CAC0 is
| |  | (33) |
Therefore,
CAC0 can be expanded as
| | 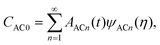 | (34) |
with
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ψACn
ψACn =
λnψACn(
η). The eigen functions
ψACn are Hermite polynomials in a semi-infinite domain with weight functions exp(−
η2) with the associated eigenvalues
λn = −
n.
8 Following Riaz
et al.,
8 it can be shown that in the limit of zero-wave number, the first mode decays at the slowest rate compared to the other modes and is therefore the dominant mode.
Considering the dominant mode of the perturbation concentration, CAC0 = AAC1η![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−η2), we define the growth rate of perturbation as
exp(−η2), we define the growth rate of perturbation as
| |  | (35) |
following Riaz
et al.8 For
βC/
βA = 1,
v0 is obtained from
eqn (25) as
| |  | (36) |
with boundary conditions
v0 = 0 at
η = 0 and
v0 → 0 as
η → ∞. Therefore, for
βC/
βA = 1, the above growth rate can be obtained semi-analytically.
B. Nonlinear numerical simulations
Initial and boundary conditions.
At time t′ = 0, the entire domain is quiescent, and is solute and product free, i.e.v′(x′,z′,0) = 0, CA′(x′,z′,0) = 0, and CC′(x′,z′,0) = 0. The top boundary is impermeable to the product and the fluid, and has the maximum concentration of solute: ∂CC′/∂z′(x′,0,t′) = 0, v′(x′,0,t′) = 0, and CA′(x′,0,t′) = 1. Here, v′ is the vertical component of the velocity vector in dimensionless form. Finite domain depth Lz′ and domain width Lx′ are considered. The bottom boundary is assumed impermeable to flow, solute and product, such that v′(x′,Lz′,t′) = 0, ∂CA′/∂z′(x′,Lz′,t′) = 0, and ∂CC′/∂z′(x′,Lz′,t′) = 0. Similarly, the vertical walls are impermeable to flow, solute and product, so that u′(0,z′,t′) = 0, ∂CA′/∂x′(0,z′,t′) = 0, ∂CC′/∂x′(0,z′,t′) = 0; and u′(Lx′,z′,t′) = 0, ∂CA′/∂x′(Lx′,z′,t′) = 0, ∂CC′/∂x′(Lx′,z′,t′) = 0.
Numerical methods.
The coupled nonlinear partial differential eqn (1)–(4) subject to relevant boundary conditions were solved numerically using the finite element, partial-differential equation solver Fastflo.47–49 The basic solution methods, described in previous publications by the group23,27 have been followed. For completeness, we describe these briefly here. A backward Euler time stepping scheme has been used for time discretisation. The coupled continuity and Darcy's equations were iteratively solved using the augmented Lagrangian method at each time step. Two convergence criteria for velocity v and pressure p have been satisfied at each time step: (i) the normalized velocity difference between two successive iterations, averaged over all corner nodes  for the m-th time step and n-th iteration; (ii) the divergence of velocity satisfies continuity such that ∇′·v′ ≤ 2 × 10−11.
for the m-th time step and n-th iteration; (ii) the divergence of velocity satisfies continuity such that ∇′·v′ ≤ 2 × 10−11.
Tests were carried out to ensure that the growth and the evolution of the fingering patterns were independent of mesh and time step resolutions. Six-noded triangular elements with quadratic interpolation were used. The minimum number of nodes required for convergence was found to increase with Da/Ra2. The results were found to be independent of time-step for 1.88 ≤ t′ ≤ 3.76. The Grid Péclet number and Courant number criteria for the minimum required time step was also satisfied, which ensured stability and accuracy of the solutions.5
The numerical algorithm was validated against results of Andres and Cardoso27 for zero-density contribution of the product.
C. Methods to find the time for onset of convection
In the linear stability analysis considering the dominant mode of the self-similar diffusion operator, the time for onset of convection, toc′, corresponds to the time at which the maximum growth rate with respect to the wave number becomes positive. This time denotes the critical time for the onset of instability of the boundary layer.
In the nonlinear simulations, the time for onset of convection tdc′, is obtained by noting the first local minimum in the solute dissolution flux at the interface as a function of time. Beyond this time, convective fingers become noticeable and influence mass transport by convection.4 This method has been previously used by Hidalgo and Carrera50 for an inert system and Andres and Cardoso23 for a reactive system.
The linear stability results using the dominant mode (DM) and the quasi-steady state approximation (QSS) are in good agreement. For the inert system, the predicted onset times are consistent with the previously published literature,8,10,11 thus validating our methodologies. For the reactive cases, the deviation is even smaller. The general variation of the onset time with reaction strength predicted from nonlinear numerical simulations is in agreement with that obtained from linear stability analysis. For inert systems, Hassanzadeh et al.5 reported the time for onset of convection from numerical simulation to be almost an order of magnitude higher than that obtained from linear stability analysis. In the present work, the ratio of time for onset of convection obtained from nonlinear simulations, tdc, to that obtained from linear stability (QSSA and Dominant Mode), toc, is of this order and is therefore acceptable.
D. Power-averaged mean number of fingers
The power-averaged mean number of fingers,27,39 at a given time instant, has been obtained by computing the fast Fourier transform (FFT) of the vertically-averaged solute concentration profile,  . The power-averaged mean number of fingers in the simulation domain is defined as
. The power-averaged mean number of fingers in the simulation domain is defined as  , where fi are the Fourier modes of the fast Fourier transform X(f,t) and Pi = ∣X(f)∣2 is the corresponding power in the Fourier space.
, where fi are the Fourier modes of the fast Fourier transform X(f,t) and Pi = ∣X(f)∣2 is the corresponding power in the Fourier space.
Acknowledgements
P. G. gratefully acknowledges the Dr Manmohan Singh Scholarship from St. John's College, Cambridge and the grant of study leave from Jadavpur University, Kolkata, India. We thank Csaba Katai and Phanos Anastasiou, undergraduate Research Project students, for carrying out some of the numerical simulations.
References
-
IPCC, in Special Report on Carbon Dioxide Capture and Storage, ed. B. Metz, et al., Cambridge University Press, 2005 Search PubMed.
- H. E. Huppert and J. A. Neufeld, Annu. Rev. Fluid Mech., 2014, 46, 255–272 CrossRef.
- A. Riaz and Y. Cinar, J. Pet. Sci. Eng., 2014, 124, 367–380 CrossRef CAS.
- H. Emami-Meybodi, H. Hassanzadeh, C. P. Green and J. Ennis-King, Int. J. Greenhouse Gas Control, 2015, 40, 238–266 CrossRef CAS.
- H. Hassanzadeh, M. Pooladi-Darvish and D. W. Keith, AIChE J., 2007, 53, 1121–1131 CrossRef CAS.
- J. A. Neufeld, M. A. Hesse, A. Riaz, M. A. Hallworth, H. A. Tchelepi and H. E. Huppert, Geophys. Res. Lett., 2010, 37, L22404 CrossRef.
- D. R. Hewitt, J. A. Neufeld and J. R. Lister, J. Fluid Mech., 2013, 719, 551–586 CrossRef CAS.
- A. Riaz, M. Hesse, H. A. Tchelepi and F. M. Orr, J. Fluid Mech., 2006, 548, 87 CrossRef CAS.
- H. Hassanzadeh, M. Pooladi-Darvish and D. W. Keith, Transp. Porous Media, 2006, 65, 193–211 CrossRef CAS.
-
D. A. S. Rees, A. Selim and J. P. Ennis King, Emerging Topics in Heat and Mass Transfer in Porous Media, Springer, Netherlands, 2008, pp. 85–110 Search PubMed.
- M. Chan Kim and C. Kyun Choi, Phys. Fluids, 2012, 24, 044102 CrossRef.
- D. Pritchard, J. Fluid Mech., 2013, 722, 1–4 CrossRef.
- A. Slim, J. Fluid Mech., 2014, 741, 461–491 CrossRef CAS.
- M. Chan Kim, Chem. Eng. Sci., 2015, 126, 349–360 CrossRef.
- V. Loodts, L. Rongy and A. De Wit, Chaos, 2014, 24, 043120 CrossRef CAS PubMed.
- R. Farajzadeh, B. Meulenbroek, D. Daniel, A. Riaz and J. Bruining, Comput. Geosci., 2013, 17, 515–527 CrossRef.
- T. J. Kneafsey and K. Pruess, Transp. Porous Media, 2010, 82, 123–139 CrossRef CAS.
- S. Backhaus, K. Turitsyn and R. E. Ecke, Phys. Rev. Lett., 2011, 106, 104501 CrossRef PubMed.
- A. C. Slim, M. M. Bandi, J. C. Miller and L. Mahadevan, Phys. Fluids, 2013, 25, 024101 CrossRef.
- T. F. Faisal, S. Chevalier, Y. Bernabe, R. Juanes and M. Sassi, Int. J. Heat Mass Transfer, 2015, 81, 901–914 CrossRef CAS.
- J. Ennis-King and L. Paterson, Int. J. Greenhouse Gas Control, 2007, 1, 86–93 CrossRef CAS.
- S. S. Cardoso and J. T. Andres, Nat. Commun., 2014, 5, 5743 CrossRef CAS PubMed.
- J. T. Andres and S. S. Cardoso, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046312 CrossRef PubMed.
- K. Ghesmat, H. Hassanzadeh and J. Abedi, J. Fluid Mech., 2011, 673, 480–512 CrossRef CAS.
- D. Pritchard and C. N. Richardson, J. Fluid Mech., 2007, 571, 59–95 CrossRef CAS.
- L. T. Ritchie and D. Pritchard, J. Fluid Mech., 2011, 673, 286–317 CrossRef.
- J. T. Andres and S. S. Cardoso, Chaos, 2012, 22, 037113 CrossRef PubMed.
- M. Chan Kim and C. Kyun Choi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 53016 CrossRef PubMed.
- T. J. Ward, K. A. Cliffe, O. E. Jensen and H. Power, J. Fluid Mech., 2014, 747, 316–349 CrossRef CAS.
- T. J. Ward, O. E. Jensen, H. Power and D. S. Riley, J. Fluid Mech., 2014, 760, 95–126 CrossRef CAS.
- M. A. Budroni, L. A. Riolfo, L. Lemaigre, F. Rossi, M. Rustici and A. De Wit, J. Phys. Chem. Lett., 2014, 5, 875–881 CrossRef CAS PubMed.
- M. Chan Kim, Chem. Eng. Sci., 2015, 134, 632–647 CrossRef CAS.
- T. J. Ward, O. E. Jensen, H. Power and D. S. Riley, Phys. Fluids, 2015, 27, 116601 CrossRef.
- V. Loodts, C. Thomas, L. Rongy and A. De Wit, Phys. Rev. Lett., 2014, 113, 114501 CrossRef CAS PubMed.
- C. Wylock, A. Rednikov, B. Haut and P. Colinet, J. Phys. Chem. B, 2014, 118, 11323–11329 CrossRef CAS PubMed.
- V. Loodts, L. Rongy and A. De Wit, Phys. Chem. Chem. Phys., 2015, 17, 29814–29823 RSC.
- I. Cherezov and S. S. S. Cardoso, Phys. Chem. Chem. Phys., 2016, 18, 23727–23736 RSC.
- C. Thomas, V. Loodts, L. Rongy and A. De Wit, Int. J. Greenhouse Gas Control, 2016, 53, 230–242 CrossRef CAS.
- A. De Wit, Phys. Fluids, 2004, 16, 163 CrossRef CAS.
-
L. Marini, Geochemical Sequestration of Carbon Dioxide, Elsevier, 2007 Search PubMed.
-
Roscoe Moss Company, Handbook of groundwater development, Wiley, 1990 Search PubMed.
- G. P. D. De Silva, P. G. Ranjith and M. S. A. Perera, Fuel, 2015, 155, 128–143 CrossRef CAS.
- National Chemical Database Service, Royal Society of Chemistry, URL: cds.rsc.org.
- A. C. Lasaga, J. Geophys. Res.: Solid Earth, 1984, 89(B6), 4009–4025 CrossRef CAS.
- Lecture notes of University of Wisconsin-Green Bay, URL: http://https://www.uwgb.edu/dutchs/Petrology/SolnCO3.htm.
- M. L. Szulczewski, M. A. Hesse and R. Juanes, J. Fluid Mech., 2013, 736, 287–315 CrossRef.
- CSIRO, Fastflo Tutorial Guide, CSIRO, Australia, 2000.
- A. N. Campbell, S. S. S. Cardoso and A. N. Hayhurst, Proc. R. Soc. London, Ser. A, 2005, 461, 1999–2020 CrossRef CAS.
- A. N. Campbell, S. S. S. Cardoso and A. N. Hayhurst, Chem. Eng. Sci., 2005, 60, 5705–5717 CrossRef CAS.
- J. J. Hidalgo and J. Carrera, J. Fluid Mech., 2009, 640, 441 CrossRef CAS.
|
| This journal is © the Owner Societies 2017 |
Click here to see how this site uses Cookies. View our privacy policy here. 





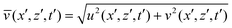 , while the average speed over the whole computation domain at each time instant has been obtained by evaluating
, while the average speed over the whole computation domain at each time instant has been obtained by evaluating  .
.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914. The inert system in Fig. 3(d) exhibits very weak motion, with severely curtailed finger formation and a sparse finger presence. However, for βC/βA = 1 and 1.5 [Fig. 3(e) and (f)], a large number of prominent sinking fingers are distributed throughout the domain, with new fingers forming at the interface. In these cases, the numbers of fingers are almost double of that in the inert case. For intermediate reaction strength, Da/Ra2 = 1 × 10−3, with beta ratio 1 and 1.5 at a dimensionless time of t′ = 34
914. The inert system in Fig. 3(d) exhibits very weak motion, with severely curtailed finger formation and a sparse finger presence. However, for βC/βA = 1 and 1.5 [Fig. 3(e) and (f)], a large number of prominent sinking fingers are distributed throughout the domain, with new fingers forming at the interface. In these cases, the numbers of fingers are almost double of that in the inert case. For intermediate reaction strength, Da/Ra2 = 1 × 10−3, with beta ratio 1 and 1.5 at a dimensionless time of t′ = 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252, the average speed of the whole domain is maintained at ∼70% of the peak speed obtained before the fingers reach the bottom of the domain. For high reaction strength, Da/Ra2 = 2.49 × 10−3, this ratio is maintained at ∼75%. However, for the inert system at the same dimensionless time, the average speed is reduced to 30% of the maximum speed before fingers hit the bottom boundary. Thus, a reaction accompanied by heavier or equal density product formation as the solute can significantly enhance convective mixing and maintain it long term.
252, the average speed of the whole domain is maintained at ∼70% of the peak speed obtained before the fingers reach the bottom of the domain. For high reaction strength, Da/Ra2 = 2.49 × 10−3, this ratio is maintained at ∼75%. However, for the inert system at the same dimensionless time, the average speed is reduced to 30% of the maximum speed before fingers hit the bottom boundary. Thus, a reaction accompanied by heavier or equal density product formation as the solute can significantly enhance convective mixing and maintain it long term. , and
, and  . These plots reveal valuable information about the early-time growth of the boundary layer and long-term dynamic behaviour of the fingering region. Situations with four different combinations of Da/Ra2 and βC/βA are discussed. Each curve represents one time instant, and the same time range is covered in all the plots. The boundary layer grows from the top interface (left) to the bottom of the domain (right) in the figures. At small reaction strength, Da/Ra2 = 0.15 × 10−3 and βC/βA = 1.5 [Fig. 5(a)], upon onset of convection, swelled regions start appearing in concentration profiles. This structure is maintained for some time, after which the concentration gradient is sharpened close to the interface as more solute is conveyed down from the interface. This behaviour is similar to that for inert situations reported by Andres and Cardoso.27 As the product density increases (βC/βA = 10, [Fig. 5(b)]), convection is established more rapidly. More prominent sharpening of the concentration gradient is observed demonstrating pronounced convective removal of solute from the interface and its effective transport towards the bottom of the domain.
. These plots reveal valuable information about the early-time growth of the boundary layer and long-term dynamic behaviour of the fingering region. Situations with four different combinations of Da/Ra2 and βC/βA are discussed. Each curve represents one time instant, and the same time range is covered in all the plots. The boundary layer grows from the top interface (left) to the bottom of the domain (right) in the figures. At small reaction strength, Da/Ra2 = 0.15 × 10−3 and βC/βA = 1.5 [Fig. 5(a)], upon onset of convection, swelled regions start appearing in concentration profiles. This structure is maintained for some time, after which the concentration gradient is sharpened close to the interface as more solute is conveyed down from the interface. This behaviour is similar to that for inert situations reported by Andres and Cardoso.27 As the product density increases (βC/βA = 10, [Fig. 5(b)]), convection is established more rapidly. More prominent sharpening of the concentration gradient is observed demonstrating pronounced convective removal of solute from the interface and its effective transport towards the bottom of the domain.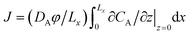 , or in dimensionless form, J′ = JLc/DAφCs. Reaction strengths ranging from Da/Ra2 = 0–2.49 × 10−3 are investigated for βC/βA = 0, 1 and 1.5.
, or in dimensionless form, J′ = JLc/DAφCs. Reaction strengths ranging from Da/Ra2 = 0–2.49 × 10−3 are investigated for βC/βA = 0, 1 and 1.5.



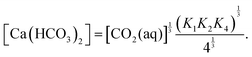
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) ,
,![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) .
.

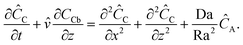
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) = v0(z,t)eikx,
= v0(z,t)eikx,

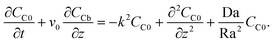
 , eqn (22)–(24) become
, eqn (22)–(24) become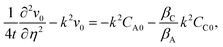
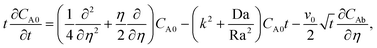

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(σt).
exp(σt).
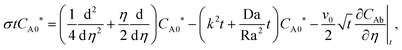

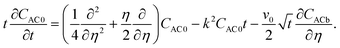

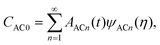
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ψACn = λnψACn(η). The eigen functions ψACn are Hermite polynomials in a semi-infinite domain with weight functions exp(−η2) with the associated eigenvalues λn = −n.8 Following Riaz et al.,8 it can be shown that in the limit of zero-wave number, the first mode decays at the slowest rate compared to the other modes and is therefore the dominant mode.
ψACn = λnψACn(η). The eigen functions ψACn are Hermite polynomials in a semi-infinite domain with weight functions exp(−η2) with the associated eigenvalues λn = −n.8 Following Riaz et al.,8 it can be shown that in the limit of zero-wave number, the first mode decays at the slowest rate compared to the other modes and is therefore the dominant mode.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−η2), we define the growth rate of perturbation as
exp(−η2), we define the growth rate of perturbation as

 for the m-th time step and n-th iteration; (ii) the divergence of velocity satisfies continuity such that ∇′·v′ ≤ 2 × 10−11.
for the m-th time step and n-th iteration; (ii) the divergence of velocity satisfies continuity such that ∇′·v′ ≤ 2 × 10−11.
 . The power-averaged mean number of fingers in the simulation domain is defined as
. The power-averaged mean number of fingers in the simulation domain is defined as  , where fi are the Fourier modes of the fast Fourier transform X(f,t) and Pi = ∣X(f)∣2 is the corresponding power in the Fourier space.
, where fi are the Fourier modes of the fast Fourier transform X(f,t) and Pi = ∣X(f)∣2 is the corresponding power in the Fourier space.








