Regarding the torsional flexibility of the dihydrolipoic acid's pharmacophore: 1,3-propanedithiol†
Annalisa
Vigorito
,
Camilla
Calabrese
,
Ettore
Paltanin
,
Sonia
Melandri
and
Assimo
Maris
 *
*
Dipartimento di Chimica G. Ciamician, Università degli Studi di Bologna, Via Selmi 2, 40126 Bologna, Italy. E-mail: assimo.maris@unibo.it; Tel: +39 051 2099502
First published on 22nd November 2016
Abstract
The conformational space of antioxidant dihydrolipoic acid has been explored through the investigation of its pharmacophore, 1,3-propanedithiol. Five of the possible 25 non-equivalent isomers (namely: gGGg′, gGGg, g′AGg, gAGg and g′AGg′) were observed in the 59.6–74.4 GHz frequency region using free-jet absorption rotational spectroscopy. Furthermore, for three of them, the 34S mono-substituted isotopologues were also detected in natural abundance. Theoretical simulations show that the balance of steric and electronic intramolecular interactions arises on a shallow conformational potential energy surface and suggest that in polar solvents the flexibility of the dithiol chain is greater than that in the isolated phase.
Introduction
Thiols are organic compounds containing a carbon-bonded sulphydryl (–SH) group. Although thiols may be considered sulfurated analogues of alcohols, their properties change significantly due to the size, electronegativity and polarizability differences between oxygen and sulfur atoms.Since the difference in electronegativity between S and H is small, the SH bond presents low polarity and shows hydrogen bonds weaker than those formed by the OH bond; on the other hand, sulphydryl groups can react forming sulfur–sulfur (–S–S–) covalent linkages, as in the case of proteins, where disulfide bonds formed between cysteine residues play an active role in their molecular folding and stability. Actually, the thiol/disulfide pair is a redox couple, with the following oxidation reaction: 2 –SH ↔ –S–S– + 2H+ + 2e−, and it is precisely this feature that makes it essential in several biochemical processes, involving both macromolecules containing cysteine residues and relatively small molecules, such as tripeptide glutathione1 (γ-Glu–Cys–Gly) and dihydrolipoic acid, which act as reducing agents. In particular, dihydrolipoic acid (DHLA hereafter, Fig. 1) is one of the most powerful cellular antioxidants (reduction potential −0.32 V).2 The oxidation of DHLA to lipoic acid involves the 1,3-propanedithiol terminal chain (13PDT hereafter, Fig. 1) which, thanks to the formation of an intramolecular disulfide bridge, becomes the 1,2-dithiolane cycle.3,4
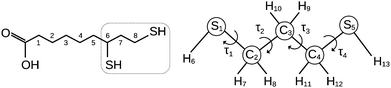 | ||
| Fig. 1 Sketch of dihydrolipoic acid (IUPAC: 6,8-dimercaptooctanoic acid) and 1,3-propanedithiol with the numbering of atoms and the torsional angles used in the text. | ||
Due to the high polarizability of the sulfur atom, thiols coordinate metals that behave as soft Lewis acids, and this is the reason why, since ancient times, they have also been known as mercaptans, that is, mercury capturers. Furthermore, the thiol-metal binding affinity is of relevance in biological systems: for instance metallothionein proteins are able to bind both physiological and xenobiotic heavy metals through the disulfide binding of their cysteine residues;5 iron–sulfur clusters constitute the active site of iron–sulfur proteins,6 and the already mentioned glutathione and DHLA create stable metal-sulfides.7,8 In particular, it has been evidenced that the bi-dentate 13PDT tail of DHLA efficiently acts as a metal chelator agent. Moreover, differently from other molecules, DHLA is able to cross the blood–brain barrier and for this reason it can be used as a drug to mobilize metal atoms attached to the brain cells towards the blood stream.3
Interested in the widespread biological activity of DHLA, we focused our attention on its structural features. Since DHLA contains a relatively long substituted alkyl chain, it is characterized by high torsional flexibility and its conformational space is described by nine dihedral angles giving rise to 39 = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 683 possible rotamers. As the full exploration of this space is a huge task, we based the present study on the conformational preferences of 13PDT, which represents the pharmacophoric group of DHLA. We used the high resolution of millimeter wave spectroscopy to obtain detailed structural information on the different conformations present in the cold and isolated environment of a free jet expansion. The experimental results were then rationalized and explained through a thorough and extensive comparison with theoretical calculations obtained under the same isolated conditions or in the simulated aqueous environment.
683 possible rotamers. As the full exploration of this space is a huge task, we based the present study on the conformational preferences of 13PDT, which represents the pharmacophoric group of DHLA. We used the high resolution of millimeter wave spectroscopy to obtain detailed structural information on the different conformations present in the cold and isolated environment of a free jet expansion. The experimental results were then rationalized and explained through a thorough and extensive comparison with theoretical calculations obtained under the same isolated conditions or in the simulated aqueous environment.
Experimental and computational details
A commercial sample of 13PDT (C3H8S2, Mw = 108.23 g mol−1, 99%) was purchased from Sigma-Aldrich and used as received, while carrier gases (Ar and He) were purchased from SIAD. 13PDT is a smelly, pale yellow liquid under ambient conditions. Its melting point is −79 °C, and its boiling point is 169 °C. The rotational spectrum of 13PDT was recorded in the 59.6–74.4 GHz frequency region using a millimeter-wave Stark-modulated free jet absorption spectrometer. Details of the experimental setup are given elsewhere.9–11 Briefly, a stream of carrier gas (Ar at P0 = 20 kPa or He at P0 = 40 kPa) was bubbled through the sample cooled in an ice bath and then expanded to about Pb = 0.5 Pa through a 0.3 mm diameter pinhole nozzle. The resolution and the estimated accuracy of the frequency measurements are about 300 kHz and 50 kHz, respectively.Characterization of the stable structures was done using standard geometry full-optimizations followed by calculations of the analytical second derivatives. The computations were run applying second-order Møller–Plesset (MP2) perturbation theory12,13 in combination with both Pople's 6-311++G(d,p)14,15 and Peterson and Dunning's aug-cc-pVTZ16,17 triple-valence basis sets. Internal rotation pathways were explored varying the involved dihedral angles by regular steps, whereas all the other internal coordinates were freely optimized. For this purpose only the less computationally demanding Pople's basis set was utilized. Finally, in order to simulate the effect of a polar solvent, both the minima and the internal motion pathways were investigated using a polarizable continuum model18 at the same levels of calculation as for the isolated phase. All quantum mechanical computations were performed using the Gaussian 09 (revision D.01) quantum chemistry package.19 Molecular graphics images were produced using the freely available UCSF Chimera20 and Gmolden21 packages.
Results and discussion
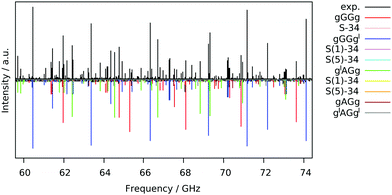
The free jet broadband rotational spectrum of 13PDT, recorded using Ar as a carrier gas (Fig. 2), appears to be quite dense reflecting the presence of various species. Typically in supersonic expansion beams, for a given molecule, the detectable species are conformational22 or tautomeric23 isomers, isotopologues,24 low energy vibrational satellites25 and torsional states generated by the tunnel effect between symmetrically equivalent isomers.26 Since 13PDT is a saturated compound, no tautomeric effects are involved but different conformers could be detected.Conformational analysis
For a complete conformational analysis, a 4-dimensional space defined by two skeletal torsional angles (SCCC, τ2 and τ3 in Fig. 1) and two sulphydryl dihedral angles (HSCC, τ1 and τ4 in Fig. 1) has to be considered. Three staggered positions (namely anti, gauche and gauche′, depending on an anticlockwise or a clockwise rotation, respectively) are possible for each dihedral angle, giving rise to 34 = 81 rotamers. Depending on the backbone orientation, the structures belong to nine “skeletal families”: AA, AG, AG′, GA, GG, GG′, G′A, G′G, and G′G′, where “A” and “G” stand for anti and gauche, respectively. Considering the position of the two terminal hydrogen atoms, each skeletal family consists of nine conformers: aa, ag, ag′, ga, gg, gg′, g′a, g′g, and g′g′, where “a” and “g” again stand for anti and gauche, respectively. However, due to the symmetry of the molecule, the number of non-equivalent backbone structures decreases to 4 families: AA, AG/AG′/GA/G′A, GG/G′G′ and GG′/G′G. Taking into account the orientation of the SH groups as well, 8 pairs and 16 quartets of equivalent conformers can be identified and 25 distinguishable rotamers are obtained. The list of non-equivalent conformers, including their symmetry group and degeneracies, is given in Table 1 with the ab initio zero-point corrected relative electronic energy values.19 The two more stable and nearly isoenergetic conformers are gGGg and gGGg′, whereas due to the steric hindrance of the sulfur atoms, the GG′ conformers lie 11 kJ mol−1 above. The data are in overall agreement with the ones reported for the condensed phase: vibrational spectroscopic studies show that the GG, AG and AA skeletal arrangements exist in the liquid phase, while GG is the only stable form in the crystalline phase.27 It is worth noting that rotational studies on the oxygen analogue 1,3-propanediol (C3H8O2) showed that its skeletal structure is constrained to the GG′ conformation, which is the less stable one for 13PDT.28,29 Thus, the strong intermolecular hydrogen bond between the hydroxyl groups causes 1,3-propanediol to behave almost oppositely to 13PD.| Conf. | Γ irr | n | MP2/6-311++G(d,p) | MP2/aug-cc-pVTZ | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ΔE0 | ΔE0,aq | A e/Be/Ce (MHz) | |μa/b/c| (D) | ΔE0 | ΔE0,aq | A e/Be/Ce (MHz) | |μa/b/c| (D) | |||
| a Minimum not reached: during the optimization process, the aGG′a species relaxes to the aGG′g′ species. | ||||||||||
| gGGg | C 2 | 2 | 0 | 39 | 5842/1439/1332 | 0/2.8/0 | 43 | 0 | 5658/1491/1364 | 0/2.7/0 |
| gGGg′ | C 1 | 4 | 17 | 107 | 5204/1606/1423 | 0.9/1.9/0.5 | 0 | 14 | 5164/1633/1440 | 0.9/1.9/0.4 |
| aGGg′ | C 1 | 4 | 235 | 366 | 5141/1657/1466 | 1.2/1.3/0.7 | 187 | 233 | 5138/1672/1478 | 1.0/1.2/0.7 |
| g′GGg′ | C 2 | 2 | 263 | 258 | 5618/1482/1348 | 0/0.8/0 | 178 | 123 | 5488/1532/1381 | 0/1.1/0 |
| aGGg | C 1 | 4 | 302 | 348 | 6001/1417/1330 | 0.2/1.5/1.0 | 336 | 287 | 5749/1485/1375 | 0.1/1.8/0.9 |
| aGGa | C 2 | 2 | 658 | 653 | 6460/1348/1292 | 0/0.0/0 | 640 | 557 | 5923/1464/1379 | 0/0.8/0 |
| g′AGg | C 1 | 4 | 151 | 100 | 8769/1105/1035 | 0.4/2.0/0.2 | 280 | 131 | 8742/1113/1040 | 0.5/2.0/0.0 |
| gAGg | C 1 | 4 | 217 | 149 | 8944/1090/1030 | 0.7/1.0/0.9 | 333 | 173 | 8821/1101/1037 | 0.8/1.1/0.7 |
| gAGg′ | C 1 | 4 | 308 | 219 | 9290/1078/1016 | 0.4/0.6/0.3 | 401 | 217 | 9123/1090/1025 | 0.4/0.7/0.4 |
| g′AGg′ | C 1 | 4 | 310 | 183 | 9125/1093/1021 | 0.1/1.5/1.3 | 399 | 189 | 9048/1101/1027 | 0.2/1.6/1.2 |
| aAGg | C 1 | 4 | 457 | 431 | 9190/1098/1032 | 0.3/0.4/0.1 | 505 | 390 | 9014/1110/1043 | 0.4/0.7/0.3 |
| gAGa | C 1 | 4 | 469 | 427 | 9118/1115/1043 | 1.5/1.5/0.0 | 555 | 429 | 8950/1126/1051 | 1.4/1.4/0.1 |
| g′AGa | C 1 | 4 | 469 | 404 | 9525/1091/1021 | 1.2/2.3/0.9 | 556 | 407 | 8870/1134/1052 | 1.1/2.3/1.0 |
| aAGg′ | C 1 | 4 | 607 | 503 | 8961/1125/1045 | 0.0/0.2/1.3 | 610 | 432 | 9347/1100/1031 | 0.1/0.1/1.4 |
| aAGa | C 1 | 4 | 767 | 735 | 9370/1124/1045 | 1.2/0.7/1.0 | 764 | 649 | 9141/1136/1058 | 1.1/0.9/1.2 |
| gAAg | C 2 | 2 | 159 | 3 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 531/897/865 531/897/865 |
0/0.5/0 | 369 | 127 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 746/896/865 746/896/865 |
0/0.7/0 |
| gAAg′ | C s | 2 | 207 | 0 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 547/896/864 547/896/864 |
0/0.5/1.3 | 408 | 129 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 772/895/865 772/895/865 |
0/0.7/1.3 |
| aAAg | C 1 | 4 | 462 | 310 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 396/908/872 396/908/872 |
0.7/1.7/0.8 | 591 | 356 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 455/911/875 455/911/875 |
0.6/1.7/0.7 |
| aAAa | C 2v | 1 | 804 | 655 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 209/921/879 209/921/879 |
0/2.8/0 | 816 | 602 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129/928/886 129/928/886 |
0/2.7/0 |
| gGG′g | C 1 | 4 | 923 | 958 | 4637/1755/1361 | 1.0/2.0/0.3 | 890 | 807 | 4604/1802/1387 | 1.1/2.1/0.2 |
| aGG′g | C 1 | 4 | 1184 | 1158 | 4601/1817/1381 | 1.8/2.2/1.0 | 1145 | 1001 | 4531/1884/1410 | 1.6/2.4/0.9 |
| g′GG′g | C 1 | 2 | 1200 | 1182 | 4741/1727/1358 | 0.9/2.0/0.8 | 1122 | 1007 | 4685/1779/1384 | 0.9/2.2/0.7 |
| gGG′g′ | C 1 | 2 | 1272 | 1170 | 4549/1860/1420 | 0.4/2.8/0.7 | 1229 | 1053 | 4525/1915/1451 | 0.3/2.8/0.6 |
| aGG′g′ | C 1 | 4 | 1473 | 1215 | 4504/1920/1440 | 0.7/2.8/0.1 | 1441 | 1105 | 4488/1962/1462 | 0.6/2.8/0.0 |
| aGG′a | C 1 | 2 | 1800 | 1474 | 4542/1912/1439 | 0.5/2.5/1.1 | 1752 | —a | 4604/1914/1456 | 0.6/2.4/1.1 |
Rotational spectrum
Guided by the values of the theoretical rotational constants (A, B and C, Table 1), which are directly related to the molecular mass distribution of each conformer, and those of the electric dipole moment components (μa, μb, and μc, Table 1), which give rise to the selection rules and intensities of rotational transitions, the spectra of nine species could be identified. The main features observed in the spectrum belong to the gGGg′, gGGg and g′AGg conformers whereas less intense lines are assigned to the corresponding 34S (natural abundance 4.3%) mono-substituted isotopologues and to the gAGg conformer.Since conformational relaxation processes through low energy barriers (around 400 cm−1) are common in Ar expansions,30 the presence of other conformers was checked using a lighter carrier gas, He instead of Ar, and the g′AGg′ species was then detected. Measured transition lines were fitted31 to Watson's S-reduced semirigid asymmetric rotor Hamiltonian (Ir representation)32 achieving the spectroscopic parameters summarized in Table 2. The conformational assignment was further confirmed by the values of the spatial coordinates of the S atoms, obtained from the experimental rotational constants of normal and isotopic species using Kraitchman's substitution method (rs).33 The equilibrium (re) ab initio predictions are compared to the rs structure in Fig. 3 and Table 3. Although a direct comparison between ab initio structures (referring to the equilibrium geometry) and experimental data (related to the ground vibrational state) must be considered with care, it is worth noting that the rotational constants and the substitution coordinates are better reproduced by Pople's basis set instead of the more extended Dunning's one.
| gGGg | Parent | 34S1 = 34S5 | |
|---|---|---|---|
| a Standard error in parentheses in the units of the last digit. b Values in squared brackets are fixed to the parent species ones. c Number of transitions. d Root mean square deviation of the fit. e Yes (y) or no (n) observation of a-, b-, and c-type transitions, respectively. f Minimum and maximum J quantum numbers for the observed rotational transitions. | |||
| A 0 (MHz) | 5815.075(9)a | 5774.18(3) | |
| B 0 (MHz) | 1437.049(4) | 1402.80(2) | |
| C 0 (MHz) | 1325.975(5) | 1294.99(2) | |
| D J (kHz) | 1.666(5) | 1.62(2) | |
| D JK (kHz) | −19.151(9) | −18.9(1) | |
| D K (kHz) | 71.9(1) | 71.7(5) | |
| d 1 (kHz) | −0.3640(6) | [0.3640]b | |
| d 2 (kHz) | −0.0148(2) | [−0.0148] | |
| N | 45 | 19 | |
| RMSd (kHz) | 50 | 53 | |
| a/b/ce | n/y/n | n/y/n | |
| J min–Jmaxf | 5–23 | 5–14 | |
| gGGg′ | Parent | 34S1 | 34S5 |
|---|---|---|---|
| A 0 (MHz) | 5364.435(3) | 5323.76(1) | 5329.96(1) |
| B 0 (MHz) | 1543.221(3) | 1507.18(2) | 1505.478(9) |
| C 0 (MHz) | 1382.752(3) | 1351.53(1) | 1350.551(9) |
| D J (kHz) | 2.082(6) | 2.06(1) | 2.053(9) |
| D JK (kHz) | −18.596(4) | −18.29(6) | −18.43(6) |
| D K (kHz) | 53.85(3) | 53.6(2) | 53.9(2) |
| d 1 (kHz) | −0.5320(5) | 0.54(3) | −0.498(9) |
| d 2 (kHz) | −0.0229(2) | — | −0.024(2) |
| H J (Hz) | −0.047(5) | — | — |
| N | 97 | 27 | 30 |
| RMSd (kHz) | 42 | 52 | 43 |
| a/b/ce | y/y/y | n/y/n | n/y/n |
| J min–Jmaxf | 5–24 | 5–15 | 5–17 |
| g′AGg | Parent | 34S1 | 34S5 |
|---|---|---|---|
| A 0 (MHz) | 8767.42(2) | 8741.83(2) | 8682.972(2) |
| B 0 (MHz) | 1100.891(4) | 1070.453(5) | 1075.142(5) |
| C 0 (MHz) | 1029.212(5) | 1002.296(5) | 1005.547(5) |
| D J (kHz) | 0.205(4) | [0.205] | [0.205] |
| D JK (kHz) | −4.95(1) | [−4.95] | [−4.95] |
| D K (kHz) | 71.8(6) | 76.6(6) | [71.8] |
| d 1 (kHz) | −0.0296(6) | [−0.0296] | [−0.0296] |
| N | 49 | 18 | 16 |
| RMSd (kHz) | 35 | 47 | 39 |
| a/b/ce | n/y/n | n/y/n | n/y/n |
| J min–Jmaxf | 3–24 | 3–14 | 3–13 |
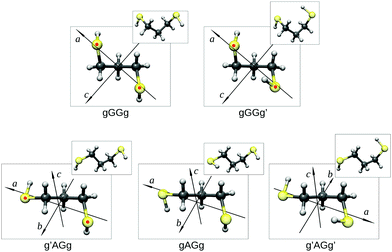 | ||
| Fig. 3 The observed conformers of 13PDT (re) showing their principal axis system and the substitution coordinates of the S atoms (rs, indicated as red points). | ||
| a | b | c | |||
|---|---|---|---|---|---|
| a Constain's errors34 expressed in units of the last decimal digit. b From MP2/6-311++G(d,p) geometries. c From MP2/aug-cc-pVTZ geometries. d Imaginary value. | |||||
| gGGg | S1 | r s | 2.0858(9)a | 0.550(3) | 0.15(1) |
| r e | 2.087 | −0.545 | −0.153 | ||
| r e | 2.041 | −0.562 | −0.155 | ||
| S5 | r s | 2.0858(9) | 0.550(3) | 0.15(1) | |
| r e | −2.087 | −0.545 | 0.153 | ||
| r e | −2.041 | −0.562 | 0.155 | ||
| gGGg′ | S1 | r s | 1.9892(2) | 0.592(3) | 0.17(1) |
| r e | 1.947 | −0.603 | −0.174 | ||
| r e | 1.927 | −0.607 | −0.173 | ||
| S5 | r s | 2.0377(8) | 0.542(3) | 0.168(9) | |
| r e | −1.993 | −0.557 | 0.175 | ||
| r e | −1.975 | −0.561 | 0.175 | ||
| g′AGg | S1 | r s | 2.5786(6) | 0.282(6) | 0.10(2) |
| r e | 2.573 | 0.285 | −0.103 | ||
| r e | 2.566 | 0.284 | −0.102 | ||
| S5 | r s | 2.3669(7) | 0.543(3) | i0.02(8)d | |
| r e | −2.367 | 0.540 | −0.037 | ||
| r e | −2.354 | 0.544 | −0.035 | ||
Information encoded in the measured spectral intensities was then analyzed. First the predicted μb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μc ratios were confirmed for all detected rotamers. Then, the relative intensities of the Q-branch lines of the gGGg′, gGGg and g′AGg conformers provided a direct indication of the population's distribution at the rotational levels, which is consistent with a temperature of 5–7 K. Finally, from the observed intensity values weighted on both the structural degeneracy and the square values of the calculated dipole moment components, the conformational relative abundances could be estimated as gGGg′
μc ratios were confirmed for all detected rotamers. Then, the relative intensities of the Q-branch lines of the gGGg′, gGGg and g′AGg conformers provided a direct indication of the population's distribution at the rotational levels, which is consistent with a temperature of 5–7 K. Finally, from the observed intensity values weighted on both the structural degeneracy and the square values of the calculated dipole moment components, the conformational relative abundances could be estimated as gGGg′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gGGg
gGGg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g′AGg
g′AGg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gAGg
gAGg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g′AGg′ = 13
g′AGg′ = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 in Ar and 13
0 in Ar and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9
9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in He expansion. These values are in qualitative agreement with the predictions derived by the calculated relative energies (MP2/aug-cc-pVTZ 13.0
1 in He expansion. These values are in qualitative agreement with the predictions derived by the calculated relative energies (MP2/aug-cc-pVTZ 13.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.2
5.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.0
3.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.3
2.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6 and MP2/6-311++g(d,p) 13.0
1.6 and MP2/6-311++g(d,p) 13.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.1
7.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.4
6.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.5
4.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.8) and reveal that in Ar expansion the conformational relaxation of g′AGg′ onto g′AGg takes place. Other conformers of 13PDT were expected to be observed considering their theoretical abundances, but they were not detected. The lack of observation of the higher-energy GG and AG rotamers can be explained considering both the values of the electric dipole moment components (as in the case of gAGg′) and the relaxation to lower-energy conformers in the supersonic jet. Regarding the most stable conformers of the AA species, the reason for their non-disclosure is ascribed to the low values of the electric dipole moment components.
2.8) and reveal that in Ar expansion the conformational relaxation of g′AGg′ onto g′AGg takes place. Other conformers of 13PDT were expected to be observed considering their theoretical abundances, but they were not detected. The lack of observation of the higher-energy GG and AG rotamers can be explained considering both the values of the electric dipole moment components (as in the case of gAGg′) and the relaxation to lower-energy conformers in the supersonic jet. Regarding the most stable conformers of the AA species, the reason for their non-disclosure is ascribed to the low values of the electric dipole moment components.
The experimental findings confirm that the structural arrangements adopted by 13PDT are different from the 1,3-propanediol ones, as already suggested by the computational results. Due to the lower strength of the SH hydrogen bond with respect to the OH one, the conformational preferences of 13PDT arise from a balance of electronic and steric effects, whereas the intramolecular hydrogen bond interaction is the main driving force in the case of the analogue 1,3-propanediol. As a consequence, the population of 13PDT spreads on a larger number of conformers. Moreover, it should be noted that, due to the lack of a dominant interaction, the changes in the conformational relative energy values obtained at different levels of calculation are not negligible.
Internal rotation pathways
A complete description of the conformational behavior of 13PDT requires the knowledge of the lowest energy connection paths between the minima in addition to their characterization. 2D sections of the four-dimensional conformational hyperspace were calculated exploring the sulphydryl internal rotation coordinates (τ1 and τ4) on a regular grid with Δτ = 15°. This approach was successful in the case of GG, AG and AA backbone arrangements but, for the high energy GG′ conformers, the SH rotations induce skeletal rearrangement towards more stable GG forms. The obtained potential energy surfaces (PESs), reported in Fig. 4 as contour level maps, show that the interconversion barriers for the SH rotation are in the 300–600 cm−1 range. For an easier interpretation of the 2D-PESs, the corresponding 1D-sections, at the level of the minima, are given in the ESI.† In agreement with the experimental evidence, the interconversion barrier from the g′AGg′ to g′AGg conformer appears low enough (about 300 cm−1) to allow its relaxation in the free jet expansions.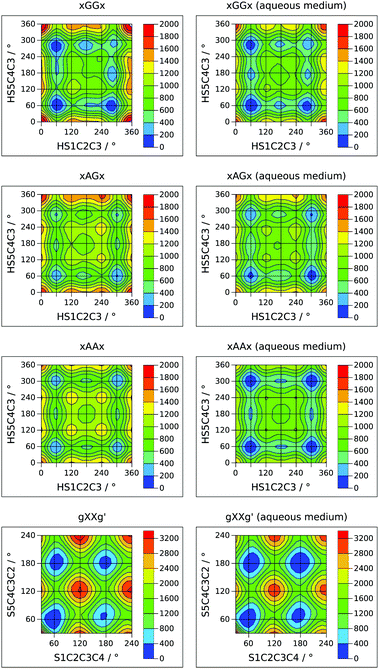 | ||
| Fig. 4 Theoretical 2D sections of the conformational PES (cm−1) of 13PDT under isolated conditions (left side) or in a polar medium (right side). | ||
The investigation of the backbone internal rotation pathways is a more challenging task because, during the exploration of the PES as a function of τ2 and τ3, the rearrangement of the SH groups easily takes place, introducing additional variables to the model and thus preventing the achievement of a 2D-PES. Nevertheless, choosing a gg′ orientation of the SH groups and varying the τ2 and τ3 dihedral angles in the τ = 30°–240° range by steps of Δτ = 10°, we could obtain a 2D-PES including the gGGg′, gGAg′, gAGg′, and gAAg′ species (see left side of Fig. 4). The calculated SCCC internal rotation barriers (1100–1600 cm−1) are higher than the sulphydryl ones and are compared with the CCCC ones estimated for butane.35
In order to extrapolate these results to an environment closer to the biological one, the effect of a polar medium was simulated using a polarizable continuum model.18 The relative energy of the minima and the 2D-PESs achieved using water's dielectric constant (εr = 78.3553) are reported in Table 1 and in the right side of Fig. 4, respectively. As a general result, the 2D-PESs appear to be flattened: most of the minima are closer in energy and also the interconversion skeletal barriers decrease, indicating that in a polar solvent the torsional flexibility of 13PDT is even greater than that in the gas phase. In particular, the stabilization energies due the polar medium increase with the “anti character” of the skeletal arrangement, being 14–16 kJ mol−1 for GG, 16–17 kJ mol−1 for AG, and 17–18 kJ mol−1 for the AA species. Consequently, the gAAg and gAAg′ conformers become the most stable minima. Concerning the GG′ forms, two trends can be recognized: the stabilization energies are 19–20 kJ mol−1 if the sulfur electronic clouds face each other (aGG′a and aGG′g′) and 15–17 kJ mol−1 otherwise. However, all the GG′ conformers remain the less stable ones.
PDB search and data analysis
The great flexibility related to the relatively flat PES of 13PDT suggests that the conversion between conformers might be feasible also in DHLA and can be considered a relevant factor in its biological activity. Indeed, many of the calculated barriers are low enough to be surmounted under room temperature conditions. To confirm this picture, a search for the DHLA ligand was carried out on the Worldwide Protein Data Bank (http://www.wwpdb.org).36 Inquiring about DHLA or its functional form dihydrolipoamide resulted in seven matches (PDB ID: 1DXM,371WOR,382PNR,392Q8I,401Y8N,411Y8O,41 and 1Y8P41) that are related to seven X-ray diffraction resolved macromolecular structures. Looking at the ligand conformations depicted in Fig. 5, two considerations can be made. Firstly, in all cases the alkanoyl chain assumes an anti arrangement, moving the carboxyl polar head away from the 13PDT pharmacophore and thus hindering their interaction. Secondly, different surroundings induce different structural arrangements of the 13PDT tail, evidencing its high degree of flexibility. These findings validate the assumption that the presence of the alkanoyl chain does not alter the torsional properties of the 13PDT frame. Hence, the 13PDT molecule can be considered as a reliable probe of DHLA's bio-active site behavior.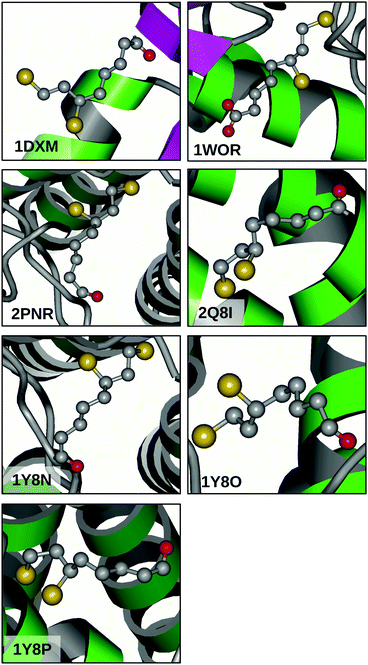 | ||
| Fig. 5 X-ray diffraction structures of the DHLA ligand in different biological environments available from the Protein Data Bank using the reported PDB identifiers. | ||
Conclusions
In this work, five different conformers and five 34S isotopologues of 13PDT have been characterized using rotational spectroscopy, which allows resolution at the quantum state level. Moreover, the interconversion dynamics among the conformers has been elucidated via quantum mechanical calculations. The transferability of the 13PDT monomer torsional properties to the related DHLA pharmacophoric group has been supported by the analysis of several DHLA structural PDB data.Due to the relatively easy capability to change its conformation, the 13PDT appears to be free to adapt its shape depending on the surroundings, in order to maximize the intermolecular interactions, providing a possible rationale for the different biochemical roles played by DHLA in cellular processes.
Acknowledgements
This work was supported by the University of Bologna through the “Ricerca Fondamentale Orientata” grants to AM and SM (RFO2014, RFO2015-2016). The authors thank Prof. Luca Dore for the use of the GESP software for the digital signal processing of the spectral data. AM thanks the CINECA award under the ISCRA initiative (HP10C7VAM5), for the availability of high performance computing resources.References
- F. Q. Schafer and G. R. Buettner, Free Radical Biol. Med., 2001, 30, 1191–1212 CrossRef CAS PubMed.
- L. J. Reed, B. G. DeBusk, I. C. Gunsalus and C. S. Hornberger, Science, 1951, 114, 93–94 CrossRef CAS PubMed.
- K. P. Shay, R. F. Moreau, E. J. Smith, A. R. Smith and T. Hagen, Biochim. Biophys. Acta, 2009, 1790, 1149–1160 CrossRef CAS PubMed.
- L. Packer and E. Cadenas, J. Clin. Biochem. Nutr., 2011, 48, 26–32 CrossRef CAS PubMed.
- M. Tomas, A. Tinti, R. Bofill, M. Capdevila, S. Atriana and A. Torreggiani, J. Inorg. Biochem., 2016, 156, 55–63 CrossRef CAS PubMed.
- R. Lill, Nature, 2009, 460, 831–838 CrossRef CAS PubMed.
- S. J. S. Flora and V. Pachauri, Int. J. Environ. Res. Public Health, 2010, 7, 2745–2788 CrossRef CAS PubMed.
- L. Patrick, Altern. Med. Rev., 2003, 7, 456–471 Search PubMed.
- S. Melandri, W. Caminati, L. B. Favero, A. Millemaggi and P. G. Favero, J. Mol. Struct., 1995, 352/353, 253–258 CrossRef CAS.
- S. Melandri, G. Maccaferri, A. Maris, A. Millemaggi, W. Caminati and P. Favero, Chem. Phys. Lett., 1996, 261, 267–271 CrossRef CAS.
- C. Calabrese, A. Maris, L. Evangelisti, L. B. Favero, S. Melandri and W. Caminati, J. Phys. Chem. A, 2013, 117, 13712–13718 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- R. Krishnan, J. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- D. E. Woon and T. H. Dunning, Jr, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. Couch, D. Greenblatt, E. Meng and T. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- G. Schaftenaar and J. Noordik, J. Comput.-Aided Mol. Design, 2010, 14, 123–134 CrossRef.
- D. Loru, I. Pena, J. L. Alonso and M. Eugenia Sanz, Chem. Commun., 2016, 52, 3615–3618 RSC.
- S. Melandri, L. Evangelisti, A. Maris, W. Caminati, B. M. Giuliano, V. Feyer, K. C. Prince and M. Coreno, J. Am. Chem. Soc., 2010, 132, 10269–10271 CrossRef CAS PubMed.
- E. A. Arsenault, D. A. Obenchain, Y. J. Choi, T. A. Blake, S. A. Cooke and S. E. Novick, J. Phys. Chem. A, 2016, 120, 7145–7151 CrossRef CAS PubMed.
- A. Maris, L. Favero, R. Danieli, P. G. Favero and W. Caminati, J. Chem. Phys., 2000, 113, 8567–8573 CrossRef CAS.
- C. Calabrese, Q. Gou, A. Maris, S. Melandri and W. Caminati, J. Phys. Chem. B, 2016, 120, 6587–6591 CrossRef CAS PubMed.
- J. N. Som and D. K. Mukherjee, J. Mol. Struct., 1975, 26, 120–123 CrossRef CAS.
- W. Caminati, S. Melandri and P. G. Favero, J. Mol. Spectrosc., 1995, 171, 394–401 CrossRef CAS.
- D. F. Plusquellic, F. J. Lovas, B. H. Pate, J. L. Neill, M. T. Muckle and A. J. Remijan, J. Phys. Chem. A, 2009, 113, 12911–12918 CrossRef CAS PubMed.
- R. S. Ruoff, T. D. Klots, T. Emilson and H. S. Gutowski, J. Chem. Phys., 1990, 93, 3142–3150 CrossRef CAS.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS.
- J. K. G. Watson, in Vibrational Spectra and Structure, ed. J. R. Durig, Elsevier, New York/Amsterdam, 1977, vol. 6 Search PubMed.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17–25 CrossRef CAS.
- C. C. Costain, J. Chem. Phys., 1958, 29, 864–874 CrossRef CAS.
- Y. Mo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 164–171 CAS.
- H. M. Berman, K. Henrick and H. Nakamura, Nat. Struct. Mol. Biol., 2003, 10, 980 Search PubMed.
- M. Faure, C. Cohen-Addad, M. Neuburger and R. Douce, Eur. J. Biochem., 2000, 267, 2890–2898 CrossRef CAS PubMed.
- H. H. Lee, D. J. Kim, H. J. Ahn, J. Y. Ha and S. W. Suh, J. Biol. Chem., 2004, 279, 50514–50523 CrossRef CAS PubMed.
- D. G. Vassylyev, C. N. Steussy and Y. Devedjiev, J. Mol. Biol., 2007, 370, 407–416 CrossRef PubMed.
- M. Kato, J. Li, J. Chuang and D. T. Chuang, Structure, 2007, 15, 992–1004 CrossRef CAS PubMed.
- M. Kato, J. L. Chuang, R. M. Wynn and D. T. Chuang, EMBO J., 2005, 24, 1763–1774 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Ab initio structural parameters and energy values for all conformers, mono-dimensional sections of the bi-dimensional conformational potential energy surfaces and measured transitions used in the fit. See DOI: 10.1039/c6cp05606g |
| This journal is © the Owner Societies 2017 |