Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The premolten layer of ice next to a hydrophilic solid surface: correlating adhesion with molecular properties†
Jonathan F. D.
Liljeblad
 ,
István
Furó
and
Eric C.
Tyrode
*
,
István
Furó
and
Eric C.
Tyrode
*
Department of Chemistry, School of Chemical Science and Engineering, KTH Royal Institute of Technology, SE-100 44 Stockholm, Sweden. E-mail: tyrode@kth.se
First published on 23rd November 2016
Abstract
In order to establish the potential correlation between the macroscopic ice adhesion and the molecular properties of the premolten layer (PML), the adhesion strength between ice and hydrophilic silica has been measured as a function of temperature. In addition, temperature-dependent molecular properties have been determined using techniques that are sensitive to different aspects of the PML, specifically total internal reflection (TIR) Raman, vibrational sum frequency (VSFS) and NMR spectroscopies. The ice shear adhesion strength was observed to increase linearly with decreasing temperature until −25 °C, where a plateau marked the adhesive strength having reached the cohesive strength of ice. Interestingly, at temperatures higher than −20 °C the ice samples slid on smooth (Ra < 0.4 nm) silica surfaces. This sliding behavior was not observed on rougher silica surfaces (Ra ∼ 6 nm). By varying the penetration depth of the evanescent field, TIR Raman was used to establish an upper limit to the thickness of the PML in contact with silica (<3 nm even at −0.3 K below the bulk melting temperature). Additional quantitative determination of the temperature-dependent thickness of the PML was obtained from 2H NMR measurements in mesoporous silica particles. Finally, the inherently surface specific technique, VSFS, which probed changes in the hydrogen bond environment, indicated at approximately −25 °C the onset of PML, followed by a marked structural change occurring just a fraction of a degree below the melting temperature. Jointly, the experimental approaches link, strongly and consistently, ice adhesion to the PML properties. Specifically, it is inferred that the premolten layer facilitates sliding and contributes to the observed friction behavior, provided its thickness is comparable to the surface roughness of the underlying silica substrate.
Introduction
Perhaps surprisingly, the statement of water being not solely in the state of either bulk ice or bulk liquid – while having been first floated by Faraday1 – only gained general acceptance in the 1990s.2,3 Since then, a barrage of modern experimental techniques have provided irrefutable evidence for premelting of ice and, moreover, showed that this is a rather general phenomenon that occurs in many materials.2 Premelting arises at the surface of ice and manifests itself in structures that are more disordered, and molecules that are more mobile, than those in the crystalline phase. As a surface phenomenon, it is expected to influence properties defined by the state of the surface, which include among other things, the reaction and release of trace gases from ice, as well as adhesion and friction.4 Interestingly, charge and mass transfer via pre-molten layers to and from hailstones is the pre-condition of the charge build up preceding lightning.3Despite having gained acceptance as a phenomenon, there is no detailed, molecular, experimentally, and consistently tested understanding of premelting.5,6 The core problem is illustrated by the fact that experimental techniques differ by orders of magnitude when it comes to estimating either the extension of the PML or its temperature dependence!3,5,7 This apparent cacophony persists when looking at other derived molecular properties of the PML. It is also reflected by the lack of established terminology – PML is called disordered interface by equally many and quasi-liquid layer or liquid-like layer by some. The lack of agreement in the estimated PML properties has often been attributed to impurities.8 While impurities may certainly be a factor, the apparently divergent results of experiments performed under very similar conditions but with different experimental methods suggest other underlying reasons: firstly, the use of methodologically inherent but, to each other, incompatible definitions of molecular order and dynamics when interpreting the results from different type of experiments and, secondly, experimental artifacts.
The aim of the research presented here is to link the temperature dependent macroscopic properties of adhesion and friction to the corresponding molecular properties of the PML. Specifically, we explore the PML that arises at the silica–ice interface using four different experimental approaches to extract information. The first consist of macroscopic shear adhesion measurements performed on a home-built apparatus. The remaining three are spectroscopic methods: total internal reflection (TIR) Raman spectroscopy,9 NMR spectroscopy, and vibrational sum frequency spectroscopy (VSFS).10,11 Although TIR Raman and NMR are very different from each other in the way they detect water molecules being in a state that is not that of bulk ice, they shall furnish reassuringly consistent information about the extension of the PML. For simplicity and for being able to compare our results to those previously reported, we shall define this extension as “thickness”. Yet, one should be acutely aware that the PML is (despite being often depicted in such manner) probably not a well-defined layer with sharp boundaries. Rather, the PML is an assembly of molecules whose behavior gradually resembles bulk ice as the distance to the defining interface (here, silica) increases. The thickness of the PML is then dependent on the threshold, either given or set up, by a particular experimental method for detecting water molecules behaving differently from molecules in ice. In the NMR studies below, this threshold is set by the reorientational dynamics of molecules. In TIR-Raman the spectrum responds to changes in vibration frequencies influenced by intermolecular interactions, in particular hydrogen bonds whose strength and arrangement defines the state of the material: ice, liquid water, or PML. In contrast to NMR and TIR-Raman, VSFS shall be used to probe in a very sensitive manner the state of the water molecules closest to the silica surface.
Due to its abundance on Earth, silica is a natural choice for a model hydrophilic solid surface that provides strong dipolar interactions and a rich hydrogen bond platform. The silica–ice interface also offers distinct advantages for studying the PML. First, it is available in pure form both as a flat surface that can be assessed by VSFS, TIR Raman, and shear adhesion measurements, but also as a surface in controlled-size pores with the large surface-to-volume ratios required for probing the PML using a relatively surface insensitive method like NMR. Second, it can be made very smooth which, as will be shown below, has important implications for the shear adhesion measurements. That being said, there exist a body of work that addresses the state of PML at the silica–ice interface, which include ellipsometry,12,13 VSFS,14 X-ray,15 NMR,16 and even ice adhesion measurements.17 However, the discord in terms of the description of the PML properties is as vivid as for the ice/vapour interface, with estimations for the PML layer extension ranging from non-existent,13,14 to tens16 and hundreds of nanometers.12,18 We will consider some of the potential causes of these discrepancies, and bring a more consistent understanding of the PML properties at this relevant mineral/ice interface.
Experimental
Materials
Water (H2O) was obtained from an Integral 15 Millipore filtration unit (resistivity of 18.2 MΩ cm and total organic carbon < 3 ppb) and D2O (resistivity higher than 1.1 MΩ cm) was purchased from Larodan Fine Chemicals and used as received. The IR-grade fused silica hemispheres (arithmetic average roughness, Ra < 0.7 nm and 10 mm in diameter) were custom-made by CVI-Melles Griot and the flat fused silica windows (Ra ≤ 0.4 nm and 12.5 mm in diameter) were obtained from Laser Components GmbH, Olching, Germany. Mesoporous silica particles of approximately 150 μm (mesh 80/120) in diameter were obtained from CPG Inc., with nominal mean pore diameter of 187.8 nm, and specific pore volume of 1.33 cm3 g−1. Chromosulphuric acid from Merck was used for cleaning the silica surfaces and particles.Surface roughness
The profilometry of the silica samples was performed using a NewView 5010 (Zygo Corporation, CT, USA) optical profilometer equipped with a 20× objective. Measurements were taken over a 0.33 × 0.44 mm area with a lateral resolution of 0.69 × 0.69 μm per pixel. The Zygo Metro pro version 9.1.6 software was used to record and process the data, as well as calculating the Ra and RMS roughness values. The topographical images were extracted from the profilometer raw data using a software developed in-house (see ESI8† for details).Roughness parameters with higher lateral resolution were obtained from AFM topography images using a Dimension FastScan (Bruker) atomic force microscope operated in tapping mode. The images were recorded using two Hz scan rate with FastScan A cantilevers featuring a resonance frequency of 1.4 MHz, a nominal spring constant of 18 N m−1, and a tip radius of 5 nm. For each sample a small and large scale image (10 × 10 μm and 2 × 2 μm, respectively) was recorded. Roughness parameters were calculated using the NanoScope Analysis version 1.5 software (Bruker).
Ice adhesion measurements
The home-built shear-adhesion-measurement device (see ESI1† for details) features a temperature controlled stainless steel sample chamber, and a pneumatic piston (CDQSB25-30D, SMC Corp.) equipped with a force sensor (LCMFD-200N, Omegadyne, Sunbury, OH, USA) connected to a plastic pushing rod. The voltage output (at the mV level) from the force sensor was recorded with a TC-08 computer interface (Pico Technology, Cambridgeshire, UK) and a LabView program. To achieve a reproducibly increasing force, an adjustable flow restriction valve (AS1002F, SMC Corp.) was fitted in the air supply line before the piston, and the flow adjusted to 10 mL min−1 at an inlet pressure of 2.8 bar. A pressure regulator (AW30-F02H, SMC Corp.) maintained a constant air pressure to the valve. The sample chamber was thermally insulated with a cork jacket and the temperature of the silica samples was monitored with a thermocouple mounted directly on one of the silica substrates. The temperature of the chamber's baseplate was controlled by a Julabo fluid recirculating cooler (Julabo FP50-ME).The ice/silica samples were prepared by placing a Teflon cylinder (internal diameter and wall thickness of 10 and 1 mm, respectively) filled with degassed water (0.8 mL) on top of the silica windows. The temperature of the chamber was then reduced to −20 °C to quickly freeze the sample. The intended measuring temperature was subsequently set and the sample was allowed to equilibrate for at least 20 minutes before performing the ice adhesion measurement.
TIR Raman spectrometer
The Raman spectra were collected in a home-built spectrometer described in detail elsewhere.19 The beam from the 532 nm CW laser (Laser Quantum, UK) is focused on the sample position with a Gradium lens (focal length 80 mm). An ultra-long working distance objective (M-Plan Apo 50X, NA 0.55, Mitutoyo, Japan) attached to a microscope was used to collect the Raman scattered light which was subsequently directed first through a long-pass filter and then to a combined spectrometer and CCD camera (Shamrock 303i, Newton DU940N-BV, Andor, Ireland). The surface sensitivity results from the Total Internal Reflection (TIR) geometry where the penetration depth of the evanescent field exciting the molecules is governed, among other things, by the angle of incidence (aoi) of the laser beam.9,20 For the silica/ice system investigated here the minimum effectively achievable penetration depth is ≈70 nm at 80° aoi. Polarization optics in the beam path enables selective recording of different combinations of polarizations of the excitation laser and Raman scattered light. In this work, unless otherwise stated, the spectra were recorded using S polarized incident light and y polarized scattered light (i.e. perpendicular to the plane of incidence of the excitation laser). Laser power densities are described in detail in the Laser heating section below. The presented spectra have been smoothed using running average over five data points, then baseline subtracted, and finally normalized to the highest intensity peak.VSF spectrometer
The home built VSF spectrometer used in this research has been described in detail elsewhere.21 Briefly, an 800 nm/90 fs/1 kHz pulse train is generated by a Integra-HE amplifier seeded by a Ti:light oscillator (both from former Quantronix, now Amplitude, France). The tunable IR pulses are produced in a parametric amplifier, HE-TOPAS-C (Light Conversion, Lithuania) pumped by 75% of the output power from the Integra-HE. The remaining power is converted to a bandwidth-tunable picosecond pulse in a home-built pulse shaper. The IR and 800 nm pulses are directed through the silica hemisphere in a co-propagating geometry and overlapped in space and time on the silica/ice interface. The angles of incidence, fixed at 70° and 55° for the 800 nm and IR beams respectively, are selected for preferentially enhancing the high wavenumber OH-stretching region.21 A combined spectrometer (Shamrock SR303i-B, Andor, Ireland) and EM-CCD camera (Newton DU971N-UVB, Andor, Ireland) was used to record the sum frequency (SF) signal. A detailed description of the power and power densities at the sample position is given in the Laser heating section below. A normalization procedure based on recording the non-resonant SF response from a gold coated silica hemisphere was applied to the data.21 Spectra were smoothed using running average over five data points, which resulted in a typical resolution of 3 cm−1.A model function featuring a sum of complex Lorentzians (eqn (1)) has been fitted to the data using the Levenberg–Marquardt algorithm in a commercial software (Origin 9.0) to extract the non-resonant contribution to the signal ANR, as well as the amplitude An, the resonance frequency ωn, and the homogeneous line width Γn of the nth vibrational mode (ωIR represents the tunable IR frequency). This approach is necessary since both constructive and destructive interference between peaks occurs in VSF spectroscopy.
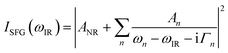 | (1) |
Before fitting, the data were normalized by the Fresnel factors which depend on the IR frequency and the specific experimental geometry employed21 (see ESI6† and ESI7† for details).
Spectroscopy cell and sample preparation
A custom-made sample cell (see ESI2† for details) was used for in situ freezing and temperature control of the silica/ice samples investigated with TIR Raman and VSF spectroscopies. Cooling fluid was circulated in the stainless steel cell body that features a cylindrical sample chamber (volume ≈0.5 mL) with tubing attached for injection of fluid. The open end of the chamber was fitted with a fused silica hemisphere (r = 5 mm) sealed with a Viton O-ring and clamped to the cell body with holders made out of a high thermal conductivity polymer (CoolPoly-E5101, Cool Polymers/Celeanese, RI, USA). The hemisphere was cleaned by immersion in chromosulphuric acid for at least two hours followed by repeated rinsing in ultrapure water. A cork jacket provided thermal insulation of the sample cell. To avoid frost formation on the hemisphere surface its exterior was purged with a small laminar flow of dry cold air. Initially, the temperature of an ice sample was measured using a thermocouple mounted in close proximity to the silica/ice interface to establish a calibration curve relating the temperature of the sample and the cooling fluid. Thereafter, the experimental temperature was set by the cooling fluid according to the calibration curve. Furthermore, after each experiment (i.e. measuring the full temperature series for a given sample) the temperature of the cell was slowly (in 0.1 K/10 minutes steps) increased until the ice sample began to melt to obtain an absolute temperature reference and verify the calibration curve. Before freezing at approximately −20 °C, with the sample cell turned upside down and the hemisphere facing down, degassed ultrapure water was injected to fill the cell, leaving a small air bubble inside which served to accommodate for the expansion upon freezing. The sample was left to equilibrate at least 30 min before carrying out measurements at a given temperature.The ice samples prepared were polycrystalline. Nevertheless, as the crystal sizes were at least ten times larger than the diameter of the laser beams used to probe the interfacial region, all the vibrational spectroscopy data shown here were obtained from single crystals of unknown orientation. The borders between crystals could be easily identified by the grain boundaries at the melting point, as well as by direct inspection of light microscope images using polarized light. SF spectra were collected in several different ice samples, showing an overall similar trend in the variation of the spectral features with temperature. However, for consistency and ease of comparison, the SF data presented here result from measurements carried out in a single ice sample.
Laser heating
A major concern when investigating the properties of the premolten layer is potential disturbances that the probing methods may induce. This is particularly relevant for TIR Raman and VSFS, where focused laser beams are directed towards the sample surface. We tested the heating effect experimentally, employing inverted white-light microscopes set above the sample positions in both spectrometers.21 Silica/ice samples were prepared and equilibrated at essentially the bulk melting point of ice (a few hundredths of a degree below 0 °C). Then, the power densities of the relevant laser beams were slowly increased until melting was first observed in the irradiated area. The microscope images provided sufficient contrast to observe the formation of thin wetting films of just a few tens of nanometers thick.22 Measurements were then performed using power densities half to one order of magnitude lower than the experimentally determined threshold. For the broadband IR laser beam this threshold was determined at ∼3200 cm−1, which is the peak absorption frequency in bulk ice. Note also that both the visible laser (800 nm) in VSF and the excitation beam in TIR Raman (532 nm) are totally internally reflected at the silica/ice interface, and thus do not propagate into the bulk ice beyond the penetration depth of the evanescent field. For the TIR Raman measurements, the power at the sample position of the 532 nm laser was 10 mW, with a projected beam waist of <10 μm. In the VSF measurements the power of the ∼100 fs IR laser varied between 0.2–0.5 mW depending on the central wavelength, while that of the 800 nm visible beam was typically 15 mW. The projected beam waists for the IR and visible pulses were ∼0.3 mm and ∼0.4 mm, respectively.NMR samples and setup
The mesoporous silica particles were cleaned by immersion in chromosulphuric acid at ∼40 °C for approximately four hours, followed by a rinsing procedure and vortex mixing, where the water volume was exchanged at least 20 times. The particles were then dried at ∼125 °C for several hours, before finally being placed in a 5 mm NMR tube and topped up with D2O. The sample contained 26 mg porous silica that filled the NMR tube up a column of ∼1 cm height. The nominal pore volume of the silica used can be obtained from the specific pore volume of 0.035 cm3. Prior to the experiment, the liquid level was reduced to ca. one mm above the level of the top of the water-saturated porous silica column. The total heavy water content of the sample (mw = 109.6 mg) was established from the mass difference after having dried the sample at 106 °C in an oven (that is, after having performed the NMR experiments). From the specific pore volume and the known density of D2O, the fraction of all added water contained within the pores was found to be xpore = 0.35.The NMR experiments were performed on a Bruker Avance III 500 NMR spectrometer with 76.8 MHz resonance frequency for 2H. A conventional broadband-observe probe was used to detect the time-domain 2H NMR signal as recorded after a single-pulse excitation. The length of the excitation pulse was set to 1 μs that corresponds to a pulse angle of ca. 11° (calculated form the 90° pulse length calibrated using the liquid 2H NMR signal above melting). The actual temperature of the sample versus the set temperature was calibrated in situ with Pt100 temperature sensors. The accuracy of the calibration (within the ±0.1 K precision of the temperature regulator system used) was tested by recording the characteristic signature (the appearance of a narrow peak) of melting in a bulk D2O sample.
Identification and measurement of the NMR signal of premolten water
Measuring the amount of water molecules in the premolten layer was based on the fact that, under the current detection regime, bulk D2O ice does not provide a central peak in the NMR spectrum but only the quadrupolar Pake pattern that is becoming increasingly featureless towards the melting point as a result of the increasing frequency of molecular jumps in ice. This feature is in stark contrast to the spectra recorded by quadrupole echo detection where a central peak appears.23 This behavior, connected to the nature of the molecular jumps,23,24 will be further investigated in detail elsewhere. Here it suffices to say that the spectra recorded for ice in porous silica differs from that in bulk ice, by the presence of a large central peak of ca. 8–10 kHz line width at all explored temperatures (see ESI10† for details). This 2H NMR peak is assigned to the premolten layer.25–27One disadvantage with single-pulse detection is that probe ringing introduces transients, which can be significantly suppressed by introducing a few microseconds waiting time after the excitation pulse. However, as a consequence of this waiting time, the broad spectrum of the ice component becomes strongly distorted, a problem that is amplified by the effect of the remaining transients. Hence, extracting the intensity of the peak assigned to the premolten layer requires extensive baseline correction that is nonetheless, rather straightforward at low temperatures, where a simple linear baseline correction suffices. However, closer to the melting point (see the discussion below concerning the melting point in pores) the spectrum of the ice component becomes increasingly motionally averaged23 and thereby narrower. Hence, distinguishing between the still much broader ice peak and the relatively narrower premolten peak becomes less evident. In addition, close to the melting point a “central” peak even in the spectrum of bulk ice can be observed. Yet, at the highest temperature below the melting point explored here, the relative intensity of that peak is more than one order of magnitude lower than that of the premolten peak. These effects jointly form one factor that limits our uppermost temperature to ca. 1.5 °C below the pore melting point of ice.
The other limiting factor is the distribution of pore sizes in the explored porous glass. As described by the Gibbs–Thomson equation,28 materials melt in pores at temperatures inversely proportional to the pore size. Hence, a size distribution leads to a distribution of the pore melting points (indeed, this is the way one often detects pore size distribution in NMR cryoporometry29,30). For this reason, ice in pores smaller than the average size melts at temperatures lower than the average pore melting temperature. This is actually detectable by the appearance of a small and narrower peak on the top of the premelting peak. Coincidentally, the onset of this effect is also around ca. 1–1.5 °C below the average pore melting point of ice.
NMR intensity calibration and the extraction of the PML thickness
The 2H integral intensity of the premolten peak IPML![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) raw(T) recorded at different temperatures was first corrected as IPML(T) = IPML
raw(T) recorded at different temperatures was first corrected as IPML(T) = IPML![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) raw(T)/iac(T) with relative variation of the integral intensity iac of perdeuterated acetone compared to its value at 5 °C (that is, iac(5 °C) = 1 while iac(−30 °C) = 1.25). This latter procedure accounts for the intensity variation of the 2H NMR signal because of the inverse proportionality of the nuclear magnetization to the temperature (Curie's law) and because of the temperature dependence of NMR probe response.30 As resulted by this correction, IPML(T) is directly proportional to the number of water molecules in premolten state. In addition, the 2H integral intensity Itotal was recorded at 5 °C where all ice was molten (note that bulk melting temperature for D2O is 3.8 °C). Considering that the fraction of water imbibed into the pores was xpore = 0.35, the relative amount of premolten water within the pores can be obtained as
raw(T)/iac(T) with relative variation of the integral intensity iac of perdeuterated acetone compared to its value at 5 °C (that is, iac(5 °C) = 1 while iac(−30 °C) = 1.25). This latter procedure accounts for the intensity variation of the 2H NMR signal because of the inverse proportionality of the nuclear magnetization to the temperature (Curie's law) and because of the temperature dependence of NMR probe response.30 As resulted by this correction, IPML(T) is directly proportional to the number of water molecules in premolten state. In addition, the 2H integral intensity Itotal was recorded at 5 °C where all ice was molten (note that bulk melting temperature for D2O is 3.8 °C). Considering that the fraction of water imbibed into the pores was xpore = 0.35, the relative amount of premolten water within the pores can be obtained as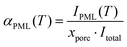 | (2) |
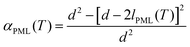 | (3a) |
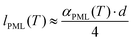 | (3b) |
Results and discussions
Ice adhesion on neat silica
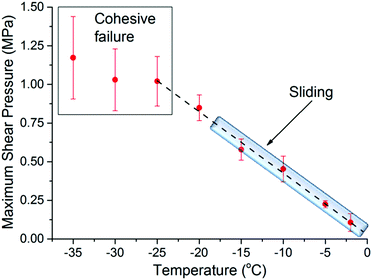
Fig. 1 shows the maximum shear adhesion pressure (i.e. the pressure where failure occurs) of ice on ultra-smooth silica substrates (Ra < 0.4 nm) as a function of temperature (note that the shear adhesion differs from the tensile adhesion, which is typically an order of magnitude higher for silica/ice interfaces).3,17,18 The data shows that the adhesion strength first increases almost linearly as the temperature decreases, and then remains, within error, approximately constant at temperatures below −25 °C. Depending on the temperature of the measurement, three different behaviors were noticed. The first, defined as cohesive failure and observed at −25 °C and lower temperatures, is characterized by traces of ice left behind on the substrate upon removal of the ice cylinder. In this range, the strength of the adhesion is at least comparable to, if not higher than, the cohesive strength of the bulk ice. The larger error bars in this regime are a consequence of the stochastic breaking process occurring in the bulk (Fig. 1). The second, defined as adhesive failure and observed between −20 °C and −25 °C, is assigned to cases where the ice cylinder, at a given pressure, suddenly detaches completely from the substrate, leaving behind a clean silica surface. The third and most interesting behavior was observed between 0 °C and ∼−20 °C, when the ice cylinder was seen to consistently slide on the silica surface when performing the adhesion measurements (see movie in ESI†). This latter behavior has been rarely reported in the ice adhesion literature.4,17The sliding behavior is particularly worth remarking, because on rougher silica substrates (vide infra) ice does not slide at any temperature, detaching exclusively by adhesive or cohesive failure. The general trend depicted in Fig. 1, with an almost linear increase of the adhesion strength followed by a cohesive regime, as well as the sliding behavior for smoother samples is in agreement with what has been previously reported by Jellinek.17,18 Although not experimentally proven, it was suggested then that the transition from sliding to adhesive/cohesive failure, was influenced by the thickness of the PML relative to the surface roughness. The underlying argument is that the premolten layer promotes sliding, provided it is sufficiently thick to prevent mechanical interlocking by ice engaging groves in the substrate surface: the molecular properties of the premolten layer should then govern the macroscopic adhesion. To establish such correlation we make use of vibrational spectroscopy and NMR.
The thickness of the premolten layer
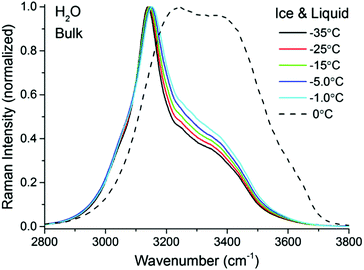
A closer examination and fitting of the ice spectra in Fig. 2, together with those collected at other polarization combinations (see ESI3†), reveal the presence of at least four resolvable bands, centered at approximately 3050, 3140, 3270, and 3375 cm−1. Although these bands associated with the OH stretching modes have been previously identified,32–35 the detailed assignments remain a source of debate, mainly because of the complicated interplay between OH-bonds of different strengths and in particular, their intermolecular coupling dynamics.36–38 Agreement is found, however, in the assignment of the dominant ∼3140 cm−1 peak in Fig. 2 to the collective in-phase OH stretch of tetrahedrally coordinated water molecules.32,33,35–37 Without going further in the assignment of the remaining bands, for the purpose of the general discussion of the TIR Raman spectra below, it suffices to stress the spectral differences between the solid and liquid forms of H2O, namely sharp bands at lower wavenumbers are linked to strongly hydrogen bonded molecules in ice, while broader features at higher wavenumbers are accordingly associated to more loosely coordinated molecules in the liquid.
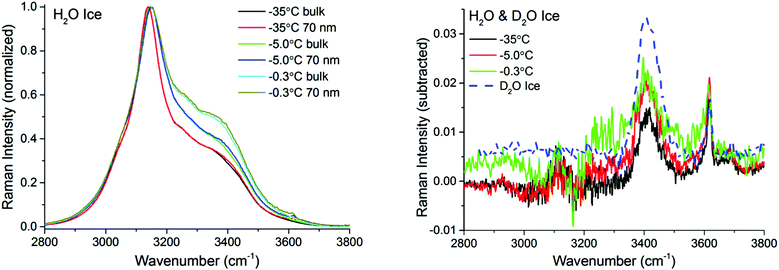
Fig. 3 left shows pairs of closely overlapping TIR Raman spectra from the “surface” and bulk collected at three different temperatures, ranging from −35 °C to −0.3 °C. The difference spectra (Fig. 3 right) are significant, and show two clear peaks at ∼3410 cm−1 and ∼3620 cm−1, with essentially temperature-independent centre positions and absolute intensities. The observed lack of temperature dependence is inconsistent with the expected behavior of a premolten layer, particularly when approaching the melting point. In order to determine the origin of the peaks in the difference spectra, experiments were also performed with D2O ice. Replacing the hydrogen atoms of water by the heavier deuterium red-shifts all the ice spectral features by ∼900 cm−1, which should leave in principle, no bands in the OH stretching region. However, the same features observed for H2O ice remained for D2O ice (dashed line in Fig. 3 right), which implies that the bands do not arise from either ice or the PML. They are instead assigned to SiOH groups trapped within the bulk fused silica substrate.42,43
To make certain that potential spectral features from the PML were not obscured by substrate bands, additional TIR Raman measurements were performed with D2O ice (Fig. 4). As previously recognized,32,37,38 the patterns of the spectral features in D2O ice are not identical to those of H2O ice. Notwithstanding, they show obvious resemblance, with a more intense peak at low frequencies (i.e. 2330 cm−1), followed by weaker and broader bands at higher wavenumbers (note that D2O ice melts at +3.8 °C). The difference spectra in the OD stretching region shown in the inset of Fig. 4 may reveal ever slightly higher intensities for the bands associated with weaker hydrogen bonds close to the melting point; however, within error, no significant differences are observed at the two extreme temperatures recorded.
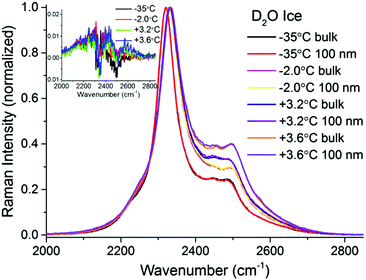 | ||
| Fig. 4 TIR Raman Sy spectra of D2O ice (melting temperature +3.8 °C) next to a fused silica substrate at various temperatures, collected at two penetration depths: “bulk” and 100 nm. The spectra have been normalized to the peak centred at ∼2330 cm−1. The inset (magnification shown in ESI4†) shows the surface contribution (subtraction of bulk spectrum from 100 nm spectrum for each temperature). | ||
There are two possible explanations for these results: (i) the PML thickness is very small compared to the shortest penetration depth of the evanescent wave, and/or (ii) its spectral features are not significantly different from those of bulk ice. Option (ii) can be discarded, considering previous IR measurements on thin ice films,40 as well as confocal Raman measurements on porous silica samples (data to be presented elsewhere), that indicate that the PML vibrational spectra clearly differs from that of ice, resembling more that of liquid or supercooled water. This is further substantiated with the sum frequency results described below. Hence, we infer that the thickness of the PML is lower than the detection limit of TIR Raman at all temperatures measured. Specifically, from the subtracted spectra shown in Fig. 3 and 4 and using as model for the PML the spectra of supercooled water, the PML thickness as determined by TIR Raman, is conservatively estimated to be thinner than 3 nm, even at temperatures as close as 0.3 °C from the bulk melting temperature.
Following the procedure described in detail in the Experimental section, the estimated thickness of the premolten layer lPML (see eqn (3b)) as a function of temperature is presented in Fig. 5. The temperature scale in Fig. 5 is relative to the approximate mean pore melting point of 3.3 °C as obtained by conventional cryoporometric experiments (the bulk melting point inside the pores is suppressed as predicted by the Gibbs–Thomson equation).30
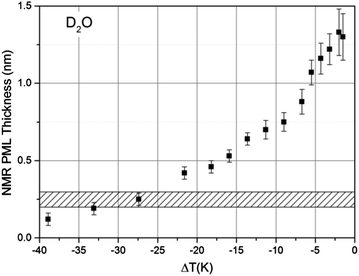 | ||
| Fig. 5 The thickness of the PML layer derived (see lPML in eqn (3b)) from 2H NMR measurements as a function of temperature, measured on porous silica particles imbibed with D2O. The ΔT is relative to the approximate mean pore melting point that is ∼3.3 °C for the silica particles used. The shaded area indicates the customary range given for the thickness of a monolayer of water in the liquid state. | ||
While premelting has been frequently detected by NMR both in pores but also on free-standing small ice particles,44 the preferred detection method has been 1H NMR.16 Yet, in the 1H NMR spectrum the signals from ice and premolten water cannot be as easily distinguished45 as in the corresponding 2H NMR spectrum, particularly when approaching the melting point where the molecular mobility in ice increases.23 This is illustrated in the ESI10† where it is shown that the 2H NMR signal of the PML layer can be clearly distinguished upon comparison of the spectra recorded in bulk ice and ice imbibed in the porous glass.
Further support for the identification of the PML–NMR signal can be obtained by comparing the signal intensity in porous glasses with varying pore sizes. As indicated by eqn (3a) in the Experimental details, the relative intensity of the signal αPML is inversely proportional to the mean pore diameter, a fact that has been verified both for water45 and other liquids exhibiting premelting.46 For the same reason, premelting in porous materials was typically observed by NMR in systems with small pore sizes. Notwithstanding, as it has been demonstrated the PML thickness is sensitive to the curvature of the pore wall.46 Consequently, porous silica particles with rather large pores (i.e. 187.8 nm) were selected in this study to facilitate the comparison of the NMR data with the TIR Raman and VSFS observations on flat surfaces.
The only comparable temperature-dependent data set we are aware of has been collected in Vycor glasses with 4–50 nm pore diameter;16 Vycor glasses typically exhibit far less regular pore structures and broader pore size distributions30 than those manufactured by Controlled Pore Glasses. In contrast to the data presented in Fig. 5, the data from Ishizaki et al.16 seem to indicate that the premolten layer grows continuously up to complete melting. We believe the data within a few degrees to the pore melting temperature, were wrongly attributed to the PML16 since the contribution of completely molten pore volumes was neglected. Hence, the data from Ishizaki et al.16 reflects not the extension of the premolten layer but instead the width of their pore size distribution (see NMR section in Experimental details). As an additional contributing methodological reason, the 1H NMR spectrum of the premolten phase is narrower (ca. 3 kHz broad45) than the corresponding 2H NMR spectrum (ca. 8–10 kHz, vide supra), while the 1H spectrum of the liquid within molten pores is ca. 6 times broader (>0.5 kHz, caused by magnetic field inhomogeneity to which 1H is more sensitive, in direct proportionality to its high gyromagnetic factor) than the corresponding 2H NMR spectrum. Hence, the NMR signal contributions from the premolten layers and molten pores cannot be easily distinguished by 1H NMR employed by Ishizaki et al.16
The NMR data show a progressively faster increase in the PML thickness as the temperature approaches the melting point but, due to the limitations discussed above, the thickness at temperatures ΔT < 1.5 K, could not be assessed. Still, this latter temperature range was accessible by TIR-Raman, yielding a thickness estimate of <3 nm. On the other hand, the NMR data presented in Fig. 5 shows that around ΔT ∼ 25 K the PML becomes less than a monolayer thick. Notwithstanding, even in that region we find that a very small fraction of water molecules exhibits some rapid re-orientational dynamics, which is the underlying reason for motionally averaging out the static quadrupole coupling and thereby obtaining a broad, yet isotropic peak. The statement “less than a monolayer thickness” implies that, in this temperature range, the premolten fraction is not any longer a continuous layer (and, thereby, may not be called PML) but a collection of individual molecules that behave more like defects in a crystalline structure.
VSF spectroscopy: PML onset and molecular insight
In contrast to TIR-Raman, VSF spectroscopy is intrinsically surface specific because only molecules in a non-centrosymmetric environment (which is always the case at an interface) can contribute to the sum frequency generation. This removes the need for background subtraction. In addition, data can be recorded in different polarization combinations, which facilitate spectral assignments. In light of the essentially negative result (that is, the absence of a signal that can be assigned to PML) by TIR-Raman and the concluded lack of PML signature in previous spectroscopic experiments on silica or silica-like surfaces,13,14 one important function of the VSFS experiments was to verify both (i) the existence of molecules at the silica–ice interface that are not in the state characteristic of bulk ice and (ii) verify that the system evolves with temperature on a manner that is consistent with the NMR results presented in Fig. 5.In Fig. 6 the VSF spectra recorded in the SSP, PPP, and SPS polarization combinations for −38 °C ice and liquid water, both in contact with silica, are shown for reference. In contrast to TIR-Raman, the VSF spectra present additional bands at higher wavenumbers, demonstrating that at the interface there is a significant larger fraction of water molecules that form weaker hydrogen bonds. We stress that this, in ice, is not a signature of PML but the expected behaviour at an interface to which water cannot or has more limited options to hydrogen bond. We recall that the experimental geometry used, preferentially enhances the SF response at high wavenumbers making it easier to detect changes in the bands at high frequencies21 (Fresnel factor corrected spectra can be found in ESI7†). When compared with the VSF spectra of liquid H2O, the ice spectra at −38 °C displays lower absolute intensities, but at the same time sharper and more prominent bands at lower wavenumbers. As described in more detail below, this difference in absolute intensities is attributed to the conflicting molecular ordering imposed by the underlying ice crystal and the negatively charged silica surface.
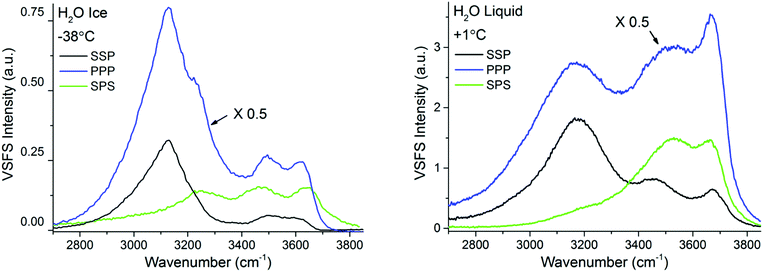 | ||
| Fig. 6 VSF spectra recorded in the SSP, PPP, and SPS polarization combinations of H2O ice at −38 °C (left) and H2O liquid at +1 °C (right). Note that the intensity in the PPP spectra has been divided by 2 for ease of comparison. The spectra fitted and corrected by the Fresnel factors can be found in ESI7.† | ||
The features observed at higher wavenumbers, mainly at ∼3350 cm−1, ∼3450 cm−1, ∼3550 cm−1, and ∼3630 cm−1 are in turn linked to under-coordinated water molecules present in the top half bilayer, close or in direct contact to the silica substrate. The first two resonances are near in frequency to features observed at the single crystal ice/vapour interface below 200 K,51,52 which were tentatively assigned to three-coordinated water molecules with dangling lone pairs.51 The remaining bands at the blue end of the spectra (Fig. 6), not observed at the ice/vapour interface, are in turn assigned to weakly hydrogen bonded water molecules in direct contact to the fused silica surface. The high frequency of these modes would indicate that the molecules or moieties participating in the H-bond pair do not accept themselves any additional H-bonds.54,55 Although the peak position of the highest frequency mode closely corresponds with the band assigned in TIR Raman to bulk SiOH groups (see Fig. 3), the OH feature in the SF spectra rapidly exchanges when in contact with D2O,19 which indicates that it originates from accessible surface groups. Nonetheless, SF experiments using silica surfaces with varying Si–OH group densities (to be presented elsewhere), suggest that this latter band may indeed be linked to weakly hydrogen bonded surface silanol groups.
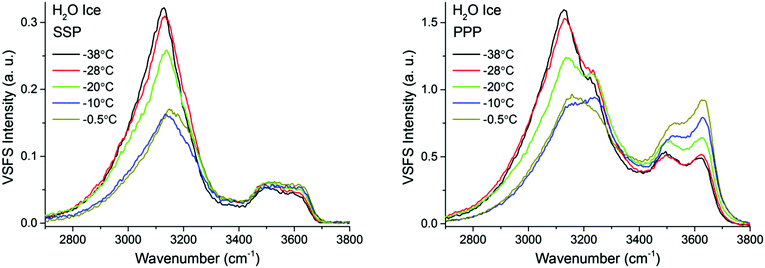 | ||
| Fig. 7 VSF spectra recorded in the SSP (left), and PPP (right) polarization combinations of H2O ice in contact with fused silica at various temperatures ranging from −38 °C and −0.5 °C. SPS spectra, as well as the Fresnel factor corrected spectra can be found in ESI5 and ESI7.† | ||
At temperatures exceeding −0.5 °C and in a limited temperature interval before reaching the bulk melting temperature, the VSF spectral features display a contrasting behaviour as shown in Fig. 8, where both SSP and PPP spectra are presented. First and most remarkably, the overall intensity of the SF response rapidly increases, remaining however, substantially lower than when in contact with liquid water (note the liquid spectra in Fig. 8 have been rescaled for ease of comparison). Second, a new band at ∼3400 cm−1, reminiscent of one of the dominant bands in the liquid spectra (see normalized spectra in ESI7† to better apprehend this change), appears gradually. Another detail worth noting is the appearance of a well resolved shoulder in the −0.3 °C spectra at ∼3050 cm−1, that coincides in frequency with a similar feature observed in the bulk Raman spectra of H2O ice (see Fig. 2).
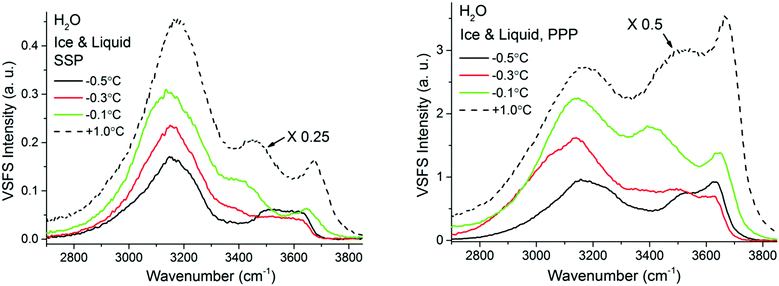 | ||
| Fig. 8 VSF spectra recorded in the SSP (left), and PPP (right) polarization combinations of H2O ice in contact with fused silica at various temperatures ranging from −38 °C and −0.5 °C. SPS spectra, as well as the Fresnel factor corrected spectra can be found in ESI5 and ESI7.† VSF spectra recorded in the SSP (left), and PPP (right) polarization combinations of H2O ice in contact with fused silica at various temperatures ranging from −0.5 °C to −0.1 °C. The corresponding spectra for liquid water are also added for reference. Note that the liquid water spectra, shown as dashed lines, have been divided by 4 or 2 for ease of comparison. SPS spectra, as well as the Fresnel factor corrected spectra can be found in ESI7.† | ||
The most important variations of the spectral features as a function of temperature are summarized in Fig. 9, where the fitted amplitudes of selected peaks at different polarization combinations are shown. All fitted parameters, including additional details of the fitting procedure can be found in the ESI11.†Fig. 9 highlights the three distinct temperature ranges with qualitatively different behaviors: stable spectra below −28 °C, and significant changes but with very different character between −25 °C and −10 °C on one hand, and less than a degree below the bulk melting temperature on the other hand.
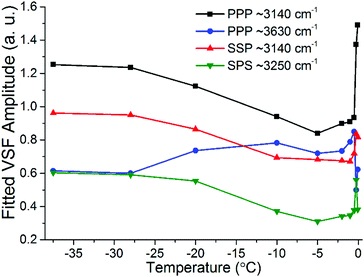 | ||
| Fig. 9 Fitted amplitudes of selected modes in the VSF spectra collected in the SSP, PPP and SPS polarization combinations. Note that the amplitudes have been normalized by the corresponding bandwidths. For ease of comparison the amplitude values for the ∼3630 cm−1 band in PPP have been multiplied by −1 as they display an opposite phase. Additional fitted parameters and details of the procedure can be found in the ESI11.† | ||
The first detectable changes take place in the temperature range between −25 °C and −10 °C with the marked decrease of the bands linked to 4-coordinated water molecules that are not in direct contact to silica, and which in principle connect the surface bilayers (i.e. “stitching” modes). The appearance of changes in the spectral features can be interpreted as the onset of the PML at the ice/silica interface, which we note is curiously ∼60 °C above the estimated onset temperature for the ice/vapour interface based on measurements using the same technique.14,56 A lower SF intensity implies a broadening of the orientational distribution and/or a decrease in the number of molecules having that particular configuration.10,11 Interestingly, during this first transition, the features linked to water molecules in direct contact to the silica substrate, show an opposite behavior, increasing in the PPP, and to a much lower extent, also in the SSP spectra (Fig. 7 and 9), suggesting a narrowing of their average orientation. This behavior can be considered as the first evidence of the conflicting ordering imposed by the underlying ice crystal and the silica substrate, which becomes more apparent at higher temperatures (see below). In this region, the NMR-derived PML thickness is 1–3 monolayers thick, that – in a typical liquid-like material – is sufficient for losing some spatial/orientational correlation. Hence, this is consistent with the orientational distribution inferred above.
From ∼−10 °C and up to approximately −0.5 °C the spectral features, besides some small changes in the high frequency modes, remain largely constant suggesting limited structural changes in this temperature range. On the NMR side, one can note that in the −10 °C to −1.5 °C range there are no dramatic changes in either the line width of the PML signal or in the extension of the PML.
It is only when approaching the bulk melting temperature that dramatic onset of a new behavior is observed (Fig. 8 and 9); unfortunately, we lack NMR data in this interval, but TIR Raman sets a limit of <3 nm for PML thickness at −0.3 °C. The overall increase in spectral intensity is linked to the thickening of the PML, as the negative charge of the silica substrate start imposing an ordering of the interfacial water molecules with their dipole moment oriented towards the silica surface, which is in clear contrast to the ordering enforced by the underlying ice crystal. This conflict is exemplified for example with the increased amplitude and probable change in phase of the ∼3450 cm−1 band, which would essentially indicate a flip of the average relative polar orientation14,20 of the contributing water molecules just a fraction of a degree below the bulk melting temperature (Fig. 8 and 9). Indeed, evidence of this change in orientation upon melting can be found in previous studies of the single crystal ice (basal plane)/silica interface, where a flip of 180° was concluded from examining the SF interference patterns between −20 °C ice and liquid water at a constant frequency of 3150 cm−1.14 We note however, that our fitted data from a single ice crystal but of unknown orientation, do not support such a change in phase for the ∼3125 cm−1 peak upon melting, but instead for that of the neighbouring band at ∼3250 cm−1 when going through the first transition associated to the PML onset (see Fig. 7 and ESI11†).
The significant lower intensity of the SF ice spectra at −0.1 °C compared to the water spectrum at +1 °C (Fig. 8), is an indication that the PML thickness is always smaller that the SF probing depth at the silica/water interface (i.e. just a few molecular layers). The significant increase in SF intensity upon melting is not unique to silica, as a similar behaviour has been recently reported to occur with another negatively charged surface, specifically muscovite mica.57 Finally, we note that as the PML becomes thicker it is also likely that SF signal can be generated from the retreating ice/PML interface. We speculate that this could be origin of the 3050 cm−1 feature resolved in the −0.3 °C spectra (Fig. 8). However, a more conclusive picture and interpretation of the experimental data must await new theoretical calculations and models.
Concluding remarks
The three techniques used to probe the molecular properties of the premolten layer at the silica/ice interface have provided consistent information. At the lowest explored temperatures starting from approximately −25 °C and below (that is, relative to the bulk or pore melting in the particular set of explored samples), NMR indicated that very few water molecules (i.e. less than a monolayer coverage), possess rotational freedom that permits them to contribute to the peak assigned to the premolten state. In this region, VSFS reveals no temperature dependence down to −38 °C. Hence, whatever order exists at very low temperatures seems to persist up to ∼−25 °C. In summary, there is no indication of a premolten layer at the lowest explored temperatures.Our data jointly set the onset temperature for PML to approximately −25 °C. Somewhere around this point the VSF spectral parameters start to show a temperature dependent variation and to indicate a growing disorder at the interface while the NMR-derived thickness exceeds that of a monolayer. At the highest explored temperature of 1.5 K below the melting point, the NMR-derived PML thickness is ∼1.5 nm; this is consistent with the upper limit of 3 nm at −0.3 °C determined from TIR-Raman. The information obtained by NMR, TIR Raman, and VSFS, specifically the onset temperature and thickness are also in good agreement with a previous X-ray reflectivity study on the PML properties of single crystal ice in contact with amorphous silica15 and the results of recent theoretical work.58
VSFS yielded richer information still, in the form of the onset of another trend at approximately −0.5 °C, a temperature region that could not be explored by NMR, and which was interpreted in terms of additional growth of the PML. Yet, VSFS also provided evidence that the thickness remains limited to just a few molecular layers even at −0.1 °C. Interestingly, upon formation of the PML, the SF results imply that the net average orientation of the tetrahedrally coordinated water molecules found in the second or third molecular layers from the surface (i.e. bilayer “stitching” modes), broadens, while those molecules in direct contact to the silica substrate show the opposite trend. This behaviour is explained by the conflicting order imposed by the negatively charged fused silica surface on the one side, and the underlying ice crystal on the other. As the melting temperature is approached and the interfacial ice structure relaxes, the influence of the silica surface charge arising from deprotonation of the surface silanol groups increases, aligning more water molecules in the PML, resulting in an increase of the SF spectral intensity, yet without ever reaching the values observed in the presence of liquid water.
Of course, there are also some discrepancies, like for example the apparent doubling in the NMR-derived PML thickness between −10 and −1 °C, a temperature range where limited changes are observed in VSFS. This can be attributed to the fact that the two techniques probe different aspects of the PML, but perhaps also to experimental specificities, as NMR measurements were carried out with polycrystalline D2O ice, while in VSFS they were made with single crystal H2O, though of unknown orientation.
The measured properties of the PML are clearly correlated to the macroscopic ice adhesion measurements. In particular, the transition between the sliding and the non-sliding behaviour observed at approximately −20 °C (Fig. 1). With some caution, commanded by the assumptions involved in the evaluation of the NMR data, the onset of sliding seems to coincide with having a PML that, in addition, has a thickness that exceeds the average surface roughness. In connection to this inference, we note that in rougher silica surfaces with a Ra of ∼6 nm (measured in a 2 × 2 μm area, see ESI9†), ice did not slide at any temperature, which also highlights the potential importance of the surface roughness relative the PML thickness in the sliding mechanism. Having said this, the value of the arithmetic surface roughness, Ra, will depend on the lateral resolution and extension of the probed area (see ESI8 and ESI9†). In this regard, we observed ice to slide at −10 °C on silica surfaces of intermediate roughness, with a Ra of ∼0.7 nm when measured in 2 × 2 μm area, but with a Ra of ∼22 nm when measured in a profilometer for an area of 0.33 × 0.44 mm (see ESI8 and ESI9†). This stresses the importance of the micron or submicron roughness for the PML lubricating sliding to take place.
Our adhesion measurements do not address directly ice friction, particularly not kinetic friction where, except at low sliding speeds, the effects of frictional heating seem to dominate.59 Yet, the lack of consistent information about the premolten layer seems to hinder a more complete analysis just as well as the evaluation of the performance of theoretical models. We hope that our work will provide some progress toward alleviating that shortcoming. In addition, we point out that sliding shear adhesion is, indeed, directly related to static friction.
Acknowledgements
This work was financially supported by the Swedish Foundation for Strategic Research (SSF-FFL5 program) and the Swedish Research Council (VR). Per M. Claesson, Eduardo Figueroa Karlström, and Lasse Makkonen are acknowledged for helpful and inspiring discussions. Matthew Fielden is thanked for performing the AFM measurements. Torbjörn Pettersson is acknowledged for providing the software used for analysing the profilometer data.References
- M. Faraday, Proc. R. Soc. London, 1859, 10, 440–450 CrossRef.
- J. G. Dash, A. W. Rempel and J. S. Wettlaufer, Rev. Mod. Phys., 2006, 78, 695–741 CrossRef CAS.
- V. F. Petrenko and R. W. Whitworth, Physics of Ice, Oxford University Press, 1999 Search PubMed.
- L. Makkonen, J. Adhes. Sci. Technol., 2012, 26, 413–445 CAS.
- T. Bartels-Rausch, H. W. Jacobi, T. F. Kahan, J. L. Thomas, E. S. Thomson, J. P. D. Abbatt, M. Ammann, J. R. Blackford, H. Bluhm, C. Boxe, F. Domine, M. M. Frey, I. Gladich, M. I. Guzmán, D. Heger, T. Huthwelker, P. Klán, W. F. Kuhs, M. H. Kuo, S. Maus, S. G. Moussa, V. F. McNeill, J. T. Newberg, J. B. C. Pettersson, M. Roeselová and J. R. Sodeau, Atmos. Chem. Phys., 2014, 14, 1587–1633 CrossRef.
- Y. Li and G. A. Somorjai, J. Phys. Chem. C, 2007, 111, 9631 CrossRef CAS.
- O. Björneholm, M. H. Hansen, A. Hodgson, L.-M. Liu, D. T. Limmer, A. Michaelides, P. Pedevilla, J. Rossmeisl, H. Shen, G. Tocci, E. Tyrode, M.-M. Walz, J. Werner and H. Bluhm, Chem. Rev., 2016, 116, 7698–7726 CrossRef PubMed.
- J. S. Wettlaufer, Phys. Rev. Lett., 1999, 82, 2516–2519 CrossRef CAS.
- D. A. Woods and C. D. Bain, Soft Matter, 2014, 10, 1071–1096 RSC.
- Y. R. Shen, in Nonlinear Spectroscopy for Molecular Structure Determination, ed. R. W. Field, E. Hirota, J. P. Maier and S. Tsuchiya, Blackwell Science, Oxford, UK, 1998, pp. 249–271 Search PubMed.
- G. L. Richmond, Chem. Rev., 2002, 102, 2693–2724 CrossRef CAS PubMed.
- Y. Furukawa and I. Ishikawa, J. Cryst. Growth, 1993, 128, 1137–1142 CrossRef CAS.
- D. Beaglehole and P. Wilson, J. Phys. Chem., 1994, 98, 8096–8100 CrossRef CAS.
- X. Wei, P. B. Miranda, C. Zhang and Y. R. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 085401 CrossRef.
- S. Engemann, H. Reichert, H. Dosch, J. Bilgram, V. Honkimäki and A. Snigirev, Phys. Rev. Lett., 2004, 92, 205701 CrossRef CAS PubMed.
- T. Ishizaki, M. Maruyama, Y. Furukawa and J. G. Dash, J. Cryst. Growth, 1996, 163, 455–460 CrossRef CAS.
- H. H. G. Jellinek, Can. J. Phys., 1962, 40, 1294–1309 CrossRef.
- H. H. G. Jellinek, J. Colloid Sci., 1959, 14, 268–280 CrossRef CAS.
- E. Tyrode and J. F. D. Liljeblad, J. Phys. Chem. C, 2013, 117, 1780–1790 CrossRef CAS.
- E. Tyrode, M. W. Rutland and C. D. Bain, J. Am. Chem. Soc., 2008, 130, 17434–17445 CrossRef CAS PubMed.
- J. F. D. Liljeblad and E. Tyrode, J. Phys. Chem. C, 2012, 116, 22893–22903 CrossRef CAS.
- R. V. Klitzing, Adv. Colloid Interface Sci., 2005, 114–115, 253–266 CrossRef PubMed.
- R. J. Wittebort, M. G. Usha, D. J. Ruben, D. E. Wemmer and A. Pines, J. Am. Chem. Soc., 1988, 110, 5668–5671 CrossRef CAS.
- F. Fujara, S. Wefing and W. F. Kuhs, J. Chem. Phys., 1988, 88, 6801–6809 CrossRef CAS.
- I. Furó and J. Daicic, Nord. Pulp Pap. Res. J., 1999, 14, 221–225 CrossRef.
- J. Rault, R. Neffati and P. Judeinstein, Eur. Phys. J. B, 2003, 36, 627–637 CrossRef CAS.
- T. Sparrman, M. Öquist, L. Klemedtsson, J. Schleucher and M. Nilsson, Environ. Sci. Technol., 2004, 38, 5420–5425 CrossRef CAS PubMed.
- C. L. Jackson and G. B. McKenna, J. Chem. Phys., 1990, 93, 9002–9011 CrossRef CAS.
- J. Mitchell, J. B. W. Webber and J. H. Strange, Phys. Rep., 2008, 461, 1–36 CrossRef CAS.
- O. V. Petrov and I. Furó, Prog. Nucl. Magn. Reson. Spectrosc., 2009, 54, 97–122 CrossRef CAS.
- O. Petrov and I. Furó, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 011608 CrossRef PubMed.
- E. Whalley, Can. J. Chem., 1977, 55, 3429–3441 CrossRef CAS.
- V. Buch and J. P. Devlin, J. Chem. Phys., 1999, 110, 3437–3443 CrossRef CAS.
- J. R. Scherer and R. G. Snyder, J. Chem. Phys., 1977, 67, 4794 CrossRef CAS.
- T. Shigenari and K. Abe, J. Chem. Phys., 2012, 136, 174504 CrossRef PubMed.
- F. Li and J. L. Skinner, J. Chem. Phys., 2010, 133, 244504 CrossRef CAS PubMed.
- L. Shi, S. M. Gruenbaum and J. L. Skinner, J. Phys. Chem. B, 2012, 116, 13821–13830 CrossRef CAS PubMed.
- L. De Marco, W. Carpenter, H. Liu, R. Biswas, J. M. Bowman and A. Tokmakoff, J. Phys. Chem. Lett., 2016, 7, 1769–1774 CrossRef CAS PubMed.
- H. H. Richardson, J. Mol. Struct., 2006, 799, 56–60 CrossRef CAS.
- V. Sadtchenko and G. E. Ewing, J. Chem. Phys., 2002, 116, 4686–4697 CrossRef CAS.
- R. L. Walker, K. Searles, J. A. Willard and R. R. H. Michelsen, J. Chem. Phys., 2013, 139, 244703 CrossRef PubMed.
- R. K. Iler, The chemistry of silica: solubility, polymerization, colloid and surface properties, and biochemistry, Wiley, 1979 Search PubMed.
- B. A. Morrow and A. J. McFarlan, J. Phys. Chem., 1992, 96, 1395–1400 CrossRef CAS.
- Y. Mizuno and N. Hanafusa, J. Phys., Colloq., 1987, 48(C1), 511–517 CrossRef.
- R. Valiullin and I. Furó, J. Chem. Phys., 2002, 117, 2307–2316 CrossRef CAS.
- O. V. Petrov, D. Vargas-Florencia and I. Furó, J. Phys. Chem. B, 2007, 111, 1574–1581 CrossRef CAS PubMed.
- C. Medcraft, D. McNaughton, C. D. Thompson, D. R. T. Appadoo, S. Bauerecker and E. G. Robertson, Phys. Chem. Chem. Phys., 2013, 15, 3630–3639 RSC.
- A. Wong, L. Shi, R. Auchettl, D. McNaughton, D. R. T. Appadoo and E. G. Robertson, Phys. Chem. Chem. Phys., 2016, 18, 4978–4993 RSC.
- V. Buch, T. Tarbuck, G. L. Richmond, H. Groenzin, I. Li and M. J. Shultz, J. Chem. Phys., 2007, 127, 204710 CrossRef CAS PubMed.
- T. Ishiyama, H. Takahashi and A. Morita, J. Phys. Lett., 2012, 3, 3001–3006 CAS.
- M. J. Shultz, P. Bisson and T. H. Vu, Chem. Phys. Lett., 2013, 588, 1–10 CrossRef CAS.
- H. Groenzin, I. Li, V. Buch and M. J. Shultz, J. Chem. Phys., 2007, 127, 214502 CrossRef PubMed.
- P. J. Bisson and M. J. Shultz, J. Phys. Chem. A, 2013, 117, 6116–6125 CrossRef CAS PubMed.
- K. Ohno, M. Okimura, N. Akai and Y. Katsumoto, Phys. Chem. Chem. Phys., 2005, 7, 3005–3014 RSC.
- C. J. Tainter, Y. Ni, L. Shi and J. L. Skinner, J. Phys. Lett., 2013, 4, 12–17 CAS.
- X. Wei, P. B. Miranda and Y. R. Shen, Phys. Rev. Lett., 2001, 86, 1554–1557 CrossRef CAS PubMed.
- E. Anim-Danso, Y. Zhang and A. Dhinojwala, J. Phys. Chem. C, 2016, 120, 3741–3748 CrossRef CAS.
- D. T. Limmer and D. Chandler, J. Chem. Phys., 2014, 141, 8 CrossRef PubMed.
- B. N. J. Persson, J. Chem. Phys., 2015, 143, 224701 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the ice-adhesion measuring device, movie showing the sliding behavior of ice on silica, details of the vibrational spectroscopy sample cell, TIR Raman spectra collected for ice at different polarization combinations, Raman D2O ice spectra at different temperatures, silica/ice SF spectra collected in the SPS polarization combination, Fresnel factor corrected VSF spectra, detailed fitting parameters of the SF spectra, AFM and profilometry images and roughness measurements, and raw 2H NMR spectra of the PML. See DOI: 10.1039/c6cp05303c |
| This journal is © the Owner Societies 2017 |