 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic anisotropy of a CoII single ion magnet with distorted trigonal prismatic coordination: theory and experiment†
Yan
Peng‡
ab,
Tilmann
Bodenstein‡
bc,
Karin
Fink
*b,
Valeriu
Mereacre
a,
Christopher E.
Anson
a and
Annie K.
Powell
 *ab
*ab
aInstitute of Inorganic Chemistry, Karlsruhe Institute of Technology, Engesserstrasse 15, 76131 Karlsruhe, Germany. E-mail: annie.powell@kit.edu
bInstitute of Nanotechnology, Karlsruhe Institute of Technology, P.O. Box 3640, 76021 Karlsruhe, Germany. E-mail: karin.fink@kit.edu
cqLEAP Center for Theoretical Chemistry, Department of Chemistry, Aarhus University, Langelandsgade 140, 8000 Aarhus C, Denmark
First published on 11th October 2016
Abstract
The single ion magnetic properties of Co(II) are affected by the details of the coordination geometry of the ion. Here we show that a geometry close to trigonal prismatic which arises when the ligand 6,6′-((1Z)-((piperazine-1,4-diylbis(propane-3,1-diyl))bis(azanylylidene))bis(methanylylidene))bis(2-methoxyphenol) coordinates to Co(II) does indeed lead to enhanced single-ion behaviour as has previously been predicted. Synthesis of the compound, structural information, and static as well as dynamic magnetic data are presented along with an analysis using quantum chemical ab initio calculations. Though the complex shows a slight deviation from an ideal trigonal prismatic coordination, the zero-field splitting as well as the g-tensor are strongly axial with D = −41 cm−1 and E < 0.01 cm−1. For the lowest Kramers doublet (S = 1/2) g∥ = 7.86 and g⊥ < 0.05 were found. In contrast, the second Kramers doublet possesses a rhombic g-tensor with g∥ = 2.75 and g⊥ = 4.35. Due to large spin–orbit coupling resulting in very different g tensors, it is not possible to simulate the temperature dependence of the magnetic susceptibility with a spin Hamiltonian of the form H = D(Sz2 − S(S + 1)/3) + E(Sx2 − Sy2) + μBgS·B using an effective spin S = 3/2. Calculations on model complexes show the influence of the coordinating atoms and the deviation from the ideal trigonal prismatic coordination. As the distortion is reduced towards idealised D3h, the zero field splitting increases and the g-tensor of the second Kramers doublet also becomes axial.
Introduction
Since the discovery of the first 3d SIM (single-ion magnet), an Fe(II) complex with a trigonal pyramidal coordination geometry in 2010,1 the family of SIMs based on 3d ions has grown rapidly. The magnetic behaviour of these compounds results from the interplay between ligand-field splitting and spin–orbit interaction that can generate large anisotropy, which is a key ingredient for SMMs (single molecule magnets).2–4 With the development of this area, it has become obvious that magnetic anisotropy is the main criterion for engendering slow relaxation of the magnetisation, although other mechanisms may contribute to the relaxation processes.5 In particular, Co(II) complexes are known to show a wide range of zero field splittings. In his review, Boča gives values in the range from −38 cm−1 to +83 cm−1.6 Low coordination numbers are promising because they can split the d-orbitals in such a way that a nearly degenerated ground state occurs, facilitating the spin–orbit coupling and thus enhancing the magnetic anisotropy.7,8 Currently, the quest for transition-metal-based SIMs is focused on low-coordinate metal species with coordination numbers of two to five, which possess large axial (D) and small rhombic zero-field splitting parameters (E) resulting in slow magnetic relaxation.4,7,8 Only recently have examples of seven- and eight- coordinated Co(II) compounds been reported which show slow relaxation.9,10 For 3d ion-based SIMs, the SMM behaviour is usually only visible under a small applied external field that suppresses the fast magnetic tunnelling and very few mononuclear complexes based on 3d ions show slow relaxation of the magnetisation without field.11–18 Recently, Ruiz and co-workers predicted the properties of 3d SIMs based on the coordination numbers and electronic structures of paramagnetic centres.2 For a Co(II) system, SMM behaviour could occur either via the trigonal pyramidal (large positive D values) or the trigonal prismatic (large negative D values) coordination modes. Such a trigonal prismatic coordination was realised in two homoleptic Co(II) complexes.15–17 In the first complex, Co(II) is coordinated by nitrogen (trispyrazoloximate) and derivatives and the complex shows a large negative value for D (−115 cm−1) and a spin reversal barrier of 152 cm−1.15 The second is coordinated by oxygen via six salicylaldehyde Schiff bases with a barrier of 76 cm−1. In the first coordination sphere, both compounds show only a very small distortion from an ideal trigonal prism. Although both complexes possess a strong axial zero field splitting (E/D is very small), there is a significant difference in the g-tensor. While the anisotropy of the g values obtained from magnetisation and NMR data is small in the first complex (g∥ = 2.9 and g⊥ = 2.2) it is, according to quantum chemical calculations, strongly axial in the second compound (g∥ = 7.57 and g⊥ = 0.56) whereas the corresponding magnetisation data was fitted with S = 3/2 and an isotropic giso = 3.05.Here, we present the synthesis and characterisation of an air stable Co(II) compound with a trigonal prismatic coordination geometry. Although there is deviation from idealised trigonal prismatic coordination arising from the combination of nitrogen and oxygen in the first coordination sphere and the stiffness of the ligand, the compound exhibits slow magnetic relaxation without application of a dc field. The Orbach energy barrier of 56 cm−1 is relatively high for a Co(II)-based SIM. The electronic structure and the magnetic properties were analysed in detail by quantum chemical calculations. The effect of the distortion from the ideal trigonal prismatic coordination was investigated by calculating the situation for model complexes where the coordination was changed stepwise from that of the synthesized complex to an ideal trigonal prism with either 6 O or 6 N coordinating atoms.
Experimental
General information
All chemicals were used as received without any further purification and all manipulations were performed under aerobic conditions. Powder X-ray diffraction was carried out on a STOE STADI-P diffractometer, using Cu-Kα radiation with λ = 1.5406 Å. Elemental analyses (C H N) were performed using an Elemental Vario EL analyzer.X-ray crystal structure
Data were measured at 150 K on a Stoe IPDS II diffractometer with graphite-monochromated Mo-Kα radiation. The structure was solved by dual-space direct methods (SHELXT) and refined by full-matrix least-squares using SHELX-2014.19§Magnetic measurements
Magnetic susceptibility data (1.8–300 K) were collected on powdered samples using a SQUID-based sample magnetometer, Quantum Design model MPMS-XL instrument under a 1000 Oe applied magnetic field. Magnetisation isotherms were collected at 2, 3, and 5 K between 0 and 7 T. Ac susceptibility measurements were carried out under an oscillating ac field of 3 Oe and ac frequencies ranging from 1 to 1500 Hz. Data were corrected for diamagnetism using Pascal constants and a sample holder correction.Preparation of 6,6′-((1Z)-((piperazine-1,4-diylbis(propane-3,1-diyl)) bis(azanylylidene))bis(methanylylidene))bis(2-methoxyphenol) (H2L)
A mixture of o-vanillin (3.04 g, 20 mmol) and 1,4-bis(3-aminopropyl)piperazine (2.0 g, 10 mmol) was refluxed for 4 h in EtOH (50 mL). The resultant yellow precipitate was filtered and washed well with cold EtOH followed by ether and then dried in air. Yield 90% (4.23 g). Anal. calc. (found) % for C26H36N4O4: C, 66.64 (66.55); N, 11.96 (11.80); H, 7.74 (7.82).Preparation of [CoII(L)] (1)
A mixture of H2L (46.8 mg, 0.1 mmol), Co(NO3)2·6H2O (29 mg, 0.1 mmol) in 2 mL of DMF was stirred for 10 minutes. Then, Et3N (50 mg, 0.5 mmol) was added to the mixture under stirring. After 1 minute stirring, the solution was filtered and left undisturbed. Red-brown block-shaped crystals of 1 were grown from the filtrate overnight in 50% (37.8 mg, based on Co) yield. Anal. calc. (found)% for C26H34CoN4O4: C, 59.42 (59.45); N, 10.66 (10.55); H, 6.52 (6.50).Quantum chemical methods
Complete active space self-consistent field (CASSCF) and spin–orbit configuration interaction (SOCI) calculations were performed for compound 1. For Co, O and N, a def2-TZVPP basis set was used while C and H were equipped by a def2-SVP basis set.20,21All calculations were performed with the Bochum suite of ab initio programs.22–26 The active space was spanned by the five 3d orbitals of Co. The CASSCF orbitals were obtained by averaging over the ten S = 3/2 states. In the SOCI calculations, the scaled-nucleus spin–orbit operator27 (ξ = 0.61) was constructed and diagonalised within the active space. Dynamic correlation was considered for the first two quartet states by the averaged coupled pair functional (ACPF)28 variant of the MCCEPA program26 with reference wave-functions based on this active space. The 3d orbitals of Co and the lone pairs of the ligands were included in the correlation treatment. Test calculations showed that an expansion of the active space by addition of a further d-shell or inclusion of occupied ligand orbitals has no influence on the CASSCF reference wave-functions. Since we use a multi-reference configuration interaction type rather than a perturbation approach to treat dynamic correlation it is unlikely that extension of the active space will have a significant influence on the results. For the model complexes, only the core orbitals (1s for O and N, 1s2s2p for Co) were kept frozen. The influence of the correlation energy on the SOCI calculations was considered by shifting the diagonal elements of the lowest CASSCF state by ΔEcor = (E(24A1)ACPF − E(24A1)CAS) − (E(14A1)ACPF − E(14A1)CAS) thus correcting the first excitation energy. This method is denoted as SOCI* in the following.29 The χT characteristics were calculated by numerical differentiation at a finite magnetic field of B = 1 T and averaged over the three Cartesian directions.25 In the ESI,† we attempt to assess the accuracy of these calculations and inter alia describe additional calculations taking into account the dynamic correlation for the first seven quartet states. The higher excited states which were not explicitly treated by the ACPF method were shifted down by the average correlation energy ΔEcor of the seven lowest states 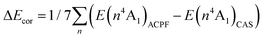 , thus correcting the lowest excitation energies. However, completely neglecting the higher states did not change the results.
, thus correcting the lowest excitation energies. However, completely neglecting the higher states did not change the results.
For the field dependence of the magnetisation data, SOCI* calculations were performed for different fields (B = 0.1 T to B = 7.0 T in steps of 0.1 T). Here, the Zeeman-operator was added to the Hamiltonian for the SOCI* calculations. From the resulting energies of the electronic states with and without magnetic field, the susceptibility was obtained from:
 | (1) |
 | (2) |
 | (3) |
The first approach for calculating the g-matrix consists of sampling a hemisphere of different field directions around the cobalt centre. The angular resolution of the grid points on the hemisphere is 4°. For each point, the Zeeman splitting was calculated using finite perturbation theory and the g-factor was extracted using an effective spin of S = 1/2. The first magnetic main axis was assigned to the direction of the largest splitting. The second axis corresponds to the direction with the largest splitting in the plane perpendicular to the first axis. The third axis was found by orthogonalisation. In the second approach, we constructed the Zeeman matrix within the active space and transformed it into the basis of the respective Kramers doublet. With these matrix elements, the Abragam–Bleaney tensor G = ggT was constructed and diagonalised to yield the magnetic axes and g-factors.30D and E values were determined by the effective Hamiltonian approach31 for an S = 3/2 pseudo-spin from the numerical effective Hamiltonian:
 | (4) |
![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) i are the orthogonalised projections of the wave functions for the lowest states in the SOCI (SOCI*, respectively) calculation on to the quartet ground state of the CASSCF calculation where the z-axis of the complexes was chosen along the direction of g∥.
i are the orthogonalised projections of the wave functions for the lowest states in the SOCI (SOCI*, respectively) calculation on to the quartet ground state of the CASSCF calculation where the z-axis of the complexes was chosen along the direction of g∥.
In the model complexes the chelating ligand was substituted by ammonia and water molecules. While the positions of nitrogen and oxygen were taken from the experimental structure and the systematic structural changes, the positions of the hydrogen atoms were optimized in a DFT-D3/B3LYP structure optimization32–35 for the 4A1 ground state.
Analysis of the dynamic magnetic susceptibility data and determination of relaxation times and processes
The dispersion-expressions36–38 given below were used to fit the out-of-phase (χ′′) as well as the in-phase (χ′) data.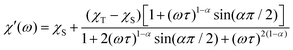 | (5) |
 | (6) |
Here, χT and χS denote the thermodynamic and adiabatic limits of χ, respectively, α is known as the Debye distribution parameter. The curves were fitted with a focus on describing the maxima of the out-out-phase part correctly. Therefore, only the data points around the maxima of χ′′ were used for the fits. Inclusion of α does not significantly change the relaxation times (see Tables S1 and S2, ESI†).
The field-dependent data were modelled using the terms for direct (m = 2, 4) and QTM processes together with a field-independent offset OH:
| τ−1 = AHmT + B1/(1 + H2B2) + OH | (7) |
In the fitting procedure, the first term vanished (infinitesimally small values for A). The reason for this is unclear, and we cannot exclude that the direct term is hidden under the QTM curve. Similar behaviour has been observed for other complexes.39,40 However, since the temperature-dependent curves also did not improve upon adding a direct term proportional to T, we removed the term AHmT altogether from the relaxation expressions. The temperature dependent data was thus fitted using:
| τ−1 = τ0−1 exp(−U/kT) + CTn + OT | (8) |
with OT = B1/(1 + (1200 Oe)2μ0−2B2). We were not able to find a reasonable fit using a variable Raman exponent n. Instead, fits were obtained for fixed n ranging from 2 to 9 with n = 9 giving a reasonable result.41 The parameters were obtained by an iterative procedure. In the first step, the Orbach parameters were optimised while the Raman parameters were kept fixed. Next, the Raman parameters were obtained for a constant Orbach term. These two steps were repeated until all values reached convergence.
Results and discussion
Geometric and electronic structure
The trigonal prismatic air-stable complex [CoII(L)] (H2L = 6,6′-((1Z)-((piperazine-1,4-diylbis(propane-3,1-diyl)) bis(azanylylidene))bis(methanylylidene))bis(2-methoxyphenol)), complex 1, was obtained as dark red crystals from the reaction of H2L with Co(NO3)2·6H2O in DMF in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in the presence of Et3N (Scheme 1). The purity of the complex was confirmed by powder X-ray diffraction (Fig. S1, ESI†) and elemental analysis. The X-ray single-crystal structure analysis reveals that complex 1 crystallises in the monoclinic space group P21/n. As shown in Fig. 1a, the neutral molecule consists of one deprotonated Schiff-base ligand (L2−) encapsulating one Co(II) ion in a slightly distorted trigonal prismatic coordination environment. The top and bottom planes of the prism are formed by one piperazine nitrogen, and one nitrogen and oxygen of the corresponding Schiff base arms in such a way, that always one oxygen and one nitrogen of the different arms are on top of each other (Fig. 1b). The normals of these planes are tilted with respect to each other by 6° (Fig. 1b) and twisted by 3° (Fig. 1c). We assume that the tilting angle is caused by the piperazine unit. The two N atoms of piperazine (N1, N2) are much closer to each other (2.47 Å) than the N–O pairs (2.81 Å). The Co–Npiperazine distances are longer than the Co–Nimino distances, and both of these Co–N distances are longer than the Co–Ophenol distances (Table 1). The Co(II) atoms are well-separated with an interatomic distance longer than 7.02 Å (Fig. 1d), thus precluding any significant intermolecular magnetic interactions.
1 in the presence of Et3N (Scheme 1). The purity of the complex was confirmed by powder X-ray diffraction (Fig. S1, ESI†) and elemental analysis. The X-ray single-crystal structure analysis reveals that complex 1 crystallises in the monoclinic space group P21/n. As shown in Fig. 1a, the neutral molecule consists of one deprotonated Schiff-base ligand (L2−) encapsulating one Co(II) ion in a slightly distorted trigonal prismatic coordination environment. The top and bottom planes of the prism are formed by one piperazine nitrogen, and one nitrogen and oxygen of the corresponding Schiff base arms in such a way, that always one oxygen and one nitrogen of the different arms are on top of each other (Fig. 1b). The normals of these planes are tilted with respect to each other by 6° (Fig. 1b) and twisted by 3° (Fig. 1c). We assume that the tilting angle is caused by the piperazine unit. The two N atoms of piperazine (N1, N2) are much closer to each other (2.47 Å) than the N–O pairs (2.81 Å). The Co–Npiperazine distances are longer than the Co–Nimino distances, and both of these Co–N distances are longer than the Co–Ophenol distances (Table 1). The Co(II) atoms are well-separated with an interatomic distance longer than 7.02 Å (Fig. 1d), thus precluding any significant intermolecular magnetic interactions.
| Co1–O3 | 2.0018 (12) | N4–Co1–N3 | 157.49 (6) |
| Co1–O1 | 2.0106 (12) | O3–Co1–N2 | 136.92 (5) |
| Co1–N4 | 2.1547 (14) | O1–Co1–N2 | 87.16 (5) |
| Co1–N3 | 2.1570 (14) | N4–Co1–N2 | 80.95 (5) |
| Co1–N2 | 2.2650 (14) | N3–Co1–N2 | 118.89 (5) |
| Co1–N1 | 2.2880 (14) | O3–Co1–N1 | 87.55 (5) |
| O3–Co1–O1 | 132.22 (6) | O1–Co1–N1 | 136.20 (5) |
| O3–Co1–N4 | 84.85 (5) | N4–Co1–N1 | 120.19 (5) |
| O1–Co1–N4 | 86.01 (5) | N3–Co1–N1 | 80.02 (5) |
| O3–Co1–N3 | 86.39 (5) | N2–Co1–N1 | 65.80 (5) |
| O1–Co1–N3 | 84.61 (5) | Co–Coadj | 7.0151 (6) |
The electronic structure calculations reveal a splitting of the ionic 4F ground state of Co(II) over the range of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 cm−1 as a result of the trigonal prismatic ligand field (see Table 2). The 4A1 ground state is separated from the next states by about 1924 cm−1 (ACPF). Due to spin–orbit interaction, mainly with the second quartet state, the 4A1 ground state splits into two Kramers doublets, E1 and E2, with a spin–orbit splitting of 82 cm−1 (SOCI*). The next excited states follow at 2000 cm−1 (see Fig. 2). Analysis of the SOCI wave functions shows that the lowest two Kramers doublets consist of 90% contributions of the 4A ground state. Thus, the low-lying energy spectrum, consisting of the two Kramers doublets, can be described by a pseudo-spin of S = 3/2 using the spin Hamiltonian H = D(Sz2 − S(S + 1)/3) + E(Sx2− Sy2). The numerical effective Hamiltonian is given in Table 3. The resulting D tensor in cm−1 is:
180 cm−1 as a result of the trigonal prismatic ligand field (see Table 2). The 4A1 ground state is separated from the next states by about 1924 cm−1 (ACPF). Due to spin–orbit interaction, mainly with the second quartet state, the 4A1 ground state splits into two Kramers doublets, E1 and E2, with a spin–orbit splitting of 82 cm−1 (SOCI*). The next excited states follow at 2000 cm−1 (see Fig. 2). Analysis of the SOCI wave functions shows that the lowest two Kramers doublets consist of 90% contributions of the 4A ground state. Thus, the low-lying energy spectrum, consisting of the two Kramers doublets, can be described by a pseudo-spin of S = 3/2 using the spin Hamiltonian H = D(Sz2 − S(S + 1)/3) + E(Sx2− Sy2). The numerical effective Hamiltonian is given in Table 3. The resulting D tensor in cm−1 is:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 839 cm−1 (CASSCF) and 17
839 cm−1 (CASSCF) and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 878 cm−1 (SOCI)); the values in parenthesis correspond to the shift of the CASSCF ground state energies by the difference of the ACPF correlation energies for the two lowest quartet states and the SOCI* energies obtained with this shift
878 cm−1 (SOCI)); the values in parenthesis correspond to the shift of the CASSCF ground state energies by the difference of the ACPF correlation energies for the two lowest quartet states and the SOCI* energies obtained with this shift
| CASSCF | Energy (cm−1) | SOCI | Energy (cm−1) |
|---|---|---|---|
a ACPF energy shift of the ground state (see Experimental section).
b The values in brackets correspond to the SOCI* method calculations. The next states follow at ∼18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. 000 cm−1.
|
|||
| 4A1 | 0 (−358)a | E1 | 0 |
| E2 | 101 (82)b | ||
| 4A1 | 1567 | E3 | 1675 (2001) |
| E4 | 1884 (2189) | ||
| 4A1 | 4667 | E5 | 4435 (4764) |
| E6 | 4773 (5102) | ||
| 4A1 | 4915 | E7 | 5186 (5516) |
| E8 | 5493 (5821) | ||
| 4A1 | 6340 | E9 | 6506 (6834) |
| E10 | 6641 (6969) | ||
| 4A1 | 9409 | E11 | 9357 (9686) |
| E12 | 9668 (9998) | ||
| 4A1 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
E13 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508 (10 508 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 838) 838) |
| E14 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 699 (11 699 (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 028) 028) |
||
 | ||
| Fig. 2 Lowest electronic states obtained from the ab initio calculations. The CASSCF excitation energies are shifted by the ACPF correction (see Table 2). | ||
| M s | −3/2 | −1/2 | 1/2 | 3/2 |
|---|---|---|---|---|
| −3/2 | 0.06 + 0.00i | −0.34 − 2.05i | 0.48 − 0.04i | 0.00 + 0.00i |
| −1/2 | −0.34 + 2.05i | 81.75 + 0.00i | 0.00 + 0.00i | 0.48 − 0.04i |
| 1/2 | 0.48 + 0.04i | 0.00 + 0.00i | 81.75 + 0.00i | 0.34 + 2.05i |
| 3/2 | 0.00 + 0.00i | 0.48 + 0.04i | 0.34 − 2.05i | 0.06 + 0.00i |
Diagonalisation of the D-tensor yields strong axial anisotropy with D = −41 cm−1 and |E/D| = 0.006 (for the g-factors, see magnetic properties).
In an ideal trigonal prismatic coordination, the first two quartet states in the CASSCF calculation as well as the two orbitals at 750 cm−1 and 1300 cm−1 in Fig. 3, should be degenerate. In D3h symmetry, the ground state is an eightfold degenerate 4E′. This state is split by first order spin orbit coupling into four Kramers doublets. We expect that the axial zero field splitting is increased if the distortion of the coordination is reduced. We also note that in the electronic spectrum of 1 in the UV/Vis range the ligand bands dominate and it is not possible to extract information regarding the d–d transitions (Fig. S4, ESI†).
 | ||
| Fig. 3 Natural orbitals of the state-average CASSCF calculation.42 On the energy axes, the diagonal elements of the CASSCF Fock-matrix are shown. | ||
To gain deeper insights we performed calculations on model complexes where we started from the distorted structure, fixed the O and N atoms of the first coordination sphere and saturated them by H atoms (water and ammonia ligands, respectively). Although modeling nitrogen donors with ammonia and oxygen donors with water is something of a simplification in terms of what the second coordination sphere of the ligand field can provide for further “ultra fine-tuning”, this is also standard practice in theoretical approaches for describing 3d complexes.
Starting from model complex (model a), we went in three steps to the idealised trigonal prismatic coordination (Table 4, see details in ESI†), by first assimilating the angles of the two top and bottom triangles (model b), than making the corresponding planes coplanar (model c) and finally imposing full D3h symmetry to the positions of Co and the first coordination sphere regardless of the kind of atom (model d) and the homoleptic derivatives (models e, and f). In the cases b–f, bond lengths and angles were averaged. For all these model complexes, we calculated the energy of the lowest two quartet states at ACPF level and the lowest two Kramers doublets in SOCI* calculations.
As expected, the two complexes with D3h symmetry (e and f) show the strongest splitting because of first order spin–orbit coupling. The four lowest Kramers doublets which correspond to the 4E′ state are located at ca. 0 cm−1, 300 cm−1, 700 cm−1, and 1000 cm−1, respectively. With increasing distortion, the energies of the second quartet states are systematically increased. As a result, spin–orbit coupling becomes a second order effect and the splitting of the first quartet state into two Kramers doublets is diminished. We also note that an equally strong reduction of the zero-field splitting was observed in a study on a Ni(II) complex with large magnetic anisotropy.43
Table S3 and Fig. S5 (ESI†) give the detailed comparison of the results. In particular the zero-field splitting of the first two Kramers doublets is influenced by the details of the calculations. For CASSCF we have a ZFS of 101 cm−1, with two correlated states 82 cm−1 and for seven correlated states 85 cm−1. The latter two values are rather similar and this points to the fact that the underlying physics remains the same for all three methods and although the agreement with the experimental data is not excellent it is in the range of what can be expected from a quantum chemical calculation.
For fields up to ca. 4 T the agreement for the field dependence of the calculated and measured magnetisation is surprisingly good – calculated and measured susceptibilities differ only by ca. 12%. Taking into account that the susceptibilities are obtained as numerical second derivatives and without any fitting parameter the agreement with the experimental values is far better than might be expected and underlines the rather unusual behaviour of the Co(II) ion – but then it always was a “Kobold”.
Magnetic properties
Magnetic measurements were performed on polycrystalline powder samples. As shown in Fig. 4 (left), the χT value at 300 K is 2.46 cm3 K mol−1 and is higher than the expected value of 1.875 cm3 K mol−1 for one isolated Co(II) ion (S = 3/2) centre with g = 2 but falls within the range 2.1–3.4 cm3 K mol−1 typical for a single non-interacting high spin d7 Co(II) ion with a considerable orbital angular momentum contribution. The χT value remains roughly constant in the high temperature range (300–50 K), then decreases abruptly to 1.83 cm3 K mol−1 at 2.0 K due to zero field splitting of the Co(II) ion. The magnetisation was measured up to 7 T dc field at 2, 3, and 5 K. The lack of saturation of the magnetisation at higher field (Fig. 4) also implies the presence of significant magnetic anisotropy. The widely used spin Hamiltonian given in eqn (9) describes the magnetic anisotropy qualitatively:| H = D(Sz2 − S(S + 1)/3) + E(Sx2 − Sy2) + gμBS·B | (9) |
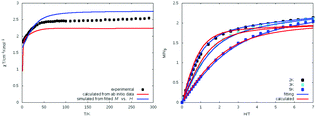 | ||
| Fig. 4 Experimental, fitted, and calculated plots of χT vs. T (left) and of M vs. H for 1 (right). The χT plot was simulated directly from ab initio energies without using a spin Hamiltonian. | ||
In an alternative, and as it turns out, very useful approach the χT characteristics as well as the field dependent magnetization data (M vs. H) were simulated directly from the SOCI* calculations allowing for the presence of a finite magnetic field and without the use of any effective spin Hamiltonian (Fig. 4). In these calculations, all 3d7 states are involved, but only the lowest two Kramers doublets are populated in the Boltzmann distribution. The simulated curves are in a surprisingly good agreement with the experimental data obtained from the magnetisation measurements. This is a further demonstration of the importance of the large magnetic anisotropy of 1 in terms of its affect on the ground and excited state within this compound.45
In order to calculate the g-factors and magnetic axes, two different approaches were considered (see Quantum chemical methods for details). In the first approach the Zeeman interaction was included in the SOCI using finite perturbation theory.25 In the second method, the Zeeman splitting is taken into account using first-order degenerate perturbation theory within the ground-state Kramers doublet.30 The first method has two advantages. Firstly, it can be used for any spin multiplicity whereas the second approach is only valid for well-isolated pseudo-spins. Secondly, the response of the wave functions to the magnetic field is included in the calculations and higher order terms can be analysed and this is important when considering the availability of excited states in terms of tunnelling and other relaxation processes. On the other hand, the second method has the advantage that numerical differentiation is avoided and the g-values can be directly obtained from the Zeeman integrals.
Resulting from this, the calculated g-factors using the SOCI wave functions are based on a pseudo-spin of S = 1/2 and confirm the high uniaxial anisotropy of 1 with g1 = 8.12, g2 = 0.59, g3 = 0.11, for method 1 and g1 = 8.14, g2 = 0.084 and g3 = 0.073 (Table S3, ESI†) for method 2. The obtained easy axes of these methods differ only by ∼4° which is in line with the grid resolution of method 1. As expected, the direction of the easy axis is along the C3 axis of the trigonal prism, i.e. perpendicular to the plane of the paper in Fig. 1a. Since the g-factors are very small in the plane perpendicular to the easy axis, the other two axes are not well-defined. The isotropic g-factors amount to 2.94 and 2.74, respectively. The energy differences for the determination of g2 and g3 in the finite field approach are rather small, i.e. on the limit of the numerical accuracy. Therefore, we assume that the values for g2 and g3 obtained by method 2 (directly from the Zeeman integrals) are more reliable in the present case. The principal values of the G-tensor become smaller upon inclusion of dynamic correlation effects (SOCI*) i.e. g1 = 7.86, g2 = 0.04, g3 = 0.05. For the second Kramers doublet we obtained g1 = 2.70, g2 = 4.35 and g3 = 4.39, again with a pseudo-spin of S = 1/2. For both Kramers doublets, g1 is parallel to the easy axis. From these results, it becomes apparent why the description of the magnetic susceptibility by the spin Hamiltonian given in eqn (9) with S = 3/2 fails for higher temperatures (Fig. S5, ESI†). Here, the second Kramers doublet becomes populated. In eqn (9), the same g-tensor is used to describe the magnetic behaviour of both Kramers doublets, but simply scaled with different Ms values. Nevertheless, at least in terms of the principal axis the Zeeman energies can be described using g ≈ 8/3 and S = 3/2.
By comparing the g-values of the model complexes (Table 4), the effect of the local coordination symmetry can clearly be seen. As the models become more symmetric, the rhombicity in the D- and G-tensor diminish and eventually in model d these properties become axial. Finally, in the entirely D3h symmetric complexes e and f, the anisotropy of the second Kramers doublet also becomes uniaxial with all anisotropy-axes (D-tensor, g-tensor of the first Kramers doublet and g-tensor of the second Kramers doublet) being collinear. However, because of the first order spin orbit coupling discussed above the Zeeman splittings of the first and second Kramers doublets do not show the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio implied by the spin Hamiltonian for S = 3/2.
1 ratio implied by the spin Hamiltonian for S = 3/2.
In order to gain further insights and to probe the dynamic magnetic behaviour, ac susceptibility measurements were carried out on 1 in the temperature range 1.8–10 K under zero dc field and 3.0 Oe ac field oscillating at frequencies between 1 and 1500 Hz. A frequency-dependent signal was observed in the χ′′ versus T plot below 10 K (Fig. S2, ESI†) suggesting slow relaxation of the magnetisation, generally attributed to a SMM behaviour. However, relaxation barriers cannot be extracted from this data due to the presence of a broad peak at higher frequencies indicating the presence of quantum tunnelling (QTM) effects. Therefore, ac susceptibility measurements were obtained at static dc fields from 300 Oe to 1500 Oe. When different dc fields are applied, the χ′′ versus frequency signal at 4.3 K dramatically changes with the magnitude of the applied field (Fig. S3, ESI†). The broad signal observed without dc field shows a clear maximum and diminishes when the dc field is increased. At fields stronger than 600 Oe the maximum in the high frequency range disappears under our measurement conditions. Additionally, a new peak appears at about 10 Hz with the application of the dc field. With increasing strength of the dc field, the peak shifts towards lower frequencies and enhances in magnitude. This behaviour is similar to what was found for previously reported trigonal prismatic mononuclear Co(II) complexes.2 The peak shift is negligible between 900 Oe and 1500 Oe, therefore, the variation of the χ′′ versus frequency signal with the temperature was studied at 1200 Oe dc applied field. The χ′′ versus frequency signal for complex 1 shows only one peak (Fig. 5) which is shifted to higher frequencies when the temperature is increased. This indicates a thermally activated regime and confirms the predicted SMM behaviour.
The field- and temperature-dependence of the measured ac data were analysed using a generalised Debye model36–38 (Fig. 6, left and Fig. S3, ESI†). The resulting relaxation times (see Tables S1 and S2, ESI†) were modelled using the expressions for spin–lattice relaxation given in the Experimental section.41,46
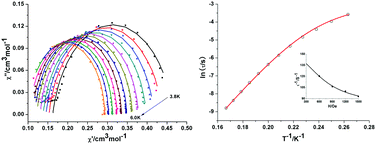 | ||
| Fig. 6 Cole–Cole plots of data for 1 measured at 1200 Oe between 3.8 K and 6.0 K (lines for fitting) (left); Plots of ln(τ) vs. T−1: The red line shows the fit to the data using eqn (10) with U = 56.65 cm−1 at 1200 Oe dc field. Inset: Field dependence of the magnetic relaxation time, τ, at 4.3 K for a microcrystalline sample of 1 and its approximation by τ−1 = B1/(1 + H2B2) + OH. Parameters A, B1 and B2 have the same meaning as in eqn (10). The parameter OH accounts for a field-independent offset at 4.3 K (right). | ||
Cole–Cole plots of χ′ versus χ′′ between 3.8 and 6.0 K (Fig. 6, left) have semicircular profiles, indicative of a single relaxation process. The plot was fitted with CC-Fit,47 which uses a generalized Debye model.36–38 The extracted parameters (see the ESI†) are similar to those extracted from the χ′ and χ′′ data with B1 = 65.60 s−1, and B2 = 1.88 × 10−6 Oe−2, respectively, together with a field-independent offset were used and found to be sufficient to model the field-dependence. For the temperature-dependent data, the QTM term itself was used as a constant offset. We thus identify an Orbach process displaying a typical SMM spin-reversal barrier of U = 56.65 cm−1 together with τ0 = 2.24 × 10−10 s−1, as well as a Raman process with exponent n = 9 (typical for a second-order Raman process in an isolated Kramers pair),41,46,48 with a prefactor of C = 1.00 × 10−4 K−9 s−1. Thus, the full expression for the spin-relaxation containing all terms necessary to describe the observed behaviour of 1 (Fig. 6) is given by eqn (10):
τ−1 (H,T) = B1/(1 + H2B2) + CT9 + τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−U/kT). exp(−U/kT). | (10) |
The spin reversal barrier of 56.65 cm−1 is slightly lower than the calculated energy difference between the lowest Kramers doublets of 82 cm−1. The deviation is typical for such compounds and primarily caused by quantum tunnelling and it is difficult to formulate general rules in terms of optimising SMM behaviour in Co(II) systems as a result of several physical effects influencing the performance of SIMs as reviewed recently by Atanasov et al.4 Nevertheless, an important message from the analysis we have performed is that the directions of the magnetic axes for the first two Kramers doublets are a key factor. We can show that when, as here, they are rather different and this difference is critically dependent on the distortion from an ideal prismatic coordination, this leads to significant changes in the spin–orbit coupling. That in turn provides a “fine-adjustment” in terms of tuning the parameters relevant to SMM behaviour.
Conclusions
In the mononuclear [CoII(L)] compound the Co(II) ion has a slightly distorted trigonal prismatic coordination geometry. Magnetic studies demonstrate its slow magnetic relaxation even in the absence of an applied dc field and the relaxation barrier of 57 cm−1 is found when applying a small dc field. Because of other relaxation mechanisms, most likely QTM,4 the measured barrier is smaller than the spin–orbit splitting obtained from ab initio calculations. DC magnetic measurements are in good agreement with ab initio calculations but could not be modelled reasonably using the single-ion spin Hamiltonian eqn (9) for S = 3/2. Although ground state anisotropy is formally considered in this Hamiltonian, it is not sufficient on its own in cases where there are orbitally degenerate states. For the given compound and its models, the calculations show a very different behaviour of the lowest two Kramers doublets with application of an external magnetic field: Whereas the ground state is uniaxial, the first excited state shows a rhombic behaviour, which is not taken into account for in the Zeeman terms in eqn (9). Calculations on the model complexes indicate that axiality for both states can be achieved through symmetry constraints within the first coordination sphere. The calculations further indicate that even small deviations from trigonal prismatic coordination reduce spin–orbit coupling and thus deteriorate the SMM behaviour significantly.In future investigations, we will focus on the effects of structural distortion and coordination number on the magnetic behaviour of mononuclear Co(II) SIMs with a view to finding an optimised building block for the construction of mixed metal polynuclear single molecule magnets incorporating Co(II) ions.
Acknowledgements
We thank the DFG for funding within the collaborative research center SFB/TRR88 “3MET”, projects A1 and A3. T. B. thanks the Danish Research Council (FNU) for funding.Notes and references
- D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224 CrossRef CAS PubMed.
- S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236 CrossRef CAS PubMed.
- M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 177, 289 Search PubMed.
- W. Lin, T. Bodenstein, V. Mereacre, K. Fink and A. Eichhöfer, Inorg. Chem., 2016, 55(5), 2091 CrossRef CAS PubMed.
- R. Boča, Coord. Chem. Rev., 2004, 248, 757 CrossRef.
- M. Dey and N. Gogoi, Angew. Chem., Int. Ed., 2013, 52, 12780 CrossRef CAS PubMed.
- P. P. Power, Chem. Rev., 2012, 112, 3482 CrossRef CAS PubMed.
- X.-C. Huang, C. Zhou, D. Shao and X.-Y. Wang, Inorg. Chem., 2014, 53, 12671 CrossRef CAS PubMed.
- L. Chen, J. Wang, J.-M. Wei, W. Wernsdorfer, X.-T. Chen, Y.-Q. Zhang, Y. Song and Z.-L. Xue, J. Am. Chem. Soc., 2014, 136, 12213 CrossRef CAS PubMed.
- T. Jurca, A. Farghal, P.-H. Lin, I. Korobkov, M. Murugesu and D. S. Richeson, J. Am. Chem. Soc., 2011, 133, 15814 CrossRef CAS PubMed.
- W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C.-J. Chang, J. Am. Chem. Soc., 2010, 132, 18115 CrossRef CAS PubMed.
- D. Weismann, Y. Sun, Y. Lan, G. Wolmershauser, A. K. Powell and H. Sitzmann, Chem. – Eur. J., 2011, 17, 4700 CrossRef CAS PubMed.
- J. M. Zadrozny, M. Atanasov, A. M. Bryan, C. Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125 RSC.
- Y.-Y. Zhu, C. Cui, Y.-Q. Zhang, J.-H. Jia, X. Guo, C. Gao, K. Qian, S.-D. Jiang, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802 RSC.
- Y.-Y. Zhu, Y.-Q. Zhang, T.-T. Yin, C. Gao, B.-W. Wang and S. Gao, Inorg. Chem., 2015, 55, 5475 CrossRef PubMed.
- V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M. E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792 CrossRef CAS PubMed.
- Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 10467 CrossRef CAS PubMed.
- (a) G. M. Sheldrick, Acta Crystallogr., 2015, A71, 3 Search PubMed; (b) G. M. Sheldrick, Acta Crystallogr., 2015, C71, 3 Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 2397 RSC.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef.
- V. Staemmler, Theor. Chim. Acta, 1977, 45, 89 CrossRef CAS.
- U. Meier and V. Staemmler, Theor. Chim. Acta, 1989, 76, 95 CrossRef CAS.
- J. Wasilewski, Int. J. Quantum Chem., 1989, 36, 504 CrossRef.
- K. Fink, C. Wang and V. Staemmler, Inorg. Chem., 1999, 38, 3847 CrossRef CAS.
- K. Fink and V. Staemmler, Theor. Chim. Acta, 1993, 87, 129 CrossRef.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- R. J. Gdanitz and R. Ahlrichs, Chem. Phys. Lett., 1988, 143, 413 CrossRef CAS.
- Relativistic electronic structure theory, part 2: Applications, ed. P. Schwerdtfeger, Elsevier, Amsterdam, 2004 Search PubMed.
- H. Bolvin, ChemPhysChem, 2006, 7, 1575 CrossRef CAS PubMed.
- R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theory Comput., 2009, 5, 2977 CrossRef CAS PubMed.
- TURBOMOLE V 6.6 2014, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH since 2007, available from http://www.turbomole.com.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2001, 32, 1456 CrossRef PubMed.
- H. B. G. Casimir and F. K. du Pré, Physica, 1938, 5, 507 CrossRef CAS.
- P. Debye, Polar Molecules, Chemical Catalogue Company, New York, 1929 Search PubMed.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341 CrossRef CAS.
- E. Colacio, J. Ruiz, E. Ruiz, E. Cremades, J. Krzystek, S. Caretta, J. Cano, T. Guidi, W. Wernsdorfer and E. J. K. Brechin, Angew. Chem., Int. Ed., 2013, 52, 9130 CrossRef CAS PubMed.
- E. Carl, S. Demeshko, F. Meyer and D. Stalke, Chem. – Eur. J., 2015, 21, 1 CrossRef PubMed.
- K. N. Shrivastava, Phys. Status Solidi B, 1983, 117, 437 CrossRef CAS.
- R. A. D. Wentworth, Coord. Chem. Rev., 1972, 9, 171 CrossRef CAS.
- M. Gruden-Pavlović, M. Perić, M. Zlatar and P. García-Fernández, Chem. Sci., 2014, 5, 1453 RSC.
- M. P. Shores, J. J. Sokol and J. R. Long, J. Am. Chem. Soc., 2002, 124, 2279 CrossRef CAS PubMed.
- A. V. Palii, J. M. Clemente-Juan, E. Coronado, S. I. Klokishner, S. M. Ostrovsky and O. S. Reu, Inorg. Chem., 2010, 49, 8073 CrossRef CAS PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Clarendon Press, Oxford, 1970 Search PubMed.
- N. F. Chilton, CC-Fit, http://www.nfchilton.com/cc-fit.html.
- R. Carlin, Magnetochemistry, Springer-Verlag, Berlin, 1986 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details; crystal data and geometric information for structure 1, additional magnetic data and calculation details. CCDC 1422338. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6cp03157a |
| ‡ These authors contributed equally. |
§ X-Ray crystal structure determination: C26H34CoN4O4 (525.50 g mol−1), monoclinic, space group P21/n, a = 16.1119 (11), b = 7.0151 (6), c = 21.1805 (14) Å, β = 96.396 (5)°, ν = 2379.1 (3) Å3, Z = 4, T = 150 K, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 reflections measured, 4819 independent data (Rint = 0.0322); 316 parameters, wR2 = 0.0867, S = 0.989, R1 (3898 data with I > 2σ(I)) = 0.0326. CCDC 1422338. 727 reflections measured, 4819 independent data (Rint = 0.0322); 316 parameters, wR2 = 0.0867, S = 0.989, R1 (3898 data with I > 2σ(I)) = 0.0326. CCDC 1422338. |
| This journal is © the Owner Societies 2016 |










